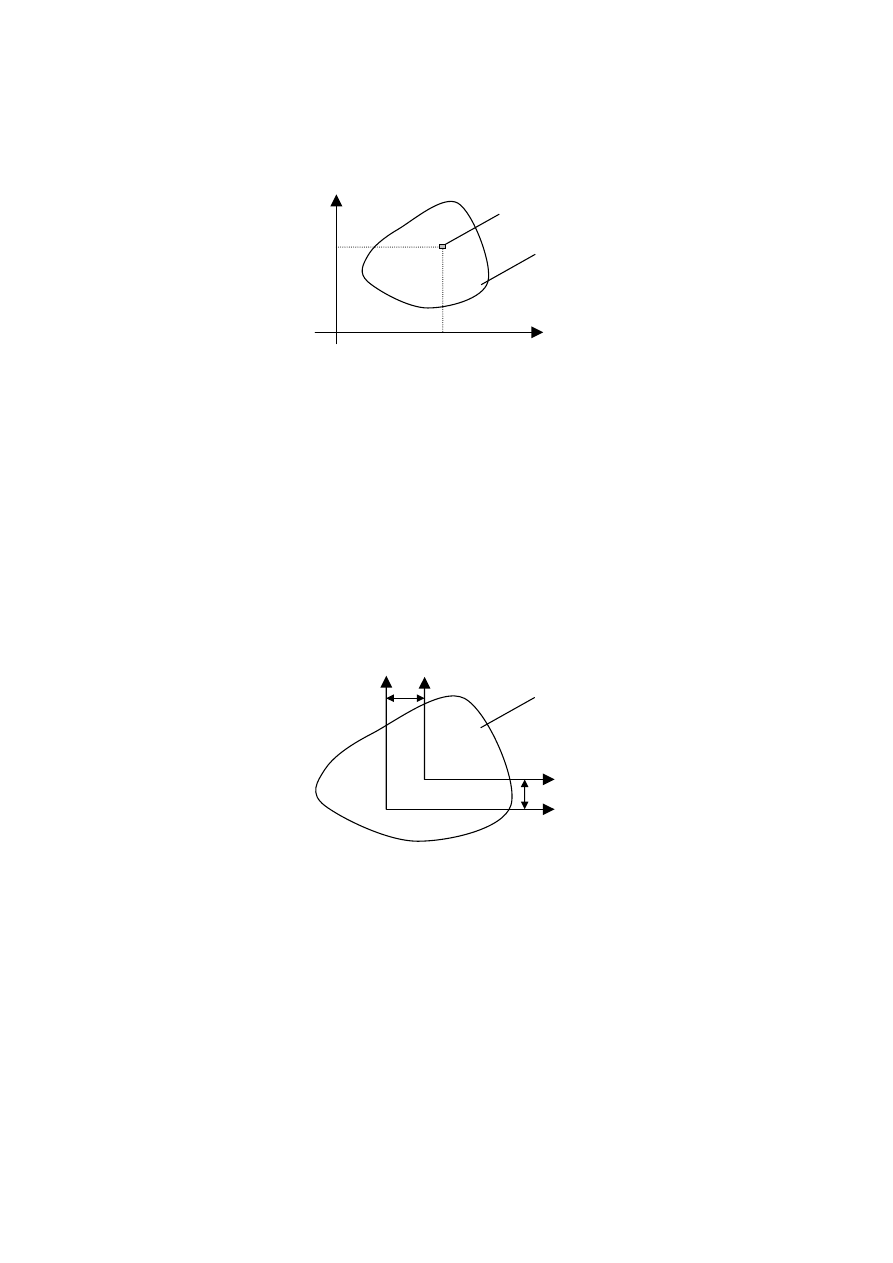
Momenty bezwładności figur płaskich - definicje i wzory

Dana jest figura płaska o polu A oraz prostokątny układ współrzędnych Oxy.

Momentem bezwładności figury względem osi x jest

dA

y

I

A

x

∫

=

2

.

Momentem bezwładności figury względem osi y jest

dA

x

I

A

y

∫

=

2

.

Momentem dewiacyjnym figury względem prostokątnego układu osi x i y jest

∫

=

A

xy

xydA

I

.

Z definicji momentów bezwładności wynika, że mogą być one tylko dodatnie.

Natomiast moment dewiacyjny może być dodatni, ujemny lub równy zero.

W przypadku równoległego przesunięcia osi układu korzystamy z twierdzenia

Steinera, wyrażonego poniższymi wzorami:

y

y

x

x

O

A

dA

a

b

x

c

y

c

y

x

A

C(b, a)

O

2

a

A

I

I

c

x

x

⋅

+

=

2

b

A

I

I

c

y

y

⋅

+

=

b

a

A

I

I

c

c

y

x

xy

⋅

⋅

+

=

gdzie osie

x

c

i

y

c

są osiami centralnymi, natomiast

b i a są współrzędnymi punktu C w

układzie

Oxy. Z rysunku wynika, że są to odległości między osiami.

Osiowe momenty bezwładności oraz dewiacyjny moment figury względem osi

centralnych można wyznaczyć korzystając z przekształconych wzorów Steinera:

2

a

A

I

I

x

x

c

⋅

−

=

2

b

A

I

I

y

y

c

⋅

−

=

b

a

A

I

I

xy

y

x

c

c

⋅

⋅

−

=

.

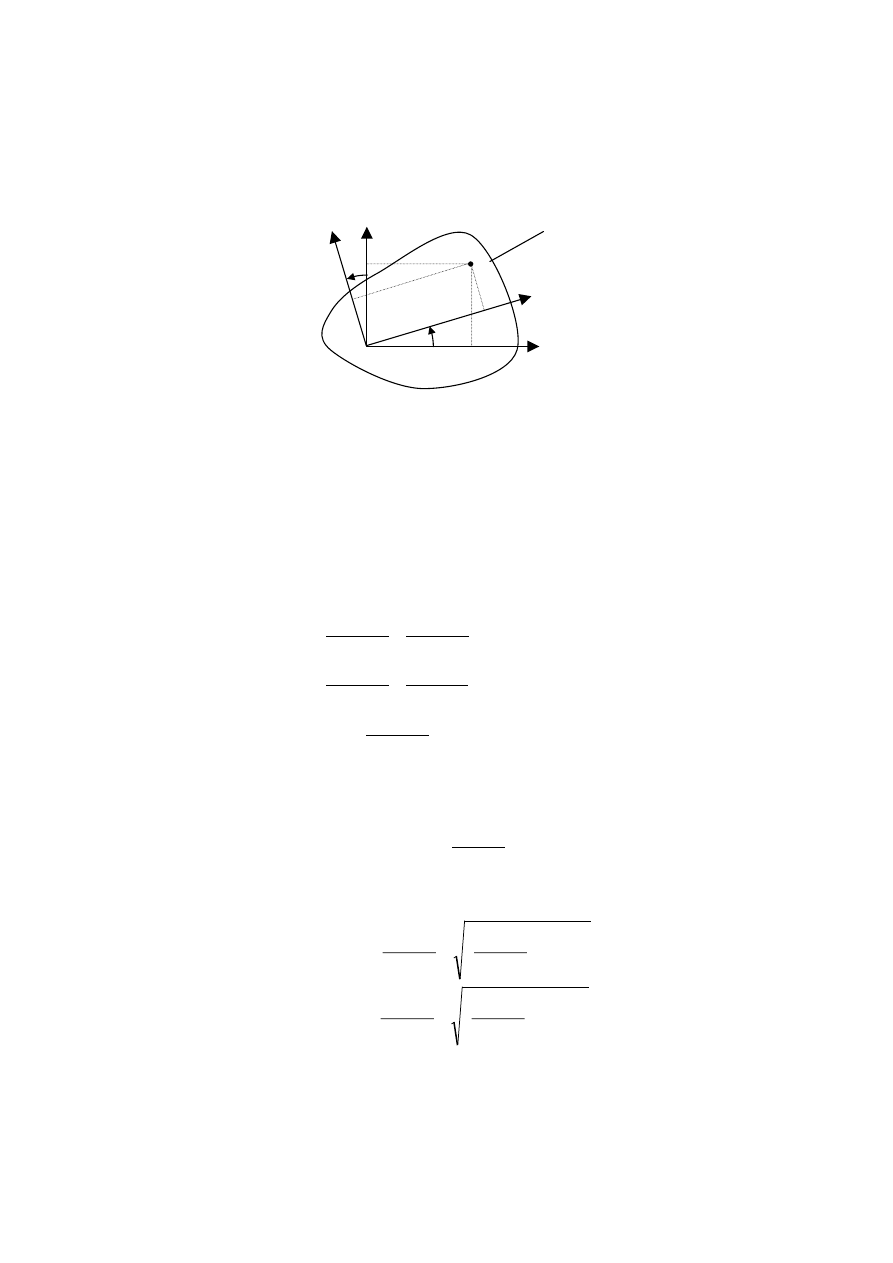
Przyjmijmy

prostokątny układ współrzędnych

Oξη obrócony o kąt φ względem układu

Oxy. Współrzędne dowolnego punktu figury płaskiej spełniają zależności:

ξ = x cos φ + y sin φ

η = y cos φ − x sin φ.

ξ

x

O

y

η

φ

A

φ

y

η

ξ

x

Wykorzystując te zależności wyznaczamy momenty bezwładności i moment
dewiacyjny w obróconym układzie

Oξη:

ϕ

ϕ

−

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

η

I

xy

y

x

A

ξ

2

2

2

2

ϕ

ϕ

+

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

ξ

I

xy

x

y

A

η

2

2

2

2

(

)

(

)

ϕ

−

ϕ

+

ϕ

ϕ

−

=

=

∫

2

2

sin

cos

I

cos

sin

I

I

ξηdA

I

xy

y

x

A

ξη

lub

(

) (

)

ϕ

−

ϕ

−

+

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

ξ

(

) (

)

ϕ

+

ϕ

−

−

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

η

(

)

ϕ

+

ϕ

−

=

2

2

2

cos

I

sin

I

I

I

xy

y

x

ξη

.

Osie układu prostokątnego, w którym moment dewiacyjny

I

ξη

= 0 nazywamy

głównymi osiami bezwładności. Kąt φ

o

między osiami prostokątnego układu

Oxy i układu

głównych osi bezwładności spełnia równanie:

y

x

xy

I

I

I

tg

−

−

=

ϕ

2

2

o

Momenty bezwładności względem głównych osi bezwładności osiągają wartości

ekstremalne:

2

2

1

2

2

xy

y

x

y

x

max

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

2

2

2

2

2

xy

y

x

y

x

min

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

.

Z powyższych wzorów wynika, że

2

1

I

I

I

I

I

I

η

ξ

y

x

+

=

+

=

+

Główna oś bezwładności, względem której moment bezwładności ma wartość

tworzy z osią x kąt

, natomiast główna oś bezwładności, względem której

max

I

I

=

1

1

ϕ

2

moment bezwładności ma wartość

min

I

I

=

2

tworzy z osią x kąt

2

ϕ

. Kierunki główne

minimalnego i maksymalnego momentów bezwładności wyznaczamy następująco:

1. I

x

> I

y

to

, natomiast

o

1

ϕ

=

ϕ

2

o

2

π

+

ϕ

=

ϕ

2. I

x

< I

y

to

2

o

1

π

+

ϕ

=

ϕ

, natomiast

o

2

ϕ

=

ϕ

3. I

x

= I

y

, I

xy

> 0 to

4

1

π

−

=

ϕ

, natomiast

4

2

π

=

ϕ

4. I

x

= I

y

, I

xy

< 0 to

4

1

π

=

ϕ

, natomiast

4

2

π

−

=

ϕ

.

Znak dodatni bądź ujemny kąta φ ilustruje poniższy rysunek.

y

y

x

O

φ > 0

O

φ < 0

x

O głównych centralnych osiach bezwładności mówimy wówczas, gdy układ osi

głównych ma początek w środku ciężkości rozpatrywanej figury płaskiej. Momenty
bezwładności względem tych osi nazywamy głównymi centralnymi momentami
bezwładności.

Jeżeli jedna z osi układu współrzędnych jest osią symetrii figury płaskiej, to moment

dewiacyjny figury w takim układzie współrzędnych jest równy zero.

W przypadku wyznaczania momentów bezwładności i momentu dewiacyjnego figury

złożonej będziemy stosować metodę superpozycji, traktując rozpatrywaną figurę jako sumę
figur elementarnych, takich jak np. prostokąt, trójkąt i fragment koła. Korzystać będziemy z
wartości momentów bezwładności i momentu dewiacyjnego dla wymienionych figur.
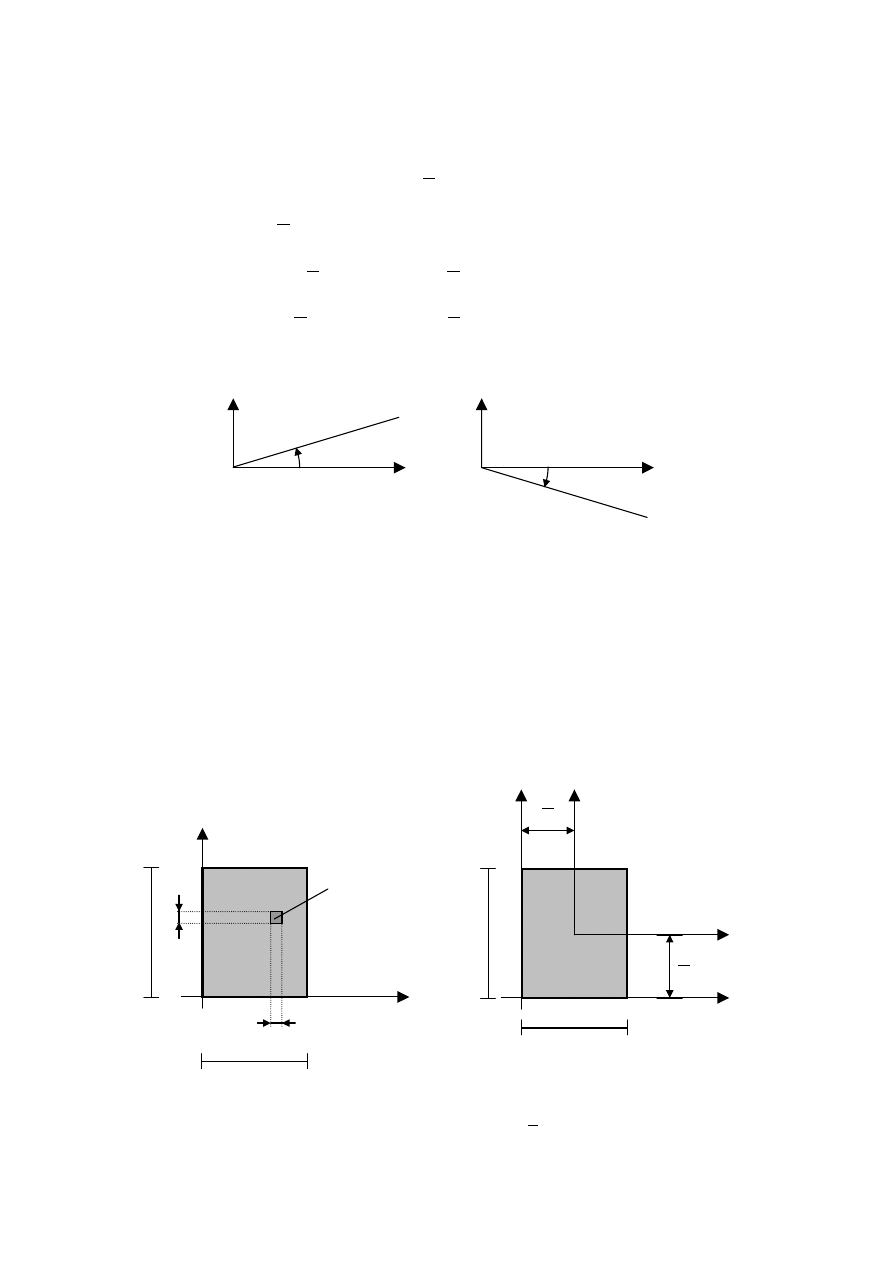
1. Prostokąt

y

O

b

y

c

C

2

b

2

h

h

y

b

dA

=dxdy

y

O

x

dx

dy

h

x

c

x

x

3

0 0

2

2

3

1

bh

dxdy

y

dA

y

I

b h

A

x

∫∫

∫

=

=

=

3

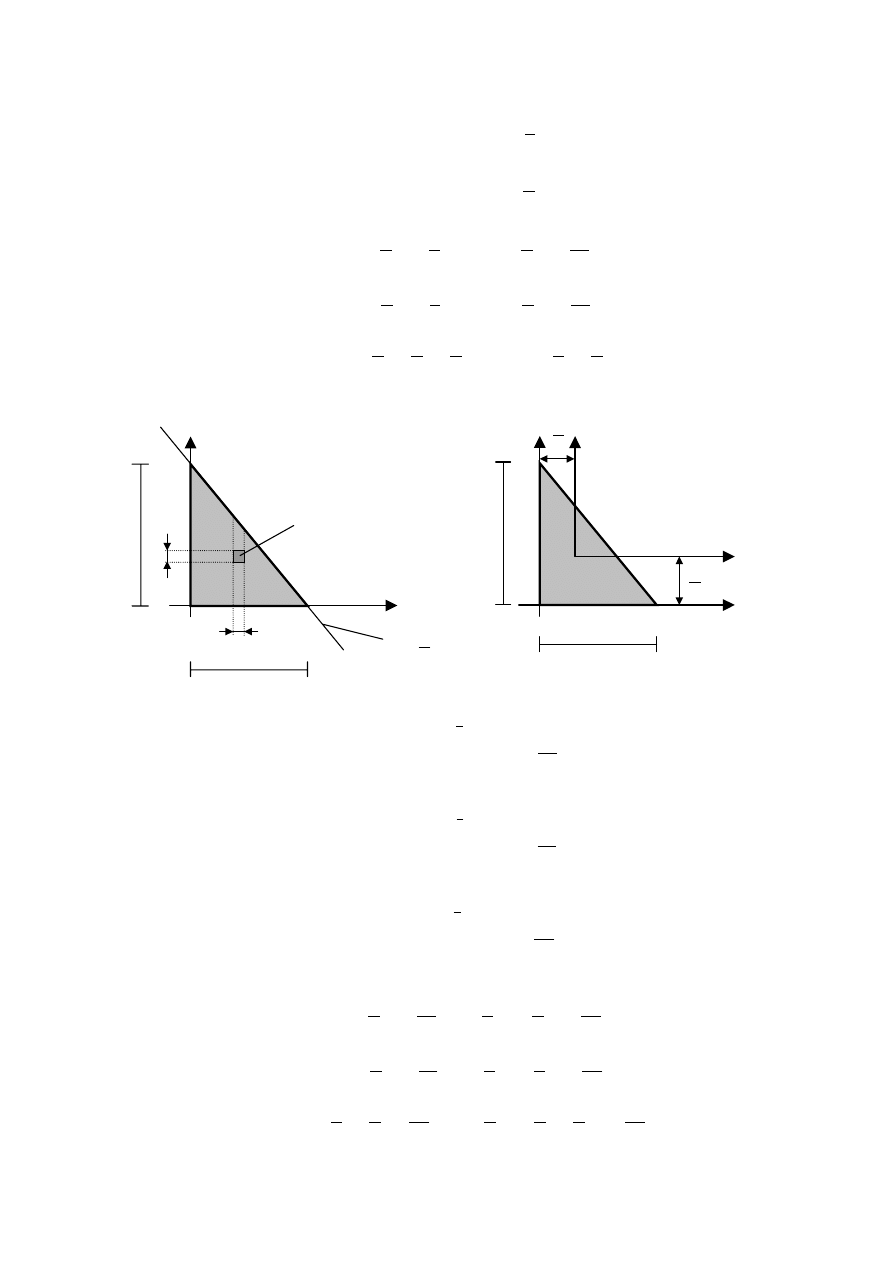
3

0 0

2

2

3

1

hb

dxdy

x

dA

x

I

b h

A

y

=

=

=

∫∫

∫

2

2

0 0

4

1

h

b

xydxdy

xydA

I

b h

A

xy

∫∫

∫

=

=

=

3

2

3

2

12

1

2

3

1

2

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

3

2

3

2

12

1

2

3

1

2

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

0

2

2

4

1

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

2. Trójkąt

b

y

O

C

y

c

3

h

3

b

h

b

dA=dxdy

y

x

O

x

dx

y

dy

y=−

h

x

b

h

+

⋅

h

x

c

x

3

0

0

2

2

12

1

bh

dx

dy

y

dA

y

I

b

b

x

1

h

A

x

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

3

0

0

2

2

12

1

hb

dx

dy

x

dA

x

I

b

b

x

1

h

A

y

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

2

2

0

0

24

1

b

h

dx

dy

xy

dA

xy

I

b

b

x

1

h

A

xy

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

3

2

3

2

36

1

3

2

1

12

1

3

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

3

2

3

2

36

1

3

2

1

12

1

3

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

2

2

2

2

72

1

3

3

2

1

24

1

3

3

h

b

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

4

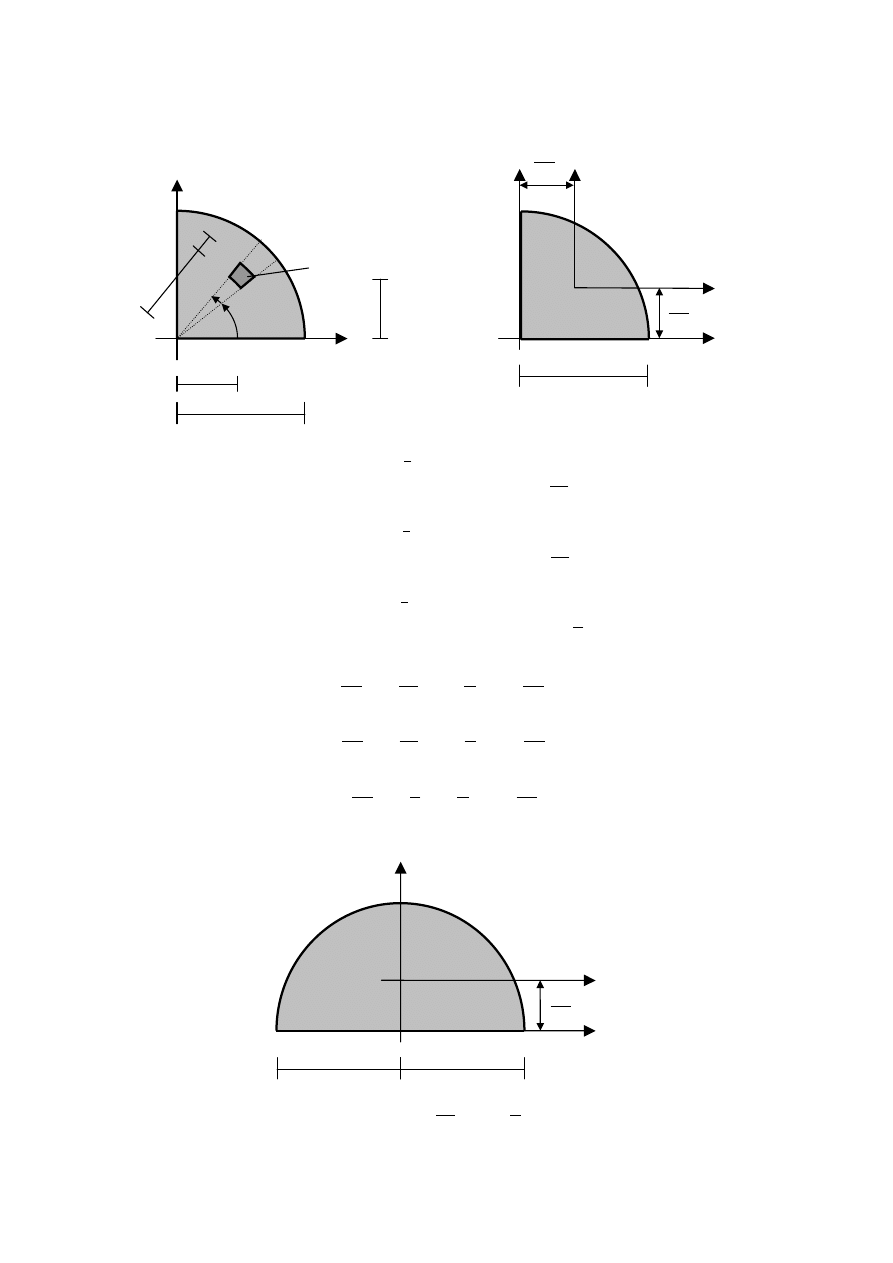
3. Ćwiartka koła

y

O

C

y

c

r

π

r

3

4

π

r

3

4

r

dA=ρdφdρ

x

O

ρ

y=ρsinφ

x=ρcosφ

dρ

φ

dφ

y

x

c

x

4

0 0

2

2

2

16

1

r

d

d

sin

dA

y

I

2 r

A

x

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

4

0 0

2

2

2

16

1

os

r

d

d

c

dA

x

I

2 r

A

y

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

4

0 0

2

8

1

os

r

d

d

c

sin

dA

xy

I

2 r

A

xy

∫∫

∫

π

=

ρ

ϕ

ϕρ

ϕ

ρ

=

=

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

x

x

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

y

y

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

4

2

2

4

2

01647

0

3

4

4

1

8

1

3

4

r

.

r

r

r

r

A

I

I

xy

y

x

c

c

−

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

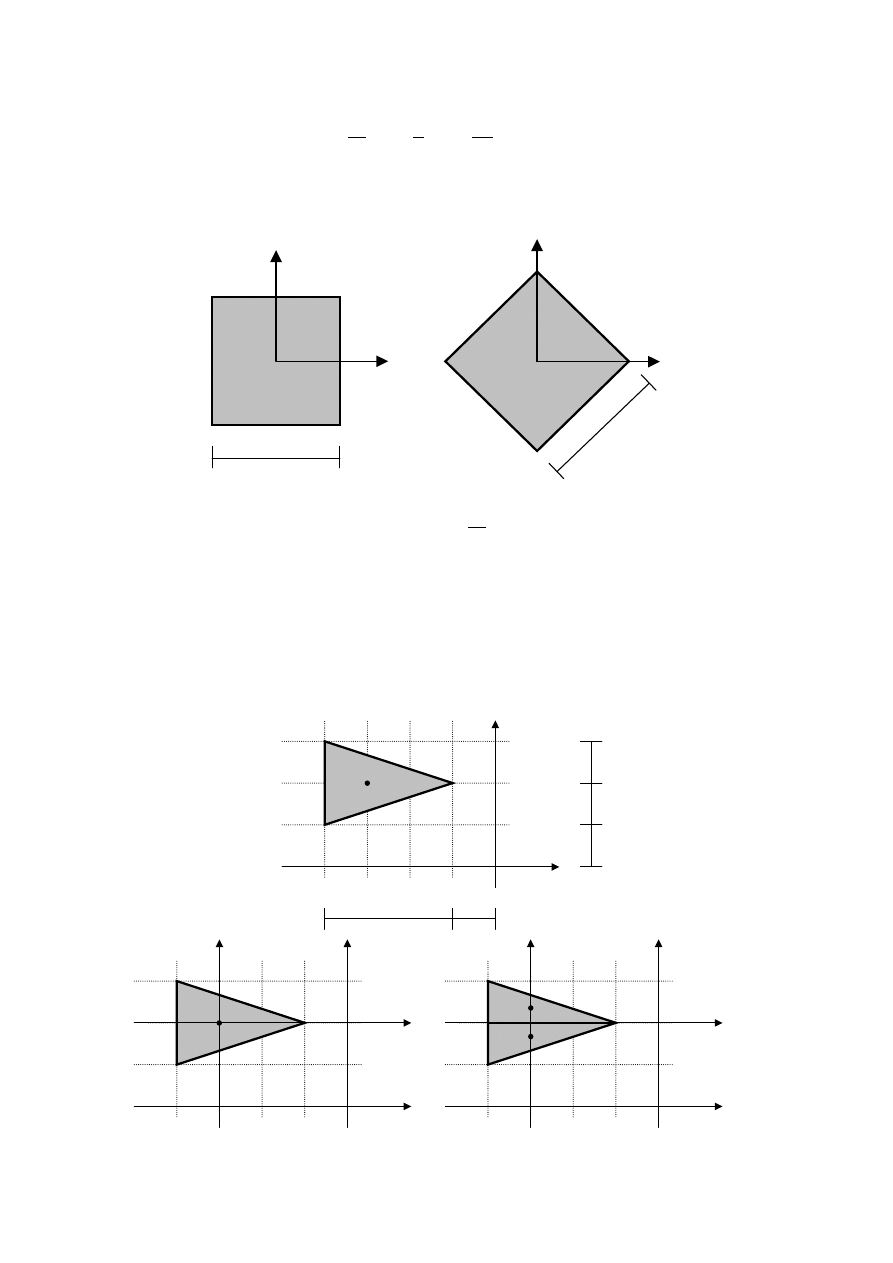
4. Półkole

O

C

r

r

π

r

3

4

y

c

=y

x

c

x

4

4

8

1

16

1

2

πr

πr

I

I

y

x

=

⋅

⋅

=

=

5

4

2

2

4

10976

0

3

4

4

1

16

1

2

r

.

r

r

r

I

c

x

≅

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

⋅

=

0

=

=

xy

y

x

I

I

c

c

5. Kwadrat

y

c

C

y

c

C

a

x

c

x

c

a

4

12

1

a

I

I

c

c

y

x

=

=

0

=

c

c

y

x

I

W przypadku kwadratu momenty bezwładności i moment dewiacyjny w dowolnym

układzie osi centralnych przyjmują podane powyżej wartości.

Przykład I

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta

równoramiennego w układzie Oxy.

C

x

y

y

c

x

c

C

O

O

C

1

C

2

y

c

a

a

a

x

y

O

a

x~

c

3

−

=

a

y~

c

2

=

C

a

3a

y

x

c

x

6

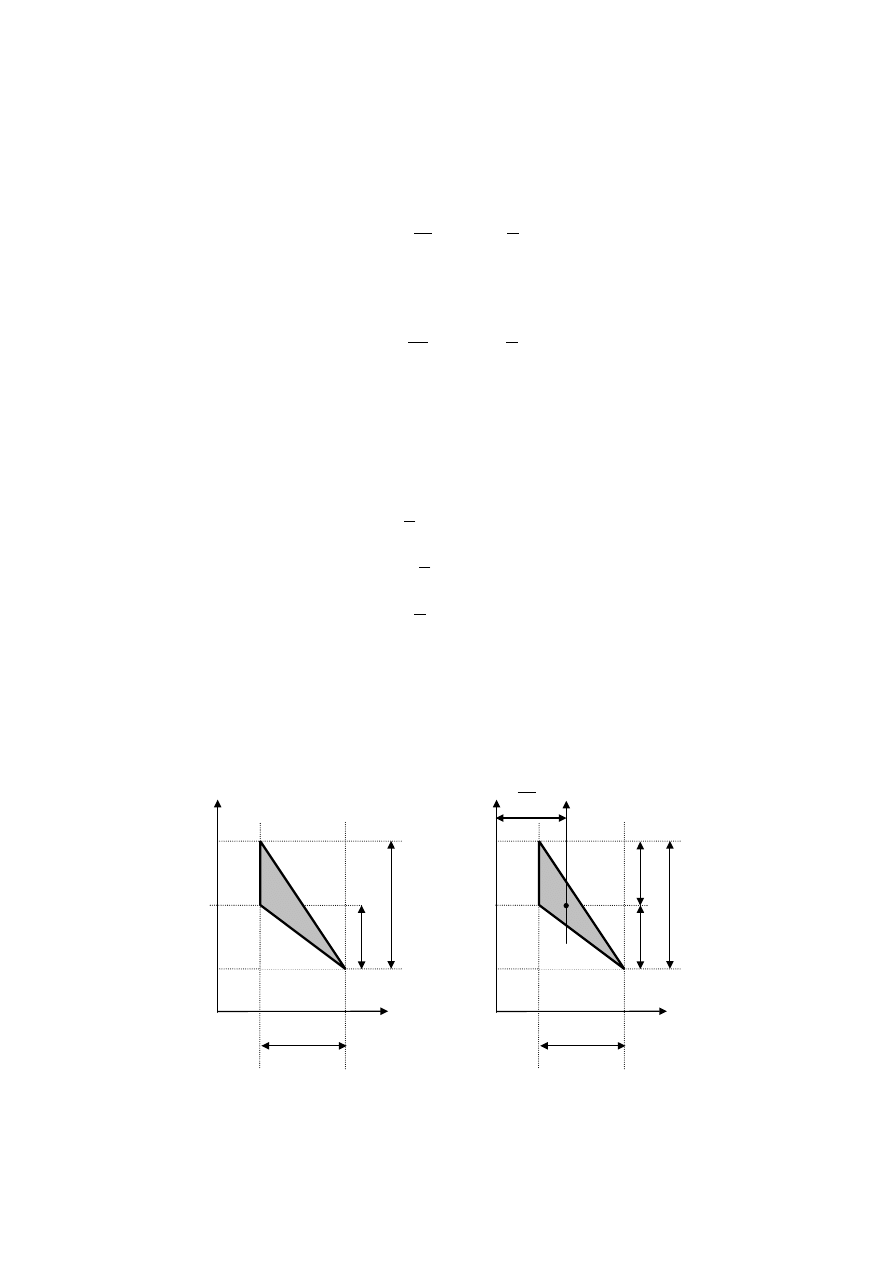
Wprowadzamy

układ osi centralnych dla trójkąta. Oś x

c

jest osią symetrii figury.

Następnie dzielimy trójkąt równoramienny na dwa trójkąty prostokątne.

Moment bezwładności trójkąta równoramiennego względem osi x

c

jest sumą

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych,
stykających się podstawą z osią x

c

.

4

3

2

1

3

12

1

2

a

a

a

I

c

x

=

⋅

⋅

⋅

=

Moment bezwładności trójkąta równoramiennego względem osi y

c

jest sumą

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych. Na
osi y

c

leżą środki ciężkości obu trójkątów, a więc

( )

4

3

2

3

3

36

1

2

a

a

a

I

c

y

⋅

=

⋅

⋅

=

Moment dewiacyjny trójkąta równoramiennego względem układu osi x

c

y

c

jest równy

zero, gdyż oś x

c

jest osią symetrii rozpatrywanej figury.

0

=

c

c

y

x

I

Aby wyznaczyć momenty bezwładności i moment dewiacyjny dla trójkąta

równoramiennego w układzie Oxy należy skorzystać z twierdzenia Steinera. Pole powierzchni
trójkąta wynosi

2

3

2

3

2

1

a

a

a

A

=

⋅

⋅

=

.

( )

4

2

2

4

2

5

12

2

3

2

1

a

.

a

a

a

y~

A

I

I

c

x

x

=

⋅

+

=

⋅

+

=

(

)

4

2

2

4

2

5

28

3

3

2

3

a

.

a

a

a

x~

A

I

I

c

y

y

c

=

−

⋅

+

=

⋅

+

=

(

)

4

2

18

2

3

3

0

a

a

a

a

y~

x~

A

I

I

c

c

y

x

xy

c

c

−

=

⋅

−

⋅

+

=

⋅

⋅

+

=

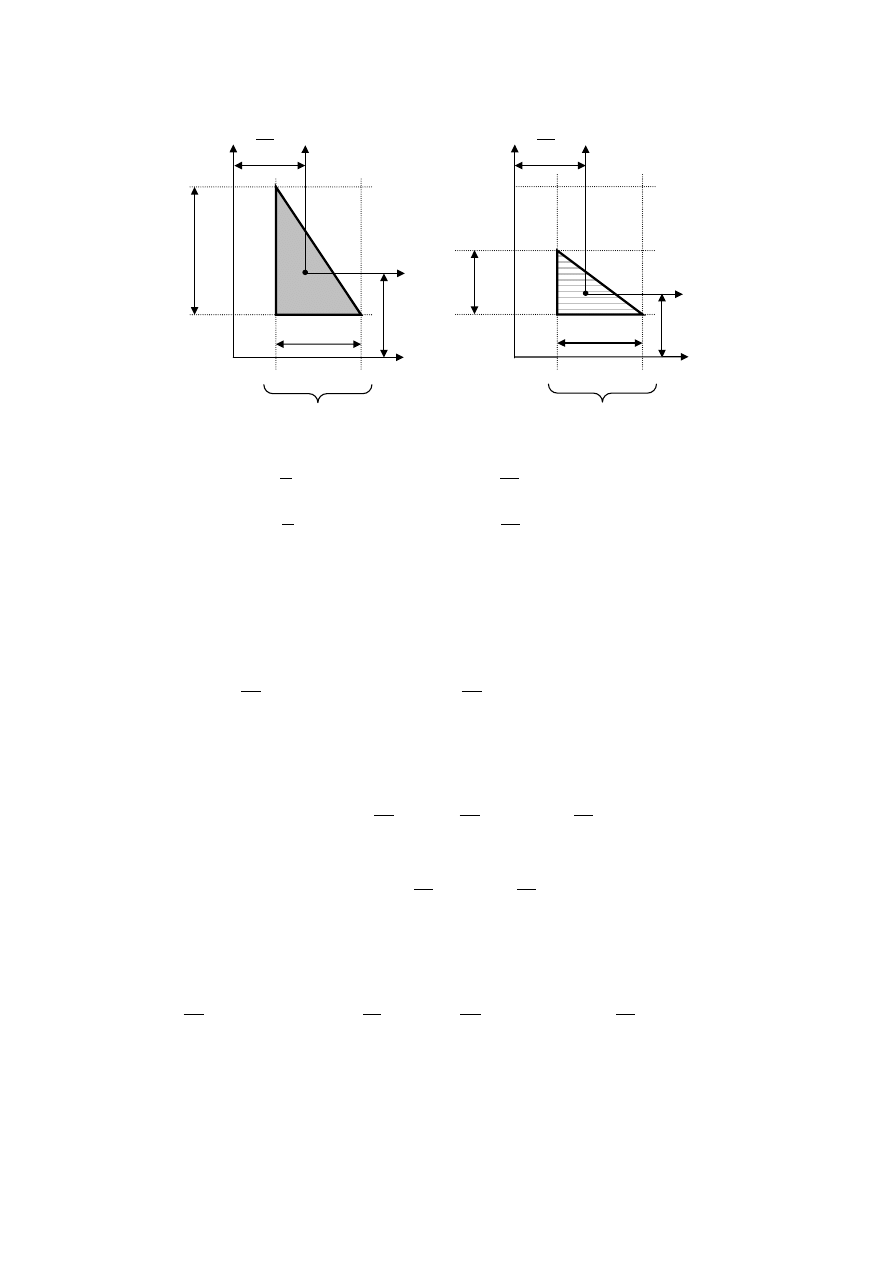
Przykład II

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta w

układzie współrzędnych Oxy.

c

y

A

B

3a

6a

8a

5a

2a

3a

C

D

a

3

10

4a

x

6a

2a

6a

3a

O

y

x

8a

5a

6a

2a

4a

2a

y

O

Rozpatrywaną figurę otrzymamy odejmując figurę II od figury I.

7

4a

O

2a

2a

6a

8a

C

1

x

y

1

c

y

1

c

x

figura I

4a

6a

a

3

10

2a

5a

3a

3a

y

2a

6a x

2

c

y

2

c

x

figura II

4a

C

2

a

3

10

O

2

I

12

6

4

2

1

a

a

a

A

=

⋅

⋅

=

,

a

x~

c

3

10

1

=

,

a

y~

c

4

1

=

,

2

II

6

3

4

2

1

a

a

a

A

=

⋅

⋅

=

,

a

x~

c

3

10

2

=

,

a

y~

c

3

2

=

.

2

2

2

II

I

6

6

12

a

a

a

A

A

A

=

−

=

−

=

Moment bezwładności względem osi x wyznaczymy jako różnicę momentu

bezwładności względem osi x figury I i figury II.

(

)

( )

( )

( )

( )

4

2

2

2

2

2

3

2

2

II

II

2

1

I

I

II

I

159

3

6

3

4

36

1

4

12

6

4

36

1

2

1

a

a

a

a

a

a

a

a

a

y~

A

I

y~

A

I

I

I

I

c

x

c

x

x

x

x

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

⋅

−

⋅

+

⋅

⋅

=

=

⋅

+

−

⋅

+

=

−

=

W przypadku wyznaczania momentu bezwładności względem osi y nie musimy

dzielić figury. Bok BD trójkąta jest równoległy do osi y i do osi

. Moment bezwładności

względem osi

obliczymy korzystając ze wzoru

c

y

c

y

( )

4

3

3

3

16

4

3

36

1

36

1

a

a

a

h

b

I

c

y

=

⋅

⋅

=

⋅

⋅

=

Moment bezwładności względem osi y wyznaczymy z wykorzystaniem wzoru Steinera

4

2

2

4

2

a

72

3

10

6

3

16

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

=

⋅

+

=

a

a

a

x~

A

I

I

c

y

y

c

W celu obliczenia momentu dewiacyjnego traktujemy rozpatrywany trójkąt jako

różnicę figury I i figury II.

(

)

( ) ( )

( ) ( )

4

2

2

2

2

2

2

2

2

II

II

1

1

I

II

I

94

3

3

10

6

3

4

72

1

4

3

10

12

6

4

72

1

2

1

1

a

a

a

a

a

a

a

a

a

a

a

y~

x~

A

I

y~

x~

A

I

I

I

I

c

c

y

x

c

c

y

x

xy

xy

xy

c2

c

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

−

−

⋅

⋅

+

⋅

⋅

−

=

=

⋅

⋅

+

−

⋅

⋅

+

=

−

=

Przykład III

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższej figury w

układzie współrzędnych Oxy.

8

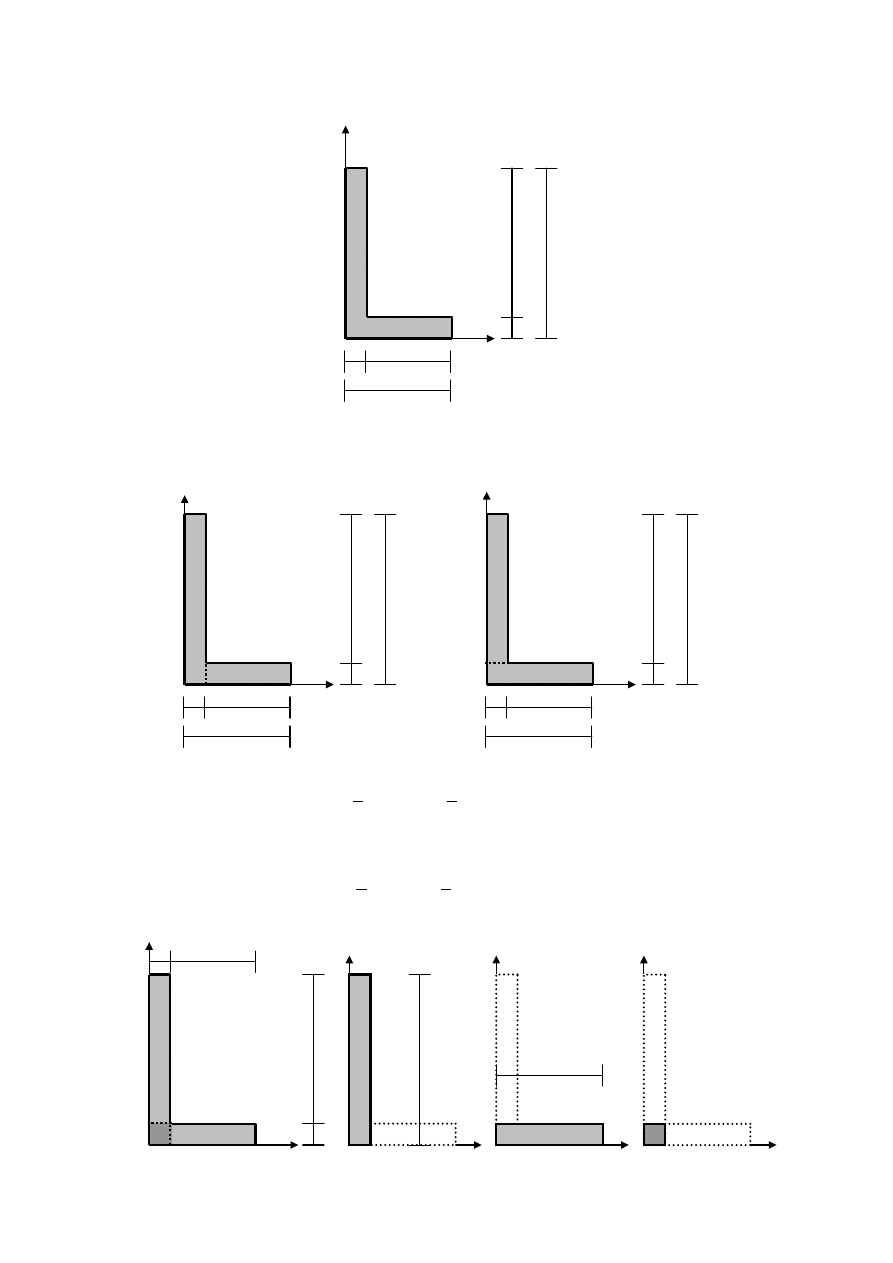
O

x

5a

a

4a

y

a

7a 8a

Przed wyznaczeniem momentu bezwładności rozpatrywanej figury względem osi x

dokonamy jej podziału na dwa prostokąty, tak żeby każdy prostokąt jednym bokiem stykał się
z osią x.

a

7a

4a

a

5a

8a

x

y

y

x

5a

a

4a

a

7a 8a

( )

4

3

3

172

4

3

1

8

3

1

a

a

a

a

a

I

x

=

⋅

⋅

+

⋅

⋅

=

W celu obliczenia momentu bezwładności figury względem osi y dokonamy jej

podziału na dwa prostokąty, z których każdy jednym bokiem styka się z osią y.

( )

4

3

3

44

5

3

1

7

3

1

a

a

a

a

a

I

y

=

⋅

⋅

+

⋅

⋅

=

Dla wyznaczenia momentu dewiacyjnego zastosujemy jeszcze inny podział.

a

7a

x

y

x

y

y

5a

4a

a

x

y

8a

x

9

Do obliczeń przyjmujemy figury składowe, zgodne z powyższym rysunkiem. Dwa

prostokąty o wymiarach 8a x a i a x 5a mają część wspólną w postaci kwadratu o boku a, dla
którego moment dewiacyjny będzie uwzględniony dwukrotnie. Należy więc w obliczeniach
moment dewiacyjny dla tego kwadratu, traktowanego jako trzecia figura, przyjąć ze znakiem
minus.

( )

( )

4

2

2

2

2

2

2

22

4

1

5

4

1

8

4

1

a

a

a

a

a

a

a

I

xy

=

⋅

⋅

−

⋅

⋅

+

⋅

⋅

=

.

10