
1
I
T
P
W
ZPT
Co uzyskaliśmy do tej pory...
Jaka jest
skutecznoś
ć...

2
I
T
P
W
ZPT
Przykład...
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
Redukcja argumentów pozwoli
obliczyć, że funkcja ta
jest zależna od
7 argumentów!
X = {x
3
, x
5
, x
6
, x
7
, x
8
, x
9
,
x
10
}
Synteza układów cyfrowych str. 32
3
I
T
P
W
ZPT
Ustalenie zbiorów A i B
A = {x
7
, x
8
,
x
9
}
X = {x
3
, x
5
, x
6
, x
7
, x
8
, x
9
,
x
10
}
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
1 0
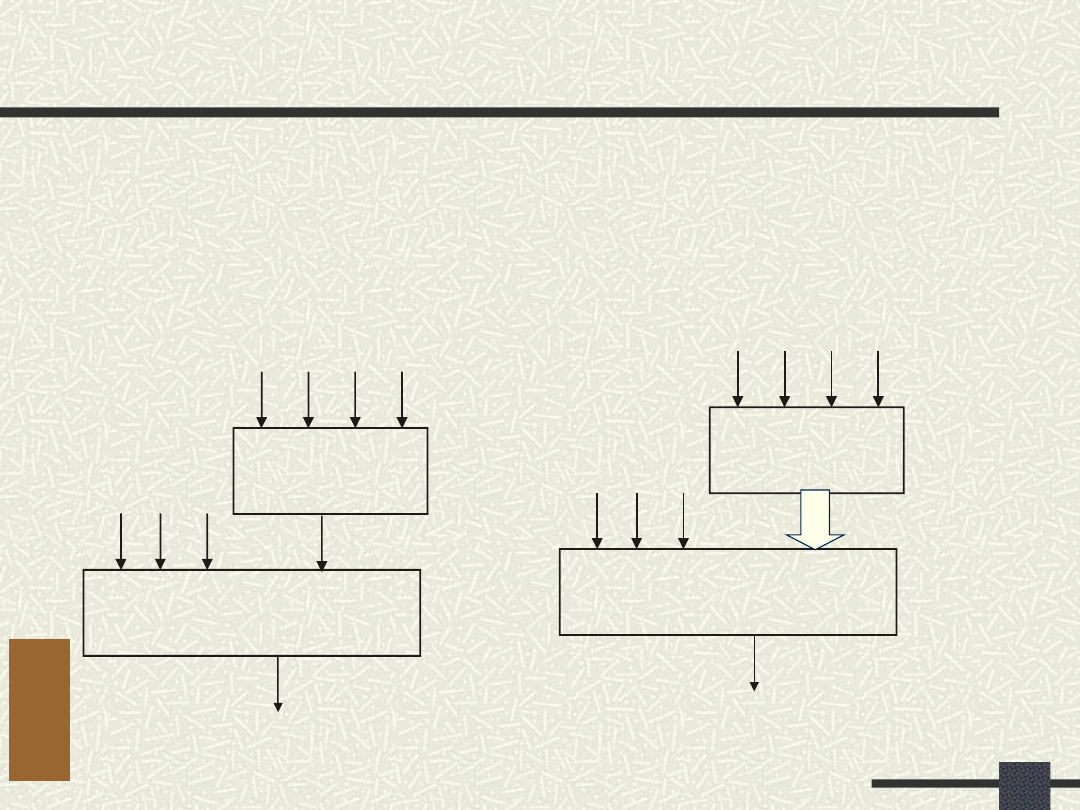
Więcej wyjść z bloku G???
B = {x
3
, x
5
, x
6
,
x
10
}
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
4
I
T
P
W
ZPT
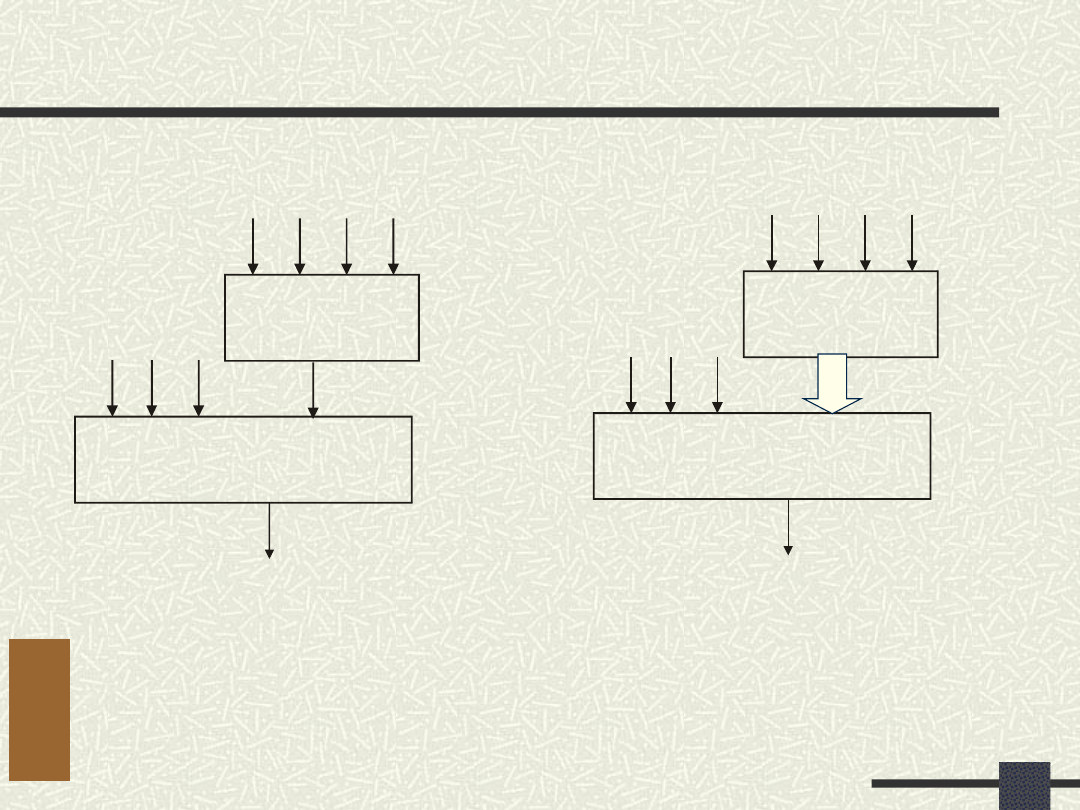
Realizacja w strukturze FPGA
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
1 0
2 komórki 4/1
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
3 najwyżej 4 komórki 4/1
5
I
T
P
W
ZPT
Ta sama funkcja w systemie Altery
MAX+PLUSII
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
realizuje tę
funkcję na
23 komórkach
!!!
6
I
T
P
W
ZPT
Niestety bezpośrednie
zastosowanie dekompozycji
funkcjonalnej w komputerowych
systemach projektowania jest – ze
względu na ogromną złożoność
obliczeniową – bardzo trudne
Oprogramowanie uniwersyteckie:
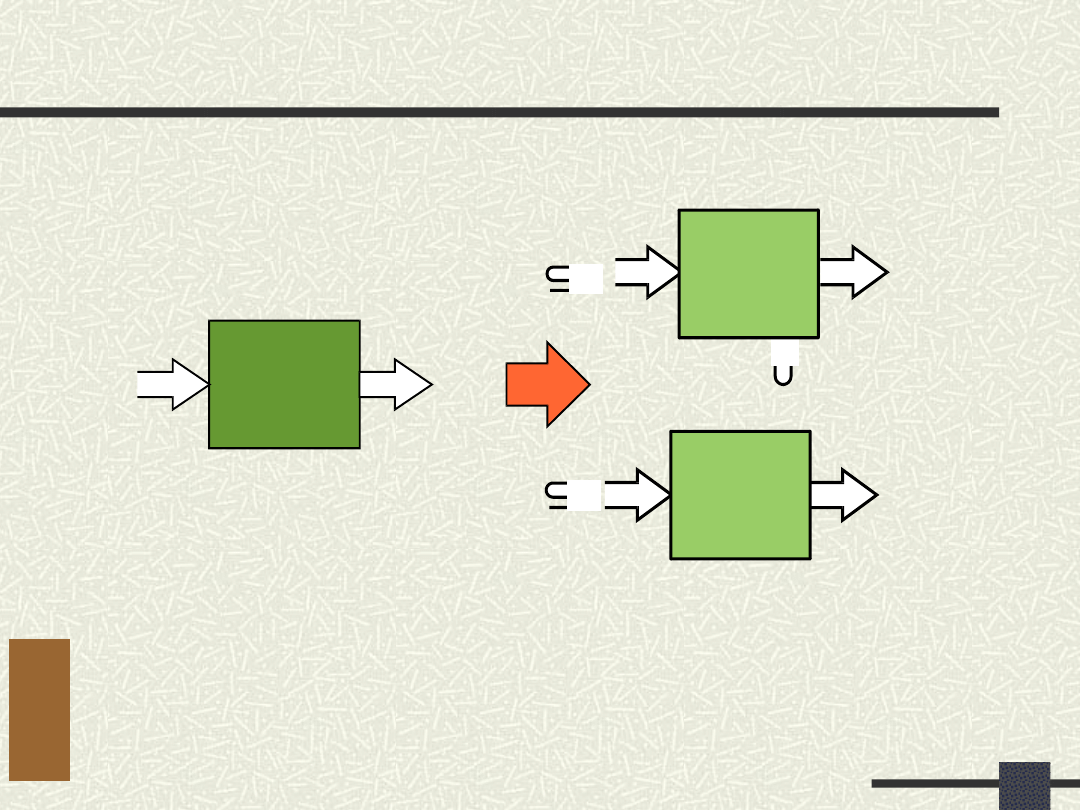
Nasza propozycja polega na zastosowaniu wspomagającej procedury
dekompozycji równoległej
SIS (Berkeley) oferuje metodę balansu procedur minimalizacji i dekompozycji
7
I
T
P
W
ZPT
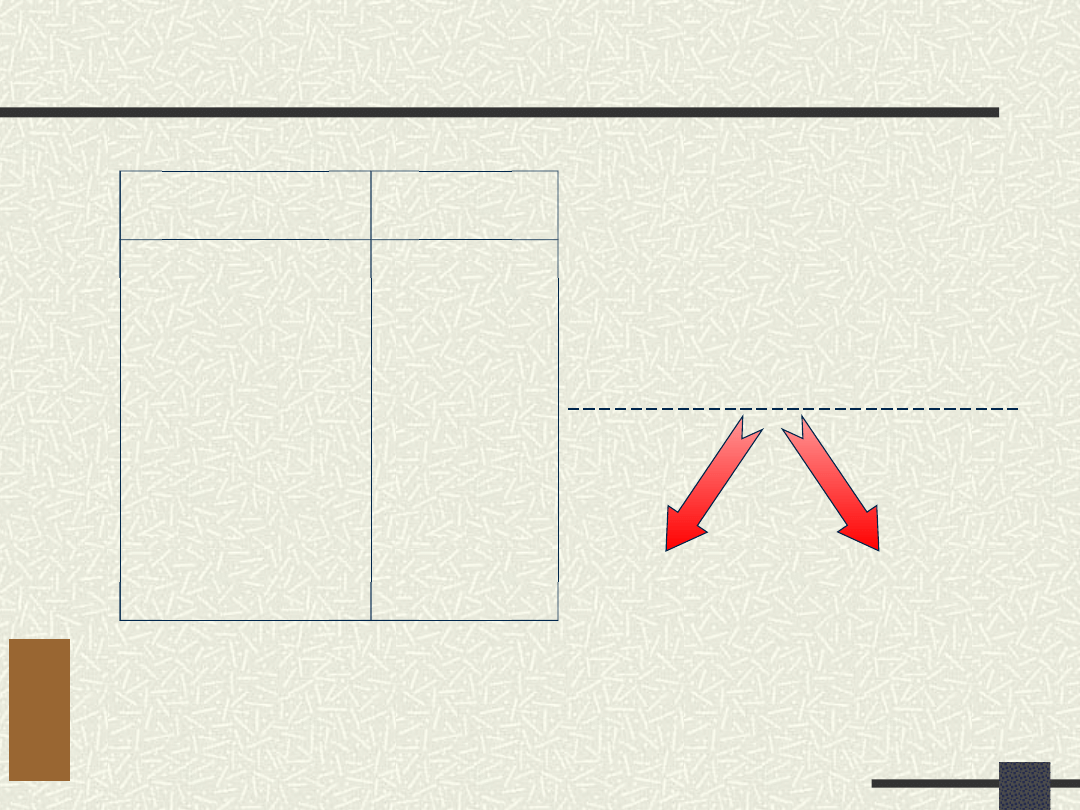
Dekompozycja równoległa
X
Y
Y
H
Y
G
Y
=
Y
H
X
H
Y
G
X
G
X
G
F
X
H
Y
H
Y
G
=
F
U
8
I
T
P
W
ZPT
Dekompozycja równoległa -
przykład
y
1
: {x
1
, x
4
}, {x
4
, x
5
}
y
2
: {x
2
, x
3
, x
5
}
G
= {y
1
, y
3
}
y
4
: {x
2
, x
5
}, {x
5
, x
6
}, {x
1
, x
6
},
H= {y
2
, y
4
}
X
g
= {x
1
, x
4
}
X
h
={x
2
, x
3
, x
5
}
y
3
: {x
1
, x
4
}
x
1
x
2
x
3
x
4
x
5
x
6
y
1
y
2
y
3
y
4
1
0
1
0
0
0
1
0
0
0
-
2
1
0
0
0
1
1
0
0
1
-
3
1
1
0
1
1
1
1
1
1
0
4
1
1
0
1
0
0
-
0
1
1
5
1
1
1
1
1
1
1
0
-
0
6
0
0
1
0
1
1
-
0
0
-
7
0
1
1
0
0
1
0
1
-
0
8
1
0
1
1
1
0
1
-
1
1
9
1
0
0
1
1
0
1
0
-
1
10
0
1
1
1
0
1
0
1
1
1
9
I
T
P
W
ZPT
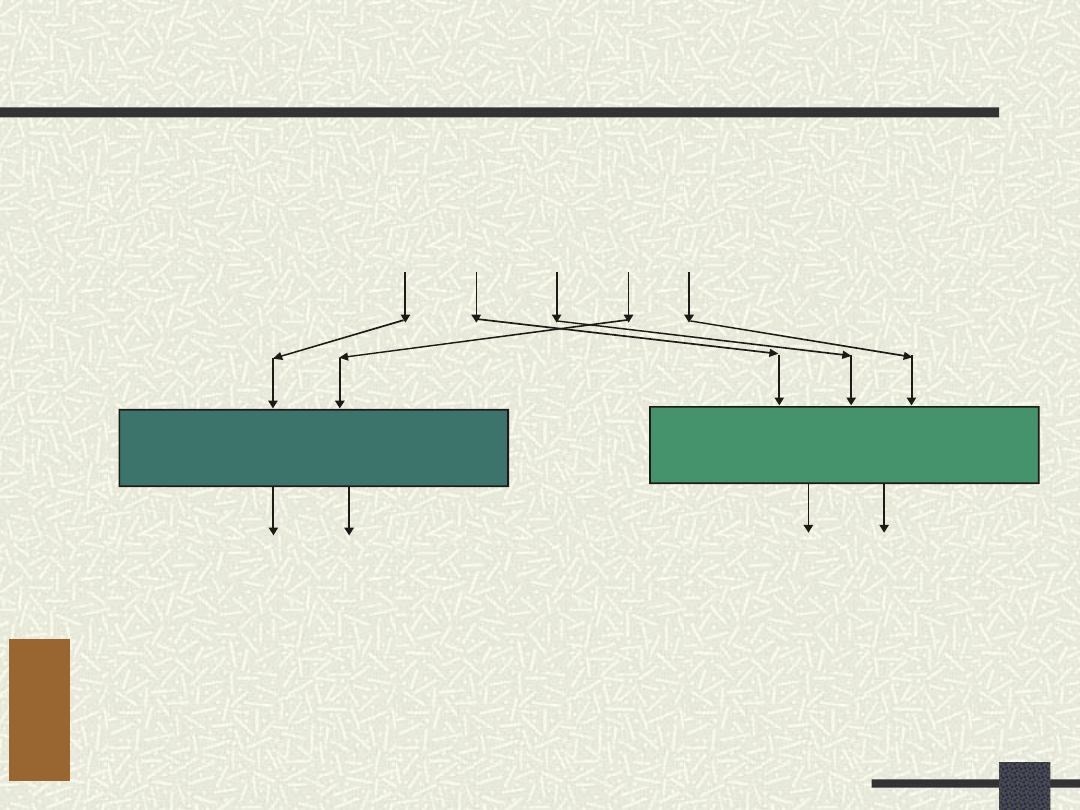
Dekompozycja równoległa -
przykład c.d.
y y
1
3
x x x x
1
2
3
4
x
x
5 6
y y
2
4
G
H
10
I
T
P
W
ZPT
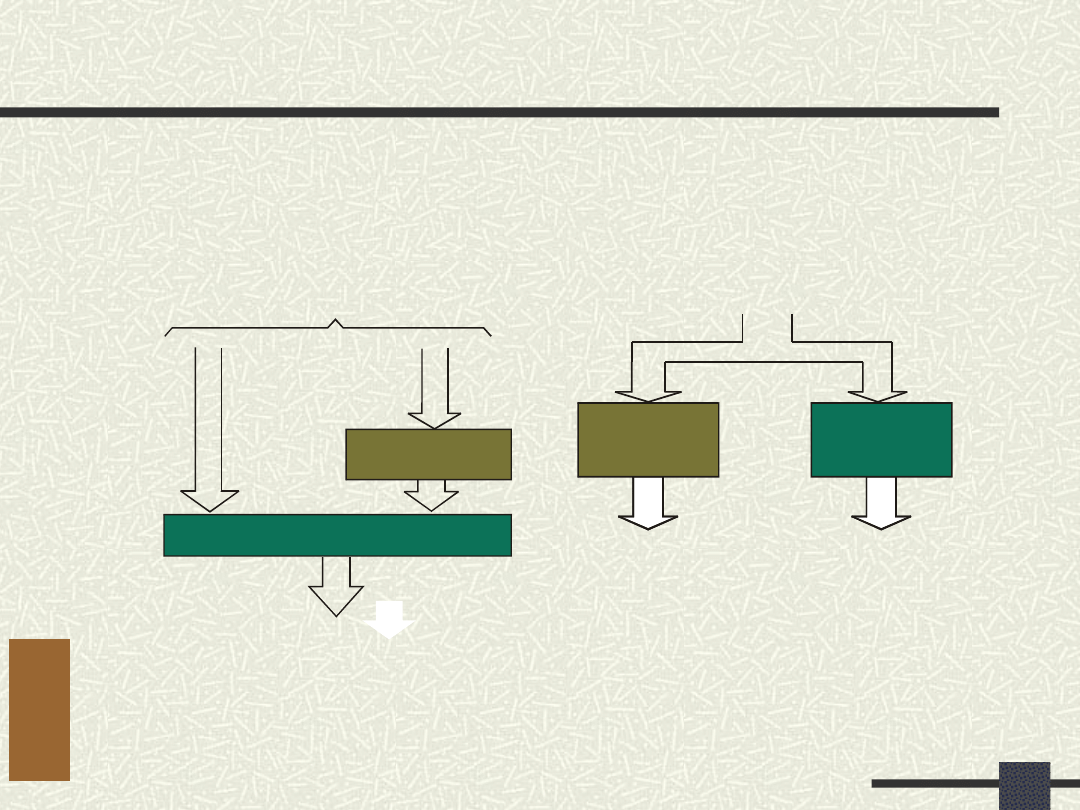
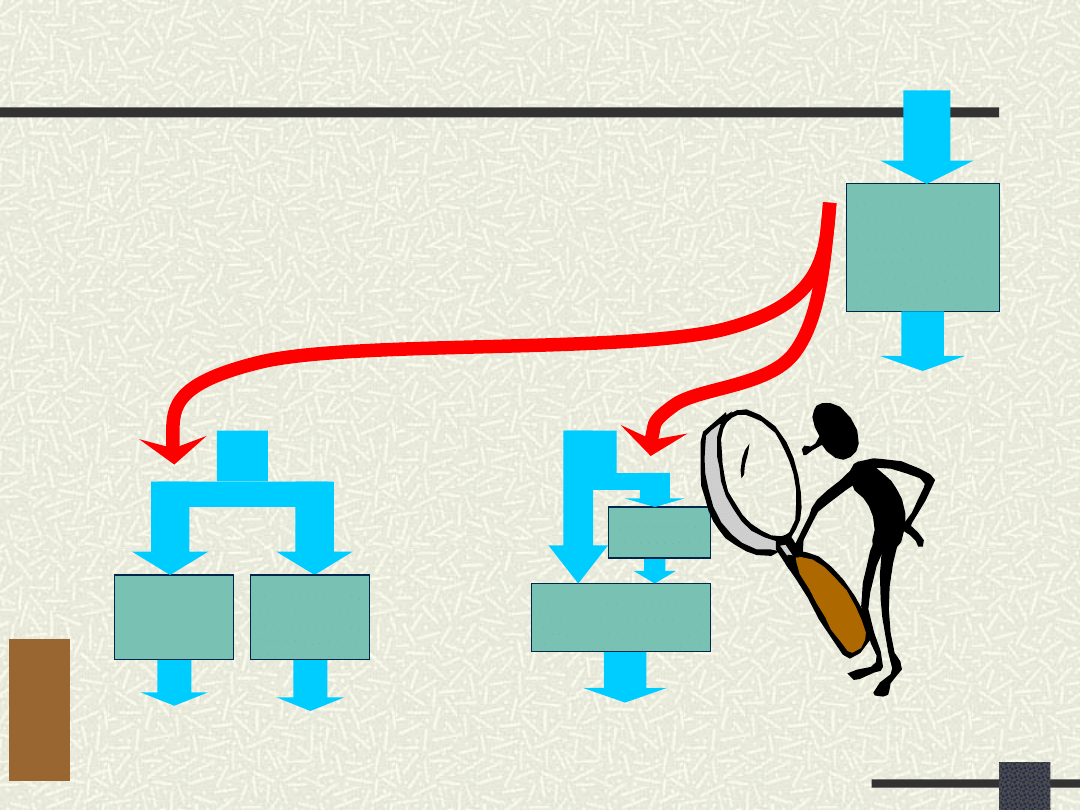
Algorytmy dekompozycji
Y
A
B
X
G
H
X
Y g
Y h
G
H
Szeregowa
Równoległa
11
I
T
P
W
ZPT
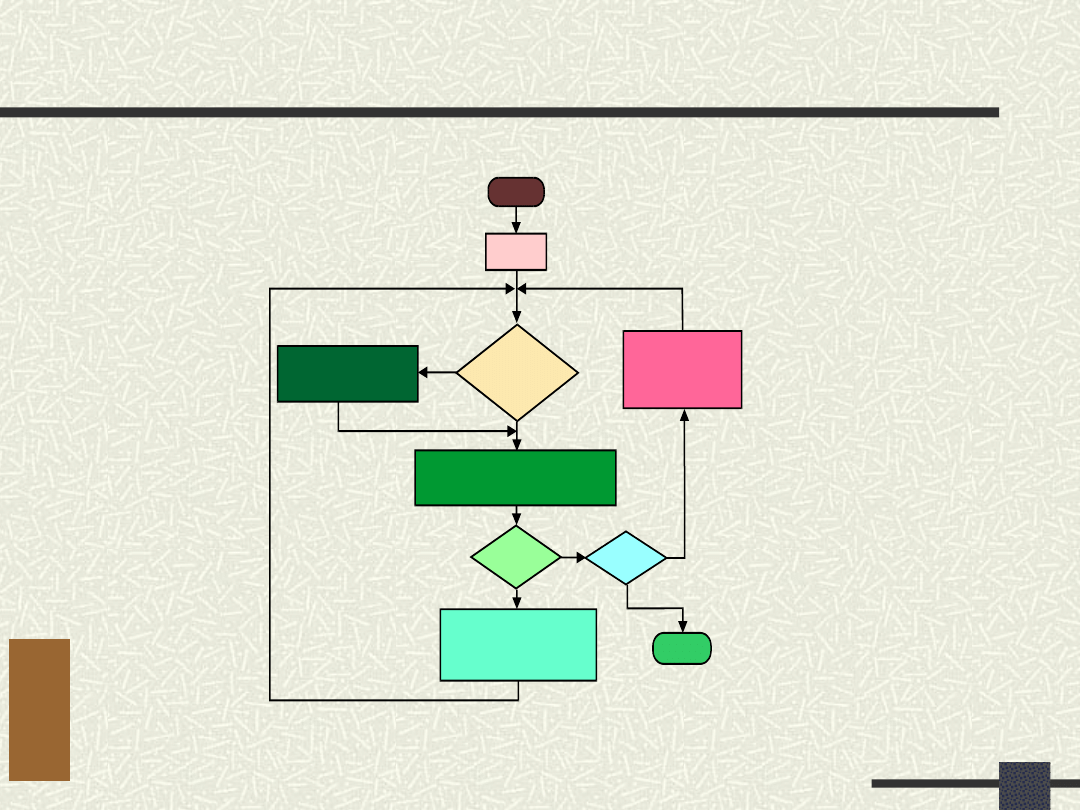
Zrównoważona dekompozycja
funkcjonalna
Metoda polegająca na wykonywaniu
Metoda polegająca na wykonywaniu
na przemian dekompozycji szeregowej
na przemian dekompozycji szeregowej
i równoległej, zgodnie z przyjętą strategią.
i równoległej, zgodnie z przyjętą strategią.
Zastosowana w procedurze DEMAIN
Zastosowana w procedurze DEMAIN
F
X
Y
G
H
X
Y
X
1
X
2
B
A
X
Y
1
Y
2
X
3
X
4
Dekompozycja równoległa
Dekompozycja równoległa
Dekompozycja szeregowa
Dekompozycja szeregowa
12
I
T
P
W
ZPT
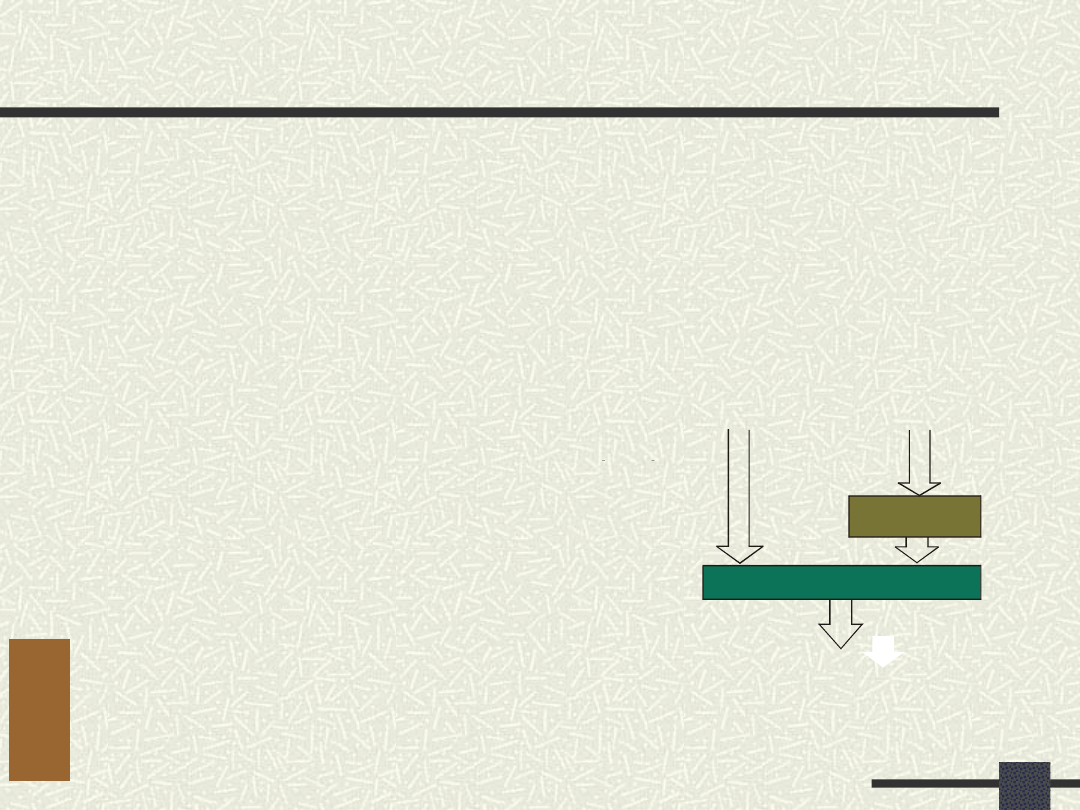
Jak dekomponuje Demain
START
D
AN
E
D
EK
O
M
PO
ZYCJA
R
Ó
W
N
O
LEG
ŁA
D
EK
O
M
PO
ZYCJA
SZER
EG
O
W
A
ISTN
IEJE ?g:=
cining:=
coutout
taktak
K
O
N
IEC
nienie
ZM
IAN
A LICZBYW
EJŚĆ/W
YJŚĆBLO
KU G
inn <
cD
ECYZJAUŻYTKO
W
N
IKA
13
I
T
P
W
ZPT
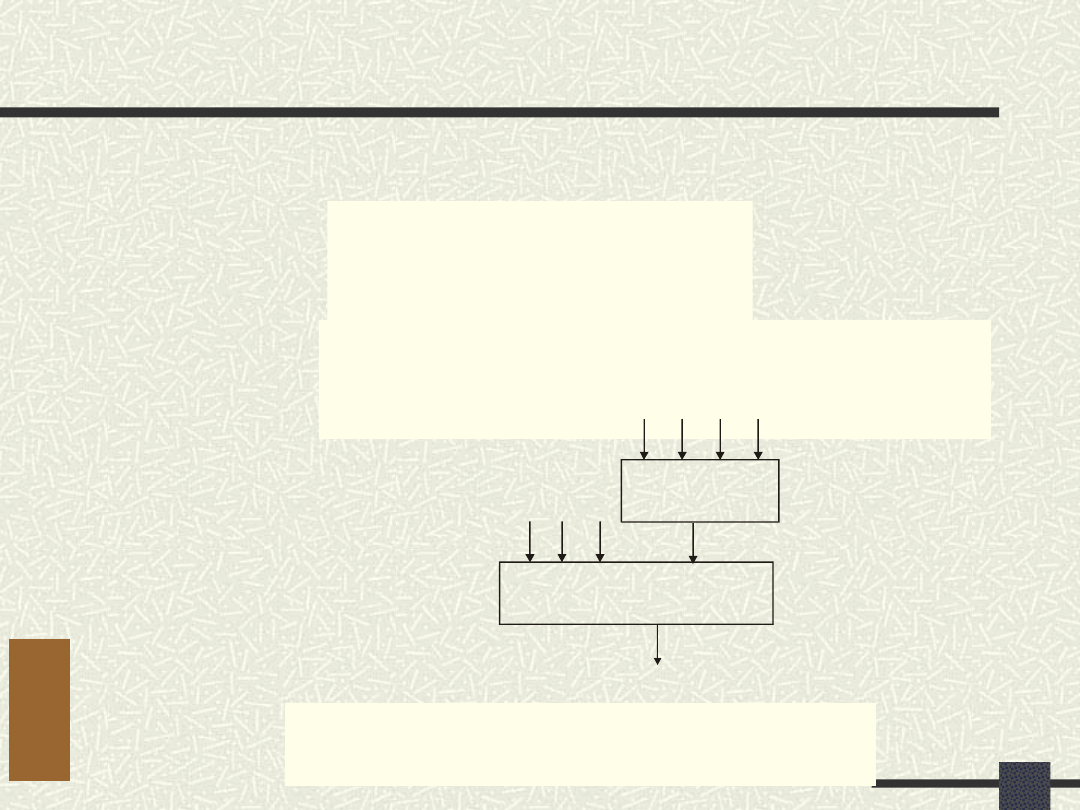
Decyzje użytkownika
The H table under consideration has 10 inputs and 2 outputs
Serial decomposition is suggested with G function parameters
assumed to be equal to the declared cell parameters
Do you prefer parallel decomposition ?: p
OR continue serial decomposition as suggested ?: s
OR continue serial decomposition with changed parameters ?: c
no. of block outputs= m
no. of block
inputs= n
c
Opcja c umożliwia również redukcję argumentów
m wyjść
G
H
n wejśc
14
I
T
P
W
ZPT
Jak obliczyć najlepszą dekompozycję
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
Opis w książce Synteza układów
cyfrowych, przykład 3.8, str. 108
1) Zredukować
argumenty
(zastosować opcję c)
2) Zastosować dekompozycję
szeregową
(opcja s)
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
15
I
T
P
W
ZPT
Przykład z
Synteza układów
cyfrowych str 32
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
Demain 2 komórki
LUT
23 komórki LUT
MAX+PLUSII
16
I
T
P
W
ZPT
Układ kombinacyjny
Inny przykład – benchmark BUL (SUC
przykład 3.9)
.type fr
.i 10
.o 2
.p 25
0101000000 00
1110100100 00
0010110000 01
0101001000 01
1110101101 10
0100010101 10
1100010001 00
0011101110 10
0001001110 10
0110000110 10
1110110010 01
0111100000 00
0100011011 00
0010111010 10
0110001110 00
0110110111 11
0001001011 11
1110001110 01
0011001011 01
0010011010 10
1010110010 00
0100110101 11
0001111010 00
1101100100 01
1001110111 11
.e
x
0
x
2
x
3
x
9
UK
y
0
y
1
17
I
T
P
W
ZPT
Specyfikacja AHDL
AHDL: 35
komórek LUT
MAX+PLUSII
SUBDESIGN bul
SUBDESIGN bul
(
(
i[1..10] : INPUT;
i[1..10] : INPUT;
o[1..2] : OUTPUT;
o[1..2] : OUTPUT;
)
)
BEGIN
BEGIN
TABLE
TABLE
(i[1..10]) => (o[1..2]);
(i[1..10]) => (o[1..2]);
B"0101000000" => B"00";
B"0101000000" => B"00";
B"1110100100" => B"00";
B"1110100100" => B"00";
B"0010110000" => B"10";
B"0010110000" => B"10";
B"0101001000" => B"10";
B"0101001000" => B"10";
B"1110101101" => B"01";
B"1110101101" => B"01";
B"0100010101" => B"01";
B"0100010101" => B"01";
B"1100010001" => B"00";
B"1100010001" => B"00";
B"0011101110" => B"01";
B"0011101110" => B"01";
B"0001001110" => B"01";
B"0001001110" => B"01";
B"0110000110" => B"01";
B"0110000110" => B"01";
B"1110110010" => B"10";
B"1110110010" => B"10";
B"0111100000" => B"00";
B"0111100000" => B"00";
B"0100011011" => B"00";
B"0100011011" => B"00";
B"0010111010" => B"01";
B"0010111010" => B"01";
B"0110001110" => B"00";
B"0110001110" => B"00";
B"0110110111" => B"11";
B"0110110111" => B"11";
B"0001001011" => B"11";
B"0001001011" => B"11";
B"1110001110" => B"10";
B"1110001110" => B"10";
B"0011001011" => B"10";
B"0011001011" => B"10";
B"0010011010" => B"01";
B"0010011010" => B"01";
B"1010110010" => B"00";
B"1010110010" => B"00";
B"0100110101" => B"11";
B"0100110101" => B"11";
B"0001111010" => B"00";
B"0001111010" => B"00";
B"1101100100" => B"10";
B"1101100100" => B"10";
B"1001110111" => B"11";
B"1001110111" => B"11";
END TABLE;
END TABLE;
END;
END;

18
I
T
P
W
ZPT
Project Information d:\maxplus2\work\bul.rpt
MAX+plus II Compiler Report File
Version 10.2 07/10/2002
Compiled: 04/18/2004 15:57:42
***** Project compilation was successful
Converted from PLA file: bul
** DEVICE SUMMARY **
Chip/ Input Output Bidir Memory Memory
LCs
POF Device Pins Pins Pins Bits % Utilized
LCs
% Utilized
bul EPF10K10LC84-3 10 2 0 0 0 %
35
6 %
User Pins: 10 2 0
Device-Specific Information: d:\maxplus2\work\bul.rpt
bul
***** Logic for device 'bul' compiled without errors.
Device: EPF10K10LC84-3
Fragment raportu MAX+PLUSII
19
I
T
P
W
ZPT
Specyfikacja VHDL
VHDL: 67
komórek LUT
MAX+PLUSII
library IEEE;
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.STD_LOGIC_1164.all;
entity bul is
entity bul is
port(i : in std_logic_vector(1 to
port(i : in std_logic_vector(1 to
10);
10);
o : out std_logic_vector(1 to
o : out std_logic_vector(1 to
2));
2));
end bul;
end bul;
architecture arch1 of bul is
architecture arch1 of bul is
begin
begin
PLA: process(i)
PLA: process(i)
begin
begin
case i is
case i is
when "0101000000" => o <=
when "0101000000" => o <=
"00";
"00";
when "1110100100" => o <=
when "1110100100" => o <=
"00";
"00";
when "0010110000" => o <=
when "0010110000" => o <=
"10";
"10";
when "0101001000" => o <=
when "0101001000" => o <=
"10";
"10";
when "1110101101" => o <=
when "1110101101" => o <=
"01";
"01";
when "0100010101" => o <=
when "0100010101" => o <=
"01";
"01";
when "1100010001" => o <=
when "1100010001" => o <=
"00";
"00";
when "0011101110" => o <=
when "0011101110" => o <=
"01";
"01";
when "0001001110" => o <=
when "0001001110" => o <=
"01";
"01";
when "0110000110" => o <=
when "0110000110" => o <=
"01";
"01";
when "1110110010" => o <=
when "1110110010" => o <=
"10";
"10";
when "0111100000" => o <=
when "0111100000" => o <=
"00";
"00";
when "0100011011" => o <=
when "0100011011" => o <=
"00";
"00";
when "0010111010" => o <=
when "0010111010" => o <=
"01";
"01";
when "0110001110" => o <=
when "0110001110" => o <=
"00";
"00";
when "0110110111" => o <=
when "0110110111" => o <=
"11";
"11";
when "0001001011" => o <=
when "0001001011" => o <=
"11";
"11";
when "1110001110" => o <=
when "1110001110" => o <=
"10";
"10";
when "0011001011" => o <=
when "0011001011" => o <=
"10";
"10";
when "0010011010" => o <=
when "0010011010" => o <=
"01";
"01";
when "1010110010" => o <=
when "1010110010" => o <=
"00";
"00";
when "0100110101" => o <=
when "0100110101" => o <=
"11";
"11";
when "0001111010" => o <=
when "0001111010" => o <=
"00";
"00";
when "1101100100" => o <=
when "1101100100" => o <=
"10";
"10";
when "1001110111" => o <=
when "1001110111" => o <=
"11";
"11";
when others => o <= "XX";
when others => o <= "XX";
end case;
end case;
end process;
end process;
end;
end;
20
I
T
P
W
ZPT
Przykład
(Leonardo Spectrum)
96 komórek LUT
.
type fr
.i 10
.o 2
.p 25
0101000000 00
1110100100 00
0010110000 01
0101001000 01
1110101101 10
0100010101 10
1100010001 00
0011101110 10
0001001110 10
0110000110 10
1110110010 01
0111100000 00
0100011011 00
0010111010 10
0110001110 00
0110110111 11
0001001011 11
1110001110 01
0011001011 01
0010011010 10
1010110010 00
0100110101 11
0001111010 00
1101100100 01
1001110111 11
.e
Leonardo Spectrum
21
I
T
P
W
ZPT
Ile komórek LUT ?
.
type fr
.i 10
.o 2
.p 25
0101000000 00
1110100100 00
0010110000 01
0101001000 01
1110101101 10
0100010101 10
1100010001 00
0011101110 10
0001001110 10
0110000110 10
1110110010 01
0111100000 00
0100011011 00
0010111010 10
0110001110 00
0110110111 11
0001001011 11
1110001110 01
0011001011 01
0010011010 10
1010110010 00
0100110101 11
0001111010 00
1101100100 01
1001110111 11
.e
y 0
0 1 3
4
7
6
y 1
0 1 2
1
6
7 9
G 1
H 1
G 2
H 2
Zagadka
4 komórki LUT
Demain
22
I
T
P
W
ZPT
Jak osiągnąć najlepszy wynik
Wynik Demaina silnie zależy od strategii
syntezy
tzn. kolejności wykonywania dekompozycji
szeregowej i równoległej
Duże znaczenie ma dekompozycja
nierozłączna
23
I
T
P
W
ZPT
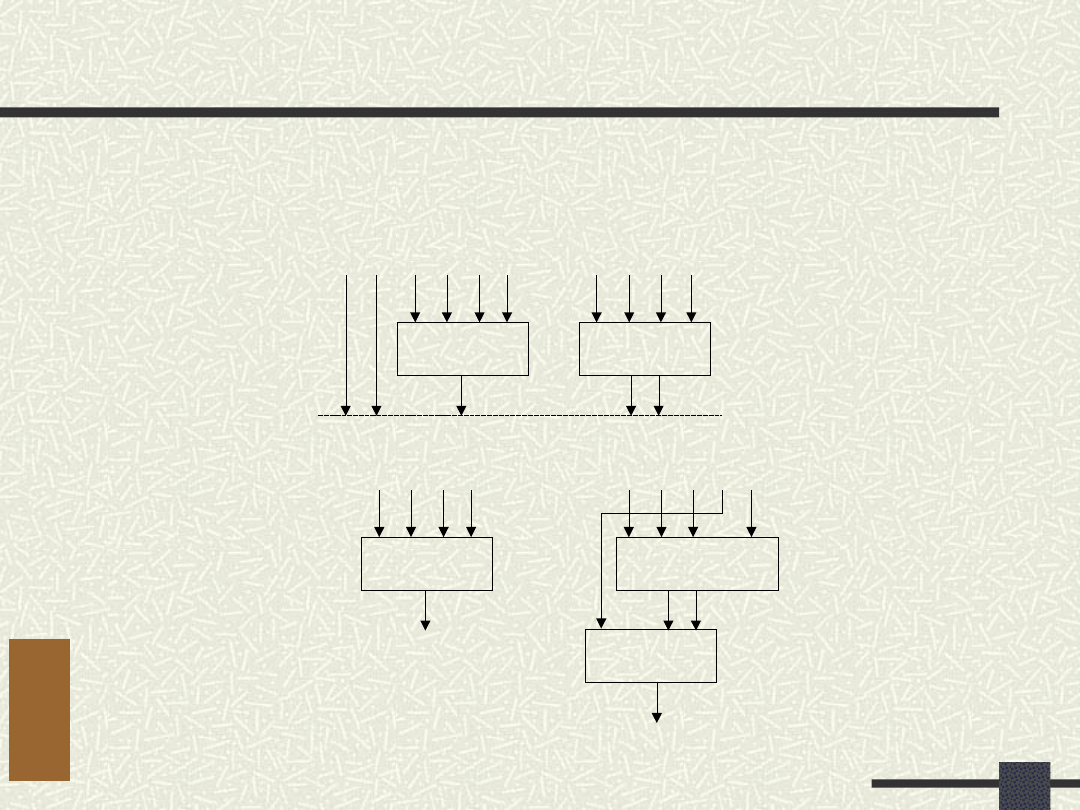
Dekompozycja funkcji BUL
y 0
0 1 3
4
7
6
y 1
0 1 2
1
6
7 9
G 1
H 1
G 2
H 2
Najpierw równoległa później szeregowa
Liczba zajętych komórek: 4
24
I
T
P
W
ZPT
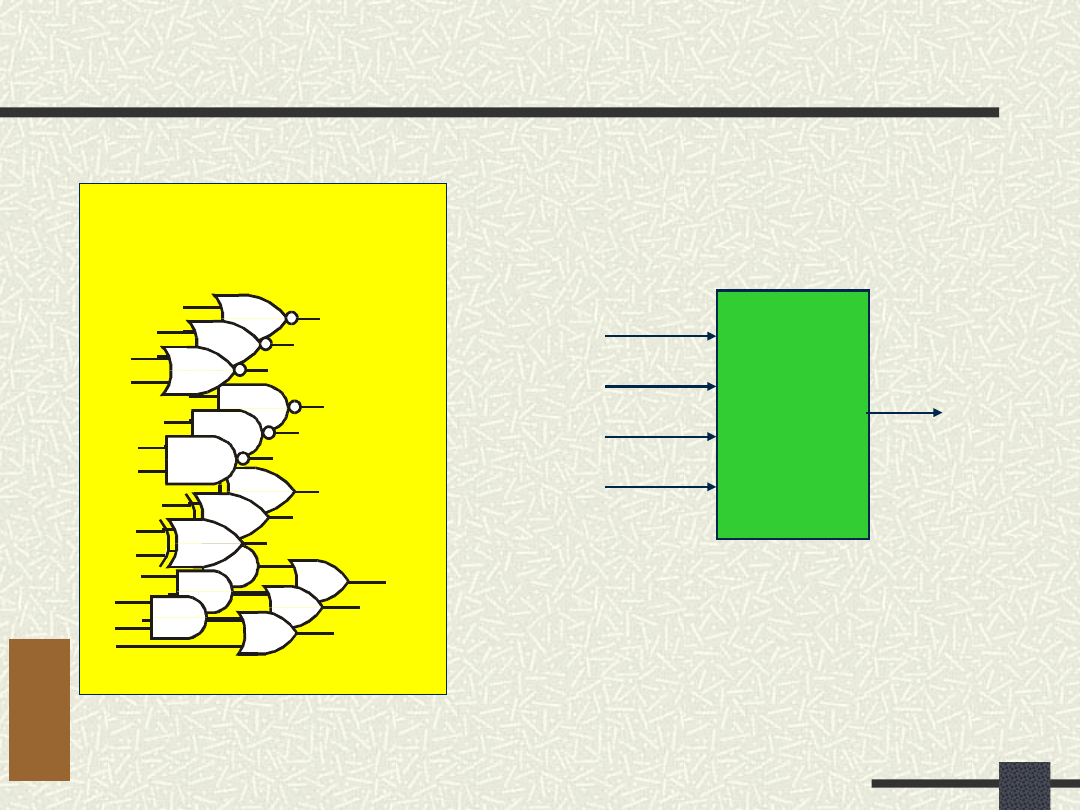
Dekompozycja funkcji BUL wg innej
strategii syntezy
8 9 1 3 4 6 0 2 5 7
( 4 / 1 )
( 4 / 1 )
( 4 / 2 )
( 4 / 2 )
( 3 / 1 )
0 1 2 3 4
0 1 2 4
0 1 2 3 4
y
0
y
1
b )
a )
c )
Najpierw szeregowa później równoległa
Liczba zajętych komórek: 7
25
I
T
P
W
ZPT
Library of gates
Przyczyna wad systemów
komercyjnych
y = f(x
1
, x
2
, x
3
, x
4
) !!!
x
1
x
2
x
3
x
4
Komórka LUT struktur FPGA
LUT
y
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
Wyszukiwarka
Podobne podstrony:
ulog w4b
ulog w4b
ulog w8b T
ulog w2
ulog w6 E
Automatyka ulog w8 id 629066 Nieznany (2)
ulog w4a
ulog demain
ulog w8a T
ulog w9b
ulog w8a e
ulog w6b
ulog w7a
ulog w9 e
ulog w1
ulog t pr 06
Zad 03-2, WEiTI - Makro, SEMESTR I, ULOG
więcej podobnych podstron