1

I

T

P

W

ZPT

Układy cyfrowe

Układy logiczne (cyfrowe) konstruowane są w różnych
technologiach i na różnych poziomach opisu.

Poziomy opisu:

1) Bramki i elementarne układy pamięciowe (przerzutniki)

2) Bloki funkcjonalne: układy arytmetyczne (sumatory), liczniki,
rejestry.

Tworzą one nowe elementy konstrukcyjne, z których buduje się
złożone układy cyfrowe o różnorodnych zastosowaniach: układy
przetwarzania sygnałów, układy sterowania, specjalizowane
procesory, układy kryptograficzne...

2

I

T

P

W

ZPT

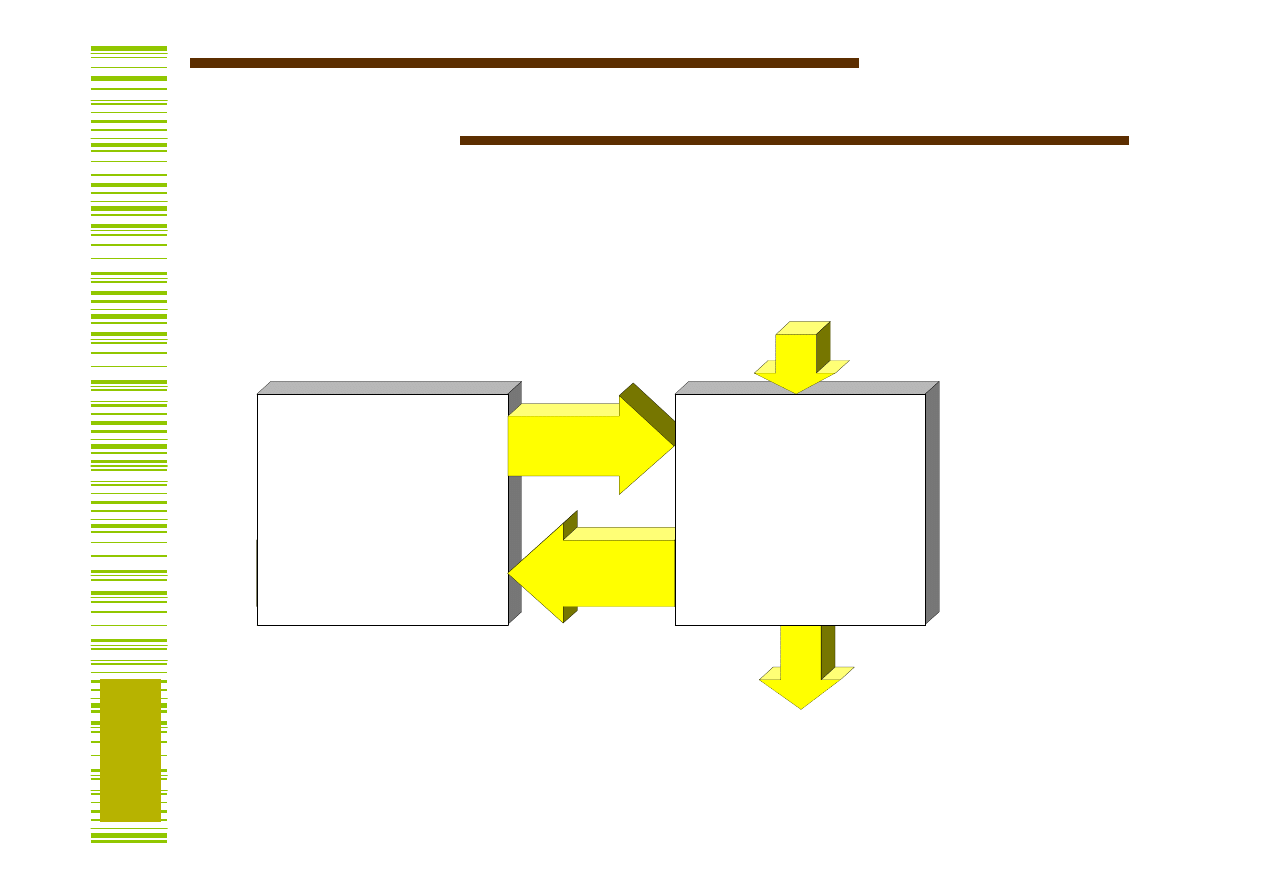
Układ

sterujący

(kontroler

)

Dane wyjściowe

Dane

wejściowe

Sygnały

sterujące

Stan części
operacyjnej

Układ operacyjny

(Datapath)

Mikrooperacje

wywoływane przez

sygnały sterujące

System cyfrowy

3

I

T

P

W

ZPT

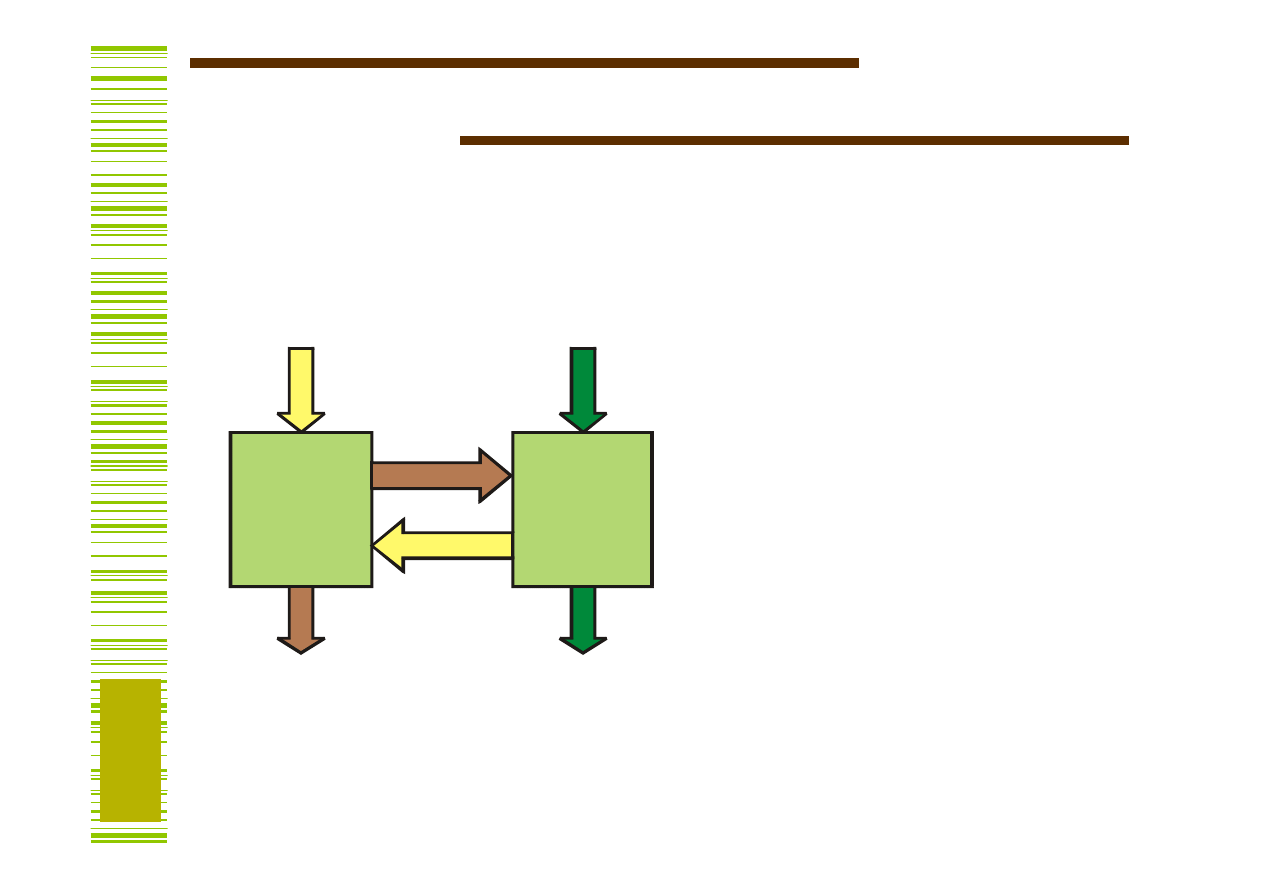
Cyfrowy zespół funkcjonalny CZF

UO - układ operacyjny US - układ sterujący

US

UO

D

F

X

P

Z

Z

Y

X

Z

D, F - przetwarzana informacja
(wektory binarne),

X - sygnały warunków,

Z - sygnały sterujące
(mikrorozkazy)

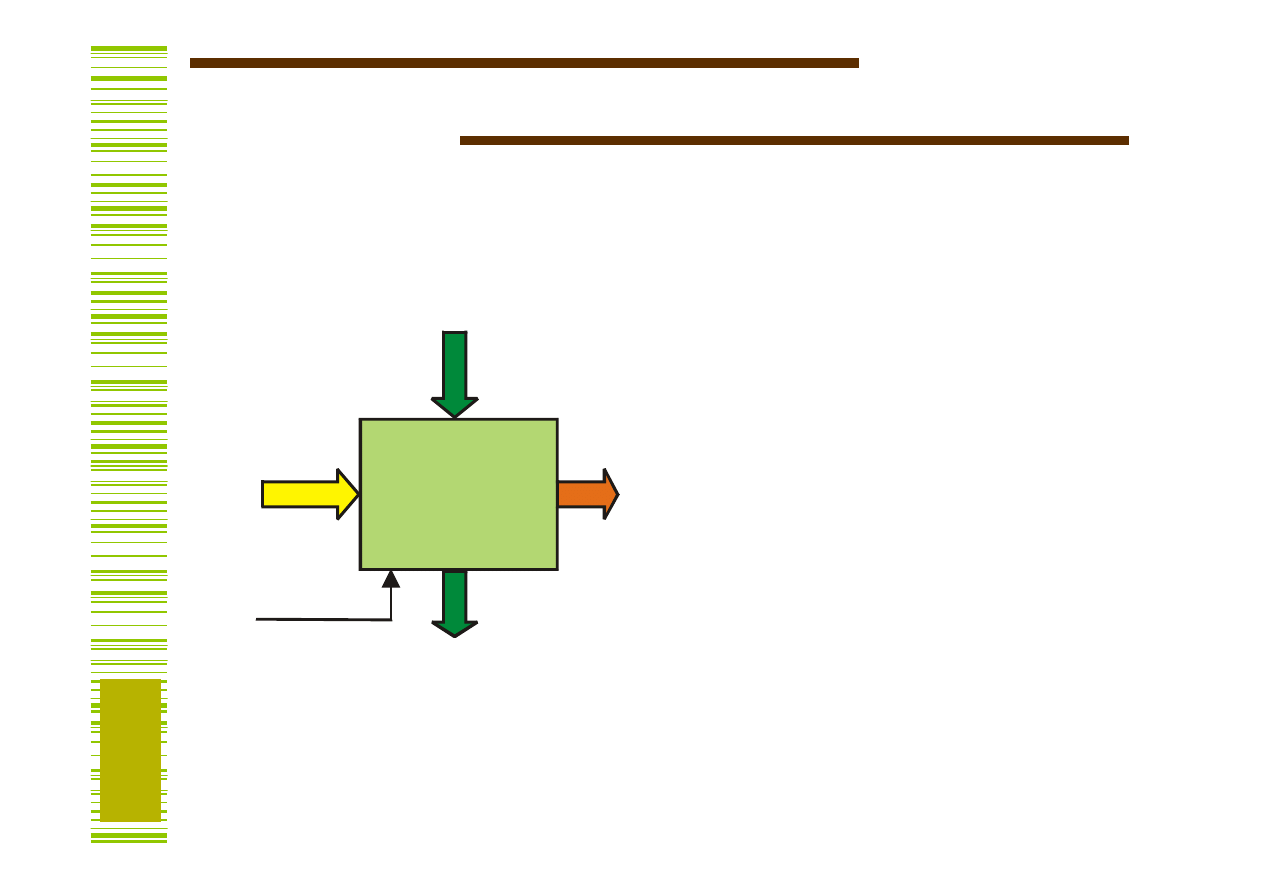
4

I

T

P

W

ZPT

Bloki funkcjonalne

X – wejścia sygnałów
reprezentujących dane
wejściowe
Y – wyjścia sygnałów
reprezentujących dane
wyjściowe,
S – wejścia sterujące,
P – wyjścia predykatowe,
sygnalizujące pewne
szczególne stany
przetwarzania danych oraz
clk – wejście zegarowe.

BF

X

Y

S

P

clk

5

I

T

P

W

ZPT

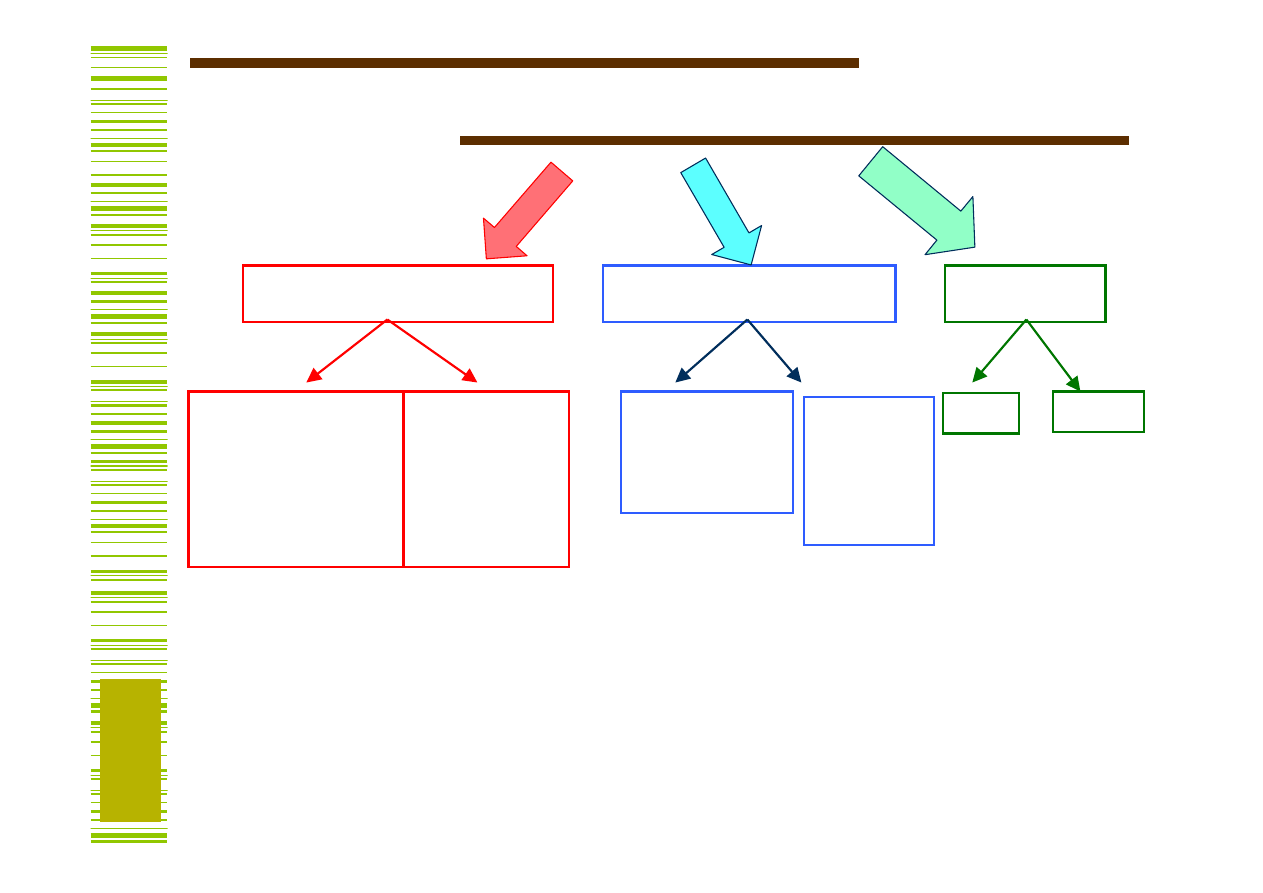
Bloki funkcjonalne

B. kombinacyjne

B. sekwencyjne

Pamięci

Układy

arytmetyczno-

-logiczne

Sumator

Układ odejmujący

Układy

Komutacyjne

MUX

DMUX

DEC

Rejestry

Równoległe
Przesuwające

Liczniki

Zliczające
W górę
W dół

ROM

(RAM)

6

I

T

P

W

ZPT

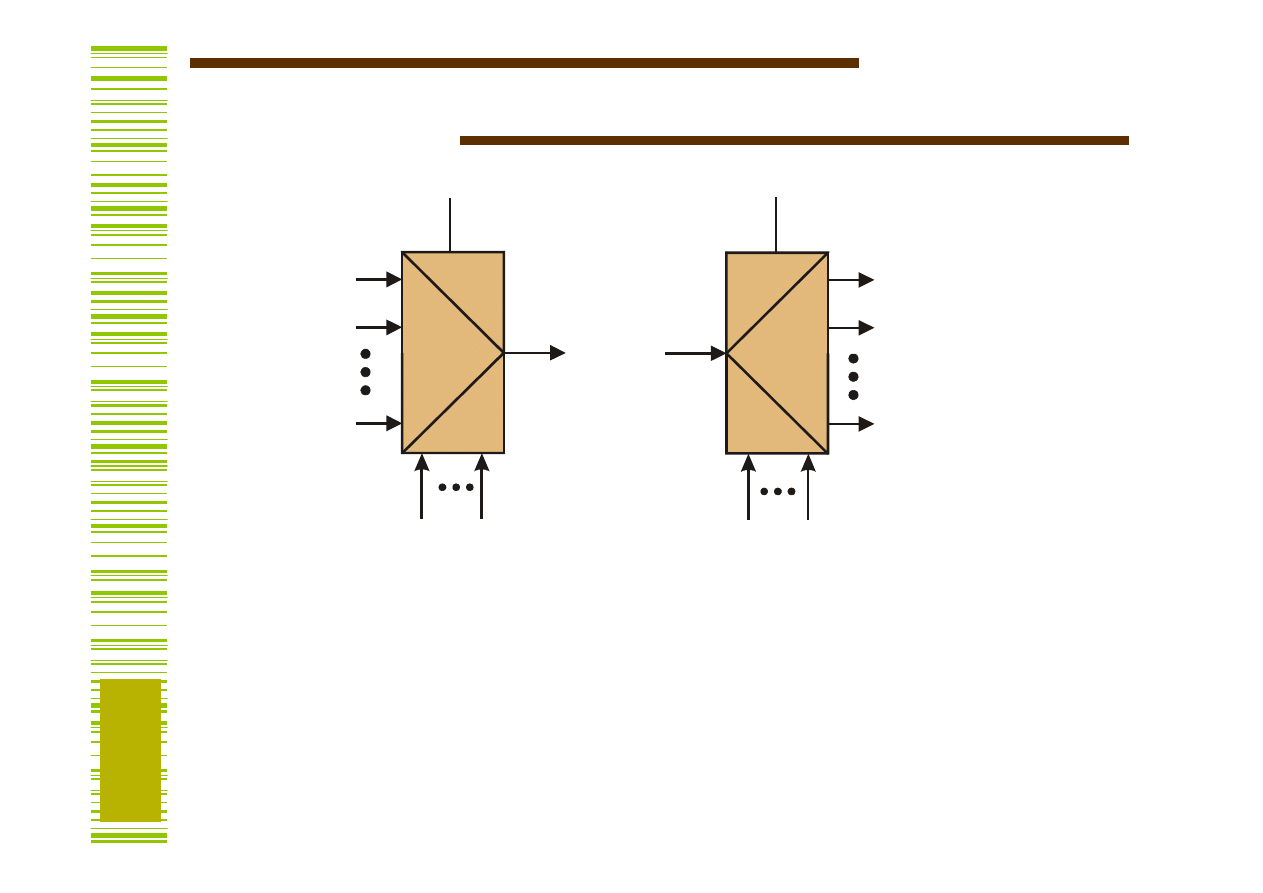
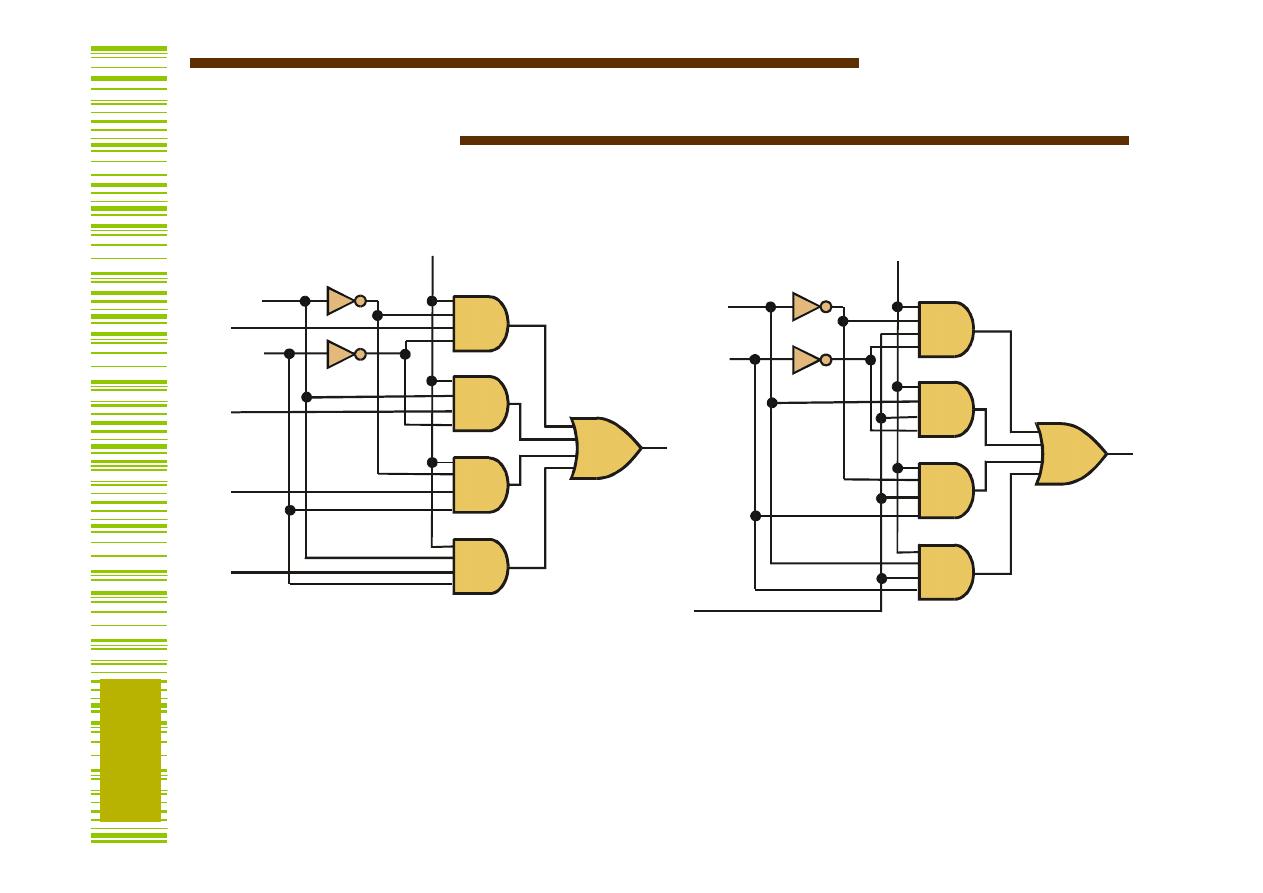
Multipleksery, demultipleksery

a

n-1

a

0

y

e

d

d

d

0

1

N-1

a

n-1

a

0

e

d

y

y

y

0

1

N-1

k = L(A),

P

k

– pełny iloczyn

∑

−

=

=

1

N

0

k

k

k

d

)

A

(

P

e

y

MUX

DMUX

N = 2

n

d

)

A

(

eP

y

k

k

=

7

I

T

P

W

ZPT

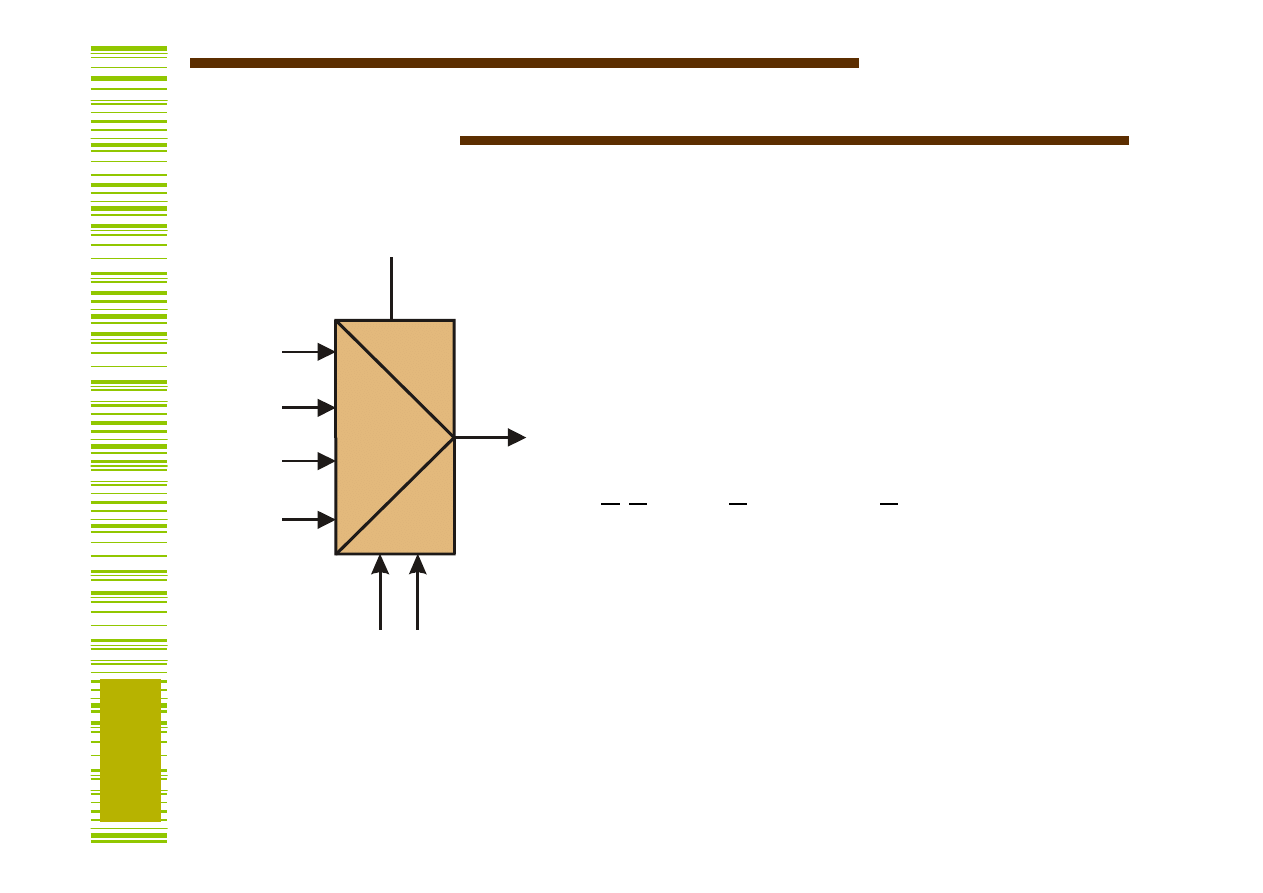
Multipleksery

∑

−

=

=

1

0

N

k

k

k

d

A

P

e

y

)

(

gdzie P

k

(A) oznacza pełny

iloczyn zmiennych

a

n–1

,...,a

0

, prostych lub

zanegowanych, zgodnie z
reprezentacją binarną liczby
k.

Dla n = 1 (MUX 2 : 1):

dla n = 2 (MUX 4 : 1):

dla n = 3 (MUX 8 : 1):

1

0

ad

d

a

y

+

=

3

0

1

2

0

1

1

0

1

0

0

1

d

a

a

d

a

a

d

a

a

d

a

a

y

+

+

+

=

7

0

1

2

6

0

1

2

5

0

1

2

4

0

1

2

3

0

1

2

2

0

1

2

1

0

1

2

0

0

1

2

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

d

a

a

a

y

+

+

+

+

+

+

+

+

=

8

I

T

P

W

ZPT

Multiplekser

e=1

0

1

2

3

0 0

0 1

1 1

0

1

1

0

1

0

1

3

0

1

2

0

1

1

0

1

0

0

1

d

a

a

d

a

a

d

a

a

d

a

a

y

+

+

+

=

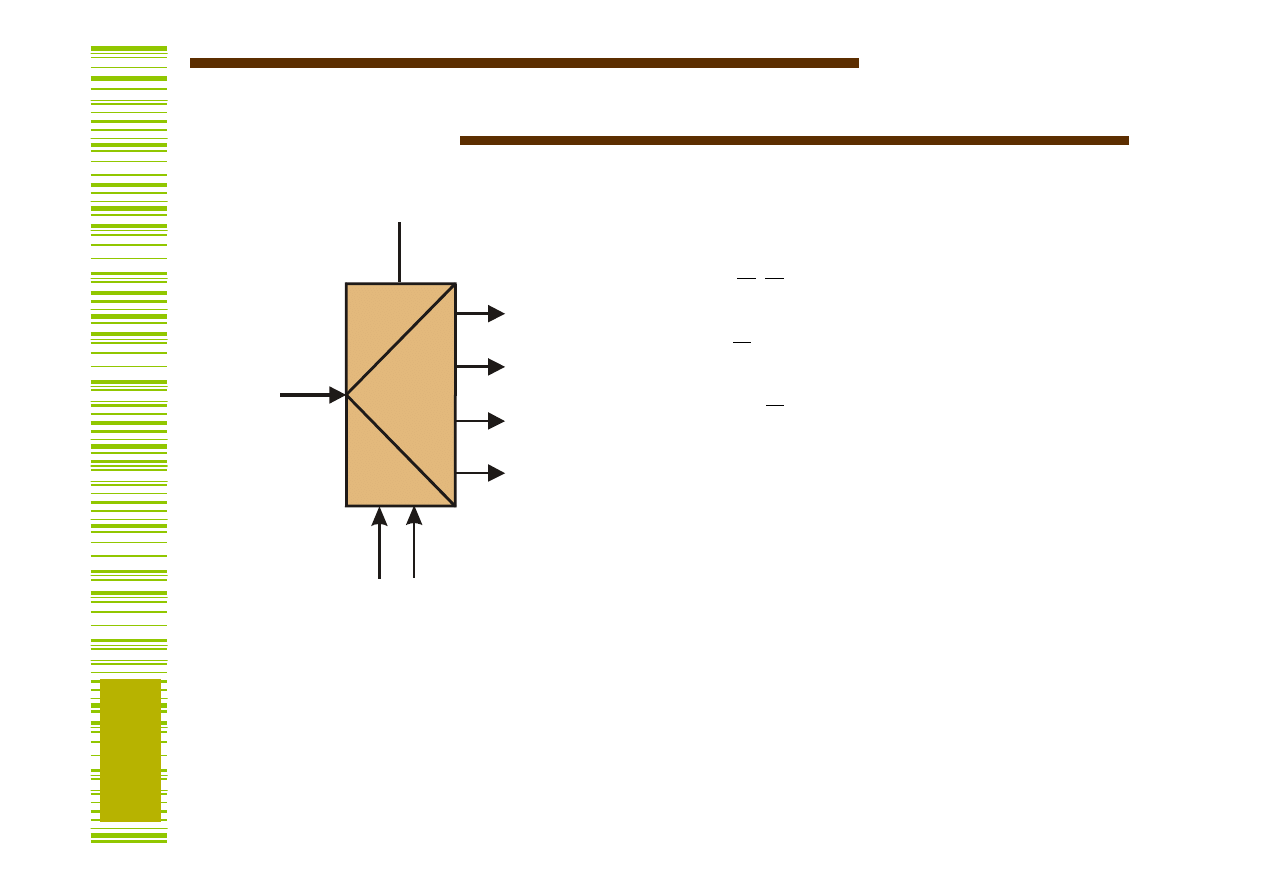
9

I

T

P

W

ZPT

Demultiplekser

e=1

1

0

1

2

3

1

0

0

0

1

0

0

0

0

0

0

1

0 0

0 1

1 1

d

a

a

y

d

a

a

y

d

a

a

y

d

a

a

y

0

1

3

0

1

2

0

1

1

0

1

0

=

=

=

=

10

I

T

P

W

ZPT

Multipleksery, demultipleksery

d

0

d

1

d

2

d

3

a

0

a

1

e

y

Multiplekser Demultiplekser

a

0

a

1

e

y

d

11

I

T

P

W

ZPT

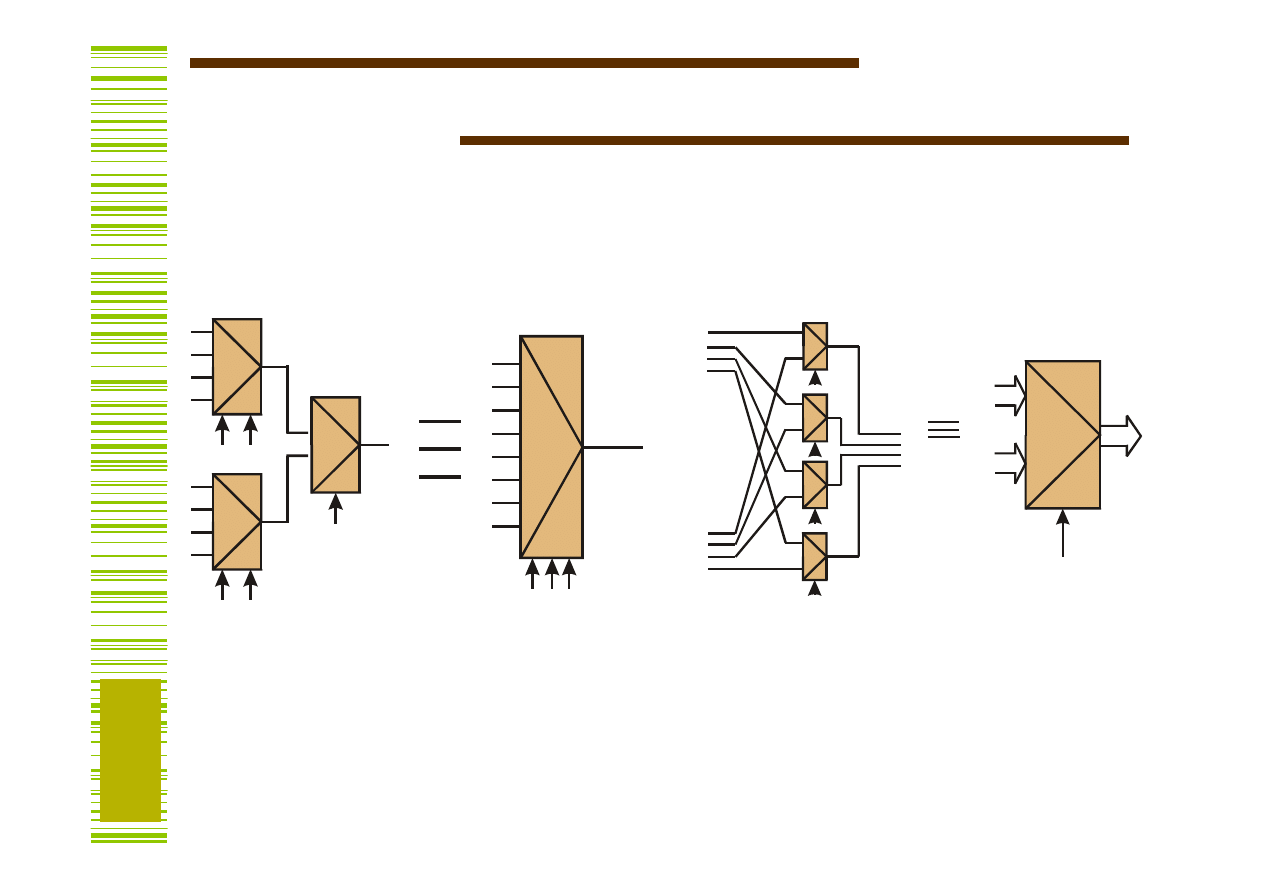
Multipleksery kaskadowe, grupowe

A

B

A

B

Multiplekser kaskadowy

Multiplekser grupowy

12

I

T

P

W

ZPT

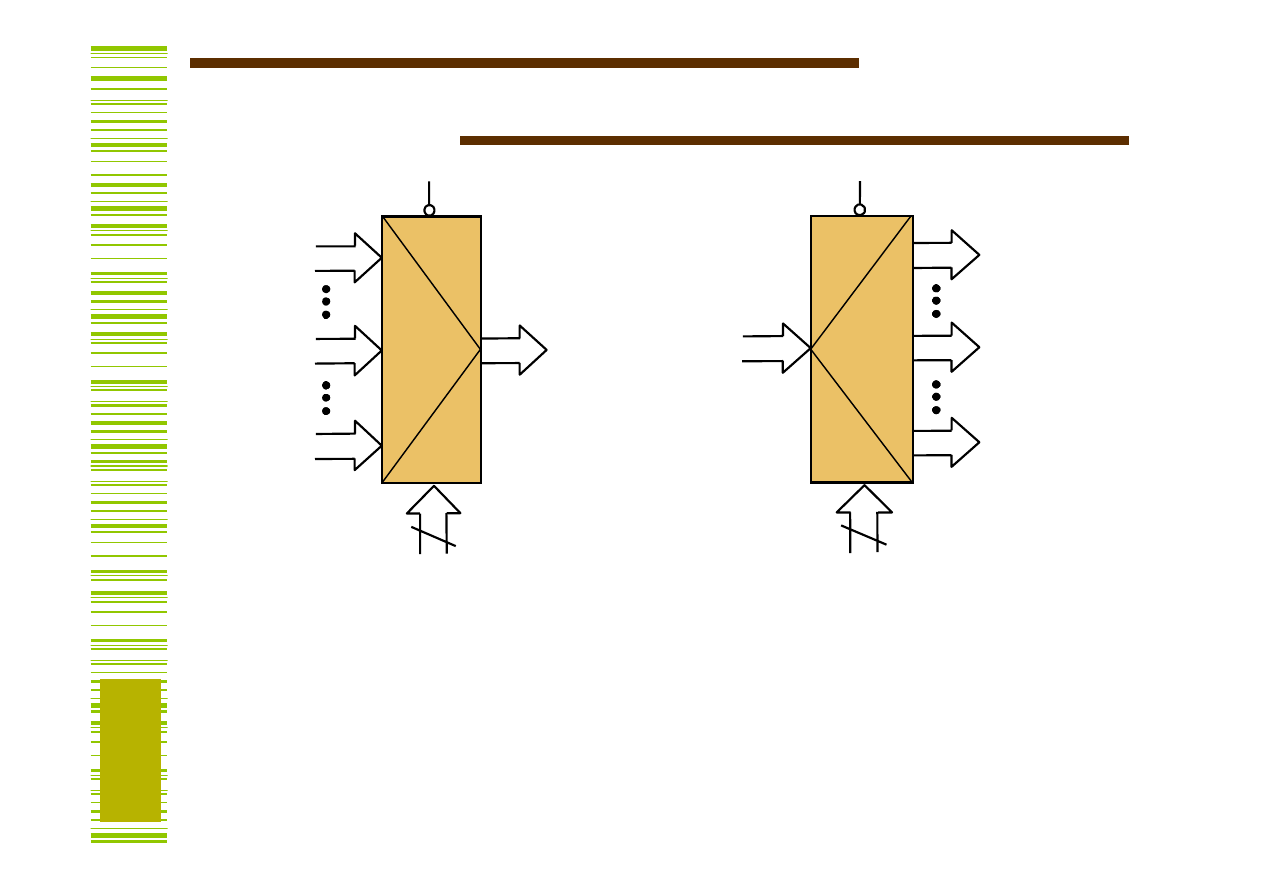
Bloki komutacyjne

Multiplekser służy do wybierania
jednego z wielu słów wejściowych i
przesyłania go na wyjście. Na wyjściu
Y pojawia się słowo wejściowe
wskazane adresem A (wg naturalnego
kodu binarnego).

Demultiplekser służy do
przesyłania słowa wejściowego
na jedno z wielu wyjść; numer
tego wyjścia jest równy
aktualnej wartości adresu.

X

0

X

j

X

N-1

Y

n

S

b

Y

0

Y

j

Y

N-1

n

S

b

X

13

I

T

P

W

ZPT

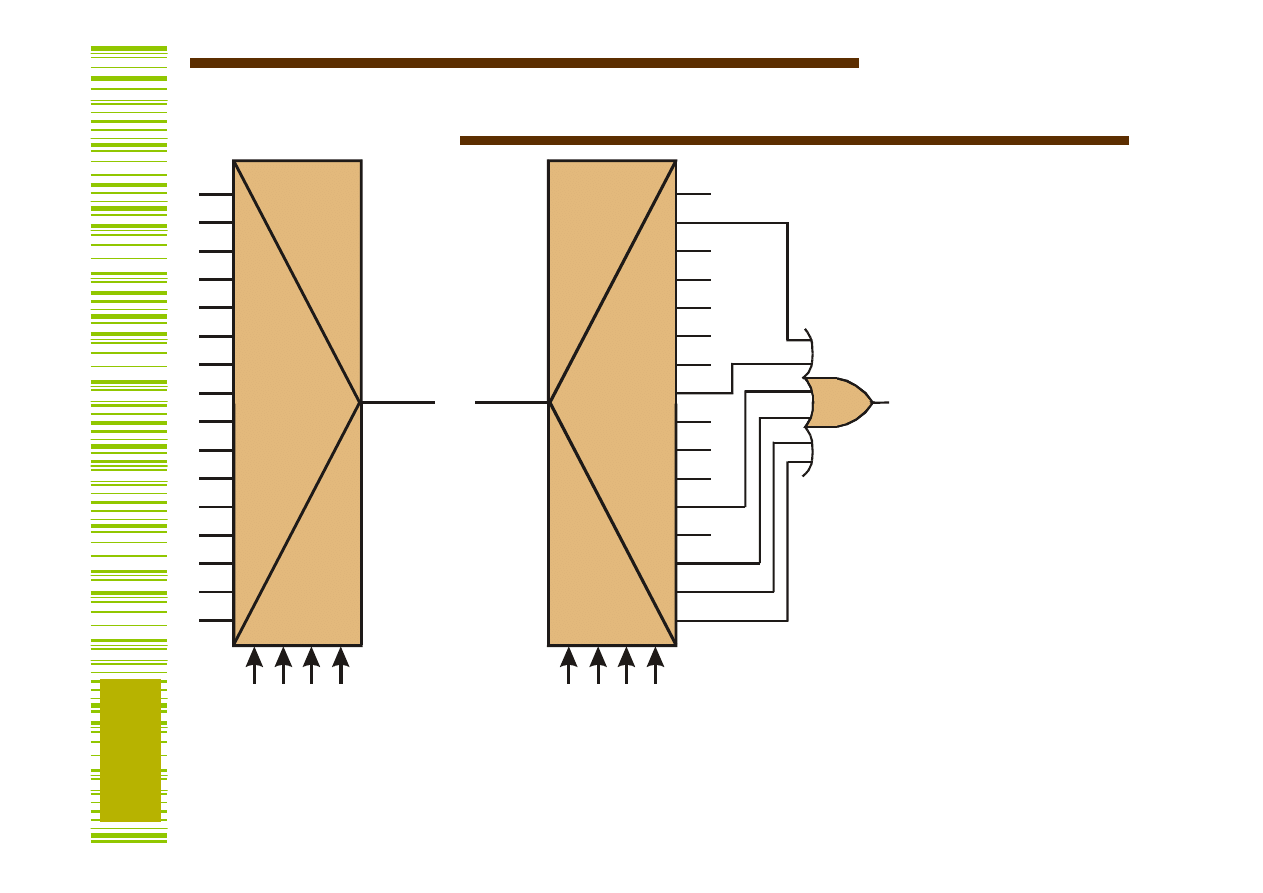
Zastosowanie MUX/DMUX do realizacji funkcji boolowskich

x1 x2 x3 x4

x1 x2 x3 x4

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

0

1

0

0

0

0

0

1

0

0

0

1

0

1

1

1

y

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

b

y

y =

Σ

(1,7,11,13,14,15)

Istnieją układy FPGA,
w których komórki są
MULTIPLEKSERAMI
Ich synteza

→

→

→

→

metody BDD

14

I

T

P

W

ZPT

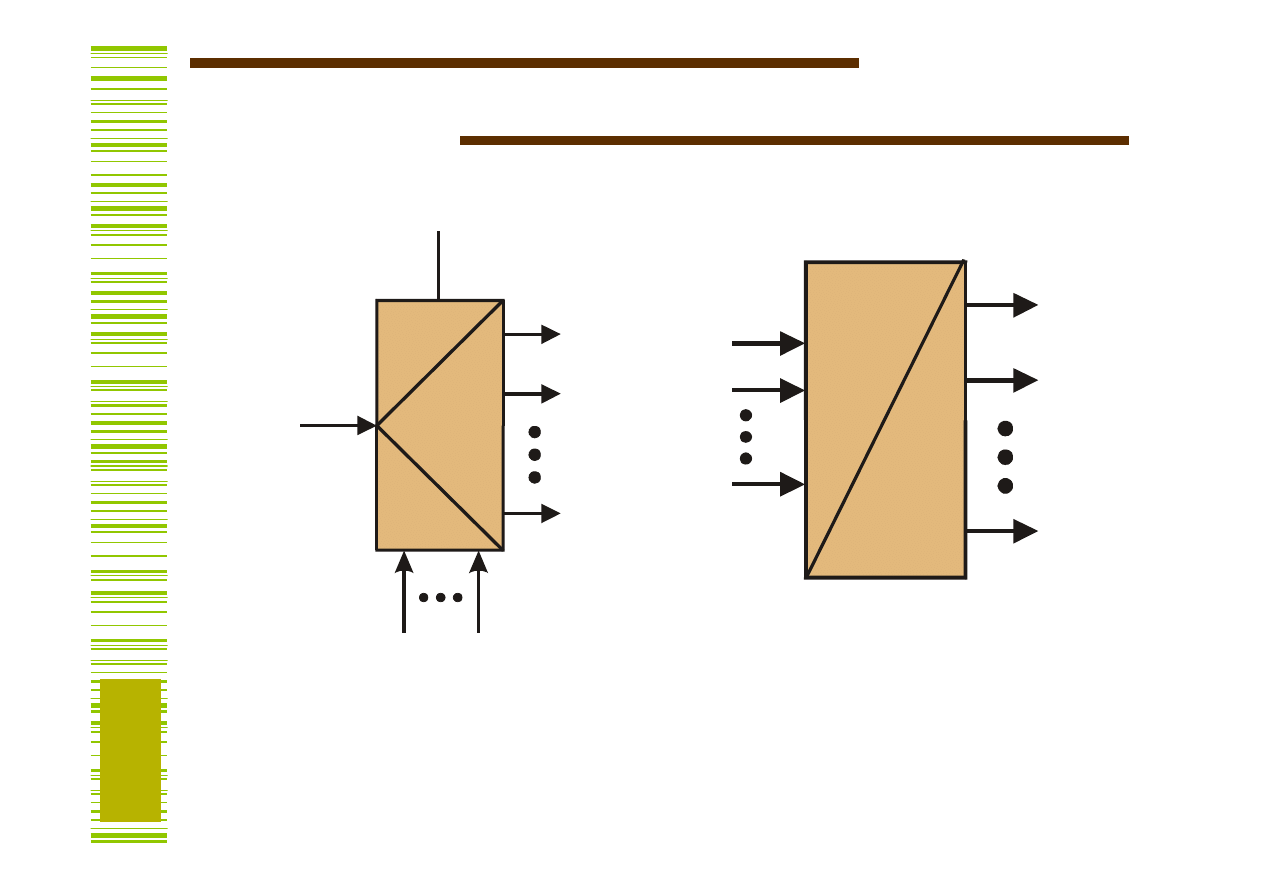
Dekoder

a

n-1

a

0

e

d

y

y

y

0

1

N-1

y

y

y

0

1

N-1

a
a

a

0

1

n-1

N = 2

n

DMUX

15

I

T

P

W

ZPT

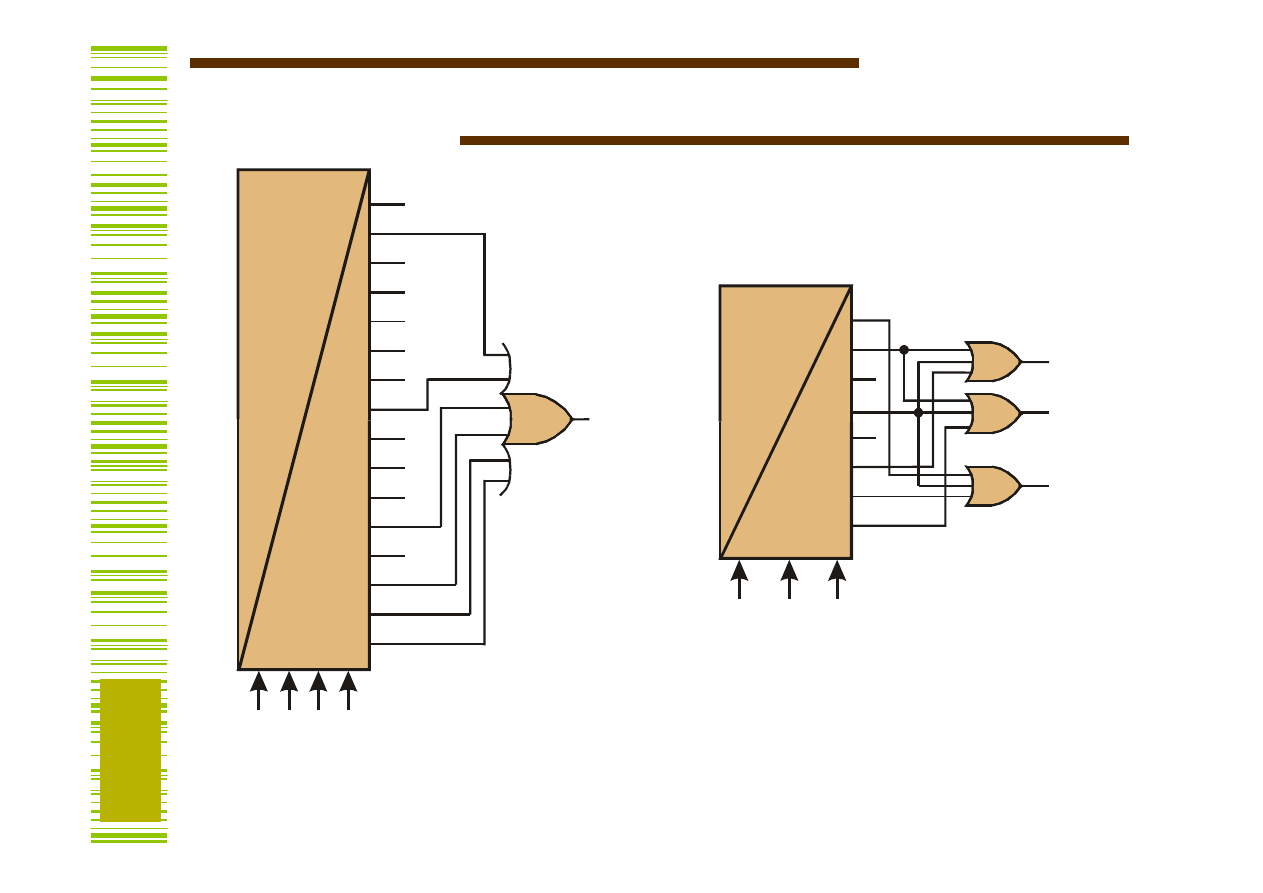
Realizacja funkcji na dekoderach

x1 x2 x3 x4

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

F

x x x

1

2

3

0

1

2

3

4

5

6

7

F

F

F

1

2

3

F

1

=

Σ

(1,3,5)

F

2

=

Σ

(1,3,7)

F

3

=

Σ

(0,3,6)

y =

Σ

(1,7,11,13,14,15)

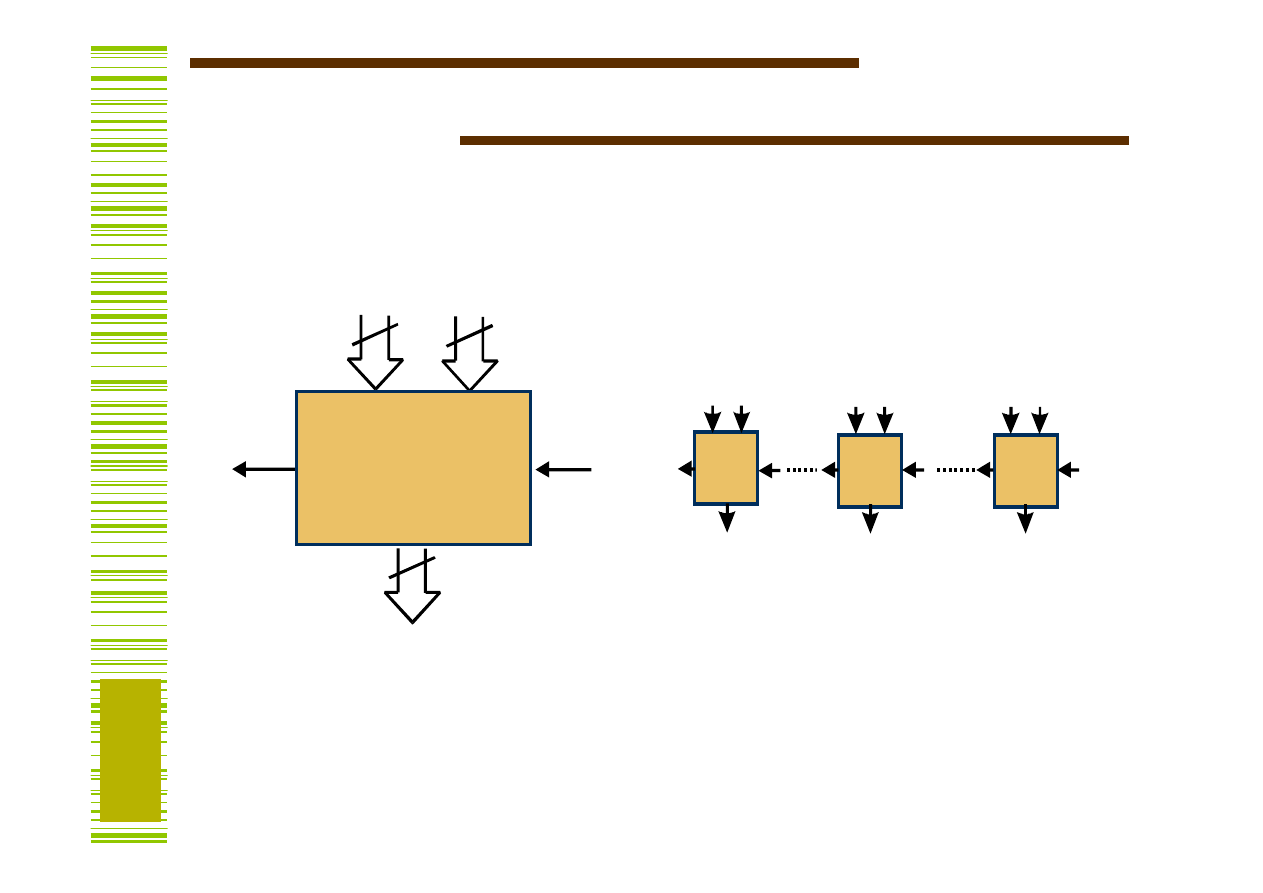
16

I

T

P

W

ZPT

Układy arytmetyczne

Najprostszy sumator – ripple carry adder

a b

a b

a

b)

b

0

0

y

0

c

1

c

0

i

i

y

i

c

i+1

c

n-1

c

i

Σ

n-1

y

n-1

c

n

Σ

Σ

n-1

Y

A

B

c

n

c

0

a)

n

n

n

Σ

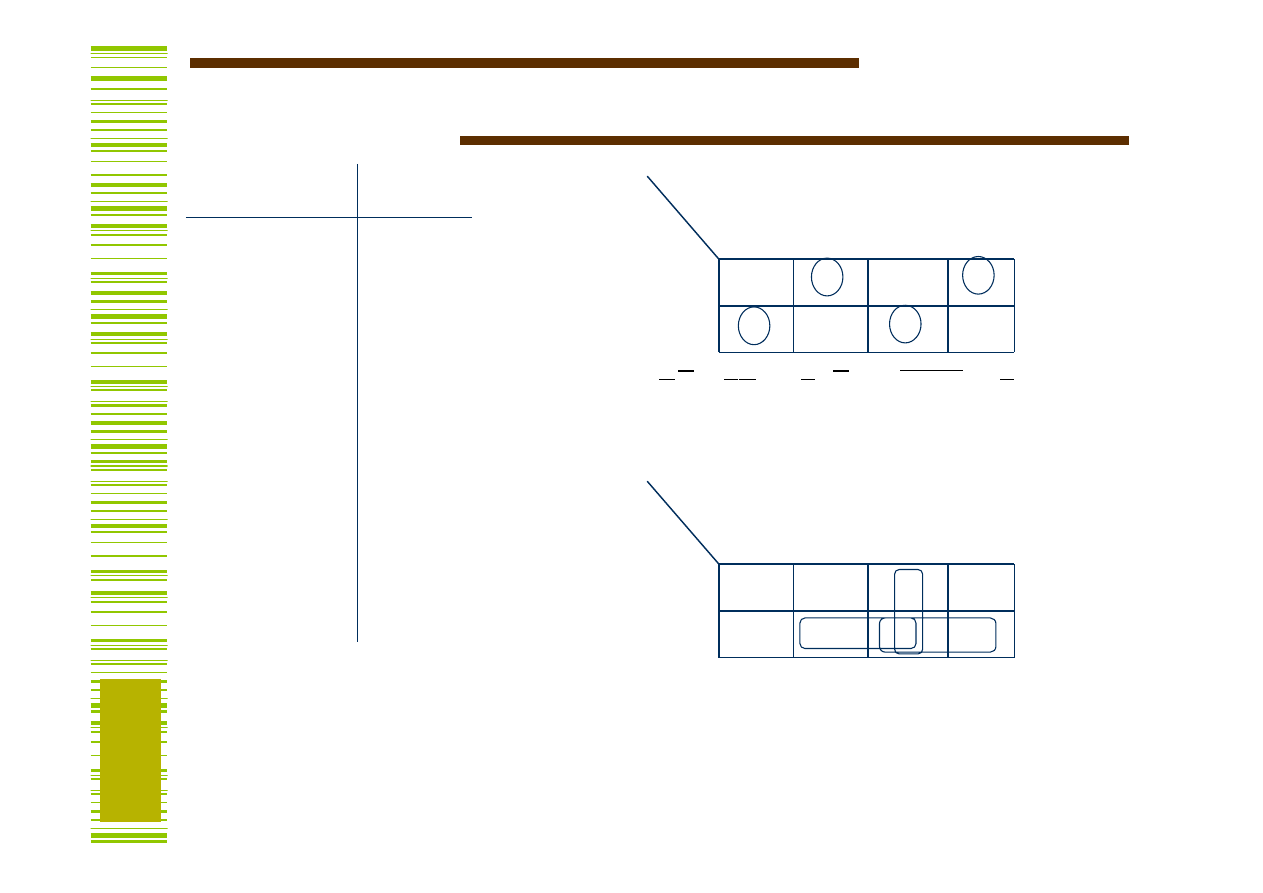
17

I

T

P

W

ZPT

Funkcje logiczne sumatora

1

1

1

0

1

0

1

0

0

0

10

11

01

00

ab

c

0

1

0

1

1

1

0

1

0

0

10

11

01

00

ab

c

( )

(

)

b

a

c

y

b

a

c

b

a

c

b

a

c

b

a

c

b

a

c

cab

y

⊕

⊕

=

⊕

∨

⊕

=

∨

∨

∨

=

)

(

)

(

b

a

c

ab

b

a

c

ab

o

c

⊕

∨

=

∨

∨

=

i

c

i

b

i

a

i

y

⊕

⊕

=

)

(

1

i

i

i

i

i

i

b

a

c

b

a

c

∨

∨

=

+

1

1

1

1

1

0

1

0

1

1

0

1

1

0

1

1

0

0

0

1

0

1

1

1

0

1

0

0

1

0

1

0

1

0

0

0

0

0

0

0

y

c

o

c

b

a

18

I

T

P

W

ZPT

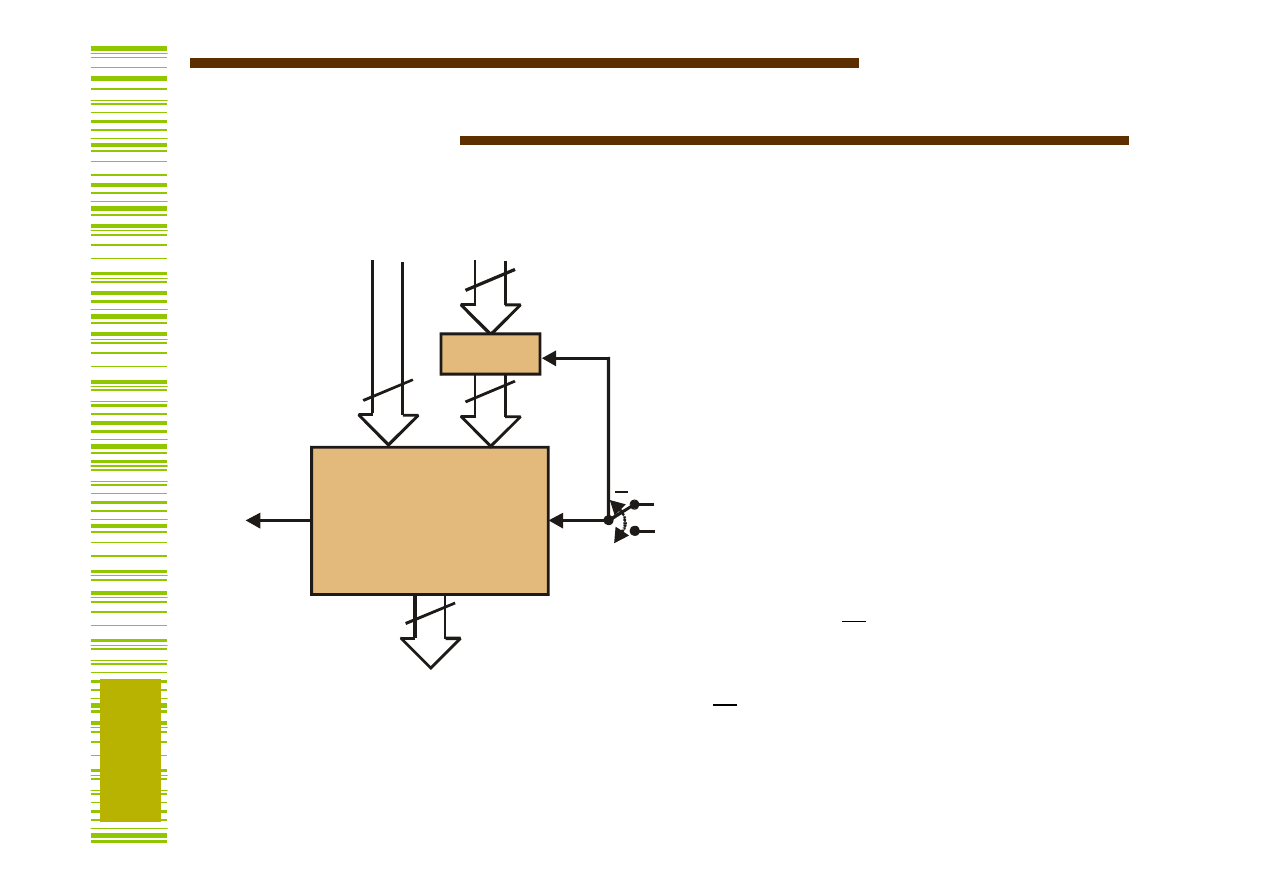
Sumator/układ odejmujący

Y

Σ

A

B

c

n

c

0

XOR

1

0

+

n

n

n

n

Y = A + B

⊕

c

0

+ c

0

;

c

0

∈

{0,1}

Dla c

0

= 0

Y = A + B

Dla c

0

= 1

Y = A + +

1 = A – B

+ 1= -B|

U2

B

B

19

I

T

P

W

ZPT

Naturalny kod binarny - NKB

A

NKB

= < a

n–1

,..., a

j

,..., a

0

>

∈

{0,1}

(

)

∑

−

=

=

=

1

0

2

n

j

j

j

NKB

D

a

L A

A

20

I

T

P

W

ZPT

Kod U2

A

U2

= <a

n–1

,..., a

j

,..., a

0

>, gdzie a

j

∈

{0,1}

<0101>│

U2

= +5│

D

; <1011>│

U2

= –5│

D

Zakres: –2

n–1

≤

A

D

≤

2

n–1

– 1

( )

∑

−

=

−

−

+

⋅

−

=

=

2

0

1

1

2

2

n

j

j

j

n

n

U2

D

a

a

L A

A

Bit a

n–1

można interpretować jako bit znaku. Jeśli a

n–1

= 0, to liczba

jest dodatnia; jeśli a

n–1

= 1 to liczba jest ujemna; pozostałe bity

stanowią uzupełnienie (różnicę) wartości liczby do najwyższej
potęgi liczby 2

21

I

T

P

W

ZPT

Sumator z przeniesieniami równoległymi

Look-ahead carry adder

W sumatorze z
przeniesieniami
równoległymi wszystkie
przeniesienia są wytwarzane
jednocześnie na podstawie
bitów sumowanych
składników.

c

i+1

= a

i

b

i

∨

c

i

(a

i

∨

b

i

)

G

i

= a

i

b

i

H

i

= a

i

∨

b

i

Wtedy:
y

i

= c

i

⊕

(H

i

)

y

i

= c

i

⊕

[(a

i

∨

b

i

) ( )] = a

i

⊕

b

i

⊕

c

i

c

i+1

= G

i

∨

H

i

c

i

i

G

i

i

b

a

∨

22

I

T

P

W

ZPT

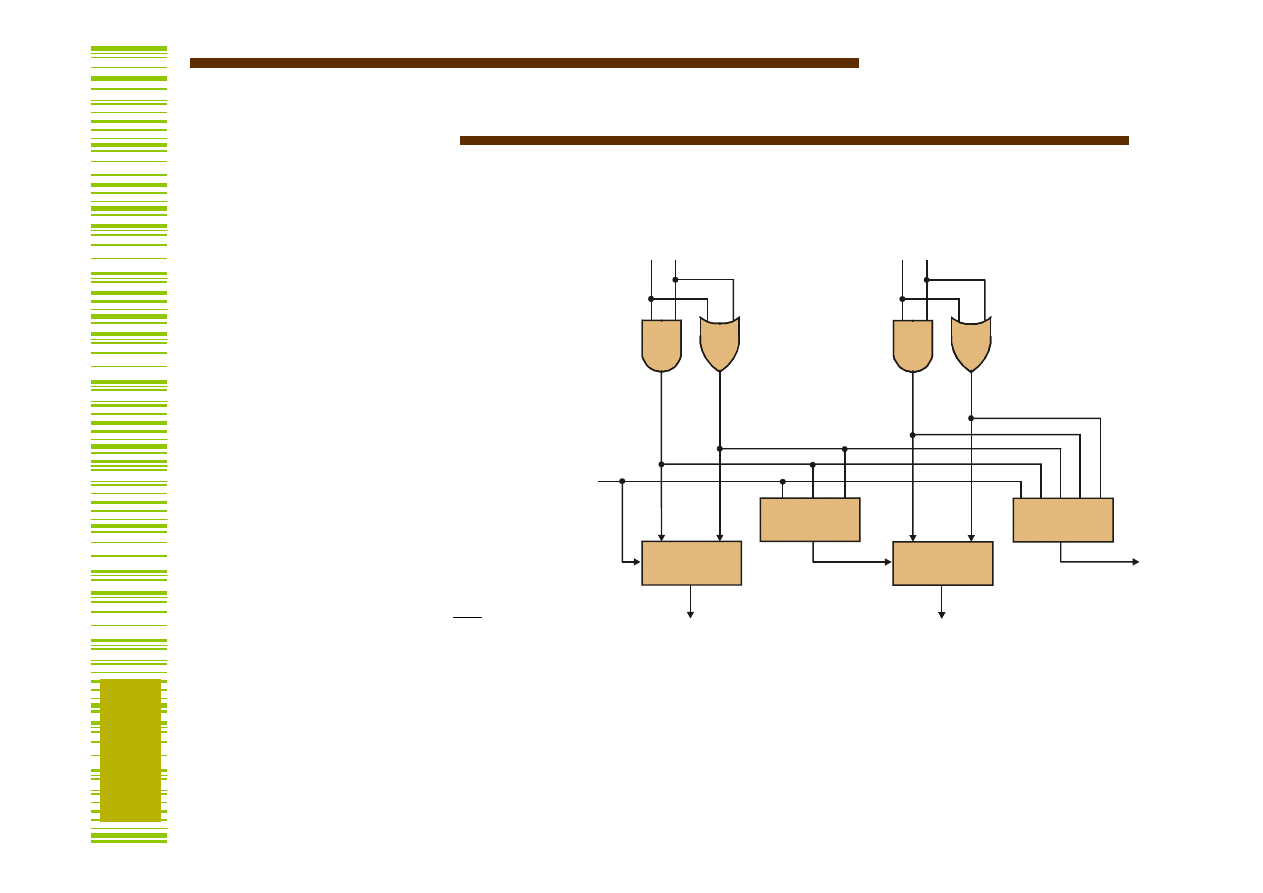
Sumator z przeniesieniami równoległymi c.d.

a0 b0

a1 b1

G0 H0

G1 H1

y0

y1

F

F

C

C

c0

c1

c2

c

i+1

= G

i

∨

H

i

c

i

c

0

c

1

= G

0

∨

H

0

c

0

c

2

= G

1

∨

H

1

c

1

=

= G

1

∨

H

1

(G

0

∨

H

0

c

0

) =

= G

1

∨

H

1

G

0

∨

H

1

H

0

c

0

(funkcja 5 arg.)

y

i

= c

i

⊕

(H

i

)

i

G

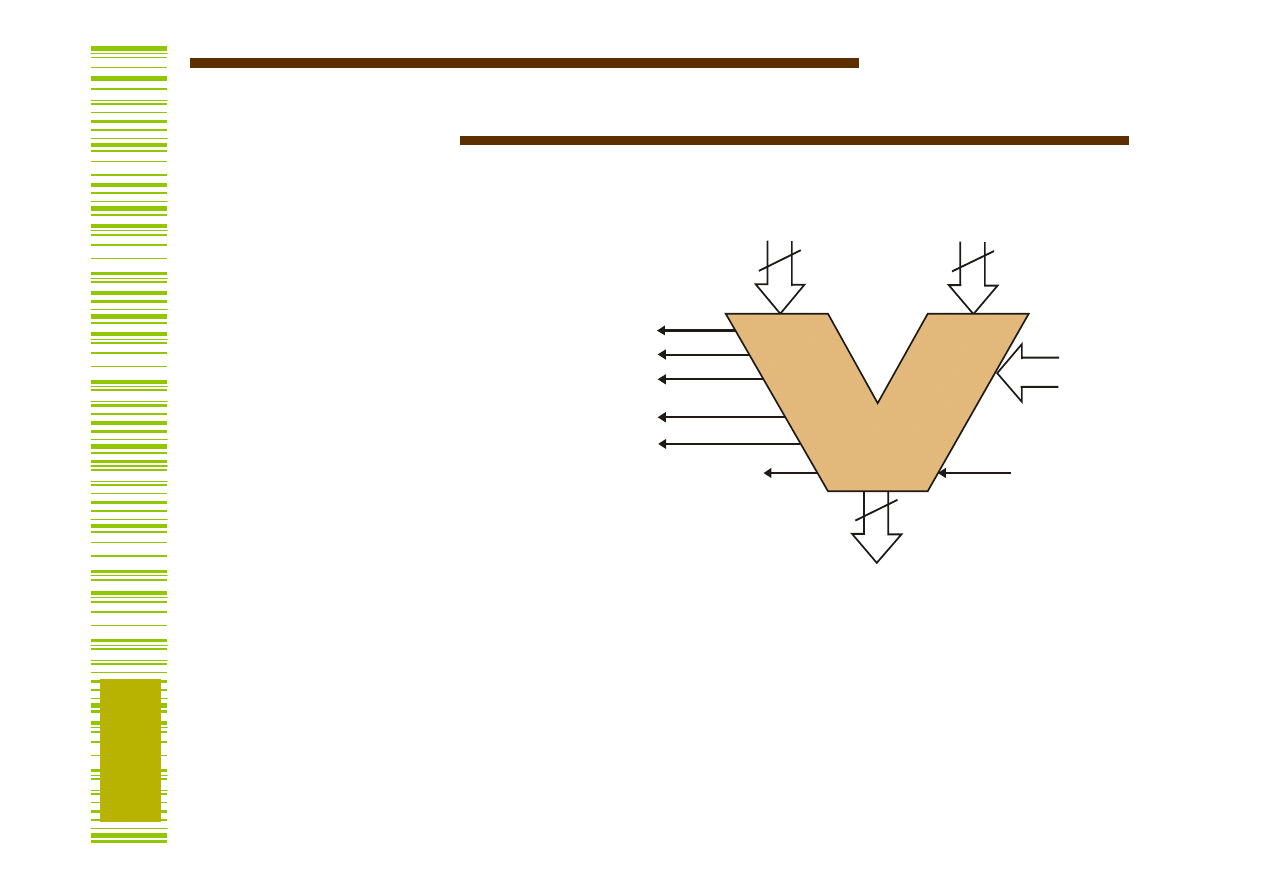
23

I

T

P

W

ZPT

Zastosowania

Jednostka arytmetyczno-logiczna

Y

B

A

n

n

n

Y

n-1

Z

OVR

P

G

c

n

c

0

S

ALU

Arytmometr (układ wykonawczy:
mikrokontrolera, procesora
sygnałowego)

Inne układy
arytmetyczne:

układy mnożące
układy kryptograficzne

...są budowane z sumatorów

24

I

T

P

W

ZPT

Komparator

A = a

3

a

2

a

1

a

0

B = b

3

b

2

b

1

b

0

A eq B = i

3

i

2

i

1

i

0

a

k

≠

b

k

Ÿ

A < B, gdy a

k

= 0, b

k

=1

A > B, gdy a

k

= 1, b

k

=0

A > B =

A < B =

k

k

k

b

a

i

⊕

=

0

0

1

2

3

1

1

2

3

2

2

3

3

3

b

a

i

i

i

b

a

i

i

b

a

i

b

a

+

+

+

B

A

B

A

gt

eq

+

25

I

T

P

W

ZPT

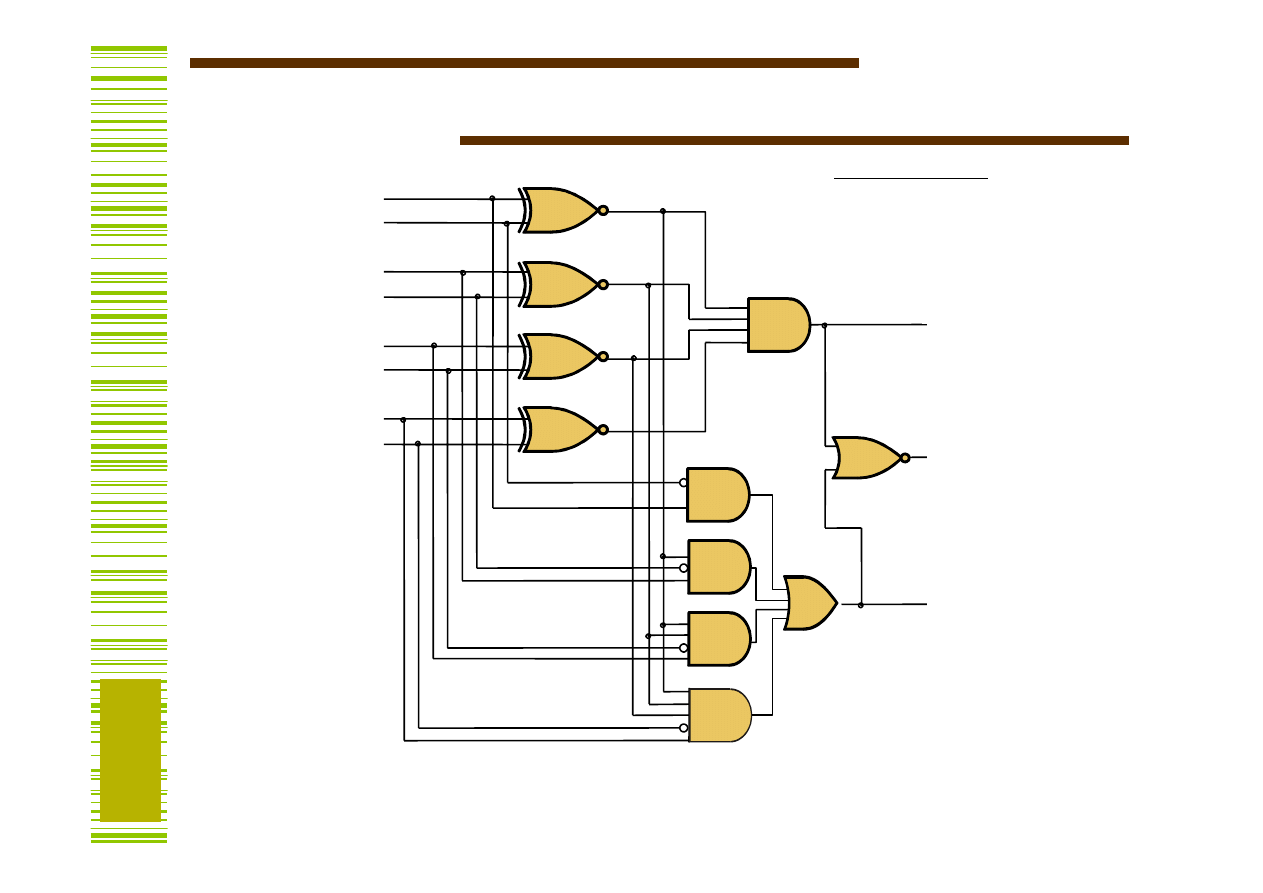
Komparator 4-bitowy

i

0

i

1

i

2

i

3

b

0

a

0

b

1

a

1

b

2

a

2

b

3

a

3

AeqB

AgtB

AltB

k

k

k

b

a

i

⊕

=

A = B

A < B

A > B