1

Automatyka i Robotyka

1. Otwarty i zamknięty układ sterowania

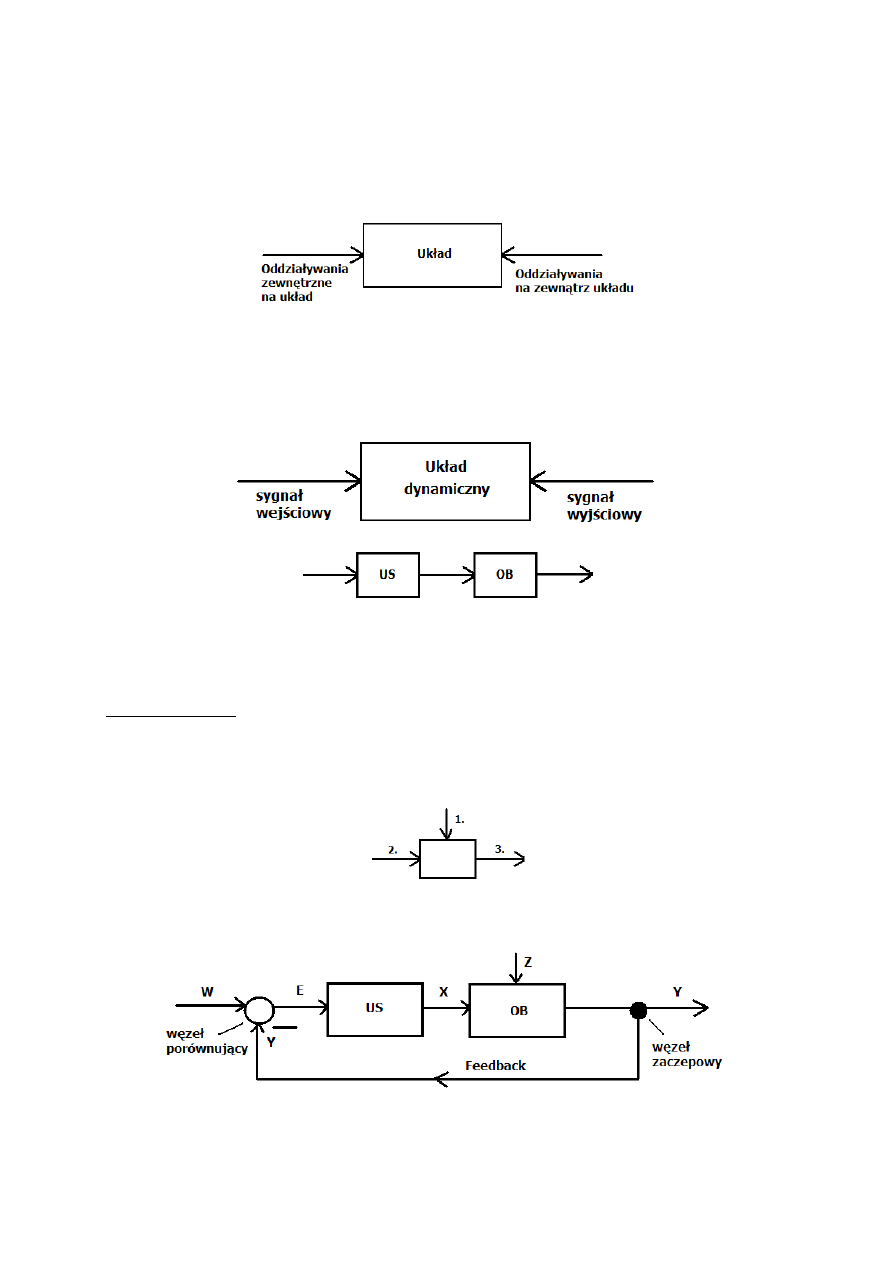
Układ – zespół elementów, w których występują oddziaływania wewnętrzne

Sterowanie – oddziaływanie na układ z założonym celem (działanie ukierunkowane na osiągnięcie

danego celu)

Układ otwarty – urządzenie sterujące wysyłające sygnał wejściowy nie wie nic obiekcie reagującym

sygnałem wyjściowym, brak kontroli reakcji na wyjściu, nie ma sprzężenia zwrotnego.

US – urządzenie sterujące i generujące sterowanie

OB – obiekt sterowania, proces lub urządzenie, w którym odbywa się ten proces lub które podlega
sterowaniu

Sygnały wejściowe:

1.

Zakłócenie – nieprzewidywalne i niekorzystne

2.

Sygnał sterujący – wielkość wymuszająca konkretną reakcję

3.

Sygnał wyjściowy – mówi o reakcji układu na sterowanie i zakłócenie

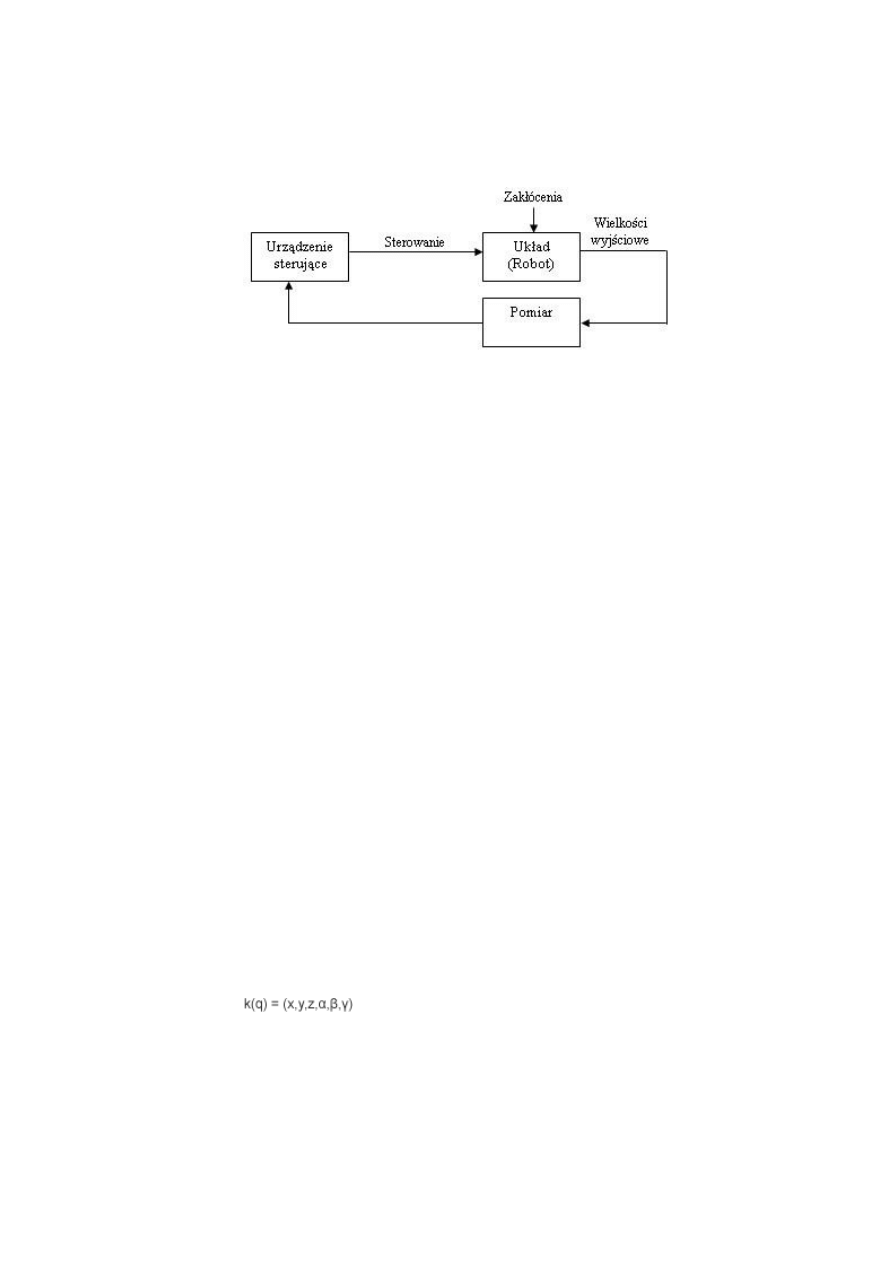
Układ zamknięty – sygnał wyjściowy wychodzący z obiektu wraca do urządzenia sterującego,

kontrola reakcji na wyjściu, czyli pętla sprzężenia zwrotnego.

W – wymuszenie

E – błąd, uchyb regulacji

X – sygnał sterujący

Y – wartość regulowana

Z – zakłócenia

2

Urządzenie sterujące porównuje sygnał zadany (wymuszenie) i wygnał wyjściowy (ich wartości) i

na podstawie różnicy tych wielkości generuje sygnał sterujący obiektem. Celem sterowania w układzie

zamkniętym jest doprowadzenie wielkości wyjściowej do wielkości zadanej.

Układ zamknięty sterowania to układ regulacji automatycznej (regulacja jest z kontrolą).

Sprzężenia zwrotne polega na zawracaniu sygnału wyjściowego na wejście. Sterowanie w układzie

zamkniętym ze sprzężeniem zwrotnym ujemnym nazywamy regulacją.

Sprzężenie zwrotne:



Ujemne

Y

W

E





Stanowi fundamentalny mechanizm samoregulacyjny. Z cybernetycznego punktu widzenia ma ono za

zadanie utrzymanie wartości jakiegoś parametru na zadanym poziomie. Zachodzi ono wtedy, gdy

jakiekolwiek zaburzenia powodujące odchylenie wartości parametru od zadanej wartości w

którąkolwiek stronę indukują działania prowadzące do zmiany wartości parametru w stronę przeciwną

(stąd nazwa "ujemne"), a więc do niwelacji (kompensacji) efektu tego odchylenia. Mówiąc obrazowo:

wartość parametru sprzężonego ujemnie zachowuje się jak niewielka kulka na dnie półkulistego

zagłębienia: każde wytrącenie jej z równowagi powoduje powtórne staczanie się w kierunku
najniższego punktu, pośrodku zagłębienia. W przypadku sprzężenia zwrotnego ujemnego wartość

parametru oscyluje, więc wokół wartości zadanej.

Sprzężenia zwrotne ujemne występują powszechnie w organizmach żywych i urządzeniach

technicznych, jako mechanizmy samoregulacji.



Dodatnie

Y

W

E





Sprzężenie zwrotne dodatnie polega na tym, że w sytuacji zakłócenia jakiegoś parametru w układzie,

układ ten dąży do zmiany wartości parametru w kierunku zgodnym (stąd - "dodatnie") z kierunkiem,

w którym nastąpiło odchylenie od "zadanej" wartości. Sprzężenie zwrotne dodatnie powoduje zatem

narastanie odchylenia. Mówiąc obrazowo: wartość parametru sprzężonego dodatnio zachowuje się jak

niewielka kulka na szczycie półkulistego wzniesienia: każde wytącenie jej z równowagi powoduje coraz

szybsze staczanie się w kierunku, w którym nastąpiło wytrącenie, aż do wypadnięcia kulki poza układ

(o ile nie zadziała odrębny bodziec hamujący). W sprzężeniu zwrotnym dodatnim wartość parametru

odchyla się więc od wartości "zadanej" tym szybciej, im dalej już się od niej znajduje.

Sprzężenie zwrotne dodatnie stosuje się w:

o Generatorze drgań

o Detektorze reakcyjnym

o Detektorze superreakcyjnym

o Mnożniku dobroci

o Przerzutniku

3

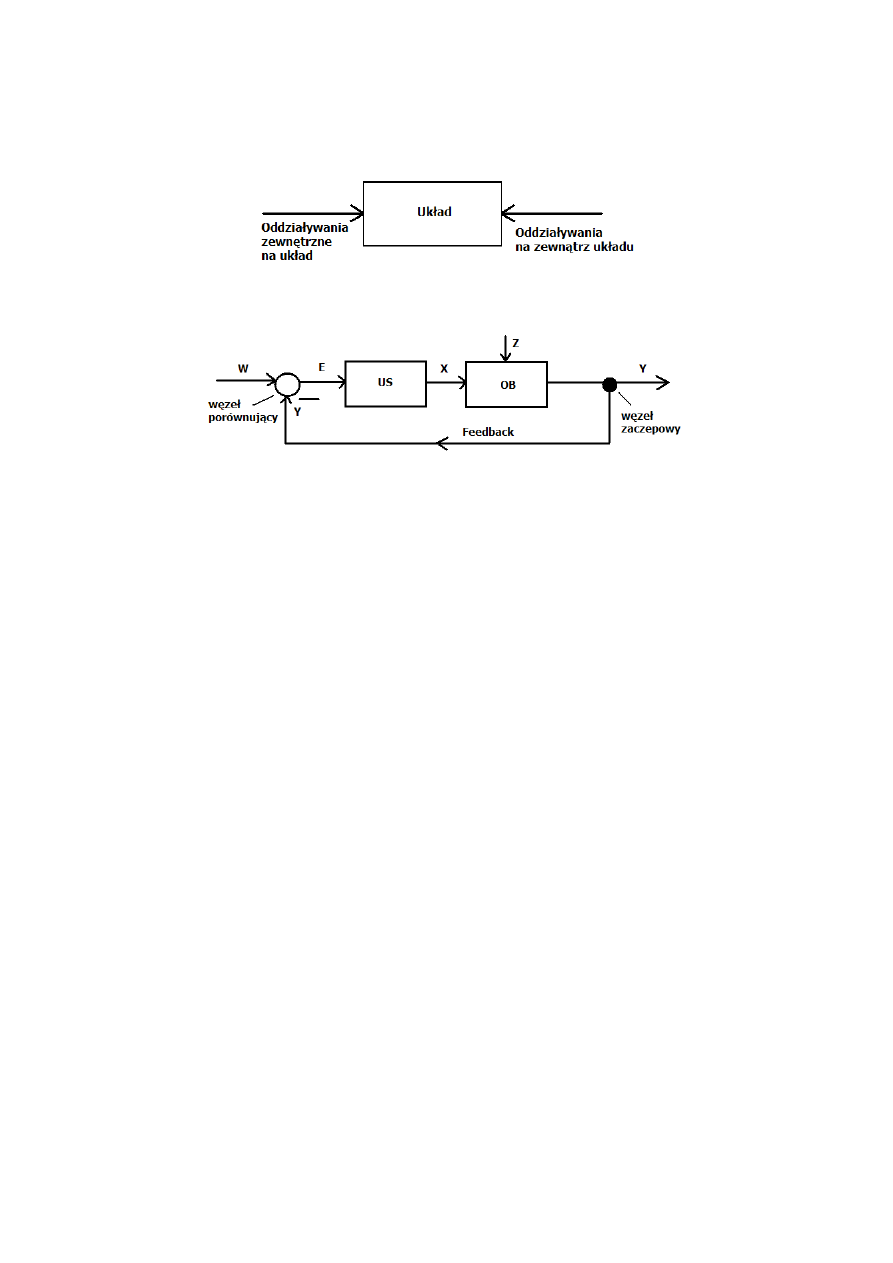
2. Podstawowe elementy układu automatycznego sterowania

Układ – zespół elementów, w których występują oddziaływania wewnętrzne

Sterowanie – oddziaływanie na układ z założonym celem (działanie ukierunkowane na osiągnięcie

danego celu)

US – urządzenie sterujące i generujące sterowanie

OB – obiekt sterowania, proces lub urządzenie, w którym odbywa się ten proces lub które podlega

sterowaniu

W – wymuszenie

E – błąd, uchyb regulacji

X – sygnał sterujący

Y – wartość regulowana

Z – zakłócenia

4

3. Metoda klasyczna i operatorowa opisu dynamiki układu

Układ Dynamiczny: zmienia swój stan.

jw

S







S – operator Laplace’a

Rozwiązanie równania różniczkowego polega na znalezieniu funkcji odpowiadającej danemu

równaniu. Rozwiązaniem równania algebraicznego są konkretne liczby. Rachunek operatorowy opiera

się na tym, że zamiast różniczkowania wprowadzamy mnożenie przez operator „s”, a zamiast

całkowania „1/s”

Metoda operatorowa – można ja stosować tylko do układów liniowych tj. zapisanymi liniowymi

równaniami różniczkowymi. Równanie

 

 

t

x

k

t

y

dt

dy

T







jest równaniem nieliniowym, ale

możemy go zlinearyzować. Wówczas otrzymamy rozwiązania przybliżone do tych z metody

operatorowej.

Równanie różniczkujące:

 

 

t

x

k

t

y

dt

dy

T







Równanie operatorowe:

   

 

s

X

k

s

Y

s

sY

T









Przejście z Y(s) do y(t) za pomocą:

 

 













0

dt

e

t

f

s

F

t

s

F(s) jest funkcją Laplace’a a f(t) jest funkcją oryginału.

Transformacja odwrotna:

 

 





 















jw

c

jw

c

st

ds

e

s

F

j

s

F

s

F





2

1

1



- Przekształcenie Laplace’a

1





- Odwrotne przekształcenie Laplace’a

Np.

 

 

 

s

A

s

X

t

A

t

x

1

1









lub

 

 

   

1

1















Ts

s

A

k

s

Y

Ts

s

X

k

s

Y

5

4. Transmitancja operatorowa

– definicja i sposób obliczania

Jest to stosunek sygnału wyjściowego do wejściowego w postaci operatorowej. Pokazuje, w

jaki sposób sygnał wejściowy pokazuje się na wyjściu:

 

 

 

s

X

s

Y

s

G



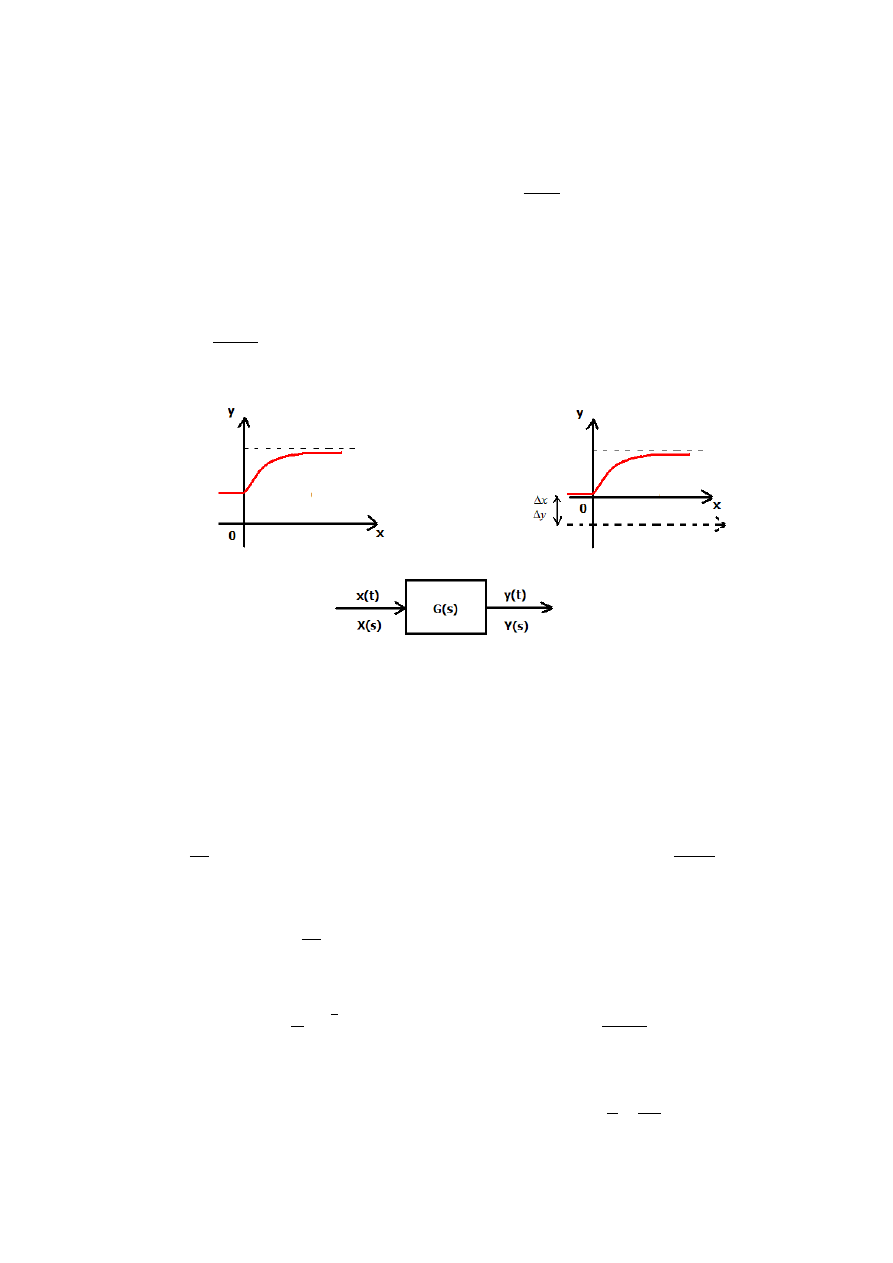
Definiując transmitancję operatorową zakładamy zerowe warunki początkowe, tzn. dla

ujemnych czasów wszystkie funkcje są równe zero. Jeżeli tak nie jest (rys.1) to przesuwamy osie

x



i

y



tak, aby warunki początkowe były zerowe (rys.2).wtedy transmitancja operatorowa przybiera

postać:

 

 

 

s

X

s

Y

s

G







rys.1

rys.2

 

   

 

 

 

s

Y

t

y

s

X

s

G

s

Y

1













Podział transmitancji:

1. Element Proporcjonalny – wyidealizowany

 

 

 

 

 

k

s

G

s

X

k

s

Y

t

x

k

t

y















2. Element Inercyjny I rzędu – rzeczywisty

 

 

   

 

 

1























Ts

k

s

G

s

X

k

s

Y

s

Y

Ts

t

x

k

t

y

dt

dy

T

3. Element Różniczkujący – wyidealizowany

 

 

 

 

s

k

s

G

s

X

s

k

s

Y

dt

dx

k

t

y

















4. Element Różniczkujący – rzeczywisty

 

 

 

sT

s

k

s

G

s

Y

e

T

k

t

y

T

t



















1





5. Element Całkujący – idealny

 

 

 

 

s

T

s

k

s

G

s

Y

d

x

k

t

y

i

1

0

























6

6. Element Całkujący – rzeczywisty

 

 

 





sT

s

k

s

G

s

Y

e

T

k

T

k

t

k

t

y

T

t





























1





7. Element Opóźniający

 





 

 

 

0

0

0

T

s

T

s

e

k

s

G

s

X

e

k

s

Y

T

t

x

k

t

y





























8. Element Oscylacyjny

 





 

2

0

0

2

2

0

2

0

2

2

1

sin

1

1

0

























































s

s

k

s

G

t

e

k

t

y

t

k

– współczynnik wzmożenia

i

T

– czas zdwojenia

0

T

– czas opóźnienia

T

- stała czasowa



- względny współczynnik tłumienia (0<



<1)

0



- pulsacja oscylacji własnych

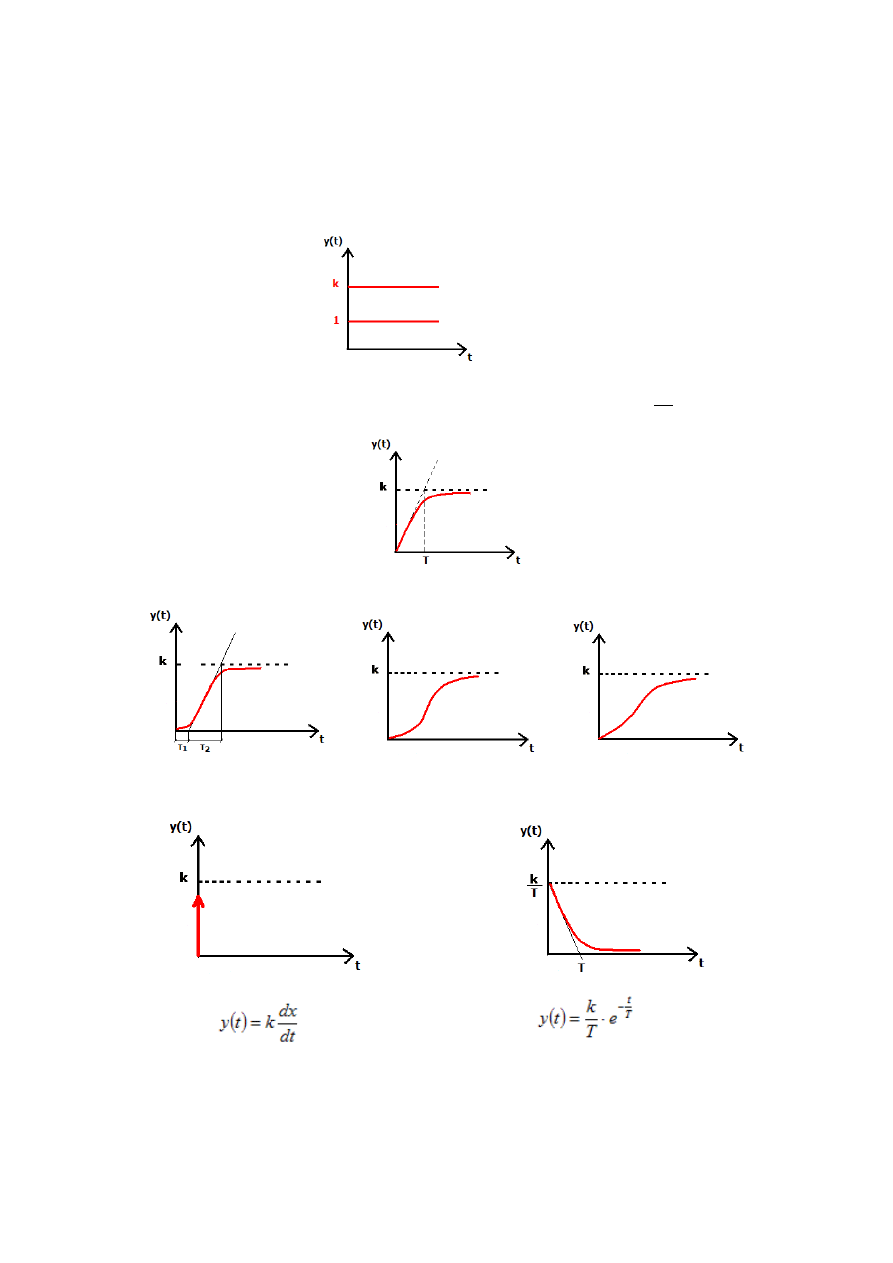
7

5. Charakterystyki czasowe układów dynamicznych

Charakterystyka dynamiczna (czasowa) – funkcja opisująca działanie obiektu w stanie

nieustalonym.

1. Człon proporcjonalny – charakterystyka czasowa skokowa

 

 

t

x

k

t

y





 



P

 



Q

2. Człony inercyjny I rzędu – charakterystyka czasowa skokowa

 

 

t

x

k

t

y

dt

dy

T







3. Człony inercyjne II i wyższych rzędów – charakterystyka czasowa skokowa

II rzędu

III rzędu

IV rzędu

4. Człon różniczkujący – charakterystyka czasowa impulsowa

Idealny:

Rzeczywisty:

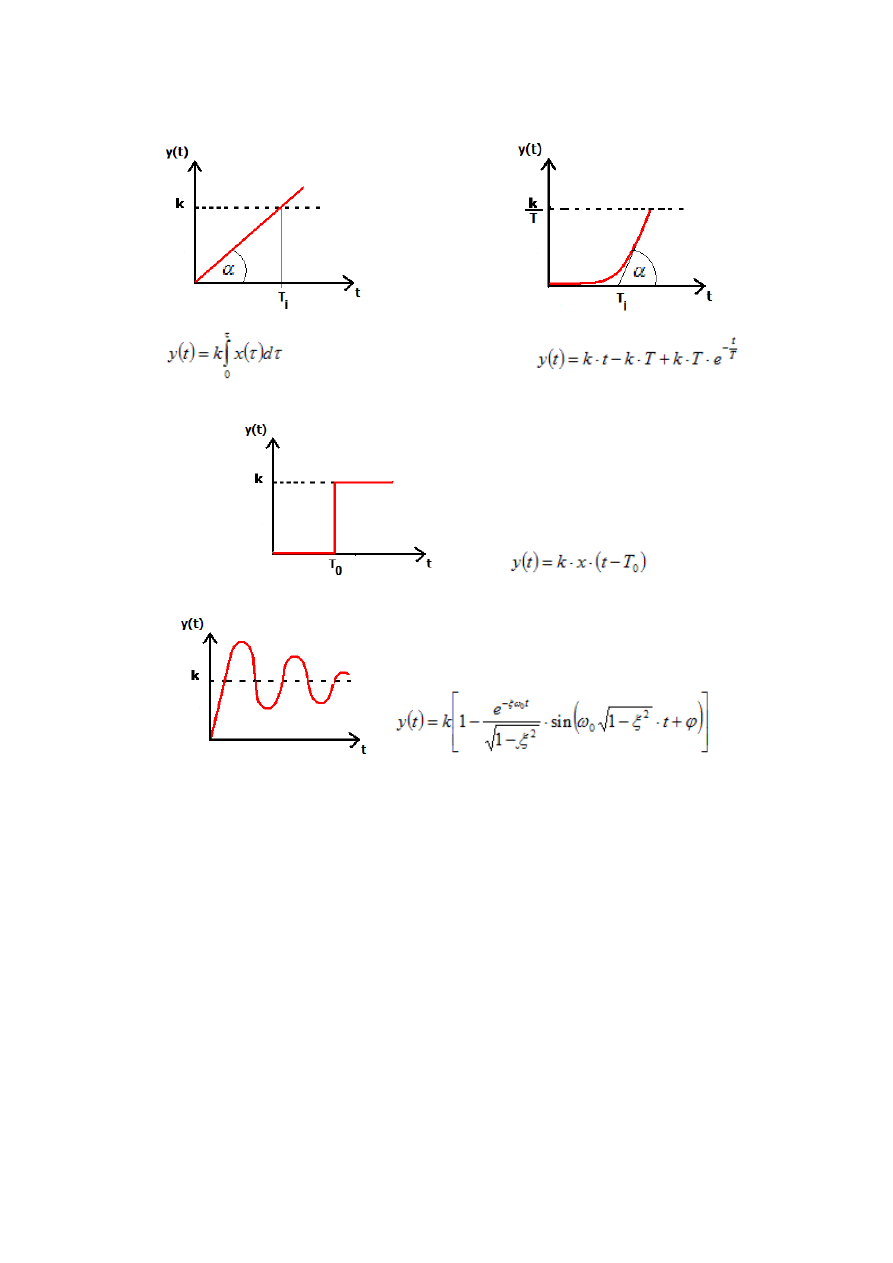
8

5. Człon całkujący – charakterystyka czasowa skokowa



tg

k



Idealny:

Rzeczywisty:

6. Człon opóźniający – charakterystyka czasowa skokowa

7. Człon oscylacyjny – charakterystyka czasowa skokowa

Charakterystyki czasowe:



Skokowe:

odpowiedź na sygnał skokowy (jednostkowy)



Impulsowe:

odpowiedź na impuls (delta Diraca)

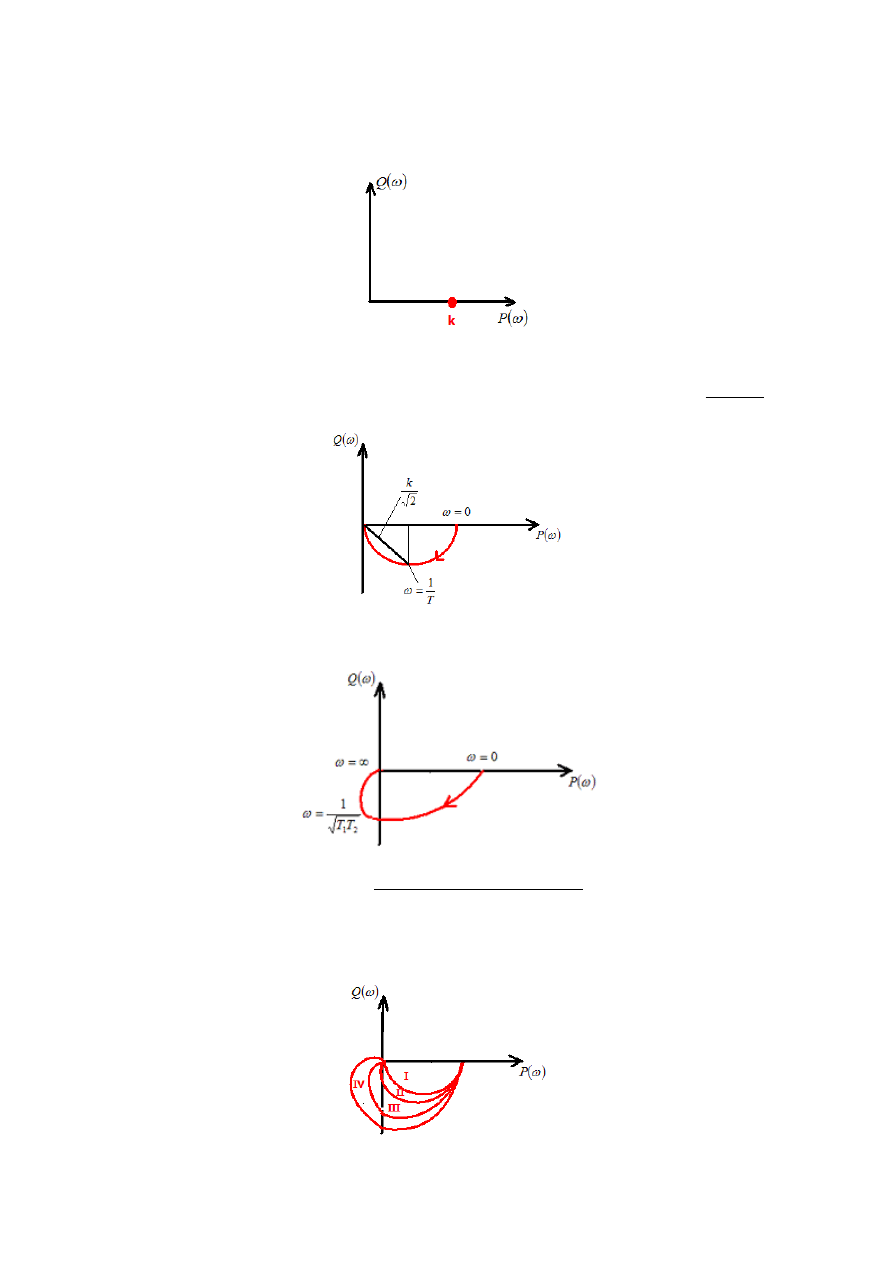
9

6. Charakterystyki częstotliwościowe

1. Człon proporcjonalny – nie zależy od częstotliwości – charakterystyka amplitudowo-fazowa:

 

 

 







jQ

P

j

G





 

k

j

G





2. Człon inercyjny I rzędu – charakterystyka amplitudowo-fazowa:

 

T

j

k

j

G









1

T – stała czasowa inercji; czas, po którym odpowiedź uzyska 60% wartości ustalonej

3. Człon inercyjny II rzędu – charakterystyka amplitudowo-fazowa:

 









2

2

2

1

2

2

2

2

2

1

2

2

1

2

1

2

1

1

T

T

T

T

T

T

jk

T

T

k

j

G

























T

1

i T

2

są to stałe czasowe odpowiedzialne za I i II opóźnienie.

4. Człony inercyjne wyższych rzędów:

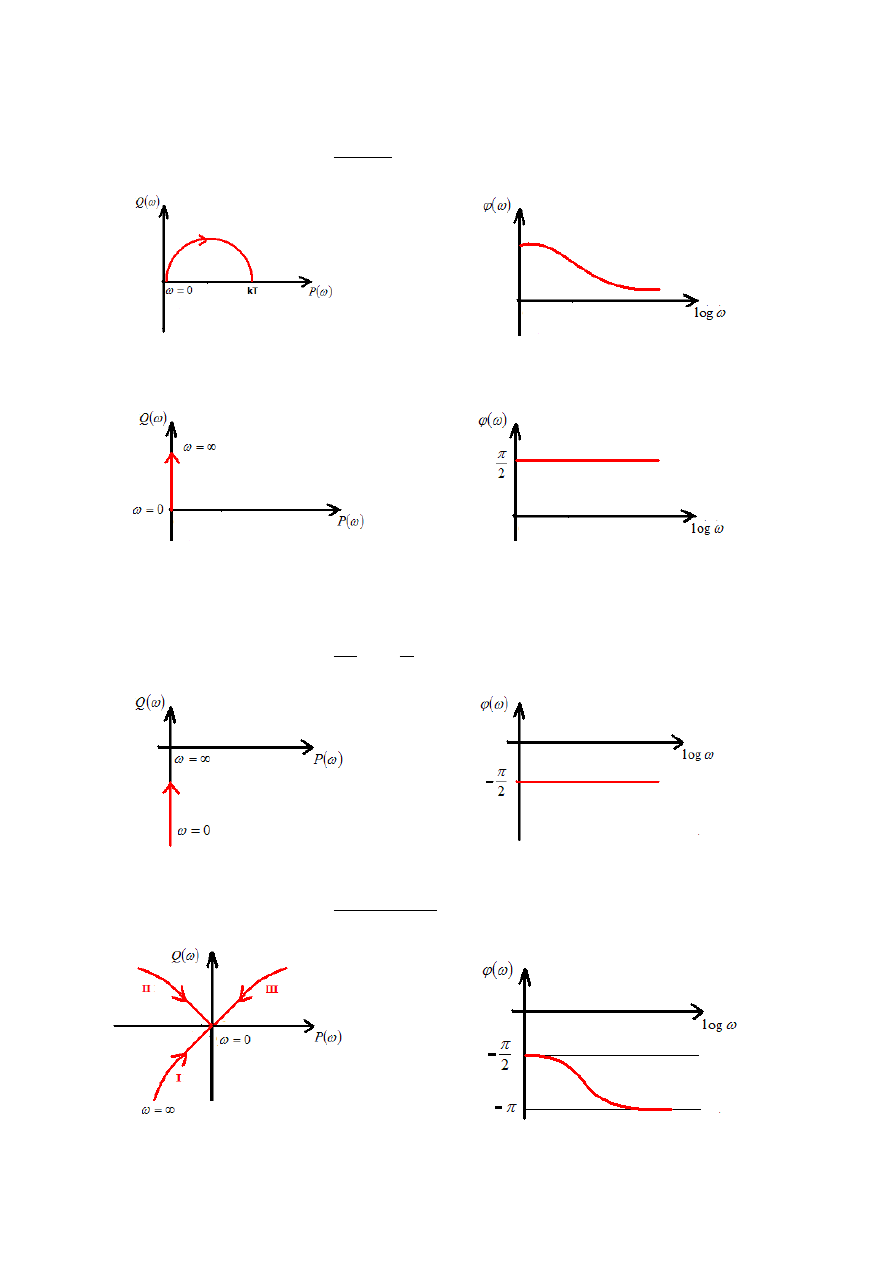
10

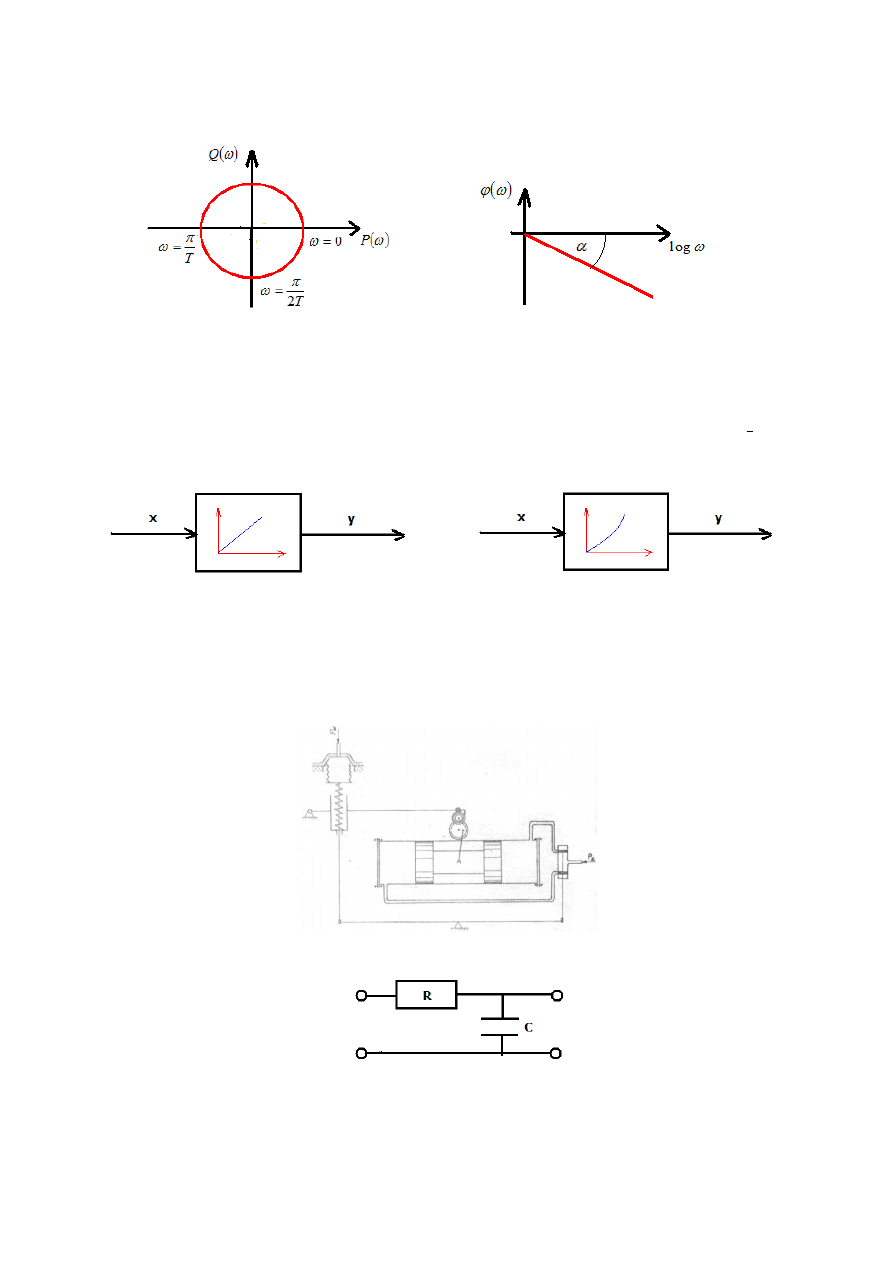
5. Człon różniczkujący:

Rzeczywisty

:

 

T

j

kj

j

G











1

Charakterystyka amplitudowo – fazowa

Charakterystyka fazowo – częstotliwościowa

Idealny

:

 





kj

j

G



 

 











j

G

arg



Charakterystyka amplitudowo – fazowa

Charakterystyka fazowo – częstotliwościowa

6. Człon całkujący:

Idealny

:

 







k

j

j

k

j

G







 

 

0

0

























Q

Q

Charakterystyka amplitudowo – fazowa

Charakterystyka fazowo – częstotliwościowa

Rzeczywisty

:

 

 





1

2

2

2









T

jk

T

k

j

G











Charakterystyka amplitudowo – fazowa

Charakterystyka fazowo – częstotliwościowa

11

7. Człon Opóźniający:

 

T

j

e

j

G









T

tg







Charakterystyka amplitudowo – fazowa

Charakterystyka fazowo – częstotliwościowa

7. Człon całkujący

Idealny:

 

 





t

d

x

k

t

y

0





Rzeczywisty:

 



t

e

kT

kT

kt

t

y











Sygnał wyjściowy nie zmienia się jedynie przy zerowej wartości sygnału wejściowego

Przykład:

1. Siłownik Tłokowy: Przykład pneumatycznego siłownika tłokowego, w którym sygnał sterujący

p

w

zmienia się w zakresie normalnym, zaś wartość ciśnienia zasilającego p

z

może przyjmować

wartości od 0,6 - 1,0 MN/m

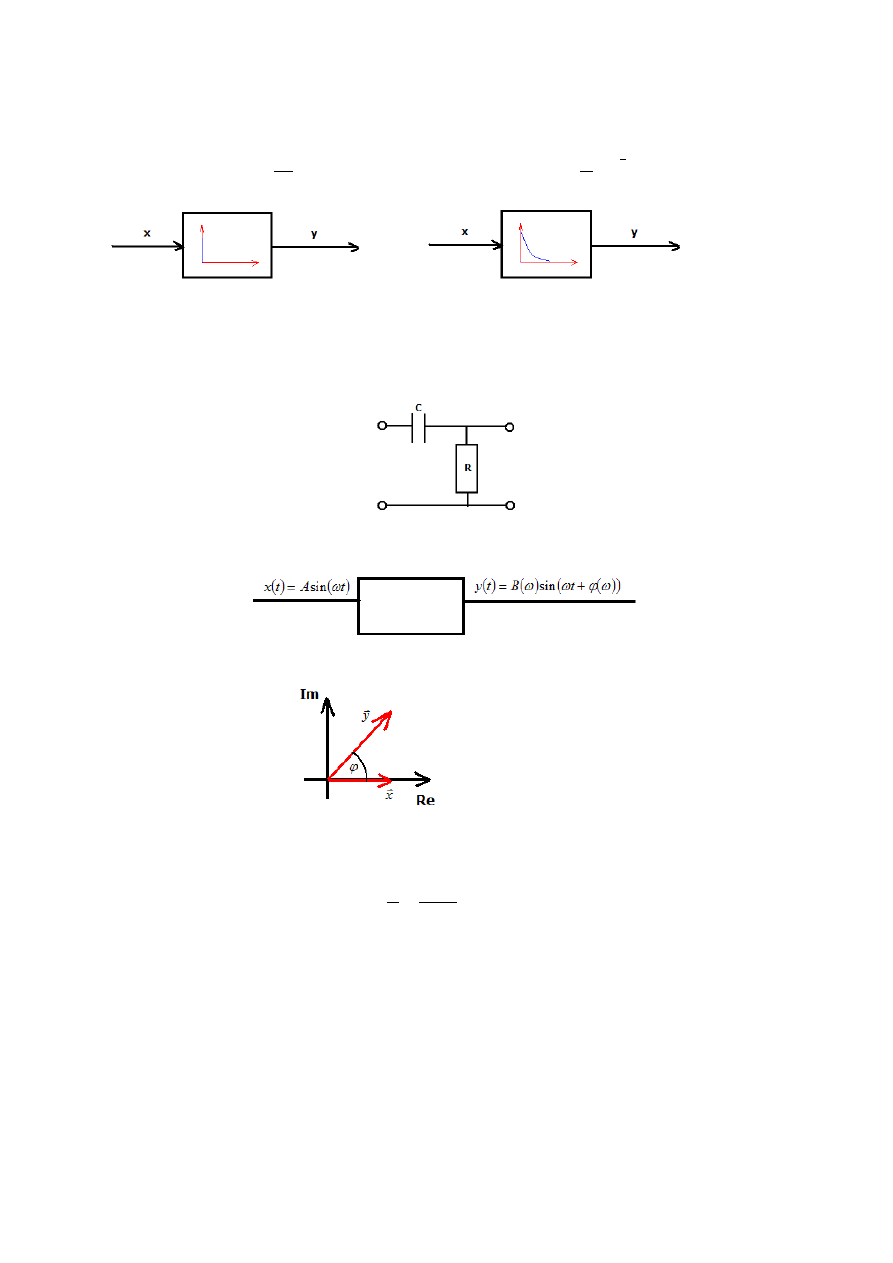
2. Urządzenie elektryczne całkujące:

12

8. Człon różniczkujący

Idealny:

 

dt

dx

k

t

y



Rzeczywisty:

 



t

e

T

k

t

y







Przesunięcie wyjściowe jest proporcjonalne do prędkości przesunięć wejściowych (reaguje na zmianę

sygnału, wykazuje działanie wyprzedzające)

Przykład:

Urządzenie elektryczne różniczkujące:

9. Transmitancja widmowa i jej sens fizyczny

Amplituda A i kąt przesunięcia fazowego



na wyjściu zależą od pulsacji



 

 

 

 

















t

j

t

j

e

B

t

y

Ae

t

x





Wektor przejściowy

y



opóźniony jest w fazie o kąt



w stosunku do

x



.

Transmitancja widmowa:

 

 

 

 

 















j

j

e

K

e

A

B

x

y

j

G











 



K

- wzmocnienie amplitudy (długość wektora amplitudy)

 





- przesunięcie fazowe

Sens fizyczny:



Dla dużych pulsacji mamy małe wzmocnienie i duże przesunięcie fazowe



Dla małych pulsacji wzmocnienie spada

Jeżeli na wejściu mamy sinusoidę, to na wyjściu też, ale będzie ona przesunięta w fazie

13

10. Wyjaśnić pojęcia

Układ stabilny:

Stabilność układu automatycznej regulacji jest to niezbędny warunek pracy układu automatycznej
regulacji mówiący o tym, że układ po wyprowadzeniu go ze stanu równowagi sam powraca do tego

stanu. Ponieważ

stan równowagi

może być różnie interpretowany stosuje się także definicję stabilności

wg. Laplace'a która mówi, że układ liniowy jest stabilny, jeżeli jego odpowiedź na wymuszenie

(zakłócenie) o ograniczonej wartości jest ograniczona.

Klasyczne kryteria stabilności układów ciągłych



Kryterium biegunów

– Wszystkie pierwiastki równania charakterystycznego układu

zamkniętego powinny być ujemne, czyli znajdować się w lewej półpłaszczyźnie płaszczyzny

zmiennej zespolonej

s

.



Kryterium odpowiedzi skokowej

– Układ zamknięty w odpowiedzi na skok jednostkowy

powinien osiągać stan ustalony w czasie dążącym do nieskończoności.



Kryterium Hurwitza

– Pierwiastki równania charakterystycznego układu zamkniętego będą

znajdować się w lewej półpłaszczyźnie płaszczyzny zmiennej zespolonej

s

(układ będzie

stabilny), jeśli spełnione zostaną 2 warunki:

o Wszystkie współczynniki równania charakterystycznego będą istnieć i mieć ten sam

znak,

o Wszystkie podwyznaczniki wyznacznika głównego (posiadającego

n

wierszy i

n

kolumn) muszą być większe od 0.



Kryterium Michajłowa

– Równanie charakterystyczne układu zamkniętego ma wszystkie

pierwiastki w lewej półpłaszczyźnie płaszczyzny zmiennej zespolonej

s

, jeśli przyrost

argumentu równania charakterystycznego w postaci widmowej

 



j

G

przy zmianie pulsacji

ω od 0 do



wynosi

2



n

, gdzie n jest stopniem równania.



Kryterium Nyquista

– Układ zamknięty jest stabilny, jeżeli charakterystyka amplitudowo-

fazowa układu otwartego nie obejmuje punktu (-1, j0).



Kryterium logarytmiczne Nyquista

– Układ zamknięty jest stabilny, jeżeli logarytmiczna

charakterystyka amplitudowa układu otwartego posiada wartość ujemną dla pulsacji

odpowiadającej przesunięciu fazowemu -π.

Układ niestabilny: wytrącony ze stanu początkowego już do niego nie wraca, ale oddala się od

niego coraz bardziej – np. śnieg na stoku i lawina.

Układ statyczny: układ regulacji (np. z regulatorem P lub PD), w którym uchyb ustalony jest

proporcjonalny do wartości wymuszenia w postaci skokowej funkcji Heaviside'a.

14

Funkcja skokowa Heaviside'a

(skok jednostkowy), jest funkcją nieciągłą, która przyjmuje wartość 0 dla

ujemnych argumentów i wartość 1 w

pozostałych przypadkach:

Często stosowanym symbolem, dla funkcji skokowej Heaviside'a jest

 

t

1

,

t

oznacza tu zazwyczaj

czas; jednak przy zastosowaniach z dziedziny mechaniki np. analizy statycznych obciążeń belek

argumentem tej funkcji jest nie czas, tylko długość belki. Funkcja ta jest używana w przetwarzaniu

sygnałów do reprezentowania sygnału włączającego się w danej chwili czasu, a także w mechanice do

reprezentowania obciążeń belek rozłożonych na pewnej części ich długości

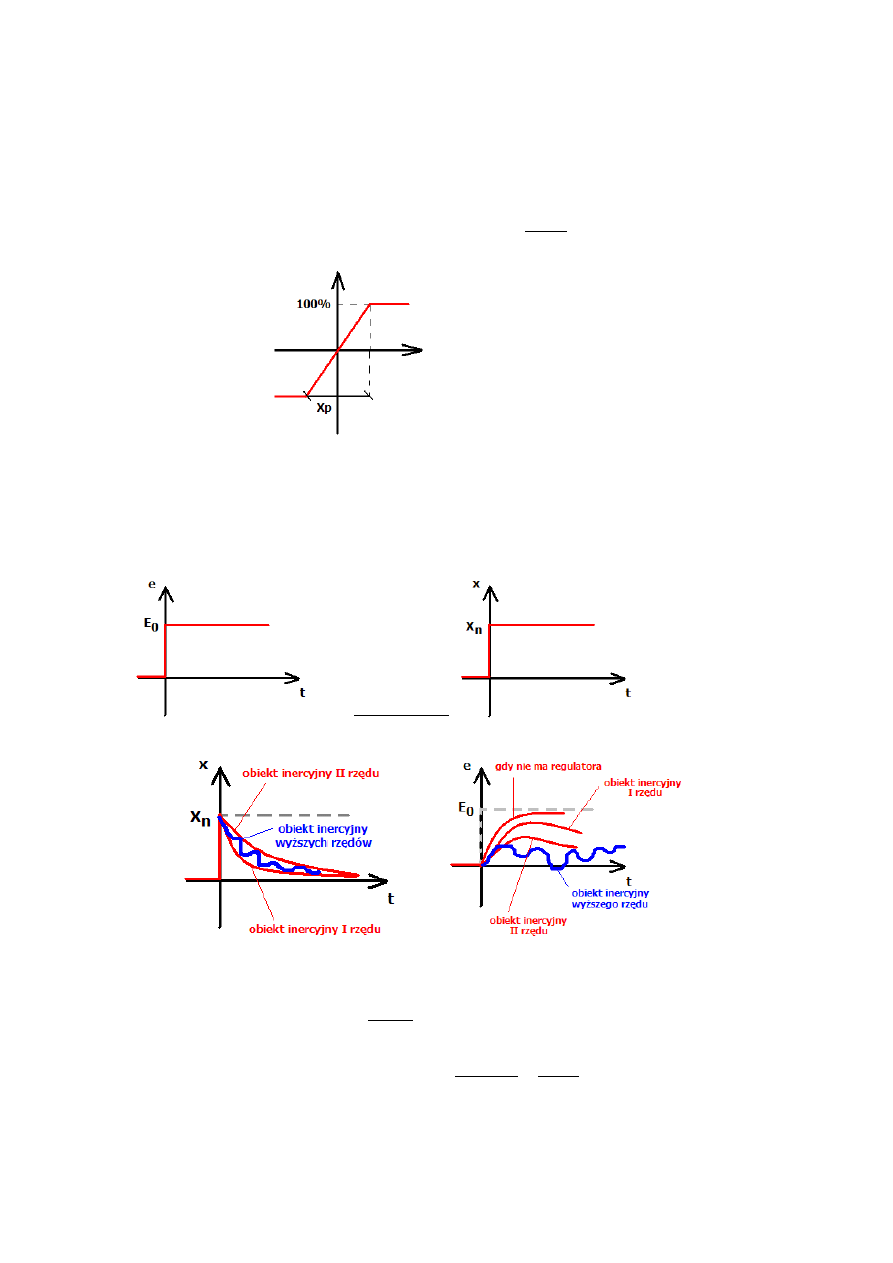
Układ astatyczny: układ regulacji (np. z regulatorem PI lub PID), w którym uchyb ustalony jest

równy 0, niezależnie od wartości wymuszenia w postaci skokowej funkcji Heaviside'a. W układach

astatycznych występują uchyby ustalone przy pobudzeniach w postaci funkcji rosnących liniowo i

parabolicznie.

15

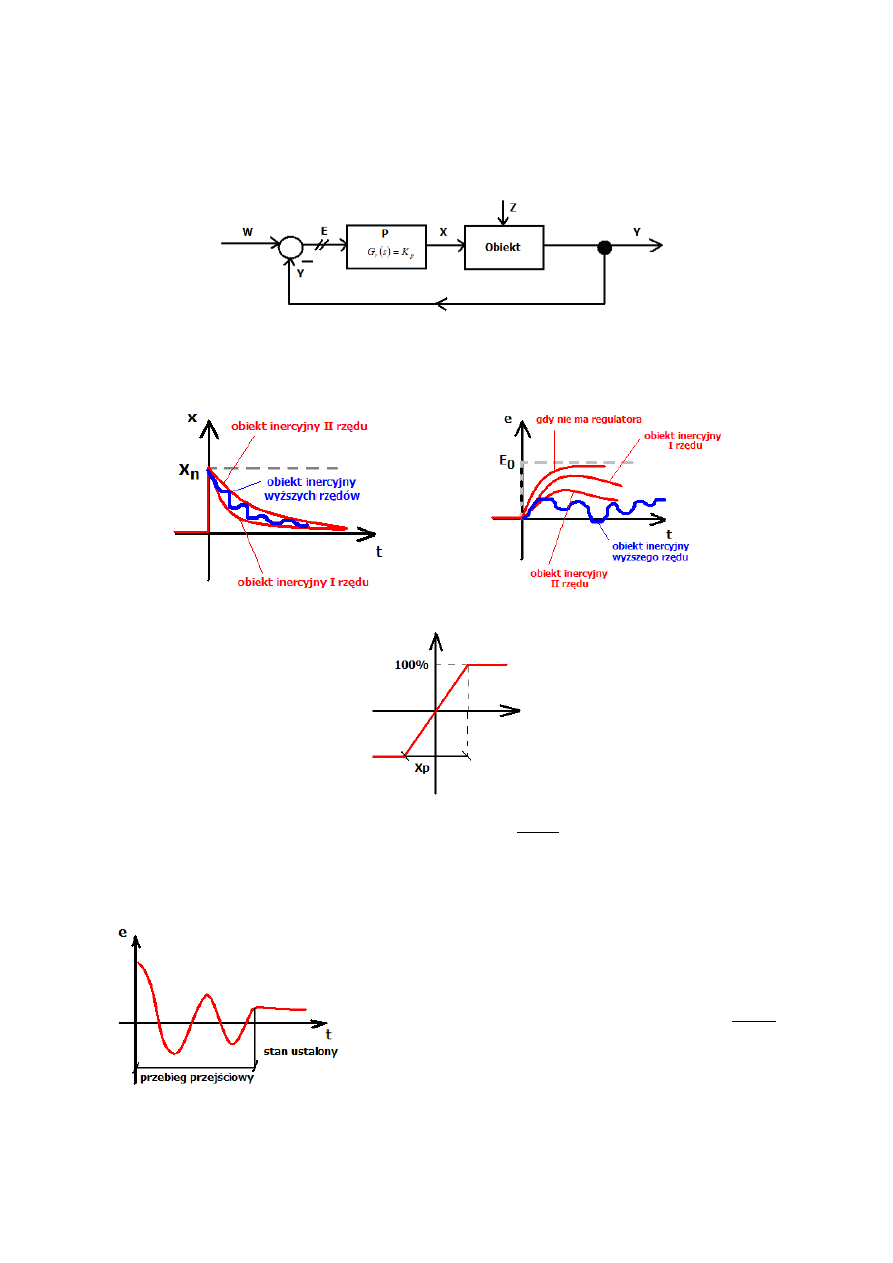
12. Zasada działania układu regulacji z regulatorem P

 

 

t

e

K

t

x

p



 

 

s

e

K

s

X

p



p

K

- współczynnik proporcjonalności

Charakterystyka statyczna (stan ustalony):

Jedyny parametr, który należy nastawić to

p

K

,

p

p

K

X

%

100



- zakres proporcjonalności

Gdy

%

100

1







p

p

X

K

Uchyb ustalony

– wartość uchybu, która pozostaje w układzie regulacji po zaniku przebiegów

przejściowych

Charakterystyka dynamiczna (zależna od czasu):

Im mniejsze wzmocnienie obiektu

p

K

tym mniejszy uchyb ustalony.

ust

p

p

ust

K

K

e

e







1

 

   

t

y

t

t

e







 

 

t

t

1

0







 

 

.

1

0

const

dla

t

z

t

z







sT

k

G

ob

ob





1

1

Transmitancja układu

0

0

0

1

1

k

k

k

k

k

k

k

k

k

k

ob

r

ob

r

ob

r











0

e

- uchyb bez regulatora

r

k

- wzmocnienie regulatora

ob

k

- wzmocnienie obiektu

16

0

k

- wzmocnienie układu otwartego

k

- wzmocnienie układu zamkniętego

Z definicji:



u

y

k



u

y

- y ustalone





ob

r

u

u

u

k

k

k

k

k

k

k

k

e

const

k

kw

y

e































































1

1

1

1

1

1

1

1

.

1

0

0

0

0

0

0

0

0

0

0

0



















uchyb ustalony jest tym większy, im większa jest zmiana wartości zadanej i im mniejsze jest

wzmocnienie układu otwartego. Układ jest tym bardziej stabilny, im mniejszy jest uchyb ustalony.

Zwiększenie wzmocnienia polepsza dokładność układu (małe

u

e

), ale pogarsza stabilność (objawia się

to oscylacyjnością),natomiast zmniejszenie

p

K

prowadzi do polepszenia stabilność kosztem

dokładności.

13. St

abilność – interpretacja fizyczna i definicja

Układ nazywamy stabilnym, jeżeli powraca do swojego stanu równowagi po ustaniu

zakłóceń. Układ jest niestabilny, jeżeli pod wpływem zakłóceń zacznie się zachowywać w sposób

niekontrolowany. Układy linowe mają jeden stan równowagi, a nieliniowe mogą mieć ich więcej.
Istnieją układy mniej i bardziej stabilne, jedne wrócą do położenia równowagi a inne nie. Układy

nieliniowe mają to do siebie, że pod wpływem zakłócenia mogą przyjąć inny stan równowagi. Jeżeli

układ linowy jest stabilny, to powraca do stanu równowagi niezależnie od wielkości zakłócenia.

Układ liniowy niestabilny nie wraca do stanu równowagi, a każde, niewielkie wymuszenie zakłóca

jego równowagę. Jeżeli układ nieliniowy jest niestabilny (tzn. stabilny lokalnie) topazy dużych

zakłóceniach nie wraca DOS tanu równowag, a przy małych może.

Przykładem układu niestabilnego jest wahadło matematyczne. Kiedy „kulka” znajduje się u

góry, mamy do czynienia z niestabilnym punktem równowagi (stan równowagi nietrwałej), a kiedy
„kulka” znajduje się na dole, mamy stabilny punkt równowagi (stan równowagi trwałej).

17

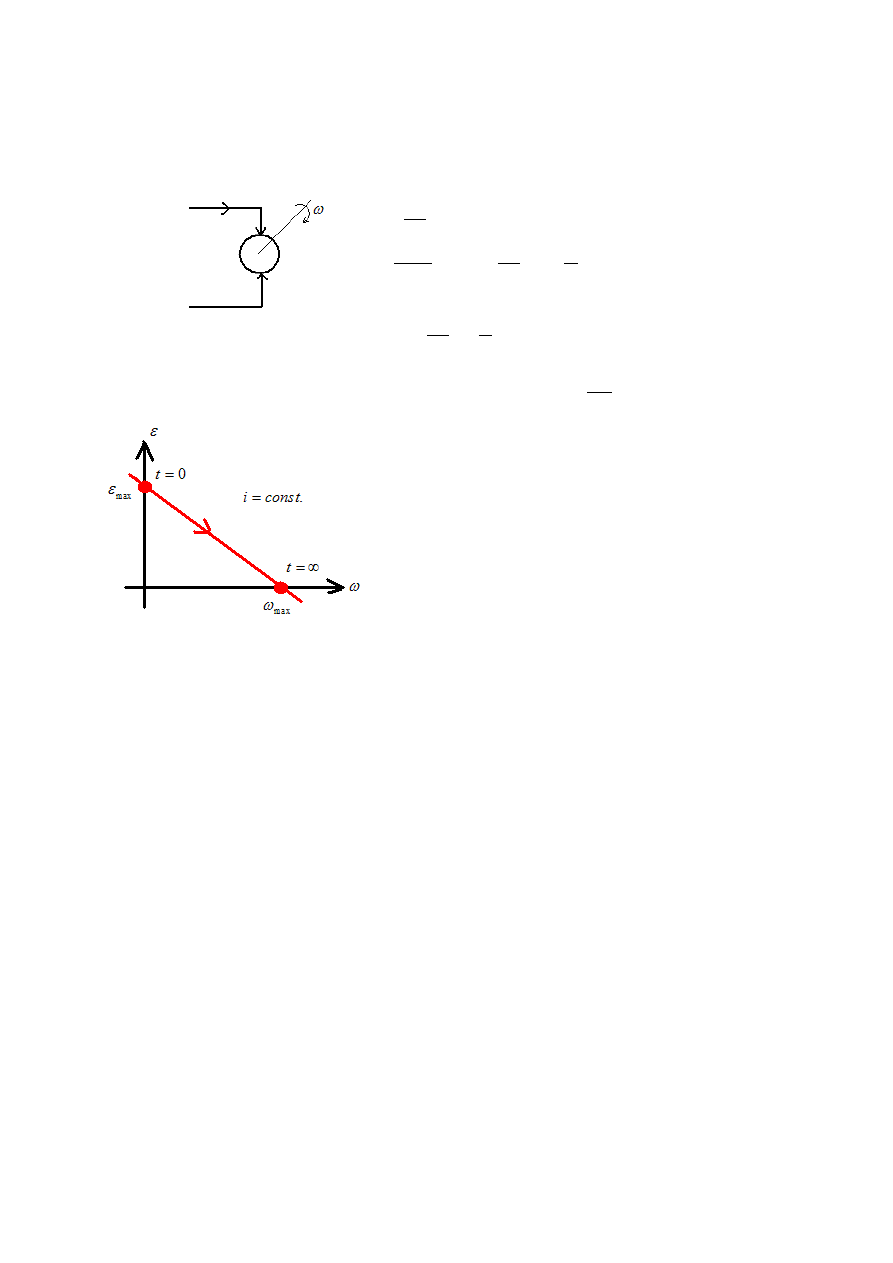
14. Płaszczyzna fazowa, trajektoria fazowa

Aby ściśle określić, co to jest stabilność, wyprowadza się współrzędne fazowe:

1. Przykład: Silnik

 

 

 

 

 

 

 

 

 

1

2

1

2

1

2

1

2

1

x

y

f

i

I

C

x

t

x

a

t

i

a

t

x

t

x

y

f

t

i

I

C

t

x

dt

t

dx

t

i

C

t

f

dt

d

I

m

m

m





































I – moment bezwładności

 

 

t

t

x





1

- prędkość

 

dt

d

t

x





2

- przyspieszenie

max

max

max

0



























Płaszczyzna x

1

i x

2

nazywana jest płaszczyzną fazową lub

płaszczyzną stanu:









2

1

x

x

Prosta

max

max







nazywana jest trajektorią fazową.

2. Przykład: Przestrzeń 3D

Ruch swobodny – ruch, w którym nie ma żadnego oddziaływania zewnętrznego. Otrzymujemy go
wtedy, gdy np. wyłączymy prąd w silniku – silnik się kręci bez wymuszenia. Jeżeli układ jest

stabilny to punkt równowagi jest w początku układu współrzędnych tzn. przy zerowym zakłóceniu

i wymuszeniu, trajektorie zbiegają się w jednym punkcie.

18

15. Warunek konieczny i wystarczający stabilności

Aby układ był stabilny, wszystkie pierwiastki jego równania charakterystycznego muszą mieć

ujemne części rzeczywiste. Jeżeli układ jest oscylacyjny, pierwiastki posiadają części urojone. Jeżeli

współczynnik tłumienia zawiera się w przedziale

1

0







to układ ma właściwości oscylacyjne, a

jego pierwiastki są zespolone i sprzężone ze sobą.

jb

a

s

jb

a

s









2

1

.

Części urojone decydują o oscylacyjności, a pierwiastki rzeczywiste decydują o stabilności

układu. Jeżeli części rzeczywiste leżą po lewej stronie układu to układ jest stabilny, a jeśli chociaż

jedne leży po prawej stronie, to układ jest niestabilny.

Kryterium Hurwitza:

0

2

1

1

2

3

4

5

1

2

3

1

0

0

0

a

a

a

a

a

a

a

a

a

a

a

a

a

a

W

n

n

n

n

n

n

n

n

n

n

n







































































3

1

4

2

5

3

1

1

2

3

1

2

1

1

0





























n

n

n

n

n

n

n

n

n

n

n

n

n

a

a

a

a

a

a

a

a

W

a

a

a

a

W

a

W

Dodatnia wartość współczynników równania charakterystycznego badanego układu sterowania

jest warunkiem koniecznym stabilności. Dla wielomianów pierwszego i drugiego stopnia jest to

zarazem warunek dostateczny.

19

16. Problem stabilności i uchybu ustalonego przy doborze

regulatora

Przypuśćmy, że charakterystyka amplitudowo – fazowa układu otwartego przebiega w pobliżu

punktu





0

,

1 j



, lecz go nie obejmuje, więc układ zamknięty jest stabilny. Może się jednak zdarzyć,

że na skutek przypadkowych zmian parametrów, układ ten przekroczy granicę stabilności i wystąpią w

nim rosnące oscylacje. Aby uniknąć sytuacji tego rodzaju wprowadza się zapas stabilności definiowany

jako zapas modułu i zapas fazy. Zapas Modułu: Wartość, o jaką trzeba zmienić moduł transmitancji

układu otwartego, przy niezmienionym jej argumencie, aby charakterystyka amplitudowo – fazowa

układu otwartego przechodziła przez punkt





0

,

1 j



, czyli aby układ zamknięty znalazł się na granicy

stabilności. Zapas modułu wyrażony, w dB:

 



















j

G

M

0

arg

- częstotliwość, dla

której przesunięcie fazowe transmitancji układu otwartego

 



j

G

0

osiąga



.Zapas Fazy: Wartość,

o jaką trzeba zmienić argument transmitancji układu otwartego przy zachowaniu niezmiennego jej

modułu, aby układ zamknięty znalazł się na granicy stabilności. Zapas fazy





to różnica między

przesunięciem fazowym równym





a wartością argumentu transmitancji

 



j

G

0

przy

częstotliwości odcięcia

0



:

 

 

1

arg

0

0

0























j

G

j

G

W dobrze tłumionych układach, tj. niepodatnych na samowzbudzenie, zapas modułu powinien wynosić

dB

12

6



, a zapas fazy





0

60

30



Problem dokładności statycznej:

Związany jest z występowaniem uchybu w stanie ustalonym. Wartość tego uchybu:

o Zależy od charakteru wymuszenia

 

t

y

0

, wartości współczynnika wzmocnienia układu

otwartego i maleje ze wzrostem tego współczynnika.

o Może być zmniejszona przez zwiększenie rzędu astatyzmu układu otwartego oraz przez

wykorzystanie pochodnych uchybu sterowania

20

17.

Porównać regulatory typu P, I, PC, PI, PD, PID

Regulator Proporcjonalny P:

 

 

 

   

t

y

t

t

e

t

e

K

t

x

p









Charakterystyki Dynamiczne

:

Charakterystyka statyczna

:

p

K

- współczynnik proporcjonalności

p

p

K

X

%

100



- zakres proporcjonalności

Uchyb ustalony e

u

to wartość uchybu, która powstaje w układzie regulacji po zaniku przebiegów

przejściowych.

Wzmocnienie regulatora:

p

r

K

K



Wzmocnienie obiektu:

ob

K

Transmitancja obiektu:

sT

K

G

O

ob





1

1

Wzmocnienie układu otwartego:

ob

r

O

K

K

K



Transmitancja układu otwartego:

ob

r

O

G

G

G



21

Wzmocnienie układu zamkniętego:

ob

r

ob

r

O

O

K

K

K

K

K

K

K









1

1





ob

r

u

u

u

k

k

k

k

k

k

k

k

e

const

k

k

y

e































































1

1

1

1

1

1

1

1

.

1

0

0

0

0

0

0

0

0

0

0

0





















Uchyb ustalony rośnie, gdy wartość zadana się zwiększa, a

O

K

maleje.

Zwiększenie wzmocnienia polepsza dokładność układu (małe

u

e

), ale pogarsza stabilność (objawia się

to oscylacyjnością),natomiast zmniejszenie

p

K

prowadzi do polepszenia stabilność kosztem

dokładności.

Regulator proporcjonalny wytwarza sygnał sterujący x(t) liniowo zależny od uchybu regulacji e(t).

uchyb ten jest proporcjonalny do wartości zakłóceń i zakłóceń przybliżeniu odwrotnie proporcjonalny

do wzmocnienia regulatora. Jest on członem bezinercyjnym, ma więc charakterystykę skokową.

Zalety i Wady:

o Szybka regulacja przy niezbyt dużej dokładności statycznej

o Jego zastosowanie zmniejsza wpływ zakłóceń, nie eliminuje ich jednak całkowicie.

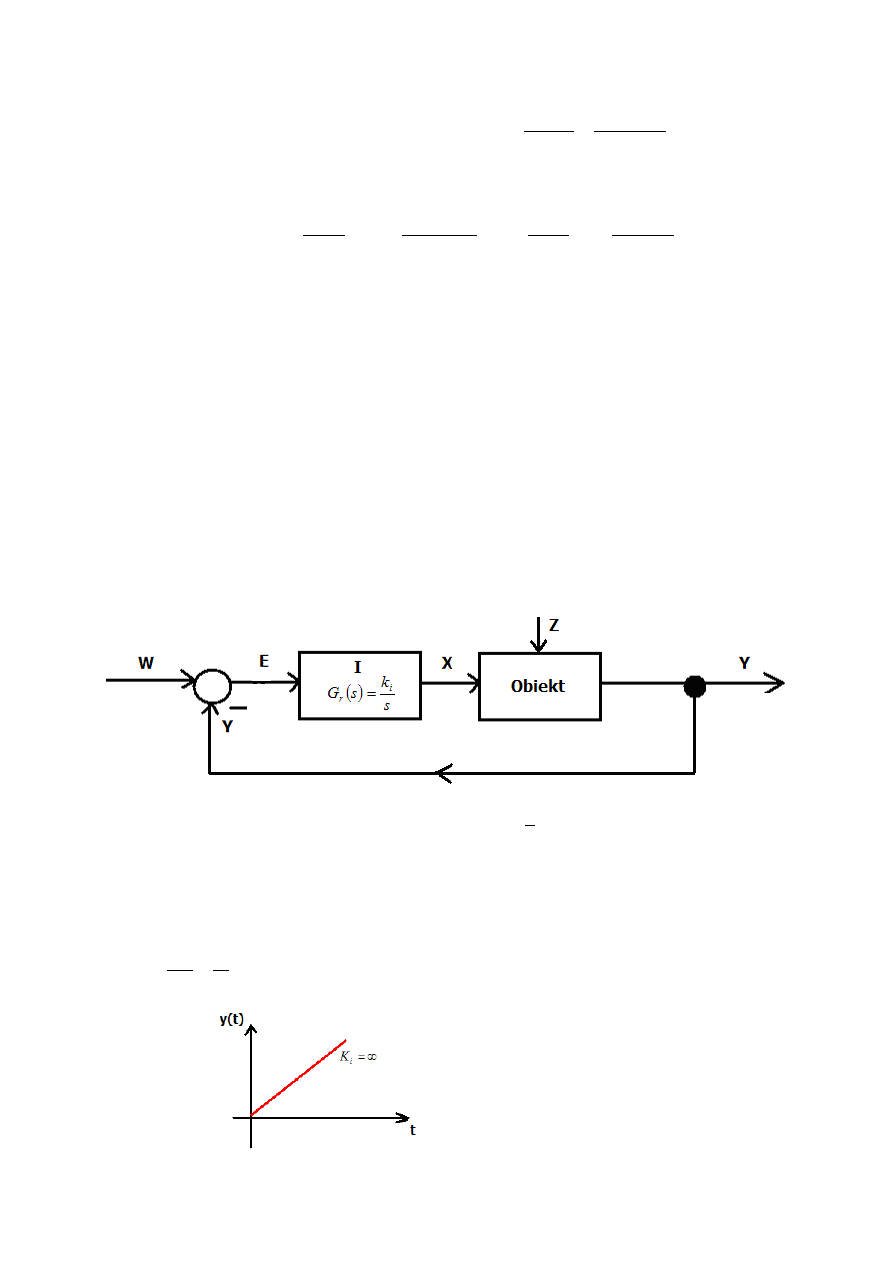
Regulator Całkujący I:

 

 

 

 

s

e

K

s

s

X

d

e

K

t

x

i

t

i

1

0











Mamy do czynienia ze stałym uchybem na wejściu, a na wyjściu sygnał wzrasta do momentu spadku

uchybu do zera. Dopiero przy zerowym uchybie sterowanie przestaje się zmieniać. Wzmocnienie

regulatora całkującego można uznać za nieskończone.

i

p

i

T

K

K

1



T

i

– czas zdwojenia, K

i

– wzmocnienie regulatora całkującego

Regulator całkujący wytwarza sygnał sterujący

proporcjonalny do uchybu regulacji e(t).

22

Zalety i Wady:

o Jest zdolny doprowadzić uchyb do zera (poprawia dokładność, ale pogarsza stabilność)

o Znacznie pogarsza stabilność i wnosi do układu opóźnienie fazowe

o Zaleta jest astatyzm układu (zwiększenie dokładności statycznej)

o Wydłużenie czasu regulacji.

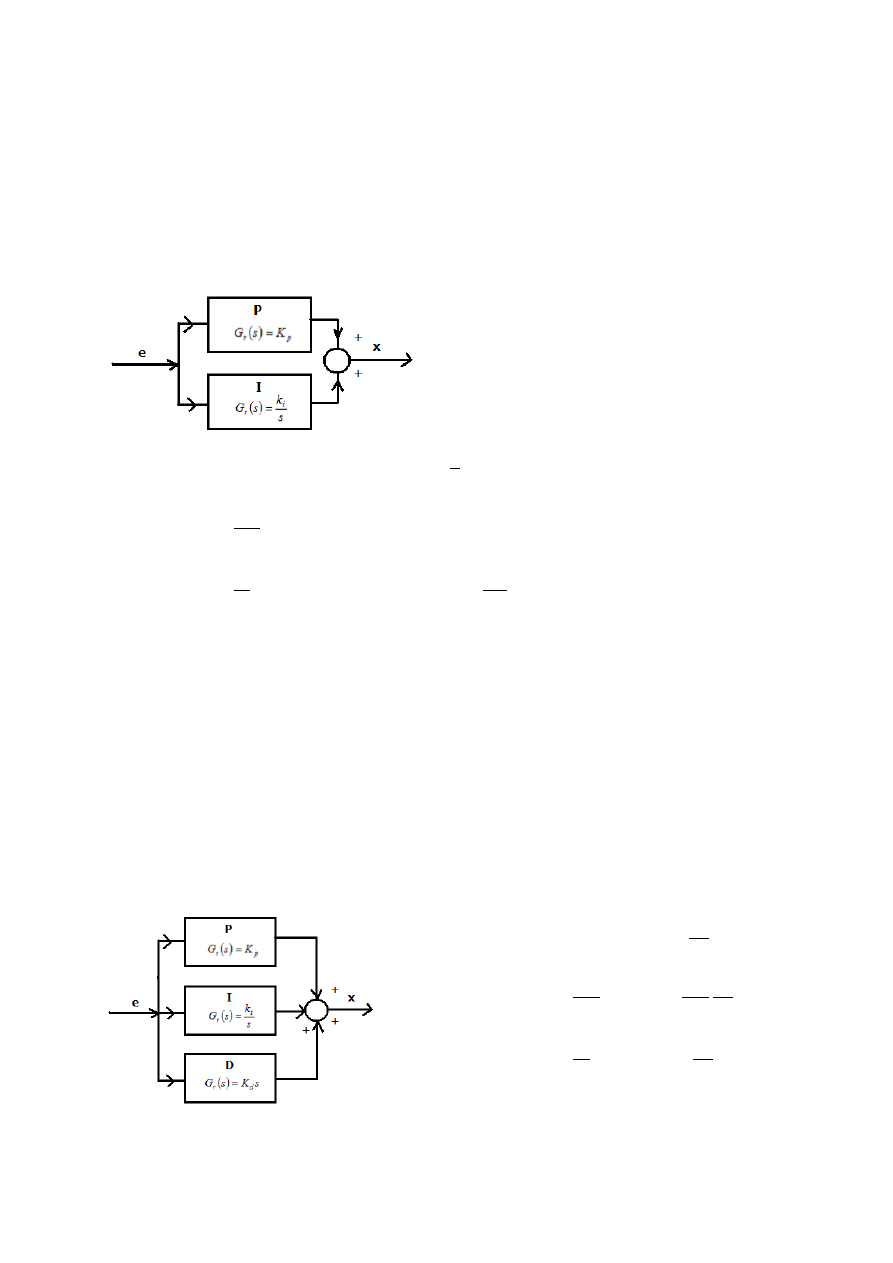
Regulator Proporcjonalno

– Całkujący PI:

 

 

 

 

 

 

 

 

 

 

 

































































s

T

K

s

G

d

e

T

t

e

K

t

x

d

e

K

K

t

e

K

t

x

K

s

K

s

G

d

e

K

t

e

K

t

x

i

p

r

t

i

p

t

p

i

p

i

p

r

t

i

p

1

1

1

1

0

0

0













Zalety i wady:

o Czas regulacji krótszy niż dla regulatora całkującego ale dwukrotnie dłuższy niż regulatora

proporcjonalnego

o Szybsza regulacja przy zachowaniu astatyzmu układu (stabilność)

o Zerowy uchyb regulacji (duża dokładność statyczna)

Znaczenie członów:

o P – zmniejsza wpływ zakłóceń, przyspieszenie reakcji (szybszy czas regulacji)

o I – doprowadzenie uchyb do zera, astatyzm układu.

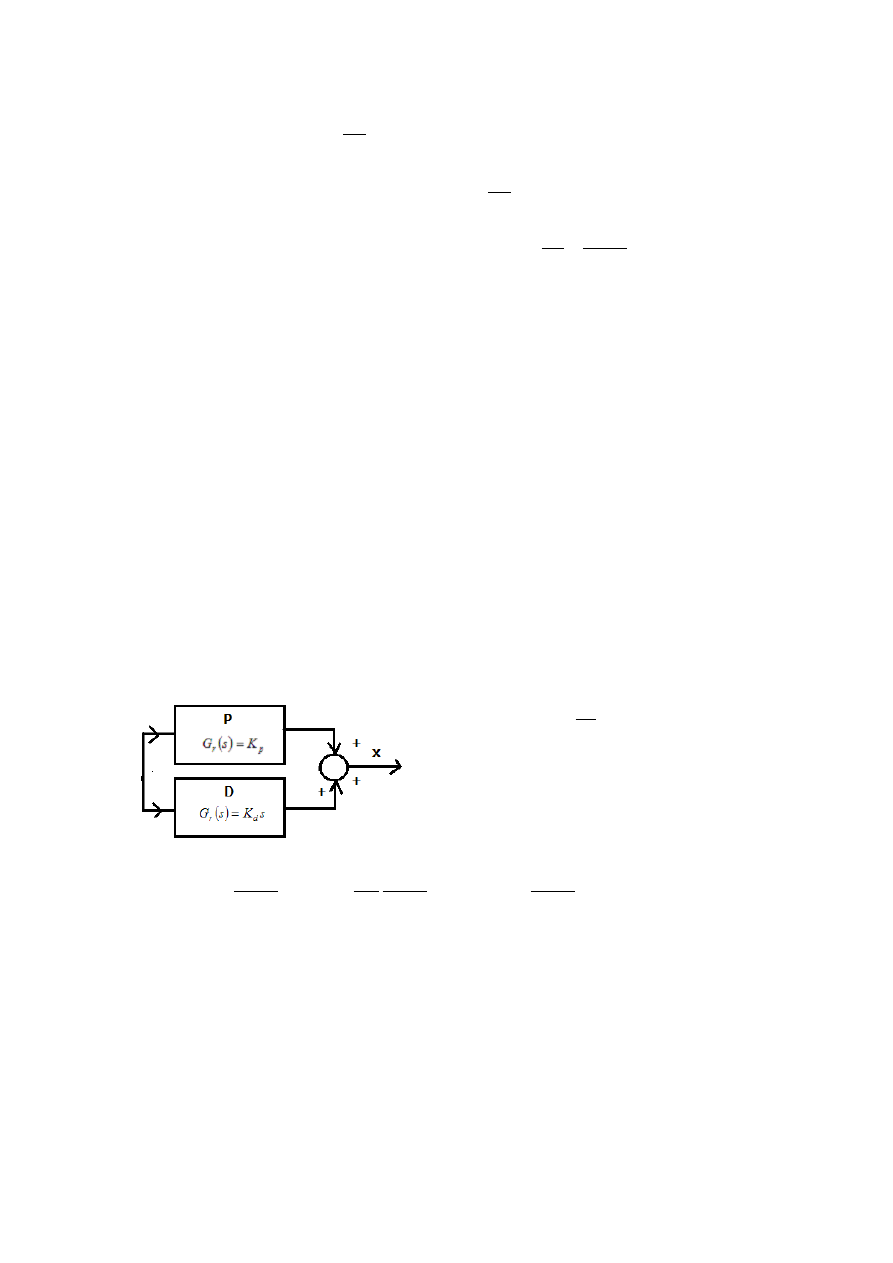
Regulator Proporcjonalno

– Całkująco - Różniczkujący PID:

 

 

 

 

 

 

 

 

 



















































dt

de

T

d

e

T

t

e

K

t

x

dt

de

K

K

d

e

K

K

t

e

K

t

x

dt

de

K

d

e

K

t

e

K

t

x

d

t

i

p

p

d

t

p

i

p

d

t

i

p

0

0

0

1













23

 

 

 

 



















s

sE

T

s

E

s

T

s

E

K

s

X

d

i

p

1

Wzór regulacji za pomocą PID

Z członem różniczkującym idealnym:

 



















s

T

s

T

K

s

G

d

i

p

r

1

1

Z członem różniczkującym rzeczywistym:

 





















sT

s

s

T

K

s

G

i

p

r

1

1

1

Powszechnie nie stosuje się regulatorów różniczkujących, różniczkujących jedynie człony
różniczkujące. Strojenie regulatora PID polega na ustawieniu odpowiednich parametrów

p

K

,

i

K

,

d

K

, lub

p

K

,

i

T

(czas zdwojenia – czas, po którym wartość odpowiedzi uchybu jest podwójna),

d

T

(czas wyprzedzenia – czas, po którym składowa proporcjonalna zrówna się ze składową

różniczkującą).

Zalety i wady:

o Najbardziej uniwersalny typ regulatora, możliwy do dostosowania do wymagań różnych

obiektów, przy odpowiedniej zmianie zastawów.

o Szybki czas reakcji (czas wyprzedzenia)
o Dobra stabilność i dokładność statyczna

Znaczenie członów:

o P – zmniejsza wpływ zakłóceń, przyspieszenie reakcji (szybszy czas regulacji), poprawia

stabilność

o I – doprowadzenie uchyb do zera, astatyzm układu, większa dokładność statyczną,

o D – zwiększa czas reakcji (czas wyprzedzenia), poprawia stabilność

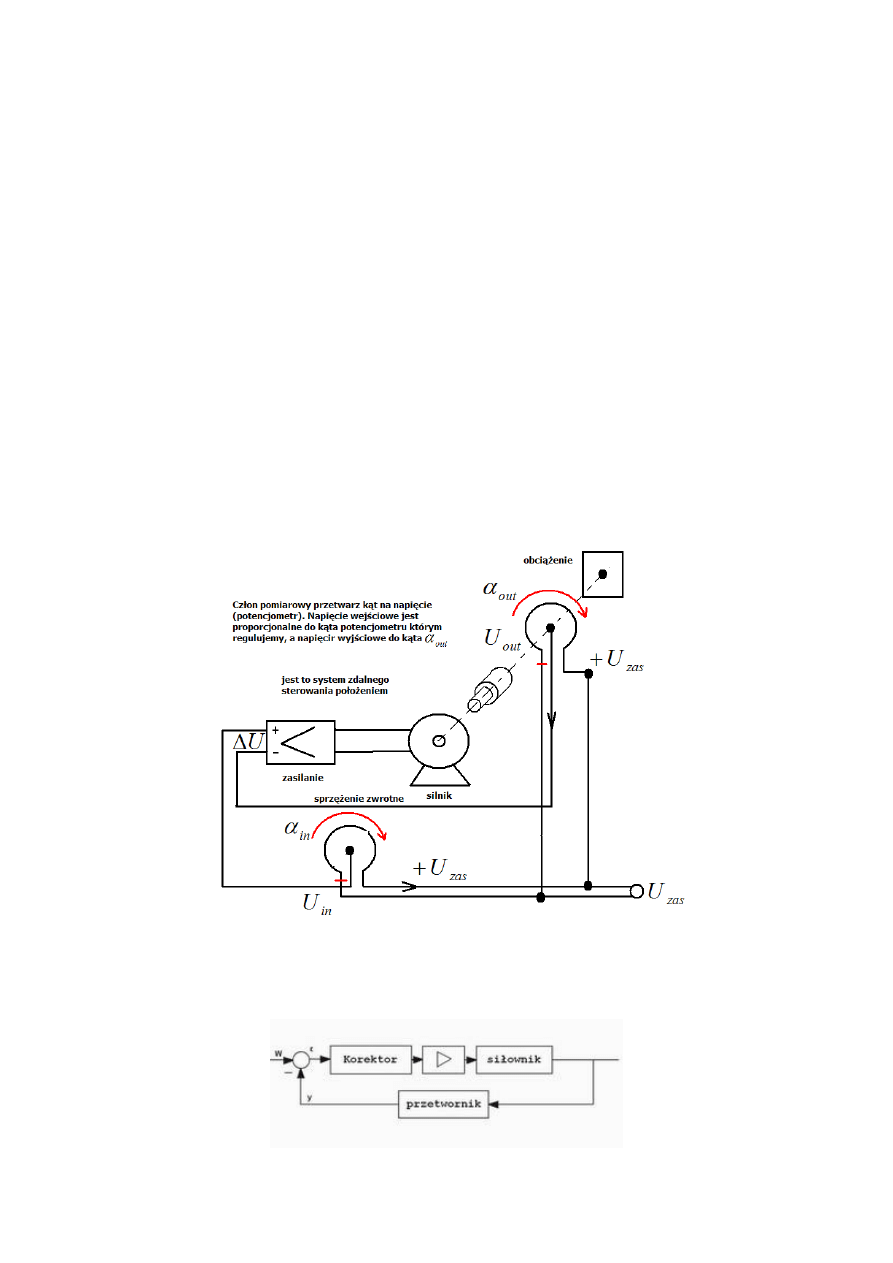
Regulator Proporcjonalno

– Różniczkujący PD:

 

 

 

 

 

s

se

K

s

e

K

s

X

dt

de

K

t

e

K

t

x

d

p

d

p









Z członem różniczkującym idealnym:

 

s

K

K

s

G

d

p

r





Z członem różniczkującym rzeczywistym:

 













































sT

s

T

K

sT

s

K

K

K

sT

s

K

K

s

G

d

p

p

d

p

d

p

r

1

1

1

1

1

Zalety i wady:

o

Szybki czas reakcji

o

Dobra stabilność

o

Mała dokładność

Człony całkujący i różniczkujący w łączeniu szeregowym dają w rezultacie regulator proporcjonalny.

24

18. Serwomechanizmy

– schemat, działanie, przykłady

Jest to zamknięty układ sterowania przemieszczeniem (układ automatyki), o strukturze

typowego układu regulacji. Wartość wzorcowa porównywana jest z przetworzonym przez przetwornik
bieżącym sygnałem wyjściowym i powstały w ten sposób uchyb podawany jest na człon korekcyjny, a

dalej na wzmacniacz. Wzmocniony sygnał trafia do siłownika, którego przemieszczenie jest wartością

wyjściową układu. Zadaniem serwomechanizmu jest likwidacja błędów regulacji (uchybu

przemieszczenia), powstających na skutek zmian wielkości wzorcowej, a więc klasyfikujemy go jako

układ nadążny. Serwomechanizm ma strukturę typowego układu regulacji, nie steruje jednak

obiektem technologicznym, lecz siłownikiem w celu usprawnienia działania toru wykonawczego.

Specyfikacją serwomechanizmów jest całkujący charakter siłownika o dynamice nie

utrudniającej regulacji, ale wnoszącej nieliniowość. Zmusza to do stosowania korektorów
proporcjonalnych, o dużym wzmocnieniu, a nawet wzmacniaczy trójpołożeniowych. Całkujący

charakter siłownika zapewnia, teoretycznie, zerowy błąd statyczny. Duże wzmocnienie w torze

głównym poprawia nadążanie układu za zmianami wzorca, ale zmniejsza zapas stabilności. Sytuację

można poprawić wprowadzając korektor regulator proporcjonalno-różniczkujący (PD).

Schemat ideowy ze sprzężeniem zwrotnym i członem pomiarowym:

out

in

U

U

U







Obrót silnika następuje o ten sam kąt, co obrót potencjometru. W układzie na

skutek bezwładności silnika występują drgania oscylacyjne.

Schemat blokowy:

25





sT

s

k

m



1

- silnik z przekładnią i obciążeniem

Transmitancja serwomechanizmu:

 

1

2

0

2

0







s

T

s

T

k

s

G

s



; k – wzmocnienie w stanie ustalonym

1





serwomechanizm oscylacyjny

1





serwomechanizm nieoscylacyjny.

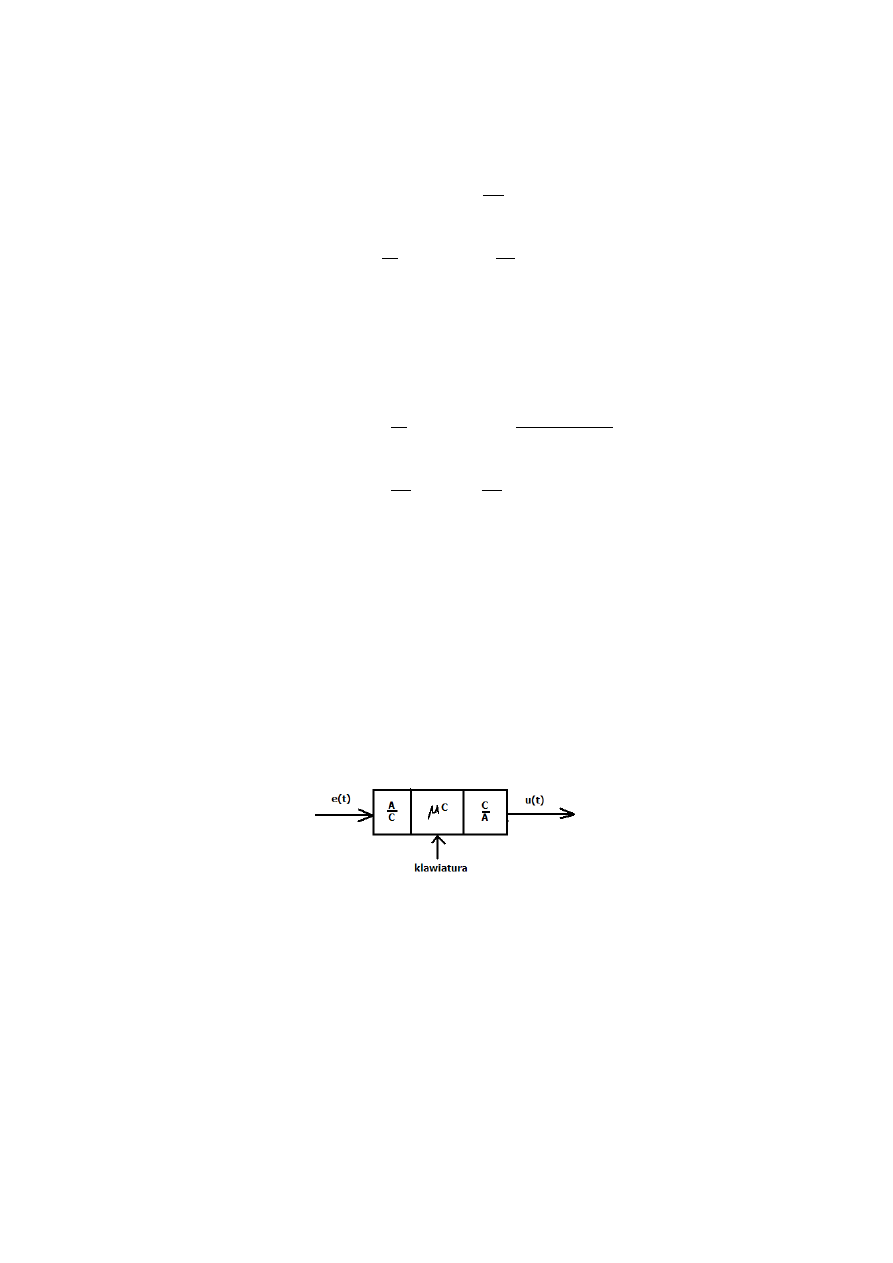
26

19. Regulatory cyfrowe, przykłady

Regulator cyfrowy: działa w oparciu o technikę komputerową i procesory.

Transmitancja operatorowa:

 



















d

p

r

sT

sT

k

s

G

1

1

Zapis matematyczny:

 

 

 





















dt

de

T

d

e

T

t

e

k

t

u

d

i

p





1

Cyfrowe urządzenia działają na zasadzie próbkowania sygnału uchybu z dużą częstotliwością (GHz)

Uchyb w chwili t

1

:

 

1

t

e

;





p

T

t

e



1

;





p

T

t

e

2

1



Uchyb:

 

0

e

;

 

1

e

; … ;

 

n

e

 

 

 

  



 

 

 

  































































1

1

1

0

0

n

e

n

e

T

T

k

e

T

T

n

e

k

n

u

T

n

e

n

e

T

T

k

e

T

n

e

k

n

u

p

d

n

k

i

p

p

p

d

n

k

p

i

p

Do zsumowania wystarczy znajomość ostatniej sumy i bieżącej próbki. Potrzebne SA jedynie

dwie komórki pamięci i jedna do poprzedniej próbki.





 





 



 









suma

a

aktua

probka

przezaca

suma

biezaca

n

e

n

S

ln

1





Regulator cyfrowy jest nieciągły, ale można go traktować jako ciągły dla dużych częstotliwości

próbkowania.

Realizacja programowania:

A/C - przetwornik analogowo – cyfrowy

C/A – przetwornik cyfrowo – analogowy

27

20. Sterowniki PLC

– budowa i programowanie

Sterownik jest urządzeniem automatyki odpowiedzialnym za sterowanie wieloma wejściami

obiektów na podstawie pomiarów wielu wyjść sterownika. W naszym przypadku sterownik pełni role
regulatora PID, a zatem regulatora proporcjonalnego całkująco – różniczkującego, dla którego sygnał

x(t) zmienia się następująco:

dt

de

T

k

d

e

T

k

t

e

k

t

x

d

p

t

i

p

p















0

)

(

)

(

)

(





Wejścia i wyjścia opisane są na listwie zaciskowej oraz przy wskaźnikach ich stanu. Te

alfanumeryczne symbole identyfikują adresy wejść/ wyjść, do których podłączone są urządzenia.

Zewnętrzne adresy używane są przez CPU do określenia, które wejścia są w stanie wysokim i które

wyjścia powinny być załączone lub wyłączone.

Urządzenia wejściowe, takie jak przełączniki, przyciski oraz inne czujniki dwustanowe,

podłączane są do listwy zaciskowej znajdującej się pod dolną osłoną PLC. Urządzenia wyjściowe, takie

jak przekaźniki, są podłączane do listwy zaciskowej znajdującej się pod górną osłoną PLC.

Programowanie - Do tworzenia programów roboczych sterowników PLC jest stosowane specjalne
oprogramowanie. Program użytkowy najczęściej składa się z pewnej liczby instrukcji ułożonych w

odpowiednim porządku logicznym odzwierciedlającym opis pracy sterowanego urządzenia. Instrukcje

podzielone są na trzy grupy:

o

Instrukcje standardowe

znajdują się w większości programów. Instrukcje standardowe

opisują: liczniki czasu, liczniki zdarzeń, połączenia logiczne, pętle programowe, inkrementacje,

negacje, przesunięcia oraz instrukcje blokowe.

o

Instrukcje specjalne

używane są do obsługi danych. Instrukcje specjalne zawierają rozkazy

przesunięcia, grupowania w tablicach, szukania, konwersji, iteracji oraz instrukcje czasu
rzeczywistego.

o

Instrukcje szybkie

umożliwiają obsługę zdarzeń w trybie przerwań, niezależnie od skanowania

PLC. Są to instrukcje obsługi szybkich liczników zdarzeń, przerwań obiektowych, aktualizacji

stanu wyjść i instrukcje transmisji.

Symbole.

Aby zrozumieć wykonywanie instrukcji PLC, konieczne jest poznanie specyficznego języka -

drabinkowego. Język logiki drabinkowej PLC składa się z powszechnie używanego zestawu symboli,

które reprezentują elementy kontroli oraz instrukcje.

Styki

Jednym z najtrudniejszych aspektów programowania PLC dla początkujących użytkowników

jest związek pomiędzy wynikiem operacji logicznej (bitem stanu), odwzorowującym rezultat działania

rozkazu, a funkcjami programowymi, które wykorzystują ten bit. Dwie z najczęściej używanych funkcji

programowych to styk normalnie otwarty (NO) oraz styk normalnie zamknięty (NC). Mówiąc

obrazowo, prąd przepływa przez styki, gdy są one zamknięte. Stykowi normalnie otwartemu (NO) jest

przyporządkowana wartość

prawda

(bit stanu = 1), gdy kontrolowane wejście lub wyjście jest w

28

stanie 1. Stykowi normalnie zamkniętemu (NC) jest przyporządkowana wartość logiczna

prawda

(bit

stanu = 1), gdy stan kontrolowanego wejścia lub wyjścia równa się 0.

Cewki

Symbol cewki przekaźnika odwzorowuje na schemacie wyjście dwustanowe. Adres tego wyjścia

odpowiada oznaczeniu fizycznego zacisku. Warunkiem załączenia cewki (ustawienia wyjścia w stan 1)

jest stan 1 bitu odzwierciedlającego rezultat zadania logicznego realizowanego przez obwód sterujący

cewki. Stan tego bitu (jako stan wyjścia) może być także wykorzystany w innych obwodach
sterowniczych.

Bloki

- reprezentują różne instrukcje lub funkcje, które są wykonywane, gdy są spełnione warunki

logiczne ich realizacji (bit stanu = 1). Typowymi funkcjami oznaczanymi jako bloki są liczniki czasu,

liczniki zdarzeń i operacje matematyczne.

29

21. Roboty przemysłowe – definicja, generacje

Robot określenie mechanicznego urządzenia wykonującego automatycznie pewne zadania. Działanie

robota może być kontrolowane przez człowieka, przez wprowadzony wcześniej program, bądź przez
zbiór ogólnych reguł, które zostają przełożone na działanie robota przy pomocy technik sztucznej

inteligencji. Roboty często zastępują człowieka przy monotonnych, złożonych z powtarzających się

kroków czynnościach, które mogą wykonywać znacznie szybciej od ludzi. Domeną ich zastosowań są

też te zadania, które są niebezpieczne dla człowieka, na przykład związane z manipulacją szkodliwymi

dla zdrowia substancjami lub przebywaniem w nieprzyjaznym środowisku.

Robot Przemysłowy - urządzenie przeznaczone do automatycznej manipulacji z możliwością

wykonania kilku ruchów względem różnych osi, zaopatrzone w chwytaki lub w narzędzia przeznaczone

do zastosowania w przemyśle. Są to roboty wykorzystywane przy szeroko pojętych zadaniach
przemysłowych. Początkowo były tylko stosowane przy przenoszeniu materiałów i spawaniu. Obecnie

zastosowanie robotów w przemyśle stale wzrasta i przedstawiony poniżej podział może nie

obejmować wszystkich dziedzin ich zastosowania.

o Jednym z kryteriów klasyfikacji jest przeznaczenie robotów, tak więc można wyróżnić następujące

klasy robotów:



Do badań naukowych



Do celów szkoleniowych



Do celów przemysłowych



Do celów badawczych pod wodą, w przestrzeni kosmicznej.

o Innym kryterium klasyfikacji robotów jest rodzaj zastosowanych napędów:



Z napędem pneumatycznym



Z napędem hydraulicznym



Z napędem elektrycznym



Z napędem mieszanym

Generacje:

o

Roboty I generacji

to roboty zaprogramowane najczęściej na określoną sekwencję czynności

(istnieje możliwość ich przeprogramowania). W robotach tej generacji stosowano przeważnie

otwarty układ sterowania tak więc robot charakteryzuje się całkowitym brakiem sprzężenia

zwrotnego od stanu manipulowanego przedmiotu.

o

Roboty II generacji

to roboty wyposażone w zamknięty układ sterowania oraz czujniki

pozwalające dokonywać pomiarów podstawowych parametrów stanu robota i otoczenia.

Roboty II generacji powinny spełniają warunek takiej taktyki przy kontakcie ze światem

zewnętrznym, aby uzyskać optymalny efekt działania. Robot powinien rozpoznawać żądany

30

obiekt nawet wówczas, gdy przemieszcza się z innymi obiektami, następnie rozpoznać ten

obiekt bez względu na jego położenie i kształt geometryczny. Takie roboty realizują te

wymagania za pomocą zespołu czujników.

o Roboty III generacji to roboty wyposażone w zamknięty układ sterowania oraz czujniki

pozwalające dokonywać złożonych pomiarów parametrów stanu robota i otoczenia. Tak

więc roboty te są wyposażone w zdolności rozpoznawania złożonych kształtów i klasyfikacji

złożonych sytuacji, a ich system sterowania powinien posiadać zdolności adaptacyjne.

Schemat układu sterowania dla robotów III generacji jest taki sam jak dla robotów II

generacji

22. Schematy kinematyczne robotów, stopnie swobody

Manipulatorem nazywamy układ N ramion połączonych ze sobą przegubami, zakończony efektorem

(chwytakiem). Pojedyncze ogniwo manipulatora zbudowane jest z przegubu oraz następującego po

nim ramienia, gdzie przegub zapewnia możliwość ruchu. Każdy przegub opisywany jest za pomocą

współrzędnej wewnętrznej (nastawy)q i przy czym i = 1, 2, ..., N.

Proste zadanie kinematyki polega na obliczeniu pozycji i orientacji członu roboczego względem

układu odniesienia podstawy dla danego zbioru współrzędnych konfiguracyjnych. Zadanie to można

traktować jako odwzorowanie opisu położenia manipulatora w przestrzeni współrzędnych

konfiguracyjnych na opis przestrzeni współrzędnych kartezjańskich. Słowo kinematyka w robotyce

odpowiada pojęciu kinematyka we współrzędnych i opisuje najczęściej zależność pomiędzy strukturą

manipulatora robotycznego, nastawami poszczególnych ramion (współrzędne wewnętrzne zapisywane

jako wektor q), a położeniem efektora. Zależność ta przedstawiana jest pod postacią macierzy K(q)
(Notacja Denavita-Hartenberga) lub pod postacią wektora k(q) (będącego "pochodną" ww. macierzy).

W tym drugim przypadku składowe orientacji uzyskane zostają poprzez zastosowanie odpowiedniej

parametryzacji macierzy R(q) będącej podmacierzą macierzy K(q). Najczęściej wektor k(q)

przedstawia się jako

gdzie trzy pierwsze składowe określają położenie, a kolejne trzy

orientację. Na podstawie wektora k(q) wyznaczyć można macierz Jakobiego stosowaną w algorytmie

Jakobianowym, a następnie określić konfiguracje osobliwe oraz manipulowalność.

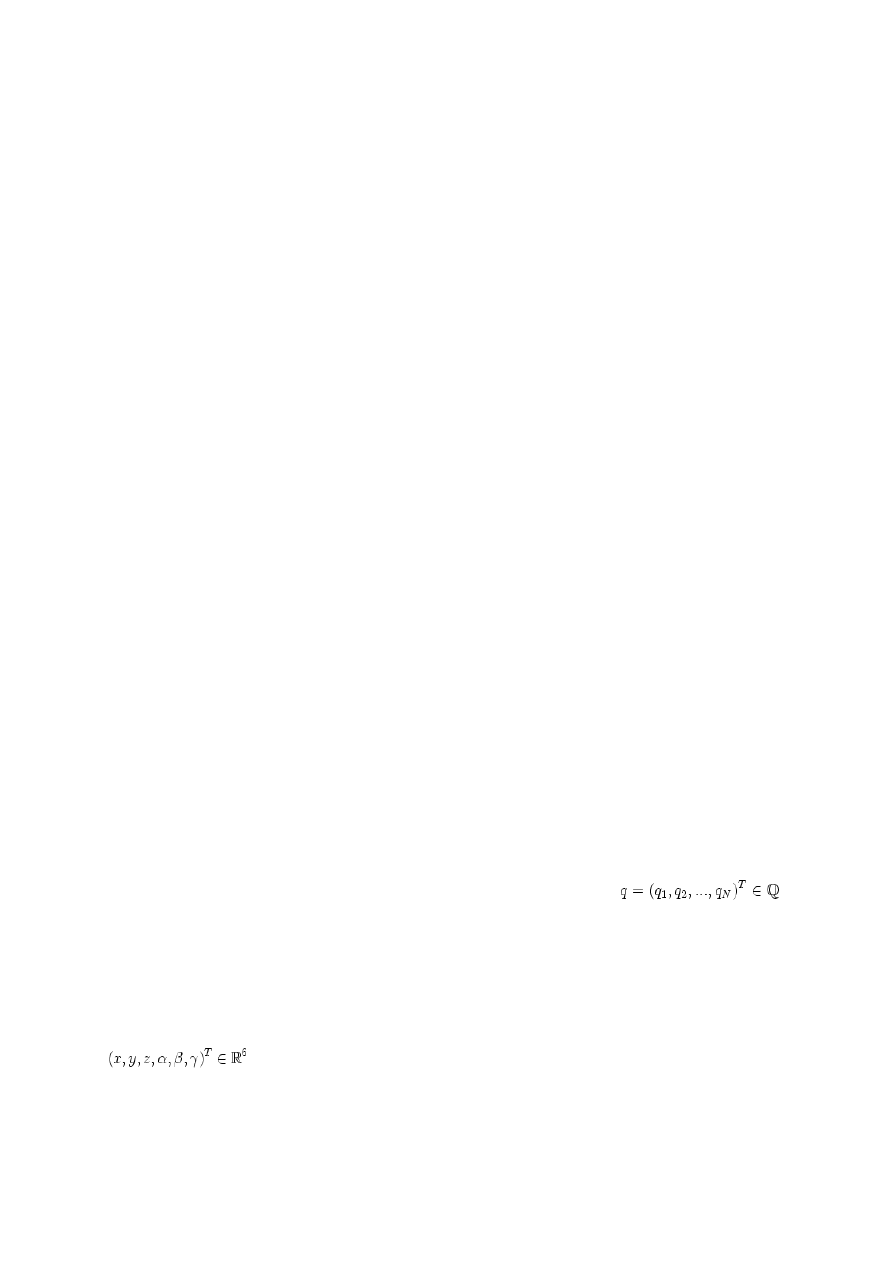
31

Stopnie swobody

Liczbę niezależnych zmiennych opisujących jednoznacznie stan (modelu) układu fizycznego

nazywa się liczbą stopni swobody tego układu. W mechanice klasycznej jest to liczba niezależnych

ruchów, jakie ciało jest w stanie zrealizować w przestrzeni. Przez niezależnych rozumie się, że żaden z

tych ruchów nie może być uzyskany poprzez superpozycję pozostałych. Ciało sztywne całkowicie

swobodne (to jest takie, na które nie nałożono żadnych więzów) ma maksymalną liczbę sześciu stopni

swobody:

o Trzy ruchy translacyjne w stosunku do osi układu współrzędnych X, Y i Z (ruch

postępowy).

o Trzy obroty względem osi równoległych do osi układu współrzędnych X, Y i Z (ruch

obrotowy).

Ciała odkształcalne mogą posiadać większą liczbę stopni swobody. Istotny jest tu podział na

ciała o skończonej liczbie stopni swobody (tzw. modele dyskretne), oraz na ciała o nieskończonej

liczbie stopni swobody (tzw. modele ciągłe).

Zgodnie z zasadami mechaniki, każdą trajektorię ciała materialnego można rozłożyć na sumę prostych

ruchów opisanych powyżej.

Ciało materialne (np. człon mechanizmu) łączone z drugim w parę kinematyczną traci pewną

ilość stopni swobody, w zależności od klasy pary kinematycznej. Ogólnie, jeżeli układ składa się z

dwóch ciał (podukładów) o odpowiednio: „n1” i „n2” stopniach swobody, oraz między tymi ciałami

występuje „w” więzów, to układ taki posiada „n1+n2-w” stopni swobody.

23. Pozycja i orientacja robotów, współrzędne

Pozycja Robota Jest określana przez położenie punktu, w którym znajduje się końcówka robota w

każdej pozycji robot ma jeszcze różne orientacje. Do zmiany orientacji potrzebne są dodatkowo 3
stopnie swobody. Tylko robot z minimum 6 stopniami swobody może przyjąć dowolną pozycję i

dowolną orientację.

Współrzędne wewnętrzne: Każdy przegub opisywany jest za pomocą współrzędnej wewnętrznej

(nastawy)

q

i

przy czym i = 1, 2, ..., N. Zmienne

q

i

po złożeniu tworzą wektor

, zwany wektorem współrzędnych wewnętrznych. Jeśli manipulator potraktujemy jako układ

sterowania, to

q

będzie odpowiadać wektorowi stanu.

Współrzędne zewnętrzne: Podczas pracy z manipulatorem ważne jest położenie i orientacja jego
efektora określane we współrzędnych zewnętrznych. Mogą one być zapisane pod postacią szóstki liczb

. W zależności od potrzeb rozmiar ten może ulec zmianie (przykładowo w danym

przypadku ważne mogą być jedynie współrzędne x oraz y). Pierwsza trójka liczb określa położenie

efektora, a kolejna - orientację.

32

Kinematyka manipulatora Ostatecznie położenie i orientacja efektora mogą być opisane we

współrzędnych zewnętrznych za pomocą wektora

oraz w funkcji współrzędnych

wewnętrznych

. Przekształcenie k :

nazywamy kinematyką

manipulatora we współrzędnych. W celu łatwiejszego opisu własności manipulatora z każdym jego
przegubem oraz efektorem możemy powiązać kartezjański układ współrzędnych, który nazywany jest

układem lokalnym. Układ

X

0

Y

0

Z

0

związany z podstawą nazywać będziemy układem bazowym i

względem niego będziemy wyznaczać położenie oraz orientację przegubów oraz efektora

manipulatora. Do opisu manipulatorów najczęściej stosuje się Notację Denavita-Hartenberga

.

24. Zadanie proste i odwrotne kinematyki robota

Zadanie proste sterowania:

Dla danej konfiguracji współrzędnych wewnętrznych należy wyliczyć pozycję i orientację

przedmiotu trzymanego przez chwytak we współrzędnych wewnętrznych (rozwiązanie jednoznaczne).

Należy podkreślić, iż bardzo często istnieje wiele sposobów orientowania układów

współrzędnych (zgodnie z notacją Denavita-Hartenberga), jednak celem analizy kinematyki prostej

jest przyjęcie najprostszej formy opisu ze względu na zmniejszenie komplikacji związanych z

obliczeniami.

Zadanie odwrotne sterowania:

Dla danej pozycji i orientacji przedmiotu należy wyznaczyć współrzędne wewnętrzne

(rozwiązanie niejednoznaczne). Kinematyka odwrotna polega na znalezieniu zmiennych przegubowych
w zależności od pozycji i orientacji końcówki roboczej.

W ogólnym przypadku jest ono trudniejsze niż zadanie kinematyki prostej, ponieważ czasami

nie istnieje jednoznaczne rozwiązanie wynikające z nieliniowości równań kinematyki.

25. Zrobotyzowane stanowisko technologiczne

Składa się z robota z układem sensorycznym oraz urządzeń technologicznych

Stanowisko służy do samoczynnej produkcji (najczęściej do prac spawalniczych, montażowych,

wszędzie tam, gdzie istnieją trudne warunki dla człowieka). Praca na takim stanowisku jest

powtarzalna i ściśle zdefiniowana (taka sama dokładność wykonania).

W przypadku spawania, robot trzyma w chwytaku, lub ma na stałe umieszczone w kiści

urządzenie spawalnicze, którym powinien dokładnie jechać po szczelinie, umiejąc korygować
trajektorię wzdłuż niej. Stanowisko zrobotyzowane powinno posiadać taśmę lub stół obrotowy. Na

stole mogą znajdować się pozycjonery, które stanowią dodatkowy stopień swobody dla

wykonywanego przedmiotu. Układ sterujący steruje jednocześnie robotem i pozycjonerem.

Rozróżniamy pozycjonery obrotowe, przechylne, podwieszane – do przesuwania robota. Układy

sensoryczne służą do sprawdzania i kontrolowania wielu parametrów wykonywanych czynności (np.

kontrolowanie szwu spawalniczego).