
1. Podstawowe podzespoły robota.
Robotem nazywamy uniwersalny system techniczny zastępujący przez swoje działanie
kinematyczne i intelektualne funkcje człowieka. Podstawowe podzespoły robota to:
-
Manipulator – utworzony przez szereg ogniw połączonych złączami, które wspólnie
tworzą łańcuch kinematyczny. Poszczególne złącza są napędzane odpowiednimi
zespołami napędowymi, które zapewniają ruchy efektora manipulatora w różnych
kierunkach.
-
Układ zasilania – przetwarza energię pierwotną dostarczaną do robota (najczęściej
elektryczną) na odpowiedni rodzaj energii stosownie do rodzaju zespołów napędowych
manipulatora. W przypadku robotów z napędami elektrycznymi jest to zwykle zestaw
wzmacniaczy mocy. W przypadku zespołów napędowych pneumatycznych lub
hydraulicznych jest to zewnętrzny kompresor z zespołem filtrów i zaworów.
-
System sensoryczny – dostarcza sterownikowi robota informacji o stanie manipulatora i
jego otoczenia. Może być to realizowane w sposób ciągły poprzez pomiar pozycji
poszczególnych osi, lub tylko przez przesyłanie informacji z dyskretnych czujników
położenia. Sensory we współczesnych robotach dzielą się na dwie grupy: sensory
wewnętrzne i zewnętrzne. Wewnętrzne związane są z łańcuchem kinematycznym
manipulatora i służą do pomiaru wzajemnych przemieszczeń i prędkości poszczególnych
złączy. Zewnętrzne służą do pomiarów wzajemnych położeń efektora robota i elementów
otoczenia.
-
Sterownik – realizuje następujące funkcje: przechowuje w pamięci sekwencje danych
dotyczących pożądanych ruchów manipulatora; zbiera i przetwarza informacje z systemu
sensorycznego robota; inicjuje i koordynuje ruchy poszczególnych zespołów napędowych
manipulatora; komunikuje się z innymi podzespołami zrobotyzowanego stanowiska.
2. Klasyfikacja struktur kinematycznych robotów.
Manipulatory klasyfikowane są jako: kartezjańskie, cylindryczne, sferyczne, typu SCARA lub
wyłącznie ze złączami obrotowymi (stawowe).
-
Manipulator kartezjański – najprostszy, wszystkie złącza są liniowe i zapewniają ruchy
wzdłuż osi X, Y, Z układu kartezjańskiego. Ruchy odbywają się w ograniczonym zakresie,
ale obszar pracy manipulatora jest bardzo duży w porównaniu z innymi strukturami.
Przestrzeń robocza ma kształt prostopadłościanu.
-
Manipulator cylindryczny – poziome ramie jest zamontowane na obrotowej kolumnie i
porusza się w kierunku pionowym i poziomym. Kolumna wykonuje ruch obrotowy,
najczęściej ograniczony do kąta pełnego. Ramie może być podnoszone lub opuszczane
wzdłuż kolumny oraz może się wysuwać w kierunku radialnym. Przestrzeń robocza tego
manipulatora jest fragmentem pionowego cylindra (wydrążonego walca).
-
Manipulator sferyczny – powstaje gdy drugie łącze manipulatora cylindrycznego zastąpimy
złączem obrotowym. Ramie może poruszać się liniowo w kierunku radialnym i może się
pochylać względem kolumny i wraz z nią obracać się w płaszczyźnie poziomej. Przestrzeń
robocza jest fragmentem sfery kulistej.
-
Manipulator typu SCARA – posiada dwa pierwsze złącza obrotowe i trzecie liniowe. Osie
złączy obrotowych są równoległe. Pierwsze złącze realizuje obrót ramienia wokół
podstawy. Drugie złącze obrotowe realizuje ruchy obrotowe przedramienia wokół osi
pionowej. Złącza obrotowe realizują ruch w przestrzeni poziomej. Ruch pionowy zapewnia
trzecie złącze o charakterze liniowym.
-
Manipulator stawowy – wszystkie jego złącza są obrotowe. Zaletą jest duża przestrzeń
robocza, która ma kształt zbliżony do sfery kulistej. Możliwe jest osiągnięcie punktów w
pobliżu środka tej sfery oraz dotarcie do wielu punktów poza przeszkodami
umieszczonymi w polu roboczym.
Zwykle na końcu ostatniego ogniwa umieszczana jest kiść, która umożliwia zamocowanie
odpowiedniego narzędzia (efektora manipulatora). Kiść jest wyposażona w dodatkowe
zespoły napędowe, które pozwalają na uzyskanie odpowiedniej orientacji efektora.

3. Opis punktu w różnych układach współrzędnych oraz transformacja przesunięcia.
Niech położenie wybranego dowolnie punktu A będzie opisana w układzie podstawowym {0}
przy pomocy wektora
0
r
A
= [
0
r
xA
0
r
yA
0
r
zA
]
T
, a jednocześnie położenie tego punktu będzie
określone w układzie przesuniętym {1} za pomocą wektora
1
r
A
= [
1
r
xA
1
r
yA
1
r
zA
]
T
. Do
wzajemnego określenia położenia obu układów wystarczy podać wektor
0
p
l
= [
0
p
xl
0
p
yl
0
p
zl
]
T
,
wyrażony w układzie podstawowym i podający położenie początku układu {1}.Te trzy
wektory połączone są zależnością:
−
=
zA
yA
xA
zl
yl
xl
zA
yA
xA
r
r
r
p
p
p
r
r
r
1
1
1
0
0
0
0
0
0
,
która może być zapisana w zwartej postaci jako:
A
l
A
r
p
r
1
0
0
+
=
.
4. Podstawowe obroty wokół osi X, Y, Z
Przekształcenie obrotu wygodnie jest przedstawić za pomocą macierzy. Wektor
współrzędnych punktu mnożymy przez macierz obrotu i mamy wektor współrzędnych po
obrocie.
Położenie punktu A w układzie współrzędnych poprzedzającym (0):
[
]
T
zA
yA
xA
r
r
r
rA
0
0
0
0
=
Macierze obrotu:
Dla osi X
−
=
θ
θ
θ
θ
θ
cos
sin
0
sin
cos
0
0
0
1
)
,
( X
R
Dla osi Y
=
θ
θ
θ
θ
θ
cos
0
sin
0
1
0
sin
0
cos
)
,
(Y
R
Dla osi Z
−
=
1
0
0
0
cos
sin
0
sin
cos
)
,
(
θ
θ
θ
θ
θ
Z
R
Położenie punktu A w układzie współrzędnych następującym:
[
]
T
zA
yA
xA
r
r
r
rA
1
1
1
1
=
Transformacja obrotu:
A
A
r
R
r
1
1
0
0
=
Przykład: obrót wokół osi X o kąt θ:
−
=
zA
yA
xA
zA
yA
xA
r
r
r
r
r
r
1
1
1
0
0
0
cos
sin
0
sin
cos
0
0
0
1
θ
θ
θ
θ
lub w zwartej postaci:
A
A
r
X
R
r
1
0
)
,
(
θ
=
5. Podstawowe właściwości macierzy rotacji
- Każda z trzech podstawowych macierzy rotacji jest ortonormalna. Po ludzku: macierz
odwrotna do macierzy ortonormalnej jest równa macierzy transponowanej. Można to
udowodnić przemnażając macierz rotacji i transpozycję tej macierzy.
- Końcowy wynik złożenia macierzy obrotów (w rotacjach złożonych) zależy od kolejności
ich wymnażania,
- Macierz rotacji złożonej będącej iloczynem macierzy rotacji podstawowych jest macierzą
ortonormalną (prawdziwe dla dowolnej liczby złożeń rotacji podstawowych)
- Dowolny obrót w układzie współrzędnych może być przedstawiony jako złożenie 3
kolejnych obrotów wokół osi bieżących układów. Należy podawać nazwy tych osi i kąty
obrotu wokół nich (np.: XYZ, ZXZ). Kąty tych obrotów to kąty Eulera. Możliwe jest 12
takich kombinacji. Wszystkie możliwości są poprawne, jednak naturalne jest XYZ:
−
=
=
β
β
β
β
α
α
α
α
γ
β
α
γ
β
α
cos
0
sin
0
1
0
sin
0
cos
cos
sin
0
sin
cos
0
0
0
1
)
,
(
)
,
(
)
,
(
)
,
,
(
,
,
Z
R
Y
R
X
R
R
Z
Y
X
−
1
0
0
0
cos
sin
0
sin
cos
γ
γ
γ
γ
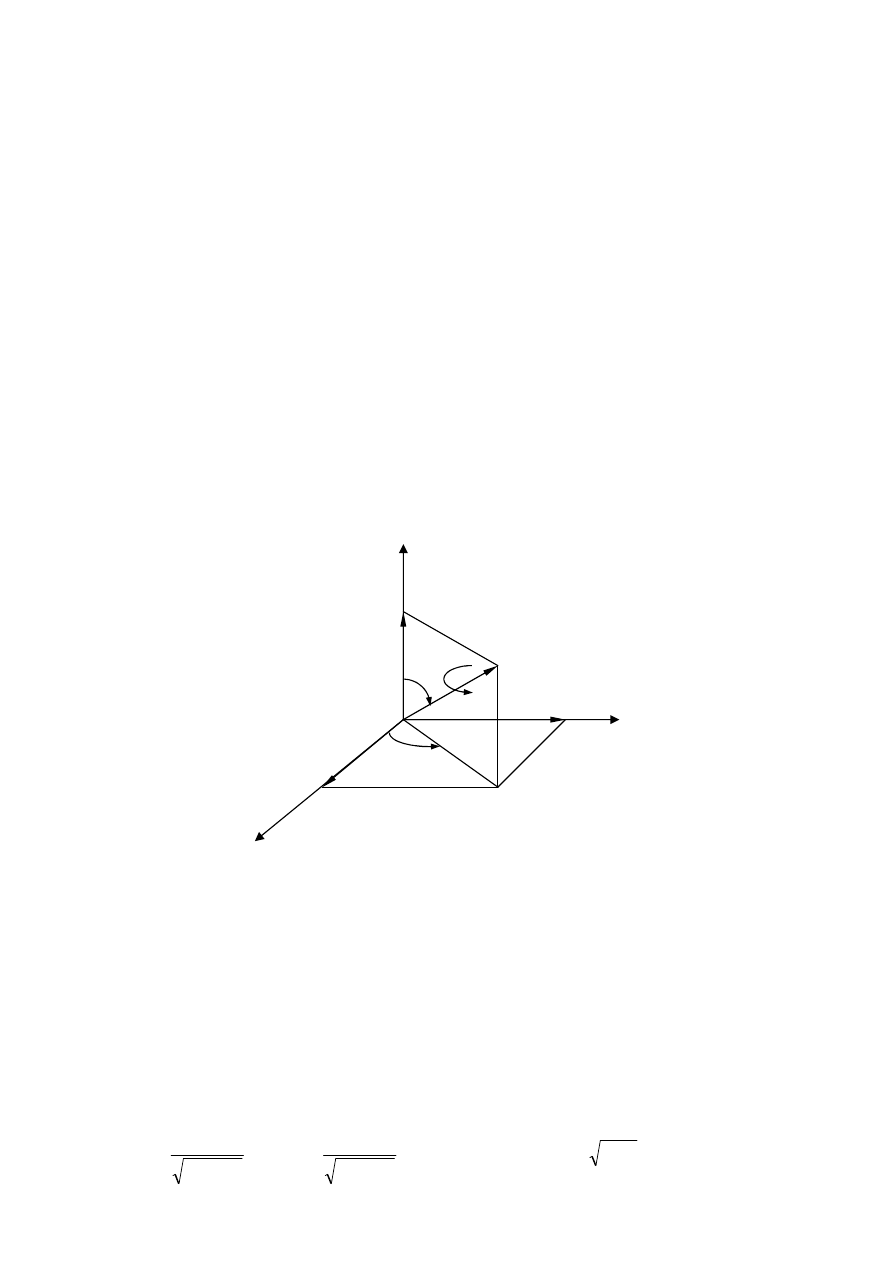
6. Rotacja wokół dowolnej osi o zadany kąt. (str. 23)
Przypadek rotacji o zadany kąt
θ
wokół dowolnie wybranej osi przechodzącej przez początek
układu współrzędnych to przypadek bardziej ogólny. Oś taka może być jednoznacznie
określona przez przyjęcie na niej wektora jednostkowego u= [u
X
u
Y
u
Z
]
T
. Wektor ten oraz
jego składowe pokazane są poniżej:
Rotacja w takim przypadku może być traktowana jako złożenie pięciu kolejnych
podstawowych rotacji:
-
dwóch początkowych rotacji, najpierw o kąt
α
wokół osi Z, a następnie o kąt
β
wokół
bieżącej osi Y. Po tych początkowych rotacjach bieżąca oś Z pokrywa się z kierunkiem
wektora u;
-
rotacji głównej o kąt
θ
wokół bieżącej osi Z;
-
dwóch końcowych rotacji, przeciwnych do rotacji początkowych, najpierw o kąt (-
β
)
wokół bieżącej osi Y, potem o kąt (-
α
) wokół bieżącej osi Z.
Stąd wzór na macierz rotacji złożonej: R(u,
θ
) = R(Z,
α
)R(Y,
β
)R(Z,
θ
)R(Y, -
β
)R(Z, -
α
)
Następnie do powyższego wzoru należy podstawić macierze rotacji podstawowych,
powoduje to powstanie macierzy, w której występują funkcje sinus i cosinus kątów
α
,
β
i
θ
.
Aby uzyskać ostateczną postać tej macierzy należy skorzystać z relacji pomiędzy
składowymi wektora u a funkcjami trygonometrycznymi kątów
α
i
β
:
2
2
cos
Y
X
X
u
u
u
+
=
α
2
2
sin
Y
X
Y
u
u
u
+
=
α
Z
u
=
β
cos
2
2
sin
Y
X
u
u
+
=
β
u
z
u
z
u
y
y
u
x
x
αααα
ββββ
θθθθ
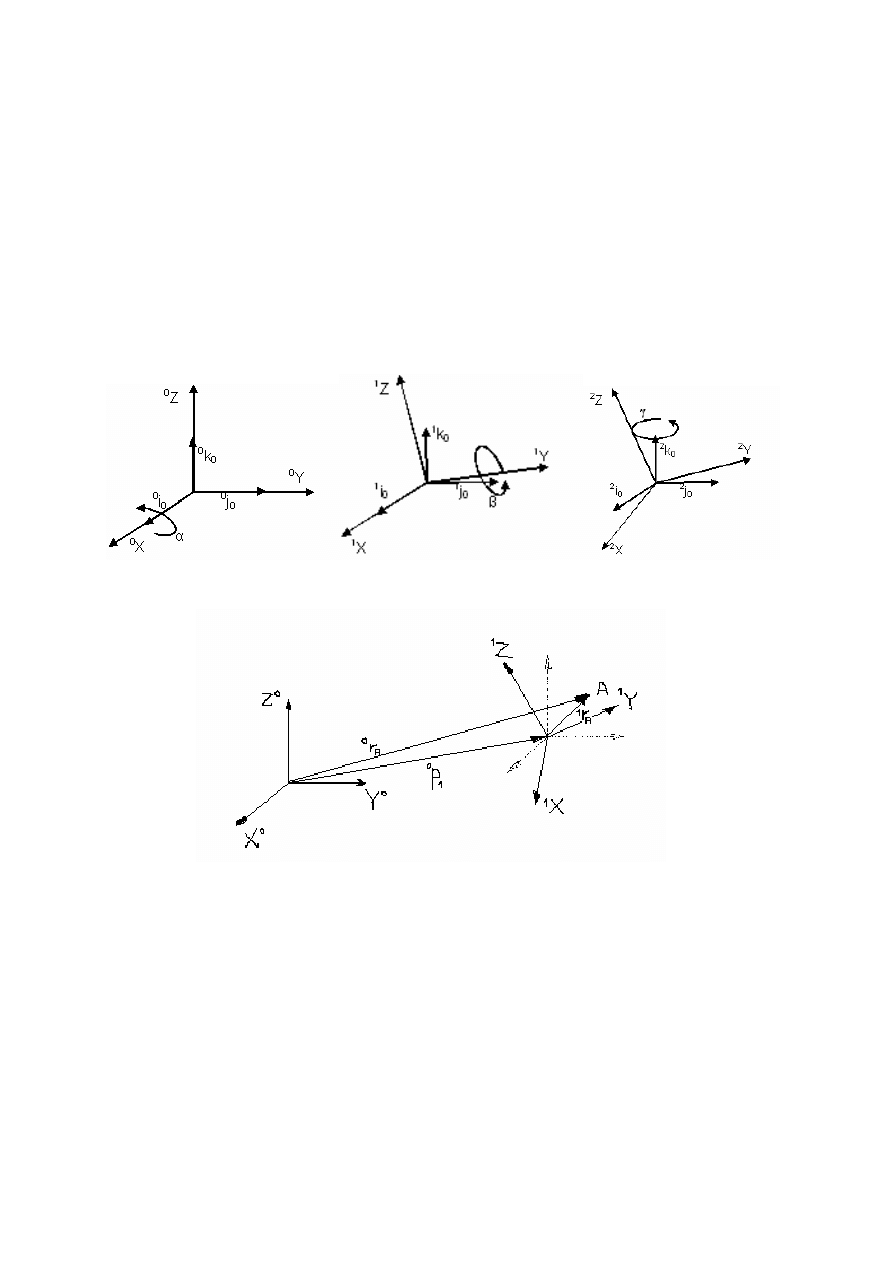
7. Sprawdź czy podana macierz może być macierzą rotacji
Macierze rotacji wokół poszczególnych osi:
−
=
a
a
a
a
X
R
cos
sin
0
sin
cos
0
0
0
1
)
0
,
(
−
=
a
a
a
a
Y
R
cos
0
sin
0
1
0
sin
0
cos
)
0
,
(
−
=
1
0
0
0
cos
sin
0
sin
cos
)
0
,
(
a
a
a
a
Z
R
By sprawdzić czy macierz jest macierzą rotacji należy sprawdzić czy nie jest jedną z tych albo
ich wymnożeniem.
8. Kąty jaw, pitch, roll.
Podstawowym złożeniem obrotów wokół stałych osi są trzy kolejne obroty wokół osi
0
X,
0
Y,
0
Z, odpowiednio o kąty α, β, γ. Układ ten utożsamiamy w tym przypadku z układem
współrzędnych związanym z ostatnim ogni-wem ruchów regionalnych. Aby odpowiednio
zoriento-wać narzędzie w przestrzeni, należy wykonać obroty o odpowiednie kąty wokół osi
tego układu współrzęd-nych. Zwyczajowo kąty te zwane są yaw (po osi X) pitch (po osi Y)
oraz roll (po osi Z). Kąt yaw odpowiada za odchylenie kierunkowe narzędzia, kąt pitch za
pochylenie narzędzia, a roll za jego obrót.
yaw
pitch
roll
Na podstawie rysunku można określić wypadkową postać macierzy rotacji złożonej jako:
(
)
( ) (
) (
)
γ
β
α
γ
β
α
,
,
,
,
,
0
2
0
1
0
0
k
R
j
R
i
R
R
roll
pitch
yaw
=
−
−
9. Transformacje jednorodne – homogeniczne
Najbardziej ogólnym przepadkiem położenia dwóch układów jest przesunięcie i rotacja.
Przesuwamy o wektor
0
P
1
i mamy nowy układ dokonując obrotu tego układu zgodnie z
macierzą rotacji
0
R
1
otrzymuje się układ ostateczny.
Związek pomiędzy opisem dowolnego punktu A w obu układach:
0
r
A
=
0
P
1
+
0
R
1
*
1
r
A
Związek ten jest bardziej złożony przy składaniu tego typu przekształceń gdyż wyrażenia
tracą jednorodność i coraz bardziej się komplikują. Aby zachować jednorodność opisu dla
dowolnych przypadków wzajemnych położeń układów współrzędnych ostatni związek
zapisuje się w postaci zwartej jako:
=
1
1
0
1
1
1
0
1
0
0
A
A
r
p
R
r
Wektory o wymiarach 4x1 i postaci
=
1
r
r)
są nazywane
uogólnionymi wektorami położenia, a niekiedy nazywane są również wektorami
jednorodnymi lub homogenicznymi. Macierz transformacji o wymiarach 4x4
=
1
0
p
R
A
nazywamy jednorodną (homogeniczną) przekształcenia.
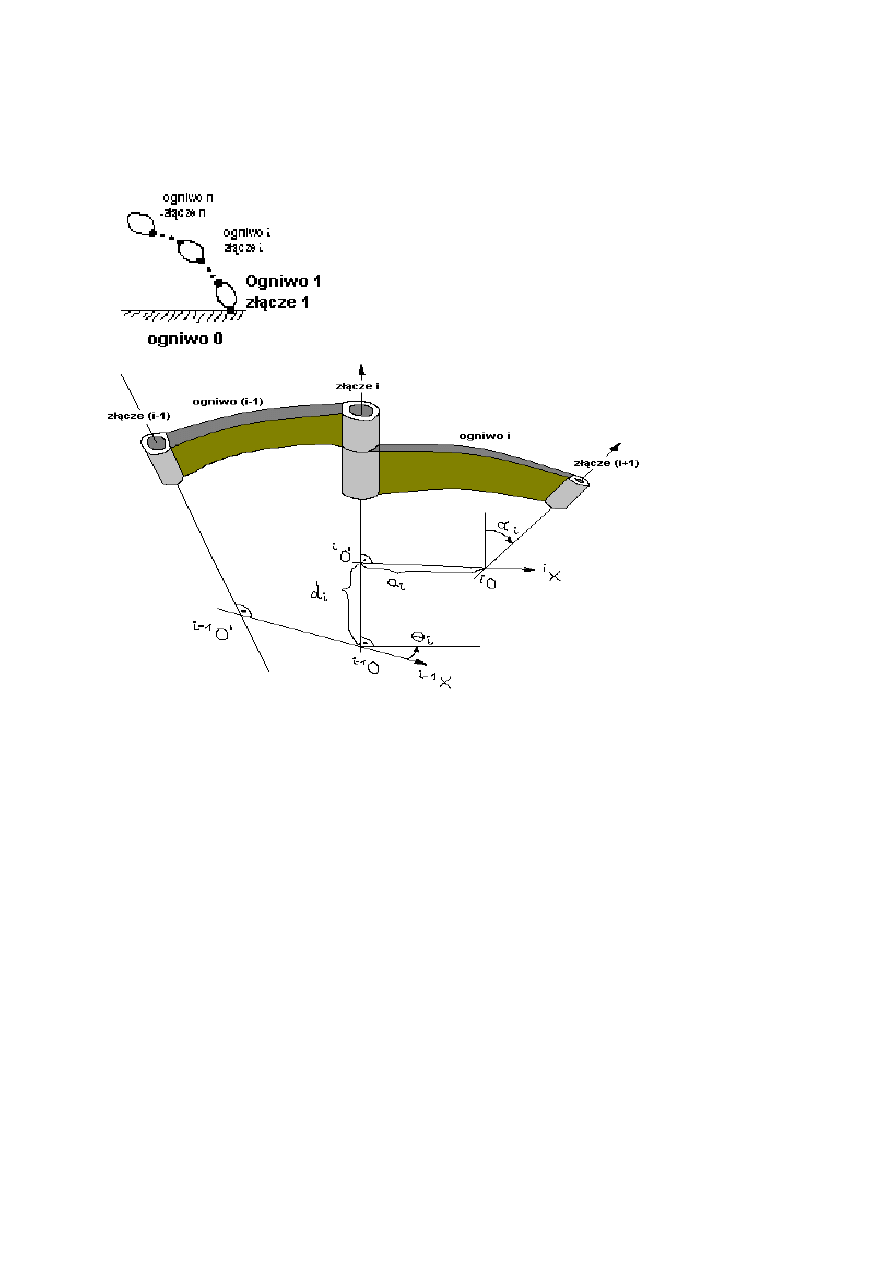
10. Notacja Denavita-Hartenberga
Manipulator robota składa się z szeregu ogniw połączonych złączami. Z każdym złączem
łańcucha kinematycznego można związać kartezjański układ współrzędnych. Przyjmuje się że
za podstawę manipulatora ogniwo 0 a kolejne numeruje się od 1 do n. Złącza numeruje się
kolejno od 1 (przy podstawie manipulatora) do n.
Dwa kolejne złącza wraz z układami współrzędnych które są związane z ogniwami zgodnie z
notacją Denavita-Hartenberga. Z ogniwem i-tym związany jest i – ty układ współrzędnych
taki sposób że:
Oś
i
Z jest osią (i+1) złącza a jej zwrot może być przyjęty dowolnie.
Os
i
X jest wspólną normalną do osi złączy i – tego i (i+1) i skierowana jest w stronę ogniw o
wyższych numerach.
Oś
i
Y jest uzupełnieniem dwóch poprzednich osi do prawoskrętnego kartezjańskiego układu
współrzędnych. Ponieważ jest ona jednoznacznie określona przez położenia osi
i
Z i
i
X
pomija się ją by zwiększyć czytelność rysunku
Zgodnie z notacją Denavita-Hartenberga tylko 4 charakterystyczne wielkości służą
jednoznacznemu określeniu położenia kolejnego układu współrzędnych względem
poprzedniego. Wielkości te to:
- kąt skręcania ogniwa α
i
mierzony wokół osi
i
X od
i-1
Z do
i
Z, zgodnie z zasadą śruby
prawoskrętnej.
- długość ogniwa a
i
mierzona wzdłuż osi
i
X od
i-1
Z do
i
Z
- przesunięcie liniowe w złączu d
i
mierzone wzdłuż osi
i-1
Z od
i-1
X do
i
X
- kąt złącza θ
i
mierzony wokół osi
i-1
Z od
i-1
X do
i
X zgodnie z zasadą próby
prawoskrętnej.

11,12: Kinematyka odwrotna: ogólne problemy i przykład postępowania. Problem
znajdowania wartości kolejnych zmiennych złączowych przy narzuconym położeniu i
orientacji narzędzia. Możliwość rozwiązania zadania kinematyki odwrotnej jest niezwykle
istotna ze względu na efektywność sterowania manipulatorem robota przemysłowego.
Zadania do wykonania przez robota są bowiem w sposób naturalny formułowane w
kategoriach pożądanych położeń i orientacji narzędzia, wyrażonych w układzie kartezjańskim
związanym z podstawą robota. Podwaliny do rozwiązania zadania kinematyki odwrotnej
stanowi znajomość kinematyki prostej manipulatora. Wektor zmiennych złączowych q jest
wyrażony w podzbiorze n-wymiarowej rzeczywistej przestrzeni wektorowej R
n
(przestrzeń
złączowa). Położenie i orientacja narzędzia są związane z podzbiorem przestrzeni R
6
(przestrzeń konfiguracji narzędzia). Do określenia konfiguracji narzędzia może służyć wektor
x należący do R
6
. Trzy składowe tego wektora określają położenie narzędzia, pozostałe trzy
określają orientację narzędzia i są z reguły kątami typu yaw-pitch-roll. W odwrotnym
problemie kinematycznym nie istnieje bezpośrednia i systematyczna procedura pozwalająca
na jego rozwiązanie. W związku z tym każdy robot musi być traktowany indywidualnie. Jest
jednakże kilka cech które mają właściwości ogólne:
Istnienie rozwiązań:
- jeżeli manipulator ma operować w przestrzeni kartezjańskiej, to liczba stopni swobody
łańcucha kinematycznego musi wynosić co najmniej sześć (odstępstwo: narzędzie osiowo
symetryczne – manipulator o pięciu stopniach swobody, do operowania na płaszczyźnie –
trzy stopnie swobody);
- przestrzeń robocza – kształt i wymiary zależą od struktury manipulatora oraz
dopuszczalnych zakresów zmiennych złączowych.
Jednoznaczność rozwiązań:
Przyczyny niejednoznaczności:
- nadmiarowość stopni swobody łańcucha kinematycznego kinematycznego stosunku do
wymiarów przestrzeni zadania;
- występowanie złączy obrotowych w łańcuchu kinematycznym.
Metody rozwiązywania:
Nie można określić ogólnego algorytmu przydatnego do rozwiązywania odwrotnego
zagadnienia kinematycznego dla każdego manipulatora. Metody można podzielić na
analityczne i numeryczne:
- rozwiązania analityczne wykorzystują metodę algebraiczną (przekształcenia
trygonometryczne) lub geometryczną (wykorzystującą geometryczne właściwości figur
płaskich lub przestrzennych do wyznaczania związków pomiędzy zbiorami rozwiązań).
Manipulatory dla których istnieją rozwiązania analityczne charakteryzują się tym, że kąty
skręcania ich ogniw są wielokrotnością kąta π/2. Rozwiązania te są proste, jeżeli trzy kolejne
osie złączy w odcinku ruchów lokalnych przecinają się w jednym punkcie.
Przy podejściu geometrycznym konieczne jest zdekompowanie przestrzennego zagadnienia
geometrycznego do szeregu zagadnień planarnych.

13 Proste i odwrotne zagadnienie kinematyczne dla prędkości
Ruchy manipulatora robota są określane zwykle w przestrzeni konfiguracji narzędzia. W
przestrzeni tej położenie i orientacja narzędzia jest wyrażana przez wektor jreR
6
. Jednakże
wykonywanie założonych ruchów nie odbywa się w sposób bezpośredni, gdyż sterowanie
robota jest realizowane przez układ napędowy robota, który oddziaływuje na poszczególne
złącza manipulatora. Konfiguracja łańcucha kinematycznego jest określona przez wektor
zmiennych złączowych
n
R
q
∈
. Relacja pomiędzy wektorem zmiennych złączowych i
wektorem konfiguracji narzędzia jest określona przez równanie kinematyki prostej
manipulatora
x = f(q)
Zwykle narzucona jest funkcja czasu x(t), którą należy realizować. Wymaga to przeliczenia
tej funkcji na odpowiadającą jej zależność q(t) w przestrzeni złączowej. Sposób przeliczania
zmiennych dla wybranej chwili czasowej omówiono w poprzednim rozdziale i pokazano, że
zadanie takie może być stosunkowo trudne. Jeżeli jednak narzucona funkcja x(t) jest
dostatecznie gładka, to można analizować zależności różniczkowe dla obu tych funkcji.
Użytecznym będzie zwłaszcza znalezienie związku pomiędzy pochodnymi względem czasu
tych funkcji, czyli prędkościami złączowymi i kartezjańskimi.
Ostatnie równanie wektorowe może być zapisane w postaci zbioru sześciu równań
skalarnych o postaci
zatem różniczki zupełne składowych wektora x będą określane przez wyrażenia
Prawe strony tych równań są liniowymi funkcjami przyrostów kolejnych zmiennych
złączowych. Zatem ostatnie równania mogą być zapisane w zwartej postaci wektorowo-
macierzowej jako
dx=J(q)dq.
Tutaj J (q) jest macierzą o wymiarach 6xn zawierającą pochodne cząstkowe funkcji
wektorów ej f (q). Macierz taka znana jest w analizie matematycznej pod nazwą macierzy
Jakobiego i przyjmuje następującą postać
W robotyce macierz J(q) jest nazywana krótko jakobianem manipulatora. Jakobian może być
traktowany jako transformacja wektora prędkości złączowych dq/dt na wektor prędkości w
przestrzeni konfiguracji narzędzia dx/dt, zachodzi bowiem zależność

Lewa strona powyższego związku może być przedstawiona w postaci dwóch składowyd
prędkości. Pierwszą z nich jest prędkość liniowa narzędzia, a drugą jego prędkość kątowa
W przypadku niektórych manipulatorów jakobian jest macierzą o mniejszej niż sześć liczbie
wierszy.
Ze względu na pożądany przebieg trajektorii narzędzia niezbądne jest w wielu
przypadkachznalezienie zależności wektora prędkości złączowych dq/dt w funkcji wektora
prędkości kartezjańskich dx/dt. Tak sformułowany problem nazywa się odwrotnym
zagadnieniem kinematycznym dla prędkości.
Jeżeli jakobian manipulatora jest kwadratową macierzą ieosobliwą, to rozwiązanie tego
zagadnienia jest szczególnie proste i wyraża się wzorem
Jednym z potencjalnych niebezpieczeństw związanych z wykorzystaniem tej zależności jest
utrata rzędu jakobianu, wtedy nie istnieje rozwiązanie odwrotnego zagadnienia
kinematycznego dla prędkości, gdyż nie można wyznaczyć macierzy odwrotnej J
-1
(q).
Konfiguracje, przy których macierz jakobian traci rząd, są nazywane konfiguracjami
osobliwymi, a odpowiadające im punkty w przestrzeni złączowej lub przestrzeni
konfiguracji narzędzia są nazywane punktami osobliwymi.
Jeżeli jakobian jest macierzą kwadratową, to zbiór punktów osobliwych otrzymuje się
rozwiązując równanie
Det(J(q)) = 0
14. Metoda wyznaczania modelu dynamiki manipulatora – podstawy. Złożone układy
zawierające podzespoły mechaniczne można modelować stosując formalizm Lagrange’a.
Bazuje on na zdefiniowaniu uogólnionych współrzędnych określających położenie mas i
uogólnionych sił działających na te masy. Dla manipulatora składającego się z szeregu ogniw
połączonych złączami, które zapewniają n stopni swobody mechanicznej definiuje się
uogólniony wektor położenia q=[q
1
q
2
… q
n
]
T
.
Podobnie definuje się wektor uogólnionych sił
działających działających kolejnych złączach τ=[τ
1
τ
2
... τ
n
]
T
, przy czym składowa τi wektora
sił odpowiada składowej qi wektora położeń, tzn. że są one albo wielkościami
charakterystycznymi dla ruchu liniowego (siła i położenie) albo obrotowego (moment siły i
położenie kątowe). Niech Ek i Ep oznaczają energię kinetyczną i potencjalną wszystkich mas
układu. Definiuje się funkcję Lagrange’a jako różnicę pomiędzy całkowitą energią kinetyczną
układu a jego całkowitą energią potencjalną.
)
(
)
,
(
)
,
(
q
E
q
q
E
q
q
L
p
k
−
≡
&
&
E
k
– zależy od wektora położeń i wektora prędkości
E
p
– zależy od wektora położeń
Ogólne związki pomiędzy funkcją Lagrange’a i siłami działającymi w złączach mogą być
wyrażone w postaci układu n równań skalarnych postaci
n
i
l
q
L
q
L
dt
d
i
i
i
≤
≤
=
∂
∂
−
∂
∂
,
)
(
τ
&
nazywanych równaniami Eulera-Lagrange’a. Należy pamiętać, że przy wyznaczaniu
pochodnych cząstkowych funkcji Lagrange’a zmienne q
i
i q
i
(z kropką na górze) traktowane
są jako wzajemnie niezależne.

15. Ogólna postać modelu dynamiki manipulatora.
Zakładamy że manipulator posiada n stopni swobody, a z jego łańcuchem kinematycznym
związane są lokalne układy współrzędnych. Aby wyznaczyć równanie modelu, należy
najpierw określić ogólną postać funkcji Lagrangea a następnie skorzystać z równań Eulera -
Lagrangea. W i – tym lokalnym układzie współrzędnych energia kinetyczna poruszającego
się elementu jest równa: dE
ki
=0.5||v||
2
dm
i
= 0.5(v
x
2
+v
y
2
+v
z
2
)dm
i
… całkowitą energię
kinetyczną i – tego można uzyskać poprzez scałkowanie elementarnej energii po wszystkich
elementach tego ogniwa. W przypadku gdy ogniwo może być traktowane jako ciało sztywne
jedynym źródłem energii potencjalnej jest grawitacja. Niech g =[gx, gy, gz 0]
T
oznacza
uogólniony wektor grawitacji wyrażony w układzie podstawowym. Wtedy energia
potencjalna elementu dm
i
którego położenie w układzie jest określone przez wektor r = T
i
*
i
r
przyjmuje postać: dE
pi
=-g
T
*r dm = -g
T
T
i
i
r dm ... energia potencjalna ogniwa i jest
otrzymywana po scałkowaniu wyrażenia po całej masie ogniwa.
i
i
i
T
mi
mi
i
i
T
pi
m
r
T
g
dm
r
T
g
dE
E
ˆ
ˆ
−
=
−
=
=
∫
∫
równania na energię kinetyczną i potencjalną pozwalają na określenie postaci funkcji
Lagranga całego manipulatora. Funkcję tą wstawiamy do l-tego równania Eulera-Lagranga i
wykonujemy wskazane przez nią całkowania. Kolejne różniczkowe równania skalarne dla
wartości l=1,2…n mogą być ostatecznie zestawione w jedno równanie wektorowo
macierzowe, które stanowi pełny opis dynamiki manipulatora:
τ
=
+
+
)
(
)
,
(
)
(
q
h
q
q
c
q
q
B
&
&
&
B-macierz inercji operatora nxn, c(q,q) wymiar nx1 wektor sprzężeń predkościowych lub sił
Coriolisa i sił dośrodkowych, h(g) – wektor sił grawitacyjnych,
τ
wymiar nx1 zawiera
uogólnione siły generowane przez zespoły napędowe w kolejnych złączach – wektor sił
złączowych.
16.Rodzaje pracy robota przemysłowego:
-ruch PTP (point to point) wystempuje w prostych czynnosciach manipulacyjnych jak
przenoszenie obiektów .Wartosci zadane w tego typu ruchu to położenie końcowe i oriętacja
efektora oraz czas trwania ruchu .nie istotny jest kształt toru.
-ruch MP multipoints wielopunktowy: gdy na drodze występują przeszkody należy je ominąć
wprowadzając dodatkowe punkty pośrednie oraz przyjmując pożądane czasy trwania etapów
między punktami ,dązymy do minimalizacji czasu trwania.
-ruch PC (path control) odtwarzanie zadanej ciągłej ścieżki (malowanie spawanie) tylko w
robotach o możliwości płynnego stewrowania każdej z osi.
17.
Planowanie trajektorii przy pomocy metody wielomianów stopnia trzeciego.
Zostanie rozważony problem przemieszczenia efektora z położenia początkowego do
zadanego położenia końcowego przy narzuconym czasie ruchu (t
f
-t
o
). Rozwiązując zadania
kinematyki odwrotnej dla obu krańcowych punktów można otrzymać wektory zmiennych
złączowych
q
o
i
q
f
. Istnieje nieskończenie wiele gładkich funkcji
q
r
(t), które mogą być użyte
do interpolacji pomiędzy punktami. Funkcja powinna być możliwie prosta, aby generowanie
jej nie obciążało nadmiernie sterownika robota. Istnieją co najmniej cztery węzły narzucone
na q
r
(t), w chwilach t
o
i t
f
. Dwa pierwsze wynikają z narzuconych położeń w tych chwilach,
czyli q
r
(t
o
)=q
o
i q
r
(t
f
)=q
f.
Dwa pozostałe wynikają z faktu, że w obu krańcowych położeniach
prędkości powinny być równe zeru, czyli q(to)=q(tf)=0. Te cztery warunki mogą być
spełnione na przykład przez wielomian stopnia trzeciego o ogólnej postaci: q
r
(t)=a
o
+a
1
(t-
t
o
)+a
2
(t-t
o
)
2
+a
3
(t-t
o
)
3
. Różniczkując względem czasu tę funkcję otrzymuje się przebieg zadanej
prędkości: q
r
(t)=a
1
+2a
2
(t-t
o
)+3a
3
(t-t
o
)
2
. Postać gładkiej trajektorii łączącej oba końcowe
punkty
3
0
3
0
2
0
2
0
0
)
(
)
(
)
(
2
)
(
)
(
)
(
3
)
(
t
t
t
t
q
q
t
t
t
t
q
q
q
t
q
f
o
f
f
o
f
r
−
−
−
−
−
−
−
+
=
stąd prędkość na tej trajektorii
będzie wielomianem stopnia drugiego
2
0
3
0
0
2
0
0
)
(
)
(
)
(
6
)
(
)
(
)
(
6
)
(
t
t
t
t
q
q
t
t
t
t
q
q
q
t
q
f
o
f
f
o
f
r
−
−
−
−
−
−
−
+
=
•
a przyśpieszenie będzie miało charakter liniowy
)
(
)
(
)
(
12
)
(
)
(
6
)
(
0
3
0
2
0
0
t
t
t
t
q
q
t
t
q
q
q
t
q
f
o
f
f
o
f
r
−
−
−
−
−
−
+
=
•
•
Z ostatniej postaci wynika, że na obu końcach trajektorii zadanej będą występowały skoki
przyśpieszenia, co oczywiście jest wadą zastosowanego podejścia.
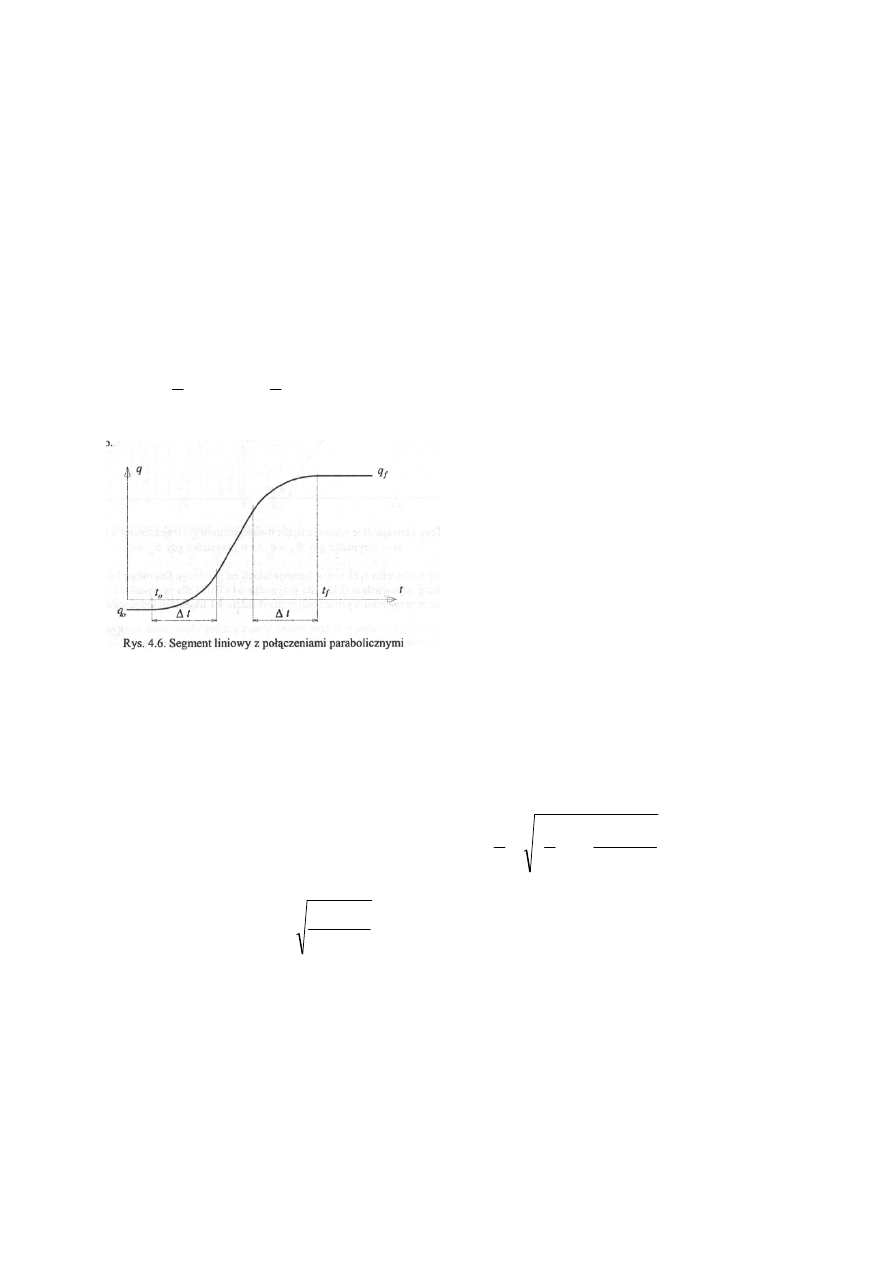
18. Planowanie trajektorii metodą odcinków liniowych ze złączkami parabolicznymi.
Najprostszą postacią funkcji łączącej punkt początkowy z końcowym dla trajektorii
jednosegmentowej jest:
f
f
f
r
t
t
t
t
t
t
t
q
t
t
a
a
q
t
q
>
≤
≤
<
−
+
=
0
0
0
1
0
0
)
(
)
(
Tylko że funkcja ta charakteryzuje się skokami prędkości zadanej w punktach początkowym i
końcowym. Aby wygenerować dostatecznie gładką funkcję można do tego liniowego
przebiegu dodać dwa paraboliczne połączenia które zapewnią ciągłość prędkości na takiej
trzyodcinkowej trajektorii. Na odcinkach parabolicznych prędkość zmiana się liniowo w
czasie a przyśpieszenie ma wartość stałą.
Założenia początkowe: oba połączenia paraboliczne charakteryzują się taką samą
bezwzględną wartością przyśpieszenia
m
q
..
wtedy przebieg q(t) będzie symetryczny względem
punktu
(
) (
)
+
+
f
f
q
q
t
t
0
0
2
1
,
2
1
. Odcinki paraboliczne muszą być tak dobrane aby
spełniać więzy dla prędkości
( )
0
)
(
.
=
=
f
t
q
t
q
&
. Przebieg taki przedstawia rysunek:
Podstawą wyznaczenia zależności pozwalających na zaplanowanie jednosegmentowej
trajektorii jest porównanie prędkości na końcu odcinka parabolicznego z prędkością na
odcinku liniowym z uwzględnieniem symetrii względem punktu środkowego.
Ostatecznie otrzymujemy równanie kwadratowe w którym niewiadomą jest czas trwania
odcinka parabolicznego
∆
t:
0
)
(
)
(
0
2
=
−
+
∆
−
∆
q
q
t
q
t
q
f
m
m
τ
&
&
&
&
gdzie
0
t
t
f
−
=
τ
Tylko jedno rozwiązanie posiada sens fizyczny:
m
f
q
q
q
t
&
&
0
2
2
2
−
−
−
=
∆
τ
τ
Aby wyrażenie podpierwiastkowe było dodatnie należy przyjąć wystarczająco długi czas
trwania segmentu:
m
f
q
q
q
&
&
0
2
−
⋅
≥
τ
Gdy w ostatnim wzorze zachodzi równość to czas trwania części liniowej spada do zera i
trajektoria składa się z faz rozpędzania i hamowania.
W bardziej ogólnym przypadku projektowania należy rozważyć trajektorię wielosegmentową
gdzie pod uwagę bierzemy niezależnie każdą składową wektora q
r
(t). Jednakże wówczas
należy mieć na uwadze że wewnętrzne punkty trajektorii stają się punktami przybliżonymi. W
związku z tym zakłada się że trajektoria powinna w zasadniczych fragmentach każdego z
segmentów przebiegać wzdłuż prostych łączących punkty węzłowe a w pobliżu każdego
punktu węzłowego wprowadzane jest połączenie paraboliczne pozwalające na gładkie
przejście do kolejnego segmentu.
Odchylenie od punktów pośrednich maleje w miarę wzrostu przyśpieszeń zespołów
napędowych które oczywiście mają zawsze ograniczone wartości .
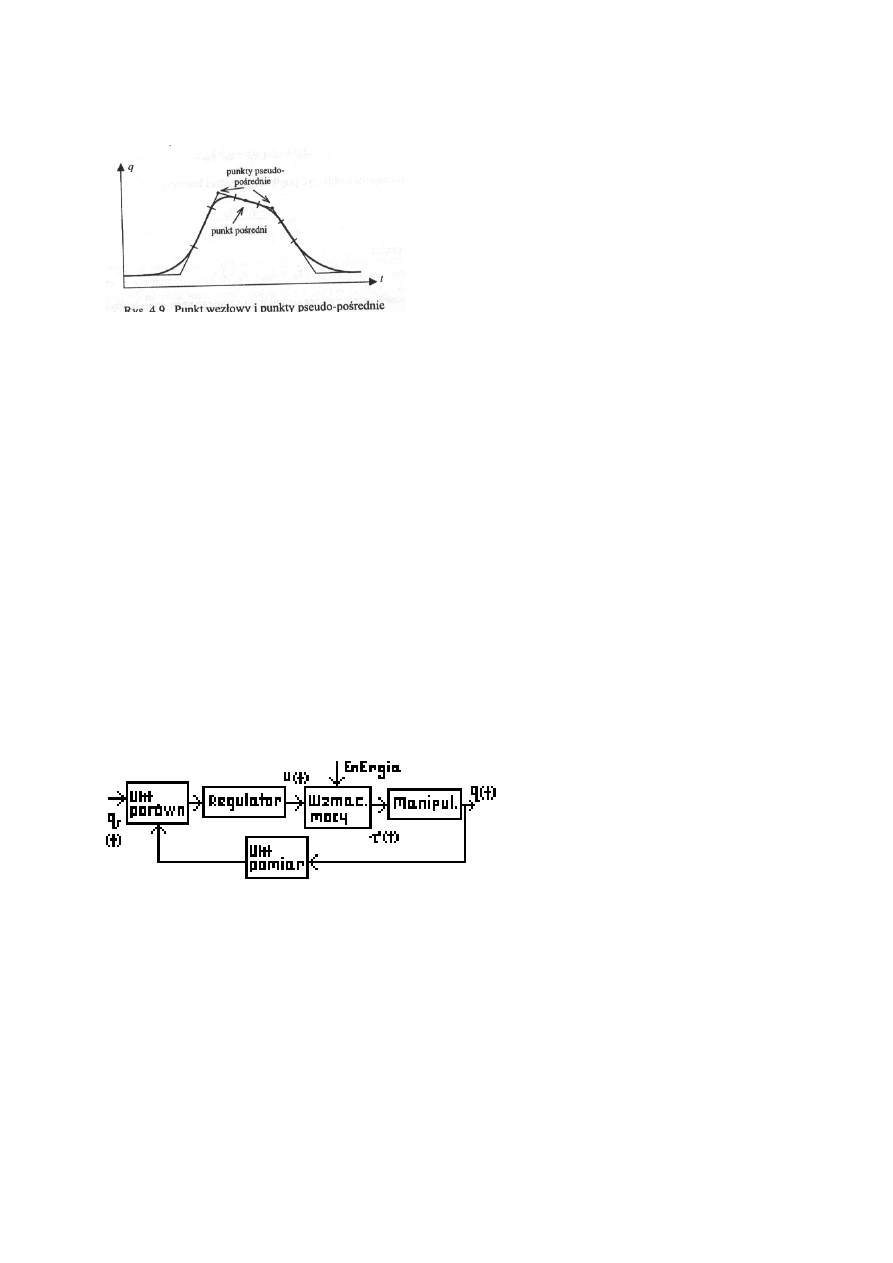
Taki sposób nie budzi zastrzeżeń w przypadku punktów pośrednich które wprowadzamy
tylko w celu ominięcia przeszkód.
Jednak metodę tę można udoskonalić tak by zapewnić dokładne przejście przez punkt
węzłowy. W tym celu wprowadza się pseudo-punkty leżące na prostej przechodzącej przez
zadany punkt i znajdujące się po obu jego stronach.
Minimalna odległość między tymi punktami musi być tak dobrana aby oba odcinki
paraboliczne połączyły się w punkcie węzłowym. Jest oczywiste że wprowadzenie dwóch
punktów pośrednich wydłuża czas realizacji trajektorii.
19. Ogólna struktura układu sterowania pozycyjnego robota.
Podstawowym zadaniem układu sterowania robota jest takie sterowanie zespołów
napędowych, aby efektor robota możliwie najdokładniej realizował zadaną trajektorię.
Najpopularniejszym rodzajem pracy robota jest realizacja ruchów jego manipulatora w
przestrzeni swobodnej, bez kontaktu z elementami otoczenia. Takie operacje jak przenoszenie
detali zawierają oczywiście fragmenty ruchów, w których występuje kontakt z otoczeniem,
lecz czas tego kontaktu jest stosunkowo niewielki w porównaniu do ogólnego czasu ruchu
efektora. Zatem warto tak planować trajektorię ruchów swobodnych i realizować ją w sposób
możliwie dokładny, aby zwiększyć szybkość wykonywania operacji technologicznych.
Układ sterowania robota, podobnie jak układ sterowania każdego obiektu dynamicznego,
składa się z szeregu typowych podzespołów tworzących razem zamknięty układ regulacji.
Cechą zamkniętego układu regulacji jest bieżące porównanie zachowania się przebiegów
wyjściowych układu z założonymi i takie sterowanie obiektu, aby minimalizować uchyb
regulacji.
Ogólna struktura zamkniętego układu sterowania pozycyjnego robota.
Manipulator jest wielowymiarowym obiektem regulacji, stąd wszystkie zaznaczone na tym
rysunku sygnały są n – wymiarowymi wektorami, a przedstawione produkty są faktycznie
złożone z n podzespołów. Zespoły napędowe manipulatora są zasilane ze wzmacniaczy mocy,
w sposób narzucony przez regulator. Z kolei regulator wypracowuje swój sygnał wyjściowy
na podstawie porównania trajektorii zadanej z trajektorią rzeczywistą. Najczęściej
porównanie to ma postać wypracowania aktualnego wektora uchybu regulacji
e(t) = q
r
(t) - q(t), chociaż w niektórych układach regulacji uwzględnia się historię przebiegu
tego uchybu lub prędkość zmian uchybu regulacji
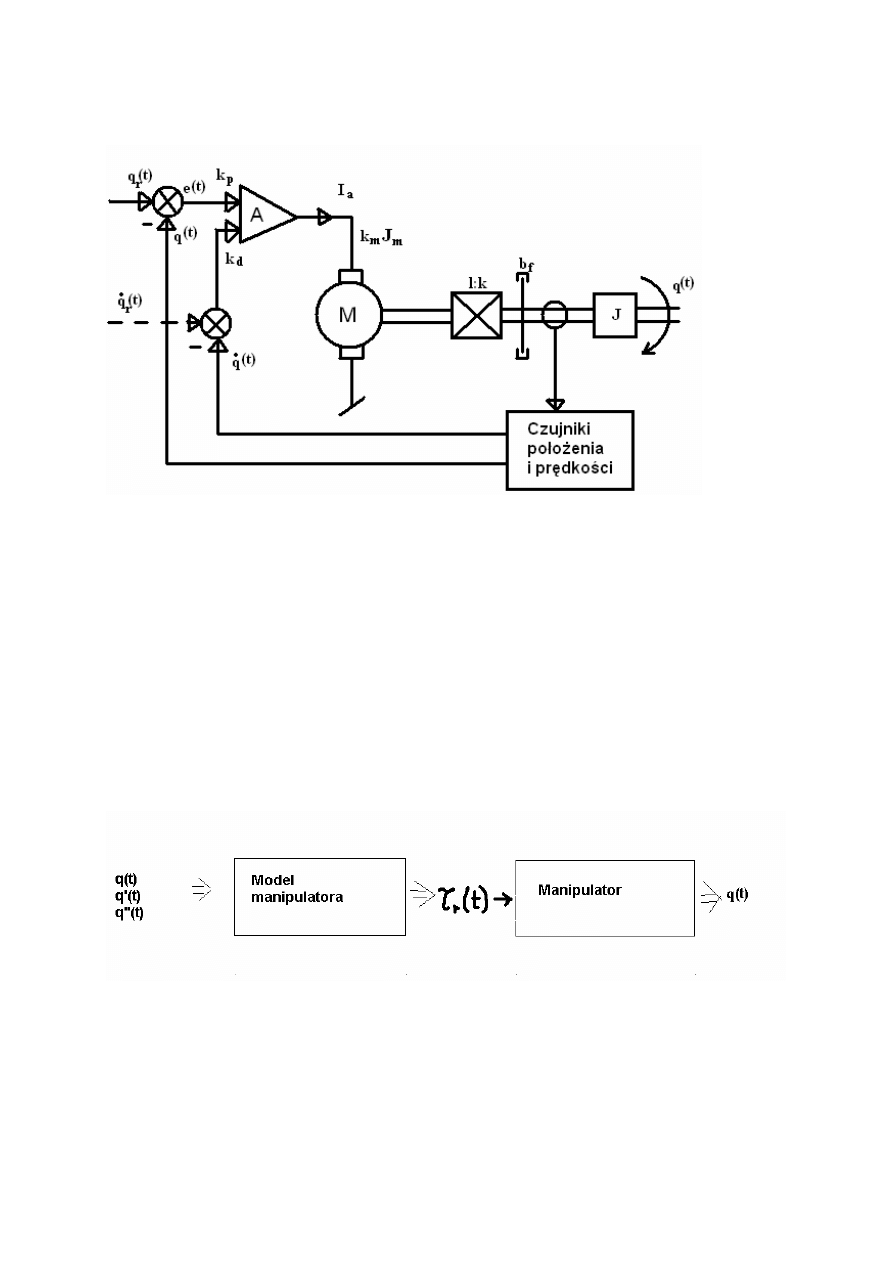
20.Klasyczny układ sterowania robota.
Większość robotów przemysłowych jest wyposażona w zespoły napędowe z silnikami prądu
stałego i przekładniami redukującymi prędkość obrotową. Każdy zespół napędowy jest
sterowany w układzie zamkniętym ze sprzężeniem pozycyjnym tworząc tak zwany
serwonapęd pojedynczej osi. Typową strukturę tego układu przedstawia poniższy rysunek.
Silnik prądu stałego jest sterowany prądowo ze wzmacniacza mocy generującego I
a
, moment
bezwładności wirnika J
m
. Wirnik silnika jest połączony ramieniem manipulatora przez
przekładnie mechaniczną o przełożeniu 1:k. Wielkość J
i
jest efektywną bezwładnością
ramienia widzianą z wału wyjściowego przekładni a b
f
jest współczynnikiem tarcia
wiskotycznego. Układ sensoryczny służy do pomiaru położenia złącza q(t) i jej prędkości
q*(t). Liniowy sterownik składa się ze wzmacniacza mocy, a jego sygnał wyjściowy jest
generowany na podstawie uchybu położenia uwzględnianego ze współczynnikiem wagowym
k
p
i sprzężenia prędkościowego uwzględnianego ze współczynnikiem wagowym k
p
.
21.Metoda wyznaczonego momentu.
Model dynamiki sztywnego manipulatora: B(q)q’’+c(q,q’)+h(q)+f(q,q’)=
τ
gdzie B(q) inercja
manipulatora, c(q,q’) siły sprzeżeń prędkościowych h(q) siły grawitacyjne f(q,q’) siły
tarcia.Na podstawie tego równania możemy dla każdej zadanej trajektorii qr(t) wyznaczyć
odpowiadający jej przebieg wektora uogólnionych sił napędowych
τ
r(t) gdy trajektoria jest
dostatecznie gładka to możliwe jest wygenerowanie przebiegu wektora sił napędowych przez
zespół napędowy robota.
23.Struktura układu napędowego oraz ogólne właściwości napędów robotów.
Podstawowymi podzespołami systemu napędowego robota są: źródło energii pierwotnej,
konwerter energii, zespoły sterowanych zaworów, elementy wykonawcze – którymi są
siłowniki lub silniki wraz z przekładami, układy pomiarowe, regulatory poszczególnych osi
oraz sterownik nadrzędny. Pokazana struktura systemu napędowego robota nie zależy od
tego jaki jest rodzaj napędu (elektryczny, hydrauliczny, pneumatyczny). W tych 3
przypadkach są inne elementy wykonawcze, zespoły sterowanych zaworów oraz konwerter
energii. Pozostałe elementy będą bardzo podobne, dotyczy to zwłaszcza sterownika
nadrzędnego i regulatorów osi. Urządzenia do pomiaru położenia i prędkości osi w zasadzie
nie zależą od czynnika energetycznego przekształcanego na pracę mechaniczną, a związane
są raczej z rodzajem złącza. Podstawowe właściwości napędów: Całkowita sprawność, Moc z
jednostki masy napędu, maksymalna siła z jednostki powierzchni czynnej.

24. Cechy charakterystyczne napędów elektrycznych robotów.
Napędy elektryczne są powszechnie stosowane w robotach stacjonarnych i mobilnych.
Spowodowane to jest m. in. następującymi ich zaletami:
-
Prosty sposób dostarczania i konwersji energii
-
Dobre dostosowanie do sterowania elektronicznego
-
Wysoka sprawność energetyczna
-
Dokładność i powtarzalność lepsza niż w przypadku napędów płynowych
-
Nie zanieczyszczanie środowiska i stosunkowo cicha praca
Napędy elektryczne stosowane w robotyce charakteryzują się zakresem generowanych
momentów napędowych od 0.1 – 100 Nm i mocą 0.1 – 10 kW. Kw. W odróżnieniu od
silników elektrycznych ogólnego stosowania,
silniki do robotów musza posiadać
następujące cechy:
-
Mała bezwładność wirnika
-
Duża wartość momentu generowanego w stosunku do masy silnika
-
Duża wartość stosunku momentu szczytowego do nominalnego
-
Duży zakres regulowanej prędkości obrotowej
-
Gładki ruch wirnika z ograniczoną pulsacja prędkość i momentu
-
Wysoka precyzja pozycjonowania napędu
-
Czterokwadrantowa praca, czyli praca silnikowa lub prądnicowa w obu kierunkach
(możliwa do uzyskania dzięki zastosowaniu wzmacniaczz z modulacją szerokości
impulsów)
Charakterystyka zespołu napędowego zależy także od podzespołów mechanicznych i
elektronicznych oraz sposobu wewnętrznego sterowania. Pożądane jest, aby układ napędowy
zachowywał się w przybliżeniu jak element proporcjonalny, czyli aby sygnał wyjściowy
stosunkowo szybko i bez przeregulowań dochodził do zadanej wartości określonej przez
poziom sygnały wejściowego.
Istnieją 2 grupy napędów elektrycznych stosowanych w robotyce:
-
Napędy z wysokoobrotowym silnikiem i przekładnią redukcyjną – najpopularniejsze;
przekładnia redukuje prędkość i powiększa generowaną siłę; najczęściej stosowane są
silniki o 1500-6000 obr/min i przekładni 1:50 – 1:200
-
Bezprzekładniowe napędy z wysokomomentowym silnikiem
Rodzaje silników stosowanych w napędach z przekładnią redukcyjną:
-
Silniki pradu stałego z mechanicznym komutatorem i magnesami trwałymi
-
Bezszczotkowe silniki z magnesami trwałymi – większa niezawodność, bo nie ma
komutatora, mniejsze zakłócenia el-magn., lepsze odprowadzanie ciepła z uzwojeń,
mniejsza inercja wirnika, waga i wymiary niż klasyczny silnik
-
Silniki krokowe – z magnesami trwałymi na wirniku – mała sprawność <- ograniczony
zakres generowanych momentów, używane w małych robotach; o zmiennej reluktancji –
przyspieszenie wirnika nieciągłe, wymagają specjalnej procedury sterującej zasilaniem
poszczególnych cewek, używane w robotach specjalnych precyzyjnych
-
Silniki indukcyjne – prosta konstrukcja, niezawodność, duży zakres prędkości obrotowej i
moment napędowy przy zatrzymanym wirniku, duża sprawność energetyczna, trudne
sterowanie -> wąskie zastosowanie
25.Cechy napędów pneumatycznych.
Napędy pneumatyczne są obecnie stosowane w lekkich manipulatorach robotów
przemysłowych o stosunkowo małej dokładności i robotach kroczących bez względu na ich
strukturę kinematyczną. Podstawową zaletą układów pneumatycznych jest prostota
konstrukcji, niski koszt i wysoka niezawodność pracy. Napędy te mogą być również z
powodzeniem stosowane w środowiskach wybuchowych lub narażonych na promieniowanie
radioaktywne, gdzie stosowanie napędu elektrycznego jest wykluczone.
Cechy napędów pneumatycznych robotów: siłowniki jednostronnego działania ze sprężyną
zwrotną, siłowniki dwustronnego działania, siłowniki beztłoczyskowe o sprzężeniu
magnetycznym.

26.Czujniki położenia i prędkości stosowane w robotyce.
Podstawowymi sensorami wewnętrznymi pośrednimi są czujniki położenia. Najczęściej
stosowane są następujące rodzaje czujników: potencjometry, transformatorowe czujniki
położenia kątowego (resolwery), przetworniki kodowe, przetworniki obrotowe-impulsowe.
Prędkość w ruchu obrotowym czy liniowym może być otrzymywana przez różniczkowania
położenia względem czasu. W zasadzie można stosować tę metodę w dwóch wariantach. W
pierwszym różniczkowanie odbywa się w sposób analogowy, w drugim cyfrowy. Obie te
metody są wykorzystywane we współczesnych robotach przemysłowych. Do pomiaru
prędkości z wykorzystaniem różniczkowania analogowego stosowane są prądniczki
tachometryczne (liniowy związek pomiędzy siłą elektromotoryczną indukowaną w cewce a
pochodną strumienia magnetycznego skojarzonego z tą cewką). Do cyfrowego stosuje się
przetworniki obrotowo-impulsowe lub obrotowo kodowe i opiera się na przybliżaniu
pierwszej pochodnej położenia kątowego przez odpowiednią różnicę pierwszego rzędu.
27.Czujniki sił i momentów stosowane w robotyce.
głównie stosujemy metody bezpośrednie –nadgarstkowy czujnik sił uogólnionych czujnik jest
przed uchwytem narzędzia czujnik ten zawiera element o kształcie krzyża na każdym z
ramion są czujniki odkształceń działające na zasadzie zmienej rezystancji na podstawie
pomiaru rezystancji można wnioskować o siłach działających w 3 kierunkach. Ortogonalnych
oraz momentow sił wokół tych osi.-czujniki palcowe umieszczane na wewnętrznych
częsciach chwytaka są to elementy z pasków elastycznych przewodzących na podstawie
pomiaru rezystancji uzyskujemy informacje o pochwyceniu elementu .Bardziej wyrafinowana
wersja to zespół pasków lub walcow łączonych w wiersze i kolumny co ułatwia ich
polączenie i zastosowanie.
28.Kierunki rozwoju systemów sensorycznych robotów.
Współczesny rozwój robotyki wskazuje na potrzebę szerszego wykorzystania zewnętrznych
sensorów położenia. Są nimi zwykle czujniki optoelektroniczne, w tym laserowe, czujniki
ultradźwiękowe oraz systemy wizyjne, Szczególne nadzieje związane są z systemami
wizyjnymi robotów przemysłowych. Istnieje już wiele udanych aplikacji przemysłowych z
wykorzystaniem kamer CDD. Zwykle stosowany jest standard telewizyjny polegający na
akwizycji obrazów z częstotliwością 25Hz. Systematycznie tanieją kamery i przetworniki o
bardzo dużych szybkościach akwizycji obrazów (do 1000 na sekundę), które pozwalają już na
efektywną realizację sprzężenia wizyjnego w torze sterowania robota przemysłowego.
29.Metody programowania robotów.
Programowanie robota to wprowadzenie do pamięci sterownika wszystkich informacji
niezbędnych do realizacji pożądanych trajektorii i interakcji z otoczeniem. Metody
programowania robotów można podzielić na trzy grupy: programowanie sekwencyjne,
programowanie przez uczenie, programowanie tekstowe.
Cechy programowania sekwencyjnego.
Programowanie sekwencyjne było powszechnie stosowane w starszych konstrukcjach
robotów z napędami hydraulicznymi lub pneumatycznymi i jest w dalszym ciągu stosowane
w konstrukcjach, które nie posiadają możliwości pomiaru bieżących wartości zmiennych
złączowych. Na każdej osi robota umieszczony jest zestaw mikro-wyłączników
mechanicznych lub fotoelektrycznych. Po zadaniu pozycji ograniczników ruchu osi,
programowanie sprowadza się do zadawania kolejności ruchów osi oraz zaciskania lub
zwalniania chwytaka. W każdym kroku wykonywany jest ruch tylko jednej osi określonego
położenia. W pierwszych robotach wykorzystujących tą metodę, programowanie odbywało
się za pomocą matrycy diodowej – wiersze odpowiadały poszczególnym osiom manipulatora,
a kolumny kolejnym krokom programu. Później matryca diodowa została zastąpiona
pamięciami elektrycznymi programowanymi przy użyciu prostej klawiatury.
Zaletą tej metody programowania jest bardzo duża prostota i czytelność struktury programu.
Podstawową wadą jest brak możliwości koordynacji ruchów w kilku złączach. Zatem metoda
ta jest odpowiednia do programowania prostych, powtarzalnych czynności manipulacyjnych,
typowych dla obsługi maszyn. Nie można jednak realizować ruchów po zadanych torach,
gdyż należałoby przedstawić je w postaci dyskretnych punktów w przestrzeni roboczej, a na
to nie pozwala z reguły pojemność pamięci.
Programowanie przez uczenie.
Polega na przeprowadzeniu manipulatora wzdłuż zadanej trajektorii przy jego ręcznym
sterowaniu, z wykorzystaniem panelu sterowania i zapamiętaniu tej trajektorii. Panel
sterowania służy do niezależnego zadawania ruchu poszczególnych osi, przy czym w fazie
uczenia sterowanie osi odbywa się w torze otwartym. Sygnały wyjściowe systemu sensorów
wewnętrznych są wykorzystywane do zapamiętywania trajektorii z dostatecznie dużą
rozdzielczością. Panel sterowania często jest wyposażony w joystick ułatwiający
sprowadzenie efektora do pożądanej pozycji. Z panelu sterowania wprowadzane są również
instrukcje dodatkowe: otwieranie i zamykanie chwytaka, czekanie przez określony czas,
nadawanie odpowiednich wartości dwustanowym wyjściom zewnętrznym uruchamiającym
inne urządzenia. Kolejne instrukcje podstawowe i dodatkowe są zapamiętywane w pamięci
programu i w trakcie jego wykonywania są poddawane interpretacji. Programowanie przez
uczenie zapewnia kontrolowanie procesu tworzenia instrukcji, umożliwia ich graficzne
przedstawianie na odpowiednich wyświetlaczach oraz poprawianie wprowadzonych
instrukcji.
Programowanie tekstowe.
Polega na tworzeniu w trybie off-line symbolicznego zestawienia pożądanych operacji robota
przy użyciu języka programowania. Instrukcje języka opisują podstawowe ruchy robota,
działanie chwytaka i obsługę wejść i wyjść układu sterowania. Poszczególne pozycje
manipulatora są reprezentowane przez zmienne nazwowe stanowiące parametry formalne
instrukcji. Instrukcje wprowadzania danych przyporządkowują tym zmiennym wartości
rzeczywiste. Języki programowania tekstowego zawierają standardowe instrukcje skoków
bezwarunkowych i warunkowych, tworzenia pętli, arytmetyczne i logiczne. W zależności od
wykorzystywanej metody opisu operacji wykonywanych przez robota, języki programowania
można podzielić na:
– Języki programowania powstałe w wyniku rozszerzenia lub modyfikacji typowych
języków,
nazywane językami robotycznie-zorientowanymi.
– Języki programowania obiektowo-zorientowane.

30. Języki programowania robotów
Wykorzystywane są w programowaniu tekstowym. W zależności od wykorzystywanej
metody opisu operacji wykonywanych przez robota, języki programowania dzielimy na 2
grupy:
♦
Języki programowania powstałe w wyniku rozszerzenia lub modyfikacji typowych języków,
nazywane językami robotycznie zorientowanymi (robot-oriented programming languages) –
program składa się z szeregu instrukcji zwanych makro-ruchami, które mogą dotyczyć opisu
przemieszczania poszczególnych ogniw łańcucha kinematycznego lub w zaawansowanych
wypadkowego ruchu efektora. Syntaktyka przypomina np. BASIC, FORTRAN, PASCAL,
LISP. Przykładowe języki to AL, VAL
♦
Języki programowania obiektowo-zorientowane (object-oriented lub task-level
programming languages) – bazują na zdefiniowaniu modelu otoczenia robota. Poszczególne
obiekty otrzymują nazwy i parametry określające ich kształt i wymiary oraz
przyporządkowanie lokalnych układów współrzędnych. W programie określa się kolejno,
które z obiektów mają być przemieszczane i w jaki sposób (pozycyjnie z zadaną wartością lub
siłowo w określonym kierunku). System programowania posiada edytor, kompilator lub
interpreter oraz interfejs wprowadzania danych obiektowych, np. z baz danych. Organizacja
przesyłu danych powinna być zgodna z systemami CAD/CAM. Przykład: AUTOPAS
Wyszukiwarka
Podobne podstrony:
odpowiedzi pdf id 332621 Nieznany
Automatyka i robotyzacja id 733 Nieznany
Automatyka i Robotyka id 73294 Nieznany
(1 ROZWOJ ROBOTYKI)id 766 Nieznany
ODPOWIEDZI FIZYKA id 332483 Nieznany
Historia robotyki, id 204124 Nieznany
odpowiedzi cz11 id 332391 Nieznany
biologia odpowiedzi zp id 88136 Nieznany
odpowiedzi biologia id 85891 Nieznany
angielski odpowiedzi zp id 2213 Nieznany (2)
odpowiedzi 11 id 332300 Nieznany
odpowiedzi edytow id 332475 Nieznany
angielski odpowiedzi zr id 2213 Nieznany (2)
odpowiedzi pdf id 332621 Nieznany
odpowiedzi do testu id 332437 Nieznany
Klucz odpowiedzi id 236518 Nieznany
Podstawy Robotyki lab3 id 36832 Nieznany
odpowiedzibezpieczenstwo id 332 Nieznany
Odpowiedzi testu BHP id 332669 Nieznany
więcej podobnych podstron