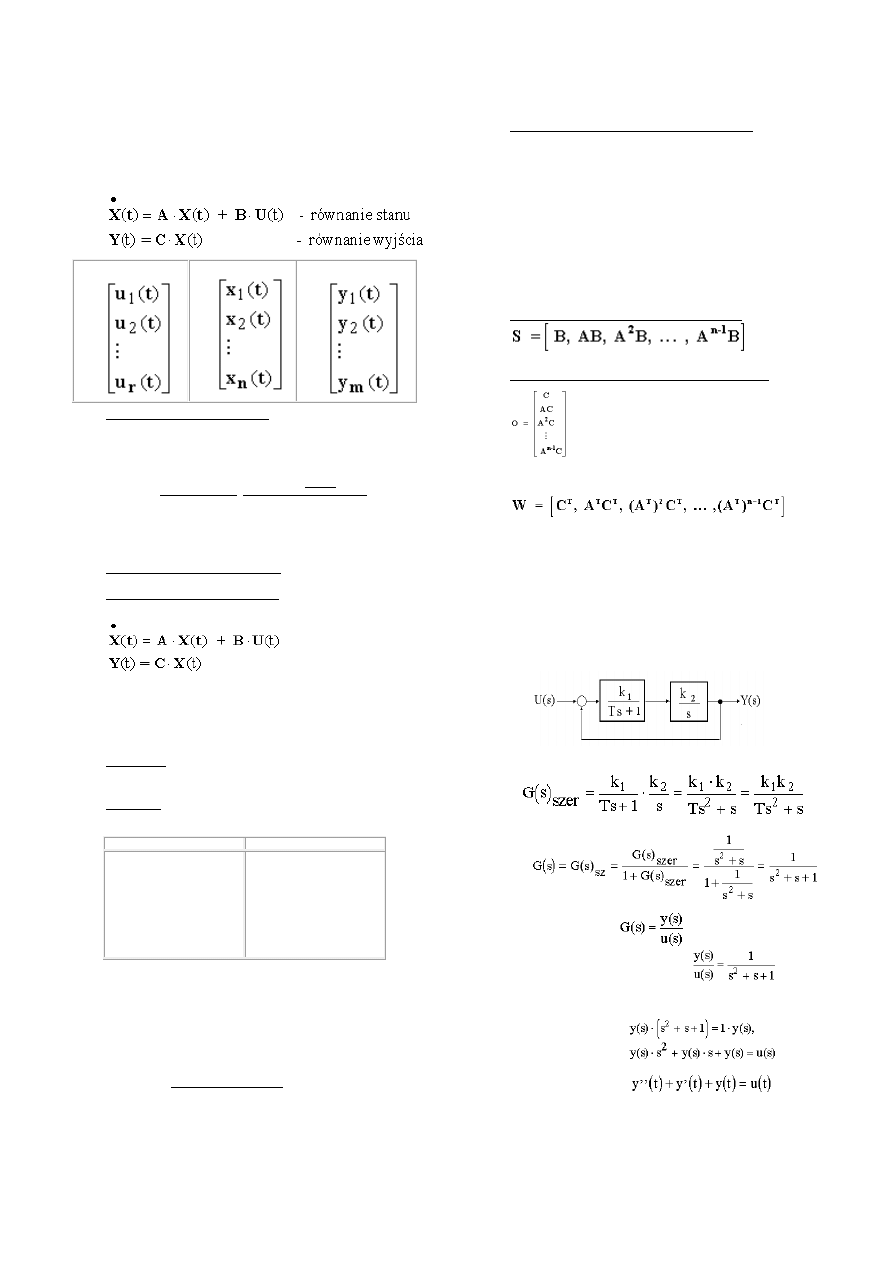
ZWIĄZEK  MIĘDZY  RÓWNANIEM  STANU,  RÓWNANIEM  WYJŚCIA  A 
MACIERZĄ TRANSMITANCJI.  
Punktem wyjścia niech będzie układ dynamiczny:  



 

liniowy, 



 

stacjonarny, 



 

wielowymiarowy. 

Układ  taki  opisują  równania  układu:  równanie  stanu  i  równanie  wyjścia: 

 

gdzie wektory U(t), X(t) i Y(t) są określone następująco:  

U(t) - wektor sygnałów 

wejściowych,   

U(t)=

  

X(t) - wektor stanu,   

X(t)=

  

Y(t) - wektor sygnałów wyjściowych, 

  

Y(t)=

 

 
ZASTOSOWANIE MACIERZY TRANSMITANCJI:  



 

analiza, rozwiązywanie zadań sterowania i badanie stabilności układów o 
wielu wejściach i wyjściach oraz układów wielopoziomowych,  



 

wyznaczanie zmiennych stanu i macierzy A, B i C równań układu,  



 

w przypadku transmitancji skalarnej G(s) dokonując zestawienia 
poznanych wyrażeń na tę transmitancję, mamy: wielomian 

charakterystyczny układu i wielomian charakterystyczny macierzy A. 
Miejsca zerowe, czyli pierwiastki charakterystyczne to wartości dla 
których transmitancja jest nieokreślona. 
Zatem macierz A i wielomian charakterystyczny pozwalają na ocenę 
własności dynamicznych układu. 

2. ZASADY DOBORU ZMIENNYCH STANU. 
a)wyboru zmiennych stanu można dokonać na podstawie:  
-analizy zjawisk zachodzących w obiekcie (układzie, procesie)  
-macierzy transmitancji  
b)na podstawie analizy zjawisk obiektu (układu, procesu) formułuje się równania opisujące 
dynamikę  układu,  należy  dążyć  aby  zmiennym  stanu  przyporządkować  sygnały 
występujące w obiekcie,  
c)w przypadku, gdy znana jest macierz transmitancji G(s), szuka się macierzy A, B i C 
spełniających równania: 
G(s) = C (sI - A)

-1

 B oraz  

 

należy jednak uwzględniać, że:  
macierz transmitancji nie dostarcza informacji o ilości zmiennych stanu,  
ten sam układ może być opisany innymi zmiennymi stanu,  
d)w ogólnym przypadku, dobór zmiennych stanu powinien uwzględniać:  
-minimalizację liczby zmiennych stanu, czyli minimalny rozmiar macierzy stanu A,  
-wybrane zmienne stanu muszą spełniać warunek niezależności liniowej,  
-jeśli  wybrano  więcej  niż  jeden  zestaw  zmiennych  stanu  to  przejście  od  jednych 
współrzędnych do innych musi być wzajemnie jednoznaczne,  
RODZAJE ZMIENNYCH STANU:  

fizykalne, fazowe, kanoniczne (nie będą omawiane),  
zmienne fizykalne:  
-wybiera się minimalną liczbę n -liniowo niezależnych wielkości reprezentujących sygnały 
fizyczne,  
-na  podstawie  relacji  określających  dynamikę  zmian  tych  wielkości  układa  się  równania 
stanu,  
zmienne  fazowe:  dobór  zmiennych  fazowych  następuje  przy  następujących  założeniach 
dotyczących układu dynamicznego, układ dynamiczny jest:  
liniowy,stacjonarny,ciągły,jednowymiarowy,  
WŁASNOŚCI FIZYKALNYCH I FAZOWYCH ZMIENNYCH STANU:  

fizykalne 

fazowe 

1. 

model  matematyczny  staje 
się modelem fizycznym,  

2. 

możliwość 

pomiaru 

wielkości fizycznych,  

3. 

można narysować  schemat 
blokowy układu,  

4. 

możliwość  syntezy  układu 
sterowania  w  przypadku 
sprzężenie 

zwrotnego 

uzależnionego  od  wektora 
stanu.  

1. 

zmienne 

fazowe 

mogą 

mieć znaczenie fizykalne,  

2. 

ułatwiają analizę dynamiki 
układów,  

3. 

ułatwiają  analizę  układów 
w  stanach  przejściowych 
(nieustalonych),  

4. 

ułatwiają 

modelowanie 

analogowe, 

ponieważ 

przez 

wprowadzenie 

elementów  całkujących  i 
proporcjonalnych.  

 
UKŁAD JEST STEROWALNY  
(całkowicie), gdy: ograniczone  przedziałami ciągłe sterowanie U(t)  przeprowadza układ z 
dowolnego stanu początkowego X(t

0

) w chwili t=t

0

 do dowolnego stanu końcowego  X(t

k

) 

w chwili t=t

k

 w skończonym przedziale czasu t

k

-t

0

=0.  

STEROWALNOŚĆ  
oznacza możliwość osiągnięcia dowolnego stanu układu w skończonym czasie za pomocą 
dopuszczalnego sterowania.  
UKŁADY NIESTEROWALNE  
to  układy,  które  są  niecałkowicie  sterowalne.  Układ  niecałkowicie  sterowalny  to  układ, 
który przy określonym doborze zmiennych stanu zawiera takie zmienne stanu, których nie 
można  za  pomocą  ograniczonego  przedziałami  ciągłego  sterowania  przeprowadzić  z 
dowolnej wartości początkowej X

i

(t

0

) do X

i

(t

k

).  

Na  podstawie  definicji  sterowalności  całkowitej  i  niecałkowitej  wprowadza  się  także 
odpowiednie pojęcia sterowalności ze względu na wyjście, które określają zmiany wektora 
sygnałów wyjściowych w chwilach t

0

 i t

k

.  

UKŁAD JEST OBSERWOWALNY  
(całkowicie), jeśli przy danym dowolnym sterowaniu U(t), istnieje skończona chwila t

k

, po 

której, na podstawie znajomości wektora sygnałów wyjściowych Y(t) i wektora sterowania 
U(t)  w  przedziale  od  t

0

  do  t

k

  można  wyznaczyć  stan  układu  X(t

0

)  w  dowolnej  chwili 

początkowej t

0

.  

OBSERWOWALNOŚĆ  

oznacza, że na podstawie przebiegu sygnału wyjściowego w skończonym przedziale czasu, 
można określić stan układu w dowolnej chwili tego przedziału.  
WŁASNOŚCI UKŁADÓW STEROWALNYCH I OBSERWOWALNYCH:  
Układ sterowalny: 
-to  układ  w  którym  wektor  sygnałów  wejściowych  oddziaływuje  na  wszystkie  zmienne 
stanu, czyli zapewnia skuteczne sterowanie,  
-zmiana wektora wejść wywołuje różne zmiany każdej współrzędnej stanu. 
Układ obserwowalny:  
-to układ w którym istnieją relacje między wszystkimi sygnałami wektora wyjściowego a 
sygnałami  wektora  stanu,  czyli  na  podstawie  przeprowadzonej  w  skończonym  czasie 
obserwacji  (analizy)  sygnałów  wyjściowych  i  sterujących  można  jednoznacznie  określić 
wektor stanu początkowego,  
-zmiana wektora stanu wywołuje różne zmiany wyjścia czyli musi zachodzić odróżnienie 
wpływu każdej zmiennej stanu na zmianę obserwowanego wektora wyjść. 
Układ niesterowalny: 
-to układ w którym wektor wejść U(t) nie ma wpływu na wszystkie zmienne stanu. 
Układzie nieobserwowalny: 
-to układ w którym między  dowolnym wektorem wyjść  Y(t) nie  zachodzą relacje  między 
wszystkimi zmiennymi stanu X(t). 
OCENA STEROWALNOŚCI I OBSERWOWALNOŚCI 
może być przeprowadzona na podstawie analizy:  
-postaci kanonicznej równania stanu i równania wyjścia,  
-bezpośredniej analizy schematu blokowego. 
WARUNEK STEROWALNOŚCI:  
Warunkiem koniecznym i dostatecznym (wystarczającym) sterowalności jest, aby macierz 

o n - 

wierszach i m - kolumnach miała rząd n, czyli n - liniowo niezależnych kolumn. 
WARUNEK 

OBSERWOWALNOŚCI: 

Warunkiem  koniecznym  i  dostatecznym  (wystarczającym)  obserwowalności  jest,  aby 
macierz:  

o  wymiarach  m  x  n  miała  rząd  n,  czyli  zawierała  n  -  liniowo 

niezależnych 

wierszy. 

Dla  ułatwienia  analizy  macierzy  O,  wprowadza  się  macierz  W,  która  jest  transpozycją 
macierzy  O.  Warunek  obserwowalności  odnoszący  się  do  macierzy  W  formułuje  się 
następująco: układ jest całkowicie obserwowalny wtedy i tylko wtedy,  gdy  rząd  macierzy 

jest równy n. 
 
UKŁAD STEROWANIA MOŻE WIĘC ZAWIERAĆ CZĘŚCI: 

SO - sterowalne i obserwowalne, 
S NO - sterowalne lecz nieobserwowalne, 
O NS - obserwowalne lecz niesterowalne, 
NS NO - niesterowalne i nieobserwowalne. 

Części te można wydzielić na podstawie:  



 

schematów blokowych,  



 

przekształceń równań stanu i równania wyjścia. 

WYZNACZYĆ TRANSMITANCJĘ ZASTĘPCZĄ OBIEKTU A NASTĘPNIE 
WYZNACZ RÓWNANIE 
CHARAKTE

RYSTYCZNE, RÓWNANIE RÓŻNICZKOWE I RÓWNANIE 

MACIERZOWE. 
Dana jest struktura regulatora o określonych transmitancjach, jak na rysunku. Dokonać 
syntezę układu i wyprowadzić równania stanu i wyjścia.  

 

1. 

Obliczenie transmitancji wypadkowej.  

a. 

transmitancja dwóch elementów połączonych 
szeregowo:  

 

b. 

transmitancja wypadkowa po uwzględnieniu sprzężenia 
zwrotnego i wartości podstawień: T=1, k

1

=1, k

2

=1:  

 

c. 

po uwzględnieniu definicji transmitancji tj. 

, transmitancja wypadkowa 

wyraża się następująco: 

, 

na podstawie powyższego wyrażenia można utworzyć 
równania stanu i wyjścia obiektu dynamicznego.  

2. 

Wyprowadzenie równań obiektu dynamicznego i macierzy.  

a. 

Wymnażając stronami równanie p.1c otrzymujemy:  

 

a po przejściu do dziedziny czasu otrzymujemy:  

, 

b. 

Otrzymane równanie jest równaniem różniczkowym II 
rzędu, zatem można utworzyć dwa równania 
różniczkowe I rzędu, które odpowiadać będą dwóm 
równaniom stanu o postaci normalnej. Jako zmienną 
stanu obieramy sygnał wyjściowy y(t) a wtedy, zgodnie 
z zasadami doboru zmiennych fazowych, można 
utworzyć relacje:  

 

Zatem równania obiektu dynamicznego są następujące: 

2 równania stanu i równanie wyjścia 

Macierze odnoszące się do powyższego układu równań są następujące: 

A=

, b=

 , c=

 , 

 
Analiza obejmuje badanie układów regulacji (regulatorów i obiektów) przy pomocy metod 
stosowanych do badania układów dynamicznych. Wynikiem analizy jest identyfikacji 
układów regulacji. 
Synteza to szereg kolejnych działań niezbędnych dla zaprojektowania układu regulacji.  
Działania te obejmują:  



 

opis matematyczny obiektu,  



 

opis zadania sterowania, czyli charakterystyki sygnału zadanego,  



 

opis zakłóceń,  



 

dobór wskaźników jakości regulacji,  



 

założenia dotyczące sygnałów układu regulacji i struktury regulatora. 

Wynikiem syntezy jest projekt układu regulacji zawierający opis matematyczny regulatora 
spełniający założenia współczynników jakości regulacji. 
RODZAJE UKŁADÓW REGULACJI 
Można wyróżnić, zależnie od przyjętego kryterium klasyfikacji, następujące rodzaje 
układów regulacji: 
a)zależnie od liczby regulowanych wielkości:  

o 

jednowymiarowe (regulacja jednej zmiennej)  

o 

wielowymiarowe 

(regulacja 

wielu 

sygnałów 

wyjściowych). 

b)poprzez analogię do układów dynamicznych:  

o 

ciągłe,  

o 

impulsowe,  

o 

liniowe,  

o 

nieliniowe 

c)ze względu na charakter sygnału zadanego y

o

(t), układy regulacji mogą być układami:  

o 

regulacji 

stałowartościowej, 

gdy 

sygnał 

y

o

(t)=y

o

=const.  

o 

regulacji  programowalnej,  gdy  przebieg  sygnału  jest 

zaprogramowany (przewidziany z góry),  

o 

regulacji  nadążnej,  gdy  sygnał  y

o

(t)  ma  charakter  nie 

przewidziany,  

o 

regulacji  ekstremalnej,  gdy  celem  regulacji  jest 

utrzymanie  sygnału  wyjściowego  lub  sygnałów 
wyjściowych  na  poziomie  wartości  ekstremalnych 
(minimalnych lub maksymalnych) 

d)ze względu na możliwość zmiany własności regulatora w czasie jego pracy:  

o 

układy  adaptacyjne,  gdy  dla  zmieniających  się  w 

czasie  pracy  równań  obiektu  następuje  dostosowanie, 
czyli adaptacja równań regulatora,  

o 

układy  optymalne,  gdy  osiąga  się  możliwie  najlepsze 

wartości  współczynników  jakości,  niezależnie  od 
struktury regulatora,  

o 

układy  suboptymalne,  gdy  przy  określonym  typie 

regulatora uzyskuje się najlepsze współczynniki jakości 

UKŁAD STATYCZNY REGULACJI to układ, którego uchyb statyczny w stanie 
ustalonym przy wymuszeniu skokowym y

o

(t) lub z(t) jest różny od zera, niezależnie od 

amplitudy wymuszenia, tzn., że w układzie statycznym występują różne od zera 
proporcjonalne do wartości skokowego lub stałego pobudzenia uchyby ustalone. 
UKŁAD ASTATYCZNY REGULACJI to układ w którym uchyb statyczny, czyli uchyb 
ustalony przy wymuszeniu skokowym jest równy 0. 
DOKŁADNOŚĆ REGULACJI to wielkość różnicy między sygnałem wartości zadanej 
y

o

(t) a sygnałem wyjściowym y(t). 

W  praktyce  dąży  się  do  uzyskania  tzw.  dokładności  wystarczającej  lub  określa  się 
dopuszczalną  bezwzględną  wartość  uchybu  dynamicznego  i  uchybu  ustalonego. 

Dokładność  dynamiczną  osiąga  się  poprzez  dobór  parametrów  i  korekcji  regulatora. 
Dokładność  statyczną  ustala  się  na  dopuszczalnym  poziomie.  Kryterium  dokładności 
statycznej jest jednoznaczne: albo układ regulacji jest astatyczny i nie ma uchybu albo jest 
statyczny  i  posiada  uchyb.  Zerowanie  uchybu  ustalonego  osiąga  się  wprowadzając  do 
regulatora  układy  całkujące.  Dążenie  do  zerowania  uchybu  może  powodować  utratę 
stabilności.  
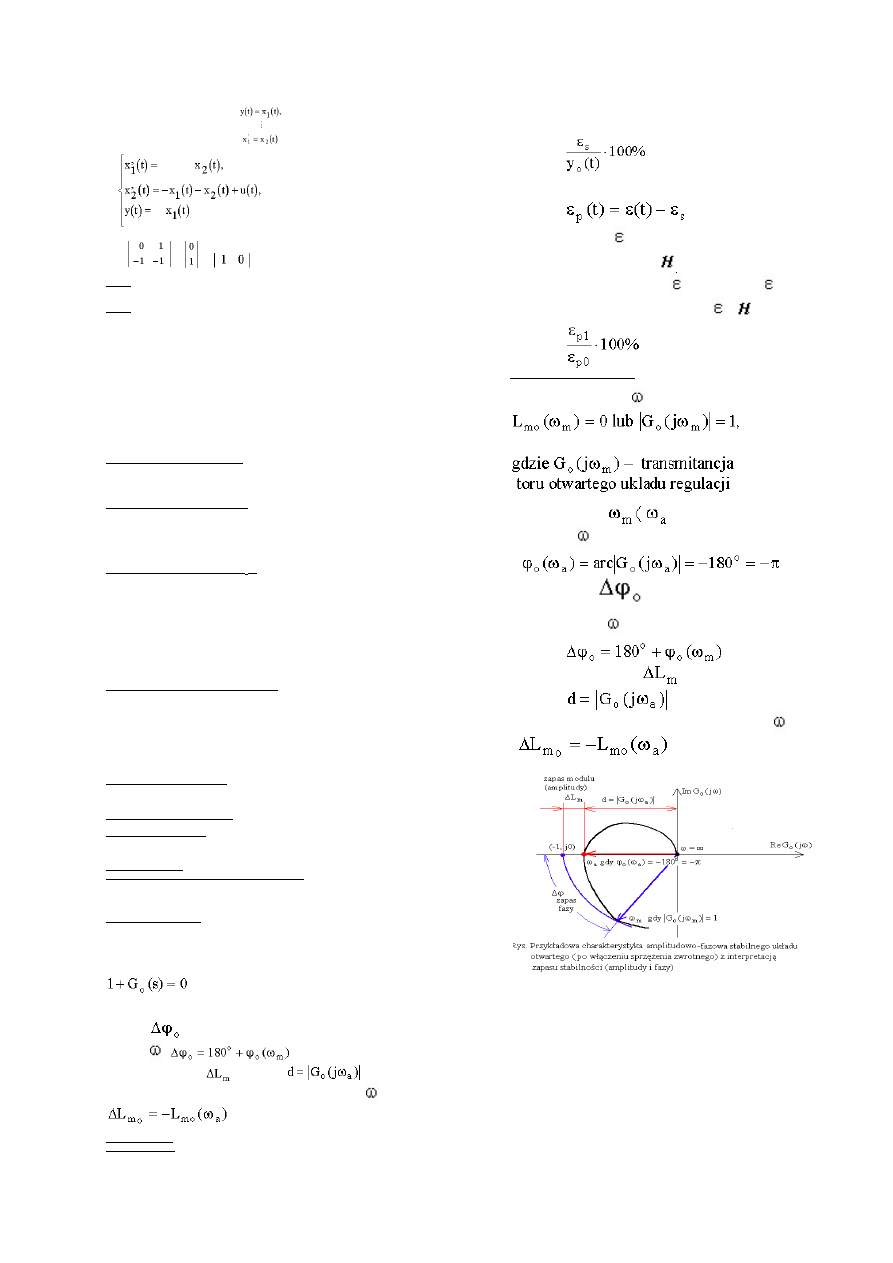
STABILNOŚĆ REGULACJI 
1)Doprowadzenie  uchybu  ustalonego  do  wartości  zerowej  osiąga  się  poprzez 
wprowadzenie  wymaganego  poziomu  (stopnia)  astatyzmu,  czyli  liczbę  biegunów 
transmitancji G

o

(s).  

2)Ocena  stabilności  zamkniętego  układu  regulacji  może  zostać  dokonana  na  podstawie 
układu  otwartego.  Mianowniki  wyrażeń  określających  transmitancję  układu  zamkniętego 
zawierają  wyrażenie  1+G

o

(s),  które  można  traktować  jak  równanie  charakterystyczne: 

 

i  znaleźć  wartości  s,  które  spełniają  to  równanie.  Aby  układ  był  stabilny,  pierwiastki 
równania  charakterystycznego  powinny  znajdować  się  w  lewej  półpłaszczyźnie  zmiennej 
zespolonej s. W praktyce do oceny stabilności stosuje się metody algebraiczne.  

6. zapas fazy 

określa odchylenie  charakterystyki fazowej od wartości -180

o

 dla 

częstotliwości 

m

. 

 

7.  zapas  modułu  (amplitudy 

)  lub  wielkość 

określa 

odchylenie  charakterystyki  amplitudowej  od  wartości  0  [dB]  dla  częstotliwości 

a

: 

 

+częstotliwość graniczna fazy i modułu 
Wskaźniki regulacji: 
Nieczestotliwosciowe: 

1. 

 wskaźnik uchybu ustalonego określa się przez podanie:  

1. wartości dopuszczalnej w jednostkach fizycznych,  
2. w jednostkach względnych  

 

2. 

czas regulacji t

r 

 

przedział czasu od chwili wymuszenie do chwili w której uchyb 
przejściowy:  

, nie przekroczy 5% wartości 

maksymalnej tj. 

po

 

3. 

współczynnik przeregulowania 

, 

iloraz największej wartości uchybu 

p1

 o znaku przeciwnym do 

po

 i 

maksymalnej wartości uchybu przejściowego (tj. 

po

), 

= 

 

Częstotliwościowe wskaźniki regulacji: 

1. 

częstotliwość graniczna modułu L

m

 charakterystyki amplitudowej 

oznacza częstotliwość 

m

. dla której 

  

2. 

częstotliwość graniczna fazy (argumentu) (warunek stabilności układu 

zamkniętego: 

) 

oznacza częstotliwość 

a

. dla której  

 

3. 

zapas fazy 

 

określa odchylenie charakterystyki fazowej od wartości -180

o

 dla 

częstotliwości 

m

. 

 

4. 

zapas modułu (amplitudy 

) lub wielkość 

 

określa odchylenie charakterystyki amplitudowej od wartości 0 [dB] dla częstotliwości 

a

: 

 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Pytania!!!!!!!!!!!!!!!!!!!!! 
DLA JAKIEJ WARTOŚCI TRANSMITANCJI GO(S) UCHYB STATYCZNY W 
STANIE USTALONYM BYŁBY ZEROWY? 
UCHYB STATYCZNY (w stanie ustalonym) s, niezależnie od amplitudy 
wymuszenia A byłby równy 0, 
gdyby granica transmitancji układu otwartego 

, gdyż: 

 

 
 
JAKIE  WŁASNOŚCI  TRANSMITANCJI  REGULATORA  GR(S)  ZAPEWNIAJĄ 
ASTATYZM UKŁADU REGULACJI? 
 
Układ astatyczny regulacji to układ w którym uchyb statyczny, czyli uchyb 
ustalony przy 
wymuszeniu skokowym jest równy 0. Uchyb statyczny (w stanie ustalonym) s 

,byłby równy 0 jeśli 

 

, co zaszłoby w przypadku gdyby transmitancja regulatora miała działanie 

całkujące: 

, czyli wystąpiłby biegun dla s=0. 

 
 
Transmitancja  operatorową  danego  elementu  liniowego  nazywamy  stosunek 
transformaty  Laplacea  sygnału  wyjściowego  do  transformaty  Laplacea  sygnału 

wejściowego, przy zerowych warunkach początkowych G(S)=Y(S)/U(S) 
Macierz  transmitancji:    Elementami  transmitancji  macierzowej  G(s)  są  transmitancje 
łączące poszczególne wejścia i wyjścia (rys. poniżej): 

 

 
 

 

 

 
 
 
 
 
 
 

Zadanko przykłądowe 

A = 

, b = 

, c = 

, d = 

 

Sprawdzić, czy powyższy układ jest sterowalny? 

1. 

Warunkiem koniecznym i dostatecznym sterowalności jest, aby macierz  

 

była rzędu n (czyli, żeby miała n - liniowo niezależnych kolumn, 
wyznacznik takiej macierzy jest różny od zera).  

2. 

Układ, którego sterowalność będziemy sprawdzać jest układem o jednym 

wejściu 

, czyli równanie stanu ma 

postać: 

, a 

macierz S nie może być osobliwa.  

3. 

Układ z jednym wejściem jest sterowalny jeśli: 

, 

w celu wyznaczenia macierzy S określamy kolejno poszczególne macierze:  

      

 

 

Jak widać w macierzy S występują 2 niezależne liniowo kolumny, a 
wartość wyznacznika jest -49, czyli wyznacznik jest różny od 0, czyli 
układ jest sterowalny.  

Sprawdzić, czy powyższy układ jest obserwowalny? 
1. 

Warunkiem koniecznym i dostatecznym obserwowalności jest, aby 

macierz 

 
była rzędu n (czyli, żeby miała n - liniowo niezależnych kolumn).  
2. 

Układ, którego obserwowalność będziemy sprawdzać jest układem o 

jednym wyjściu 

, czyli równanie wyjścia ma postać: 

, 
czyli warunkiem koniecznym i wystarczającym jest, aby macierz W nie była osobliwa, jest 

aby wartość wyznacznika det W 

0.  

3. 

Obliczenia dot. obserwowalności:  

 

Stała czasowa T – w 

układzie automatyki

, miara osiągania 

stanu ustalonego

 przez sygnał 

wyjściowy,  związana  z  czasem  trwania 

stanu  nieustalonego

  następującego  po  zmianie 

sygnału wejściowego. 
Współczynnik wzmocnienia k – parametr 

transmitancji operatorowej

, będący stosunkiem 

wartości zmiany sygnału wyjściowego do wartości zmiany sygnału wejściowego.