
Przemysław Senetra
Energetyka sem. V
Krzysztof Szadziewski
Kamil Naguszewski
Mateusz Wiński
Podstawy automatyki i robotyki
SPRAWOZDANIE
Identyfikacja obiektów automatyki
1. Wstęp
Celem ćwiczenia laboratoryjnego było zapoznanie się z metodami identyfikacja
obiektów dynamicznych sterowania i podstawowych członów występujących w automatyce na
podstawie wykonanych charakterystyk (skokowej i częstotliwościowej) oraz analiza
otrzymanych wyników podczas badania.
2. Przebieg ćwiczenia
W ćwiczeniu laboratoryjnym dokonano identyfikacji obiektów(określenie zależności
pomiędzy wejściem a wyjściem), co sprowadziło się do wyznaczenia modelu matematycznego
danych obiektów w postaci transmitancji. Dokonano tego dwoma metodami:
-identyfikacji obiektu metodą wyznaczania odpowiedzi skokowej
-identyfikacji obiektu na podstawie zdjętych charakterystyk częstotliwościowych
Metoda identyfikacji obiektu metodą wyznaczania odpowiedzi skokowej polega na
wprowadzeniu na wejście badanego obiektu funkcji skokowych oraz zarejestrowaniu
odpowiedzi układu. Następnie na podstawie przebiegu eksperymentalnej charakterystyki
skokowej zakłada się postać transmitancji aproksymującej.
Do badania charakterystyk skokowych służy układ odpowiednich przyrządów. Na spec.
tablicy ustawiamy zadaną wartość macierzy i dany sygnał wejściowy. Następnie wynik w
postaci wykresu odczytujemy na rejestratorze do tablicy.
W celu wyznaczenia charakterystyk częstotliwościowych z generatora funkcji podaje się na
zaciski wejściowe modelu laboratyjnego (tablicy) sygnał sinusoidalny. Dodatkowo sygnał z
generatora podawany jest na oscyloskop. Pomiar polega na wyznaczeniu w stanie drgań
ustalonych stosunku amplitud i przesunięcia fazowego
Na płycie czołowej modelu laboratoryjnego odzwierciedliliśmy równania macierzowe podane
odpowiednio w punktach a, b, c i d:

a)
A
=
[
0
4
−
5
1
]
B
=
[
0
0
1
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
b)
A
=
[
−
6 3
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
c)
A
=
[
0
0
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
d)
A
=
[
0
0
0
0
]
B
=
[
0
0
0
0
]
C
=
[
0
0
0
0
]
D
=
[
−
1
0
0
0
]
Rejestrator przestawiliśmy z układu X – Y na Y – t i podłączyliśmy wg rysunku nr 2
przedstawionego w punkcie 3. Podczas rejestrowania wyników na rejestratorze musieliśmy
odpowiednio dobierać skalę czasu t i skalę osi y, oddzielnie dla każdego badanego obiektu,
aby wykres zmieścił się w przedziale rejestracji. Pokrętłami u10 i u20 ustawialiśmy wartość
zadanego skoku jednostkowego przy pomocy woltomierza cyfrowego. Przebieg odpowiedzi
skokowej rejestrowaliśmy na rejestratorze przyciskając przycisk Start i Rozwiązanie.
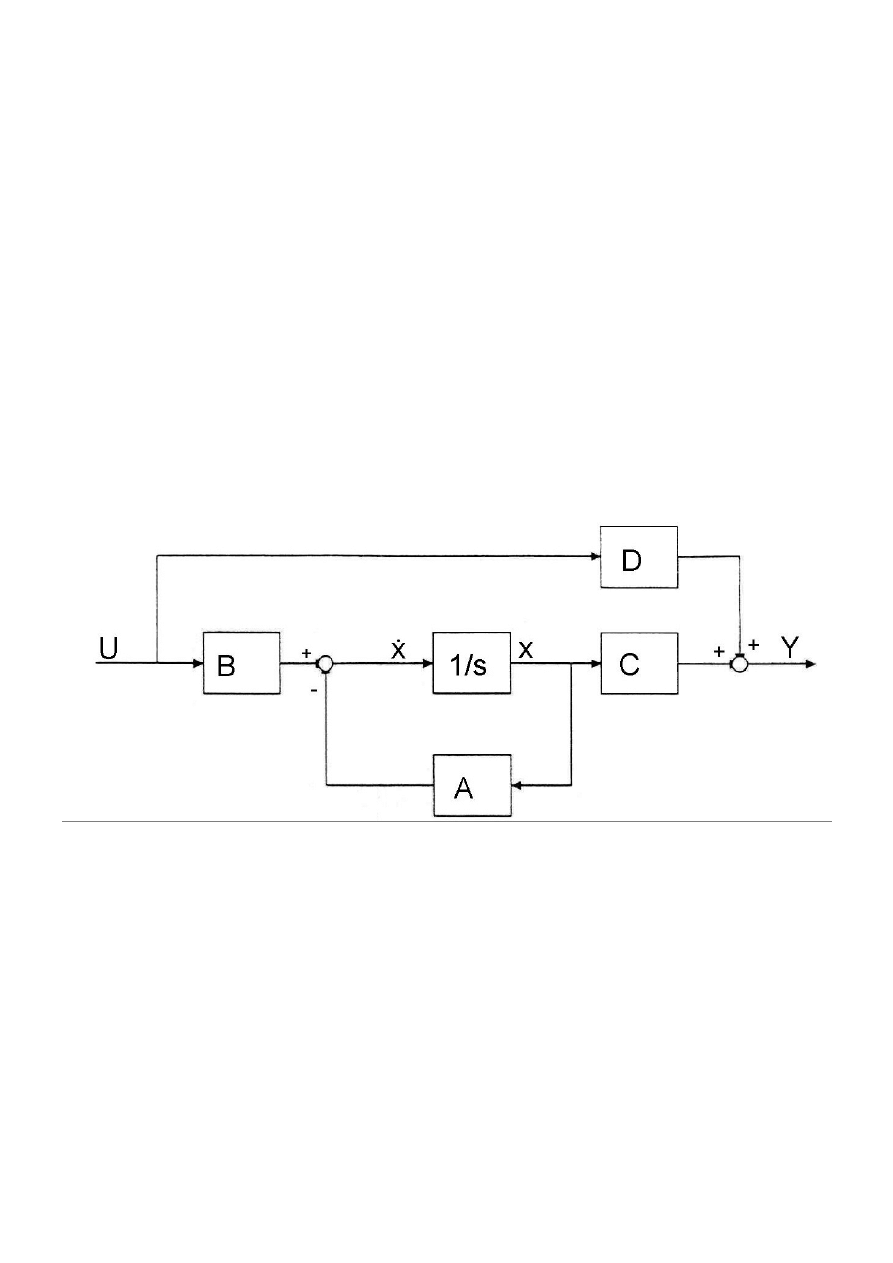
3. Schemat, opis budowy stanowiska
Stanowisko laboratoryjne pozwala na badanie właściwości liniowych układów
stacjonarnych rzędu pierwszego i drugiego.
Na stanowisku znajdował się woltomierz cyfrowy, model obiektu dynamicznego
linowego oraz rejestrator wyników. Wartości sygnału u1 oraz u2 mierzone były przy pomocy
woltomierza. Schemat płyty czołowej modelu obiektu dynamicznego linowego znajduje się
na rysunku nr 1. Na rejestratorze w funkcji Y – t rejestrowane były wyniki naszych
pomiarów. Schemat podłączenia aparatury przedstawia rys. nr 2 oraz rys. nr 3. Do
przeprowadzenia ćwiczenia używaliśmy modelu laboratoryjnego obiektu dynamicznego
liniowego podłączonego do rejestratora oraz woltomierza cyfrowego dla uzyskania dokładnych
pomiarów. Strukturę modelu odzwierciedlają równania macierzowe przy wymiarach
poszczególnych macierzy 2x2. Pozwala to na badanie liniowych układów dynamicznych do
rzędu drugiego. Elementy macierzy A, B, C, D mogą przybierać wartość A:
0
÷
±7
, B: 0,1,
C:0,
±
1, D: 0 lub –1. Wyniki pomiarów są także analizowane w komputerze przy pomocy
programu Matlab. W celu wyznaczenia charakterystyk skokowych obiektu podłączyliśmy
wyjście y1 modelu laboratoryjnego z osią y rejestratora X-Y-t, rejestrator ustawiliśmy na
rejestracje Y-t. Skalę osi y ustawiliśmy przy a) i b) na 2,5V/cm, a przy c) i d) na 2 V/cm.
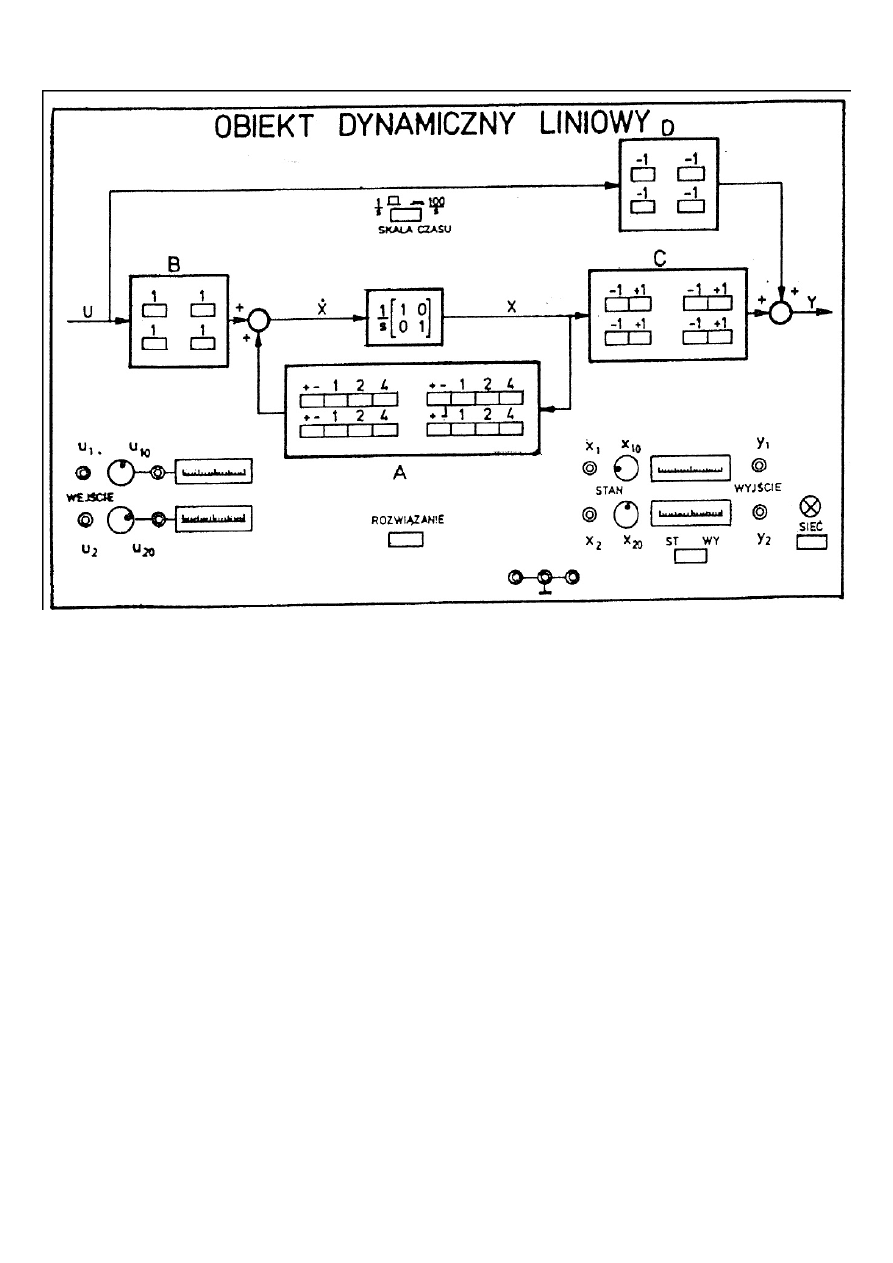
Model płyty czołowej:

4. Wyniki
Zestaw nr 12
a) Skala 2,5 V/cm
A
=
[
0
4
−
5
1
]
B
=
[
0
0
1
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
b) Skala 2,5 V/cm
A
=
[
−
6 3
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=8 V
x
10
=0
x
20
=0
c) Skala 2 V/cm
A
=
[
0
0
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
d) Skala 2 V/cm
A
=
[
0
0
0
0
]
B
=
[
0
0
0
0
]
C
=
[
0
0
0
0
]
D
=
[
−
1
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
5. Analiza wyników
Identyfikacja Teoretyczna:
G(s)
=
C
⋅
(s
⋅
I
−
A)
−
1
⋅
B
+
D
0
1
2
2
0
1
2
2
)
(
)
(
)
(
b
s
b
s
b
a
s
a
s
a
s
M
s
L
s
G
+
+
+
+
=
=
a)
U=10V
Skala rejestratora: 0,5 V/cm
=
0
4
0
0
0
0
L
M = [1 1 20]
Gdzie L=[a
2
a
1
a
0
] i M=[b
2
b
1
b
0
] dla
0
1
2
2
0
1
2
2
)
(
)
(
)
(
b
s
b
s
b
a
s
a
s
a
s
M
s
L
s
G
+
+
+
+
=
=
20
4
)
(
2
+
+
=
s
s
s
G
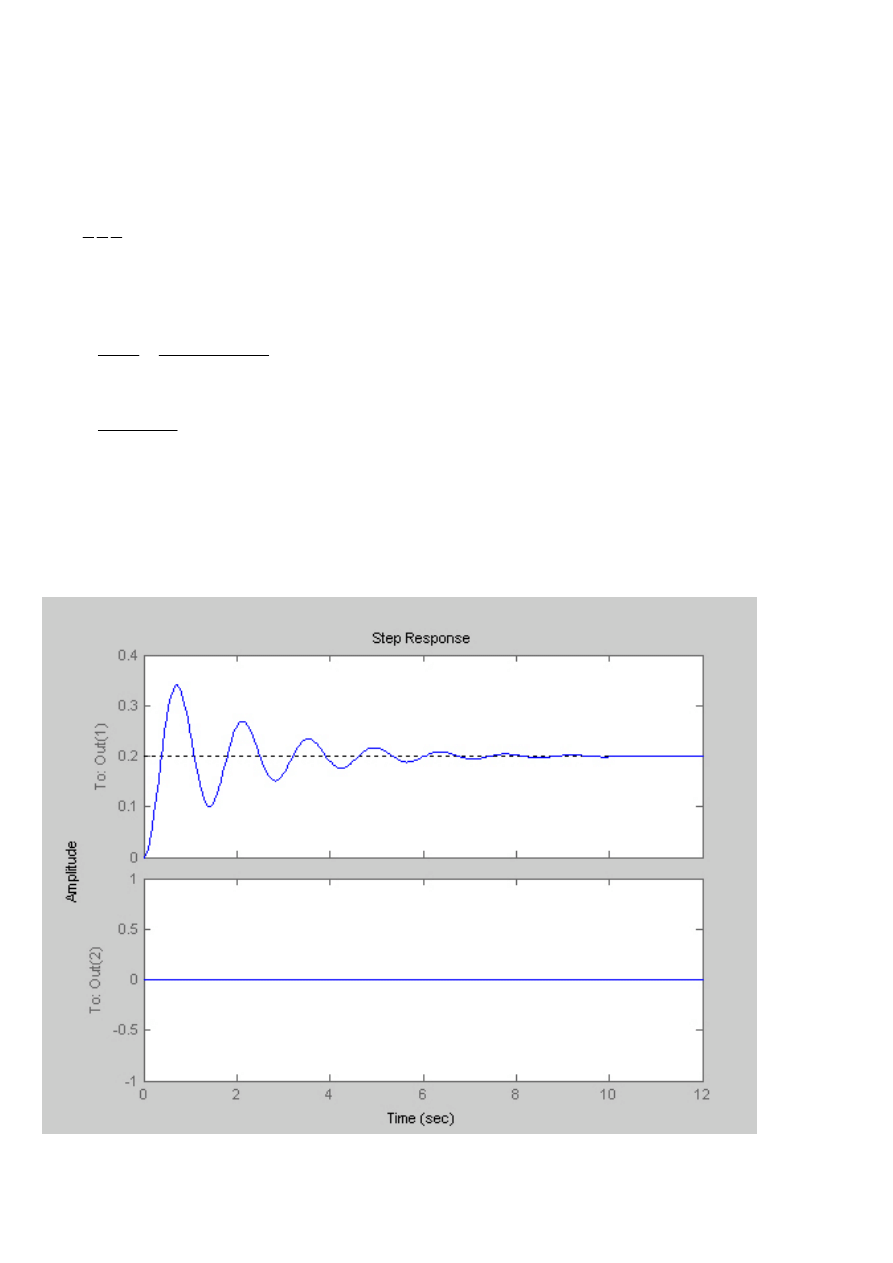
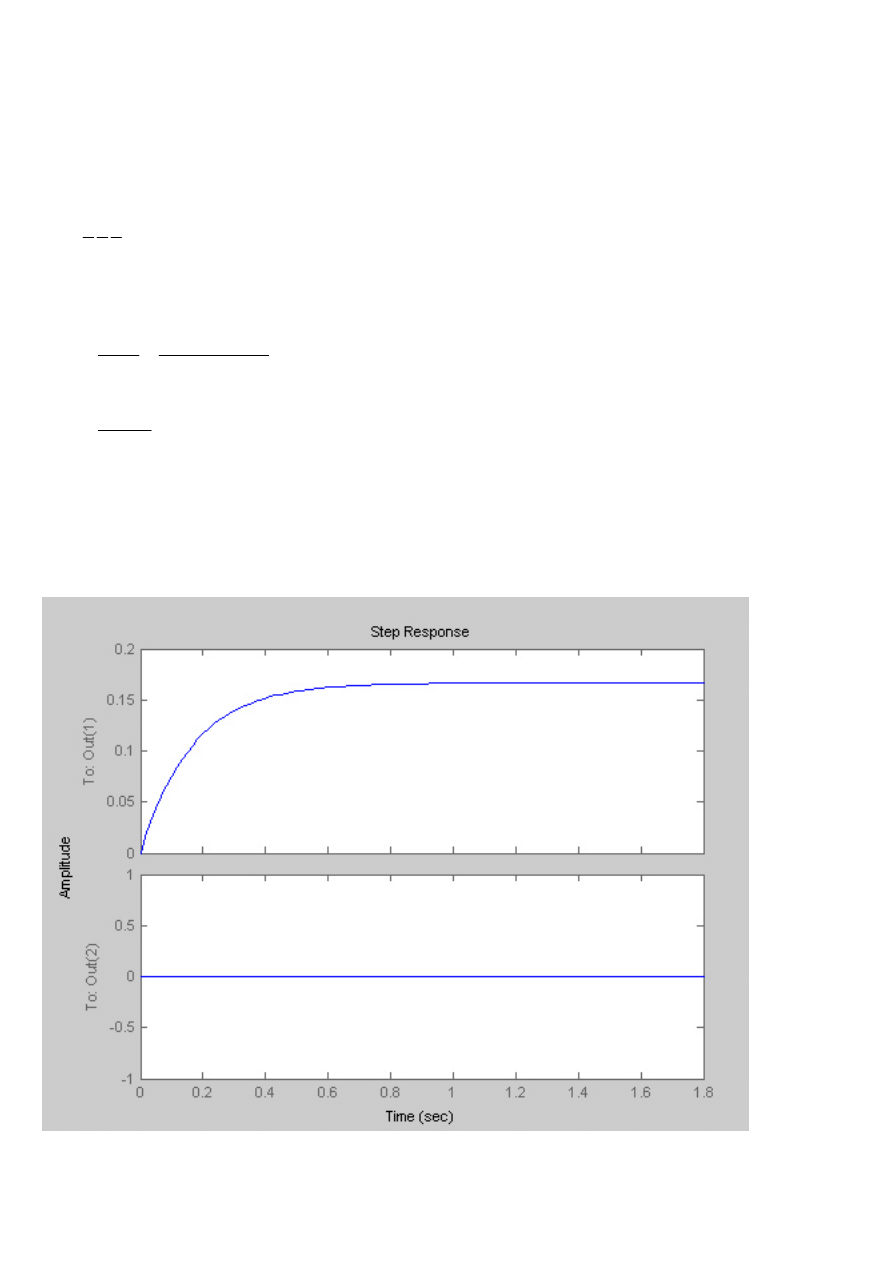
Symulacja z Matlaba
Charakterystyka skokowa
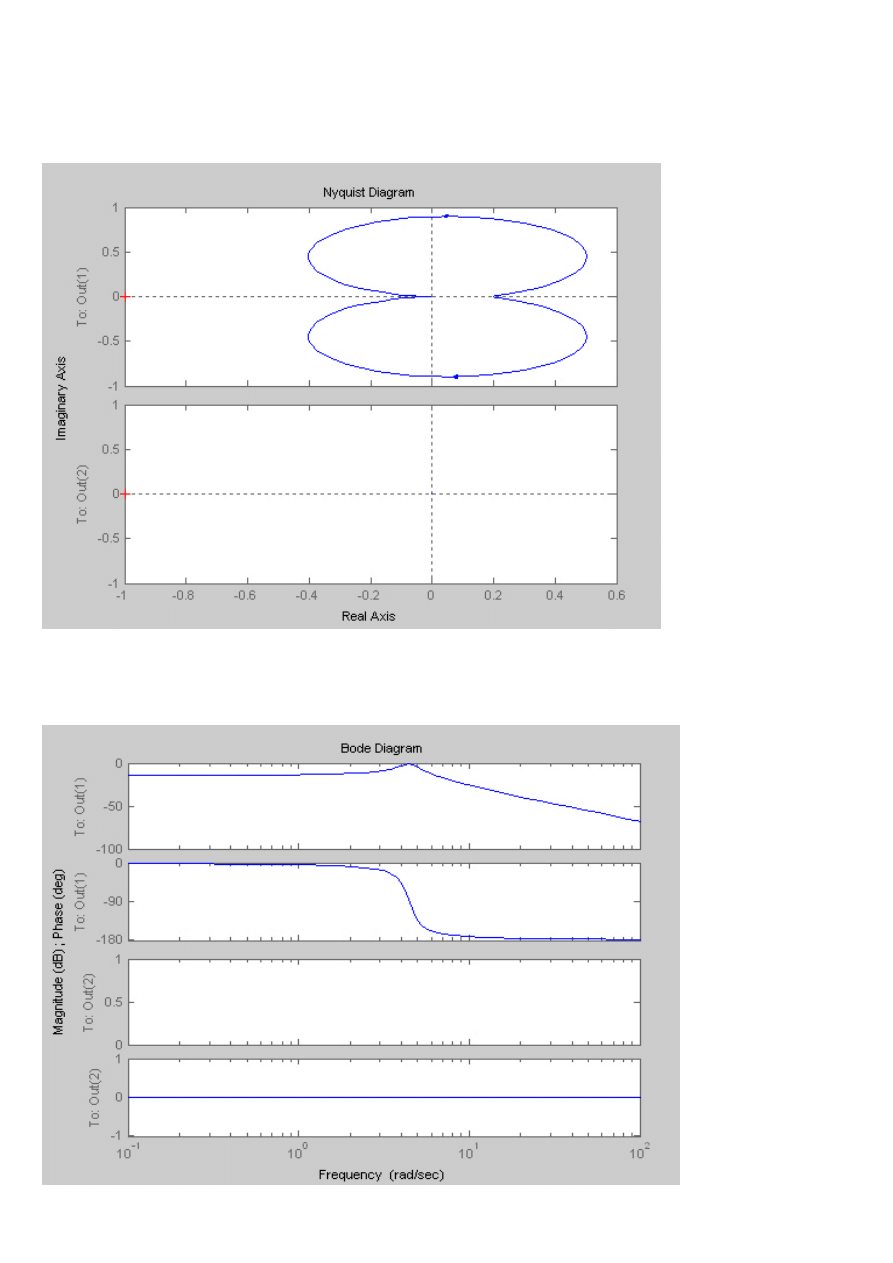
Charakterystyka Nyquista
Charakterystyka Bodego
b)
U=8V
Skala rejestratora: 0,5 V/cm
=
0
0
0
1
0
0
L
M = [1 6 0]
Gdzie L=[a
2
a
1
a
0
] i M=[b
2
b
1
b
0
] dla
0
1
2
2
0
1
2
2
)
(
)
(
)
(
b
s
b
s
b
a
s
a
s
a
s
M
s
L
s
G
+
+
+
+
=
=
s
s
s
s
G
6
)
(
2
+
=
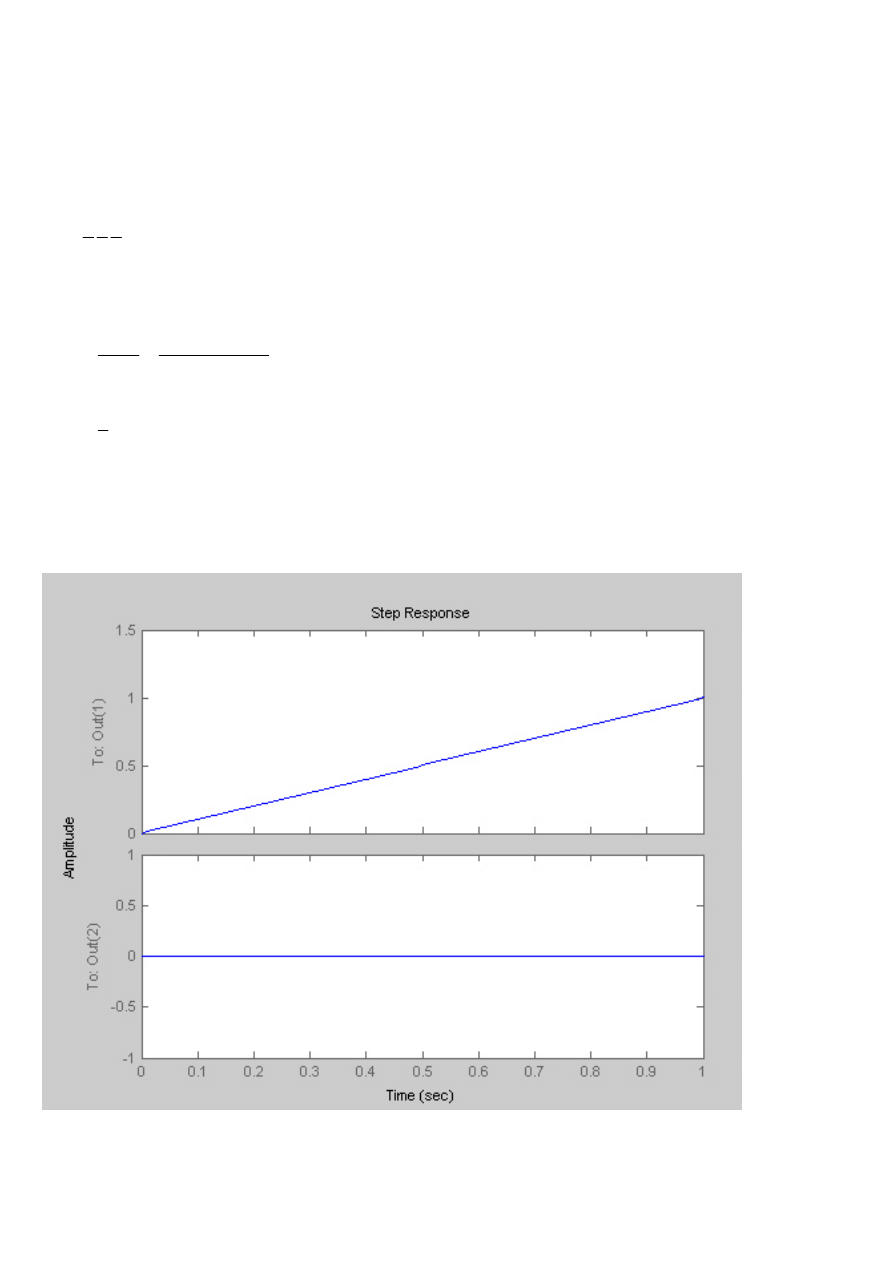
Symulacja z Matlaba
Charakterystyka skokowa
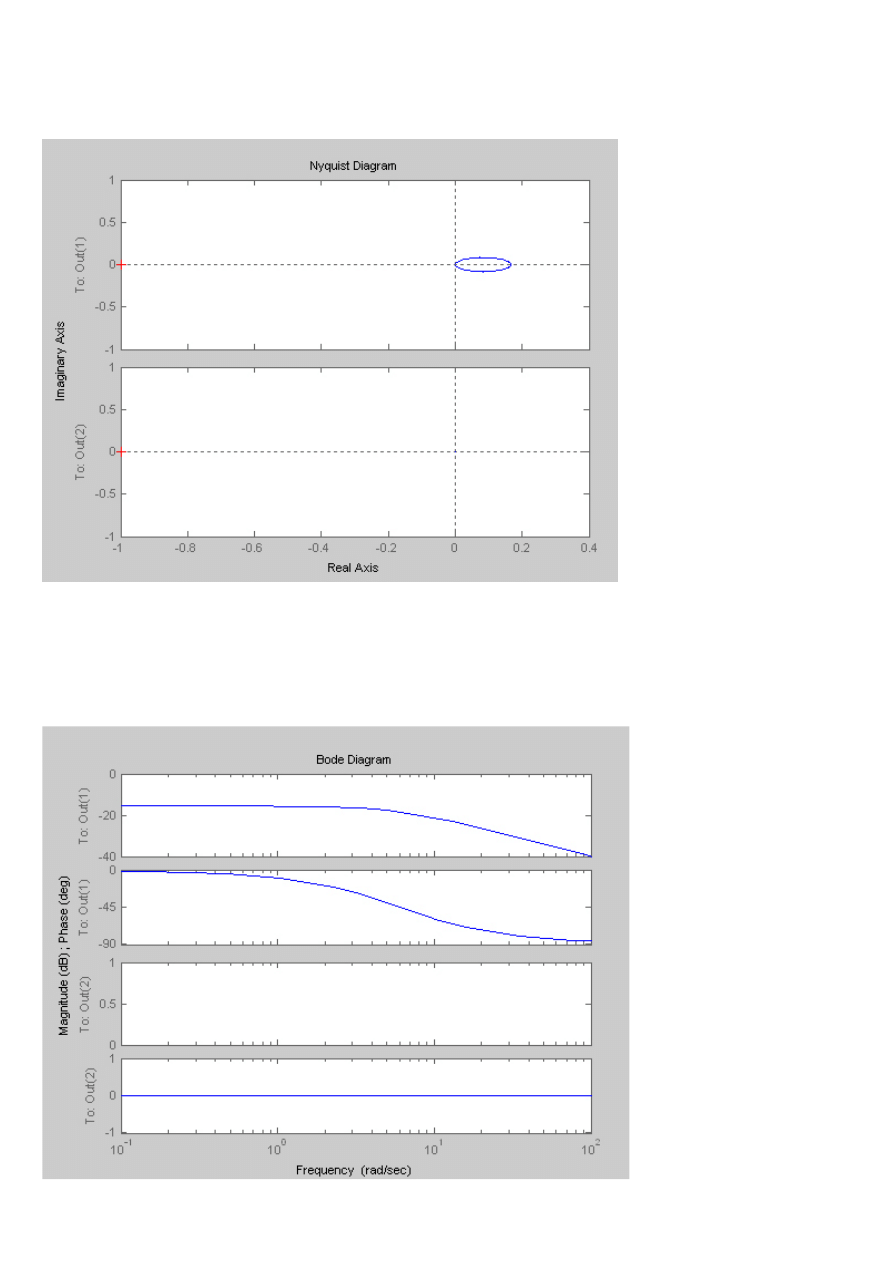
Charakterystyka Nyquista
Charakterystyka Bodego
c)
U=10V
Skala rejestratora: 2 V/cm
=
0
0
0
1
0
0
L
M = [1 0 0]
Gdzie L=[a
2
a
1
a
0
] i M=[b
2
b
1
b
0
] dla
0
1
2
2
0
1
2
2
)
(
)
(
)
(
b
s
b
s
b
a
s
a
s
a
s
M
s
L
s
G
+
+
+
+
=
=
s
s
G
1
)
(
=
Symulacja z Matlaba
Charakterystyka skokowa
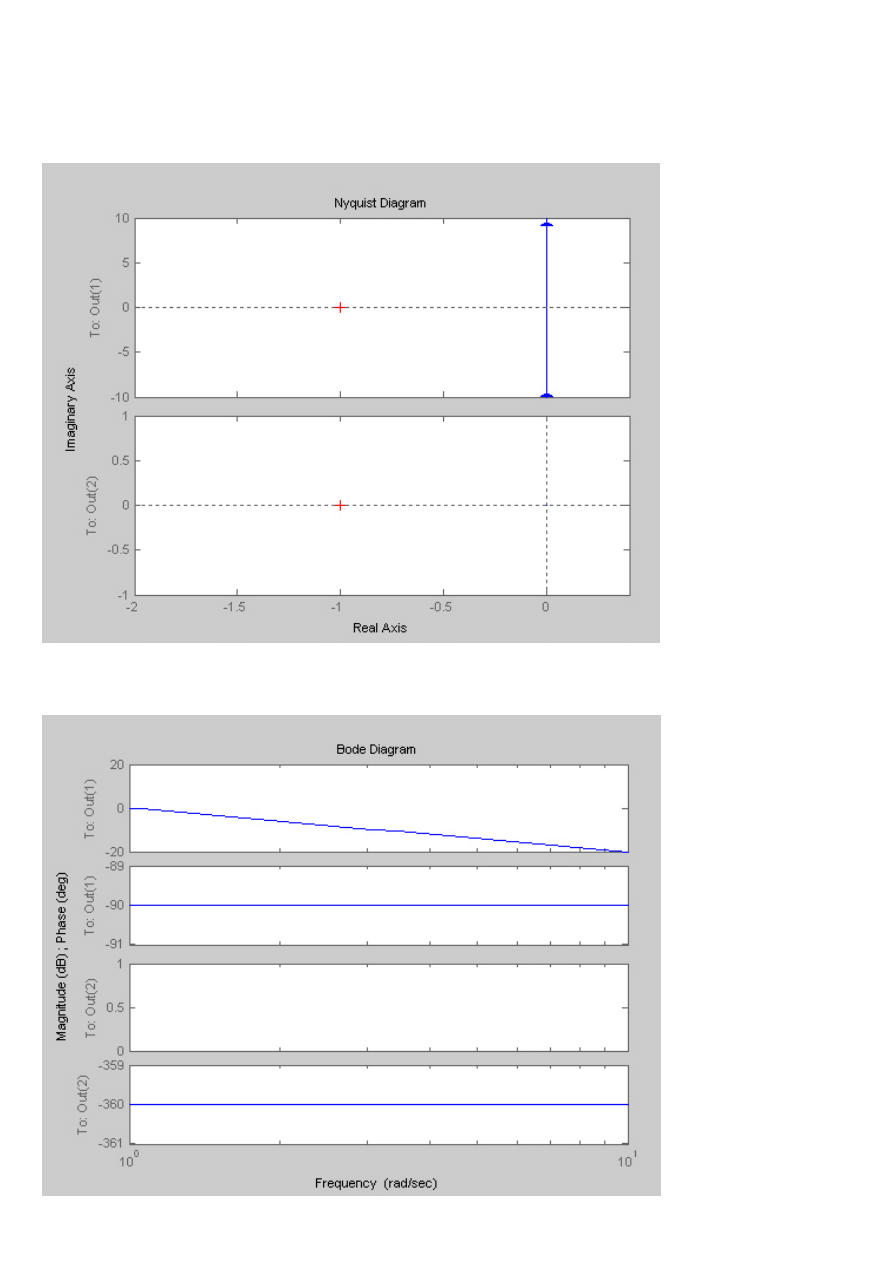
Charakterystyka Nyquista
Charakterystyka Bodego
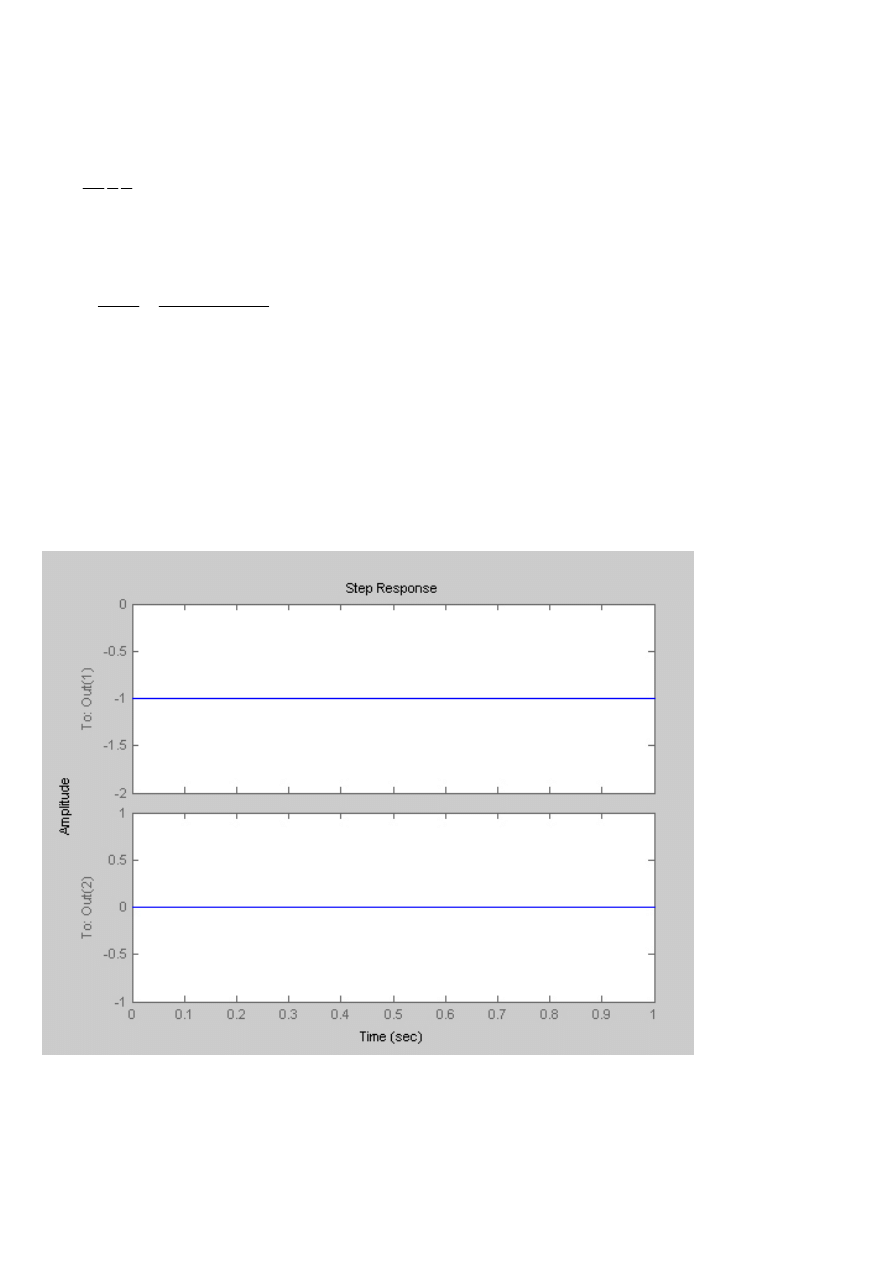
d)
U=10V
Skala rejestratora: 2 V/cm
−
=
0
0
0
0
0
1
L
M = [1 0 0]
Gdzie L=[a
2
a
1
a
0
] i M=[b
2
b
1
b
0
] dla
0
1
2
2
0
1
2
2
)
(
)
(
)
(
b
s
b
s
b
a
s
a
s
a
s
M
s
L
s
G
+
+
+
+
=
=
1
)
(
−
=
s
G
Symulacja z Matlaba
Charakterystyka skokowa
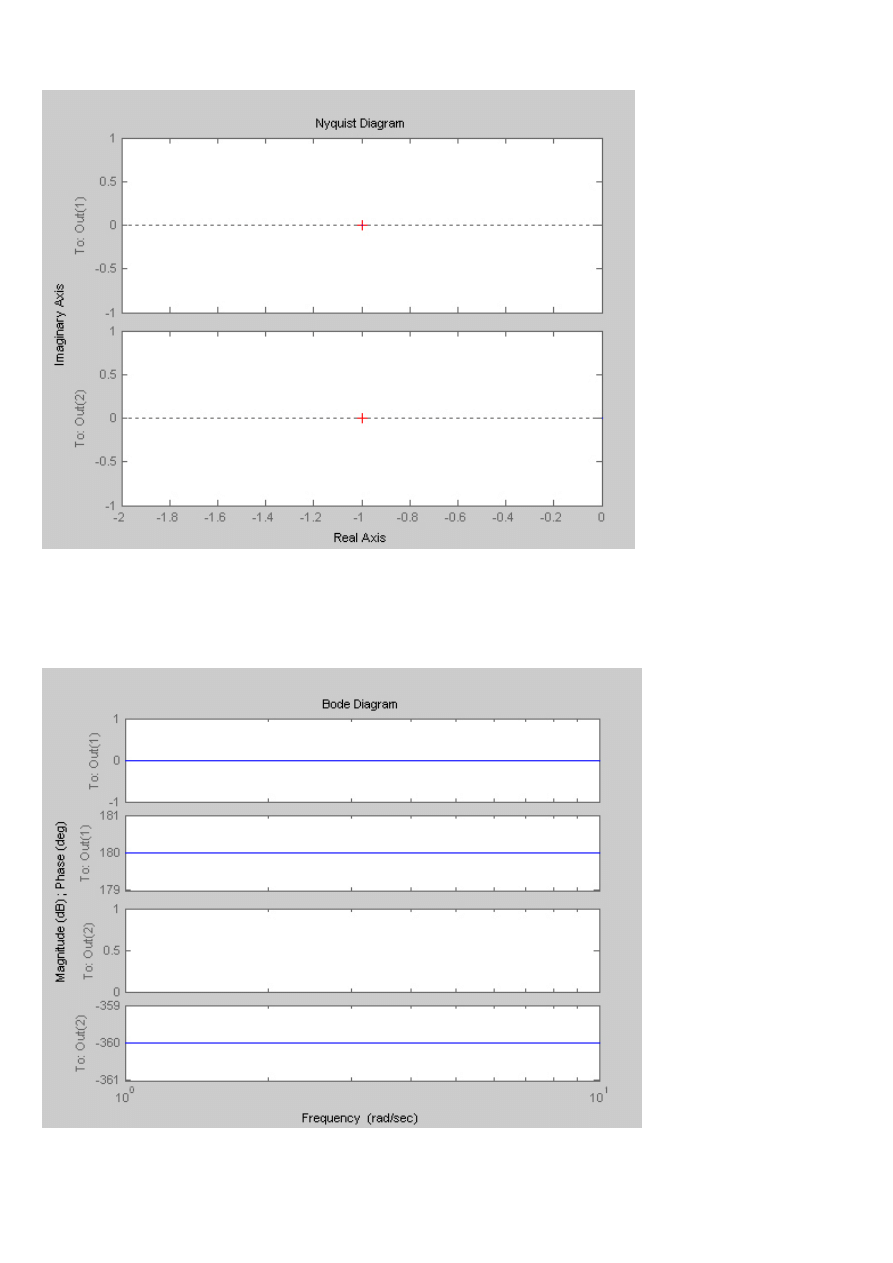
Charakterystyka Nyquista
Charakterystyka Bodego

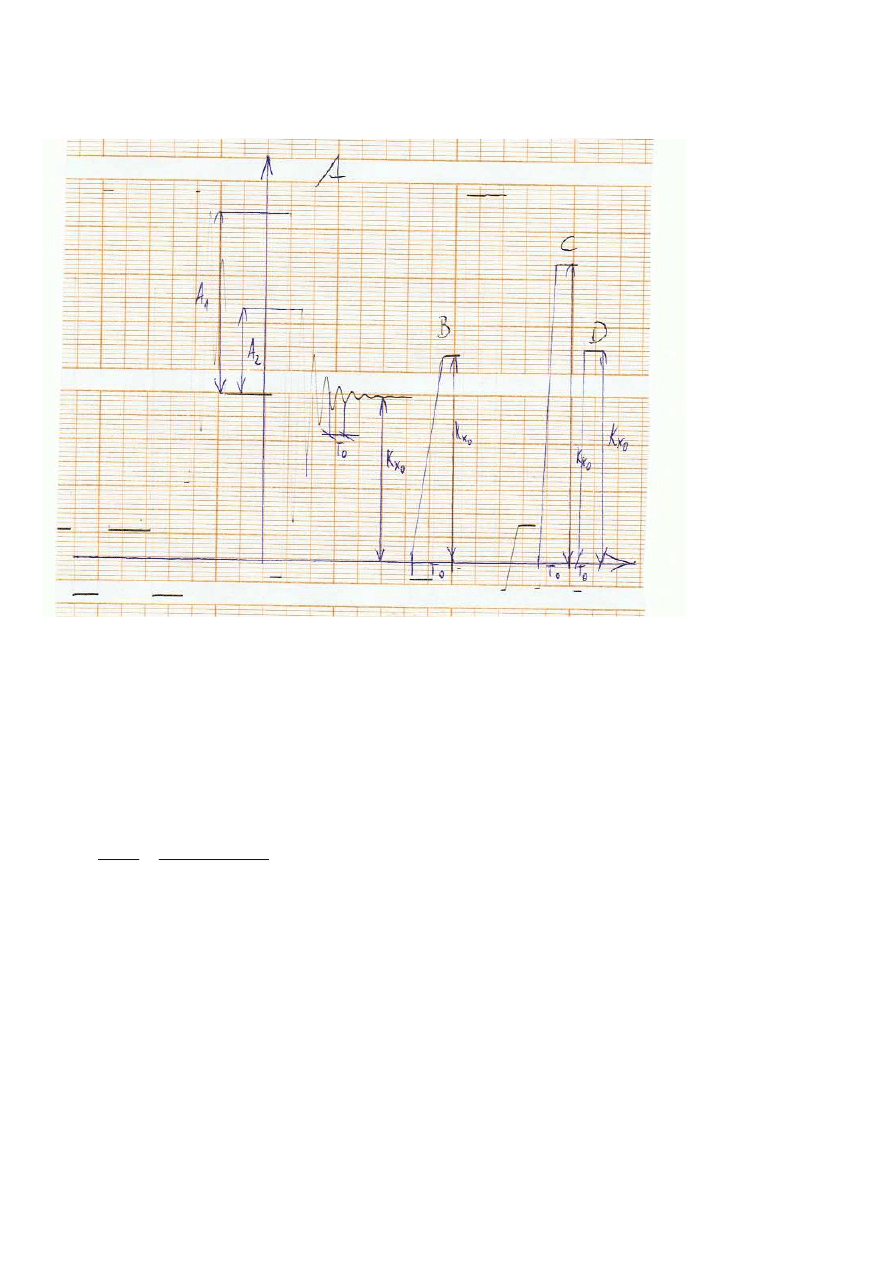
6. Identyfikacja obiektów na podstawie charakterystyk skokowych
a)
Człon oscylacyjny 2-go rzędu
A
=
[
0
4
−
5
1
]
B
=
[
0
0
1
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
35
,
0
10
5
,
3
10
0
=
=
=
U
kx
k
5
,
2
0
=
T
s
51
,
2
2
0
0
=
=
T
π
ω
19
,
0
=
ξ
3
,
6
95
,
0
2
,
2
)
51
,
2
(
51
,
2
19
,
0
2
)
51
,
2
(
35
,
0
2
)
(
2
2
2
2
2
0
0
2
2
0
+
+
=
+
∗
∗
∗
+
∗
=
+
+
=
s
s
s
s
s
k
s
G
ω
ξω
ω
b)
Człon inercyjny
A
=
[
−
6 3
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=8 V
x
10
=0
x
20
=0
538
,
0
10
0
=
=
U
kx
k
6
,
5
0
=
T
s
21
,
1
2
0
0
=
=
T
π
ω
46
,
1
46
,
0
787
,
0
)
21
,
1
(
21
,
1
19
,
0
2
)
21
,
1
(
538
,
0
2
)
(
2
2
2
2
2
0
0
2
2
0
+
+
=
+
∗
∗
∗
+
∗
=
+
+
=
s
s
s
s
s
k
s
G
ω
ξω
ω
c)
Człon całkujący
A
=
[
0
0
0
0
]
B
=
[
1
0
0
0
]
C
=
[
1
0
0
0
]
D
=
[
0
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
62
,
0
10
0
=
=
U
kx
k
s
s
k
s
G
62
,
0
)
(
=
=
d)
Człon bezinercyjny
A
=
[
0
0
0
0
]
B
=
[
0
0
0
0
]
C
=
[
0
0
0
0
]
D
=
[
−
1
0
0
0
]
U
10
=10 V
x
10
=0
x
20
=0
45
,
0
10
0
−
=
=
U
kx
k
45
,
0
)
(
−
=
=
k
s
G
7. Identyfikacja obiektów na podstawie charakterystyk częstotliwościowych
Człon 1
Lp.
f [Hz]
ω
[rad/s]
log [
ω
]
2A [V]
2B [V]
φ
Re
Im
20log[G(j
ω
)]
1
13,70
86,04
1,93
4,00
0,88
2,00
0,21
0,0077
-13,15
2
51,80
325,30
2,51
4,00
1,78
27,00
0,39
0,2020
-7,03
3
59,20
371,78
2,57
4,00
2,31
52,00
0,35
0,4550
-4,77
4
64,30
403,80
2,61
4,00
2,64
82,00
0,09
0,6535
-3,61
5
67,10
421,39
2,62
4,00
2,67
105,00
-0,17
0,6447
-3,51
6
74,60
468,49
2,67
4,00
2,11
138,00
-0,39
0,3529
-5,56
7
96,20
604,14
2,78
4,00
0,74
163,00
-0,17
0,0540
-14,66
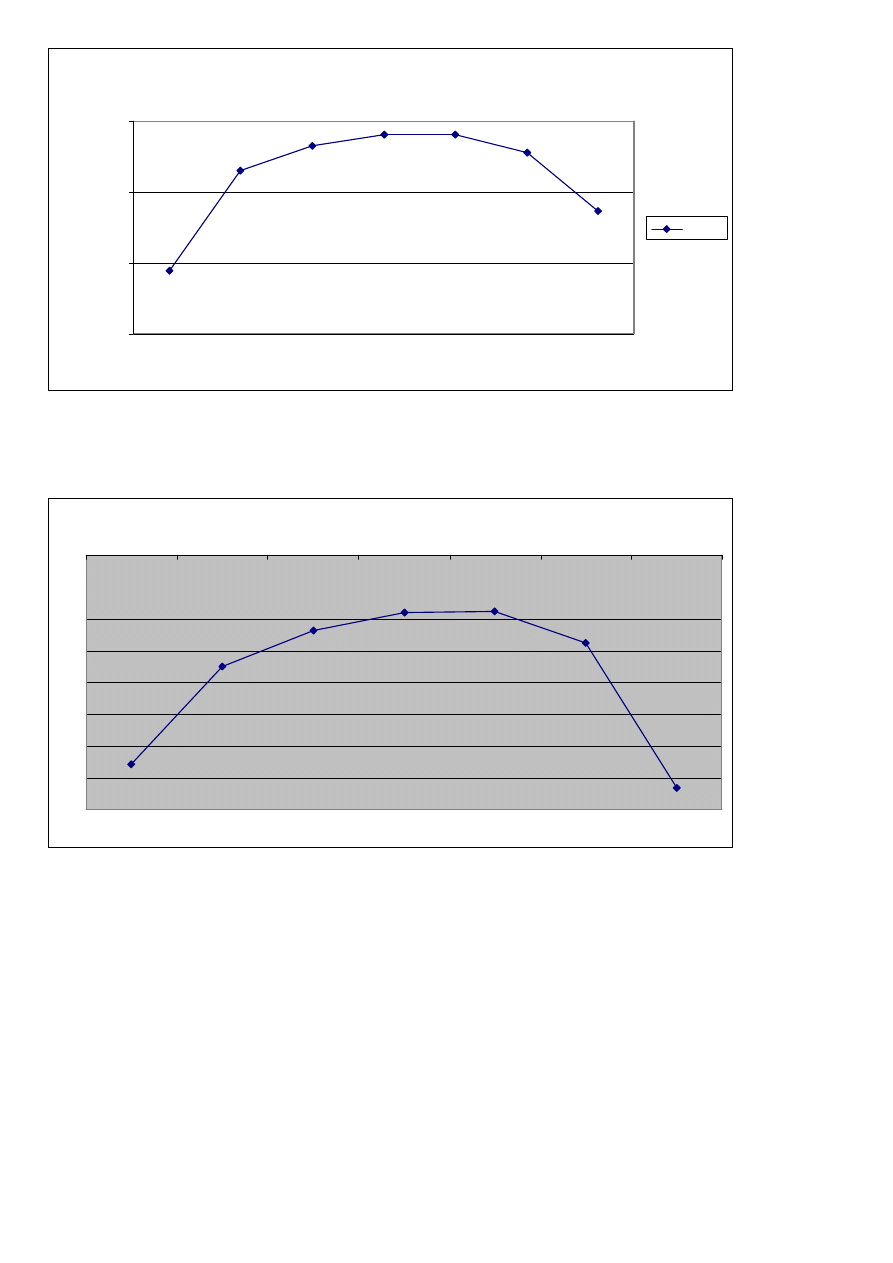
Charakterystyka amplitudowo-fazowa
0,00
0,01
0,10
1,00
Re
Im
G (jw)
Charakterystyka logarytmiczna Bodego
1,93
2,51
2,57
2,61
2,62
2,67
2,78
log(w)
2
0
lo
g
[G
(j
w
)]
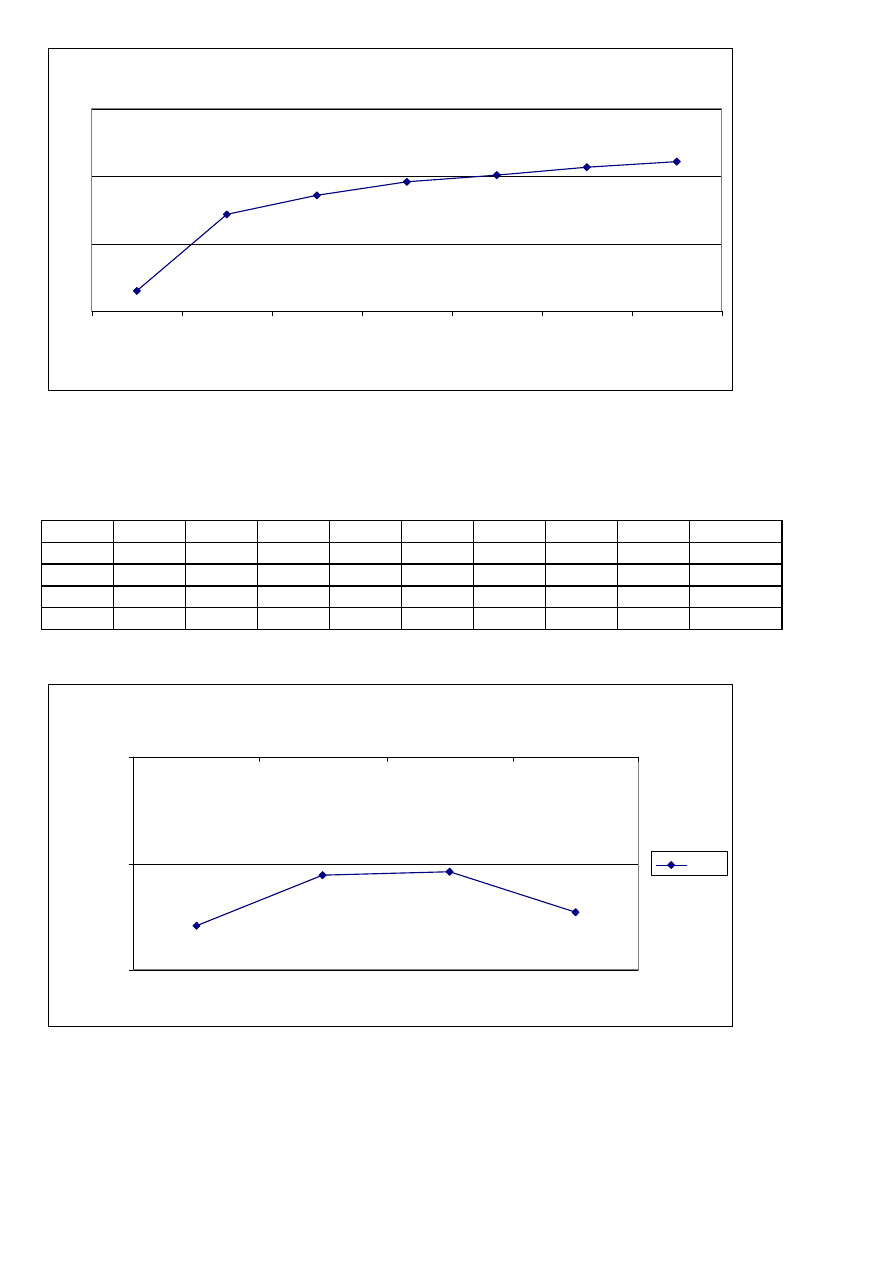
Charakterystyka logarytmiczna Bodego
1,93
2,51
2,57
2,61
2,62
2,67
2,78
log(w)
k
ą
t
fa
z
o
w
y
Człon 2
Lp.
f [Hz]
ω
[rad/s]
log [
ω
]
2A [V]
2B [V]
φ
Re
Im
20log[G(j
ω
)]
1
14,37
90,24
1,96
4,00
0,675
8,80
0,1667
0,0258
-15,46
2
60,60
380,57
2,58
4,00
0,563
33,00
0,1180
0,0766
-17,03
3
139,00
872,92
2,94
4,00
0,388
60,00
0,0485
0,0840
-20,26
4
570,00 3579,60
3,55
4,00
0,138
90,00
0,0000
0,0345
-29,24
Charakterystyka amplitudowo-fazowa
0,01
0,10
1,00
0,17
0,12
0,05
0,00
Re
Im
G(jw)
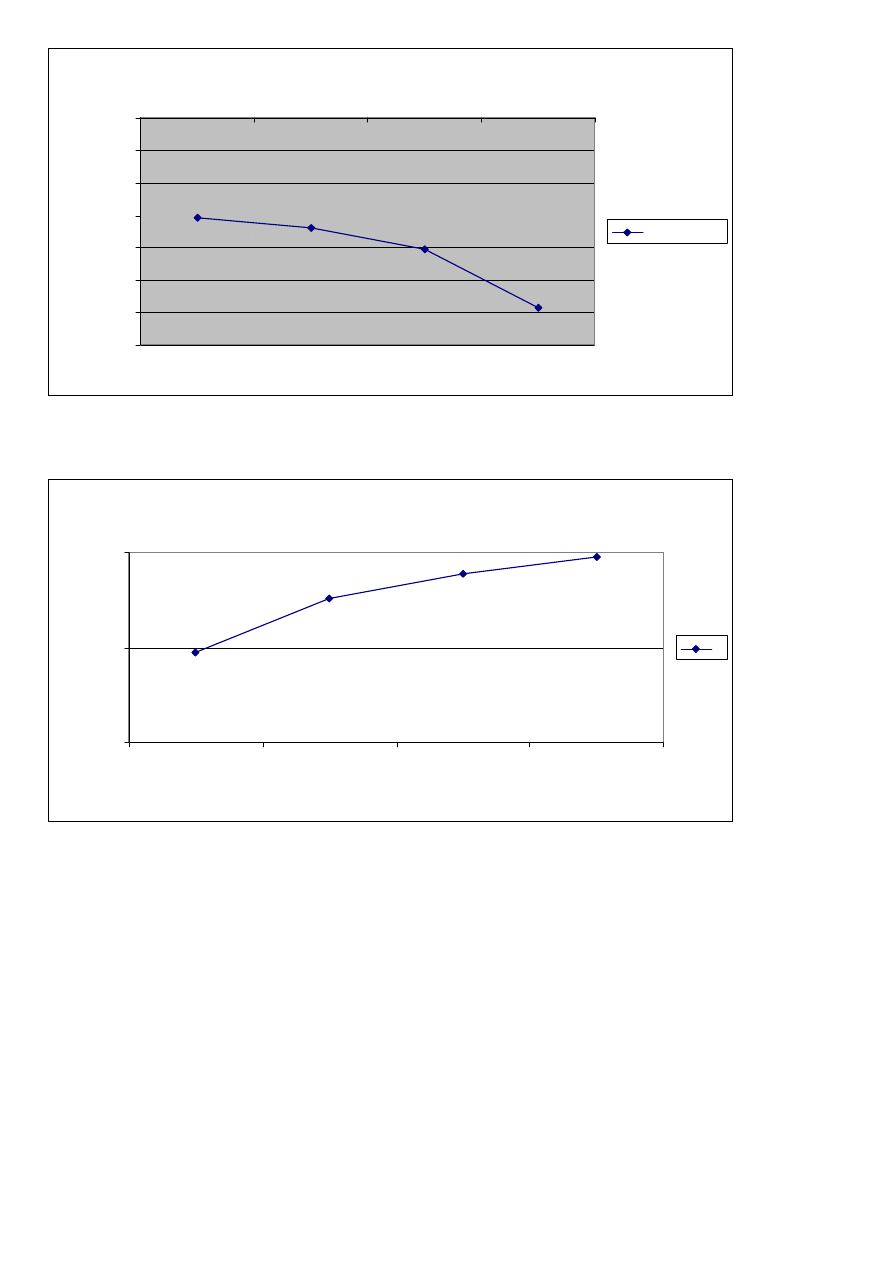
Charakterystyka logarytmiczna Bodego
-35,00
-30,00
-25,00
-20,00
-15,00
-10,00
-5,00
0,00
1,96
2,58
2,94
3,55
log(w)
2
0
lo
g
[G
(j
w
)]
20log[G(j
ω
)]
Charakterystyka logarytmiczna Bodego
1
10
100
1,96
2,58
2,94
3,55
Log(w)
k
ą
t
fa
z
o
w
y
φ
8. Wnioski
- Kształt charakterystyk zależy od dokładności sprzętu pomiarowego jak i również od
dokładności i precyzji odczytania pomiarów
Wyszukiwarka
Podobne podstrony:
automatyka10001 id 73404 Nieznany
automatyka id 73112 Nieznany (2)
automaty id 72943 Nieznany (2)
Automaty 2 id 72948 Nieznany (2)
Podstawy automatyki id 366718 Nieznany
AutomatykaCw5 id 73408 Nieznany (2)
AutomatykaCw8 id 73410 Nieznany (2)
Automatyka 7 id 73137 Nieznany (2)
AutomatykaWyklad01 id 73427 Nieznany (2)
AutomatykaCw4 id 73407 Nieznany (2)
automatyka10001 id 73404 Nieznany
automatyka wykl 1 id 73377 Nieznany
Automatyka nkf cyfrowe id 62906 Nieznany (2)
Automatyka i robotyzacja id 733 Nieznany
Automatyka ulog w8 id 629066 Nieznany (2)
4 2 RG Automaty skonczone id 38 Nieznany (2)
automatyka sprawko 2 id 73363 Nieznany
automatyka c2 id 73267 Nieznany (2)
Automatyka i Robotyka id 73294 Nieznany
więcej podobnych podstron