1

I

T
P

W

ZPT

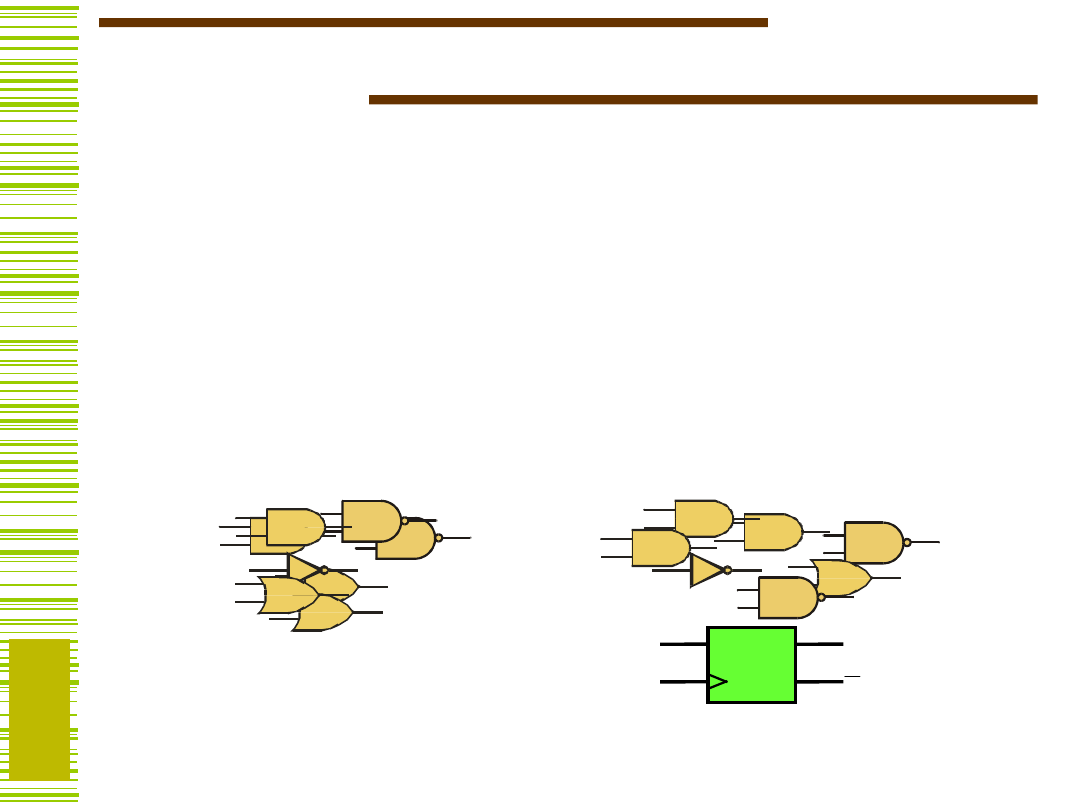
Układy logiczne

kombinacyjne

sekwencyjne

Clk

Clk

FF

D

D

Q

Q

Układy logiczne to dział techniki cyfrowej, w której
układy cyfrowe konstruowane są na poziomie bramek
logicznych i przerzutników.

2

I

T
P

W

ZPT

Funkcja boolowska

Funkcją boolowską zmiennych binarnych x

1

,... ,x

n

nazywamy

odwzorowanie:

 f: X  Y

gdzie:
X  B

n

= {0,1}  {0,1} ... {0,1},

Y  B

m

n-razy

Jeżeli X = B

 n

, to funkcję nazywamy zupełną; w przeciwnym

przypadku jest to funkcja niezupełna, zwana również funkcją
nie w pełni określoną.

  

Tablica prawdy

Formuła (wyrażenie) boolowskie

 Reprezentacje:

  

 

... i wiele innych sposobów opisu (np.

BDD)

3

I

T
P

W

ZPT

Tablica prawdy

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

7

1

1

1

1

tablicowe przedstawienie odwzorowania f

f(x

1

, x

2

, x

3

)

 

f: B

3

B

1

1

1

1

7

0

1

1

6

1

1

0

1

5

0

0

0

1

4

1

1

1

0

3

0

1

0

2

1

1

0

0

1

0

0

0

0

0

f

x

3

x

2

x

1

0

1

Funkcja niezupełna

─

─















1

n

0

j

j

j

NKB

D

2

a

A

L

A

4

I

T
P

W

ZPT

Uproszczony zapis tablicy

prawdy

 

f = [(1, 3, 5, 7, (

2, 6

)]

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

─

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

─

7

1

1

1

1

f = (

1, 3, 5, 6, 7

)

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

5

I

T
P

W

ZPT

Formuła boolowska

Formuła boolowska to wyrażenie, w którym
zmienne boolowskie połączone są operatorami:
+ (OR),  (AND), (NOT)

X

1
1
0
0

0
0
0
1

0
1
1
1

0 0
0 1
1 0
1 1

a  b

a + b

a b

a

6

I

T
P

W

ZPT

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

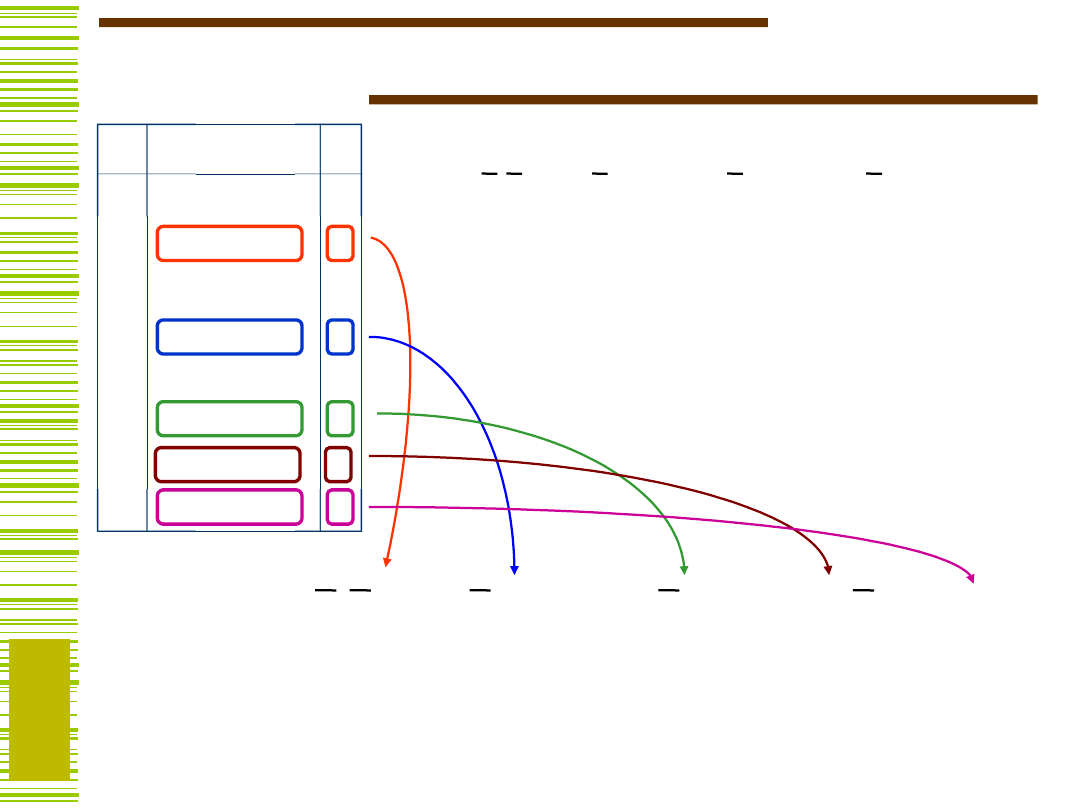
Formuła boolowska - przykład

3

2

1

x

x

x

3

2

1

3

2

1

x

x

x

x

x

x





3

2

1

x

x

x



3

2

1

x

x

x



f 

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f











Ogromne znaczenie formuł boolowskich ...

7

I

T
P

W

ZPT

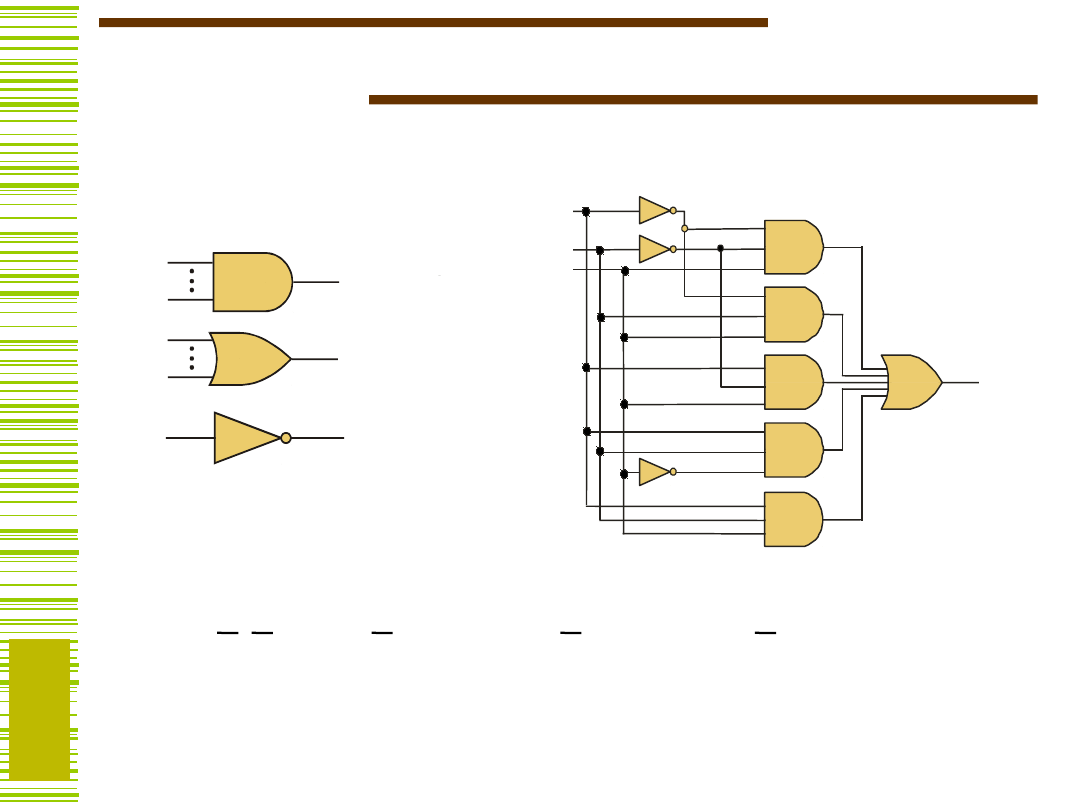
Operatory logiczne

AN
D

OR

NOT

mają swoje realizacje techniczne tzw. bramki logiczne

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f











1

2

3

4

5

x

3

x

1

x

2

f

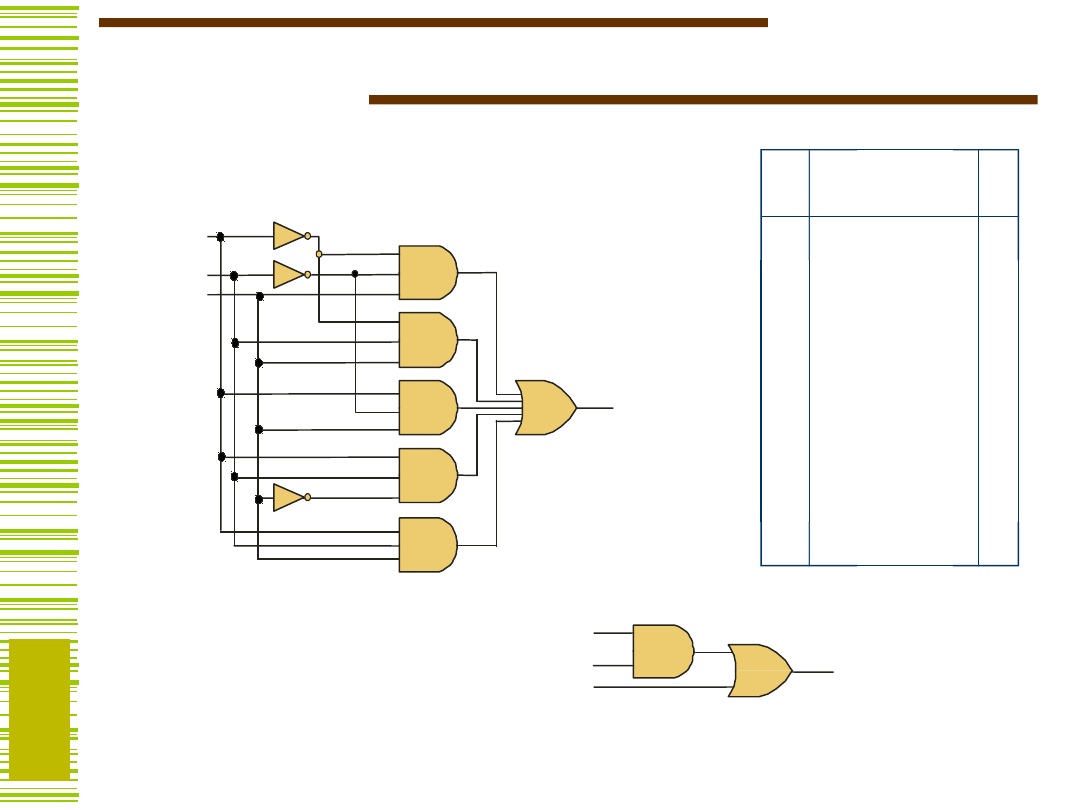
Realizacja funkcji f

1

2

3

4

5

8

I

T
P

W

ZPT

Komentarz

Zatem upraszczając wyrażenia boolowskie
będziemy mogli jednocześnie uprościć ich
realizację,

np.

zmniejszyć liczbę zastosowanych

bramek co decyduje o

kosztach realizacji

i tym

samym jest głównym czynnikiem
zwiększającym

konkurencyjność naszego

produktu na rynku

.

 

x

3

x

1

x

2

f

1

2

3

4

5

f

x
x
x

1

2

3

Podstawy teoretyczne

upraszczania wyrażeń

boolowskich zawarte są

w algebrze Boole’a.

9

I

T
P

W

ZPT

Prawa i własności algebry

Boole’a

Własności stałych

 a + 0 = a

a  0 = 0

a + 1 = 1

a  1 = a

1

a

a





0

a

a





Własności negacji

Idempotentność

a + a = a

a 

a = a

a

a 

 

Podwójna negacja

10

I

T
P

W

ZPT

Prawa i własności algebry Boole’a

c.d.

b

a

b

a

y









b

a

b

a

y









Prawa De Morgana 

Przemienność

a + b = b + a

a  b = b  a

 

Łączność

  a + (b + c) = (a + b) + c a(bc) =

(ab)c

Rozdzielność

a + bc = (a + b)(a + c)

a (b + c) = ab

+ac

11

I

T
P

W

ZPT

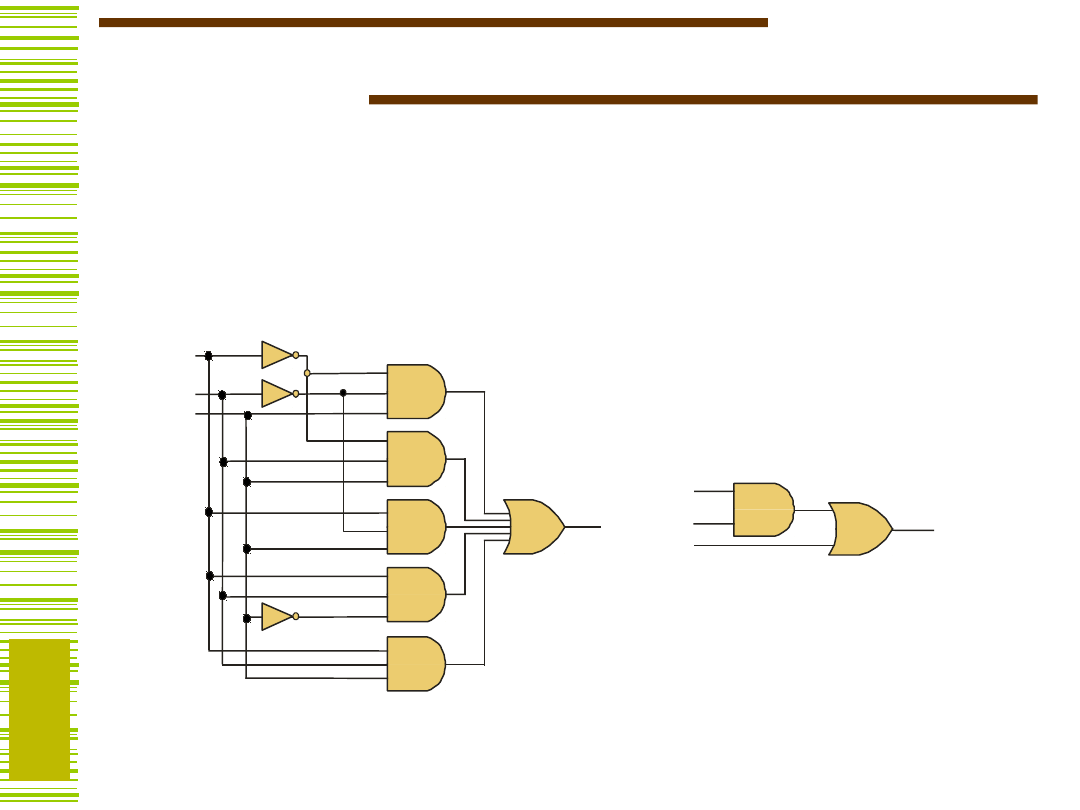
Transformacja formuły

Minimalizacja funkcji
boolowskich!!!

f

x
x
x

1

2

3

Realizacja uproszczonej

funkcji f













3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f









2

1

3

1

3

1

x

x

x

x

x

x

)

(

2

2

3

1

x

x

x

x





)

(

2

2

3

1

x

x

x

x











)

(

3

3

2

1

x

x

x

x

2

1

3

x

x

x 



=1

=
1

=
1















3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

12

I

T
P

W

ZPT

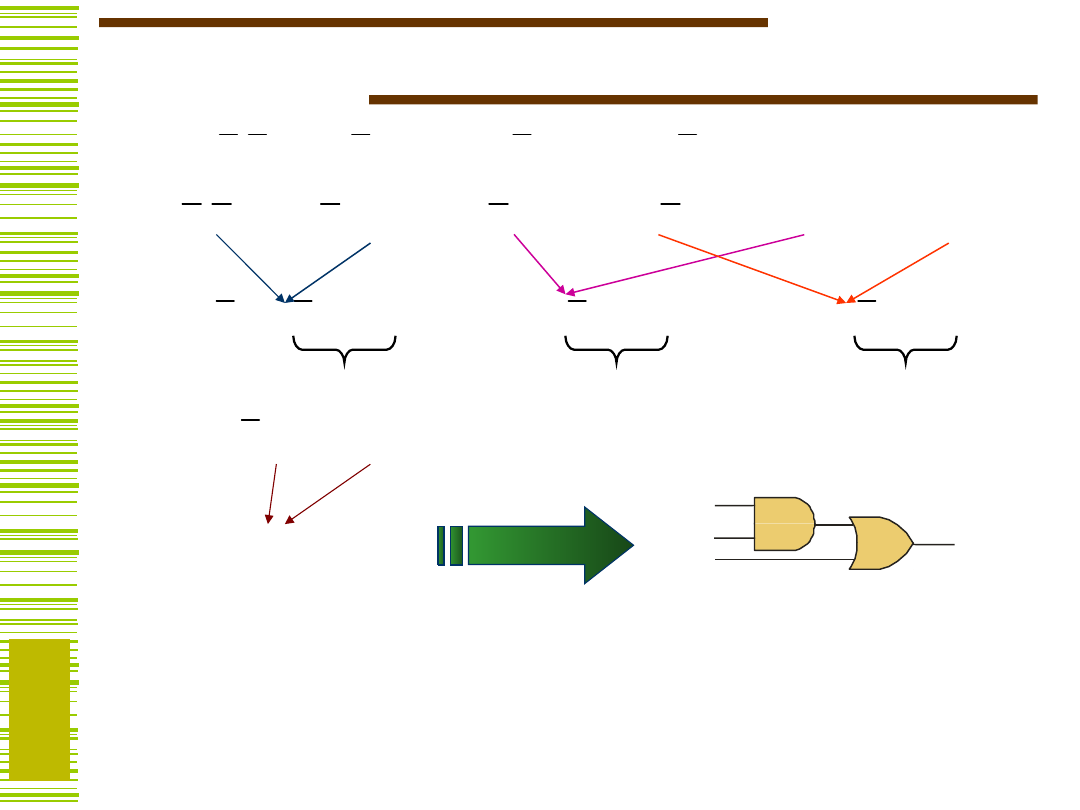
Sens fizyczny minimalizacji

x

3

x

1

x

2

f

1

3

5

6

7

f

x
x
x

1

2

3

0
1
0

0
1
0

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

0

0

0
1
1

0
1
1

1

1

13

I

T
P

W

ZPT

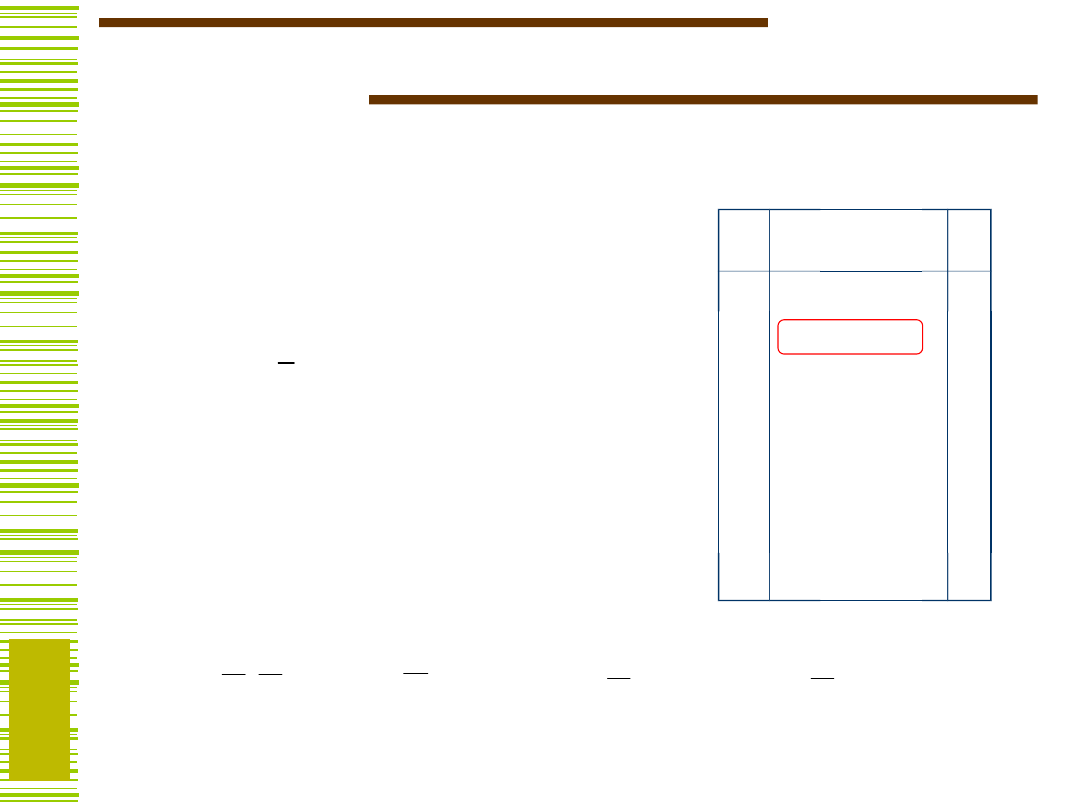
Postaci (formy) kanoniczne

Kanoniczna postać sumacyjna

(suma iloczynów)

Kanoniczna postać iloczynowa

(iloczyn sum)

14

I

T
P

W

ZPT

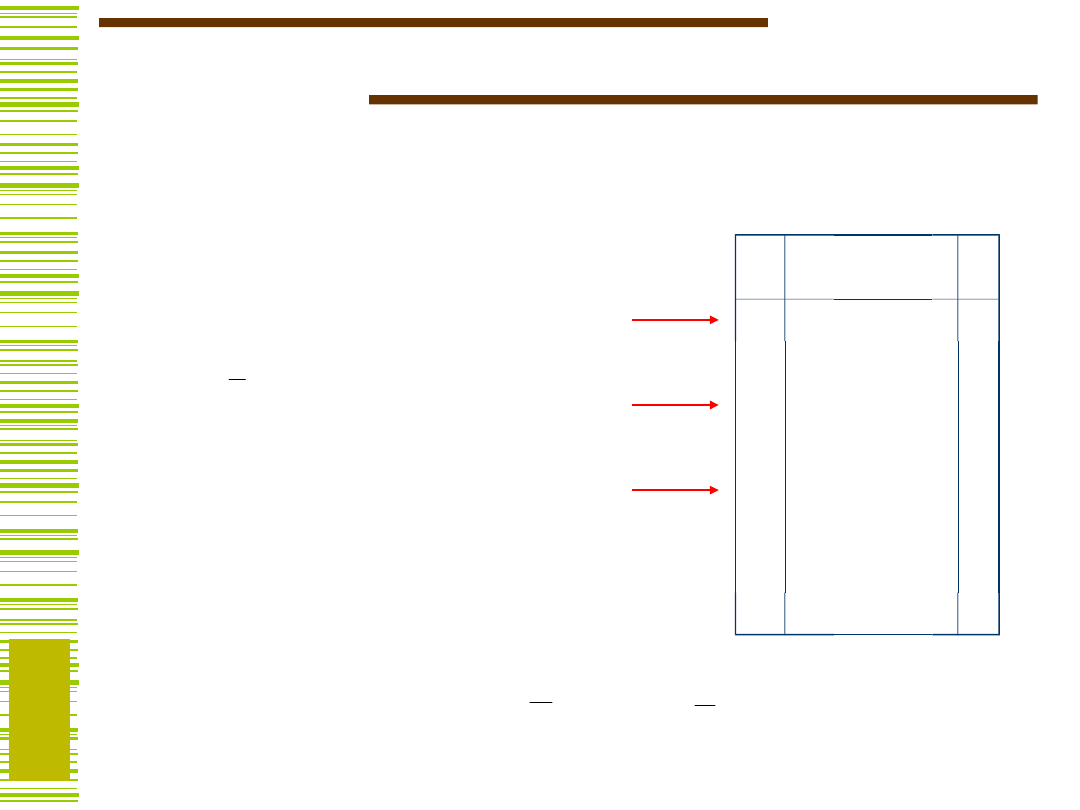
Kanoniczna postać sumacyjna

 













0

e

gdy

,

x

1

e

gdy

x,

x

e

)

f(X

x

x

x

f(X)

k

e

n

e

2

e

1

1

2

0

k

nk

2k

1k

n

V













)

(X)f(X

P

f(X)

k

k

1

2

0

k

V

n







3

2

1

x

x

x

f(X)

x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

3

2

1

x

x

x



3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x







15

I

T
P

W

ZPT

Kanoniczna postać iloczynowa

 













1

e

gdy

,

x

0

e

gdy

x,

x

e





)

f(X

x

x

x

f(X)

k

e

n

e

2

e

1

1

2

0

k

nk

2k

1k

n























)

3

2

1

x

x

(x

f











)

f(X

S

f(X)

k

k

1

2

0

k

n











x

1

x

2

x

3

f

0

0

0

0

0

1

0

0

1

1

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

)

(

3

2

1

x

x

x





)

x

x

x

3

2

1





(