WSTĘP DO

ELEKTROTECHNIKI

Izabella Mróz-Radłowska

Instytut Elektroenergetyki

II piętro p.209

Wtorek 11 -12

1. Hempowicz P. i inni. Elektrotechnika
i elektronika dla nieelektryków. WNT.
Warszawa 1999.
2. Krakowski M. Elektrotechnika
teoretyczna. Tom I. Obwody liniowe i
nieliniowe. PWN. Warszawa 1979
3. Tadeusiewicz M. Teoria obwodów.
Cz. I. Politechnika Łódzka. Łódź 2000

System jednostek SI

Dowolna wielkość fizyczna

W = W* [W]

gdzie: W* - wartość liczbowa

1[W] – jednostka wielkości

System jednostek SI

W

1

*[W

1

] = W

2

*[W

2

]

czyli





 

1

2

2

1

1

1

W

W

W

W







System jednostek SI

Początek układu SI – 1793 rok.

Ustanowienie międzynarodowego

układu jednostek SI – Generalna

Konferencja Miar w 1960.

W Polsce 1966 rok – Rozporządzenie

Rady Ministrów – Dz.U nr 25 z dnia 30

czerwca 1965, poz. 154.

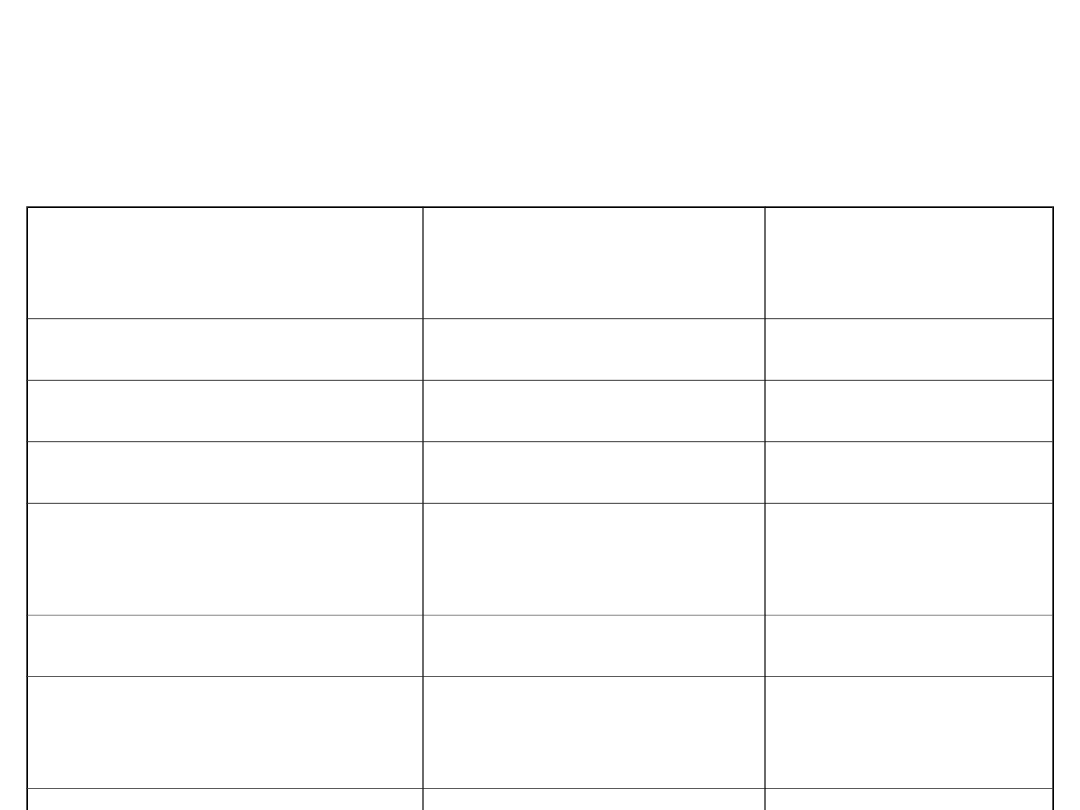
Jednostki podstawowe układu SI

Nazwa wielkości

Nazwa

jednostki

Skrót

literowy

Długość (l)

metr

m

Masa (m)

kilogram

kg

Czas (t)

sekunda

s

Natężenie prądu

(i)

amper

A

Temperatura (T)

kelwin

K

Ilość substancji

(N)

mol

mol

Światłość źródła

światła (J)

kandela

cd

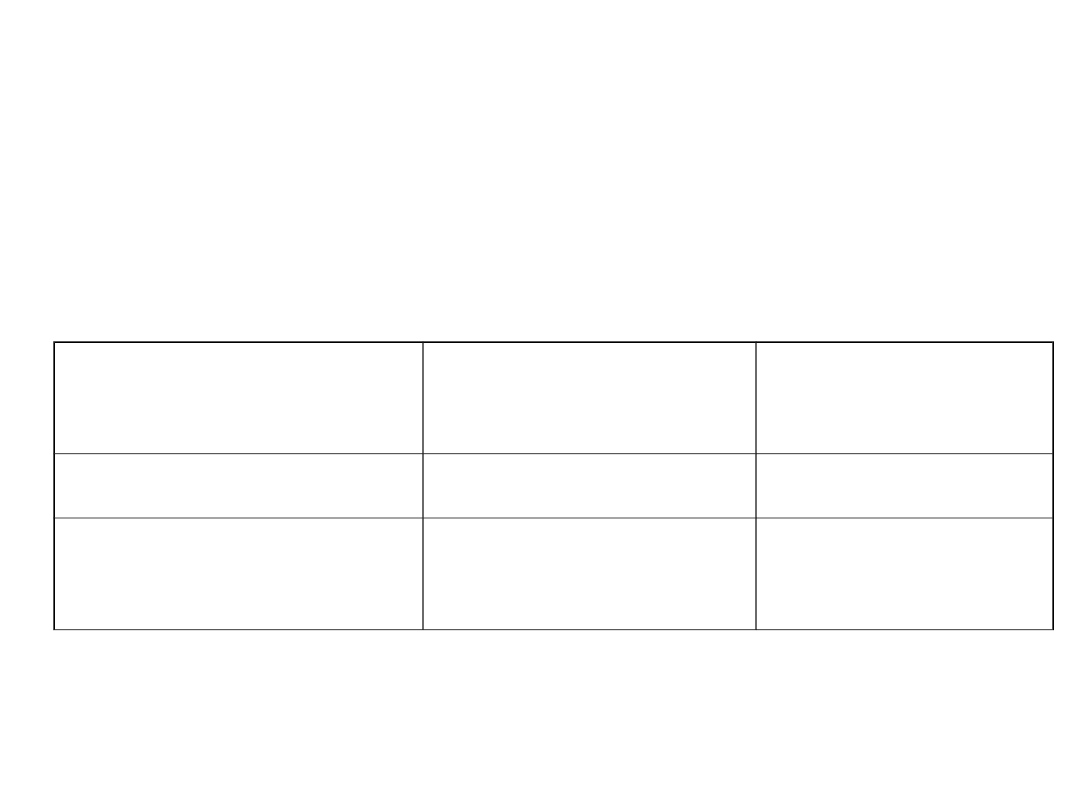
Jednostki uzupełniające układu

SI

Nazwa

wielkości

Nazwa

jednostki

Skrót

literowy

Kąt płaski

radian

rad

Kąt

przestrzenny

steradian

sr

Jednostki podstawowe układu SI

Metr

– jest długością równą 1 650

763,73 długości fali w próżni

promieniowania

monochromatycznego, emitowanego

przez izotop kryptonu 86

(promieniowanie odpowiadające

przejściu między poziomami 2p

10

i 5d

5

.

(1960)

Jednostki podstawowe układu SI

Kilogram

jest masą

międzynarodowego wzorca
(etalonu) tej jednostki,
przechowywanego w
Międzynarodowym Biurze Miar w
Sevres.

(1901)

Jednostki podstawowe układu SI

Sekunda

jest czasem trwania 9

192 631 770 okresów
promieniowania odpowiadającemu
przejściu między dwoma
nadsubtelnymi poziomami stanu
podstawowego atomu cezu 133.

(1967)

Jednostki podstawowe układu SI

Amper

jest prądem elektrycznym nie

zmieniającym się, który płynąc w dwóch

równoległych prostoliniowych

nieskończenie długich przewodach o

przekroju okręgłym znikomo małym,

umieszczonych w próżni w odległości 1

metra jeden od drugiego, wywołałby

między tymi przewodami siłę 2 •10

-7

niutona na każdy metr długości.

(1948)

Jednostki podstawowe układu SI

Kelwin

jest jednostką temperatury

termodynamicznej równą 1/273,16
temperatury bezwzględnej punktu
potrójnego wody

(1967)

Jednostki podstawowe układu SI

Mol

jest licznością (ilością)

substancji układu zawierającego
liczbę cząsteczek równą liczbie
atomów zawartych w masie 0,012 kg
czystego nuklidu węgla

12

C

Jednostki podstawowe układu SI

Kandela

jest światłością, która w

kierunku prostopadłym ma pole 1/6•10

5

m

2

powierzchni ciała doskonale czarnego,

promieniującego w temperaturze

krzepnięcia platyny pod ciśnieniem 101

325 N/m

2

(paskali)

(1967)

Jednostki uzupełniające układu

SI

Radian

jest kątem płaskim o

wierzchołku w środku koła,
wycinającym z obwodu tego koła łuk o
długości równej jego promieniowi

Jednostki uzupełniające układu

SI

Steradian

jest kątem bryłowym o

wierzchołku w środku kuli,
wycinającym z powierzchni tej kuli
pole równe kwadratowi jej promienia.

Jednostki pochodne układu SI

Dowolna jednostka wielkości W w

układzie SI

1[W] = k m

a

kg

b

s

c

A

d

K

e

cd

f

rad

g

sr

h

gdzie: k - współczynnik liczbowy
a...h – wykładniki potęg są liczbami

całkowitymi lub zerami

Jednostki pochodne układu SI

Jeżeli

k = 1

jednostka 1[W] jest jednostką

główną

,

np.

jednostka prędkości – 1 m/s lub 1 m

1

s

-1

Jednostki pochodne układu SI

Jeżeli

k  1

jednostka 1[W] jest jednostką

pokrewną

, np.

jednostka prędkości

1 km/min = 1000/60 m/s

k = 1000/60

Układ SI

Zasada spójności – w układzie SI
wartość każdej mierzalnej wielkości
fizycznej można określić za pomocą

tylko jednej

jednostki SI

(podstawowej lub pochodnej)
Oznacza to, że k = 1.

Przykład określenia jednostki

pochodnej

Wielkość: energia (lub praca, lub

ciepło).

E = F s

F = m a

a = v/t

v = s/t

Przykład określenia jednostki

pochodnej

Jednostka energii w układzie SI

1[E] = 1[F] 1[s] = 1[m] 1[a] 1[l] =

= 1[m] 1[v] 1[t]

-1

1[l] =

= 1[m] 1[l] 1[t]

-1

1[t]

-1

1[l] = 1[m]

1[l]

2

1[t]

-2

= = kg • m

2

• s

-2

= kg •

m

2

/ s

2

= 1J

Przykład określenia jednostki

pochodnej

Jednostka energii w układzie SI – dżul - J
Jednostki pozaukładowe energii:
- kilowatogodzina

1 kWh = 3,6 • 10

6

J

- kaloria 1 cal = 4,1868 J
- erg

1 erg = 10

-7

J

- elektronowolt 1 eV = 1,60206 • 10

-19

J

- British thermal unit 1 B.t.u. = 1055,06 J

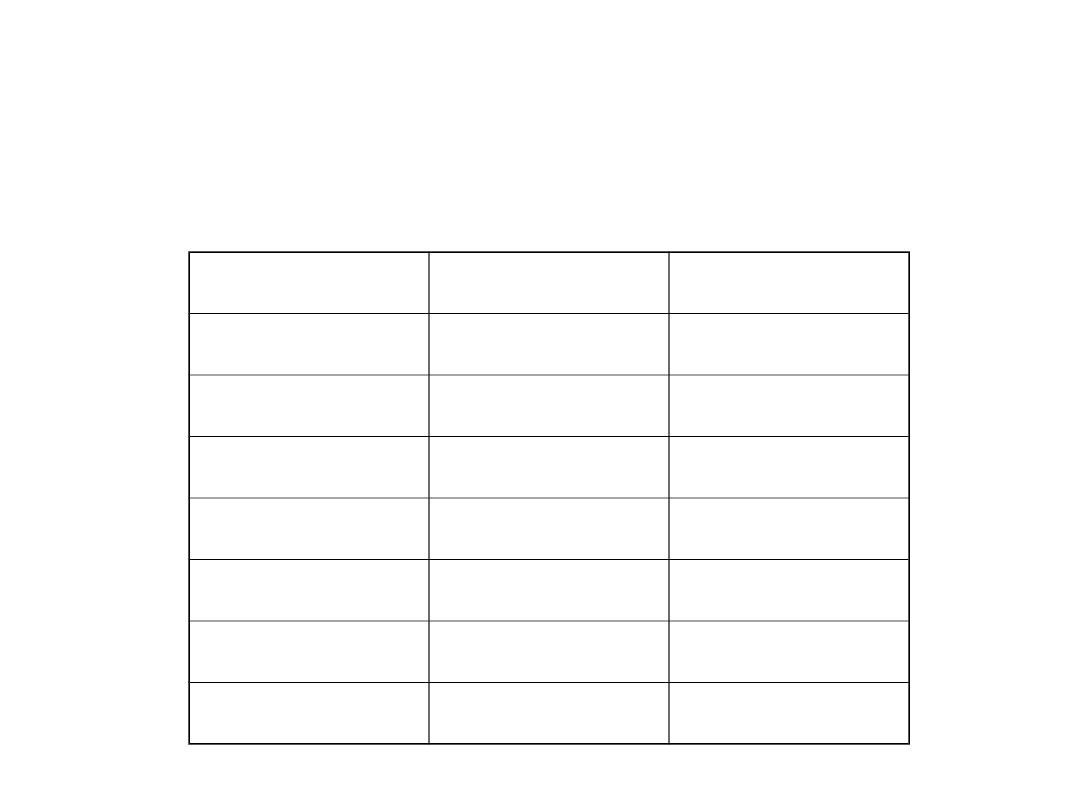
Przedrostki wielokrotne

jednostek

Nazwa

Symbol

Mnożnik

peta

P

10

15

tera

T

10

12

giga

G

10

9

mega

M

10

6

kilo

k

10

3

hekto

h

10

2

deka

da

10

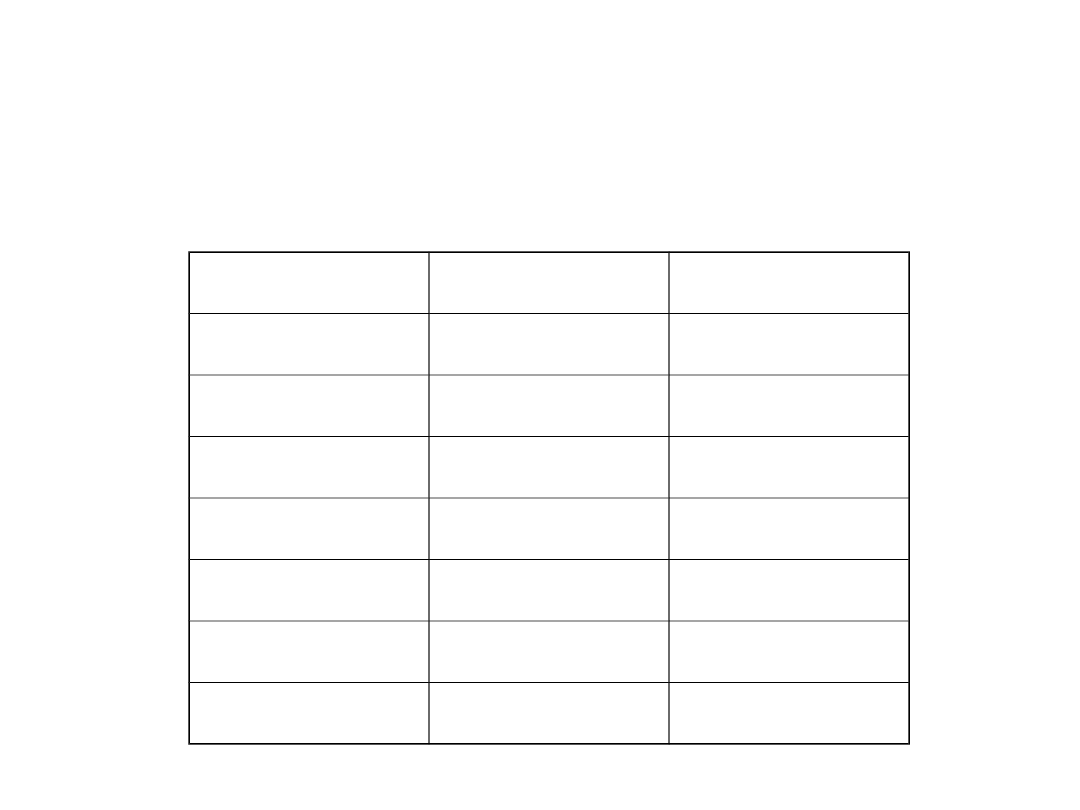
Przedrostki podwielokrotne

jednostek

Nazwa

Symbol

Mnożnik

decy

d

10

-1

centy

c

10

-2

mili

m

10

-3

mikro

µ

10

-6

nano

n

10

-9

piko

p

10

-12

femto

f

10

-15

Cechy ogólne układu SI

• Uniwersalność – może być stosowany

we wszystkich dziedzinach techniki

• Koherentność (spójność) – wszystkie

główne jednostki miar mają

współczynnik przeliczeniowy równy 1

• Dla każdej wielkości określona jest

tylko jedna jednostka miary, jedna

nazwa tej jednostki, jeden jej symbol

i jeden wymiar

Sposoby pisania równań

• Równania wielkościowe

(definicyjne)

• Równania liczbowe

Sposoby pisania równań

• Równania wielkościowe

(definicyjne) – podają zależności
między wielkościami fizycznymi.
Wielkości podstawiane są w
jednostkach głównych SI. Wynik –
w jednostce głównej SI

Sposoby pisania równań

• Równania liczbowe – podają

zależności między wartościami
liczbowymi wielkości i słuszne są
tylko przy ściśle określonych
jednostkach. Takie równania
zwykle zawierają współczynnik
liczbowy, którego wartość wynika
z przeliczenia jednostek.

Przykład pisania równań

Po włączeniu do sieci (0,24 kV)
czajnika elektrycznego przez czas 2
min płynie prąd 10 A. Obliczyć ilość
ciepła, jaka wydzieli się w czajniku.

Dane:

U = 0,24 kV

I = 10 A
t = 2 min

Przykład pisania równań

W czasie t przepływu prądu I
przepływa ładunek Q:

Q = I t

Na oporniku wydziela się energia:

W = U Q = U I t

Przykład pisania równań

Jednostki główne SI używanych w
równaniu

W = U Q = U I t

wielkości:

1[U] = V

1[I] = A

1[t] = s

1[W] = J

Przykład pisania równań

Równanie wielkościowe:

W = U I t =

= 0,24 kV • 10 A • 2 min =

= 0,24 • 10

3

V • 10 A • 2 • 60 s =

= 288 000 J = 288 kJ

Przykład pisania równań

Równanie liczbowe:

W

*

= k U

*

I

*

t

*

J

A

kV

k

min







60000

60

1

10

3









J

s

A

V

k

Przykład pisania równań

Równanie liczbowe:

W

*

= 60000 U

*

I

*

t

*

gdzie: W

*

- w J

U

*

- w kV

I

*

- w A

t

*

- w min

W

*

= 60000 • 0,24 • 10 • 2 =

= 60000 • 4,8 = 288 000 J = 288 kJ

Elementarne wiadomości o

obwodach elektrycznych

Obwód elektryczny to połączenie

elementów elektrycznych takich jak:

oporniki, kondensatory, cewki,

tranzystory, wzmacniacze, źródła

napięcia, źródła prądu.

Graficznym obrazem obwodu jest

schemat pokazujący połączenie

elementów reprezentowanych za

pomocą odpowiednich symboli.

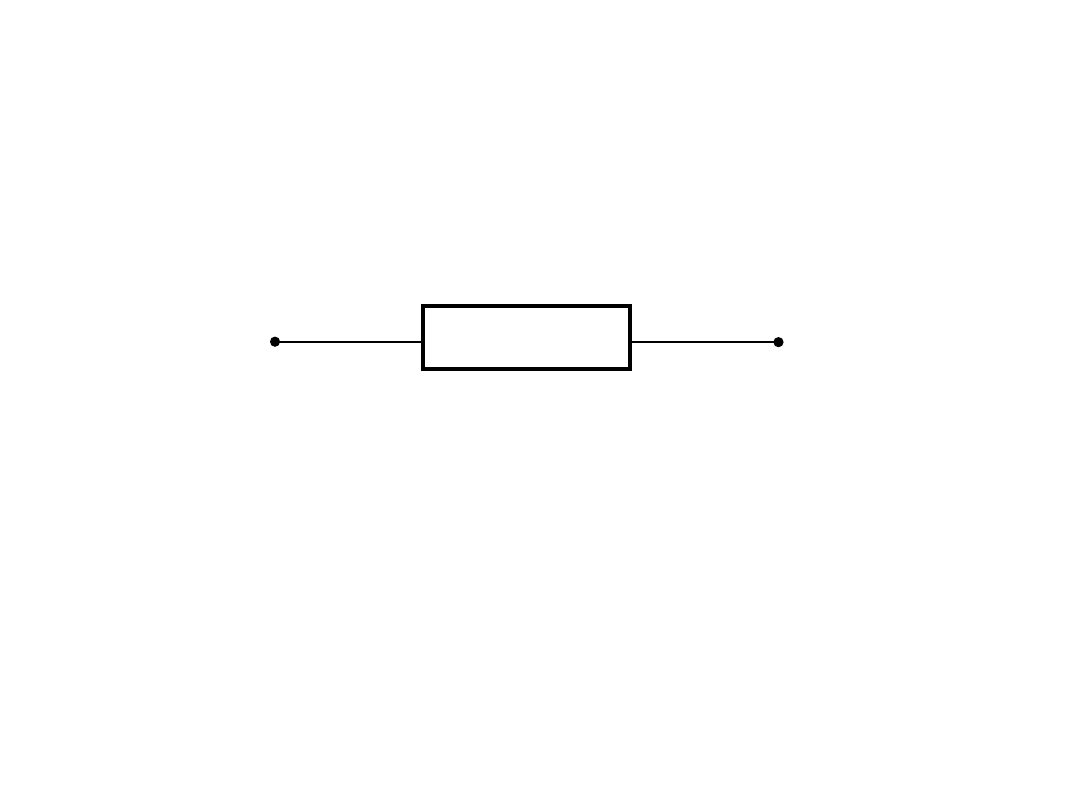
Elementarne wiadomości o

obwodach elektrycznych

Element posiadający dwie końcówki –

tworzy gałąź obwodu.

Punkty, w których łączą się dwie lub

więcej gałęzi to węzły obwodu.

1

2

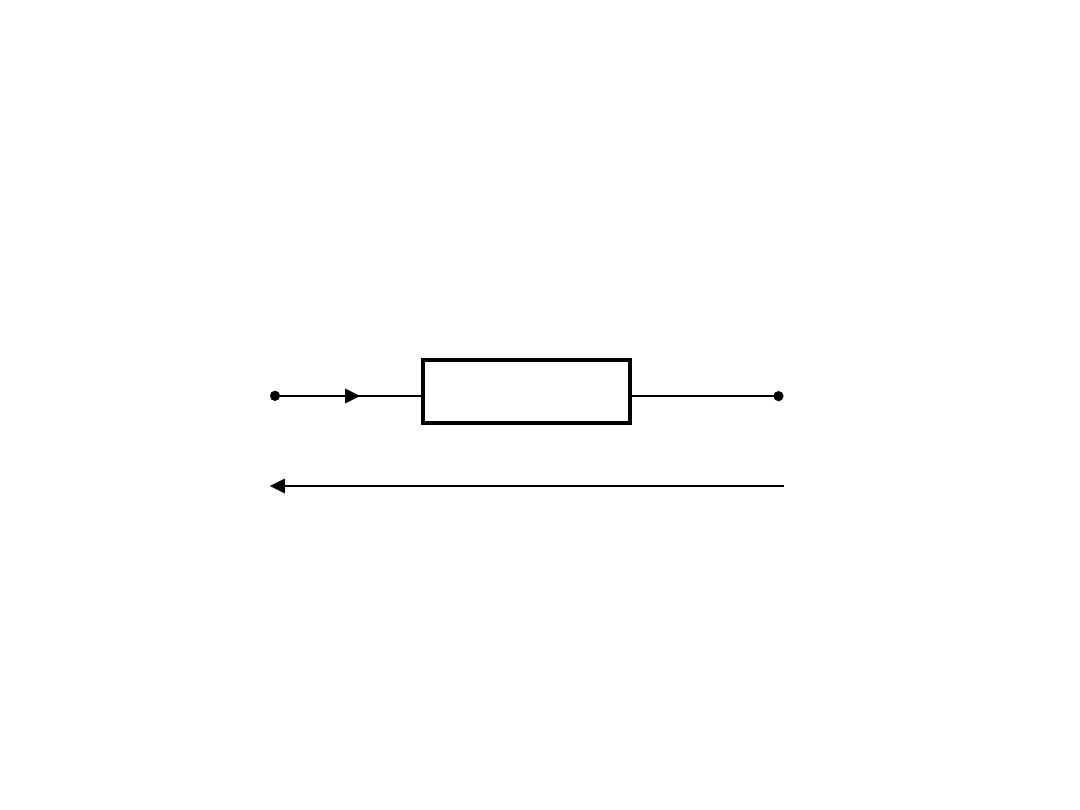
Elementarne wiadomości o

obwodach elektrycznych

1

2

i(t
)

u(t)

Ładunek elektryczny

• Elektron – elementarny nośnik

ujemnego ładunku, równego 1,6 •
10

-19

C o masie 9,108 • 10

–31

kg.

• Atom pozbawiony elektronu – jon

dodatni.

• Atom, do którego dołączył elektron

swobodny – jon ujemny.

Ładunek elektryczny

• Ładunki ujemne: elektrony lub jony.
• Ładunki dodatnie – jony.

• Prąd elektryczny

to ruch lub

zmiana w czasie ładunków:
- prąd przewodzenia
- prąd przesunięcia.

Ładunek elektryczny

• Przewodnik

(idealny) – tylko prąd

przewodzenia (ruch ładunków)

• Dielektryk

(idealny) – tylko prąd

przesunięcia (przemieszczanie ładunków

bez naruszenia struktury atomu – tzw.

polaryzacja)

• Półprzewodnik

– tej samej wielkości prądy

przewodzenia i przesunięcia

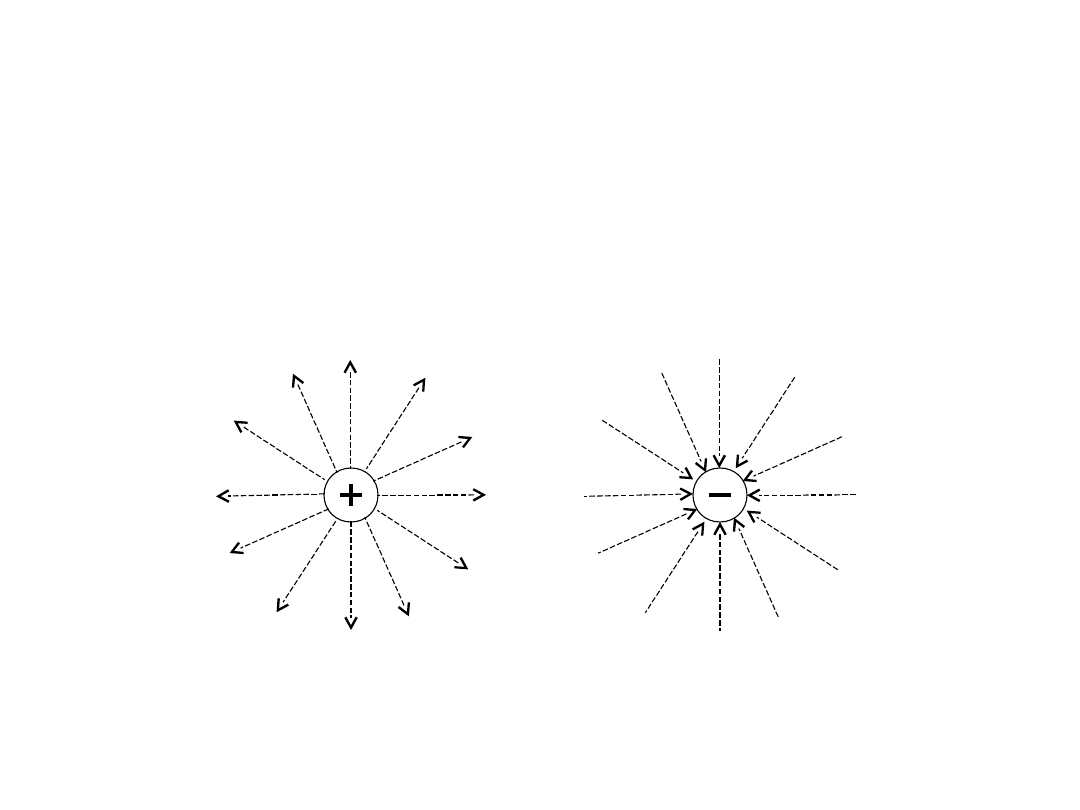
Pole elektryczne

Linie sił pola elektrycznego dla

ładunków:

dodatnieg

o

ujemnego

Pole elektryczne

Elementarna siła działająca w polu
elektrycznym na elementarny
(znikomo mały) ładunek jest
proporcjonalna do tego ładunku

dF = E dQ

(prawo Coulomba F = k

e

Q q/r

2

)

Pole elektryczne

Wielkość E – natężenie pola
elektrycznego. Jest to wektor
skierowany zgodnie z kierunkiem
siły działającej na ładunek.

Jednostka natężenia pola
elektrycznego w układzie SI

   

 

m

V

s

A

m

s

W

C

N

Q

F

E

1

1

1

1

1

1

1

1















Natężenie pola elektrycznego

Wartość natężenia pola elektrycznego w

punkcie odległym o r od ładunku

wytwarzającego to pole umieszczonego w

próżni:

gdzie:

Q – ładunek wytwarzający pole [C]

r – odległość od tego ładunku [m]


0

= 8,85 • 10

-12

F/m – przenikalność

elektryczna próżni

2

0

4

r

Q

E





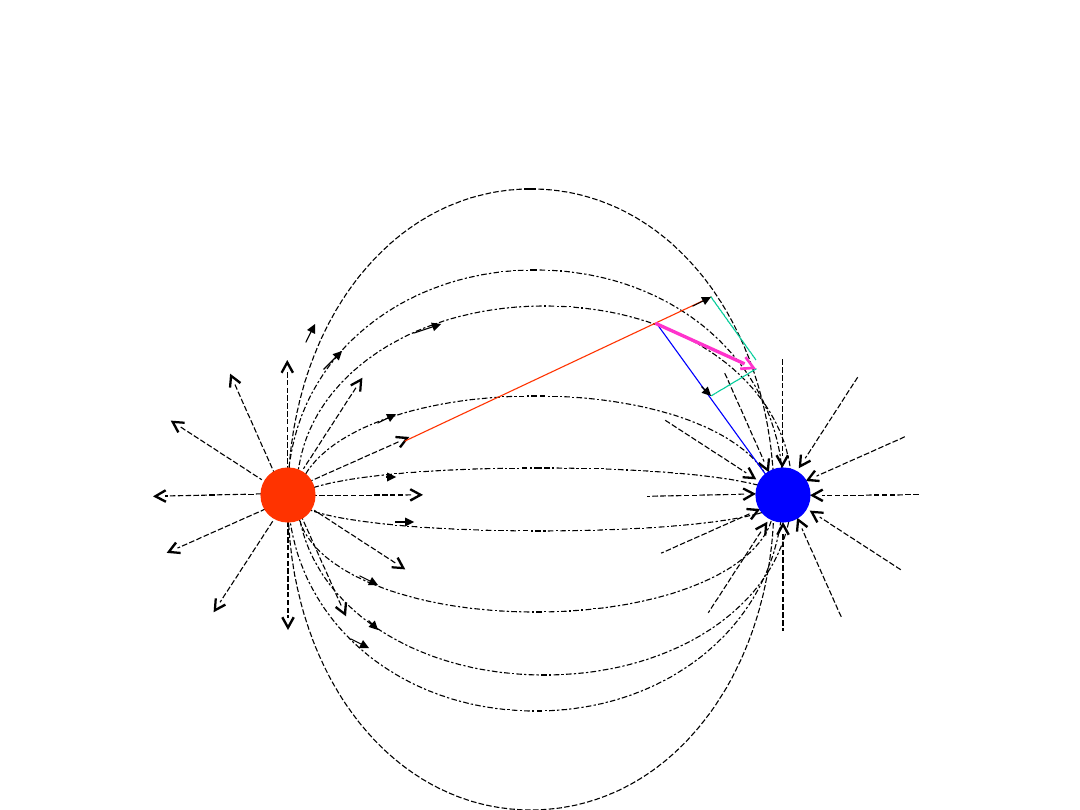
Pole elektryczne

F

1

F

2

F