1

I

T
P

W

ZPT

Wykład cz6b

2

I

T
P

W

ZPT

PRZYKŁAD 1

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0

Generujemy podziały zamknięte

Generujemy podziały zamknięte

Do zakodowania stanów
automatu M potrzebne są 3
podziały 2-blokowe, takie że:

Do zakodowania stanów
automatu M potrzebne są 3
podziały 2-blokowe, takie że:

(0)















c

b

a

3

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0

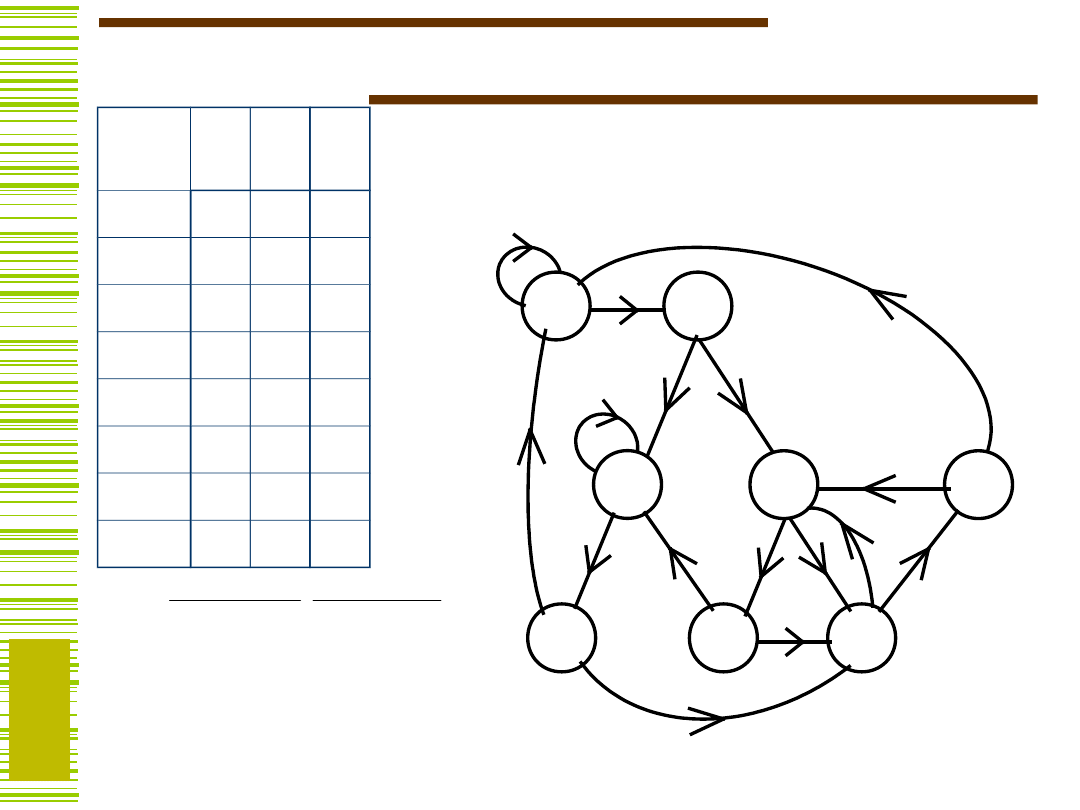
Graf par następników :

Graf par następników :





H

G,

F,

E,

;

D

C,

B,

A,

1





A,B

A,B

F,H

F,H

C,D

C,D

E,F

E,F

A,C

A,C

G,E

G,E

G,H

G,H

B,D

4

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0





G

F,

C,

B,

;

H

E,

D,

A,



G

F,

;

H

E,

C

B,

;

D

A,

;

G

F,

C

B,

;

H

E,

D,

A,

;

H

E,

D

A,

;

G

F,

C,

B,

;

A,D

A,D

D,H

D,H

B,F

B,F

+

=



2

+

=



2

5

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.





H

G,

F,

E,

;

D

C,

B,

A,

1









G

F,

C,

B,

;

H

E,

D,

A,

2





Niestety:

Niestety:

Potrzebny jest więc jeszcze jeden podział :

Potrzebny jest więc jeszcze jeden podział :





)

0

(













G

F,

;

H

E,

;

C

B,

;

D

A,

2

1

)

(0

τ 











2

1





F

E,

D,

C,

;

H

G,

B,

A,



τ

6

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.





H

G,

F,

E,

;

D

C,

B,

A,

1









G

F,

C,

B,

;

H

E,

D,

A,

2





0
0
0
0
1
1
1
1

0
1
1
0
0
1
1
0

Kodowanie wg 

1

Kodowanie wg 

1



2



2

A
B
C

D

E

F

G
H





F

E,

D,

C,

;

H

G,

B,

A,



τ





0
0
1
1
1
1
0
0

7

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.

Przy tak dobranym kodowaniu dwie funkcje
wzbudzeń Q

1

’

i Q

2

’ tego automatu będą zależne od

jednej zmiennej wewnętrznej, a trzecia Q

3

’ (w

najgorszym przypadku) od trzech zmiennych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Przy tak dobranym kodowaniu dwie funkcje
wzbudzeń Q

1

’

i Q

2

’ tego automatu będą zależne od

jednej zmiennej wewnętrznej, a trzecia Q

3

’ (w

najgorszym przypadku) od trzech zmiennych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Kto nie wierzy, niech zakoduje, obliczy funkcje
Q

1

’, Q

2

’, Q

3

’ i sprawdzi.

Kto nie wierzy, niech zakoduje, obliczy funkcje
Q

1

’, Q

2

’, Q

3

’ i sprawdzi.

Dla całego roku!

Dla całego roku!

8

I

T
P

W

ZPT

Komentarz

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

A
B
C
D
E
F
G
H

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

W szczególności dla kodowania binarnego:

W szczególności dla kodowania binarnego:

9

I

T
P

W

ZPT

Nie martwmy się…

Komputerowe

systemy

projektowania

umożliwiają

realizacje

automatów

dokładnie wg

kodowania

obliczonego

zewnętrznie przez

użytkownika

10

I

T
P

W

ZPT

Dekompozycja z autonomicznym

zegarem

Podział 

i

zbioru stanów S automatu M jest zgodny z

wejściem, jeśli dla każdego stanu S

j

 S i dla wszystkich v

l

 V



(S

j

,v

1

),



(S

j

,v

2

), ...,



(S

j

,v

l

), ...,



(S

j

,v

p

),

są w jednym bloku podziału



i

.

Warunkiem koniecznym i dostatecznym istnienia
dekompozycji automatu M, w której występuje
autonomiczny zegar o log

2

(

)

 stanach jest, aby istniał

podział zamknięty



i nietrywialny zgodny z wejściem podział



i

zbioru

stanów S tego automatu, taki że

 



i

Podział 

i

zbioru stanów S automatu M jest zgodny z

wejściem, jeśli dla każdego stanu S

j

 S i dla wszystkich v

l

 V



(S

j

,v

1

),



(S

j

,v

2

), ...,



(S

j

,v

l

), ...,



(S

j

,v

p

),

są w jednym bloku podziału



i

.

Warunkiem koniecznym i dostatecznym istnienia
dekompozycji automatu M, w której występuje
autonomiczny zegar o log

2

(

)

 stanach jest, aby istniał

podział zamknięty



i nietrywialny zgodny z wejściem podział



i

zbioru

stanów S tego automatu, taki że

 



i

11

I

T
P

W

ZPT

PRZYKŁAD 2

x

s

0

1

0

1

A

D

C

0

1

B

C

D

0

0

C

E

F

0

1

D

F

E

0

0

E

B

A

0

1

F

A

B

0

0





F

D,

B,

;

E

C,

A,

O









F

E,

;

D

C,

;

B

A,





I

Podział zgodny z wejściem:

Podział zgodny z wejściem:

Π(0)

Π

Π

O

I







I

jest zamknięty



I

jest zamknięty

12

I

T
P

W

ZPT

PRZYKŁAD 2





F

E,

;

D

C,

;

B

A,

Π 

I





F

D,

B,

;

E

C,

A,

Π

O



0

0

0

0

0

1

0

1

1

0

1

0

0
1
0
1
0
1

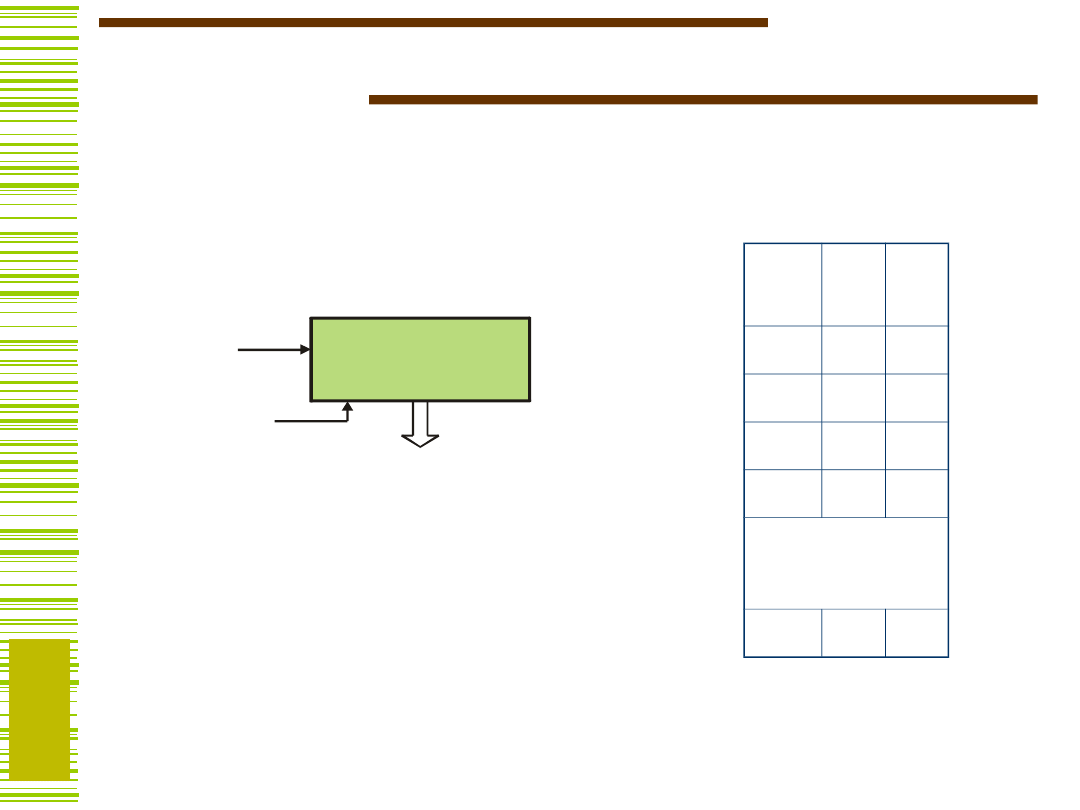
Kodowanie wg 

I

Kodowanie wg 

I

wg 

O

wg 

O

A
B
C

D

E

F

Q

1

’ = f(Q

1

,Q

2

)

Q

1

’ = f(Q

1

,Q

2

)

Q

2

’ = f(Q

1

,Q

2

)

Q

2

’ = f(Q

1

,Q

2

)

Q

3

’ = ???

Q

3

’ = ???

y = f(x,Q

3

)

y = f(x,Q

3

)

13

I

T
P

W

ZPT

E

S

0

1

S

0

S

0

S

1

S

1

S

1

S

2

S

2

S

2

S

3

S

3

S

3

S

4





S

7

S

7

S

0

Kodowanie intuicyjne

Licznik

E

clock

Q

Przykład licznika z wejściem

Enable

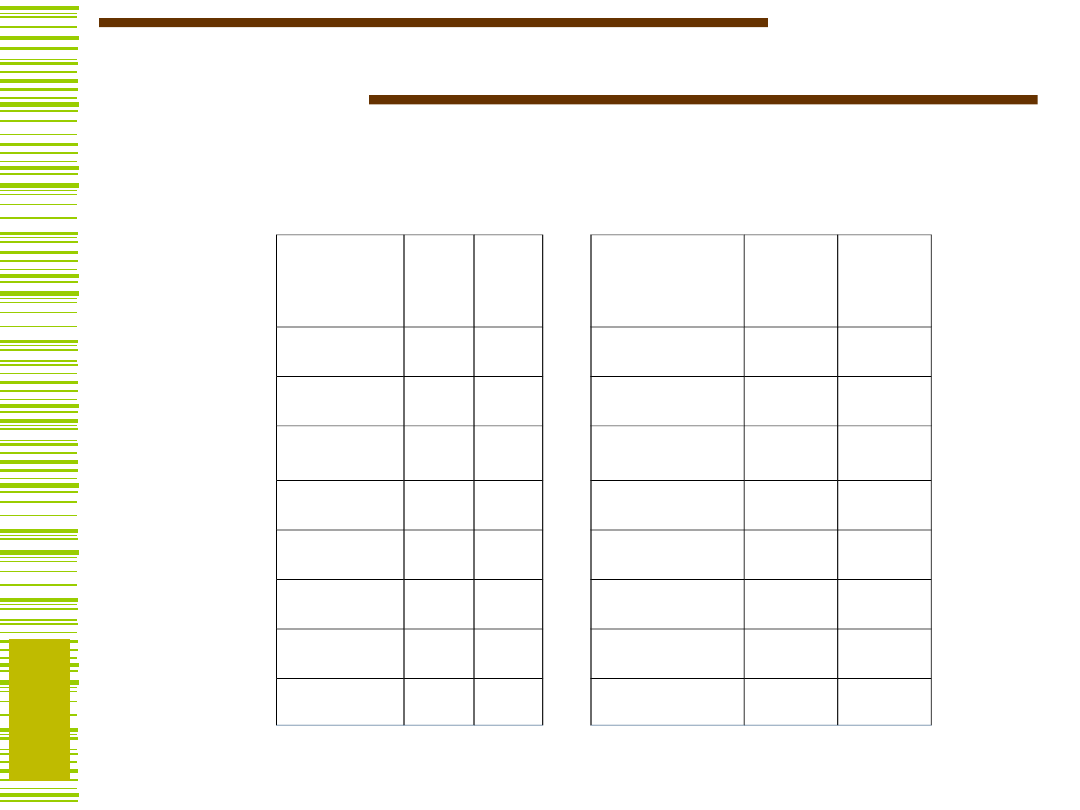
14

I

T
P

W

ZPT

E

S

0

1

E

Q2Q1Q0

0

1

S

0

S

0

S

1

000

000

001

S

1

S

1

S

2

001

001

010

S

2

S

2

S

3

010

010

011

S

3

S

3

S

4

011

011

100

S

4

S

4

S

5

100

100

101

S

5

S

5

S

6

101

101

110

S

6

S

6

S

7

110

110

111

S

7

S

7

s

0

111

111

000

S’

Q2Q1Q0

Q2’Q1’Q0’

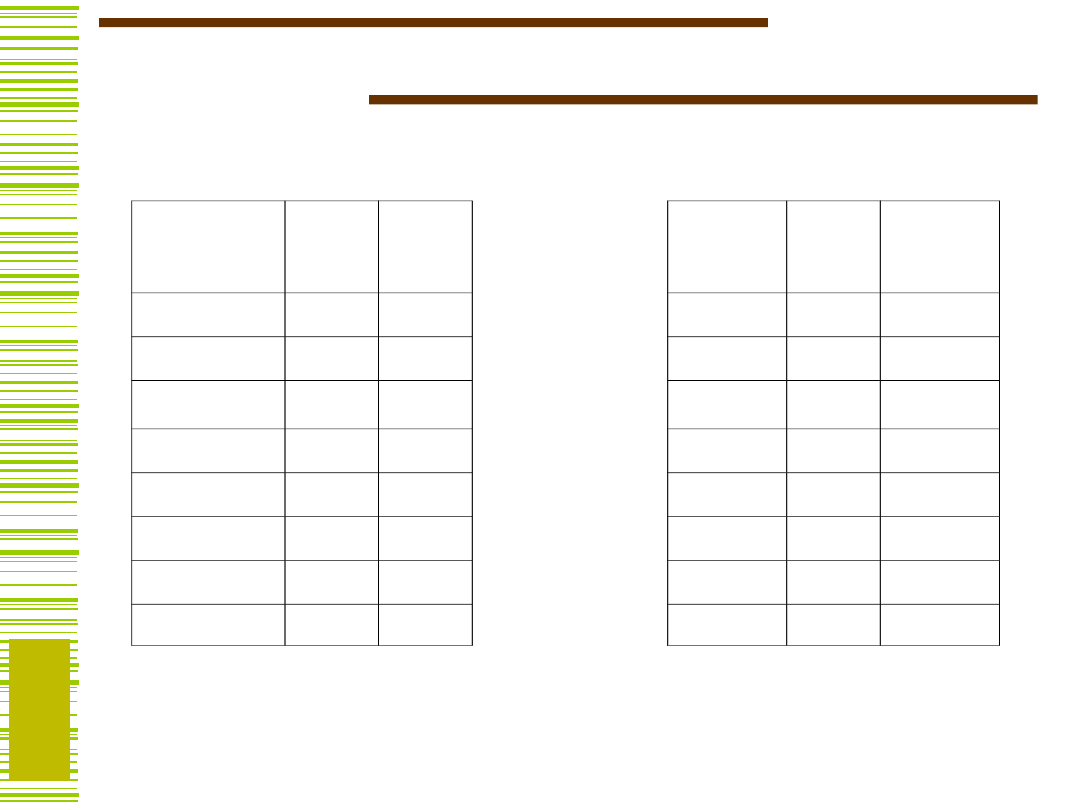
Licznik modulo 8

Tablica przejść

Tablica przejść

Zakodowana tablica przejść

kod binarny

Zakodowana tablica przejść

kod binarny

15

I

T
P

W

ZPT

E

Q2Q1Q0

0

1

E

Q2Q1Q

0

0

1

000

000

001

000

000

001

001

001

010

001

001

010

010

010

011

011

011

100

011

011

100

010

010

011

100

100

101

110

110

111

101

101

110

111

111

000

110

110

111

101

101

110

111

111

000

100

100

101

Q2Q1Q0

Q2’Q1’Q0’

Q2Q1Q

0

Q2’Q1’Q0’

Zakodowana tablica p-w

16

I

T
P

W

ZPT

E

Q2Q1Q0

0

1

E

Q2Q1Q0

0

1

0

1

0

1

000

000

001

000

0

0

0

0

0

1

001

001

010

001

0

0

0

1

1

0

011

011

100

011

0

1

1

0

1

0

010

010

011

010

0

0

1

1

0

1

110

110

111

110

1

1

1

1

0

1

111

111

000

111

1

0

1

0

1

0

101

101

110

101

1

1

0

1

1

0

100

100

101

100

1

1

0

0

0

1

Q2Q1Q0

Q2’Q1’Q0’

Q2Q1Q0

D2

D1

D0

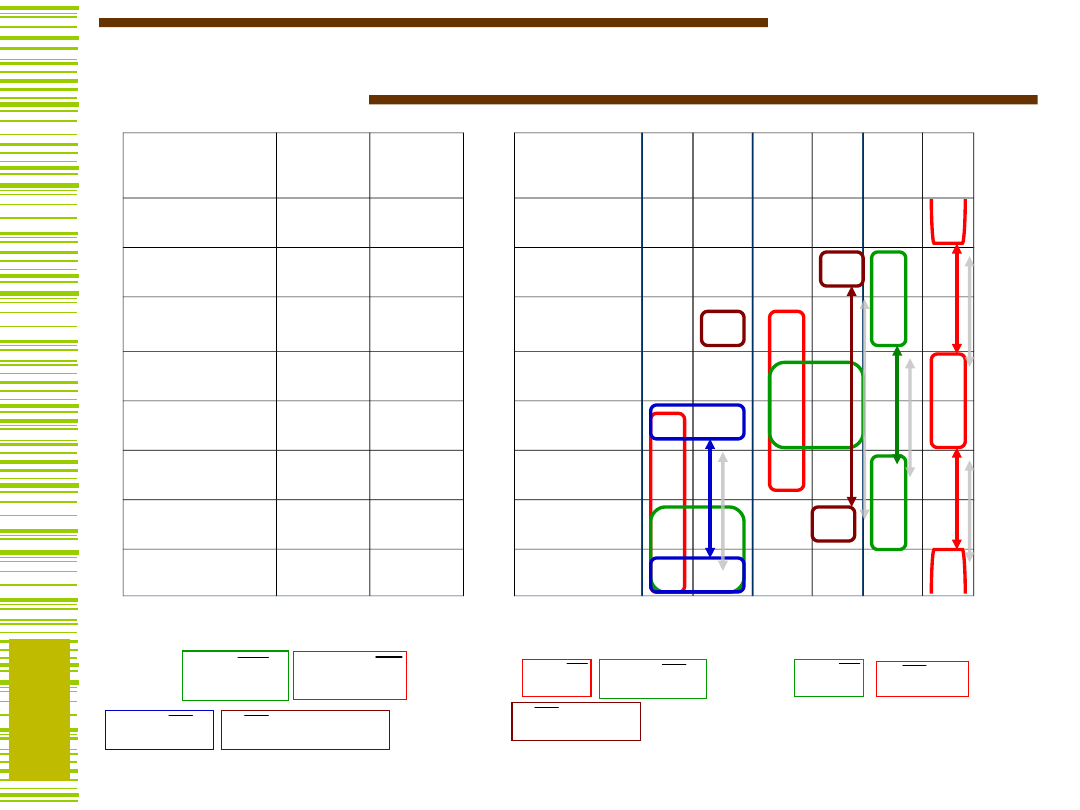
Zakodowana tablica p-w (D)

D2 =

D2 =

1

Q

Q2

0

Q

Q2



D1 =

D1 =

E

Q1

D0 =

D0 =

E

Q0

E

Q2



2Q1Q0E

Q



1Q0E

Q



0

Q

Q1



0E

Q



17

I

T
P

W

ZPT

E

Q2Q1Q0

0

1

E

Q2Q1Q0

0

1

0

1

0

1

000

000

001

000

0

0

0

0

0

1

001

001

010

001

0

0

0

1

0

1

011

011

100

011

0

1

0

1

0

1

010

010

011

010

0

0

0

0

0

1

110

110

111

110

0

0

0

0

0

1

111

111

000

111

0

1

0

1

0

1

101

101

110

101

0

0

0

1

0

1

100

100

101

100

0

0

0

0

0

1

Q2Q1Q0

Q2’Q1’Q0’

Q2Q1Q0

T2

T1

T0

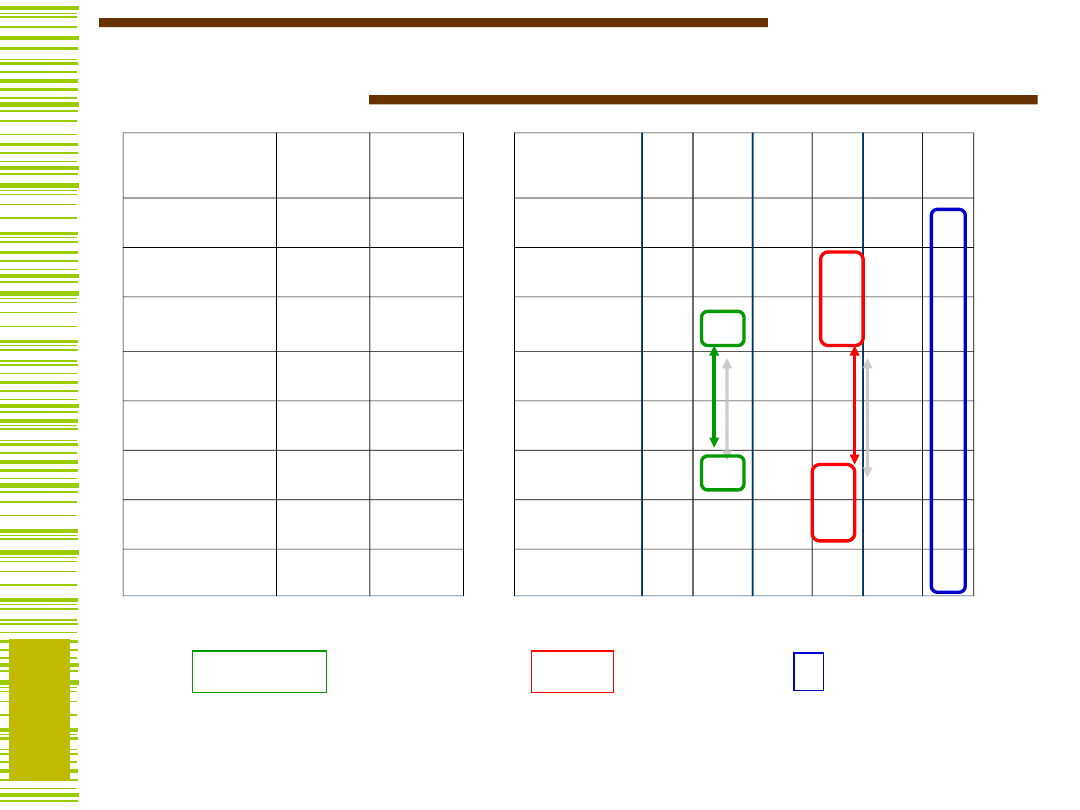
Zakodowana tablica p-w (T)

T2 =

T2 =

EQ1Q0

T1 =

T1 =

T0 =

T0 =

EQ0

E

18

I

T
P

W

ZPT

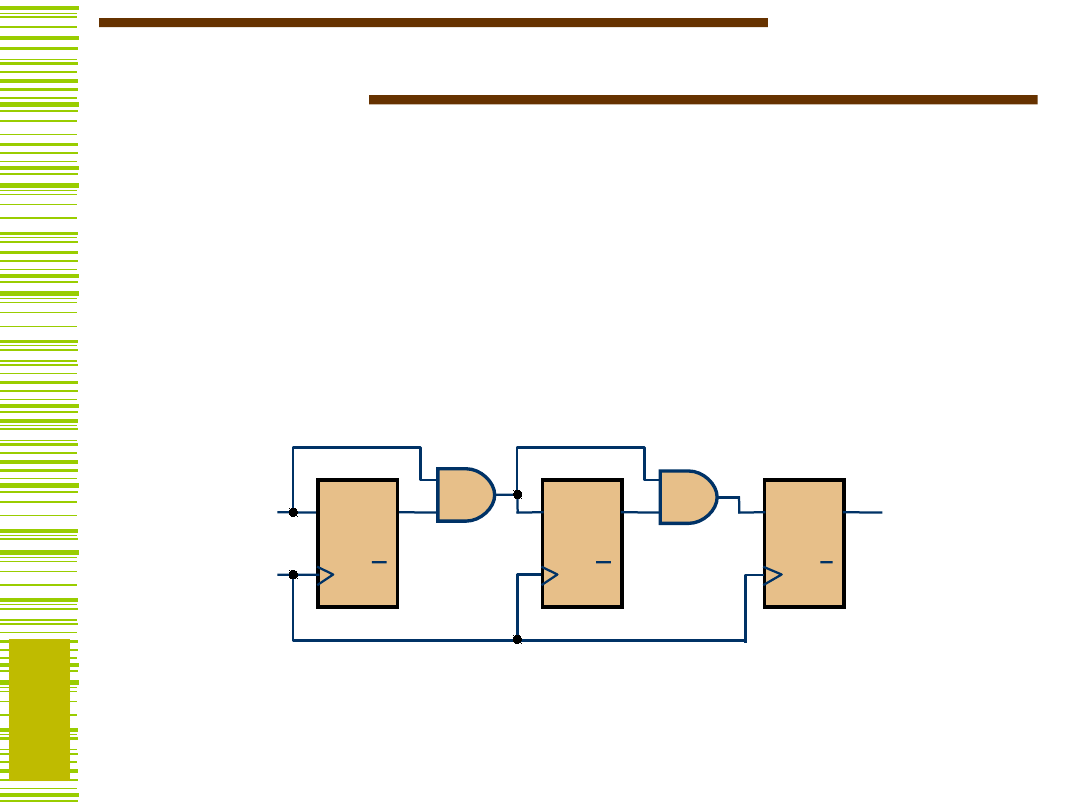
Schemat licznika

T Q

Q

Clock

T Q

Q

Enable

T Q

Q

1

1

1

0

2

0

1

0

Q

T

Q

EQ

T

EQ

T

E

T









19

I

T
P

W

ZPT

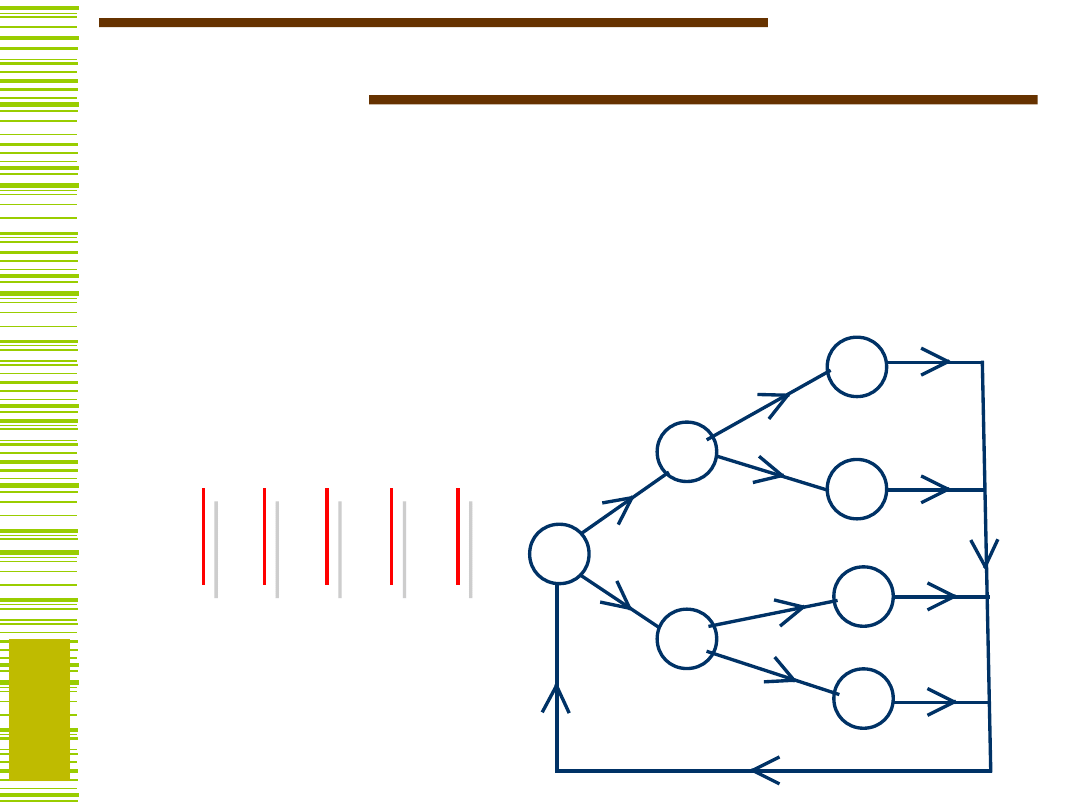
Detektor sekwencji

Zaprojektować układ sekwencyjny
Mealy’ego o jednym wejściu
binarnym i jednym wyjściu binarnym.
Układ ma badać kolejne „trójki”
symboli wejściowych. Sygnał
wyjściowy pojawiający się podczas
trzeciego skoku układu ma wynosić
1, gdy „trójka” ma postać 001, a 0,
gdy „trójka” jest innej postaci.
Sygnał pojawiający się podczas
pierwszego i drugiego skoku układu
może być nieokreślony.

Zaprojektować układ sekwencyjny
Mealy’ego o jednym wejściu
binarnym i jednym wyjściu binarnym.
Układ ma badać kolejne

„trójki”

symboli wejściowych. Sygnał
wyjściowy pojawiający się podczas
trzeciego skoku układu ma wynosić

1

, gdy

„trójka”

ma postać

001

, a

0

,

gdy

„trójka”

jest

innej postaci

.

Sygnał pojawiający się podczas
pierwszego i drugiego skoku układu
może być nieokreślony.

1

2

3

4

5

6

7

0/-

1/-

0/-

0/0

0/0

0/0

0/0

1/0

1/0

1/0

1/1

0/-

1/-

1/-

01100100110101001

01100100110101001

- -

0

- -

0

- -

1

- -

1

- -

1

- -

1

- -

0

- -

0

- -

0

- -

0

20

I

T
P

W

ZPT

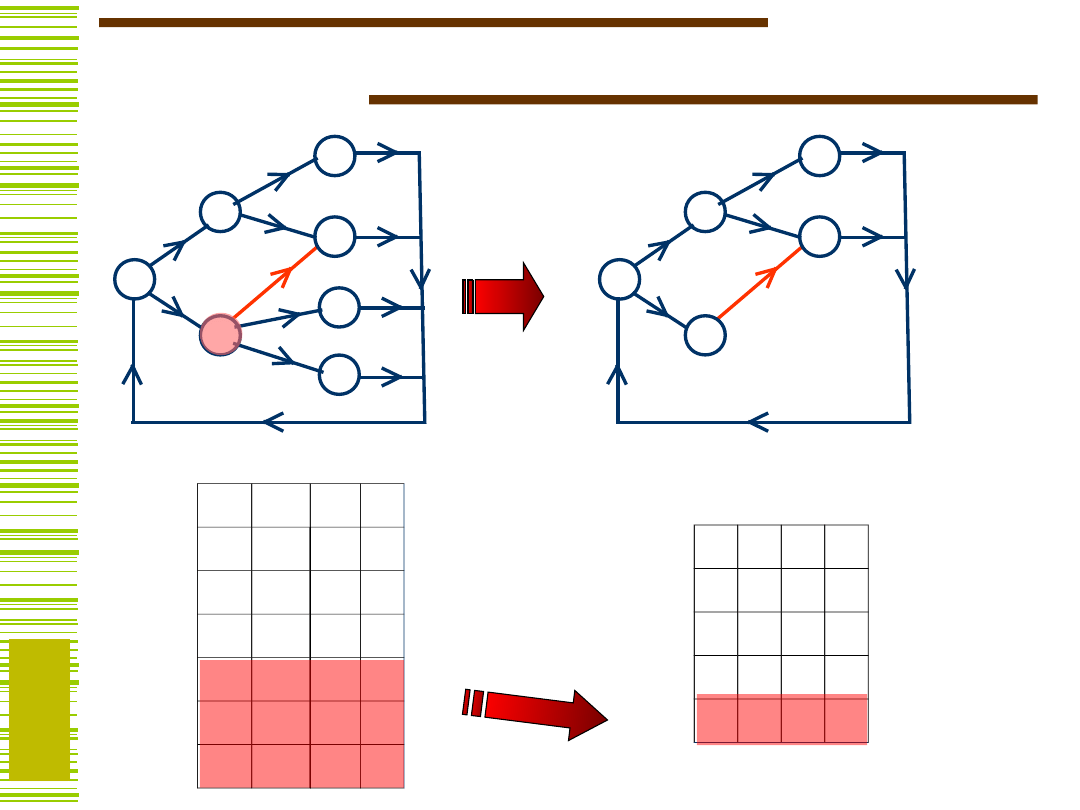
Detektor sekwencji

0/-

1/-

0/0

1

2

3

4

5

6

7

0/-

1/-

0/-

0/0

0/0

0/0

1/0

1/0

1/0

1/1

0/-

1/-

1/-

0/0

0/-

1/-

1

2

3

4

5

0/-

1/-

0/-

0/0

1/0

1/1

1/-

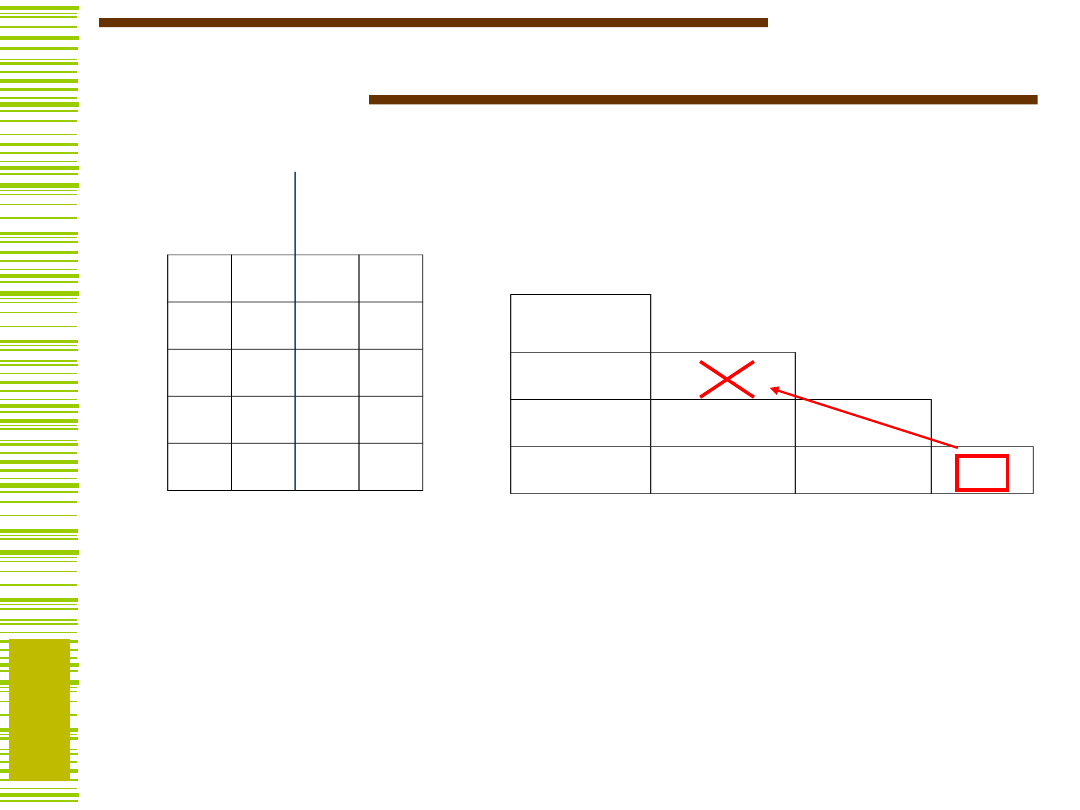
S 0 1 0 1
1 2 3 -

-

2 4 5 -

-

3 5 5 -

-

4 1 1 0 1
5 1 1 0 0

S

0

1

0 1

1

2

3

-

-

2

4

5

-

-

3

6

7

-

-

4

1

1

0 1

5

1

1

0 0

6

1

1

0 0

7

1

1

0 0

21

I

T
P

W

ZPT

Minimalizacja detektora

sekwencji

X

S

0

1

0

1

1 2

3

–

–

2 4

5

–

–

3 5

5

–

–

4 1

1

0

1

5 1

1

0

0

2 2 4, 3 5

3 2 5, 3 5

45

4 1 2, 1 3 1 4, 1 5

1 5

5 1 2, 1 3 1 4, 1 5

1 5



1

2

3

4

Bardzo dużo par zgodnych!

Bardzo dużo par zgodnych!

Do wyznaczenia MKZ wykorzystamy pary

sprzeczne, których jest znacznie mniej

(dwie).

Do wyznaczenia MKZ wykorzystamy pary

sprzeczne, których jest znacznie mniej

(dwie).

22

I

T
P

W

ZPT

Minimalizacja detektora

sekwencji

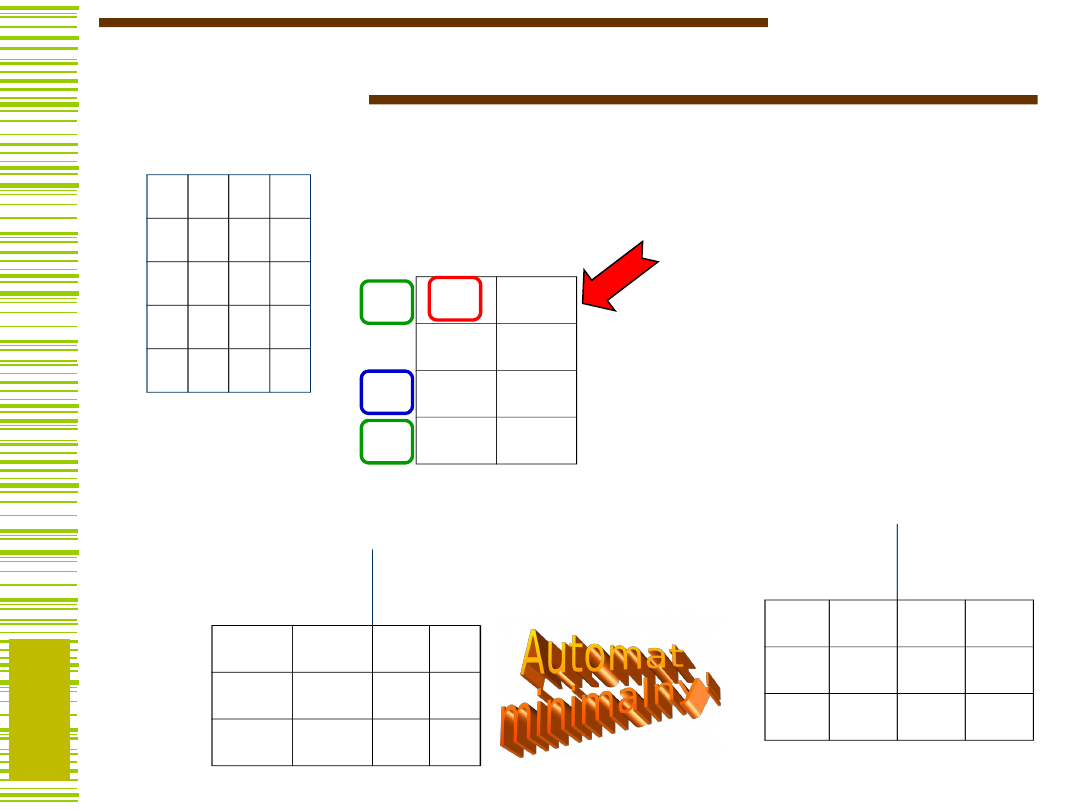
Pary sprzeczne zapisujemy w postaci wyrażenia
boolowskiego typu iloczyn (koniunkcja) dwu-
składnikowych sum.

Pary sprzeczne zapisujemy w postaci wyrażenia
boolowskiego typu iloczyn (koniunkcja) dwu-
składnikowych sum.

Na tej podstawie zapisujemy wyrażenie: (2  3) (4 

5),
które po wymnożeniu uzyskuje postać:

(2  3) (4  5) = 2 4  2 5  3 4  3 5

Na tej podstawie zapisujemy wyrażenie: (2  3) (4 

5),
które po wymnożeniu uzyskuje postać:

(2  3) (4  5) = 2 4  2 5  3 4  3 5

W detektorze sekwencji pary sprzeczne są: (2, 3); (4, 5).

W detektorze sekwencji pary sprzeczne są: (2, 3); (4, 5).

Odejmując od zbioru S = {1, 2, 3, 4, 5} wszystkich

stanów zbiory zapisane w poszczególnych

składnikach uzyskujemy rodzinę wszystkich MKZ.

Odejmując od zbioru S = {1, 2, 3, 4, 5} wszystkich

stanów zbiory zapisane w poszczególnych

składnikach uzyskujemy rodzinę wszystkich MKZ.

{1, 2, 3, 4, 5} – {2, 4} = {1, 3, 5}
{1, 2, 3, 4, 5} – {2, 5} = {1, 3, 4}

{1, 2, 3, 4, 5} – {3, 4} = {1, 2, 5}

{1, 2, 3, 4, 5} – {3, 5} = {1, 2, 4}

23

I

T
P

W

ZPT

Minimalizacja detektora

sekwencji

X

S

0 1 0 1

1

2 3 - -

2

4 5 - -

3

5 5 - -

4

1 1 0 1

5

1 1 0 0

X

S

0

1

135 125 135
134 125 135
125 124 135
124 124 135

MKZ: {1, 3, 5}, {1, 3, 4}, {1, 2, 5},
{1, 2, 4}

Funkcja przejść dla wszystkich MKZ

Funkcja przejść dla wszystkich MKZ

Dokładamy klasę {1,2,5}

Dokładamy klasę

{1,2,5}

X

S

0

1

0

1

A 135 125 135

0

0

B 125 124 135

0

0

C 124 124 135

0

1

X

S

0

1

0

1

A

B

A

0

0

B

C

A

0

0

C

C

A

0

1

Klasy: {1,3,5}, {1, 2, 4}, {1, 2, 5} spełniają

warunek pokrycia i zamkniętości

Klasy:

{

1,3,5}, {1, 2, 4},

{1, 2, 5}

spełniają

warunek pokrycia i zamkniętości

ale nie spełniają
warunku zamkniętości
– stany następne:
{1,2,5} !

ale nie spełniają
warunku zamkniętości
– stany następne:

{1,2,5} !

Klasy {1, 3, 5}, {1, 2, 4} spełniają warunek

pokrycia,

Klasy

{1, 3, 5}, {1, 2, 4}

spełniają warunek

pokrycia,

24

I

T
P

W

ZPT

...a to już było

X

S

0

1

0

1

A

B

A

0

0

B

C

A

0

0

C

C

A

0

1

Uzyskany automat był już realizowany na
przerzutnikach i bramkach – wykład cz5, plansze
13 do 20.