1
I
T
P
W
ZPT
Metody analityczne i
komputerowe
w minimalizacji funkcji boolowskich
Metoda Quine’a McCluskey’a
Metoda Espresso
a) generacja implikantów prostych
b) selekcja implikantów (tzw. pokrycie)
duża liczba różnorodnych procedur
procedury heurystyczne
iteracyjne poprawianie wyniku
2
I
T
P
W
ZPT
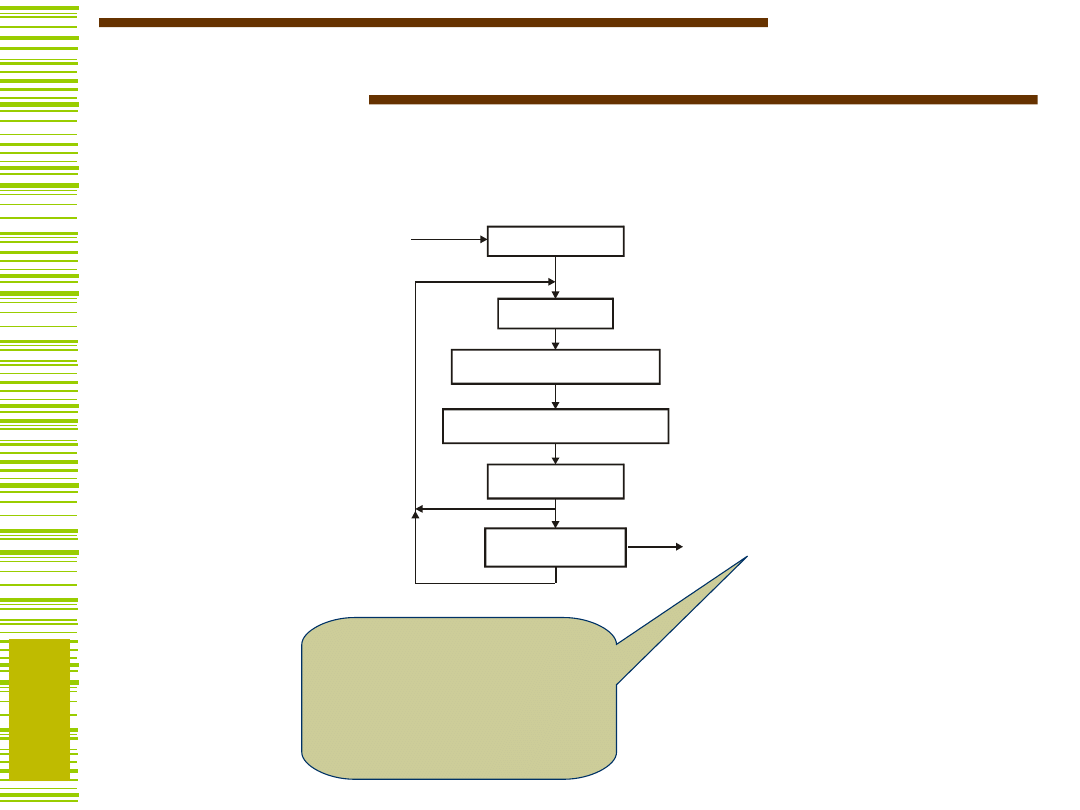
Procedury systemu ESPRESSO
Expand
Essential primes
Irredundant-Cover
Reduce
Last-gasp
F,D
F
M
Complement
(rozdział 6 w książce
SUL)
3
I
T
P
W
ZPT
Zmodyfikowana metoda ekspansji
(rozdział 3.3 książka SUL)
Łączy idee metody Quine’a McCluskey’a
oraz metody Espresso:
Metoda ta zrealizowana w programie
PANDOR jest udostępniona na
w katalogu OPROGRAMOWANIE
a) generacja implikantów prostych (wg
Espresso)
b) selekcja implikantów (wg Quine’a
McCluskey’a)
4
I
T
P
W
ZPT
Pojęcia podstawowe
Kostka K to krotka o składowych 0, 1,
reprezentująca zbiór wektorów zero-
jedynkowych.
3
1
x
x
Kostka reprezentuje niepełny
iloczyn:
K = 01 =
K = (01), to zbiór
wektorów:
0010
0011
0110
0111
5
I
T
P
W
ZPT
Oznaczenia
W standardzie espresso wektory (w
ogólności kostki), dla których funkcja f = 1
oznacza się zbiorem F.
Wektory (kostki) dla których funkcja f = 0
oznacza się zbiorem R.
f = (F, R)
6
I
T
P
W
ZPT
Przykład (EXTL)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
f
1
0
0
0
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
0
0
1
1
1
0
1
1
1
0
k
1
0
1
0
0
1
0
1
1
k
2
1
0
0
0
1
1
0
1
k
3
1
0
1
0
0
0
0
1
k
4
1
0
1
0
1
1
0
1
k
5
1
1
1
0
1
0
1
1
1
0
1
0
1
1
1
0
1
1
0
1
0
1
0
0
0
0
1
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
F
R
1 0 0 0 1 0 1
1 0 1 1 1 1 0
1 1 0 1 1 1 0
1 1 1 0 1 1 1
7
I
T
P
W
ZPT
Ekspansja
Ekspansja
jest procesem działającym na
kostkach zbiorów F i R, a jej celem jest
uzyskanie dla danej k F kostki k' tak dużej, jak
to tylko możliwe (tzn. z możliwie dużą liczbą
pozycji o wartości ) i nie pokrywającej żadnego
wektora zbioru R.
W swoich obliczeniach Ekspansja wykorzystuje
tzw. macierz blokującą B.
Ekspansja
8
I
T
P
W
ZPT
Macierz blokująca
Macierz blokująca dla danej kostki k F
powstaje
z macierzy R przez zanegowanie tych kolumn
R, których pozycje są wyznaczone przez
pozycje jedynek w kostce k F.
Macierzą blokującą (kostkę k) nazywamy macierz
B(k,R) = [b
ij
], w której każdy element b
ij
{0,1} jest
definiowany następująco:
b
ij
= 1, jeśli k
j
= 1 oraz r
ij
= 0 lub k
j
= 0 oraz r
ij
= 1;
b
ij
= 0, w pozostałych przypadkach.
Definicja oryginalna (z książki Braytona):
9
I
T
P
W
ZPT
Tworzenie macierzy blokującej
F
0 1 0 0 1 0 1
1 0 0 0 1 1 0
1 0 1 0 0 0 0
1 0 1 0 1 1 0
1 1 1 0 1 0 1
1
1
1
0
1
1
1
0
1
1
1
0
1
1
0
1
1
1
1
0
1
1
0
1
0
0
0
1
R
0
1
0
0
1
0
1
1
1
0
1
0
0
1
1
1
0
1
1
1
1
0
0
0
0
0
1
1
B
Wyznaczymy macierz blokującą dla kostki k
1
wiedząc, że
F i R są opisane macierzami:
Skoro k
1
= (0
1
00
1
0
1
), to dla uzyskania B wystarczy
w macierzy R "zanegować" kolumny drugą, piątą i siódmą.
Zatem B(k
1
,R):
10
I
T
P
W
ZPT
Pokrycie kolumnowe
Pokryciem kolumnowym
macierzy B jest zbiór
kolumn L (L {1,...,n}) taki, że dla każdego wiersza
i istnieje kolumna j L, która w wierszu i ma
jedynkę.
Pokryciem
kolumnowym
Zbiór L jest minimalnym pokryciem
kolumnowym
macierzy B, jeśli nie istnieje zbiór L’ (tworzący
pokrycie) taki, że L L’.
Pokrycie kolumnowe jest
pojęciem ogólnym,
można go tworzyć dla
każdej macierzy binarnej
11
I
T
P
W
ZPT
1
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
7
6
5
4
3
2
1
B
{L
6
, L
7
}
{L
3
, L
4
}
{L
2
, L
4
}
{L
2
, L
3
, L
7
}
Obliczanie pokrycia
kolumnowego
L =
{L
4
, L
7
}
jest pokryciem
kolumnowym.
L =
{L
2
, L
3
, L
6
}
jest pokryciem
kolumnowym.
L =
{L
2
, L
3
}
–
nie
L =
{L
2
, L
6
}
–
nie
L =
{L
3
, L
6
}
–
nie
12
I
T
P
W
ZPT
{L
6
, L
7
}
1
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
7
6
5
4
3
2
1
B
{L
3
, L
4
}
{L
2
, L
4
}
{L
2
, L
3
,
L
7
}
(L
6
+ L
7
) (L
3
+ L
4
) (L
2
+ L
4
) (L
2
+ L
3
+ L
7
) =
(
L
4
+ L
2
)(L
4
+ L
3
)(
L
7
+ L
6
)(L
7
+ L
2
+ L
3
) =
(
L
4
+ L
2
L
3
)(L
7
+ L
6
(L
2
+ L
3
)) =
(
L
4
+ L
2
L
3
)(L
7
+ L
2
L
6
+ L
3
L
6
) =
L
4
L
7
+ L
2
L
4
L
6
+ L
3
L
4
L
6
+ L
2
L
3
L
7
+ L
2
L
3
L
6
+ L
2
L
3
L
6
Obliczanie pokrycia
kolumnowego
13
I
T
P
W
ZPT
Macierz blokująca B(k,R) pozwala wyznaczyć
ekspansję kostki k oznaczaną k
+
(L,k) w sposób
następujący:
wszystkie składowe kostki k należące do L nie
ulegają zmianie, natomiast składowe nie należące do
L przyjmują wartość .
Ekspansja kostki k jest implikantem funkcji f =
(F,R).
W szczególności k
+
(L,k) jest implikantem prostym,
gdy L jest minimalnym pokryciem kolumnowym
macierzy B(k,R).
Generacja (tworzenie)
implikantów
14
I
T
P
W
ZPT
Generacja implikantów -
przykład
Dla k
2
= (1000110) i macierzy B=
1
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
1
1
0
0
0
0
0
7
6
5
4
3
2
1
zbiór L = {4,7} jest pokryciem kolumnowym B, a
więc
7
4
x
x
6
3
2
x
x
x
Natomiast dla L = {2,3,6} (inne pokrycie
kolumnowe),
k
+
(L,k) = (001) =
k
2
= (1000110)
czyli implikantem F
jest
k
+
(L, k
2
) = (00),
15
I
T
P
W
ZPT
Implikanty proste
6
3
2
4
7
4
3
6
2
2
1
1
x
x
x
I
x
x
I
x
x
I
x
I
6
3
7
7
6
6
5
5
x
x
I
x
x
I
x
I
Obliczając kolejno implikanty proste dla każdej k F
uzyskuje się:
Proszę zauważyć, że na tym zakończyliśmy
proces generacji implikantów prostych
16
I
T
P
W
ZPT
… przystępujemy do procesu
selekcji
k 5
k 4
x
1
x
2
x
3
x
4
x
5
x
6
x
7
k
1
0
1
0
0
1
0
1
k
2
1
0
0
0
1
1
0
k
3
1
0
1
0
0
0
0
k
4
1
0
1
0
1
1
0
k
5
1
1
1
0
1
0
1
7
4
3
x
x
I
1
1
x
I
5
1
k
,
k
)
0
1
(
6
2
2
x
x
I
1
k
)
(0
4
3
2
k
,
k
,
k
0)
0
(
Relacja pokrycia dla
kostek
17
I
T
P
W
ZPT
Tablica implikantów prostych
I
1
I
2
I
3
I
4
I
5
I
6
I
7
k
1
1
1
0
0
0
0
0
k
2
0
0
1
1
0
0
0
k
3
0
0
1
0
1
1
1
k
4
0
0
1
0
0
0
0
k
5
0
1
0
0
0
0
1
4
3
2
7
4
3
5
1
6
2
2
1
1
1
k
,
k
,
k
0)
0
(
x
x
I
k
,
k
)
0
1
(
x
x
I
k
)
(0
x
I
18
I
T
P
W
ZPT
Tablica implikantów prostych
Tablica implikantów prostych umożliwia wybór
(selekcję) takiego minimalnego zbioru implikantów,
który pokrywa wszystkie kostki funkcji pierwotnej
19
I
T
P
W
ZPT
Selekcja implikantów prostych
I
1
, I
2
I
3
, I
4
I
3
, I
5
, I
6
, I
7
I
3
I
2
, I
7
Inny zapis tablicy:
Minimalne pokrycie:
Minimalna formuła:
6
2
7
4
x
x
x
x
I
1
,
I
2
I
2
,
I
7
I
2
,I
3
1
1
0
0
0
0
1
0
k
5
0
0
0
0
1
0
0
k
4
1
1
1
0
1
0
0
k
3
0
0
0
1
1
0
0
k
2
0
0
0
0
0
1
k
1
I
7
I
6
I
5
I
4
I
1
I
2
I
3
7
4
3
6
2
2
x
x
I
x
x
I
Pokrycie
kolumnowe
20
I
T
P
W
ZPT
Implementacja metody – program
Pandor
Implicants table of function y1
10010
01000
01101
01000
00011
.......................
All results of function y1
y1 = !x4!x7 + x2!x6
Fragment pliku wyjściowego Pandora:
Trochę inny zapis
21
I
T
P
W
ZPT
.type fr
.i 7
.o 1
.p 9
.ilb x1 x2 x3 x4 x5 x6
x7
.ob y
1000101 0
1011110 0
1101110 0
1110111 0
0100101 1
1000110 1
1010000 1
1010110 1
1110101 1
.e
.i 7
.o 1
.ilb x1 x2 x3 x4 x5 x6 x7
.ob y
.p 2
-1---0- 1
---0--0 1
.e
E x p a n d
E s s e n tia l p r im e s
I r r e d u n d a n t- C o v e r
R e d u c e
L a s t- g a s p
F , D
F
M
C o m p le m e n t
Taki sam wynik generuje
Espresso…
…funkcja EXTL
w formacie
espresso
Więcej na temat
formatu espresso w
książce SUL
22
I
T
P
W
ZPT
Plik wejściowy i wyjściowy
przykładu
.type fr
.i 7
.o 1
.p 9
.ilb x1 x2 x3 x4 x5 x6
x7
.ob y
1000101 0
1011110 0
1101110 0
1110111 0
0100101 1
1000110 1
1010000 1
1010110 1
1110101 1
.e
.i 7
.o 1
.ilb x1 x2 x3 x4 x5 x6 x7
.ob y
.p 2
-1---0- 1
---0--0 1
.e
Skoro wyszło to
samo co w
obliczeniach za
pomocą tylko
jednej procedury
ekspansji...
...to po co są
inne
procedury
ESPRESSO
To jest za prosty
przykład!
23
I
T
P
W
ZPT
Tablica implikantów prostych
Porównanie Pandora i Espresso wymaga
szczegółowszych eksperymentów.
Można je przeprowadzić samodzielnie. Przykładowe
pliki oraz programy Pandor i Espresso są umieszczone
w katalogu Eksperymenty do wykładów cz. 3 i cz. 4.
24
I
T
P
W
ZPT
Dyskusja…
Barierą ograniczającą obliczenia systematyczną
metodą
zastosowaną w Pandorze jest ogromna złożoność
obliczeniowa zarówno w procesie generacji, jak też
w procesie obliczania pokrycia kolumnowego.
Program PANDOR został stworzony po to, aby naocznie
zaobserwować zjawisko wzrostu złożoności obliczeniowej
wraz ze wzrostem liczby argumentów funkcji.
Funkcja EXTL ma 7 implikantów (Pandor dokonuje lepszej
selekcji i oblicza ich zaledwie 5). Nie ma żadnej sprawy
w obliczeniu minimalnego pokrycia kolumnowego.
Ale…
25
I
T
P
W
ZPT
Zagadka…
.type fr
.i 10
.o 1
.p 25
0010111010 0
1010010100 0
0100011110 0
1011101011 0
1100010011 0
0100010110 0
1110100110 0
0100110000 0
0101000010 0
0111111011 1
0000010100 1
1101110011 1
0100100000 1
0100011111 1
0010000110 1
1111010001 1
1111101001 1
1111111111 1
0010000000 1
1101100111 1
0010001111 1
1111100010 1
1010111101 1
0110000110 1
0100111000 1
.e
TL27
Ile implikantów prostych
ma funkcja TL27
…a ile KAZ? Można pomylić
się o 10…
.type fr
.i 21
.o 1
.p 31
100110010110011111101 1
111011111011110111100 1
001010101000111100000 1
001001101100110110001 1
100110010011011001101 1
100101100100110110011 1
001100100111010011011 1
001101100011011011001 1
110110010011001001101 1
100110110011010010011 1
110011011011010001100 1
010001010000001100111 0
100110101011111110100 0
111001111011110011000 0
101101011100010111100 0
110110000001010100000 0
110110110111100010111 0
110000100011110010001 0
001001000101111101101 0
100100011111100110110 0
100011000110011011110 0
110101000110101100001 0
110110001101101100111 0
010000111001000000001 0
001001100101111110000 0
100100111111001110010 0
000010001110001101101 0
101000010100001110000 0
101000110101010011111 0
101010000001100011001 0
011100111110111101111 0
.end
KAZ
I dlatego TL27 obliczy zarówno
systematyczna ekspansja Pandora,
jak i Espresso. Ale już funkcja KAZ jest
z praktycznego punktu widzenia realna
do policzenia wyłącznie programem
ESPRESSO.
O innych zaletach
Pandora
na następnym wykładzie
Ale nie może to być wynik
minimalny
26
I
T
P
W
ZPT
A jak w jest w rzeczywistym
Espresso...
Komentarz tylko dla tych co
chodzą na wykłady
27
I
T
P
W
ZPT
Dalsze zalety Espresso…
Metoda Espresso jest szczególnie efektywna
w minimalizacji zespołów funkcji boolowskich.
Dla metod klasycznych synteza wielowyjściowych
funkcji boolowskich jest procesem bardzo złożonym
– trudnym do zalgorytmizowania.
Przypomnijmy przykład z poprzedniego wykładu
28
I
T
P
W
ZPT
Układy wielowyjściowe -
przykład
c
b
y
1
bd
a
abd
c
b
a
bc
c
b
y
2
bd
a
abd
3
y
bc
c
b
a
Po żmudnych obliczeniach uzyskaliśmy
wynik na 5 bramkach AND
y
1
=
(2,3,5,7,8,9,10,11,13,15)
y
2
=
(2,3,5,6,7,10,11,14,15)
y
3
=
(6,7,8,9,13,14,15)
29
I
T
P
W
ZPT
Jak obliczy Espresso?
.type fr
.i 4
.o 3
.p 16
0000 000
0001 000
0010 110
0011 110
0100 000
0101 110
0110 011
0111 111
1000 101
1001 101
1010 110
1011 110
1100 000
1101 101
1110 011
1111 111
.e
.i 4
.o 3
.p 5
11-1 101
100- 101
01-1 110
-01- 110
-11- 011
.e
E x p a n d
E s s e n tia l p r im e s
I r r e d u n d a n t- C o v e r
R e d u c e
L a s t- g a s p
F , D
F
M
C o m p le m e n t
Można sprawdzić,
że jest to taki sam
wynik jak na
planszy 30 wykładu
ULOG cz.2