Wykład 3

Układy elektroniczne

1

Minimalizacja funkcji 
boolowskich

Minimalizacja funkcji boolowskich  - polega na 

znalezieniu dla danej funkcji formuły minimalnej, 
która jest jak najmniej skomplikowana. Przy 
porównywaniu stopnia skomplikowania reguł 
wprowadza się pojęcie współczynnika 
skomplikowania.

Dla funkcji boolowskiej zapisanej przy pomocy 

kanonicznej postaci sumy, współczynnik 
skomplikowania jest równy sumie liczby mnożeń i 
sumie liczby dodawań.

W syntezie logicznej, minimalizację funkcji 

boolowskich stosuje się w celu zredukowania 
liczby potrzebnych zasobów (bramek logicznych, 
bloków bramek) do realizacji danej funkcji. 

2

Metody minimalizacji funkcji 
boolowskich

Tradycyjne:

1.

 metoda Karnaugh, 

2.

metoda Quine'a-McCluskeya, 

3.

metoda iteracyjnego konsensusu

4.

metoda Espresso (oparta na algorytmie 
ekspansji) 

Do syntezy logicznej:

1.

dekompozycja funkcji boolowskich

2.

redukcja argumentów

3

Algorytm metody Karnaugh

1.

Zapis funkcji w formie tabeli Karnaugh, używając 
kodu Greya.

2.

Zaznaczenie (możliwie największych) skupisk 
jedynek i wartości nieustalonych 

(zakładając realizację 

przy użyciu bramek NAND). 

Skupiska mogą się pokrywać. 

3.

Wybór możliwie najmniejszej liczby skupisk 
takich, by wszystkie jedynki były tam zawarte.

4.

Zapis funkcji zminimalizowanej w postaci 
kanonicznego iloczynu..

4

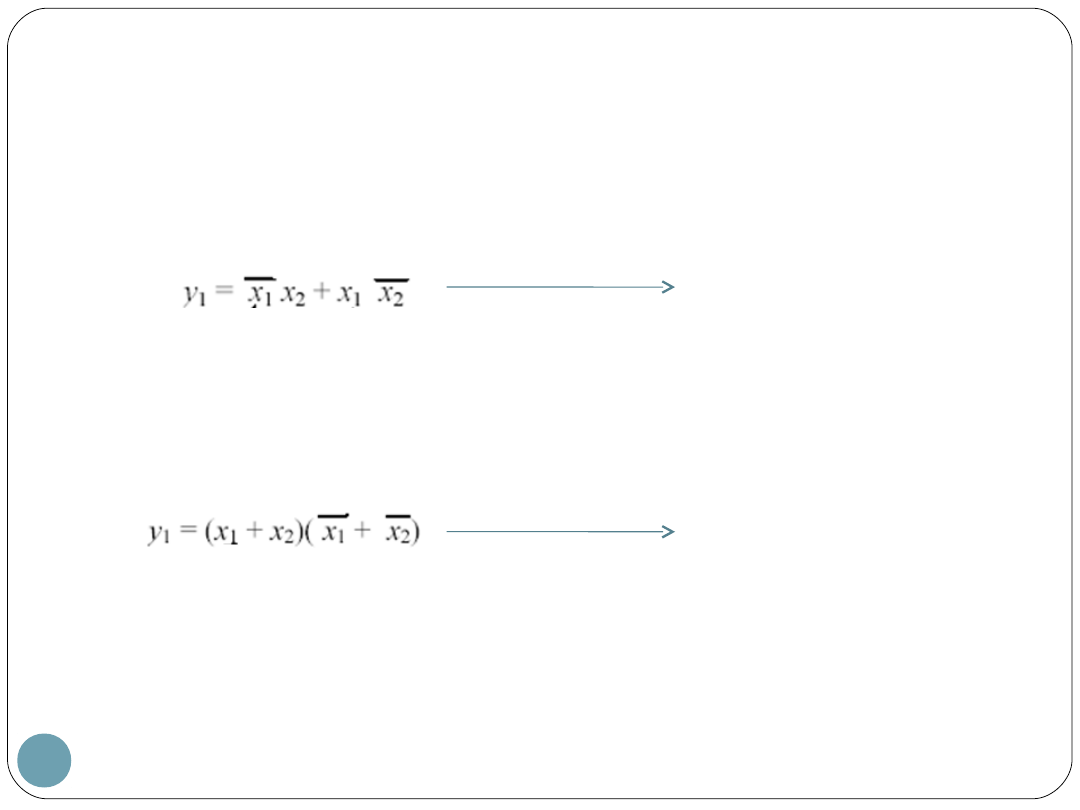
Realizacja postaci 
kanonicznych

5

?

?

Kanoniczna postać sumy 
(suma iloczynów)

Kanoniczna postać iloczynu
(iloczyn sum)

Metoda Quine’a-
McCluskeya

6

Metoda Quine’a-
McCluskeya

 Cechy:



Dużo łatwiejsza do zaimplementowania jako algorytm 
komputerowy od metody Karnaugha



znajduje minimalną postać dysjunkcyjną (sumę 
iloczynów)



Użyteczna w minimalizacji manualnej do około 6 
zmiennych wejściowych, jednak bardziej pracochłonna 
(dla prostych funkcji) od metody Karnaugh

7

Algorytm metody Quine’a-McCluskeya

1.

Wypisujemy w jednej kolumnie wektory wejściowe odpowiadające jedynkom 
oraz wartościom nieustalonym.

2.

Grupujemy te wektory rosnąco według ilości jedynek w wektorze.

3.

Porównujemy wektory o o k-tej liczbie jedynek z wektorami o k+1 liczbie 
jedynek i łączymy te które różnią się tylko jednym bitem (np. 0100 oraz 0101), 
i zapisujemy wynikowe wektory (postaci np. 010*). Plusem oznaczamy 
„połączone” wektory.

4.

Analogicznie tworzymy następne tabele dopóki występują możliwości łączenia.

5.

Wypisujemy nieoznaczone plusem implikanty jako wiersze tabeli, kolumny 
tabeli to wartości dziesiętne „jedynek”. Na przecięciach w tabeli oznaczmy 
„kółkami” związek między implikantem i wektorem wejściowym – „kółkiem 
pełnym” dla implikantów bez wartości nieustalonych, a „kółkiem pustym” dla 
implikantów zawierających w sobie wartości nieustalone.

6.

Znajdujemy kolumny z jednym „kołem pełnym” i oznaczamy cały wiersz 
odpowiedniego implikantu. Jeżeli są nieoznaczone kolumny to powtarzamy dla 
kolumn z dwoma (itd.) „kołami pełnymi”. Gdy skończą się kółka pełne 
analogicznie postępujemy z „kółkami pustymi”.

<przykład>

8

Metoda iteracyjnego 
konsensusu

9

Metoda iteracyjnego 
konsensusu

Metoda to rozpoczyna się od implikantów funkcji (mogą to 

być dowolne implikanty, w szczególności iloczyny zupełne).

Metoda iteracyjnego konsensusu to iteracyjne wykonanie 

następujących kroków:

1.

Usuń z postaci dysjunkcyjnej wszystkie pokryte implikanty

2.

Wygeneruj wszystkie (niepuste i różne od 0) konsensusy z 
par iloczynów. Dodaj je do postaci dysjunkcyjnej. Przejdź 
do kroku 1.

Algorytm kończy się w momencie, gdy nie możemy 

wygenerować nowych konsensusów, ponieważ uzyskane 
iloczyny to implikanty proste.

10