1
Eksploracja jednej zmiennej
Statystyki rozkładu częstości i wizualna
analiza danych
Wykład 2

2
Ogólny podział statystyk
Ogólny podział statystyk
Statystyki opisowe
Statystyki opisowe
Statystyki inferencyjne
Statystyki inferencyjne
3
I etap analizy wyników.
Statystyki opisowe – podsumowanie danych
Podsumowanie wyników
Liczbowe
Graficzne
Wyniki surowe nie dadzą takiego obrazu
Powinniśmy dokonać podsumowania wyników
za pomocą statystyk opisowych lub graficznego
przedstawienia danych.
Sprawdzamy czy wyniki układają się zgodnie z hipotezami.

4
Statystyki opisowe
Jak znaleźć porządek w zbiorze liczb?
Rozkład częstości

5
Rozkład częstości
Rozkład częstości – pokazuje jak często każdy
wynik się pojawił w zbiorze danych.
Jest to podsumowanie kategorii odpowiedzi w badanej
zmiennej.
Rozkładem częstości jest każde
uporządkowanie danych, które pokazuje
częstość występowania różnych wartości
zmiennej lub częstość wartości należących do
grup zmiennej
6
Zmienna
nastrój
nastrój

7
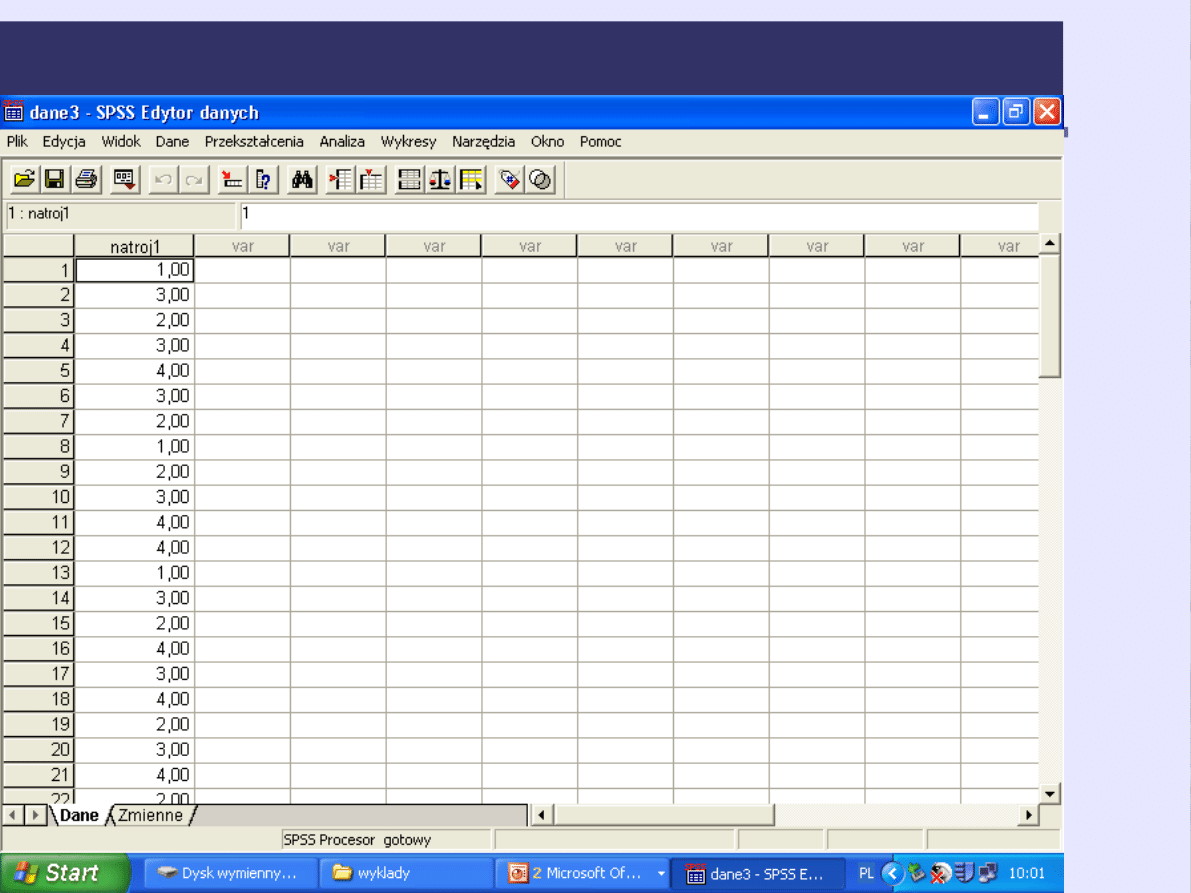
Wyniki surowe – postać numeryczna
Nastroj: 1 3 2 3 4 3 2 1 2 3 4 4 1 3 2 4 3 4 2 3 4
2 1 5 5 2 2 3 4 4 2 3 4 4 3 1 1 1 2 3 3 3 4 3 5 5
5 5 5 5
8
Wyniki surowe - dane w SPSS
9
10
Rozkład częstości - tabela
nastroj1
7
14,0
14,0
14,0
10
20,0
20,0
34,0
14
28,0
28,0
62,0
11
22,0
22,0
84,0
8
16,0
16,0
100,0
50
100,0
100,0
1,00
2,00
3,00
4,00
5,00
Ogółem
Ważne
Częstość
Procent
Procent
ważnych
Procent
skumulowany

11
Konstruowanie rozkładu częstości
W pierwszej kolumnie robimy listę możliwych
odpowiedzi (wartości zmiennej).
Jeżeli zmienna jest porządkowa, przedziałowa lub
stosunkowa uporządkowujemy jej wartości od
najmniejszej do największej.
W drugiej kolumnie zapisujemy liczebność każdej
wartości tzn. ile razy ta wartość pojawia się w
odpowiedziach osób badanych (w zbiorze danych).
W trzeciej kolumnie obliczamy procent pojawień się tej
wartości w ogóle wyników tzn. dzielimy częstość przez
ogólną ilość wyników i mnożymy razy 100.
W ostatniej kolumnie dodajemy do siebie kolejne
wartości procentów. W efekcie uzyskujemy procent
skumulowany czyli procent liczebności danej wartości i
wszystkich mniejszych w naszym zbiorze danych.

12
Histogram – wykres częstości
Histogram
Wykres liczebności poszczególnych wartości.
Liczebności przedstawione są za pomocą słupków,
których szerokość określa pewien zakres wyników.
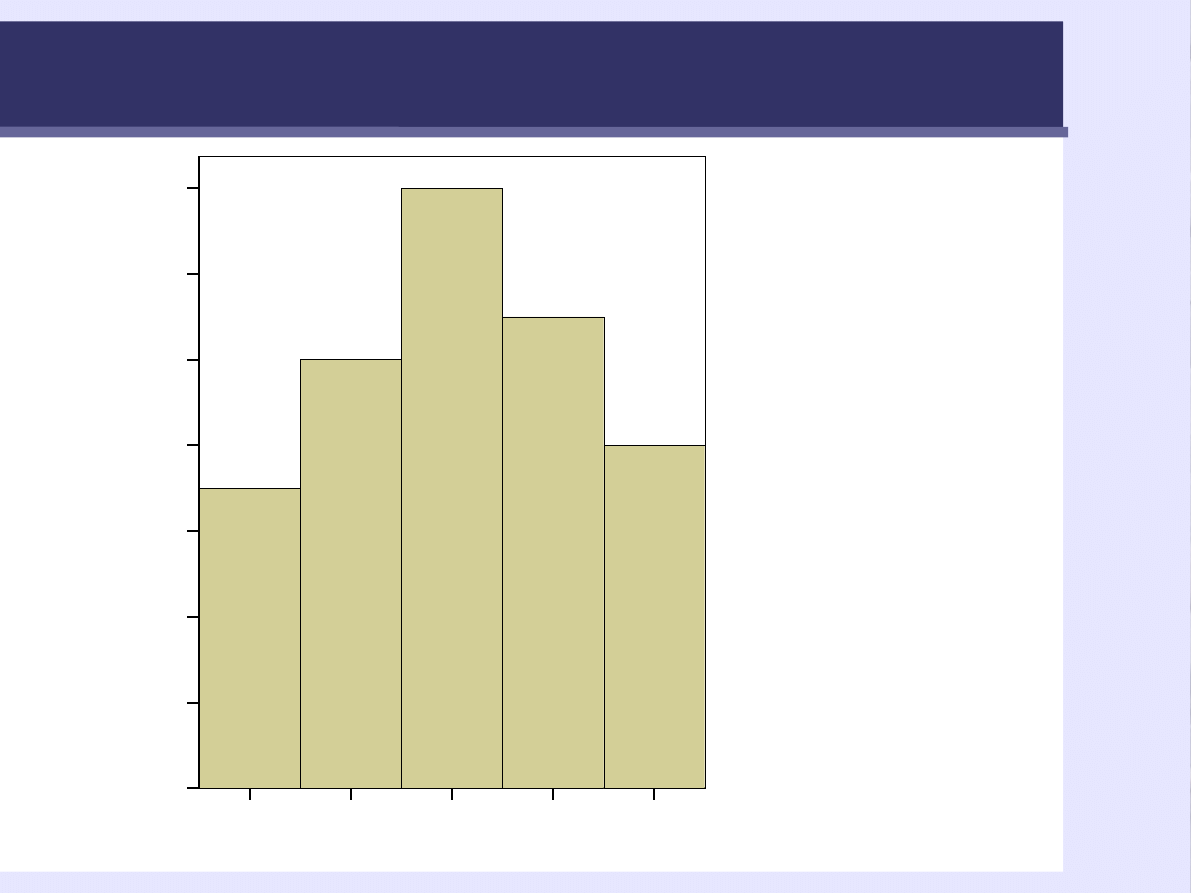
13
HISTOGRAM - wykres rozkładu częstości
1,00
2,00
3,00
4,00
5,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
14
1,00
2,00
3,00
4,00
5,00
nastroj1
0
5
10
15
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
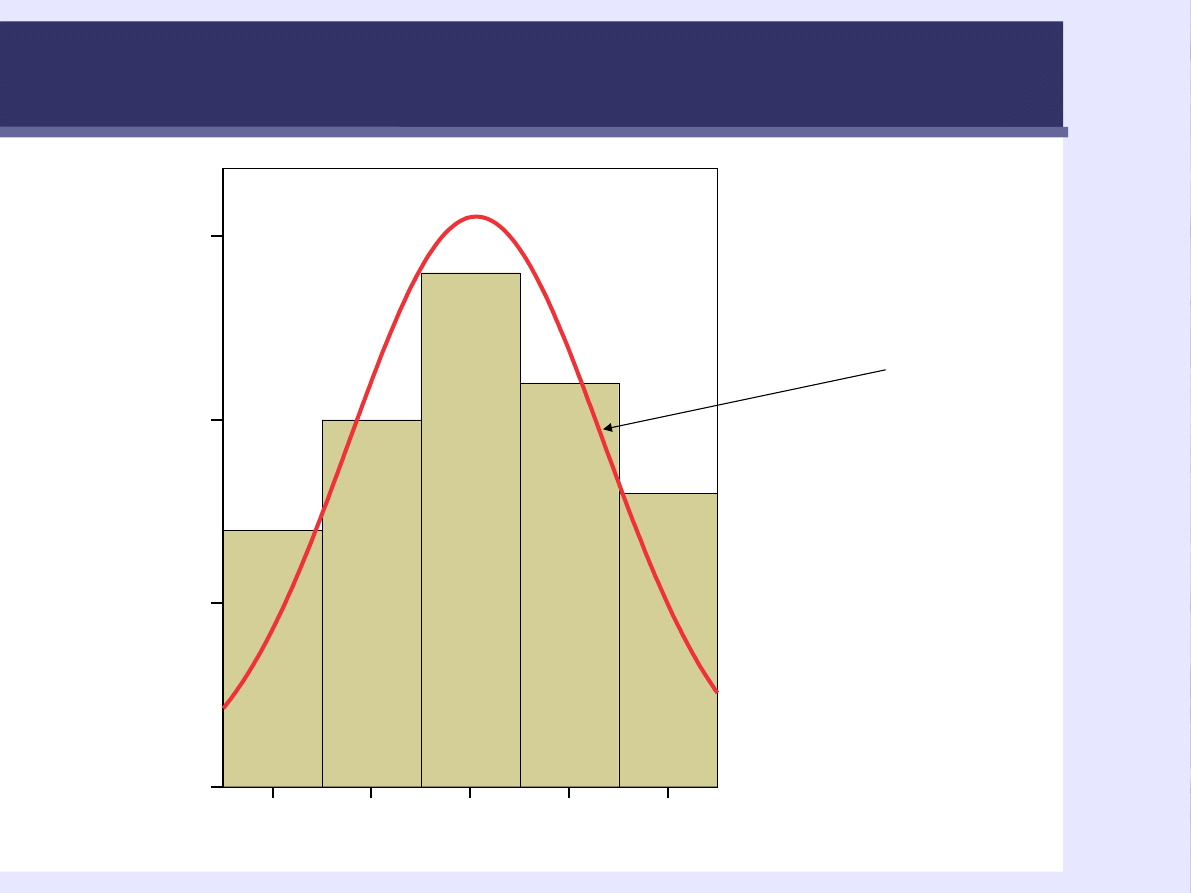
Histogram z krzywą normalną
Krzywa normalna
15
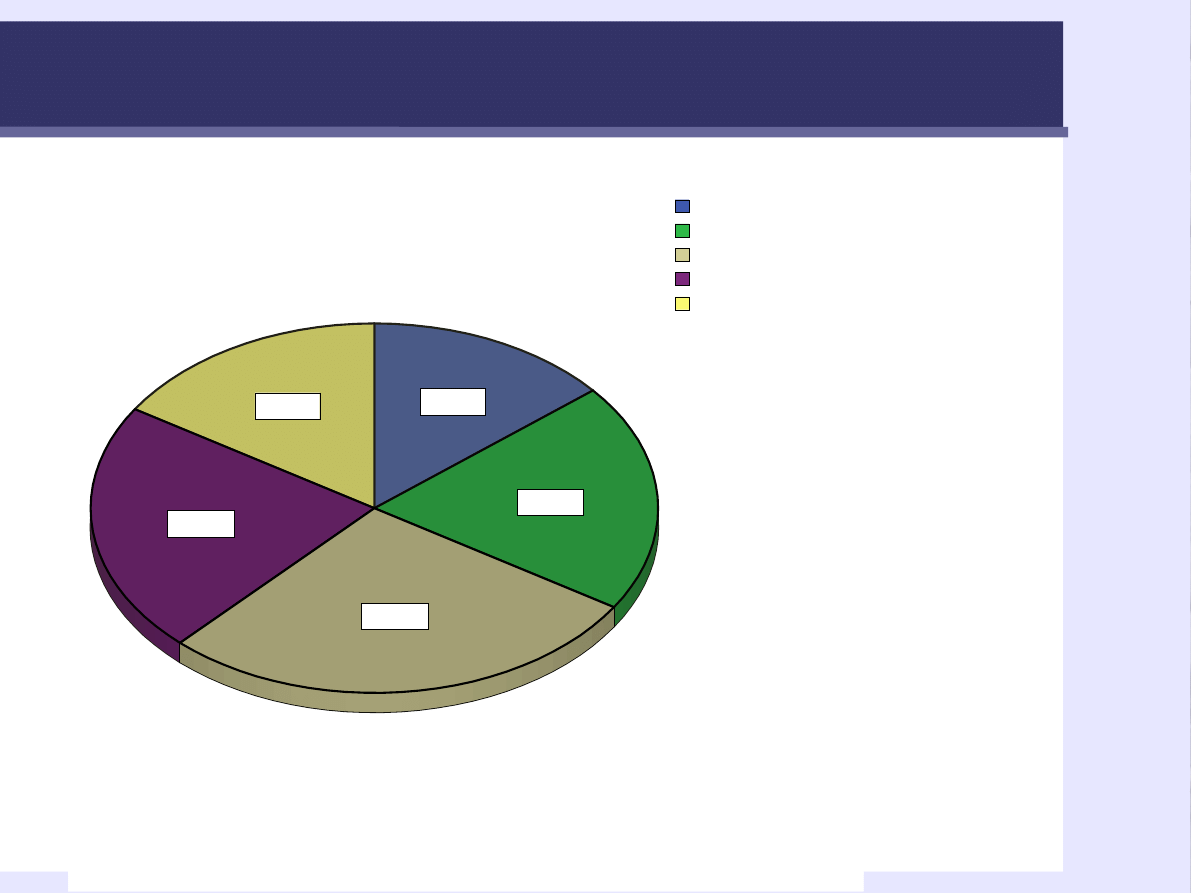
Wykres kołowy (tortowy)
14,0%
20,0%
28,0%
22,0%
16,0%
nastroj1
bardzo zły
zły
trudno powiedzieć
dobry
bardzo dobry
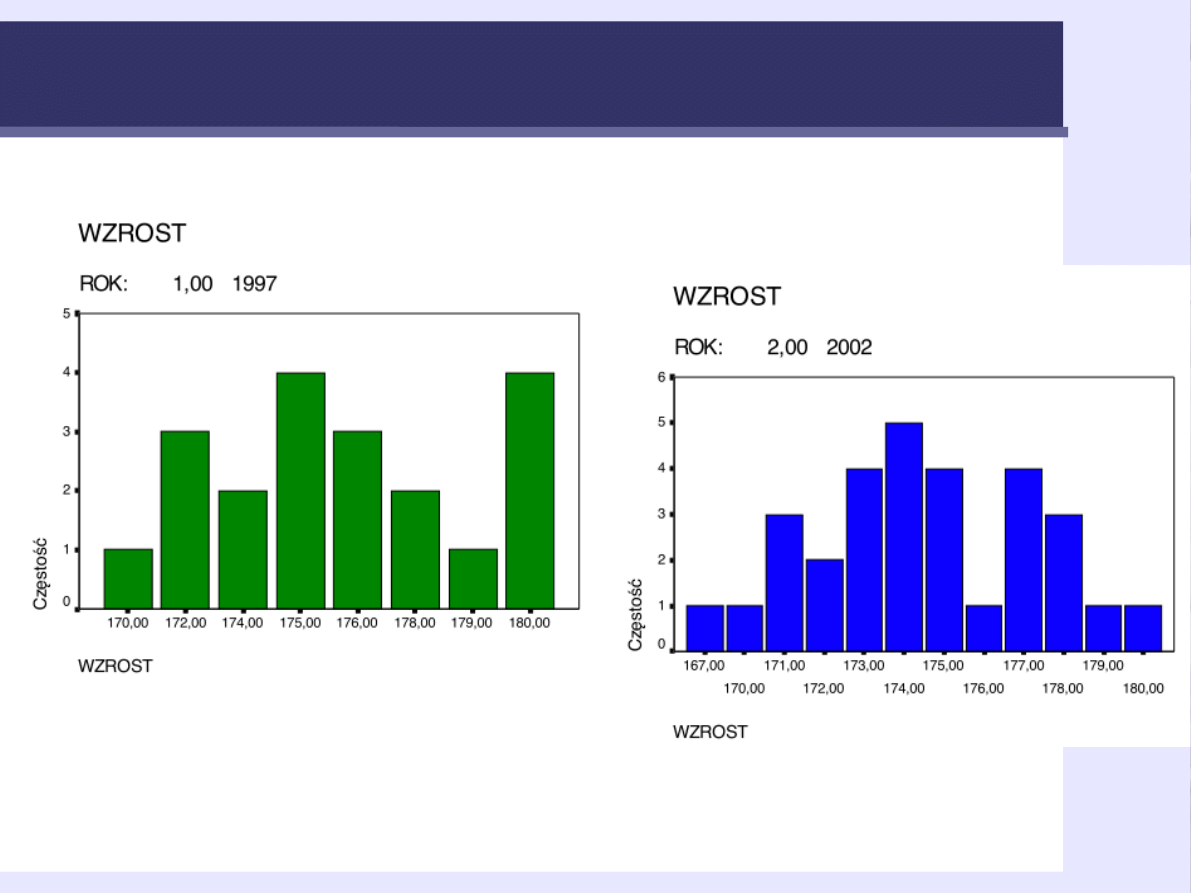
16
Wzrost Miss Polonia 1997 i 2002
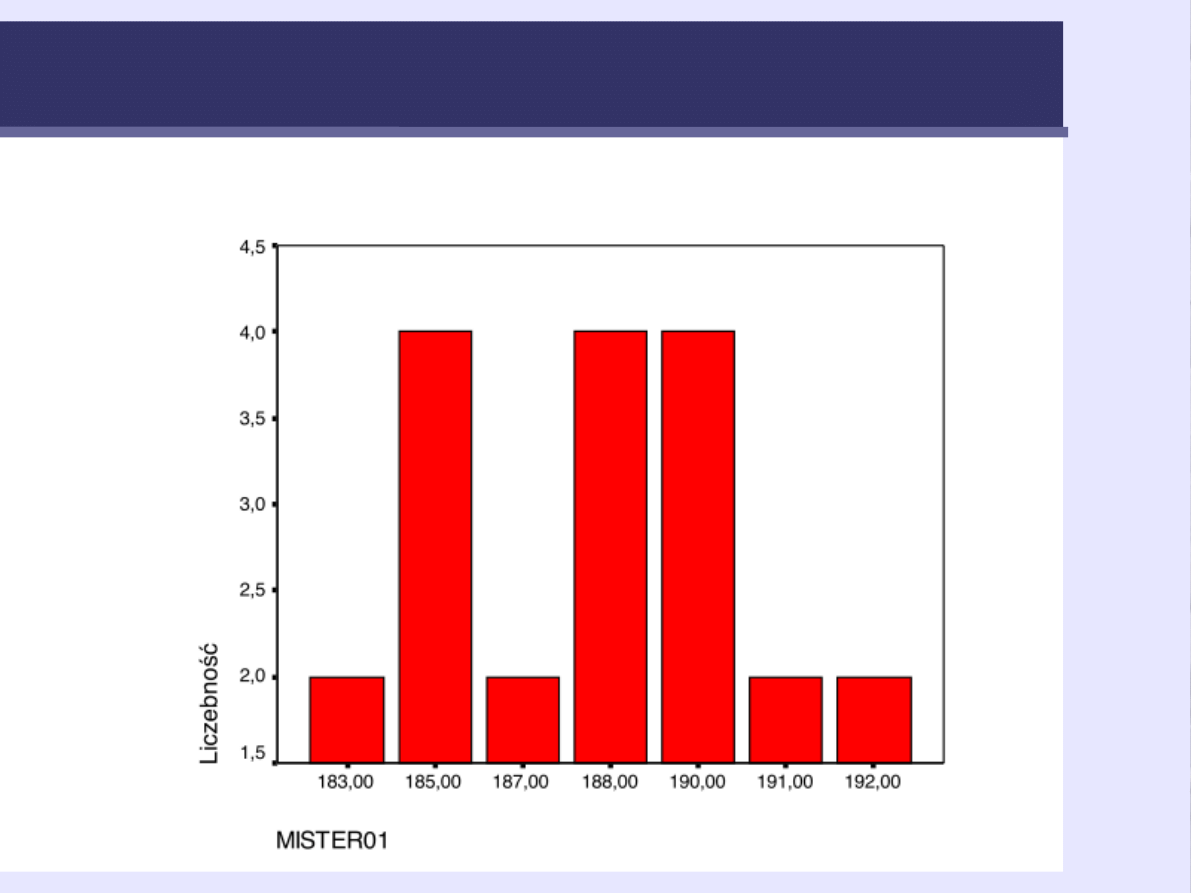
17
Mister Poland 2001

18
Charakterystyki rozkładu częstości
Miary tendencji centralnej
średnia,
mediana,
modalna lub dominanta lub moda
Miary rozproszenia wyników
zakres,
wariancja,
odchylenie standardowe
Kształt rozkładu wyników
skośność
kurtoza

19
Miary tendencji centralnej
Najpopularniejsze statystyki podsumowujące starają się przedstawić
pewną
centralną
wartość dla danych, inaczej
przeciętną
wartość
wyników pomiarów.
Wartość ta jest zazwyczaj bliska punktowi największego skupienia
pomiarów i można ją uważać za najbardziej typową dla całego zbioru.
Średnia
Mediana
Modalna
20
Średnia
(M)
Oznacza dodanie
(sumę)
wszystkich
wyników
Oznacza liczbę
obserwacji/przyp
adków
M=
∑
x
N
21
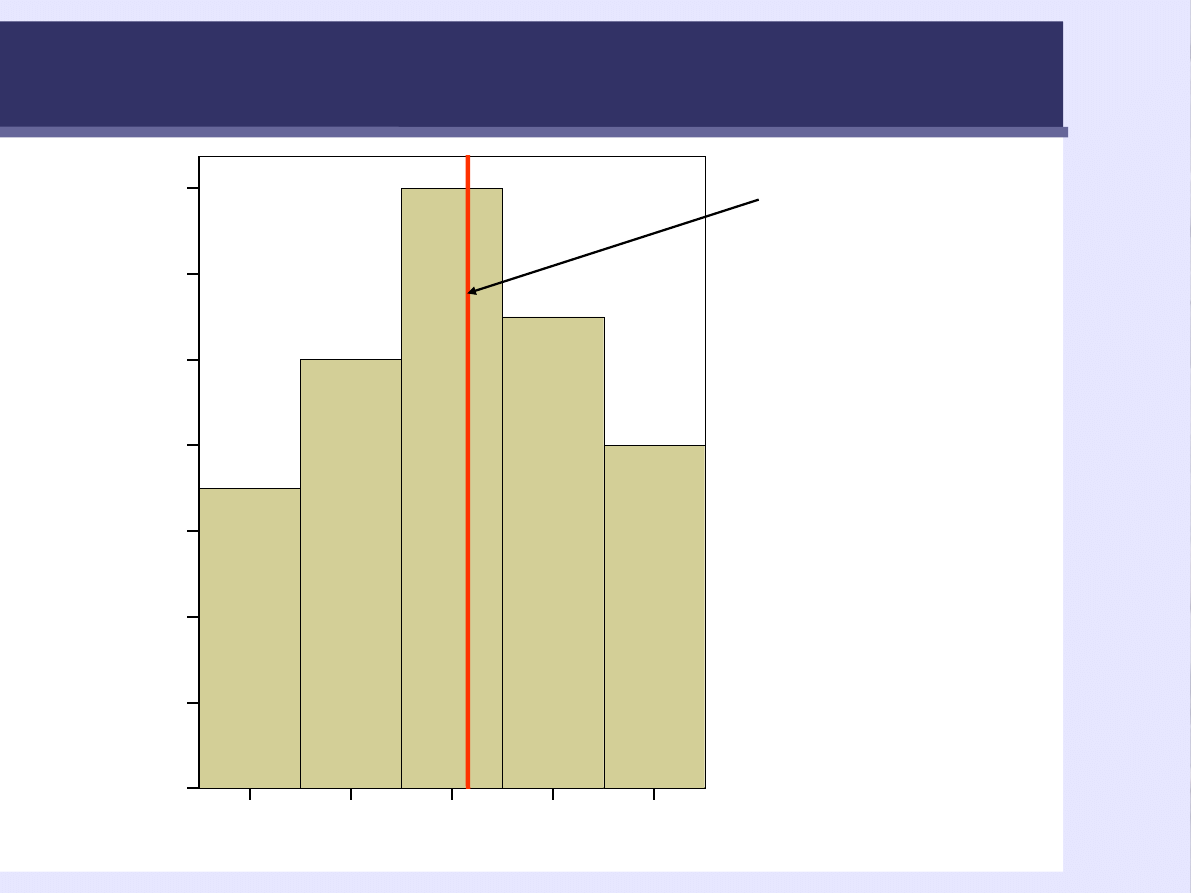
Średnia
1,00
2,00
3,00
4,00
5,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
Średnia
M = 3,06
22
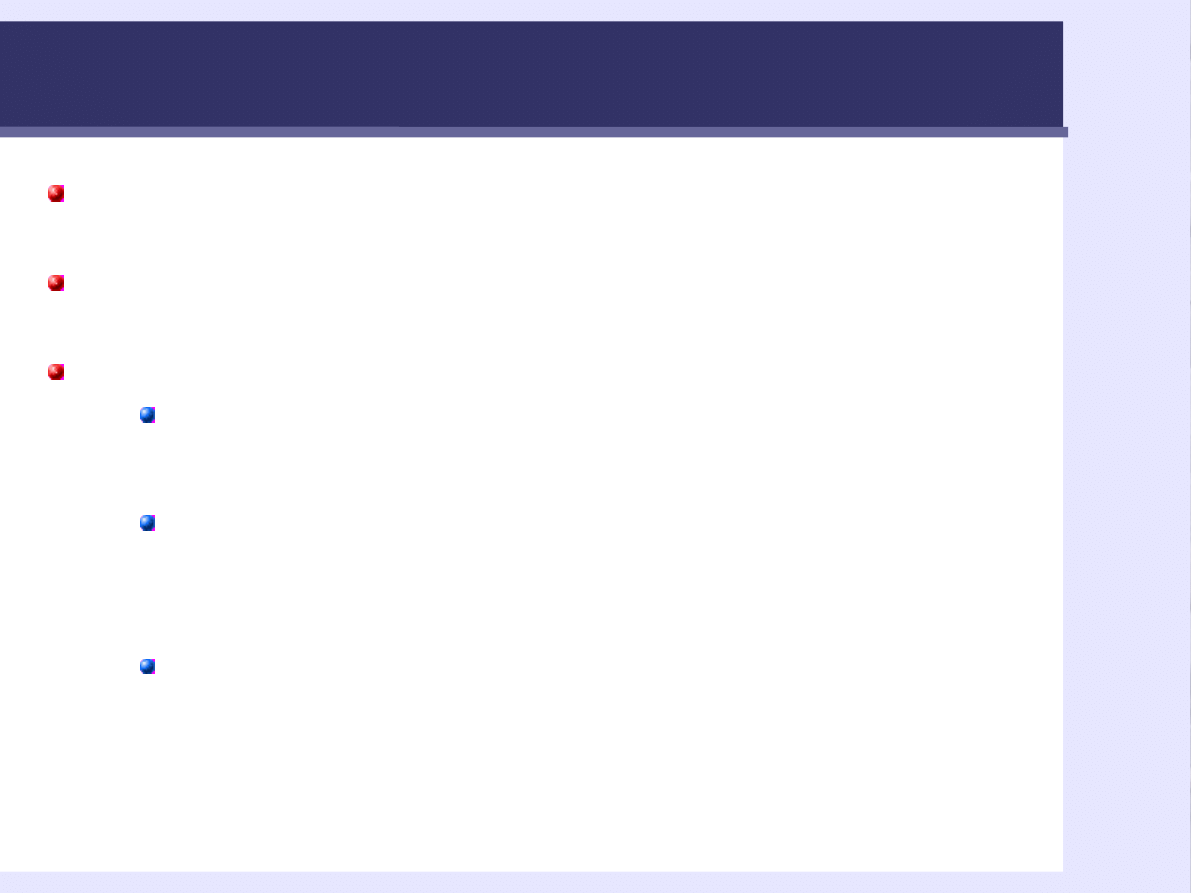
Średnia
najczęściej używana przez psychologów
Przy jej obliczaniu bierzemy
pod uwagę wszystkie wyniki
Wykorzystywana w wielu
testach statystycznych
Wady:
Reprezentując
wszystkich – może
mówić o nikim
Często jej wartość nie
występuje w wynikach
(średnia liczba dzieci
w domach 2.3??)
Jest wrażliwa na
dewiantów – skrajne
wyniki
23
0,00
3,00
6,00
9,00
12,00
15,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,2941
Std. Dev. = 2,10042
N = 51
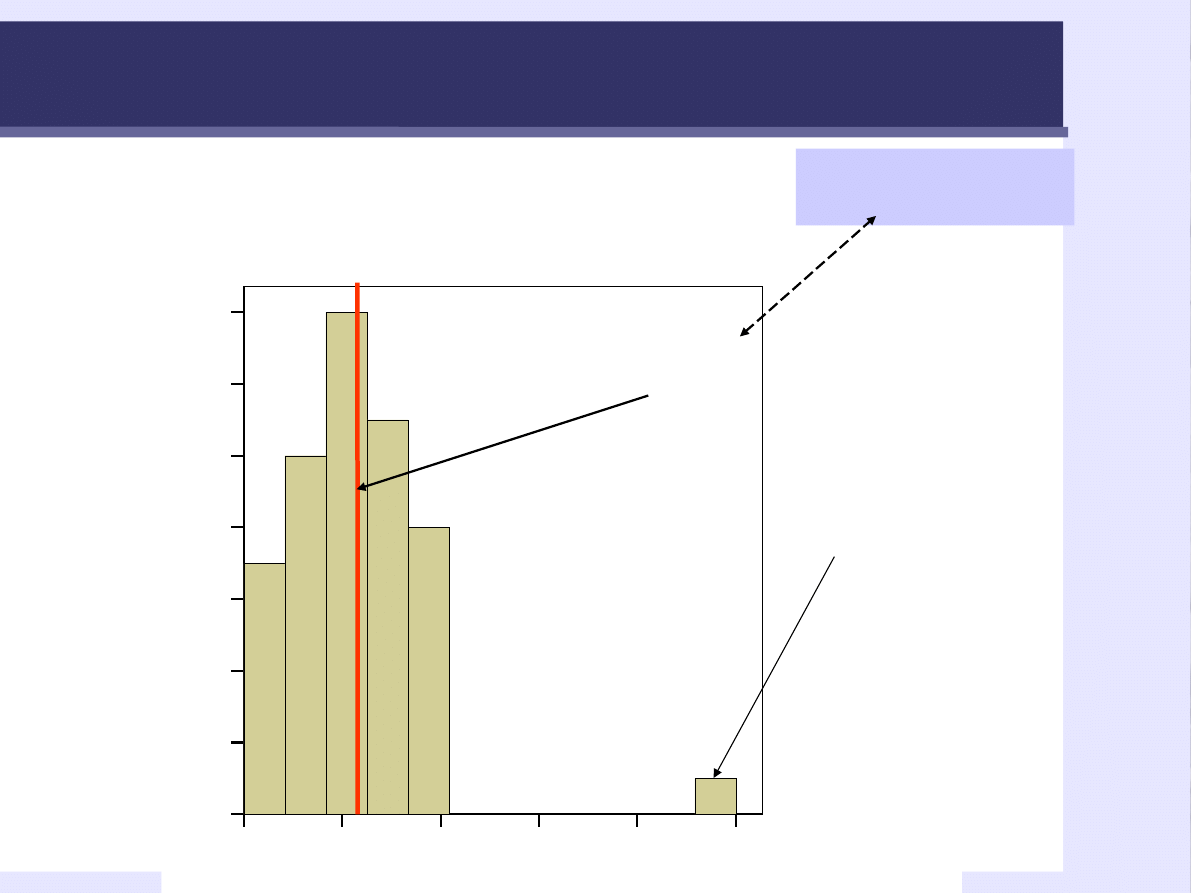
Histogram
Średnia i outlier
Średnia
M
M
= 3,29
= 3,29
Wynik odstający
(outlier,
dewiant)
Poprzednia średnia
M
M
= 3,06
= 3,06
24
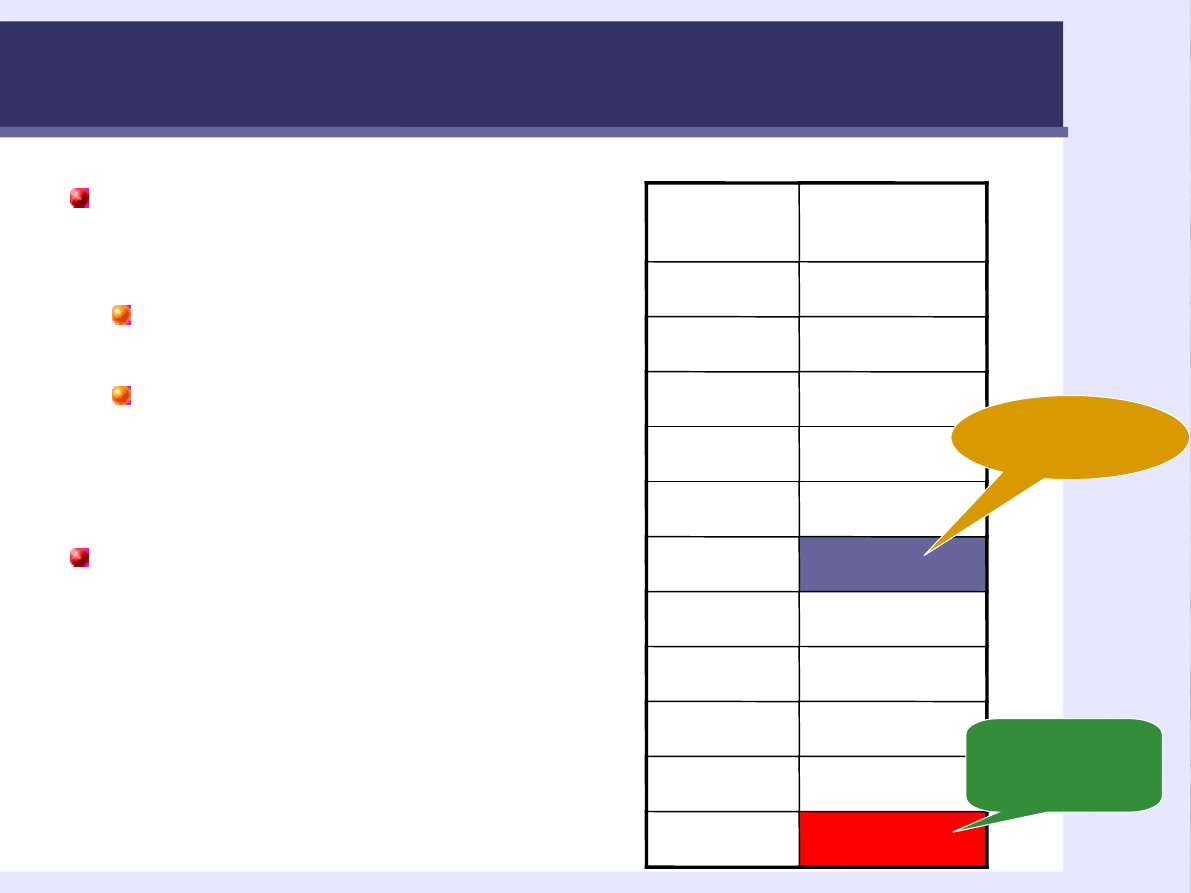
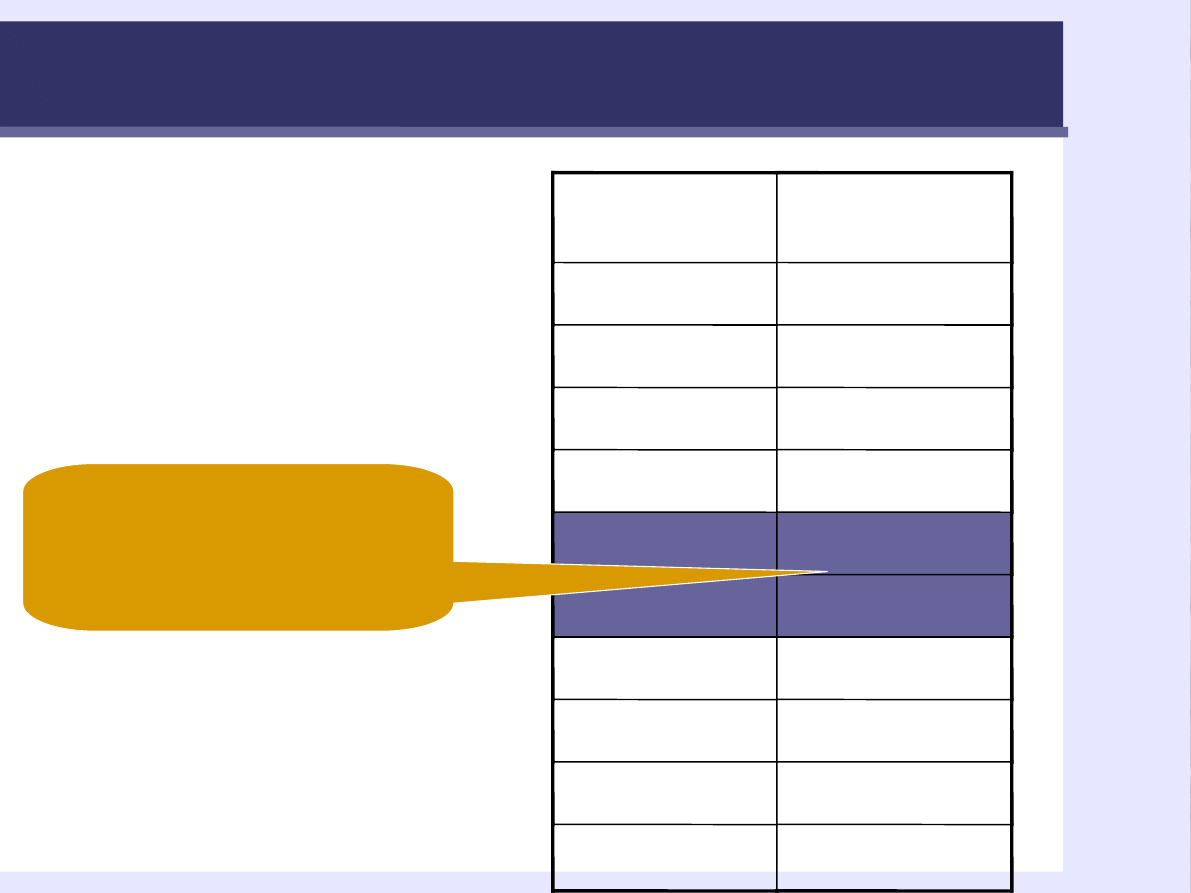
Mediana Me
Me – to wartość, która
znajduje się w środku
wszystkich wartości.
Aby ustalić Me trzeba
uporządkować wyniki.
Wynik, w tym wypadku,
6 osoby dzieli wszystkie
wyniki na połowę.
Medianę oblicza się
najczęściej wtedy gdy
pojawiają się bardzo
nietypowe wyniki
(dewianci/outliers), a nie ma
powodów, aby je eliminować
(średnia =4,05)
Kolejne
wyniki
Czas
reakcji
1
0,5
2
0,5
3
1
4
1
5
2
6
2
7
2,5
8
2,5
9
2,5
10
3
11
25
Mediana
Dziwny
wynik
25
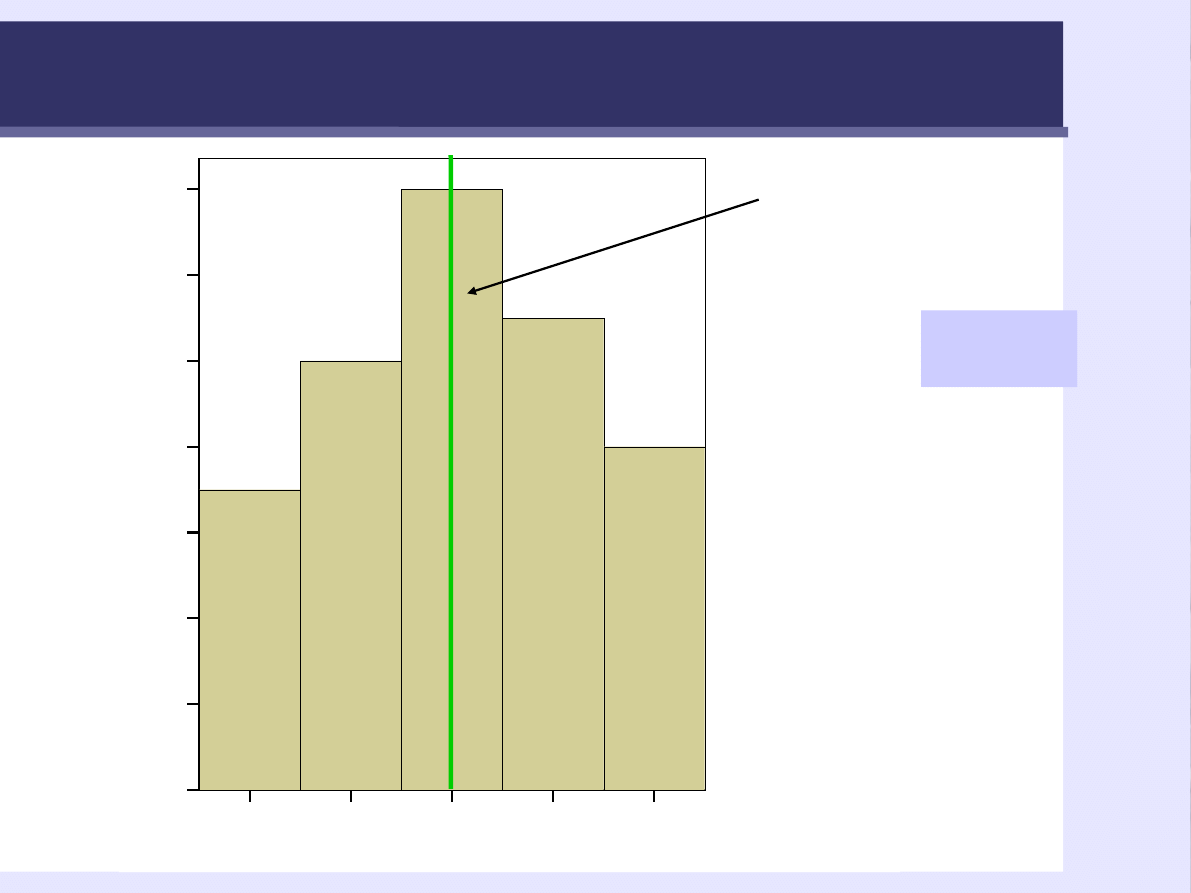
Obliczanie mediany w przypadku parzystej liczby wyników
Kolejne
wyniki
zapamiętane
1
3
2
4
3
4
4
5
5
5
6
7
7
8
8
8
9
8
10
9
Wtedy bierzemy
Wtedy bierzemy
średnią
średnią
z wyników leżących
z wyników leżących
pośrodku
pośrodku
5 + 7 / 2= 6
5 + 7 / 2= 6
26
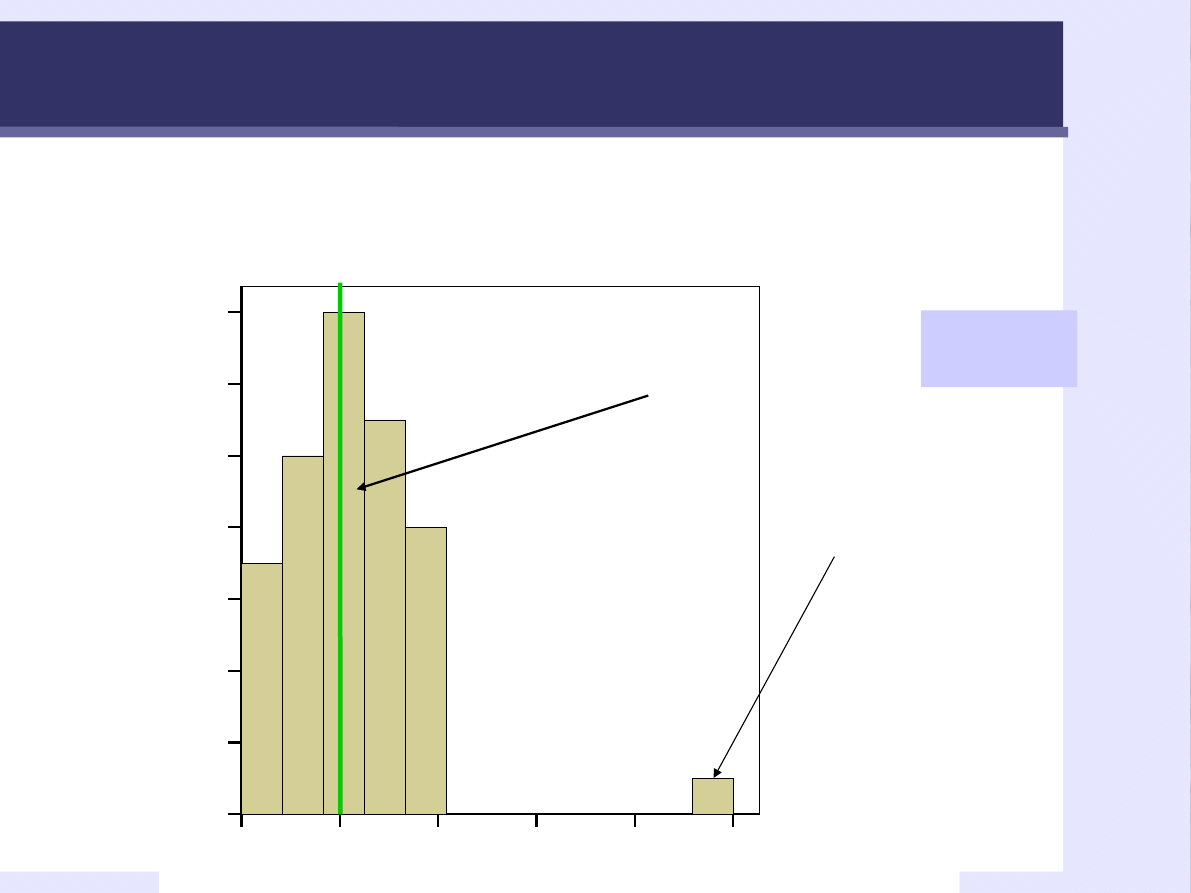
Średnia
1,00
2,00
3,00
4,00
5,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
mediana
Me
Me
= 3,00
= 3,00
średnia
M
M
= 3,06
= 3,06
27
0,00
3,00
6,00
9,00
12,00
15,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,2941
Std. Dev. = 2,10042
N = 51
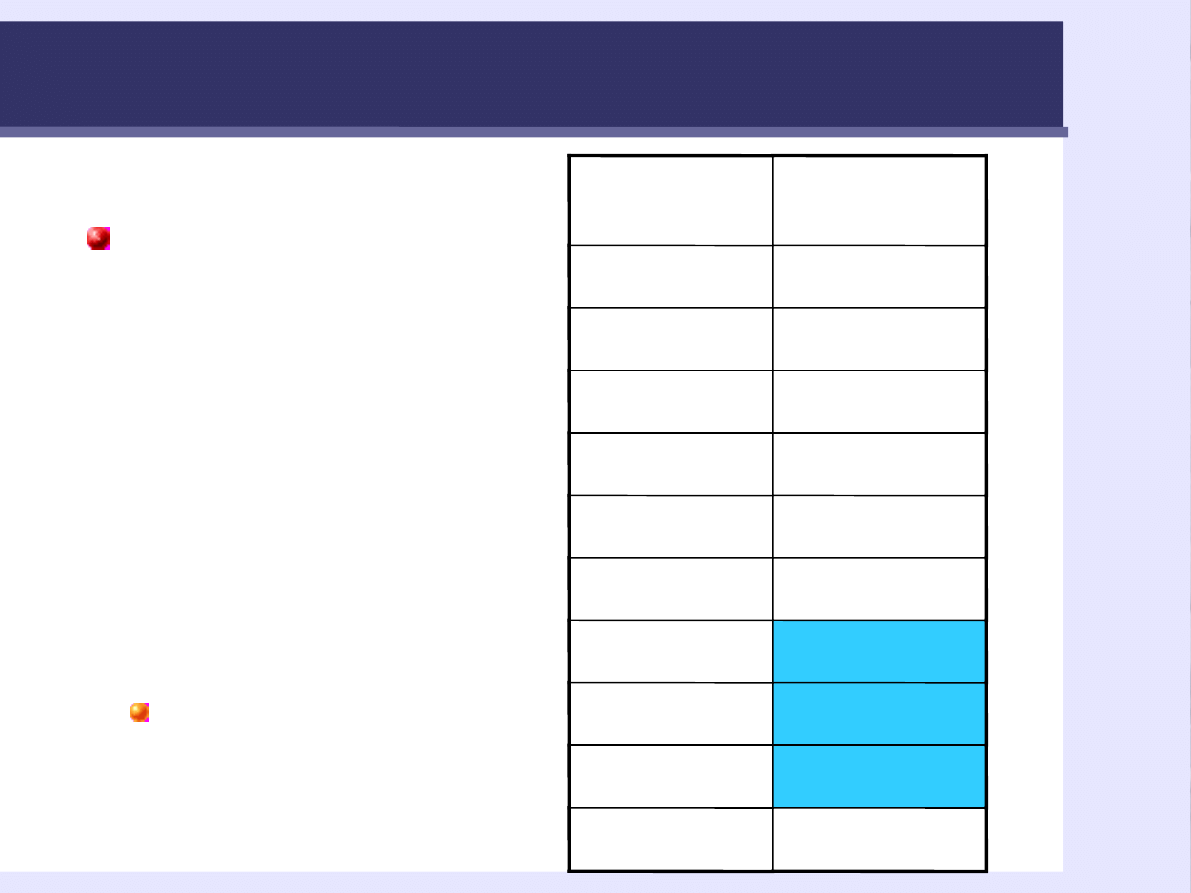
Histogram
Mediana i outlier
Mediana
Me
Me
= 3,00
= 3,00
Wynik odstający
(outlier,
dewiant)
średnia
M
M
= 3,29
= 3,29
28
Modalna = moda = dominanta Mo
Jest to najczęściej
pojawiająca się
wartość wśród
wyników
uczestników
badania, też tak jak
medianę najłatwiej
ją dostrzec po
uporządkowaniu
wyników
Modalna = 8
Kolejne
wyniki
zapamiętane
1
3
2
4
3
4
4
5
5
5
6
7
7
8
8
8
9
8
10
9
29
Średnia
1,00
2,00
3,00
4,00
5,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
modalna
Mo
Mo
= 3,00
= 3,00
średnia
M
M
=
=
3,06
3,06
mediana
Me
Me
= 3,00
= 3,00

30
0,00
3,00
6,00
9,00
12,00
15,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,2941
Std. Dev. = 2,10042
N = 51
Histogram
Modalna i outlier
Modalna
Mo
Mo
= 3,00
= 3,00
Wynik odstający
(outlier,
dewiant)
średnia
M
M
=
=
3,29
3,29
Mediana
Me
Me
= 3,00
= 3,00
31
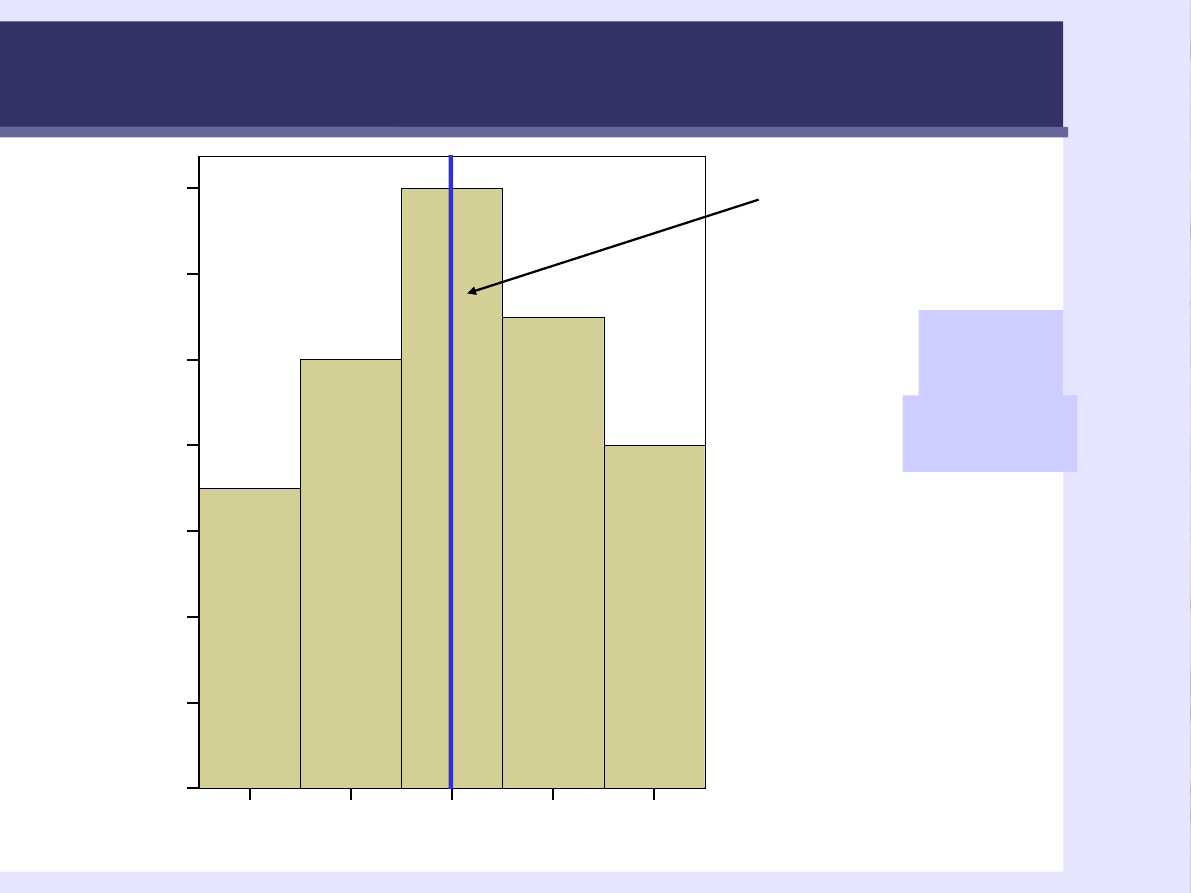
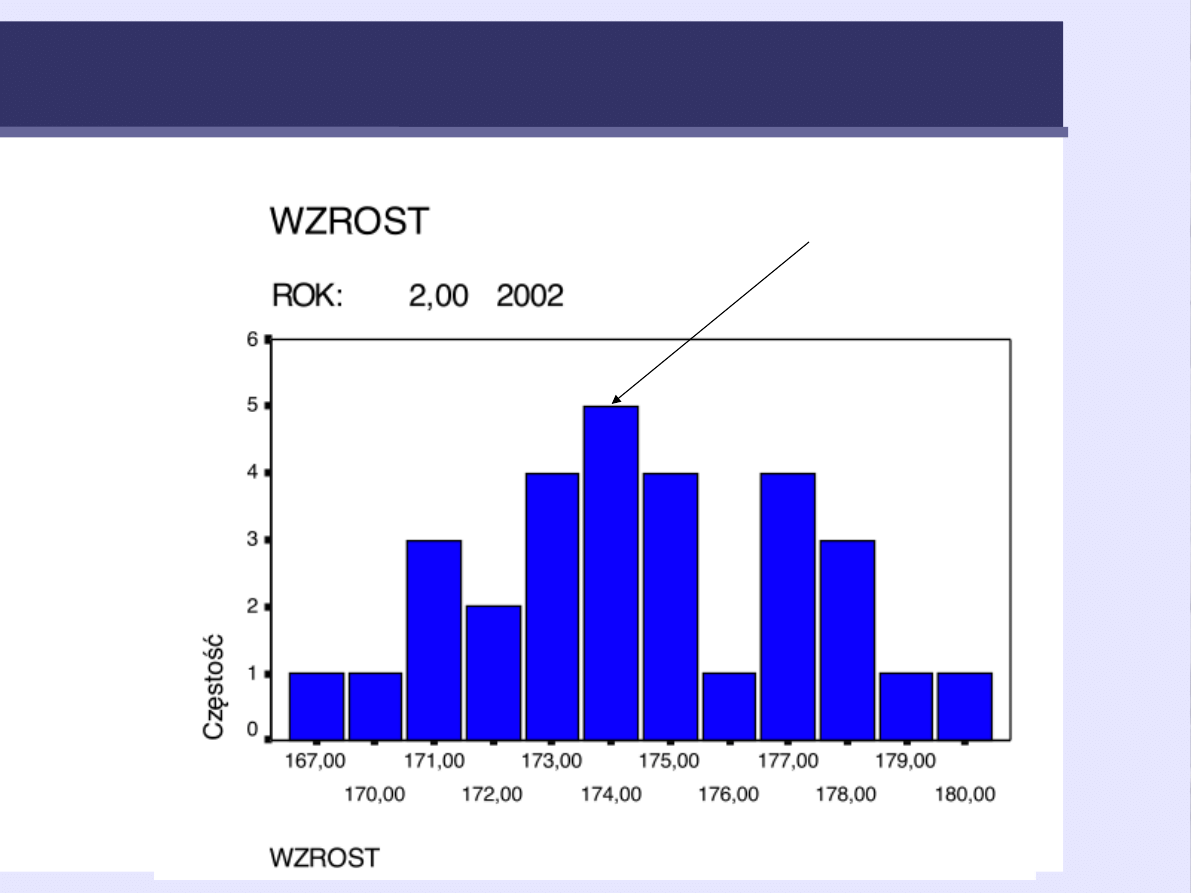
Rozkład jednomodalny
modalna
32
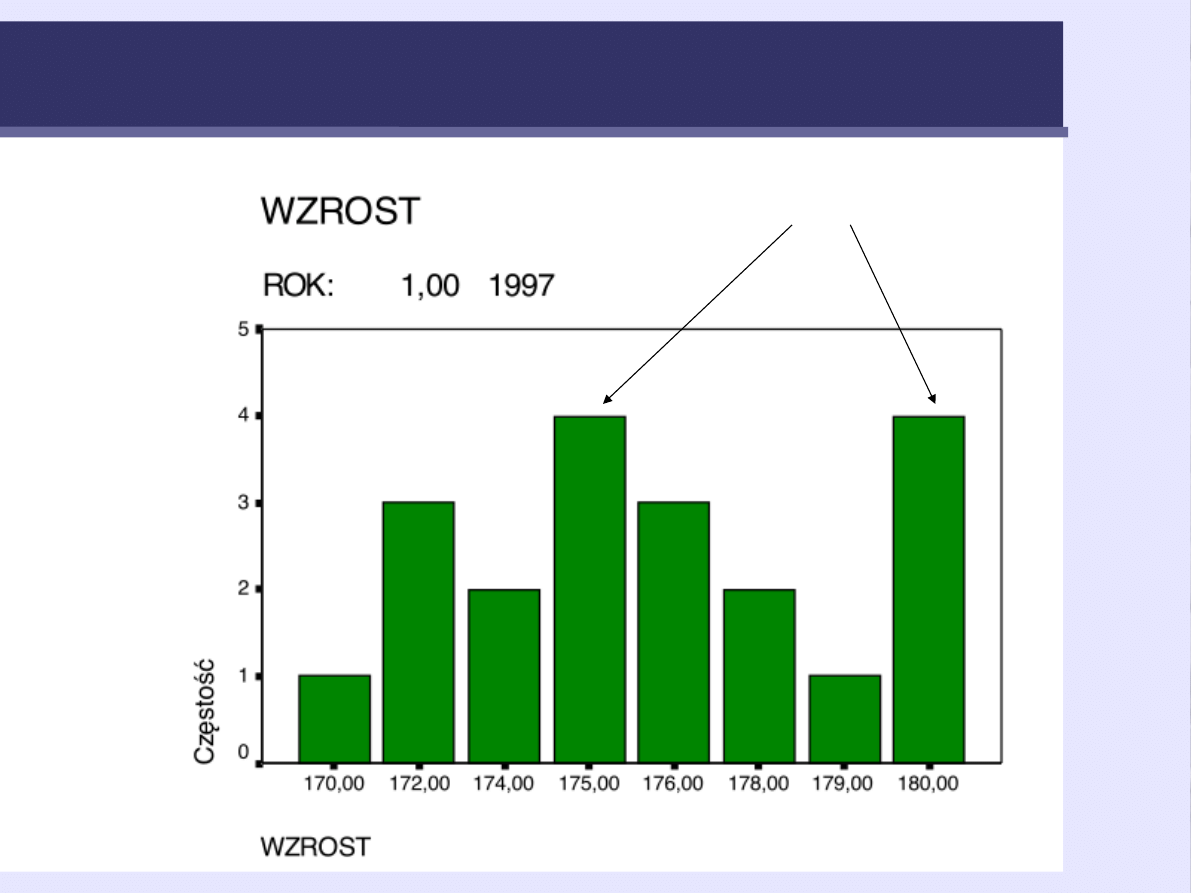
Rozkład dwumodalny
modalne
33
Modalna
Relatywnie rzadko stosowana w psychologii
Wady:
Może w ogóle nie wystąpić w wynikach (jeśli nie ma
co najmniej dwóch takich samych wyników)
3, 4, 5, 6, 7, 8 –
nie ma modalnej
Może być dwie i więcej modalnych, jeśli więcej
wyników powtarza się
2, 2, 4, 5, 6, 6, -
2 i 6 to modalne
–
rozkład
wyników dwumodalny
Może też nie odzwierciedlać prawdziwego obrazu
danych
34
Miary tendencji centralnej
Statystyki
nastroj1
51
0
3,2941
3,0000
3,00
Ważne
Braki danych
N
Średnia
Mediana
Dominanta
35
0,00
3,00
6,00
9,00
12,00
15,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,2941
Std. Dev. = 2,10042
N = 51
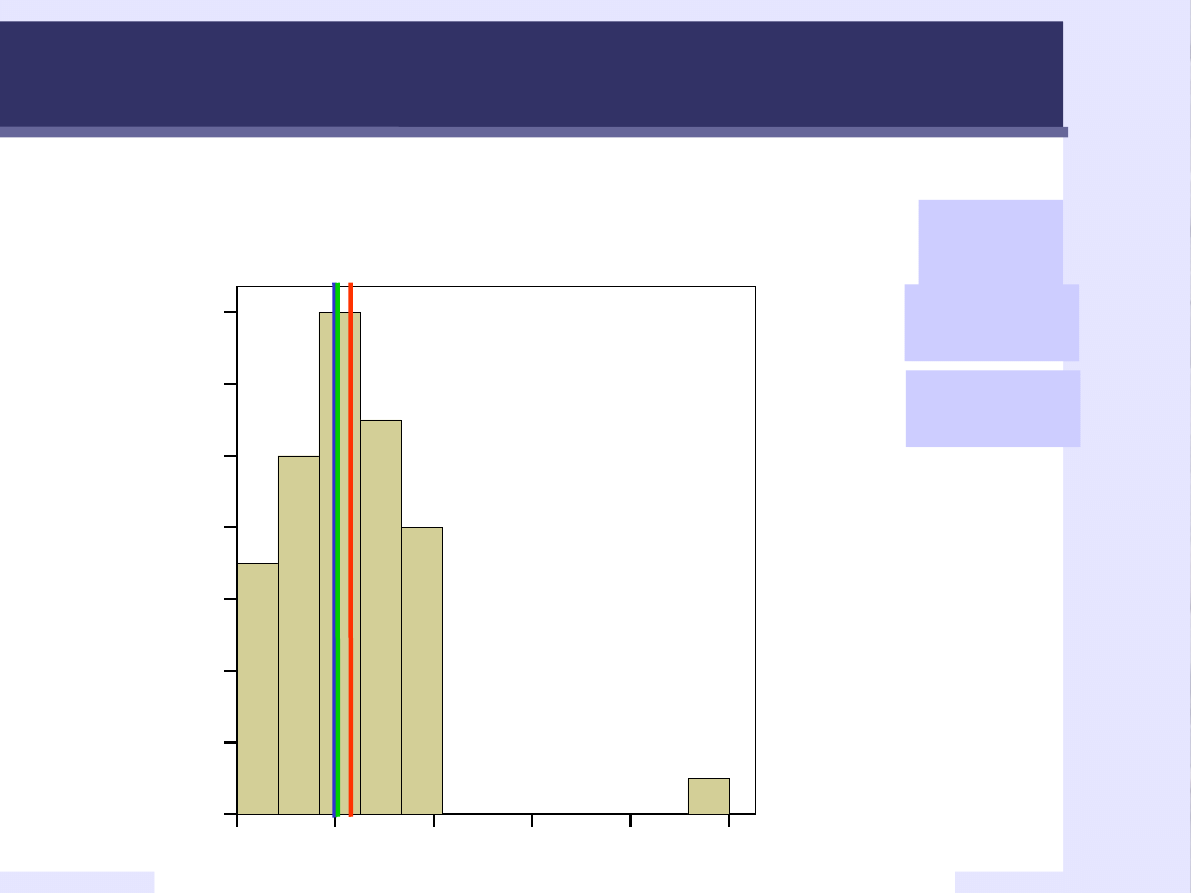
Histogram
Miary tendencji centralnej
Modalna
Mo
Mo
= 3,00
= 3,00
Średnia
M
M
=
=
3,29
3,29
Mediana
Me
Me
= 3,00
= 3,00
36
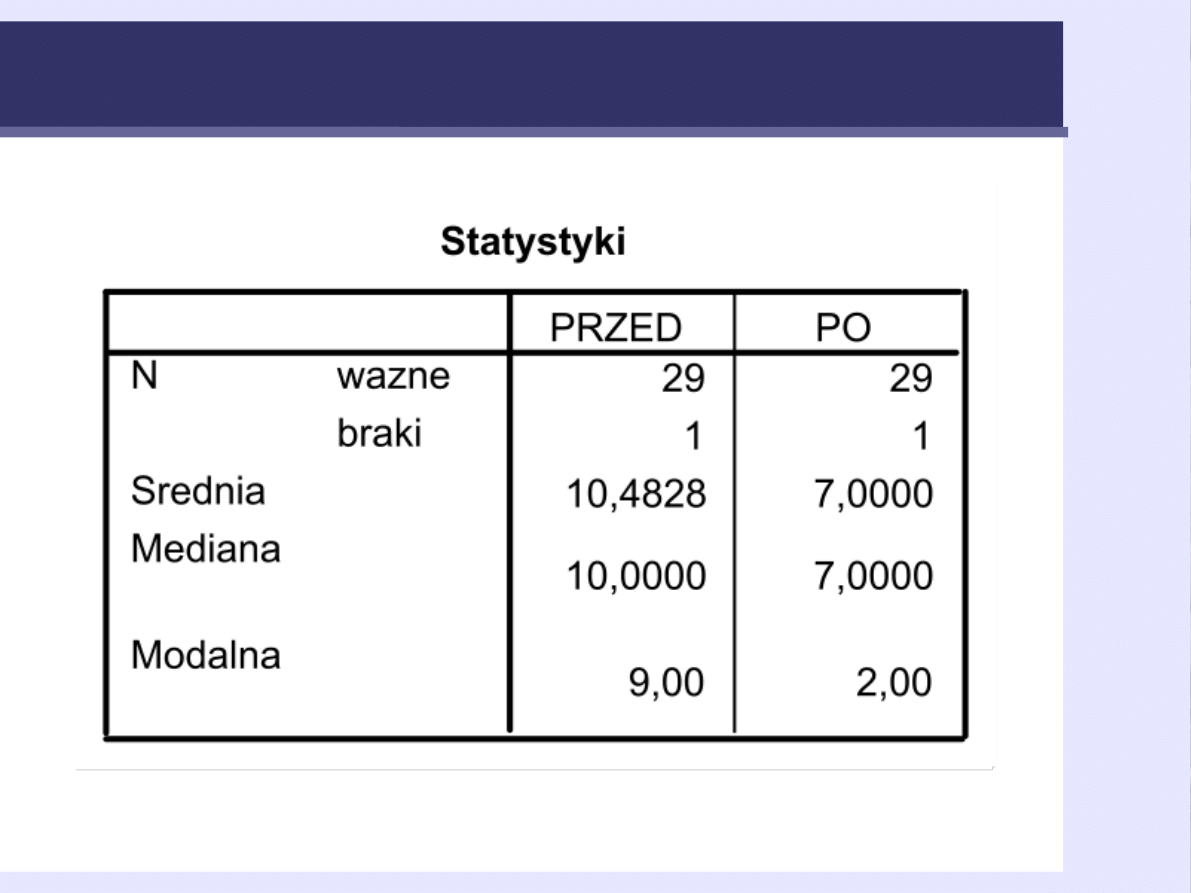
Wszystkie ...
37
Poziom pomiaru (skale) i miary które można
obliczać
nominalna
porządkowa
przedziałowa ilorazowa
średnia
mediana
modalna

38
Miary rozproszenia
Same miary tendencji centralnej nie
wystarczają do opisu danych
te same wartości mogą pochodzić z
bardzo różnych zestawów wyników
Dlatego opisujemy również, jak wyniki
są zróżnicowane.
Wykorzystywane są do tego celu tzw.
miary rozproszenia
miary rozproszenia
Zakres
Zakres
Wariancja
Wariancja
Odchylenie standardowe
Odchylenie standardowe
39
Minimum, maksimum, zakres
Minimum
– najmniejsza wartość
Maximum
– największa wartość
zakres
(rozstęp) jest rozumiany jako różnica między
największym i najmniejszym pomiarem
Nastroj:
1 3 2 3 4 3 2 1 2 3 4 4 1 3 2 4 3 4 2 3 4 2 1 5 5 2 2
3 4 4 2 3 4 4 3 1 1 1 2 3 3 3 4 3 5 5 5 5 5 5
5 − 1= 4
zakres
40
Jak bardzo każdy wynik różni się od średniej
Pięciu statystyków zapytano o to ilu mają
przyjaciół.
Wyniki: 1, 2, 3, 4, 5
M = 3
Średnią możemy rozumieć jako model
prawdziwych danych.
Czy model ten jest trafny?
Jak bardzo dane różnią się od modelu?
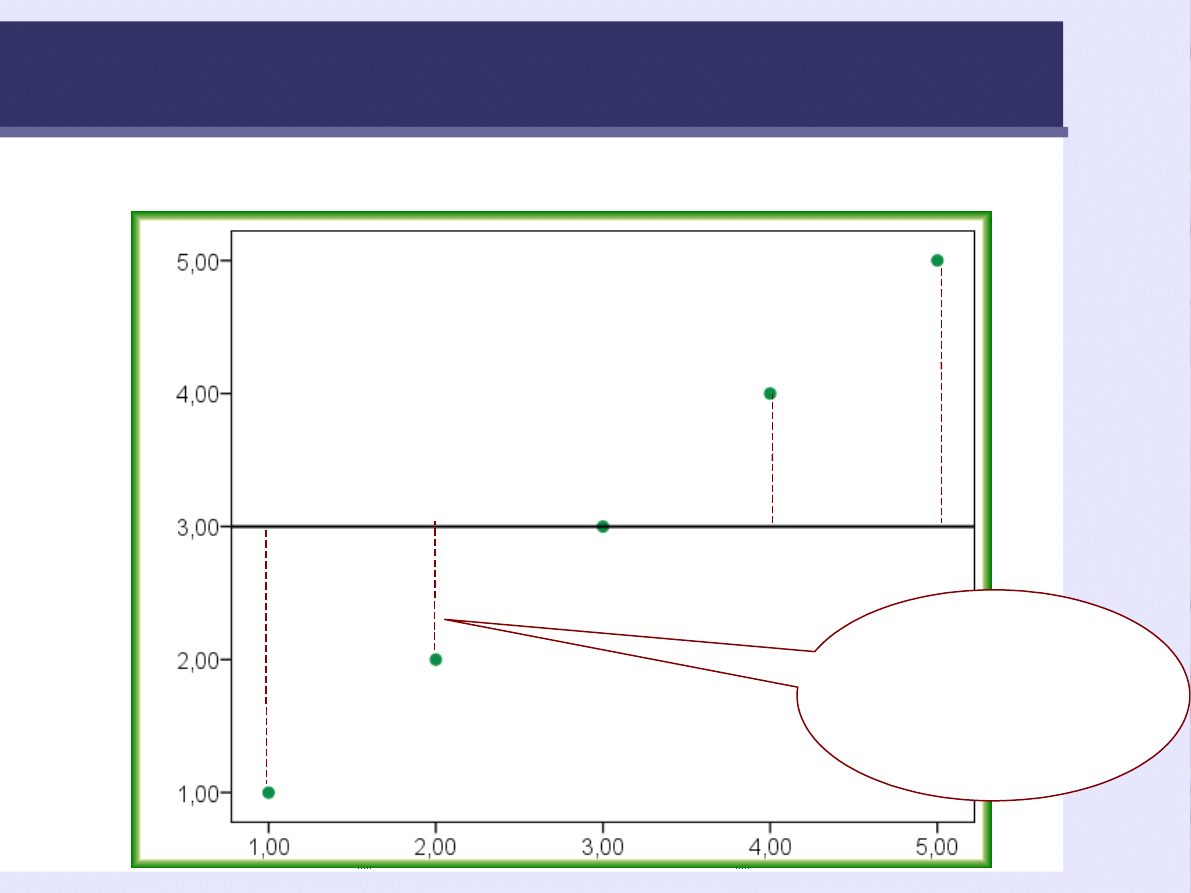
41
Odchylenie od średniej
-2
-1
+1
+2
średnia
Różnica między
wynikiem a
średnią
L
ic
z
b
a
p
rz
y
ja
c
ió
ł
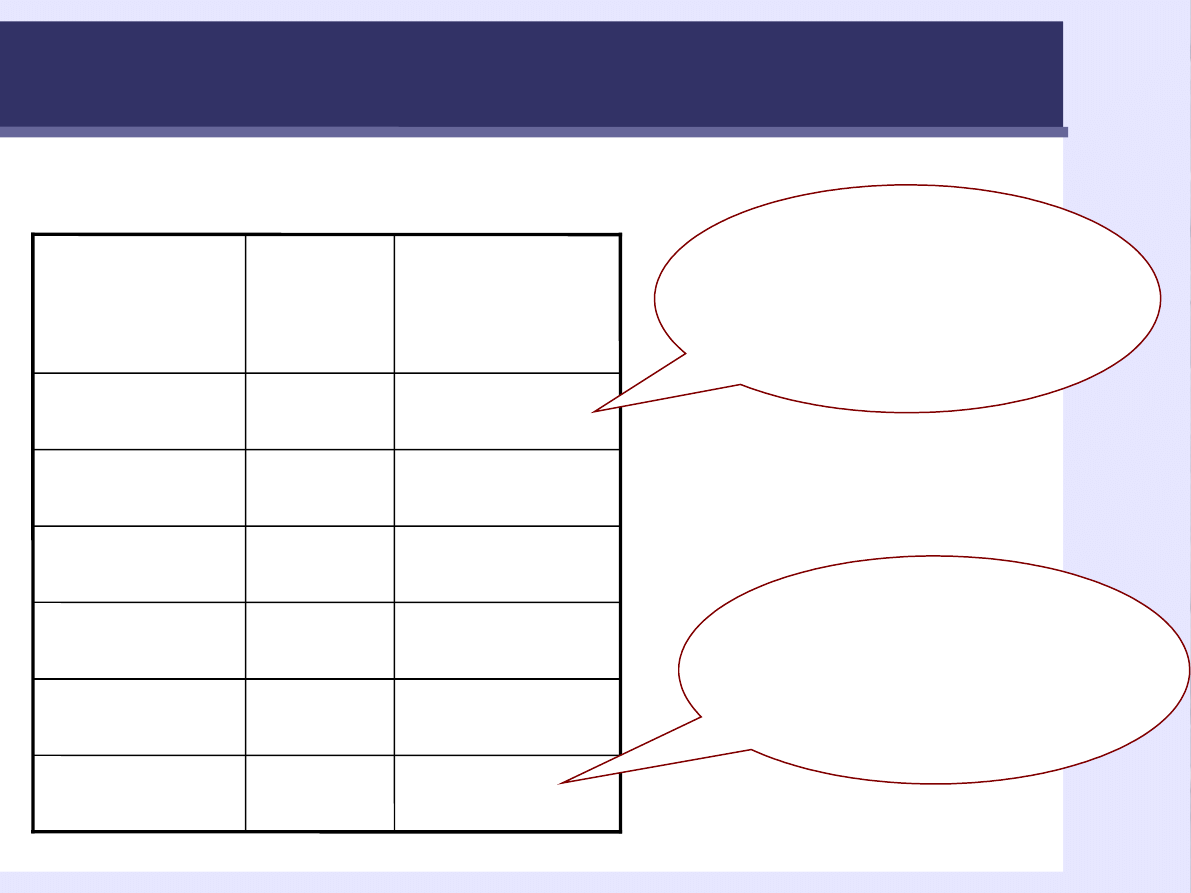
42
Odchylenie od średniej
0
Sum
a:
2
5-3
5
1
4-3
4
0
3-3
3
-1
2-3
2
-2
1-3
1
Różnica
pomiędzy
wynikiem a
średnią
(odchylenie od
średniej)
(x -
M)
Liczba
przyjaciół
W tym wypadku średnia
przecenia tego statystyka
- zawyżyła jego liczbę
przyjaciół o 2.
Dodanie wszystkich
odchyleń zawsze da
wynik zero 0

43
Właśności odchylenia od średniej
4
3
Suma odchyleń wyników od
średniej równa się zero.
Kwadrat sumy odchyleń
wyników od średniej jest
mniejszy niż kwadrat sumy
odchyleń wyników od
jakiekolwiek liczby (a)

44
Suma kwadratów (ss)
Liczba
przyjaciół
Odchylenie
od średniej
Podniesione
do kwadratu
1
-2
4
2
-1
1
3
0
0
4
1
1
5
2
4
Suma:
10
SS jest miarą
rozproszenia wokół
średniej – jest to miara
dokładności modelu
opartego o średnią
Niestety jest to miara
zależna od ilości danych
jakie zostały
zgromadzone, tzn. od
liczby przypadków.
Im więcej przypadków
tym większe SS.

45
Wariancja (zmienność)
Wariancja (variance) jest to
suma kwadratów odchyleń
wszystkich wyników od
średniej dzielona przez
liczbę wyników
N
M)
(x
=
s
2
2
UWAGA
Jeśli interesuje nas oszacowanie wariancji w populacji, wtedy dzielimy
przez (n-1), (wariancja =2.5)
Jeśli interesujemy się tylko wariancją w próbie: wtedy dzielimy przez n,
(wariancja=2)
Pakiety statystyczne podają z reguły pierwszą opcję
s
2
=
ss
N
…innymi słowy…

46
Problem jednostek pomiaru
Wariancja jest dobrą miara rozproszenia
wyników.
Bardzo często stosowana w analizie wynikach.
Problematyczny może być fakt, że wariancja
jest wyrażona w jednostkach skali na jakiej
dokonywany był pomiar podniesionych do
kwadratu
Aby uniknąć tego problemu często stosuje się
zamiennie miarę nazywaną
odchylenie
standardowe

47
Odchylenie standardowe (s, SD)
Odchylenie standardowe:
Mówi o rozproszeniu wyników wokół średniej
Zawsze kiedy mówimy o średniej należy
wspomnieć też o odchyleniu standardowym
Jego wartość jest ściśle związane z wariancją
Jednostki, w których wyrażane jest SD są takie same
jak oryginalny pomiar
Interpretacja
Interpretacja
Niskie wartości SD informują o tym, że wyniki są bardzo blisko
położone wokół średniej
SD = 0 oznacza, że wszystkie wyniki są takie same
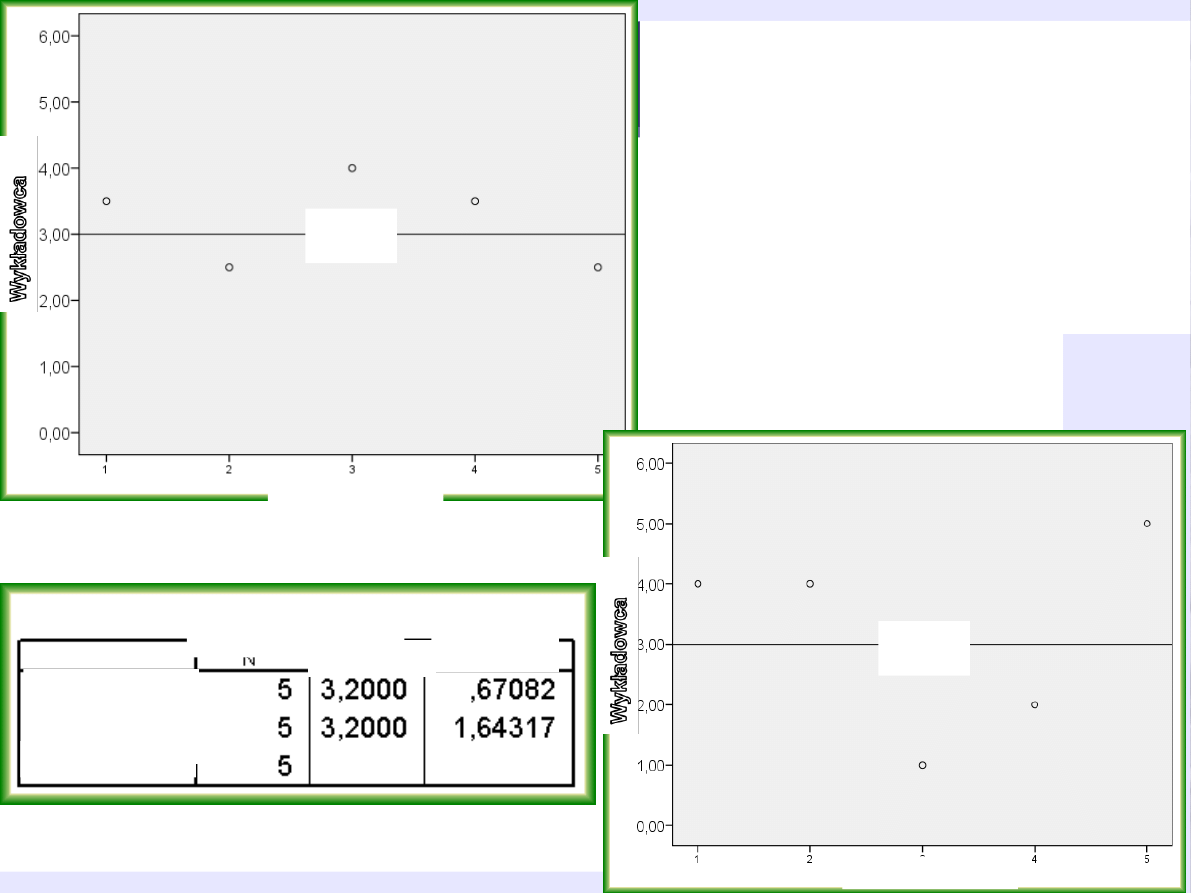
48
Dla pierwszego wykładowcy
jest małe zróżnicowanie
ocen jego wykładów jest
małe
Zróżnicowanie wyników
drugiego jest większe
średnia
SD
Wykładowca
1
Wykładowca
2
N ważne
Statystyki
opisowe
wykład
wykład
średni
a
średni
a

49
Co się stanie jak dodamy stałą do wszystkich
wyników?
Po co to robić?
Gdy mamy skalę np. od -5 do +5
Ponieważ chcemy pozbyć się wartości ujemnych
Jak to wpływa na statystyki opisowe?
Dodanie wartości stałej do wszystkich wyników zmienia
średnią, medianę i dominantę (modalną) o tę wartość.
Nie zmienia wariancji i odchylenia standardowego.
50
Dodajemy stałą do wyników – porównanie statystyk
opisowych
Statystyki
50
50
1
1
3,0600
13,0600
3,0000
13,0000
3,00
13,00
1,28428
1,28428
1,649
1,649
-,056
-,056
,337
,337
-,983
-,983
,662
,662
4,00
4,00
Ważne
Braki danych
N
Średnia
Mediana
Dominanta
Odchylenie standardowe
Wariancja
Skośność
Błąd standardowy skośności
Kurtoza
Błąd standardowy kurtozy
Rozstęp
nastroj1
nastroj10
51
Dodajemy stałą do wyników – porównanie kształtów
rozkładów
0,00
1,00
2,00
3,00
4,00
5,00
6,00
nastroj1
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 3,06
Std. Dev. = 1,28428
N = 50
nastroj1
10,00
11,00
12,00
13,00
14,00
15,00
16,00
nastroj10
0
2
4
6
8
10
12
14
C
zę
s
to
ś
ć
Mean = 13,06
Std. Dev. = 1,28428
N = 50
nastroj10

52
Związki dwóch
zmiennych
53
Zmienne i ich sposoby
reprezentacji
Zmienna pierwsza, np. samoocena:
Zmienna pierwsza, np. samoocena:
Bardzo niska
Niska
Wysoka
Bardzo wysoka
Druga zmienna, np. nastrój:
Druga zmienna, np. nastrój:
Bardzo zły
Zły
Dobry
Bardzo dobry
1
2
3
4
1
2
3
4
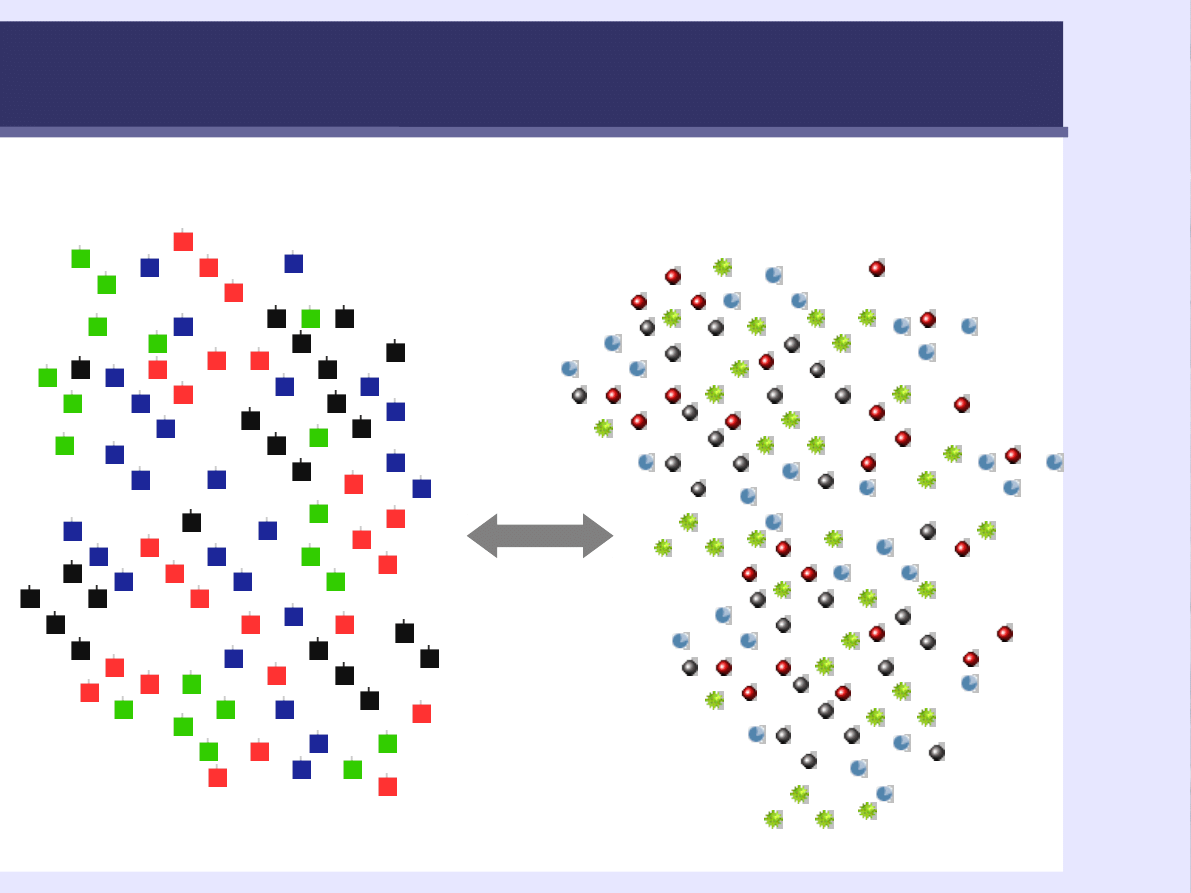
54
Zmienność
?
?
samoocena
samoocena
nastrój
nastrój
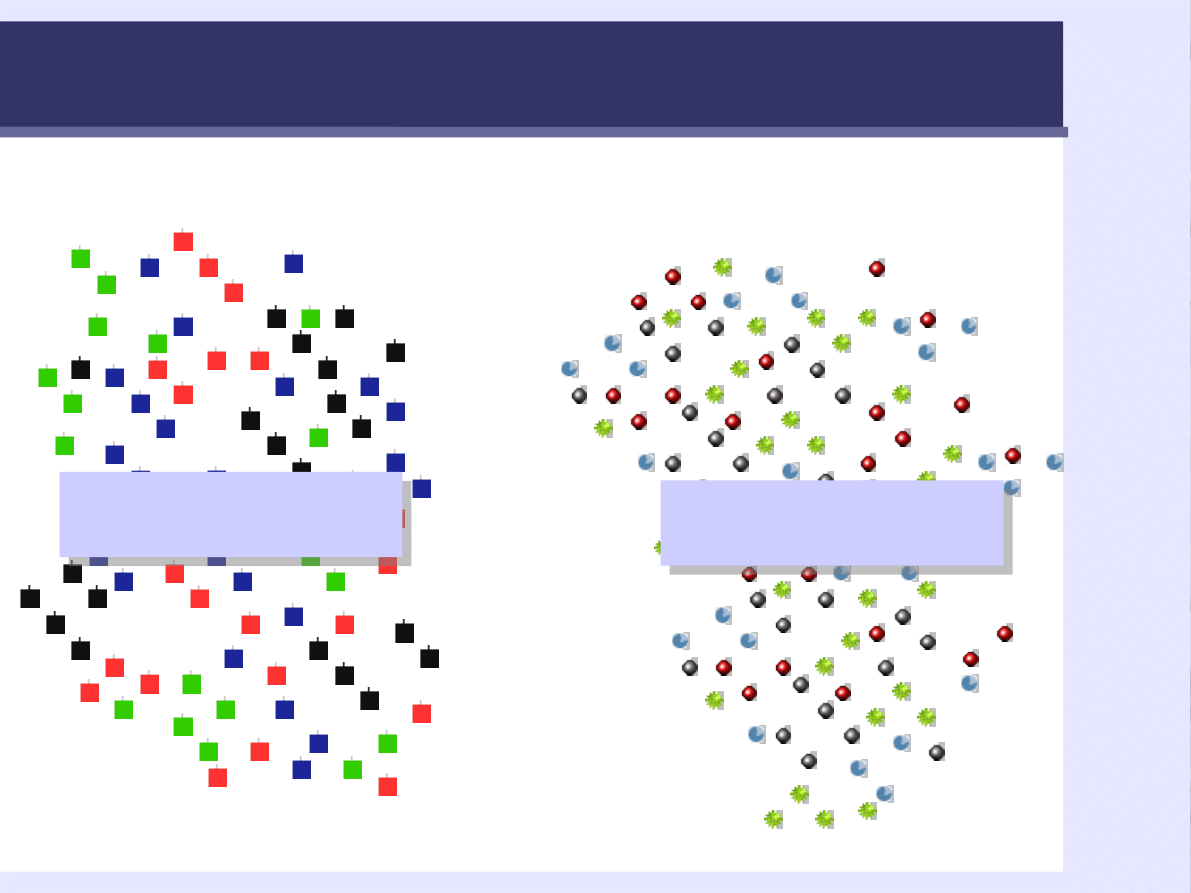
55
Schemat korelacyjny
Pomiar drugiej
zmiennej
Pomiar drugiej
zmiennej
Pomiar pierwszej
zmiennej
Pomiar pierwszej
zmiennej
samoocena
samoocena
nastrój
nastrój
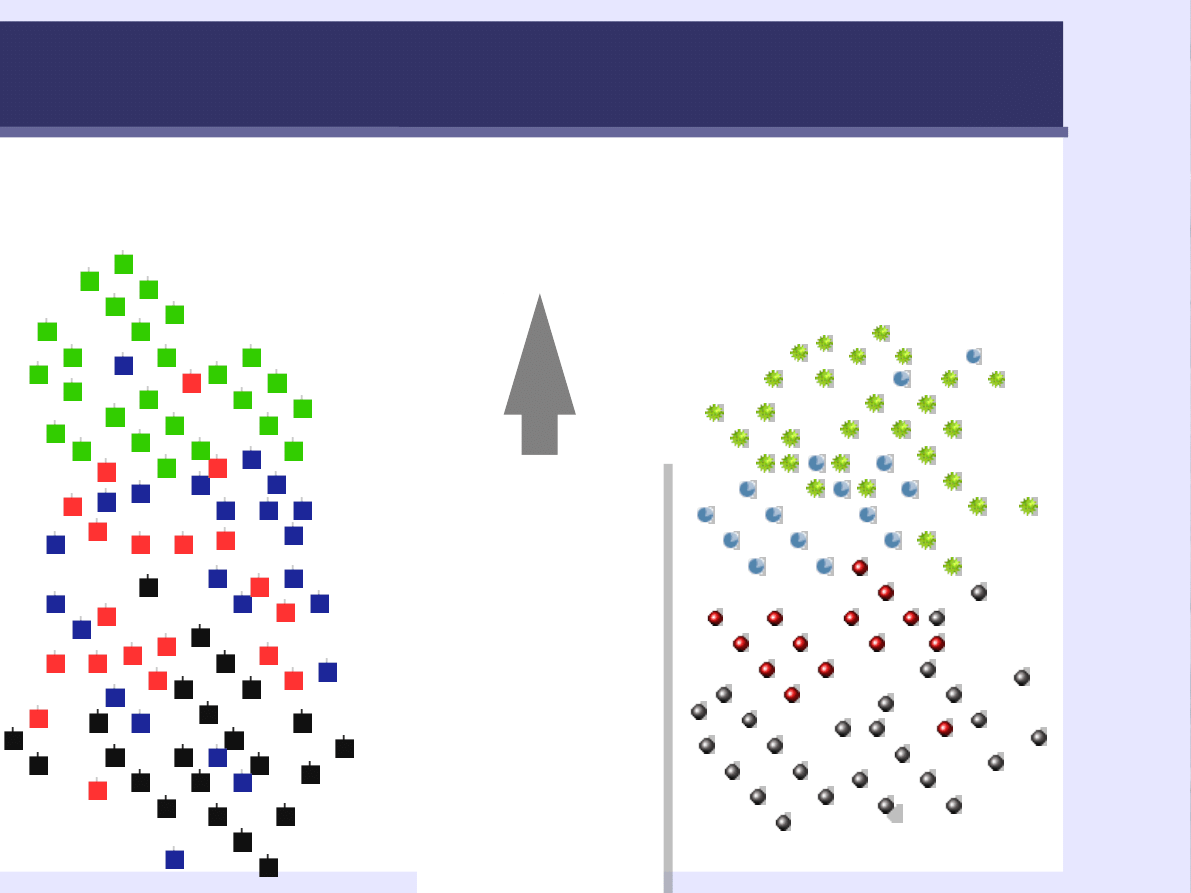
56
współzmienność
Jeżeli
wartość
pierwszej
własności
zmienia się
to wartość
drugiej
zmienia się
w
przewidywa
lny sposób.
Jeżeli
wartość
pierwszej
własności
zmienia się
to wartość
drugiej
zmienia się
w
przewidywa
lny sposób.
samoocena
samoocena
nastrój
nastrój
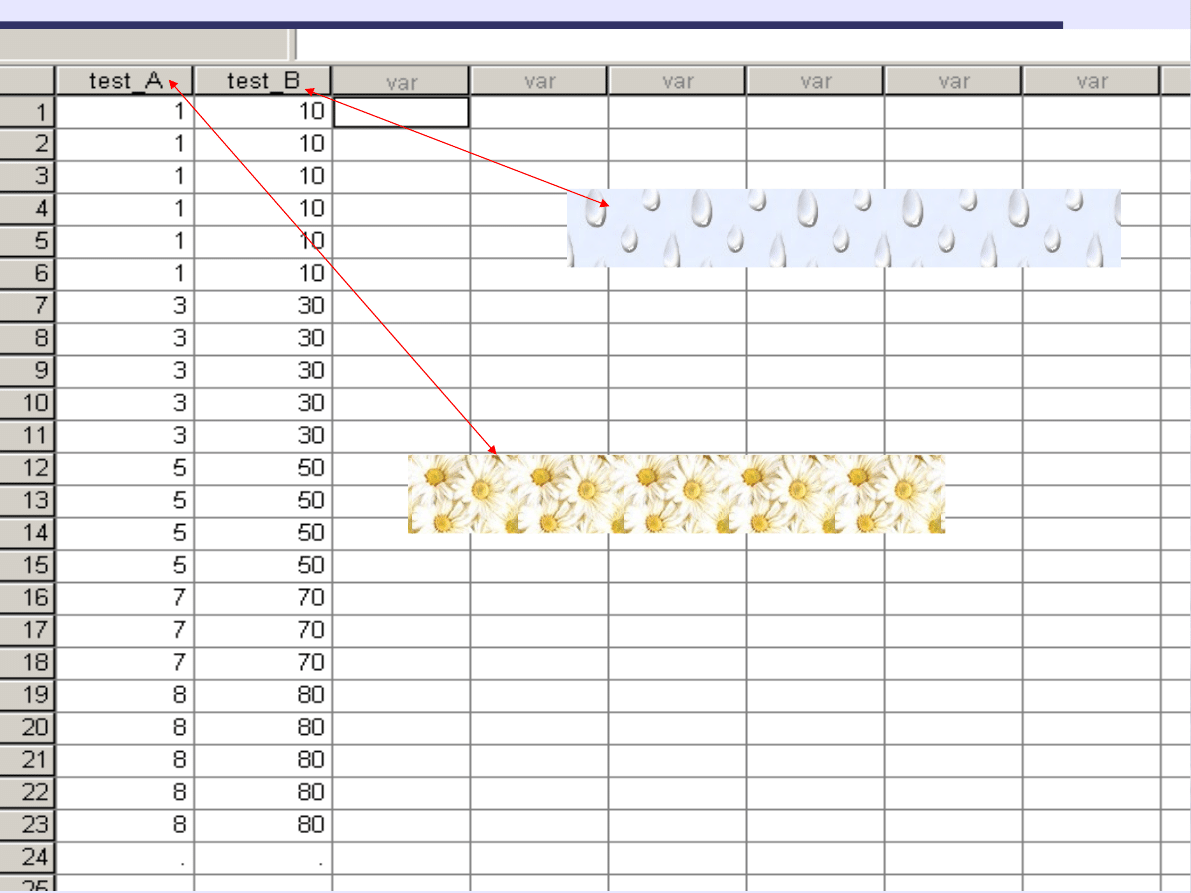
57
Średnia (M)=44,35
Odchylenie standardowe (SD) = 27,44
Średnia (M)=4,43
Odchylenie standardowe (SD) = 2,74
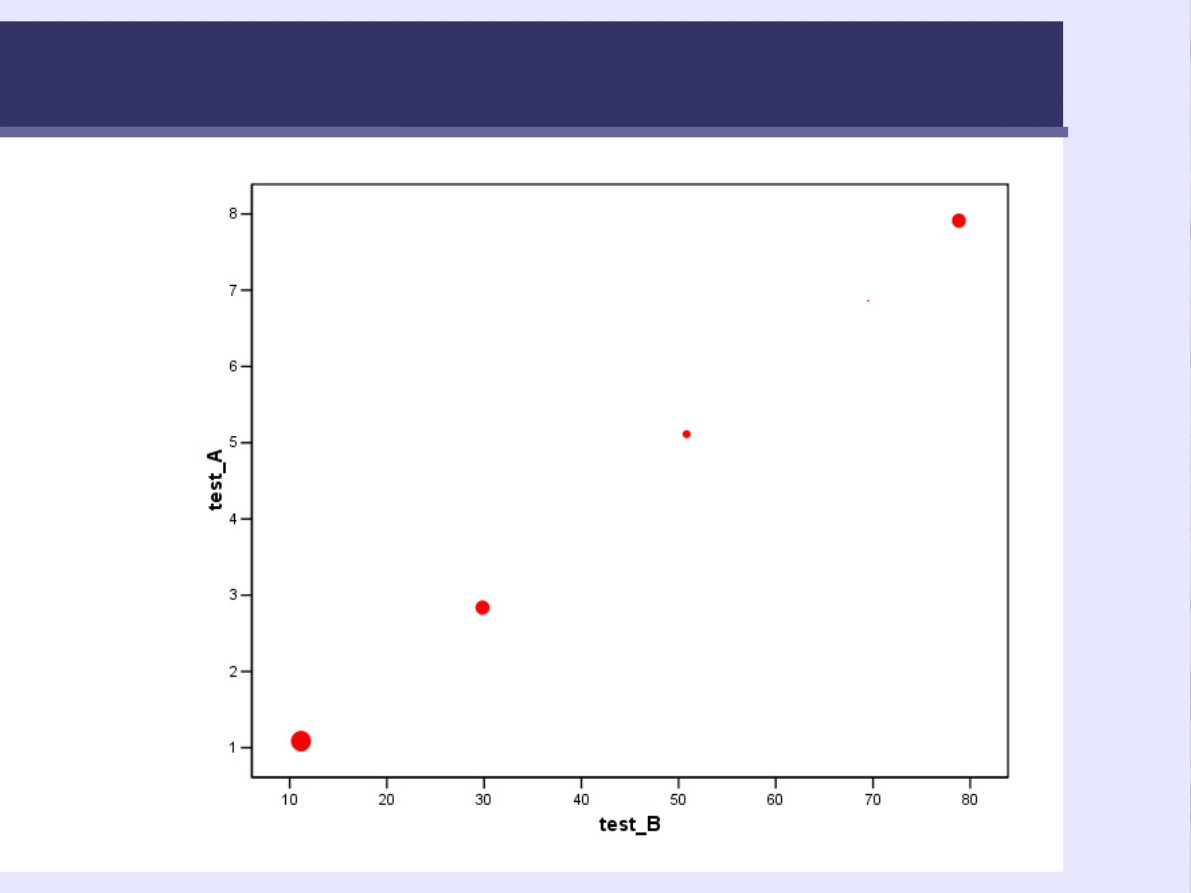
58
Związek między testem A i testem B(Wykres
rozrzutu
)
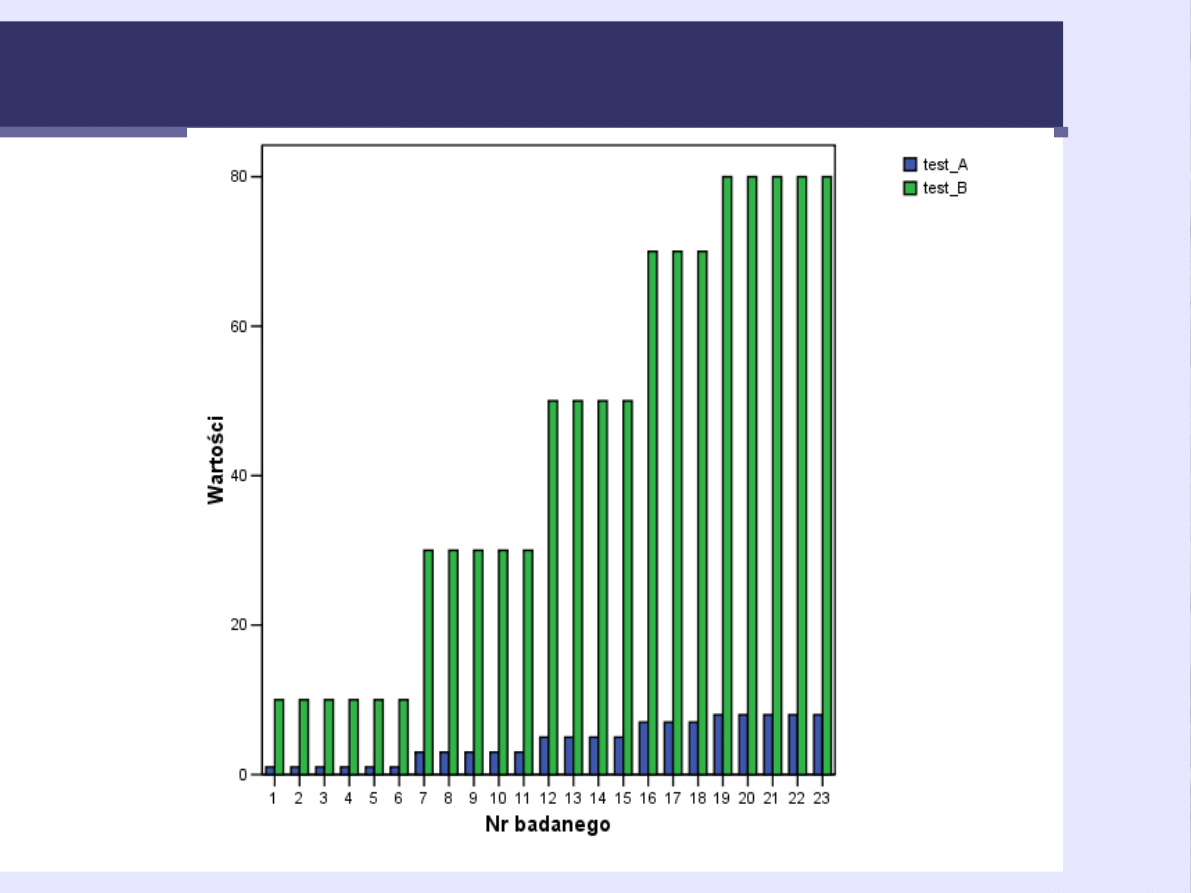
59
Jak zmieniają się wartości surowe w
obu zmiennych

60
Co to oznacza że dwie zmienne korelują ze
sobą?
Oznacza to, że ich wyniki zmieniają się wspólnie
Jeśli zmieniają się wyniki jednej zmiennej, wyniki drugiej
zmieniają się w przewidywalny sposób
Innymi słowy zmienne te są zależne od siebie
Korelacja oznacza liniowy związek dwóch
zmiennych.
Wnioskujemy o współzależności dwóch
zmiennych, a nie o relacjach przyczynowo
skutkowych.

61
Wykres rozrzutu
Zazwyczaj używa się tego rodzaju wykresu do
pokazania współzależności pomiędzy dwoma
zmiennymi
Dwa wymiary pokazujące rozkład wyników dla
dwóch zmiennych
Każdy wymiar pokazuje wartości liczbowe danej
zmiennej
Uwaga: przedstawiamy dane mierzone co
najmniej, na skali przedziałowej
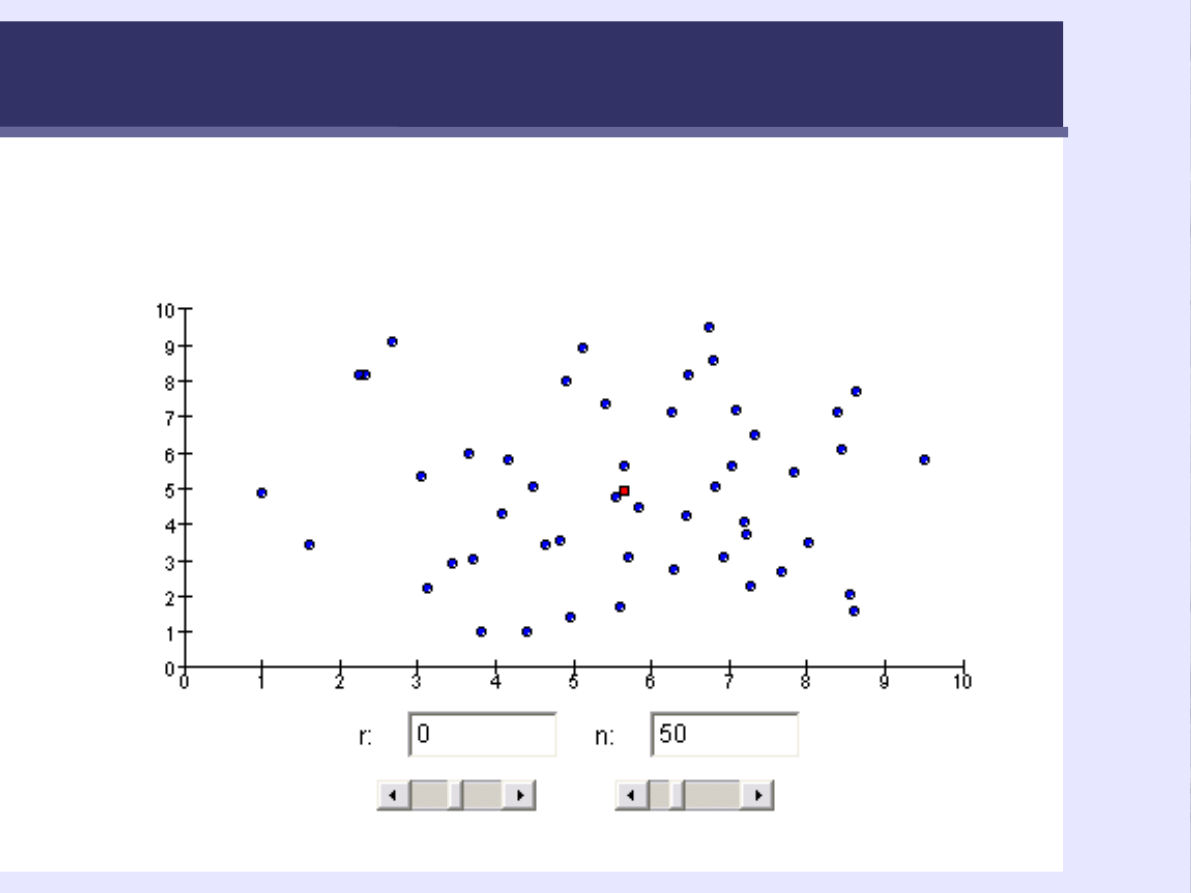
62
Przyjrzyjmy się różnym
związkom dwóch
zmiennych

63
Standaryzacj
a
wyników

64
Wartości standaryzowane
z
W celu:
porównania wyników (mierzonych różnymi
narzędziami) lub
sprawdzenia prawdopodobieństwa uzyskania danego
wyniku
przekształca się wyniki surowe na wyniki
wyrażone
w jednostkach odchylenia
standardowego
są to
wyniki standardowe
czy
standaryzowane
(SPSS).

65
Standaryzacja wyników
Proste przekształcenie liniowe każdego wyniku x w
z:
Wartość standaryzowana “z” danego wyniku =
wynik surowy (x) minus średnia (M) dzielone przez
odchylenie standardowe (SD)
Każdy
pojedynczy
wynik x
zmieniam na z
z=
x− M
SD
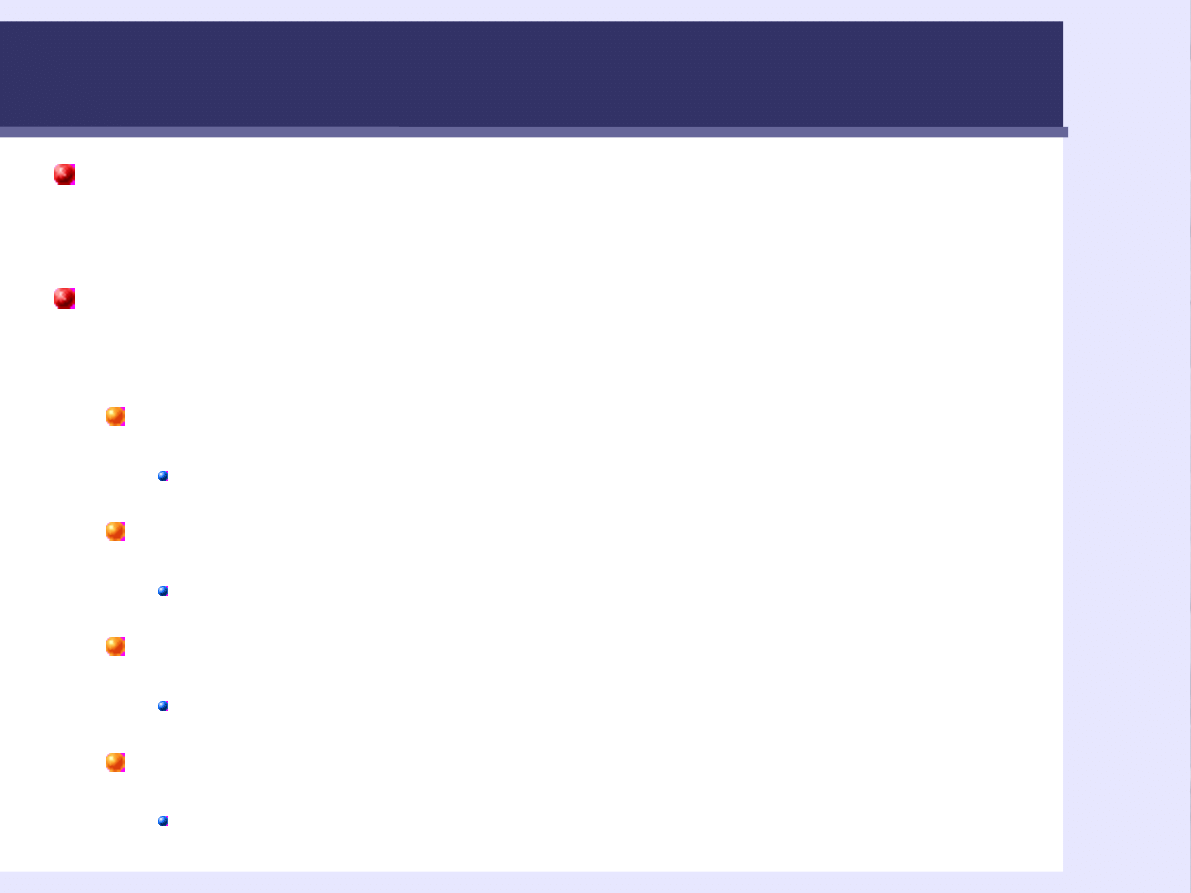
66
Właściwości wyników standaryzowanych “z” dla
próby
Średnia z danych wystandaryzowanych
jest równa 0
Wariancja i odchylenie standardowe dla
danych wystandaryzowanych są równe 1
wyniki dokładnie równe średniej
są równe zeru
wartości „z” zbliżone do średniej
są bliskie wartości “0”
wartości “z” mniejsze od średniej
są ujemne
wyniki “z” większe od średniej
są dodatnie
67
Ćwiczenie
Hrabina Zenobia de’Ouhę w teście
znajomości zasad savoir-vivre otrzymała 20
punktów
(średnia w badanej grupie hrabin wyniosła 25,
odchylenie standardowe 5).
Natomiast w teście teoretycznej wiedzy o
tańcach towarzyskich dostała 5 punkty
(średnia w grupie wyniosła 3, odchylenie
standardowe 2)
Na czym hrabina zna się lepiej?
Materiały do wykładu: Krzysztof Krejtz,
SWPS

68
odpowiedź
Widać, że hrabinie
lepiej wychodziło
tańczenie niż dobre
obyczaje
Materiały do wykładu: Krzysztof Krejtz,
SWPS

69
Współczynnik r-Pearsona
70
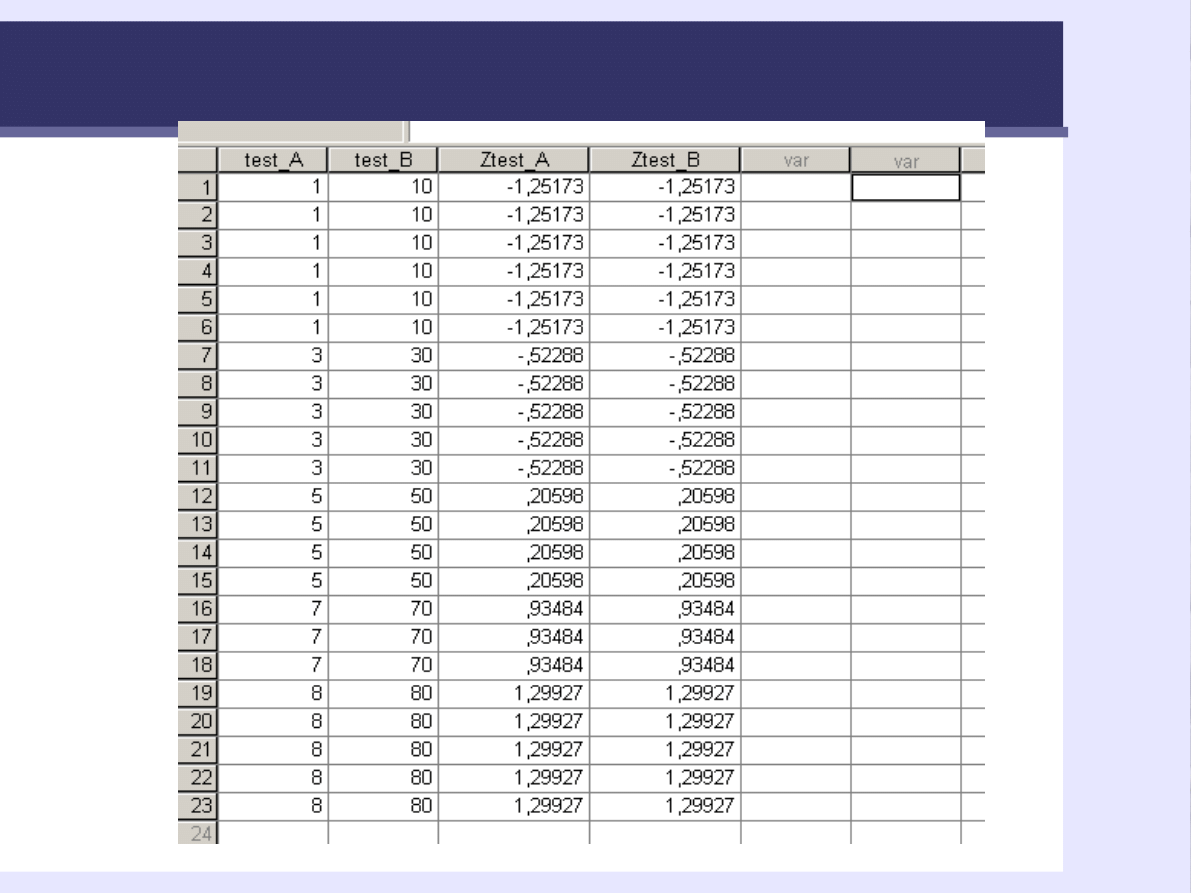
Wyniki standaryzowane zmiennych test
A i test B
71
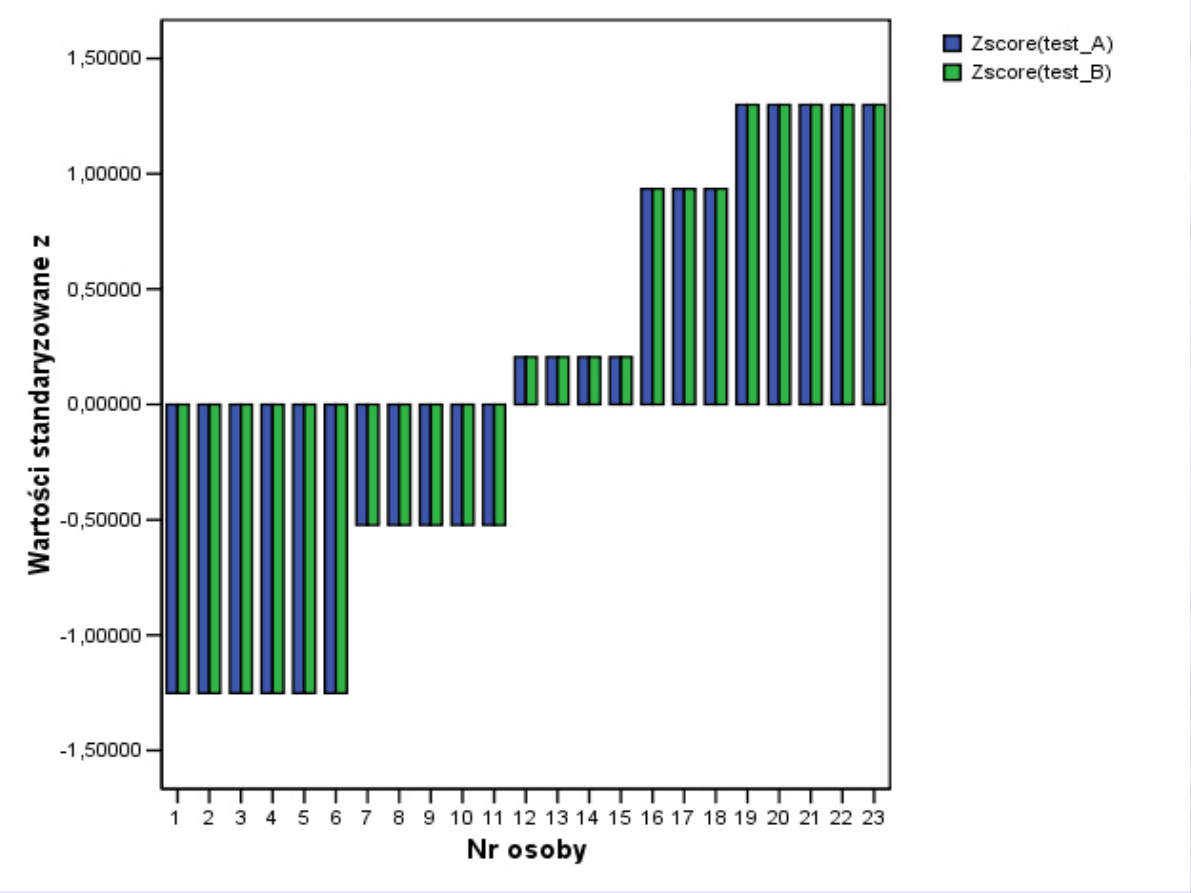
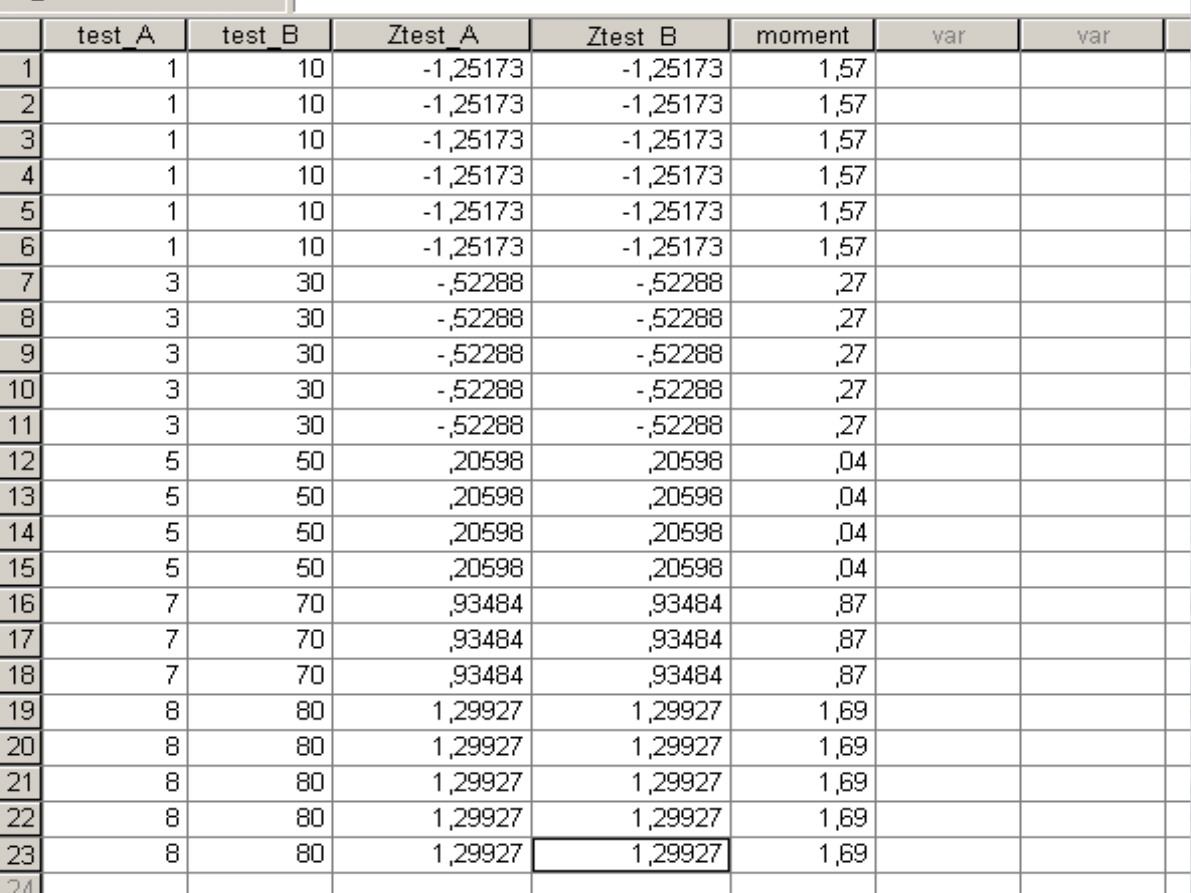
Jak zmieniają
się wartości
standaryzowan
e obu
zmiennych
72

73
współczynnik r-Pearsona
1
N
Z
Z
=
r
x
y

74
Kolejne kroki obliczania współczynnika r-
Pearsona
Wszystkie wyniki na obu skalach zamieniamy na z
(na podstawie odpowiednich średnich i odchyleń
standardowych)
Mnożymy wartości z obu zmiennych
Dodajemy iloczyny do siebie
Dzielimy przez liczbę obserwacji minus 1
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
Wyszukiwarka
Podobne podstrony:
Metodologia - SPSS - Zastosowanie komputerów - Lipiec - Statystyki, Metodologia - SPSS - Zastosowani
korelacje, Statystyka i metodologia(1)
Statystyka i metodologia 1
metodologia ćw4 notatki z literatury, Statystyka i metodologia(1)
opracowanie wykładów statystyka z metodologią
testowanie hipotez, Statystyka i metodologia(1)
Metodologia ze statystyką - Test - Sędek, Statystyka i metodologia(1)
HANDOUT (3), Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Metodologia ze statystyką, Metodol
Metodologia kog-pyt. i odp, Statystyka i metodologia(1)
Handout (2), Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Metodologia ze statystyką, Metodol
Quiz 1. skale i zmienne, Statystyka i metodologia(1)
Laboratorium 4 statystyka, Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Metodologia ze staty
testy t, Statystyka i metodologia(1)
pytania egzamin statystyka 2, Metodologia badań psychologicznych i STATYSTYKA
Metodologia kog-pyt i odp, Statystyka i metodologia(1)
Metodologia - SPSS - Zastosowanie komputerów - Lipiec - Testz statystyczne, Metodologia - SPSS - Zas
więcej podobnych podstron