Podstawowe elementy podejścia Naukowego

• Obiektywny pomiar zjawiska, które nas interesuje

• Kontrola czynników mogących zakłócić pomiar

• Zdolność weryfikowania pomiarów: własnych oraz tych dokonanych przez innych badaczy

Dwa typy nauk

• Nauki formalne: wnioskowanie dedukcyjne, niezawodność wnioskowania, Np. matematyka.

• Nauki empiryczne: wnioskowanie indukcyjne, Np. biologia, psychologia.

Wnioskowanie indukcyjne - przykładowe typy

Generalizacja:

• Proporcja Q z próby ma cechę A

Dlatego

• Proporcja Q z populacji ma cechę A.

Sylogizm statystyczny:

• Proporcja Q z populacji P posiada pewien cechę A

• Jednostka I jest członkiem populacji P

Dlatego

• Istnieje prawdopodobieństwo Q, że I posiada cechę A.

Wybór schematu badawczego

Ogólny plan prowadzenie badania, który specyfikuje:

• Dobór próby:, w jaki sposób wybiorę osoby z populacji do mojego badania

• Przydział do warunków badawczych:, w jaki sposób podzielę moje osoby na grupy badawcze (o ile w ogóle to mi będzie potrzebne)

• Typy zmiennych, jakie uwzględnione zostaną w badaniu: niezależnych, zależnych oraz kontrolowanych

• Sposób zbierania danych.

Zmienne: w eksperymencie i badaniach różnicowych

• Zmienna niezależna - zmienna, którą manipulujemy, oddziałuje na inną zmienną; (przyczyna). Musi posiadać, co najmniej dwa poziomy (dwie wartości).

- Zmienna niezależna nie manipulowana = zmienna grupująca w badaniach różnicowych (płeć, porównanie schizofreników i zdrowych)

• Zmienna zależna - jej wartości podlegają oddziaływaniom innych zmiennych (niezależnych i zakłócających); (skutek).

• Zmienne uboczne - zmienne kontrolowane oraz zmienne zakłócające.

Operacjonalizacja - Z poziomu opisu teoretycznego przechodzimy na poziom empirii.

=> tworzenie/ dobór wskaźników do pomiaru zmiennych.

=> określenie narzędzi pomiarowych oraz procedur pomiaru.

Wskaźniki

• Indicatum - to, na co wskaźnik wskazuje

• Moc zawierania - na ile wskaźnik obejmuje wszystkie obiekty indicatum

• Moc odrzucania - w jakim stopniu wskaźnik obejmuje tylko obiekty należące do indicatum

Moc zawierania vs moc odrzucania

• Wskaźnik ma doskonałą (=1) moc zawierania,

Jeżeli w zakresie wskazywanym przez wskaźnik znalazły się wszystkie obiekty należące do indicatum (nawet, jeżeli znalazły się tam inne obiekty

• Wskaźnik ma doskonałą (=1) moc odrzucania,

Kiedy wszystkie obiekty wskazane przez wskaźnik nalezą do indicatum (nawet, jeżeli nie wszystkie obiekty, indicatum są objęte wskaźnikiem)

Skale pomiarowe

Różni je stopień dokładności pomiaru

- Zmienne ciągłe - najbardziej precyzyjny pomiar

• Mogą przyjmować każdą wartość w ramach określonego przedziału Np. 1 minuty

- Czas reakcji w teście Stroopa Np. 1,03 sekundy

- Temperatura

- Zmienne dyskretne - przyjmują konkretne wartości z przedziału

- Oceny atrakcyjności na skali od 0-10, wynik w skali depresji Becka

- Zmienne kategorialne - wartości przyporządkowane konkretnym kategoriom

- Płeć - 2 kategorie

- Zawód - lekarz, nauczyciel,......

Skale pomiarowe

• Nominalna (kategorialna)

• Porządkowa (rangowa)

• Przedziałowa (interwałowa)

• Stosunkowa (ilorazowa)

Schemat Korelacyjny

W schemacie korelacyjnym mówimy o

• Współzmiennych lub zmiennych współwystępujących.

• Czasami na podstawie jednej zmiennej możemy przewidywać wartości drugiej. Wówczas zmienne te nazywamy odpowiednio:

• Predyktorem lub zmienną niezależną = zmienna na podstawie, której przewidujemy.

• Zmienną zależną = zmienna, której wartości są przewidywane.

• Nie możemy powiedzieć, która zmienna jest przyczyną, a która skutkiem.

• Poziom wnioskowania opiera się o współzmienność.

• Mówimy o tym, że zmienne zmieniają swoje wartości w przewidywalny sposób.

Schemat Różnicowy

• Interesujemy się wpływem wcześniej wybranych cech, zdarzeń naturalnych na interesujące nas zjawiska.

• Możemy patrzeć jak czynniki zdeterminowane genetycznie takie jak płeć, czy zmienne osobowościowe np. introwersja vs. ekstrawersja różnicują osoby pod względem zachowań, postaw, etc.

• Warunki poprzedzające pomiar interesującego nas zachowania nie podlegają manipulacji.

• Nie można interpretować uzyskanych danych w kategoriach przyczynowo - skutkowych.

• Tak jak w badaniach korelacyjnych możemy sprawdzać związek między interesującymi nas zmiennymi

Schemat Eksperymentalny

• Weryfikacja hipotez przyczynowo-skutkowych

• Najważniejsze cechy eksperymentów:

• Manipulacja zmienną niezależną

• Randomizacja II stopnia

• Kontrola zmiennych ubocznych

• Trafność wewnętrzna - kontrola zmiennych niezależnych i ubocznych, losowy przydział badanych do grup eksperymentalnych.

• Trafność zewnętrzna - stopień, w jakim wyniki badania mogą być generalizowane na inne sytuacje i populacje. Powtarzalność i realizm sytuacyjny.

Plan dla grup niezależnych

• Jeżeli wykonujemy badanie w planie dla grup niezależnych - schemat różnicowy lub eksperymentalny powinniśmy pamiętać o:

• Równej liczbie osób na każdym poziomie wszystkich zmiennych niezależnych.

• Łatwiej poddać analizie takie dane i łatwiej zinterpretować wyniki

• Uwaga: zwiększając plan o dodatkową zmienną lub poziom odpowiednio zwiększamy liczbę osób wymaganych w próbie: 2x2 3x3 2x2x2

Plan dla grup zależnych

• Jedna grupa badanych

• Wielokrotny pomiar tych samych zmiennych

• Manipulacja zmienną niezależną pomiędzy pomiarami

• Efekt wprawy - Pojawia się, jeżeli używamy tego samego narzędzie kilkukrotnie

• Badani często pamiętają swoje odpowiedzi z poprzedniego badania

• Efekt zmęczenia - gorsze wyniki w późniejszych pomiarach mogą być spowodowane zmęczeniem samym badaniem.

• Efekt kolejności pomiarów - Wyniki jednego pomiaru mogą wpłynąć na wyniki

pomiaru drugiego.

• Efekt zmiany badanych w czasie - nie zależny od manipulacji. Zbyt długie przerwy między pomiarami.

Rozkład częstości - pokazuje jak często każdy wynik się pojawił w zbiorze danych.

• Jest to podsumowanie kategorii odpowiedzi w badanej zmiennej.

• Rozkładem częstości jest każde uporządkowanie danych, które pokazuje częstość występowania różnych wartości zmiennej lub częstość wartości należących do grup zmiennej

Miary tendencji centralnej

• średnia,

• mediana,

• modalna lub dominanta lub moda

Miary rozproszenia wyników

• zakres,

• wariancja,

• odchylenie standardowe

Kształt rozkładu wyników

• skośność (Większość wyników gromadzi się po jednej stronie średniej)

• kurtoza

Średnia

• Przy jej obliczaniu bierzemy pod uwagę wszystkie wyniki

• Wykorzystywana w wielu testach statystycznych

• Wady:

• Reprezentując wszystkich - może mówić o nikim

• Często jej wartość nie występuje w wynikach (średnia liczba dzieci w domach 2.3??)

• Jest wrażliwa na dewiantów - skrajne wyniki

Mediana

• Me - to wartość, która znajduje się w środku wszystkich wartości.

• Aby ustalić Me trzeba uporządkować wyniki.

• Medianę oblicza się najczęściej wtedy, gdy pojawiają się bardzo nietypowe wyniki

Modalna

• Jest to najczęściej pojawiająca się wartość wśród wyników uczestników badania, też tak jak medianę najłatwiej ją dostrzec po uporządkowaniu wyników

• Relatywnie rzadko stosowana w psychologii

• Wady:

• Może w ogóle nie wystąpić w wynikach (jeśli nie ma co najmniej dwóch takich samych wyników) 3, 4, 5, 6, 7, 8 - nie ma modalnej

• Może być dwie i więcej modalnych, jeśli więcej wyników powtarza się 2, 2, 4, 5, 6, 6, - 2 i 6 to modalne - rozkład wyników dwumodalny

• Może też nie odzwierciedlać prawdziwego obrazu danych

Zakres

• Jest rozumiany jako różnica między największym i najmniejszym pomiarem

Suma kwadratów (ss)

• Wzór => ss=Σ(x−M)²

• SS jest miarą rozproszenia wokół średniej - jest to miara dokładności modelu opartego o średnią

• Niestety jest to miara zależna od ilości danych, jakie zostały zgromadzone, tzn. od liczby przypadków. (Im więcej przypadków tym większe SS.)

Wariancja

• Wzór => s²=[Σ(x−M)²] / N lub s²=ss / N

• Wariancja (variance) jest to suma kwadratów odchyleń wszystkich wyników od średniej dzielona przez liczbę wyników

• Uwaga

• Jeśli interesuje nas oszacowanie wariancji w populacji, wtedy dzielimy przez (n-1), (wariancja =2.5)

• Jeśli interesujemy się tylko wariancją w próbie: wtedy dzielimy przez n, (wariancja=2)

• Wariancja jest dobrą miara rozproszenia wyników.

• Bardzo często stosowana w analizie wynikach.

• Problematyczny może być fakt, że wariancja jest wyrażona w jednostkach skali, na jakiej dokonywany był pomiar podniesionych do kwadratu

Odchylenie standardowe (s, SD)

• Wzór => SD= √s²

• Mówi o rozproszeniu wyników wokół średniej

• Zawsze, kiedy mówimy o średniej należy wspomnieć też o odchyleniu standardowym

• Jego wartość jest ściśle związane z wariancją

• Niskie wartości SD informują o tym, że wyniki są bardzo blisko położone wokół średniej

• SD = 0 oznacza, że wszystkie wyniki są takie same

Kurtoza

• Określa stromość rozkładu częstości.

• Odnosi się do stopnia, w jakim wyniki są gromadzą się na krańcach rozkładów

• Innymi słowy odpowiadamy na pytanie jak płaski lub spiczasty jest rozkład wyników.

• Jeżeli jeden rozkład jest bardziej stromy (spiczasty) niż drugi mówi się, że jest bardziej leptokurtyczny.

• Jeżeli natomiast jest mniej stromy to mówi się, że jest bardziej platykurtyczny.

• Rozkład normalny określa się jako mezokurtyczny.

Punkty podziału uporządkowanego rozkładu wyników

• Mediana - dzieli uporządkowany rozkład wyników na 2 równe części (po 50%).

• Kwartyle - dzielą uporządkowany rozkład wyników na 4 równe części (po 25 %).

• Decyle - dzielą uporządkowany rozkład wyników na 10 równych części (po 10%).

• Percentyle - dzielą uporządkowany rozkład wyników na 100 równych części (po 1%).

Rozkład Normalny

• Kształt rozkładu wielu zmiennych, które mierzą psychologowie ma kształt mniej więcej symetryczny, przypominający dzwon.

• W populacji wiele zmiennych psychologicznych przyjmuje rozkład normalny

• Popularny w przyrodzie

Wartości standaryzowane

• W celu:

- porównania wyników (mierzonych różnymi narzędziami) lub

- sprawdzenia prawdopodobieństwa uzyskania danego wyniku

Przekształca się wyniki surowe na wyniki wyrażone w jednostkach odchylenia standardowego są to wyniki standardowe czy standaryzowane (SPSS).

• Wzór => z = (x-M) / SD

Duża próba - lepsze oszacowanie populacji, mniejszy błąd, lepsza reprezentacja populacji

(Średnia z tej próby - dobre oszacowanie średniej w populacji)

Mała próbka - większe prawdopodobieństwo błędu, możemy uzyskać wyniki z krańców

(Średnia w tej próbie byłaby zdecydowanie większa/mniejsza od średniej w populacji, duży błąd próby)

Prawo wielkich liczb - Zwiększając wielkość próby zmniejszamy prawdopodobieństwo

wystąpienia błędu próby

Teoretyczny rozkład średnich z próby

• Losujemy z populacji możliwie wiele prób ze zwracaniem

• Liczymy dla każdej próby średnią

• Średnie te traktujemy jako dane i obliczamy statystyki rozkładu

• Średnia ze średnich z tych prób byłaby bliska rzeczywistej średniej w populacji

• Co więcej rozkład z tych prób jest bliski normalnemu

Centralne Twierdzenie Graniczne - Wraz ze wzrostem liczebności prób, niezależnie od

kształtu rozkładu w populacji, rozkład z próby średnich zbliża się do normalnego ze średnią m i wariancją s2/N

Etapy testowania hipotez

• Stawiamy hipotezę badawczą

• Zbieramy dane

• Stawiamy hipotezę zerową

• Konstruujemy rozkład prawdopodobieństwa otrzymania takiego wyniku przy założeniu, że hipoteza zerowa jest prawdziwa

• Porównujemy wynik uzyskany z rozkładem

• Znajdujemy prawdopodobieństwo uzyskania takiego wyniku

• Podejmujemy decyzję o odrzuceniu bądź nie hipotezy zerowej (H0).

Jak niskie musi być prawdopodobieństwo, aby odrzucić H0

• Odrzucamy hipotezę zerową, jeśli prawdopodobieństwo uzyskania takiego wyniku jest, co najmniej p≤0,05; p≤0,01 (lepiej); p≤0,001 (najlepiej).

• Często nazywane jako

- obszar odrzucenia,

- poziom istotności

Testy t dla prób zależnych

• Porównywanie średnich dla 1 grupy badanych (dwukrotny pomiar tych samych osób)

• Stosowany w eksperymentach w planie dla grup zależnych oraz badaniach z powtarzanym pomiarem

• Weryfikacja hipotezy zerowej o braku różnic między średnimi w badaniu z powtarzanym pomiarem

• Np. u tej samej grupy osób sprawdzamy poziom samooceny przed i po manipulacji

Testy t dla prób niezależnych

• Porównywanie średnich dwóch grup badanych (różne osoby w każdym z warunków)

• Stosowane w badaniach w schemacie różnicowym i eksperymentach w planie dla grup niezależnych

• Testowanie hipotezy zerowej o braku różnic między średnimi w porównywanych populacjach

• Np. porównujemy poziom samooceny w grupie, która miała prezentację bodźców z poziomem samooceny w grupie bez manipulacji

Test t dla jednej próby - służy do porównywania średniej w próbie do określonej znanej

wartości np. znanej średniej w populacji

Stopnie swobody (df)

• Liczba stopni swobody to liczba wartości zmiennej, które mogą się zmieniać przy ograniczeniach nałożonych na dane.

• Związana z oszacowywaniem odchylenia standardowego w populacji na podstawie próby

• Liczba stopni swobody jest równa liczbie wyników minus liczba parametrów, która musi być oszacowana „po drodze” podczas oszacowywania docelowego parametru.

Test homogeniczności wariancji - test Levene'a

• Test ten mówi nam czy wariancje w naszych grupach są podobne

• Aby pojąć decyzję patrzymy na poziom istotności dla testu Levene'a

• Jeśli p>0,05 - wtedy nie ma różnic między wariancjami (nie odrzucamy hipotezy zerowej testu Levene'a)

• Jeśli p<0,05 - wówczas istnieje istotna statystycznie różnica między wariancjami w porównywanych grupach

• Wynik testu Levene'a determinuje, z którego wiersza odczytamy wyniki naszego testu t

• Jak test Levene'a nie jest istotny czytamy z wiersza,w którym mamy założenie o równości wariancji (górny)

• Jeśli test nie jest istotny czytamy z dolnego wiersza

Podając wyniki testu

• Pamiętajmy o podaniu stopni swobody i poziomu, na jakim są istotne nasze wynik oraz o interpretacji uzyskanego wyniku w odniesieniu do postawionej hipotezy

t(df)=wynik testu; p<0,05 (lub inny poziom istotności) lub n.i.

Od czego zależy wielkość testu t?

• Wielkości różnic (między średnimi lub między średnią a kryterium)

• Im większa różnica, tym większa może być wartość testu

• Wielkości wariancji dla rozkładu różnic:

• Im mniejsza wariancja tym większa może być wartość testu

• Wielkości próby:

• Im większa próba tym większa może być wartość test

Test Stroopa (1935)

• Uczestnik badania proszony jest o jak najszybsze nazwanie koloru czcionki jakim jest napisane słowo, ignorując jednocześnie jego znaczenie

• STÓŁ CZERWONY

• TRAWA ZIELONY

• Stroop (1935b) zauważył, że dłużej zajmuje osobom nazwanie koloru słowa, zwłaszcza jeśli jest ono konkurencyjną nazwą koloru

• Główne zadanie na nazywanie koloru zostało spowolnione przez konkurencyjny automatyczny proces odczytywania znaczenia słowa

Emocjonalny test Stroopa

• Głównym zadaniem badanych jest nazwanie koloru słów, które nasycone są afektem pozytywnym bądź negatywnym.

• Dłuższy czas reakcji przy słowach negatywnych, specyficznie odnoszących się do problemu.

• Pozwala na uchwycenie specyfiki przetwarzania treści afektywnych zarówno w przypadku zaburzeń emocjonalnych, jak i postaw społecznych, zwłaszcza silnie nasyconych negatywnymi odczuciami (uprzedzenia).

Kowariancja

• Miara współzmienności

• Jak obliczyć kowariancję?

• Sprawdzamy, jak wyniki każdej zbadanej osoby odchylają się od średniej (X - M) dla każdej zmiennej.

• Dla obu zmiennych mnożymy przez siebie te odchylenia - dla każdej osoby

• Dodajemy wyniki mnożenia.

• Sumę dzielimy przez liczbę osób minus jeden (N-1)

• Jeżeli wartość kowariancji jest duża i dodatnia świadczy o tym, że ludzie, którzy mieli niskie wyniki w pierwszej zmiennej mają również niskie wyniki w drugiej.

• Jeżeli wartość kowariancji jest negatywna to świadczy to że…

• Kowariancja równa zero (0) pokazuje, Że nie ma związku między zmiennymi.

• Nie bierze pod uwagę wielkości wariancji zmiennych pod uwagę.

• Wysoka wariancja jednej lub obu zmiennych będzie duża skutkuje wysokimi wskaźniki kowariancji niezależnie od rzeczywistej siły związku obu zmiennych.

• Dlatego do sprawdzenie siły związku oraz porównań dwóch związków bierzemy pod uwagę współczynniki korelacji.

Co to oznacza że dwie zmienne korelują ze sobą?

• Oznacza to, że ich wyniki zmieniają się wspólnie

• Jeśli zmieniają się wyniki jednej zmiennej, wyniki drugiej zmieniają się w przewidywalny sposób

• Innymi słowy zmienne te są zależne od siebie

• Korelacja oznacza liniowy związek dwóch zmiennych.

• Wnioskujemy o współzależności dwóch zmiennych, a nie o relacjach przyczynowo skutkowych.

Wykres rozrzutu

• Zazwyczaj Używa się tego rodzaju wykresu do pokazania współzależności pomiędzy dwoma zmiennymi

• Dwa wymiary pokazujące rozkład wyników dla dwóch zmiennych

• Każdy wymiar pokazuje wartości liczbowe danej zmiennej

• Uwaga: przedstawiamy dane mierzone co najmniej, na skali przedziałowej

Porównanie wyników dwóch zmiennych mierzonych na różnych skalach

• Ponieważ najczęściej porównujemy wyniki dwóch zmiennych mierzonych na różnych skalach, współczynnik korelacji musi brać pod uwagę różne zakresy skali

• Należy wystandaryzować wyniki obu zmiennych

• Proste przekształcenie liniowe wyników surowych (X)

• Wartość standaryzowana “z” danego wyniku “X” = wynik surowy (X) minus średnia dzielone przez odchylenie standardowe

• z = (x-M) / SD

Standaryzacja

• Zmienia statystyki rozkładu zmiennej

• Średnia =0

• Odchylenie standardowe =1

• Wartości Z leżące poniżej średniej są ujemne

• Wartości większe od średniej mają Z dodatnie

• Wartości wyrażone w jednostkach odchylenia standardowego

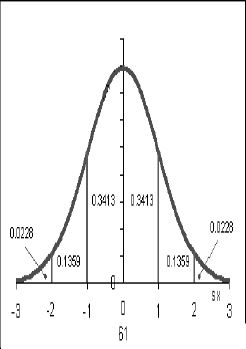
• Możemy określić prawdopodobieństwo uzyskania wyniku z danego przedziału

• Cała powierzchnia pod krzywą to 100%, więc do średniej (mediany) mamy 50%

• 68% przypadków mieści się w ramach 1 odchylenia od średniej (-1; 1)_

• Między 1 a 2 odchyleniem - 13,5%

• Około 95% w 2 odchyleniach od średniej, w 3 odchyleniach - około 99%

Współczynnik r-Pearsona

• Wzór => R =(Σ Z y∗Z x) / (N− 1)

• Kolejne kroki obliczania współczynnika r-Pearsona

• Wszystkie wyniki na obu skalach zamieniamy na z (na podstawie odpowiednich średnich i odchyleń standardowych)

• Mnożymy wartości z obu zmiennych

• Dodajemy iloczyny do siebie

• Dzielimy przez liczbę obserwacji minus 1

• Współczynnik korelacji Pearsona może przyjmować wartości z przedziału <-1;1>.

• Wartość ujemna wskazuje na negatywny związek między zmiennymi (X maleje a Y wzrasta)_

• Wartość dodatnia pokazuje na związek pozytywny pomiędzy zmiennymi (X rośnie i Y rośnie, X maleje i Y maleje)

Interpretacja współczynnika korelacji

• Korelacja oznacza liniowy związek dwóch zmiennych.

• Wnioskujemy o współzależności dwóch zmiennych, a nie o relacjach przyczynowo skutkowych.

• Sprawdzenie czy istnieje związek między dwiema zmiennymi:

• Określenie kierunku związku

• Pozytywny lub negatywny

• Pozytywny

• Wysokim wynikom na jednej zmiennej towarzyszą wysokie wyniki na drugiej zmiennej; a niskim wynikom na jednej - niskie na drugiej

• Negatywny

• Wysokim wynikom na jednej zmiennej towarzyszą niskie na innej

• Korelacja = zero

• Oznacza, Że nie ma liniowego związku między zmiennymi

• Określenie siły związku między dwiema zmiennymi

• od 0 do 1 - bez względu na znak

• (0; 1) , plus - pozytywna, 1 idealna

• (-1; 0), minus - ujemny związek, 1 idealny

• To, Że współczynnik korelacji jest ujemny nie oznacza, Że jest mniej istotny, czy silny, niż pozytywny

Wspólna zmienność, Wielkość efektu

• Wielkość efektu to ilość wariancji jednej zmiennej wyjaśniona przez wariancję drugiej zmiennej (procent wspólnej wariancji obu zmiennych).

• Kiedy mówimy o tym, że korelacje to wskaźnik współzmienności Możemy zadać pytanie o procent wspólnej wariancji obu zmiennych.

Wielkość efektu korelacji

• Szacując procent wspólnej wariancji (zmienności) obu zmiennych

• Podnosimy współczynnik korelacji do kwadratu.

• mnożymy razy 100.

• Wielkość efektu (ES) = r2 x 100

Współczynnik Rho- Spearmana (rs)

• Stosowany dla zmiennych porządkowych lub wtedy gdy nasze dane nie spełniają założeń testów parametrycznych np. brak rozkładu normalnego

• Najpierw ranguje dane obu zmiennych, potem oblicza współczynnik

• Przykład: Czy jest związek między ocenami konkursowymi z gry na skrzypcach a ocenami z gry na gitarze

Współczynnik Tau Kendalla

• Nieparametryczna korelacja

• Współczynnik ten stosuje się wtedy, gdy mamy małą próbę z dużą liczbą rang wiązanych

• Daje lepsze przewidywania co do rzeczywistej wartości korelacji w populacji niż rho-Spearmana, które jest częściej stosowane

Założenia testów parametrycznych

• Rozkład normalny zmiennej w populacji

• Sprawdzamy jaki jest rozkład: histogramy, wykresy skrzynkowe

• Wariancje w porównywanych populacjach zbliżone - założenie o homogeniczności wariancji

• Zaburzenie tego Założenia nie jest katastrofą, jeśli mamy równoliczne próbki

• Dane zbierane na skali przedziałowej i wyższej

• Nie powinno być skrajnych wyników

• Ponieważ opieramy się często na średniej i odchyleniu standardowym

Test Kołmogorova-Smirnova (test dobroci dopasowania)

• Porównuje rozkład naszych wyników w próbie do określonego rozkładu teoretycznego o takiej samej średniej i odchyleniu standardowym.

• Wartość Z Kołmogorowa-Smirnova jest oparta na największej bezwzględnej różnicy pomiędzy empirycznym a teoretycznym rozkładem skumulowanym.

• Interpretacja testu K-S dla 1 próby:

• Jeśli test ten jest nieistotny (p>0,05)_

• Rozkład naszej zmiennej nie różni się istotnie od rozkładu normalnego

• Jeśli test jest istotny (p<0,05)_

• Rozkład naszej zmiennej jest różny od rozkładu normalnego

Kiedy stosować testy nieparametryczne?

• Kiedy Założenia testów parametrycznych są zaburzone:

• Test U Manna Whitneya - schemat dla grup niezależnych

• Test znaków rangowanych Wilcoxona - schemat dla grup zależnych

• Pomiar na skali co najmniej porządkowej

• Opierają się na rangach

• Nie są wrażliwe na skrajne wyniki

Test U Manna-Whitneya

• Stosowany do testowania różnic między dwoma niezależnymi grupami

• Uznawany za nieparametryczny odpowiednik testu t dla grup niezależnych

• Założenia:

• Pomiar na skali co najmniej porządkowej

• Brak Założenia o normalności rozkładu, ale zakłada, Że rozkłady w porównywanych grupach są takie same.

• Zakłada homogeniczność wariancji (dość odporny na zaburzenie tego Założenia) - można go stosować jeśli wariancje rang w porównywanych grupach nie różnią się od siebie trzykrotnie

• Wzór => U=N₁N₂ + {[N₁(N₁+₁)] / 2} - R₁

• N₁ = 1 grupa

• N₂ = 2 grupa

• R₁ = suma rang

Test Wilcoxona

• Jeden z najbardziej popularnych testów nieparametrycznych

• Założenia:

• Skala pomiarowa co najmniej porządkowa

• Pomiary są niezależne od siebie

• H0: próbki pochodzą z identycznych populacji

• Nie ma różnic między pierwszym i drugim pomiarem (to samo założenie co przy teście t dla zależnych)

Test Chi-kwadrat χ2

• Wzór => χ ² = Σ [(O− E)²] / E

• x² - wartość statystyki `chi kwadrat'

• - częstość obserwowana - (observed frequency)

• E - częstość oczekiwana - (expected frequency)

• Porównujemy obserwowane frekwencje z oczekiwanymi.

• Jeśli wszystkie aktywności są równie popularne, obserwowane frekwencje nie powinny różnić się od oczekiwanych

• Jeśli różnice w popularności nie są przypadkowe

• Obserwowane frekwencje powinny różnić się od oczekiwanych (im bardziej tym większa szansa na istotne różnice)

Rodzaje testu Chi-kwadrat χ2

• Test χ2 dla jednej zmiennej - test zgodności

• Test χ2 niezależności dwóch zmiennych 2x2

• Szukamy związku między dwiema zmiennymi, z których każda jest na 2 poziomach stąd zapis 2x2

• χ2 dla r x 2

• Szukamy związku między dwiema zmiennymi, przy czym 1 zmienna jest dwukategorialna, druga ma więcej niż 2 kategorie

Chi-kwadrat w tabelach krzyżowych

• Przyglądając się zależności między dwoma zmiennymi kategorialnymi tworzymy tabelę krzyżową, w której zapisane są frekwencje na przecięciach wartości dwóch zmiennych

• Chi-kwadrat dla tabel krzyżowych testuje hipotezę, że zmienne zapisane w wierszach i zapisane w kolumnach są niezależne, bez wskazywania siły i kierunku zależności.

Liczebności oczekiwane w tabelach krzyżowych (E)

• Wzór => E = RT x CT / GT

• RT = ogólna liczba obserwacji w rzędzie,

• CT = ogólna liczba obserwacji w kolumnie,

• GT = ogólna liczba wszystkich obserwacji

Stopnie swobody w tabelach krzyżowych

• Stopnie swobody

• df= (liczba kolumn-1)x(liczba rzędów-1)_

• Dla tabeli 2x2 zawsze df=1

• Nie odzwierciedlają one tak jak przy teście t liczby osób badanych

• Oblicza się je na podstawie liczby kategorii uwzględnionych zmiennych w analizie.

Analiza treści

• Stone, Dunphy, Smith i Ogilvie (1966); Weber (1990)

• Metoda wykorzystująca zbiór systematycznych i obiektywnych procedur pozwalających na wyciąganie wniosków z tekstów

• Holsti (1969)

• Każda technika, która pozwala na wyciąganie wniosków na podstawie obiektywnie i systematycznie wyodrębnionych cech przekazu.

Kiedy stosujemy analizę treści?

• Badania komunikacji

• Jakie cechy własnej osoby używane są do opisu siebie w sytuacji zapoznawania się z kimś nowym?

• Badania treści stereotypów i postaw

• Jakie cechy innych grup najczęściej pojawiają się w ich opisach?

• Badania treści samoświadomości

• Jakie schematy Ja aktywizowane są w sytuacjach stresu?

• Analiza literatury

• Jaką perspektywę teoretyczną przyjmują autorzy polskich publikacji na temat wywiadu diagnostycznego?

• Analiza przekazów wizualnych

• Jaki obraz kobiety dominuje w kolorowych magazynach? Jak problem higieny prezentowany jest w reklamie?

Transkrypcje

• Transkrypcja, niejednokrotnie jest wstępną obróbką danych surowych nawet, jeżeli jest próbą dokładnego spisania słów badanego.

• Pomijane są informacje dodatkowe: ton głosu, zachowanie, mimika, itp.

• W podejściu interpretacyjnym, podkreśla się rolę zanotowania kontekstu, w jakim powstają słowa. Odchodzi się od prób idealnego oddania treści.

System kodowania (code book)

• System kodowania - spis kategorii jakościowych zawierających:

• Nazwę wraz z definicją (opisem) ich znaczenia,

• Przykłady treści, które mogą być zaklasyfikowane do każdej z kategorii, oraz

• Instrukcję kodowania dla sędziów kompetentnych.

• Obok kategorii jakościowych może zawierać skale ocen:

• np. ocena abstrakcyjności (abstrakcyjna - konkretna), pozytywności (pozytywne - negatywne), aprobaty społecznej (wysoka - niska).

Poziomy obserwowalnych jednostek analizy treści

• Grey i współpracownicy (1965) w eksperymencie metodologicznym wykazali, że wykorzystywanie do analizy szerszych jednostek kodowania, np. akapitów, powoduje, że cały przekaz klasyfikowany jest jako mniej neutralny.

Trzy typy rzetelności

• Stabilność

• Dokładność

• Spójność

Stabilność (stability)

• Polega na powtórnym zakodowaniu tych samych danych przez te same osoby.

• Np. interesujemy się treścią snów osób depresyjnych, możemy poprosić o zakodowanie wybranych snów według przygotowanego uprzednio systemu kodowania. Po upływie kilku tygodni prosimy te same osoby kodujące o powtórną klasyfikację treści tych samych snów.

Dokładność (accuracy)

• Mierzy zgodność zakodowania materiału w odniesieniu do standardu, ustalonego przez grono ekspertów lub na podstawie wcześniejszych badań.

Spójność (reproducibility)__

• W raportach z badań wykorzystujących metody jakościowe najczęściej spotkamy statystyki odnoszące się do zgodności rozumianej jako spójność kodowania materiału przez kilka osób kodujących

• Pomiar tego typu rzetelności opiera się na oszacowaniu proporcji zgodnych kategoryzacji między sędziami do wszystkich podjętych przez nich decyzji.

• W tym przypadku rzetelność często określana jest jako stopień zgodności między sędziami lub rzetelność między sędziami (inter-rater reliability).

Pi Scotta

• Uwzględnia on przypadkową zgodność między sędziami

• Uważany za statystykę konserwatywną

• Teoretycznie przyjmuje wartości od -1 do 1, gdzie -1 oznacza zupełną niezgodność między sędziami a 1 idealną zgodność, natomiast 0 oznacza zgodność pomiędzy sędziami na poziomie przypadku

• Wzór => ∏ = (Po- Pe)/( 1- Pe)

Po = (S* N zgodne) / N ogółem

S - liczba sędziów kompetentnych;

Nzgodne - liczba zgodnych kategoryzacji;

Nogółem - liczba wszystkich podjętych przez sędziów decyzji,

Pe = ∑(Pk)²

Pk = Nk / N ogółem

Kappa Cohena

• Tworzona jest tabela krzyżowa z taką samą liczbą kategorii w rzędach i kolumnach odpowiadającą liczbie kategorii systemu kodowania

• W kolumnach znajdują się klasyfikacje jednego z sędziów, a w rzędach decyzje podjęte przez drugiego z sędziów

• Wzór => K = (Po- Pe) / (1-Pe)

• Po - proporcja decyzji zgodnych; Pe - proporcja oczekiwanych decyzji zgodnych przez przypadek.

---