Instytut Materiałów Inżynierskich i

Biomedycznych

Zakład Odlewnictwa

Wydział Mechaniczny

Technologiczny

POLITECHNIKA ŚLĄSKA W

GLIWICACH

Odlewnictwo

Krystalizacja i krzepnięcie

Odlewnictwo

Krystalizacja i krzepnięcie

GLIWICE – ROK
2005

Mirosław
Cholewa

Literatura:

Literatura:



Crosley P., Douglas A., Mondolfo L.: Interfacial Energies in Heterogeneous

Crosley P., Douglas A., Mondolfo L.: Interfacial Energies in Heterogeneous

Nucleation,The Solid. of Metals, The Iron and Steel Inst. nr 110, London 1968, s.10

Nucleation,The Solid. of Metals, The Iron and Steel Inst. nr 110, London 1968, s.10



Bramfitt B.: The effect of Carbide and Nitride Addition on the heterogeneous

Bramfitt B.: The effect of Carbide and Nitride Addition on the heterogeneous

Nucleation Behavior of Liquid Iron, Metall. Trans., 1970, s. 1987

Nucleation Behavior of Liquid Iron, Metall. Trans., 1970, s. 1987



Gliksman M., Childs W.: Nucleation Catalysis in Supercooled Liquid Tin, Acta Metall.

Gliksman M., Childs W.: Nucleation Catalysis in Supercooled Liquid Tin, Acta Metall.

1962, s.925

1962, s.925



Fraś E.: Teoret. Podst. Kryst., cz. 1, skr. uczeln. nr 930 Kraków 1984, s 82

Fraś E.: Teoret. Podst. Kryst., cz. 1, skr. uczeln. nr 930 Kraków 1984, s 82

Oostdijk J.,

Oostdijk J.,

C.: Van kiem tot kristalliet. Pr. Dokt. Delft, Drukkerij J., H. Pasmans, 1967

C.: Van kiem tot kristalliet. Pr. Dokt. Delft, Drukkerij J., H. Pasmans, 1967



Chalmers B.: Principles of Solidification

Chalmers B.: Principles of Solidification

,

,

John Wiley & Sons, New York 1964, s.68

John Wiley & Sons, New York 1964, s.68



Verma A. R.: Crystal growth and dislocations. Butterworths Scientific Publications,

Verma A. R.: Crystal growth and dislocations. Butterworths Scientific Publications,

London 1953,

London 1953,



Missol W.: Energia powierzchni rozdziału faz, Wyd. „Śląsk”. Katowice 1975

Missol W.: Energia powierzchni rozdziału faz, Wyd. „Śląsk”. Katowice 1975



Braszczyński J., Krystalizacja odlewów, WNT, Warszawa 1991

Braszczyński J., Krystalizacja odlewów, WNT, Warszawa 1991



Jones H., Leak M.G.: The surface entropy of solid metals, Metall. Sci. v. 1, 1967, s. 211

Jones H., Leak M.G.: The surface entropy of solid metals, Metall. Sci. v. 1, 1967, s. 211



Jones H.: The surface energy of solid metals. Metall. Sci. v. 5, 1971, s. 15

Jones H.: The surface energy of solid metals. Metall. Sci. v. 5, 1971, s. 15



Jones H.: The grain boundary term in surface energy measurement by zero creep,

Jones H.: The grain boundary term in surface energy measurement by zero creep,

Scripta Met. v. 6, 1972, s. 423Allen B.C.: Effect of crystallographic orientation on the

Scripta Met. v. 6, 1972, s. 423Allen B.C.: Effect of crystallographic orientation on the

surface free energy and surface self-diffusion of solid molybdenum. Trans. Metall. Soc.

surface free energy and surface self-diffusion of solid molybdenum. Trans. Metall. Soc.

AIME v. 245, 1969, s. 2089

AIME v. 245, 1969, s. 2089



Guggenheim E.A.: Termodynamics, Amsterdam, North-Holland Publ.Co 1950

Guggenheim E.A.: Termodynamics, Amsterdam, North-Holland Publ.Co 1950



Burden M.H., Hunt J.D., J. Cryst. Growth, Trans., vol. 22, 1974, s. 109.

Burden M.H., Hunt J.D., J. Cryst. Growth, Trans., vol. 22, 1974, s. 109.



Tiller W., Grain size control during ingot solidification, Trans, of the Metall. Soc., v.

Tiller W., Grain size control during ingot solidification, Trans, of the Metall. Soc., v.

224, s. 448.

224, s. 448.



Witzke S., Riquet J., Durand F., Acta Metallurgica, vol.29, 1981, s. 365

Witzke S., Riquet J., Durand F., Acta Metallurgica, vol.29, 1981, s. 365



Fredrikson H., Hillert M., On formation of the central equiaxed zone in ingots.

Fredrikson H., Hillert M., On formation of the central equiaxed zone in ingots.

Met.Trans., v. 3, 1972, s. 565

Met.Trans., v. 3, 1972, s. 565



Elliot R., The formation of the equiaxed crystal zone during solidification. The British

Elliot R., The formation of the equiaxed crystal zone during solidification. The British

Foundryman, No.10, 1964, p. 164

Foundryman, No.10, 1964, p. 164



Bałandin G., Formirowanije kristalliczeskowo strojenija otliwok, Maszinistr., Moskwa

Bałandin G., Formirowanije kristalliczeskowo strojenija otliwok, Maszinistr., Moskwa

1973.

1973.



Flemings M., Solidification processing, Met. Trans., vol,5, 1974, s. 2121.

Flemings M., Solidification processing, Met. Trans., vol,5, 1974, s. 2121.



Southin R.T., Trans,TMS-AIME, v.236, 1967, s.220.

Southin R.T., Trans,TMS-AIME, v.236, 1967, s.220.



Fraś E., Krzepnięcie metali i stopów, WN PWN, Warszawa 1992.

Fraś E., Krzepnięcie metali i stopów, WN PWN, Warszawa 1992.



Kurz W., Fisher D. J., Fundamentals solidification, Trans, Tech. Publ., Paris 1984.

Kurz W., Fisher D. J., Fundamentals solidification, Trans, Tech. Publ., Paris 1984.



Chalmers B., The structure of ingots, J. Aust. Int. Met.,vol.8, 1963, s. 224.

Chalmers B., The structure of ingots, J. Aust. Int. Met.,vol.8, 1963, s. 224.



Southin R., Nucleation of equiaxed zone i cast metals, TMS-AIME, vol.229, 1967,

Southin R., Nucleation of equiaxed zone i cast metals, TMS-AIME, vol.229, 1967,

s.220.

s.220.



Ohno A., The solidification of metals. Chijin Shoken, Tokyo 1980.

Ohno A., The solidification of metals. Chijin Shoken, Tokyo 1980.



Jackson K., Hunt J., Uhlmann D., Soward T., Trans. TMS-AIME, vol. 236, 1967, p. 149.

Jackson K., Hunt J., Uhlmann D., Soward T., Trans. TMS-AIME, vol. 236, 1967, p. 149.



Langenberg F.C., Prestel G., Honeycutt C.R., Trans.

Langenberg F.C., Prestel G., Honeycutt C.R., Trans.

TMS-AIME, vol. 221, 1961, p. 993.

TMS-AIME, vol. 221, 1961, p. 993.



Kinetyka krzepnięcia

odlewów

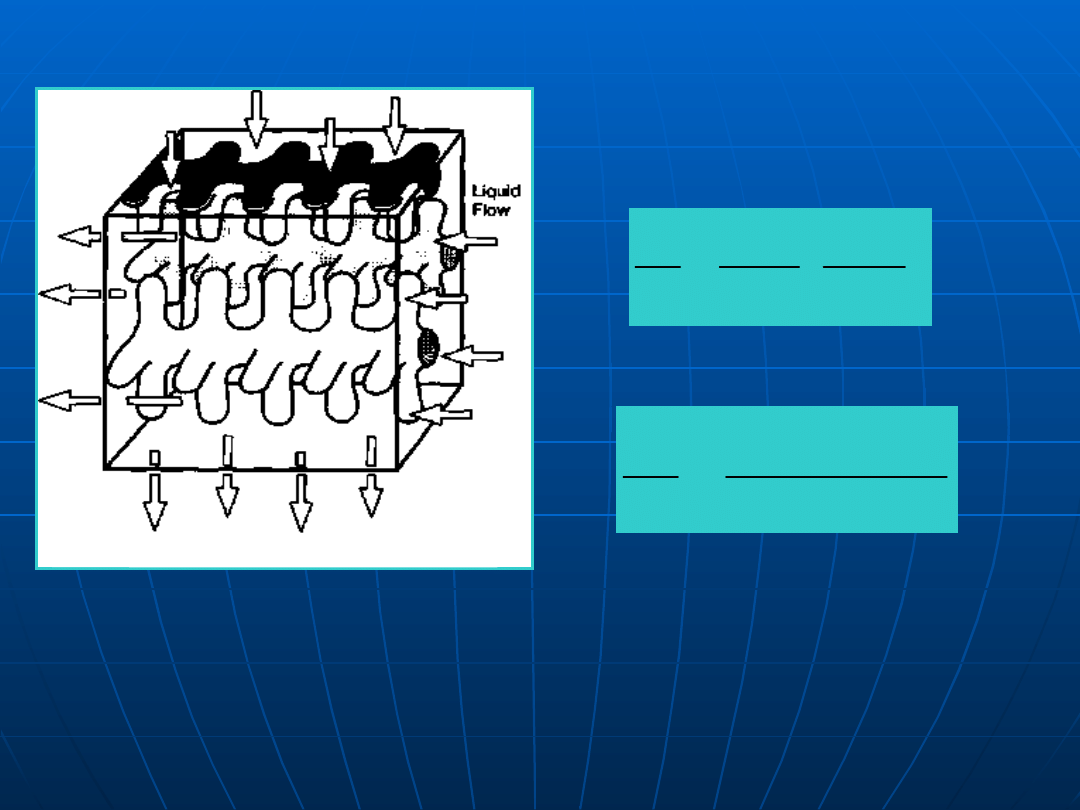
Równoważność oddziaływań fizycznych i
chemicznych











 



e

e

O

l

k

k

D

mC

v

G

1





D

C

C

m

v

G

O

E

l





gdzie:

G

l

- gradient temperatury w cieczy, v - prędkość krystalizacji.

C

O

, C

E

- stężenie

cieczy i dendrytów, m - nachylenie linii

likwidus, D - współczynnik dyfuzji

obszar jednofazowy

obszar dwufazowy

Funkcję Gibbsa, funkcję stanu można przedstawić
w następującej postaci:

A

PV

TS

U

G











Zapis dotyczy całego, dowolnego układu złożonego obejmującego
parametry ekstensywne i intensywne. Przyjmowane założenia dotyczą
zawsze ustalania jednego z nich i zmienności drugiego.

Energię swobodną rozłożono na składowe: objętościową i
powierzchniową, przy czym objętość przypisano sumie objętości
składników przed tworzeniem stopu jak i po jego wytworzeniu wraz z
powstałymi produktami reakcji między nimi. Mamy zatem dla:

objętości:

V=Vi+Vi-n (VA=0)

energii wewnętrznej:

U=UV+UA

entropii:

S=SV+SA

energii swobodnej

F=FV+FA

liczby moli

ni=nVi+nAi

zależności:

W technologiach wykorzystujących dodatkowe

W technologiach wykorzystujących dodatkowe

oddziaływania fizyczne jak np.: pola elektryczne,

oddziaływania fizyczne jak np.: pola elektryczne,

magnetyczne konieczne jest ich uwzględnienie w

magnetyczne konieczne jest ich uwzględnienie w

ogólnym bilansie energetycznym:

ogólnym bilansie energetycznym:

)

(

)

(

)

(

)

(

i

A

i

A

A

A

i

V

i

V

V

V

A

A

V

V

V

i

i

n

d

Ad

dT

S

A

F

d

dG

n

d

VdP

dT

S

PV

F

d

dG

A

F

G

PV

TS

U

G

dn

Ad

VdP

SdT

dG

































































dA

dn

BdM

Qd

VdP

SdT

dG

i

i























gdzie: S - entropia, T - temperatura, V - objętość, P - ciśnienie, Q
- ładunek elektryczny, ψ- potencjał elektryczny, M - moment
magnetyczny, B - indukcja magnetyczna, μi- potencjał chemiczny
składnika, ni - ilość składnika i (mol), ω – energia
powierzchniowa, A - powierzchnia.



Wszystkie procesy dynamicznego oddziaływania na kąpiel

Wszystkie procesy dynamicznego oddziaływania na kąpiel

można rozpatrywać jako wzrost energii Fermiego, a także

można rozpatrywać jako wzrost energii Fermiego, a także

energii wewnętrznej cieczy. Powiększa się, zatem także

energii wewnętrznej cieczy. Powiększa się, zatem także

metastabilność układu przyspieszając w ten sposób

metastabilność układu przyspieszając w ten sposób

krystalizację. Makroskopowe lub lokalne zwiększanie

krystalizację. Makroskopowe lub lokalne zwiększanie

ciśnienia w kąpieli jest termodynamicznie analogiczne do

ciśnienia w kąpieli jest termodynamicznie analogiczne do

zwiększania stopnia przechłodzenia. Znajduje to

zwiększania stopnia przechłodzenia. Znajduje to

potwierdzenie w teorii W.A. Tillera dotyczącej zarodkowania

potwierdzenie w teorii W.A. Tillera dotyczącej zarodkowania

w metalach i stopach a opisanych równaniem Clausiusa-

w metalach i stopach a opisanych równaniem Clausiusa-

Clapeyrona:

Clapeyrona:

L

V

T

dp

dT

V

T

dH

dT

dp

E

f

E

f

E









gdzie: dp wzrost ciśnienia, dTE- rzeczywiste zwiększenie
przechłodzenia, dHf – molowe ciepło topnienia, ΔVf -zmiana
jednostkowej objętości cieczy przy krzepnięciu, L - ciepło
krystalizacji



Wyznaczając następnie temperaturę T

Wyznaczając następnie temperaturę T

E

E

i

i

wstawiając ją do zależności na krytyczny promień

wstawiając ją do zależności na krytyczny promień

zarodka homogenicznego lub heterogenicznego, w

zarodka homogenicznego lub heterogenicznego, w

klasycznym rozumieniu uzyskuje się odpowiedni

klasycznym rozumieniu uzyskuje się odpowiedni

promień krytyczny (r

promień krytyczny (r

x

x

) powstały w nowych

) powstały w nowych

warunkach:

warunkach:











sin

2

2

T

T

L

G

r

E





dp

dT

T

V

r











sin

2



gdzie: ω i Θ to odpowiednio - swobodna energia
powierzchniowa między kryształem a cieczą i kąt
zwilżania



Korzystając z zależności na energię swobodną – funkcji

Korzystając z zależności na energię swobodną – funkcji

Helmholtza i potencjału termodynamicznego Herringa

Helmholtza i potencjału termodynamicznego Herringa

można wykazać współzależność i równoważność

można wykazać współzależność i równoważność

oddziaływań fizycznych i chemicznych, głównie w strefie

oddziaływań fizycznych i chemicznych, głównie w strefie

granicznej reprezentowanej przez powierzchnię kontaktu,

granicznej reprezentowanej przez powierzchnię kontaktu,

lecz także w objętości otaczającej powierzchnię kontaktu:

lecz także w objętości otaczającej powierzchnię kontaktu:



Z energii swobodnej Helmholtza:

Z energii swobodnej Helmholtza:

TS

U

F





energia swobodna powierzchni:

A

TS

U

F

A

A

A

























Ad

dT

S

n

VdP

dT

S

n

n

A

A

F

G

n

PV

F

G

TS

U

F

A

i

iA

V

i

iV

i

iA

A

A

i

iV

V

V

V

V

V









































)

(

energia użyteczna powierzchni:

gdzie: σ - napięcie powierzchniowe



W obszarze międzyfazowym gęstość, ciśnienie, skład chemiczny i

W obszarze międzyfazowym gęstość, ciśnienie, skład chemiczny i

właściwości fizyczne zmieniają się w zakresie od wartości

właściwości fizyczne zmieniają się w zakresie od wartości

charakterystycznych dla cieczy do wartości typowych dla

charakterystycznych dla cieczy do wartości typowych dla

kryształów. Dla zastosowań związanych z układami wielofazowymi,

kryształów. Dla zastosowań związanych z układami wielofazowymi,

wskazane byłoby posługiwanie się koncepcją Guggenheima

wskazane byłoby posługiwanie się koncepcją Guggenheima

uwzględniającą niezerową grubość fazy powierzchniowej o

uwzględniającą niezerową grubość fazy powierzchniowej o

cechach i własnościach dodatkowej fazy objętościowej.

cechach i własnościach dodatkowej fazy objętościowej.



Zróżnicowanie energii powierzchniowej występuje zarówno na

Zróżnicowanie energii powierzchniowej występuje zarówno na

różnych płaszczyznach krystalograficznych tego samego metalu,

różnych płaszczyznach krystalograficznych tego samego metalu,

ale także na różnych kierunkach krystalograficznych należących

ale także na różnych kierunkach krystalograficznych należących

do wspólnej płaszczyzny.

do wspólnej płaszczyzny.



Jeśli przyjąć, że energia powierzchniowa jest proporcjonalna do

Jeśli przyjąć, że energia powierzchniowa jest proporcjonalna do

niewysycenia wiązań atomowych wówczas minimalną energię

niewysycenia wiązań atomowych wówczas minimalną energię

powierzchniową będą posiadały płaszczyzny krystalograficzne

powierzchniową będą posiadały płaszczyzny krystalograficzne

gęstego upakowania atomów

gęstego upakowania atomów



Lokalny dodatkowy efekt energetyczny pozostający w związku z

Lokalny dodatkowy efekt energetyczny pozostający w związku z

topografią i morfologią kryształów wpływa na inicjowanie i

topografią i morfologią kryształów wpływa na inicjowanie i

przebieg generowania dyfuzyjnej strefy przejściowej między cieczą

przebieg generowania dyfuzyjnej strefy przejściowej między cieczą

a kryształami.

a kryształami.



Przykładowo wielkość energii krawędziowej w atmosferze

Przykładowo wielkość energii krawędziowej w atmosferze

powietrza w temperaturze 900

powietrza w temperaturze 900

o

o

C dla srebra wynosi: λ(100)=38

C dla srebra wynosi: λ(100)=38

pJ/m, λ(111)=57 pJ/m. Miedź w atmosferze wodoru w

pJ/m, λ(111)=57 pJ/m. Miedź w atmosferze wodoru w

temperaturze 1000oC posiada: λ(100)=20 pJ/m i λ(111)=34 pJ/m

temperaturze 1000oC posiada: λ(100)=20 pJ/m i λ(111)=34 pJ/m



Dla zaistnienia zarodkowania niezbędne jest stworzenie

Dla zaistnienia zarodkowania niezbędne jest stworzenie

właściwego przechłodzenia cieczy przed frontem krystalizacji.

właściwego przechłodzenia cieczy przed frontem krystalizacji.

Zarodki znajdujące się w innych obszarach odlewu powstają na

Zarodki znajdujące się w innych obszarach odlewu powstają na

granicach faz - między innymi przez kontakt ciekłego metalu z

granicach faz - między innymi przez kontakt ciekłego metalu z

elementami formy, w tym głównie układu wlewowego. Modele

elementami formy, w tym głównie układu wlewowego. Modele

opisujące ten zakres dziedziny zarodkowania to między innymi:

opisujące ten zakres dziedziny zarodkowania to między innymi:



Chalmersa – tzw. „big bang” oparty na idei zarodkowania poprzez

Chalmersa – tzw. „big bang” oparty na idei zarodkowania poprzez

kryształy zamrożone powstałe na wewnętrznej powierzchni wnęki

kryształy zamrożone powstałe na wewnętrznej powierzchni wnęki

formy

formy



Ohno – polegający na zarodkotwórczym działaniu kryształów

Ohno – polegający na zarodkotwórczym działaniu kryształów

oderwanych od powierzchni wnęki formy

oderwanych od powierzchni wnęki formy



Jaksona i in. – według, których powstaje w kąpieli dyspersja

Jaksona i in. – według, których powstaje w kąpieli dyspersja

kryształów poprzez ich nadtapianie i rozmnażanie

kryształów poprzez ich nadtapianie i rozmnażanie



Southina – w którym zarodki powstają na powierzchni ciekłego

Southina – w którym zarodki powstają na powierzchni ciekłego

metalu. Jest tzw. model deszczowy

metalu. Jest tzw. model deszczowy



Tillera lub Witzkego– o zarodkowaniu przed frontem krystalizacji

Tillera lub Witzkego– o zarodkowaniu przed frontem krystalizacji



Uwzględniające zewnętrzne pola siłowe – wymuszoną konwekcję i

Uwzględniające zewnętrzne pola siłowe – wymuszoną konwekcję i

w jej następstwie fragmentację dendrytów na skutek

w jej następstwie fragmentację dendrytów na skutek

•

-fluktuacji temperatury

-fluktuacji temperatury

•

-mechanicznego działania ciekłego metalu

-mechanicznego działania ciekłego metalu

•

-połączonego wpływu czynników: kinetycznego, stężeniowego i

-połączonego wpływu czynników: kinetycznego, stężeniowego i

cieplnego

cieplnego



W procesie zarodkowania, przy wspomaganiu zwilżania

W procesie zarodkowania, przy wspomaganiu zwilżania

fizycznymi oddziaływaniami, sumaryczna powierzchnia

fizycznymi oddziaływaniami, sumaryczna powierzchnia

międzyfazowa nie dość, że jest wielokrotnie większa niż w

międzyfazowa nie dość, że jest wielokrotnie większa niż w

tradycyjnych stopach to jeszcze dodatkowo aktywowana

tradycyjnych stopach to jeszcze dodatkowo aktywowana

może zmieniać swoją powierzchnię kontaktu w zależności

może zmieniać swoją powierzchnię kontaktu w zależności

od temperatury, lokalnego składu chemicznego,

od temperatury, lokalnego składu chemicznego,

chwilowego stężenia i intensywności zewnętrznego pola

chwilowego stężenia i intensywności zewnętrznego pola

siłowego.

siłowego.



Podsumowując można postawić tezę:

Podsumowując można postawić tezę:

zwiększenie energii powierzchniowej jest

zwiększenie energii powierzchniowej jest

skutkiem poprawnego zwilżania oraz

skutkiem poprawnego zwilżania oraz

właściwej adhezji i dyfuzji, powodując

właściwej adhezji i dyfuzji, powodując

minimalizację naprężeń i ich homogenizację

minimalizację naprężeń i ich homogenizację



Trajektoria ruchu

Trajektoria ruchu

pojedynczego jonu Fe w

pojedynczego jonu Fe w

temperaturze 1823 K

temperaturze 1823 K

rzutowana na płaszczyznę

rzutowana na płaszczyznę

poziomą YOX

poziomą YOX



jest on związany z ruchem

jest on związany z ruchem

dużej grupy sąsiednich

dużej grupy sąsiednich

jonów, co prowadzi do

jonów, co prowadzi do

stabilności lokalnej

stabilności lokalnej

struktury w czasie 6

struktury w czasie 6

·

·

10

10

-3

-3

s.

s.

Jon w tym czasie może

Jon w tym czasie może

znajdować się w stanie

znajdować się w stanie

ruchu drgającego

ruchu drgającego

względem prawie

względem prawie

nieruchomego środka

nieruchomego środka

równowagi, a następnie

równowagi, a następnie

wykonuje przeskok do

wykonuje przeskok do

nowego ośrodka drgań.

nowego ośrodka drgań.

Charakterystyki struktur atomowych

Charakterystyki struktur atomowych

metali w stanie stałym i ciekłym

metali w stanie stałym i ciekłym

Metal

Stan skupienia

stały

ciekły

Liczba

koordyna-

cyjna

Średnia

odległość

miedzy

atomami

l0

-1

nm

Temperatu

ra

K

Liczba

koordynacy

jna

Średnia

odległość

między

atoniami

10

-1

nm

Al

12

2,86

973

10,6

2,96

Zn

6—6

2,16—2,90

763

11

2,94

Hg

6—6

3,47—3,00

293

12

3,30

Na

8

3,72

373

8

4,38

Ge

4

2,34

1273

8

2,70

Bi

3—3

3,09—3,46

613

7—8

3,32



Z tabl. wynika, że dla czystych metali (Al, Zn, Hg, Na) liczba

Z tabl. wynika, że dla czystych metali (Al, Zn, Hg, Na) liczba

koordynacyjna przy roztapianiu nie zmienia się lub

koordynacyjna przy roztapianiu nie zmienia się lub

zmniejsza w niewielkim stopniu. Dla nich upakowanie w

zmniejsza w niewielkim stopniu. Dla nich upakowanie w

stanie ciekłym i stałym odpowiada jednej klasie struktur.

stanie ciekłym i stałym odpowiada jednej klasie struktur.

Dla innych metali (Bi, Ge) liczba koordynacyjna przy

Dla innych metali (Bi, Ge) liczba koordynacyjna przy

roztapianiu wzrasta. W stanie stałym metale te mają

roztapianiu wzrasta. W stanie stałym metale te mają

strukturę o mniejszym stopniu upakowania (defekty

strukturę o mniejszym stopniu upakowania (defekty

struktury), a w ciekłym — bardziej gęstą, odnoszącą się już

struktury), a w ciekłym — bardziej gęstą, odnoszącą się już

do drugiej klasy struktur. Roztapianie powoduje częściowe

do drugiej klasy struktur. Roztapianie powoduje częściowe

rozerwanie połączeń między atomami, co pozwala zapełnić

rozerwanie połączeń między atomami, co pozwala zapełnić

atomami „pustki" krystalograficzne, istniejące w sieci ciała

atomami „pustki" krystalograficzne, istniejące w sieci ciała

stałego. Wreszcie część metali, mających w stanie stałym

stałego. Wreszcie część metali, mających w stanie stałym

sieć tetragonalną (Zn, Hg, Bi), traci tetragonalność po

sieć tetragonalną (Zn, Hg, Bi), traci tetragonalność po

roztopieniu.

roztopieniu.



Ogólnie stwierdza się, że metale po stopieniu rozszerzają

Ogólnie stwierdza się, że metale po stopieniu rozszerzają

się tylko o 3 - 5% (Bi nawet się kurczy), tak że liczba i

się tylko o 3 - 5% (Bi nawet się kurczy), tak że liczba i

upakowanie najbliższych sąsiadów nie mogą ulegać

upakowanie najbliższych sąsiadów nie mogą ulegać

poważniejszym zmianom

poważniejszym zmianom

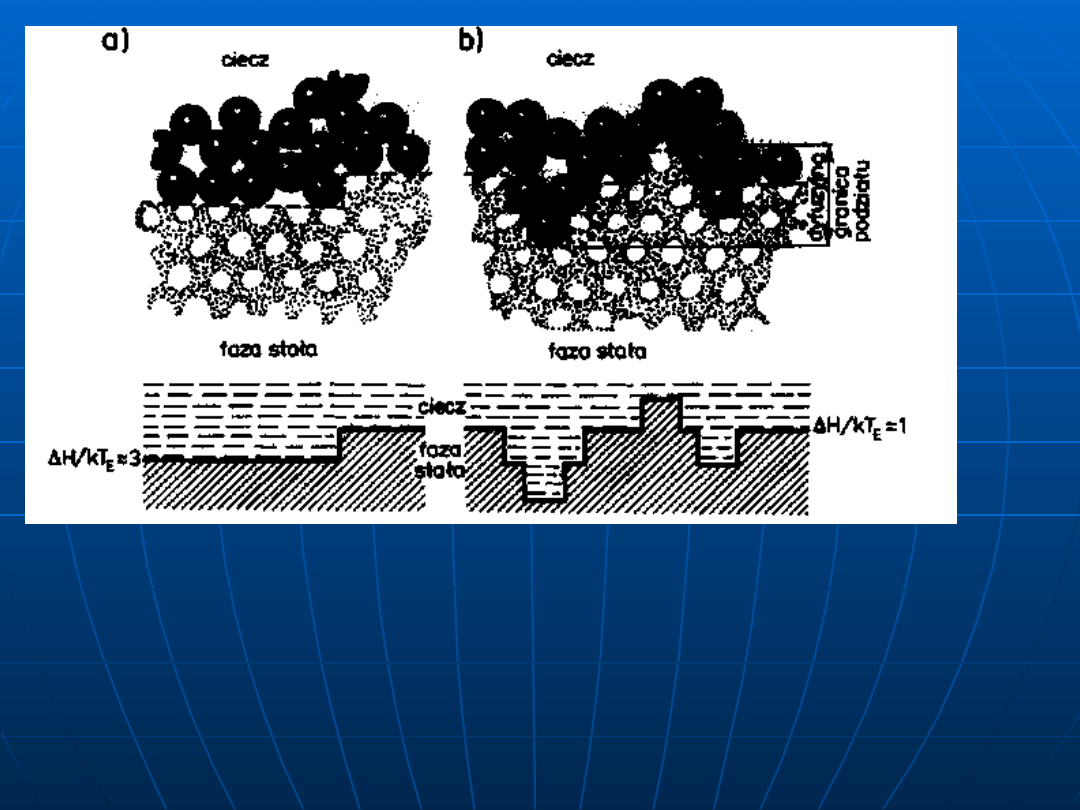
Model rozłożenia atomów w cieczy (ciemne kule) i w fazie stałej

Model rozłożenia atomów w cieczy (ciemne kule) i w fazie stałej

(jasne kule) na powierzchni:

(jasne kule) na powierzchni:

a) atomowogładkiej, b) szorstkiej — rozmytej;

a) atomowogładkiej, b) szorstkiej — rozmytej;

H

H

— entalpia,----- umowna granica rozdziału faz: ciecz — faza stała

— entalpia,----- umowna granica rozdziału faz: ciecz — faza stała



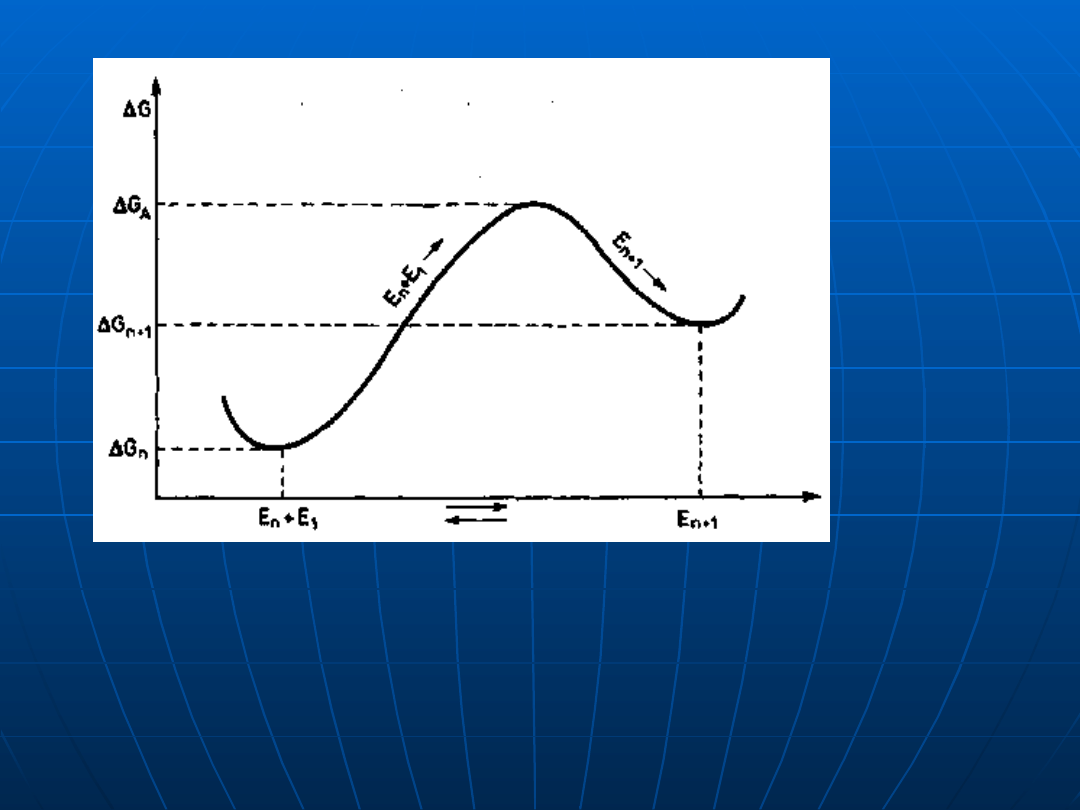
Energia swobodna układu

Energia swobodna układu

Δ

Δ

G w funkcji zmiany rozmieszczenia

G w funkcji zmiany rozmieszczenia

atomów, spowodowanej przyłączeniem nowego atomu E

atomów, spowodowanej przyłączeniem nowego atomu E

1

1

do

do

fluktuacji

fluktuacji

E

E

n

n

wg J.W. Christiana

wg J.W. Christiana



Δ

Δ

G

G

A

A

— energia stanu aktywowanego,

— energia stanu aktywowanego,

Δ

Δ

G

G

n

n

— energia fluktuacji

— energia fluktuacji

n

n

atomów,

atomów,

Δ

Δ

G

G

n+1

n+1

— energia fluktuacji

— energia fluktuacji

n +

n +

1 atomów

1 atomów



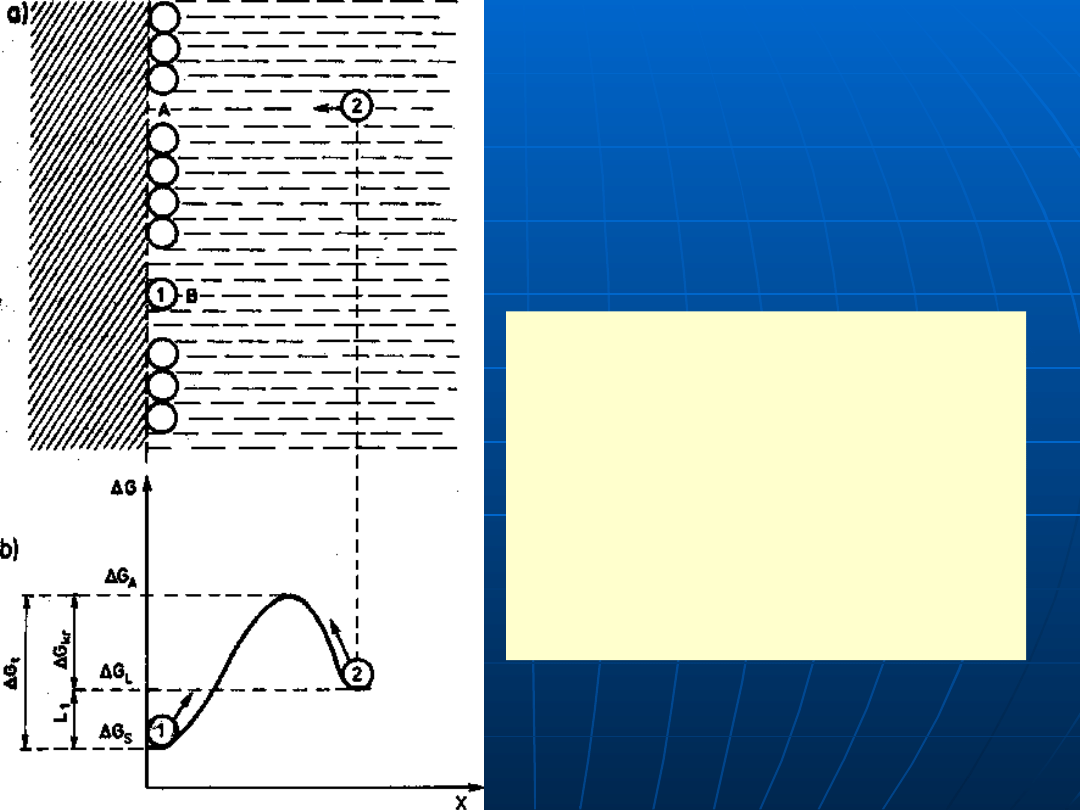
Topnienie i krystalizacja:

Topnienie i krystalizacja:



a) w układzie atomowym,

a) w układzie atomowym,



b) energetycznym;

b) energetycznym;

l

l

— atom w procesie topnienia,

— atom w procesie topnienia,

2 —

2 —

atom w procesie krystalizacji,

atom w procesie krystalizacji,

Δ

Δ

GL,

GL,

Δ

Δ

GS — energia swobodna

GS — energia swobodna

atomów w fazie ciekłej i stałej,

atomów w fazie ciekłej i stałej,

Δ

Δ

G

G

t

t

,

,

Δ

Δ

G

G

kryst

kryst

— energia aktywacji

— energia aktywacji

topnienia i krystalizacji, L

topnienia i krystalizacji, L

1

1

—

—

utajone ciepło krzepnięcia,

utajone ciepło krzepnięcia,

x

x

—

—

odległość od frontu krzepnięcia

odległość od frontu krzepnięcia



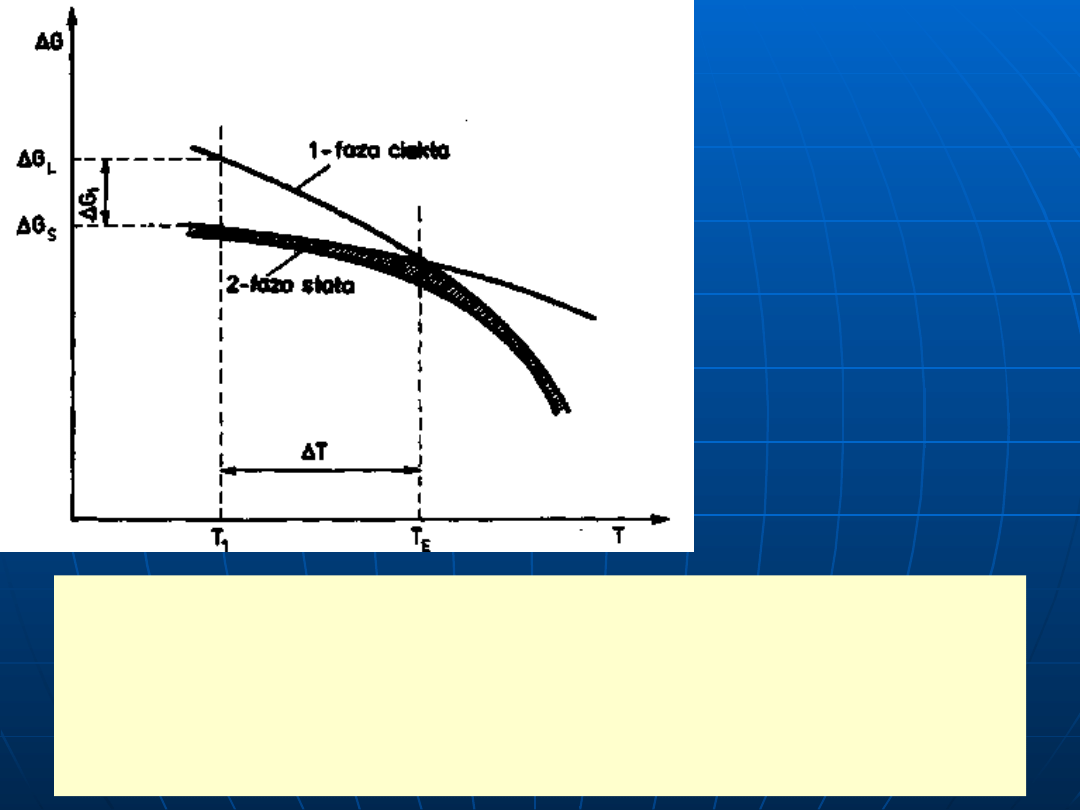
Zależność energii swobodnej fa zy stałej

Zależność energii swobodnej fa zy stałej

Δ

Δ

G

G

S

S

, i ciekłej

, i ciekłej

Δ

Δ

G

G

L

L

od

od

temperatury

temperatury

T;

T;

Δ

Δ

Gi — termodynamiczny potencjał

Gi — termodynamiczny potencjał

przemiany (krystalizacji), odpowiadający przechłodzeniu

przemiany (krystalizacji), odpowiadający przechłodzeniu

Δ

Δ

T,

T,

T

T

E

E

— temperatura równowagowa

— temperatura równowagowa



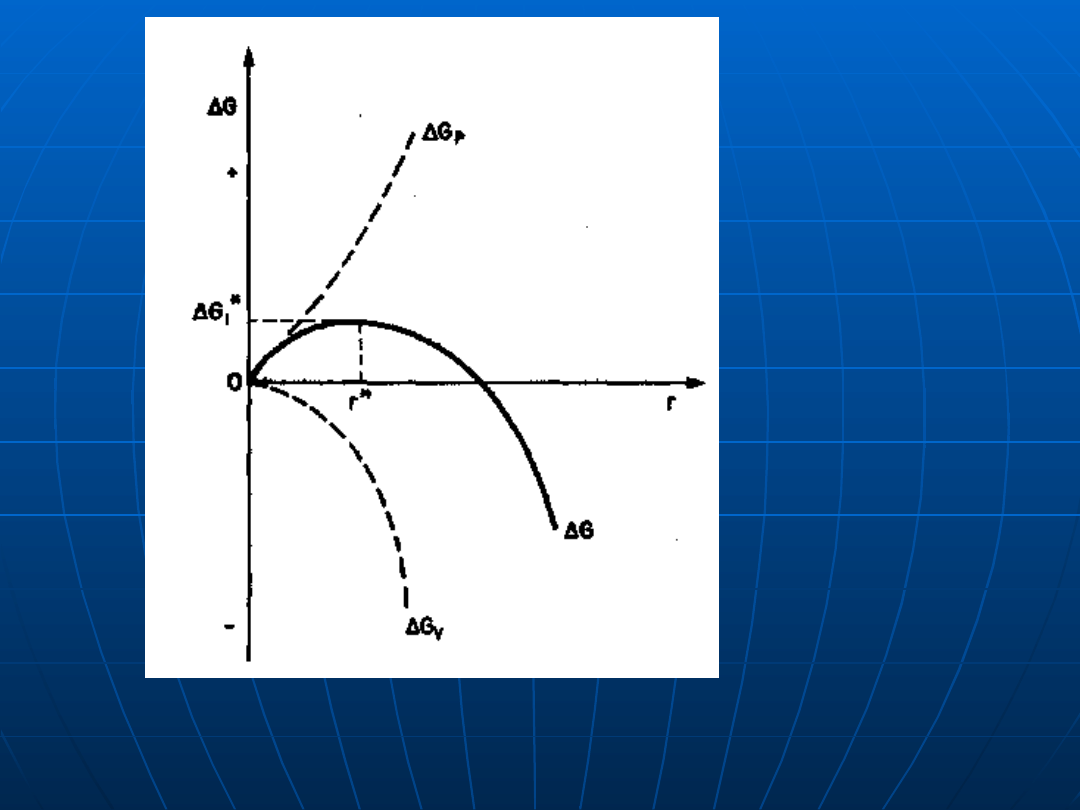
Zmiana energii swobodnej

Zmiana energii swobodnej

Δ

Δ

G, przy tworzeniu zarodka

G, przy tworzeniu zarodka

kulistego o promieniu

kulistego o promieniu

r; r*

r; r*

— promień krytyczny zarodka,

— promień krytyczny zarodka,

Δ

Δ

G

G

i

i

* — krytyczna energia swobodna zarodkowania

* — krytyczna energia swobodna zarodkowania

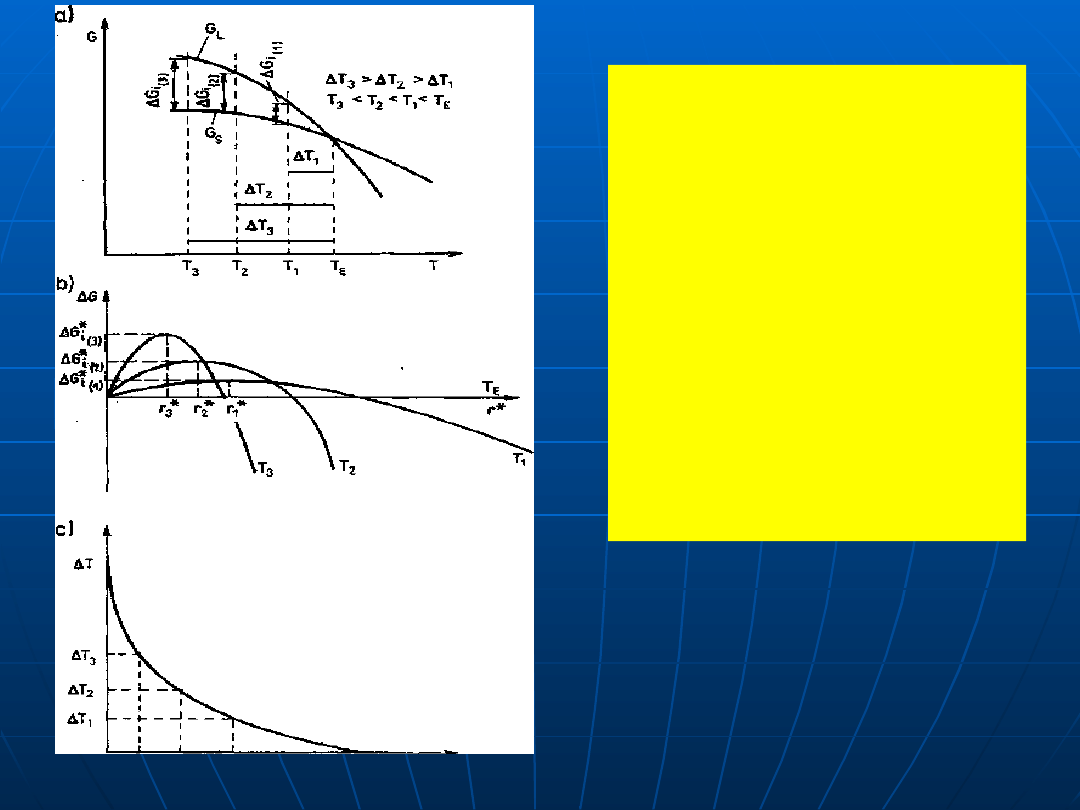
Wpływ przechłodzenia ΔT
i energii swobodnej

zarodkowania ΔG na

promień krytyczny

zarodka r*:

a) zależność

termodynamicznego

potencjału zarodkowania

ΔGi od przechłodzenia

ΔT1;

b) zależność promienia

zarodka krytycznego od

krytycznej energii

swobodnej zarodkowania

ΔGi*

i

i temperatury T;

c) zależność wielkości

zarodka krytycznego od

przechłodzenia ΔT

r*

Metal

Temperatura K

Nap. Pow.

10

-3

N/m

Metal

Temperatura K

Nap. Pow.

10

-3

N/m

Aluminium

933

860±20

Molibden

2893

2240

Antymon

900,5

395 ±20

Nikiel

1823

1924

Bizmut

544

380±10

Ołów

600

410 + 5

Chrom

1888

1420

Platyna

2273

1819

Cyna

505

525 ±10

Potas

373

573; 773

98

75; 54

Cynk

692,5

750±20

Rtęć

234,63 ;

273
373

473

573

623

500+15

470
450

430

410

400

Cyrkon

2173

1380

Gal

303

725 ±10

Iryd

2623

2310

Sód

373; 475

573

723

190; 180

171

156

Kadm

504

550±10

Kobalt

1823

1768

1936

1740

Srebro

1233,5

923

Krzem

1723

725 ±800

Srebro w fazie

stałej

1040

1235

Lit

459

430

Tytan

1998

1325

Magnez

923

520±10

Uran

1423

1020

Mangan

1533

1050

Wanad

1983

1710

Miedź -

1473

1300

Wapń

1083

255

Miedź w fazie

stałej

1100

1852

Wolfram

3653

2680

Złoto

1336

1128

Złoto w fazie

stałej

1260

1610

Żelazo

1823

1835



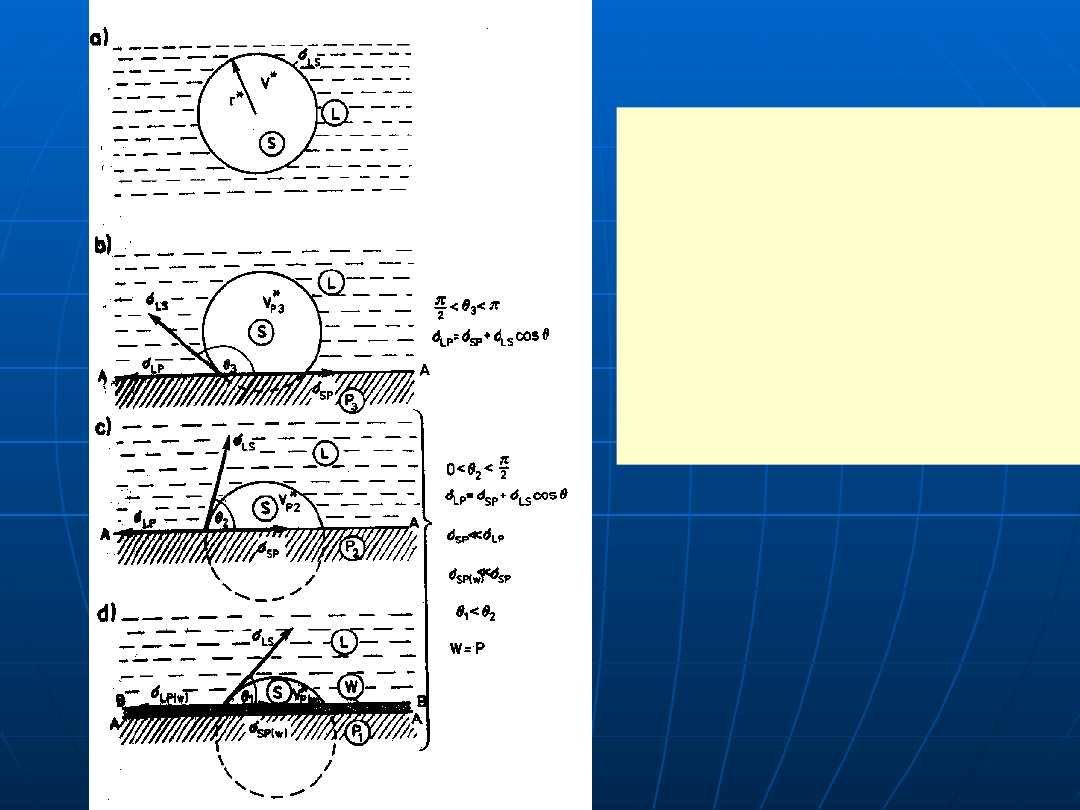
Schemat zarodka:

Schemat zarodka:



a) homogenicznego,

a) homogenicznego,



b), c), heterogenicznego,

b), c), heterogenicznego,



d) katalitycznego;

d) katalitycznego;

L — faza ciekła,

L — faza ciekła,

S

S

— faza

— faza

stała,

stała,

P

P

— podłoże,

— podłoże,

W

W

— warstwa przejściowa,

— warstwa przejściowa,

V*,r*

V*,r*

— objętość i promień

— objętość i promień

zarodka krytycznego

zarodka krytycznego



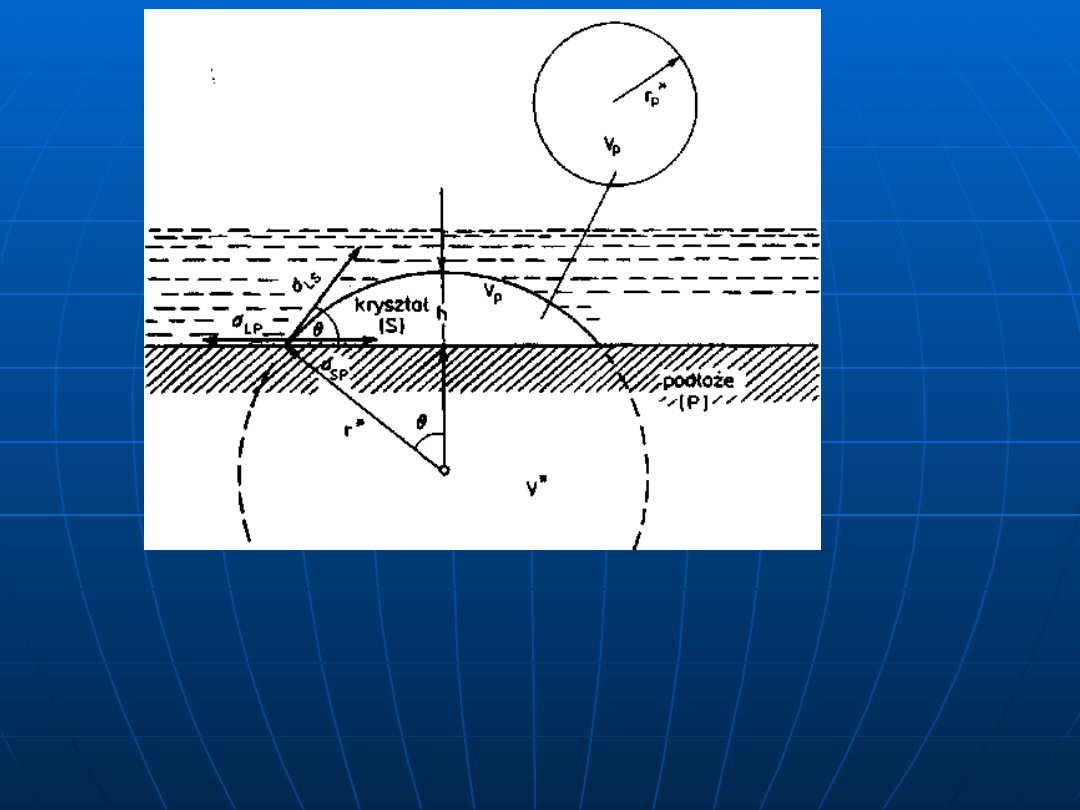
Zarodkowanie heterogeniczne (na podłożu

Zarodkowanie heterogeniczne (na podłożu

P); r*, V*

P); r*, V*

— promień i

— promień i

objętość zarodka homogenicznego, r

objętość zarodka homogenicznego, r

p

p

*,

*,

V

V

p

p

*

*

— promień i objętość

— promień i objętość

zarodka heterogenicznego (wycinka kulistego o wysokości

zarodka heterogenicznego (wycinka kulistego o wysokości

h

h

sprowadzonego do kuli)

sprowadzonego do kuli)

—_ciecz (L)



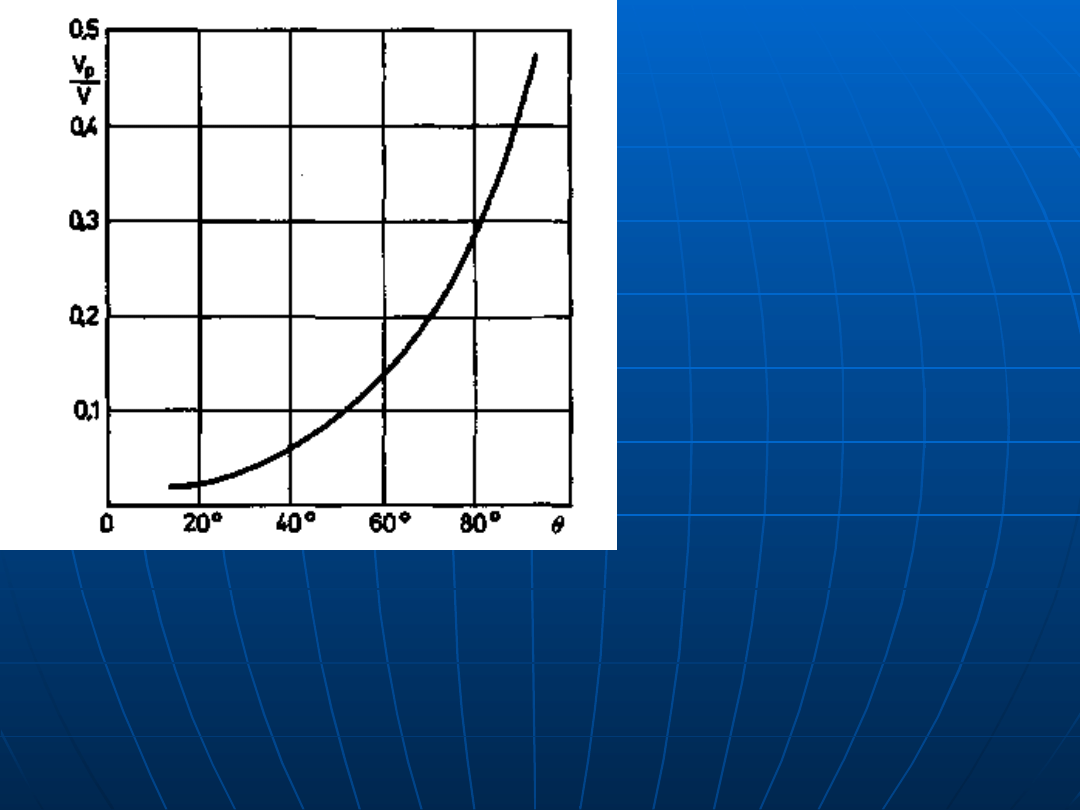
Zależność między stosunkiem objętości zarodka

Zależność między stosunkiem objętości zarodka

heterogenicznego

heterogenicznego

V*p

V*p

i homogenicznego

i homogenicznego

V

V

* a

* a

krawędziowym kątem zwilżania

krawędziowym kątem zwilżania

Θ

Θ



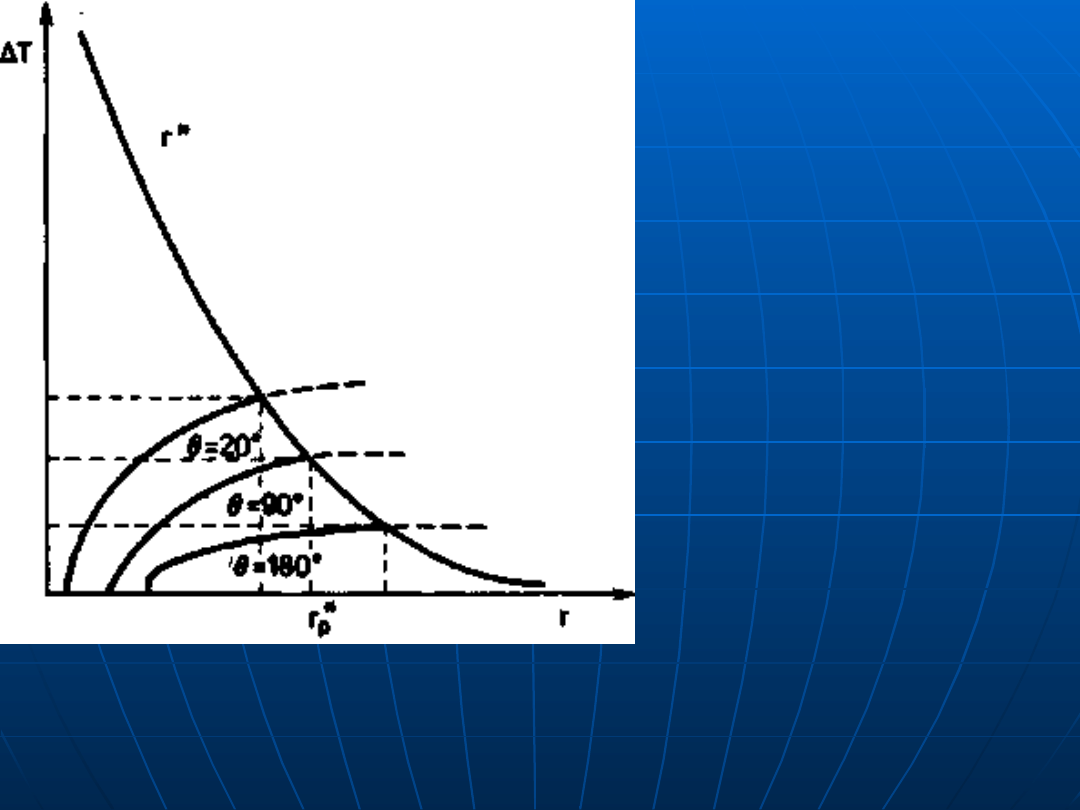
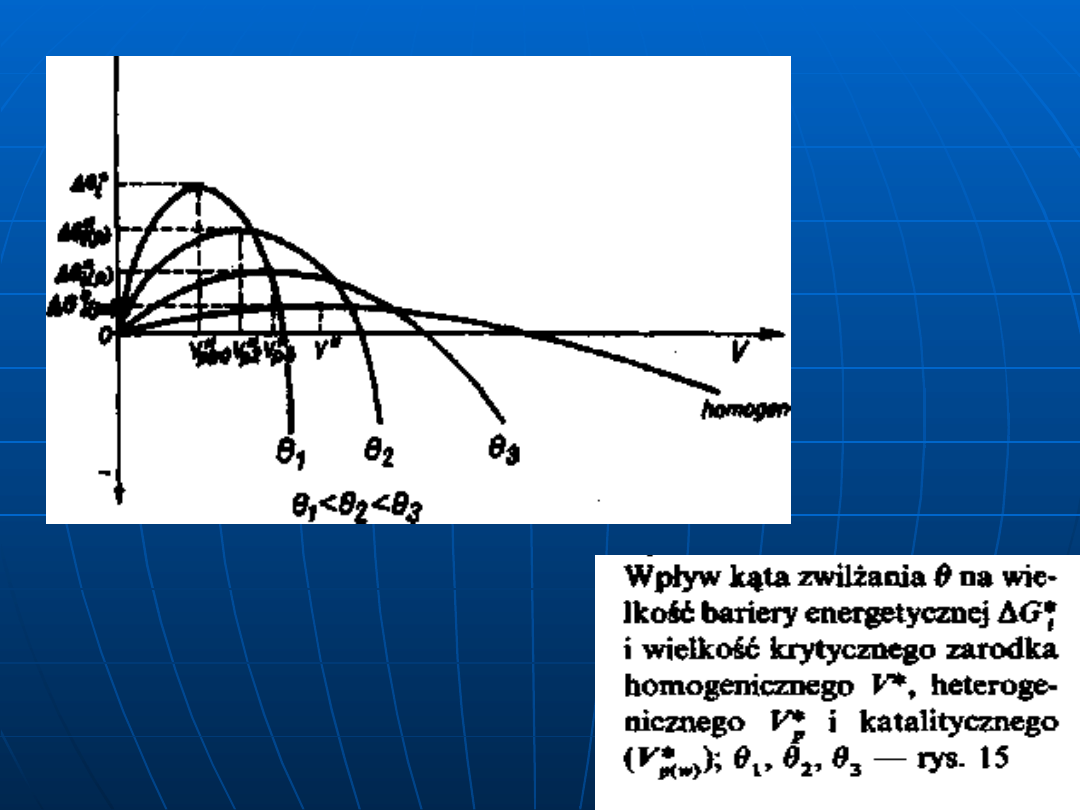
Schemat warunków zarodkowania

Schemat warunków zarodkowania

heterogenicznego w funkcji przechłodzenia

heterogenicznego w funkcji przechłodzenia

Δ

Δ

T i

T i

krawędziowego kąta zwilżania

krawędziowego kąta zwilżania



Energetyczna nadrzędność heterogenicznego zarodkowania

Energetyczna nadrzędność heterogenicznego zarodkowania

jest tak znaczna, iż nawet w czystych metalach przeważa

jest tak znaczna, iż nawet w czystych metalach przeważa

pierwszeństwo w tworzeniu zarodków heterogenicznych.

pierwszeństwo w tworzeniu zarodków heterogenicznych.

Miarą tych różnic może być wielkość przechłodzenia w

Miarą tych różnic może być wielkość przechłodzenia w

stosunku do zarodkowania homogenicznego. W badaniach

stosunku do zarodkowania homogenicznego. W badaniach

eksperymentalnych, gdzie z założenia dąży się do

eksperymentalnych, gdzie z założenia dąży się do

minimalizacji badanych objętości, chociażby dla

minimalizacji badanych objętości, chociażby dla

zmniejszenia prawdopodobieństwa oddziaływań wtrąceń

zmniejszenia prawdopodobieństwa oddziaływań wtrąceń

mogących być podkładką zarodkotwórczą, różnice w

mogących być podkładką zarodkotwórczą, różnice w

wielkości przechłodzenia mogą wynosić kilkadziesiąt stopni.

wielkości przechłodzenia mogą wynosić kilkadziesiąt stopni.

Dla przykładu podstawiając do wzoru na wielkość krytyczną

Dla przykładu podstawiając do wzoru na wielkość krytyczną

zarodka:

zarodka:



można wyznaczyć promień r* jako funkcję wielkości

można wyznaczyć promień r* jako funkcję wielkości

przechłodzenia. Przykładowa zależność dla miedzi:

przechłodzenia. Przykładowa zależność dla miedzi:

2

*

2

v

G

R











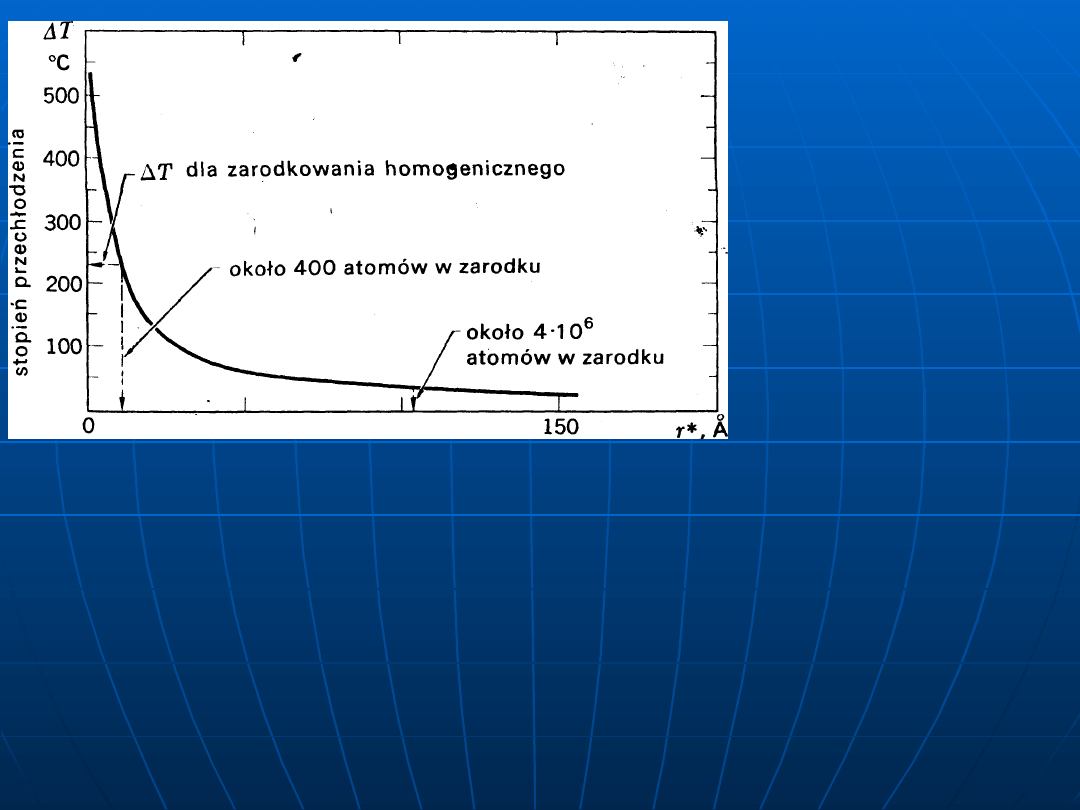
Zależność wielkości

Zależność wielkości

promienia

promienia

krytycznego

krytycznego

zarodka miedzi w

zarodka miedzi w

zależności od

zależności od

stopnia

stopnia

przechłodzenia ΔT

przechłodzenia ΔT



Podstawą analiz powinny być ze względu na procesy zarodkowania

Podstawą analiz powinny być ze względu na procesy zarodkowania

wielkości rzędu: {kilkudziesięciu ÷ kilkuset [Å]}. Wynika to z wielkości

wielkości rzędu: {kilkudziesięciu ÷ kilkuset [Å]}. Wynika to z wielkości

zarodków rzędu kilku – kilkudziesięciu [nm].

zarodków rzędu kilku – kilkudziesięciu [nm].



Na rysunku poniżej zakreskowany obszar oznacza intensywne

Na rysunku poniżej zakreskowany obszar oznacza intensywne

zarodkowanie dla kątów od 0÷25

zarodkowanie dla kątów od 0÷25

o

o

na płaszczyźnie, dla kątów 25÷45

na płaszczyźnie, dla kątów 25÷45

o

o

dla

dla

progów, krawędzi oraz 45÷90

progów, krawędzi oraz 45÷90

o

o

w szczelinach oraz 90÷120

w szczelinach oraz 90÷120

o

o

w we

w we

wgłębieniach 90÷120

wgłębieniach 90÷120

o

o

. Przy czym w większości przypadków głębokość

. Przy czym w większości przypadków głębokość

defektów powierzchniowych jest rzędu ok. 100 [Å]

defektów powierzchniowych jest rzędu ok. 100 [Å]



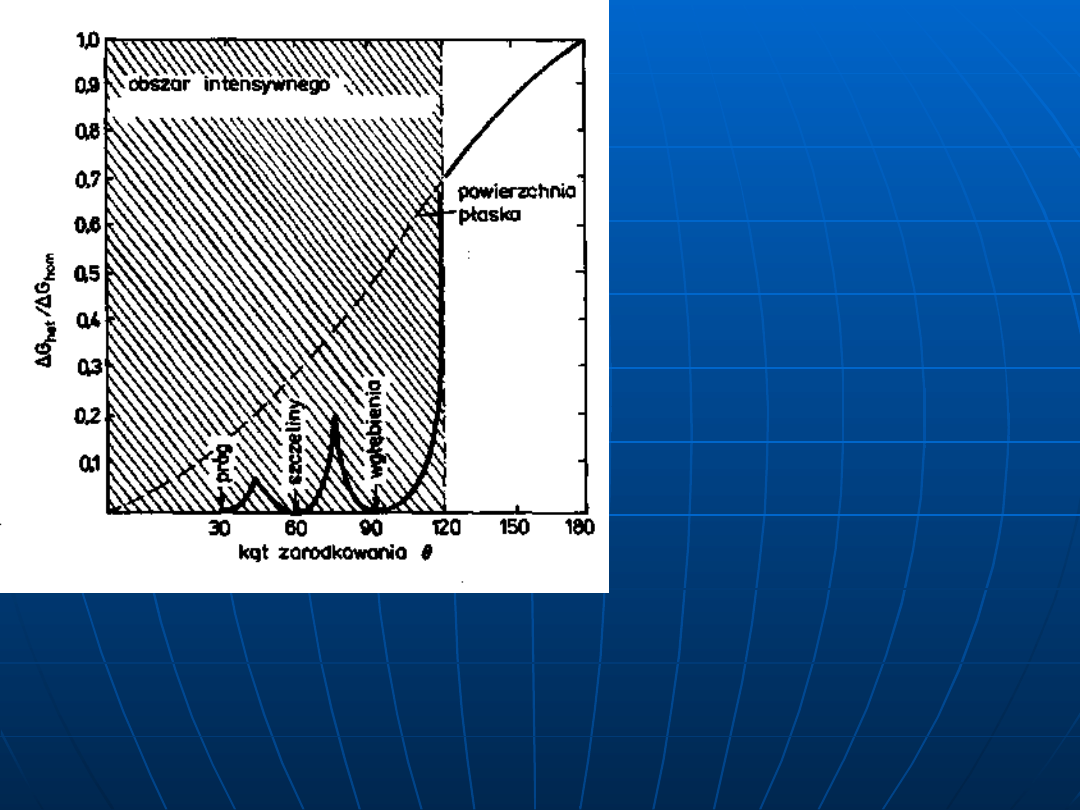
Porównanie energii stanu aktywowanego, niezbędnej do zarodkowania

Porównanie energii stanu aktywowanego, niezbędnej do zarodkowania

homogenicznego i heterogenicznego w zależności od nierówności na powierzchni

homogenicznego i heterogenicznego w zależności od nierówności na powierzchni

rozdziału fazy stałej i ciekłej

rozdziału fazy stałej i ciekłej

wg W. Missola

wg W. Missola

zarodkowania
heterogenicznego



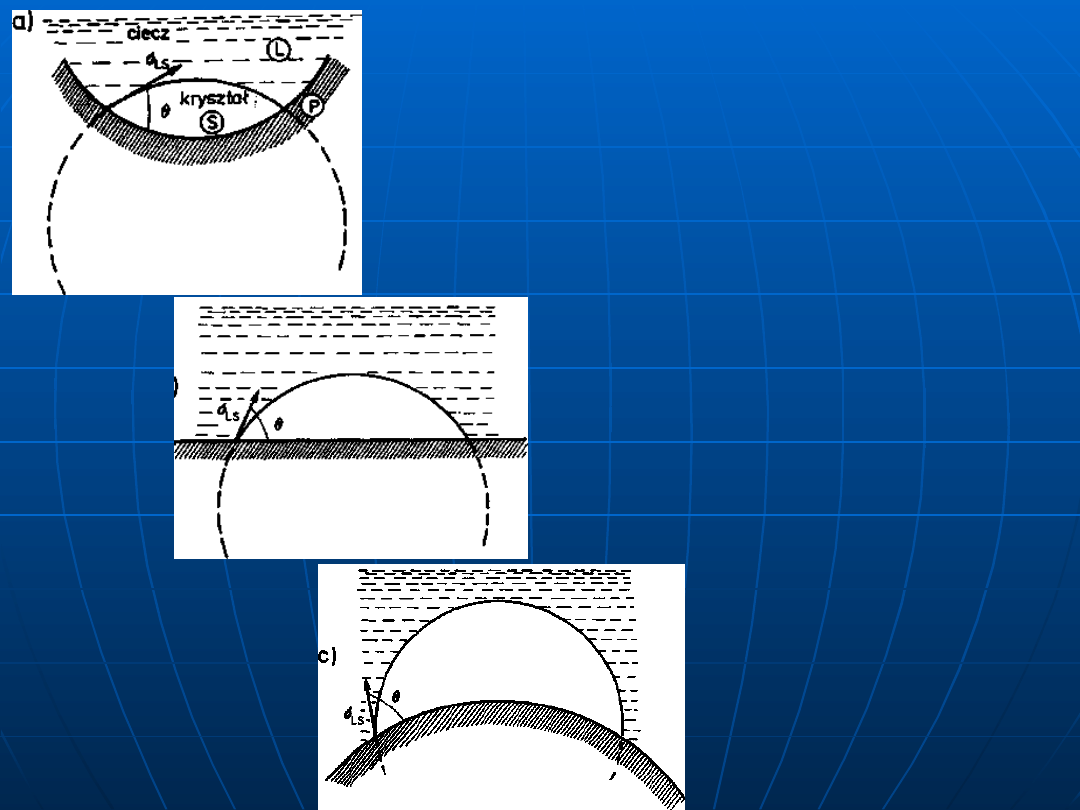
Tworzenie

Tworzenie

kryształów na

kryształów na

powierzchni

powierzchni

podłoża

podłoża

:

:



a) wklęsłej,

a) wklęsłej,



b) płaskiej

b) płaskiej



c) wypukłej

c) wypukłej



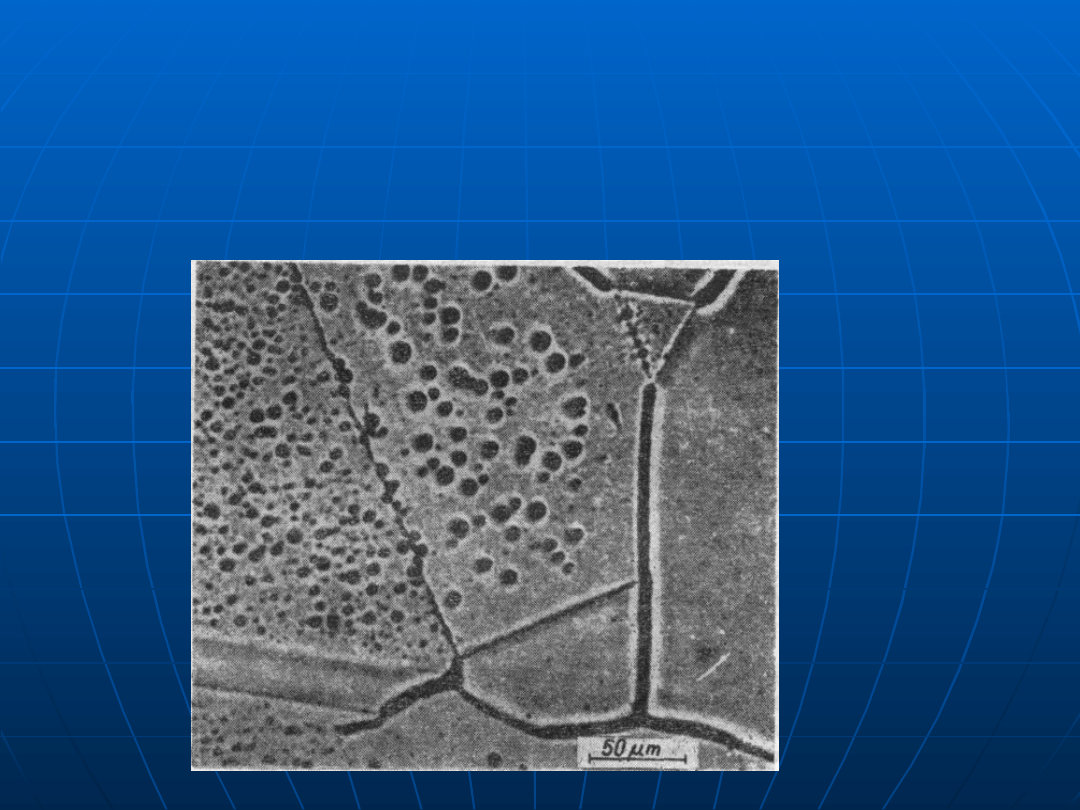
Przykładowe tworzenie jamek trawienia

Przykładowe tworzenie jamek trawienia

cieplnego na płaszczyznach (111) i (100)

cieplnego na płaszczyznach (111) i (100)

polikrystalicznego srebra (40 h, 700°C,

polikrystalicznego srebra (40 h, 700°C,

PH

PH

2

2

O/PH

O/PH

2

2

= 0,08)

= 0,08)



Kształt powierzchni międzyfazowej ciecz metaliczna – kryształ

Kształt powierzchni międzyfazowej ciecz metaliczna – kryształ

zależy m. in. od gradientu temperatury w pobliżu frontu

zależy m. in. od gradientu temperatury w pobliżu frontu

krystalizacji. Tiller dokonał szacunkowej oceny wpływu dyfuzji

krystalizacji. Tiller dokonał szacunkowej oceny wpływu dyfuzji

składnika oraz transportu ciepła [81]. Odległość, na którą

składnika oraz transportu ciepła [81]. Odległość, na którą

następuje dyfuzja w jednostce czasu przy jednostkowym

następuje dyfuzja w jednostce czasu przy jednostkowym

gradiencie stężenia jest około sto razy mniejsza niż droga

gradiencie stężenia jest około sto razy mniejsza niż droga

przemieszczenia frontu krystalizacji. Natomiast odległość, na którą

przemieszczenia frontu krystalizacji. Natomiast odległość, na którą

przenoszone jest ciepło w jednostce czasu przy jednostkowym

przenoszone jest ciepło w jednostce czasu przy jednostkowym

gradiencie temperatury jest ok. sto razy większa niż wielkość

gradiencie temperatury jest ok. sto razy większa niż wielkość

przemieszczenia frontu krystalizacji. Powierzchnia międzyfazowa,

przemieszczenia frontu krystalizacji. Powierzchnia międzyfazowa,

która szybciej reaguje na zmianę warunków termodynamicznych

która szybciej reaguje na zmianę warunków termodynamicznych

dominuje w kształtowaniu struktury

dominuje w kształtowaniu struktury



Rozwinięta powierzchnia międzyfazowa może być definiowana za

Rozwinięta powierzchnia międzyfazowa może być definiowana za

pomocą promienia krzywizny. Może być rozpatrywana w

pomocą promienia krzywizny. Może być rozpatrywana w

kategoriach przyrostu temperatury lub ciśnienia lub też zmiany

kategoriach przyrostu temperatury lub ciśnienia lub też zmiany

stężenia – głównych czynników krystalizacyjnych. Jeśli w

stężenia – głównych czynników krystalizacyjnych. Jeśli w

analizowanej przestrzeni napięcie powierzchniowe σ jest

analizowanej przestrzeni napięcie powierzchniowe σ jest

izotropowe wówczas przyrost energii swobodnej spowodowanej

izotropowe wówczas przyrost energii swobodnej spowodowanej

obecnością powierzchni zakrzywionej o promieniu r wynosi:

obecnością powierzchni zakrzywionej o promieniu r wynosi:

H

G





2





gdzie:

H

to uśredniona krzywizna



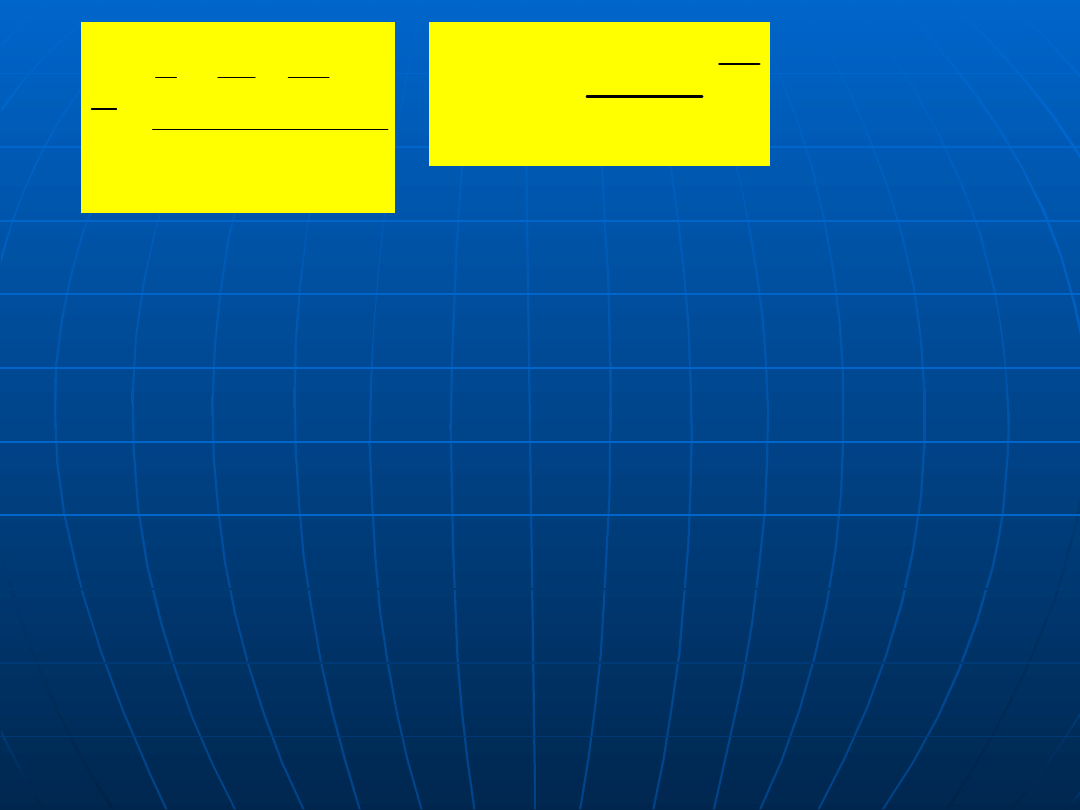
ΔGρ – zmiana energii swobodnej wywołana krzywizną

ΔGρ – zmiana energii swobodnej wywołana krzywizną



ρ1 ρ2, - zorientowane promienie główne prostopadłych krzywizn

ρ1 ρ2, - zorientowane promienie główne prostopadłych krzywizn

powierzchni kryształu.

powierzchni kryształu.



Klasyczna postać równania Gibbsa-Thomsona pokazuje zależność

Klasyczna postać równania Gibbsa-Thomsona pokazuje zależność

równowagowej temperatury krystalizacji powierzchni płaskiej Te i

równowagowej temperatury krystalizacji powierzchni płaskiej Te i

zakrzywionej Tρ frontu krystalizacji. Zależność odnosi się zasadniczo

zakrzywionej Tρ frontu krystalizacji. Zależność odnosi się zasadniczo

do czystych metali. Zakłada się równość równowagowych

do czystych metali. Zakłada się równość równowagowych

współczynników rozdziału składnika między cieczą i kryształem

współczynników rozdziału składnika między cieczą i kryształem

zakrzywionym i płaskim. Jeśli przyjąć, że promienie

zakrzywionym i płaskim. Jeśli przyjąć, że promienie

r

r

prostopadłe

prostopadłe

krzywizn są równe, co odpowiada powierzchni sferycznej wówczas

krzywizn są równe, co odpowiada powierzchni sferycznej wówczas

przyrost temperatury zależąc od promienia krzywizny r jest dwa razy

przyrost temperatury zależąc od promienia krzywizny r jest dwa razy

wyższy niż w przypadku powierzchni jednokrotnie zakrzywionej – np.

wyższy niż w przypadku powierzchni jednokrotnie zakrzywionej – np.

walcowej. Przykład wpływu obu przypadków wskazuje na skalę

walcowej. Przykład wpływu obu przypadków wskazuje na skalę

oddziaływań. Wzrost rozwinięcia powierzchni heterogenicznego

oddziaływań. Wzrost rozwinięcia powierzchni heterogenicznego

zarodkowania a tym samym wzrost powierzchni frontu wzrostu

zarodkowania a tym samym wzrost powierzchni frontu wzrostu

kryształów oraz minimalizacja promienia krzywizn celowo

kryształów oraz minimalizacja promienia krzywizn celowo

kształtowanych powierzchniowo komponentów zbrojących, prowadzi

kształtowanych powierzchniowo komponentów zbrojących, prowadzi

do zmniejszania równowagowej temperatury krystalizacji.

do zmniejszania równowagowej temperatury krystalizacji.





















F

F

dF

dF

H

2

1

1

1

2

1





H

L

T

T

e





2







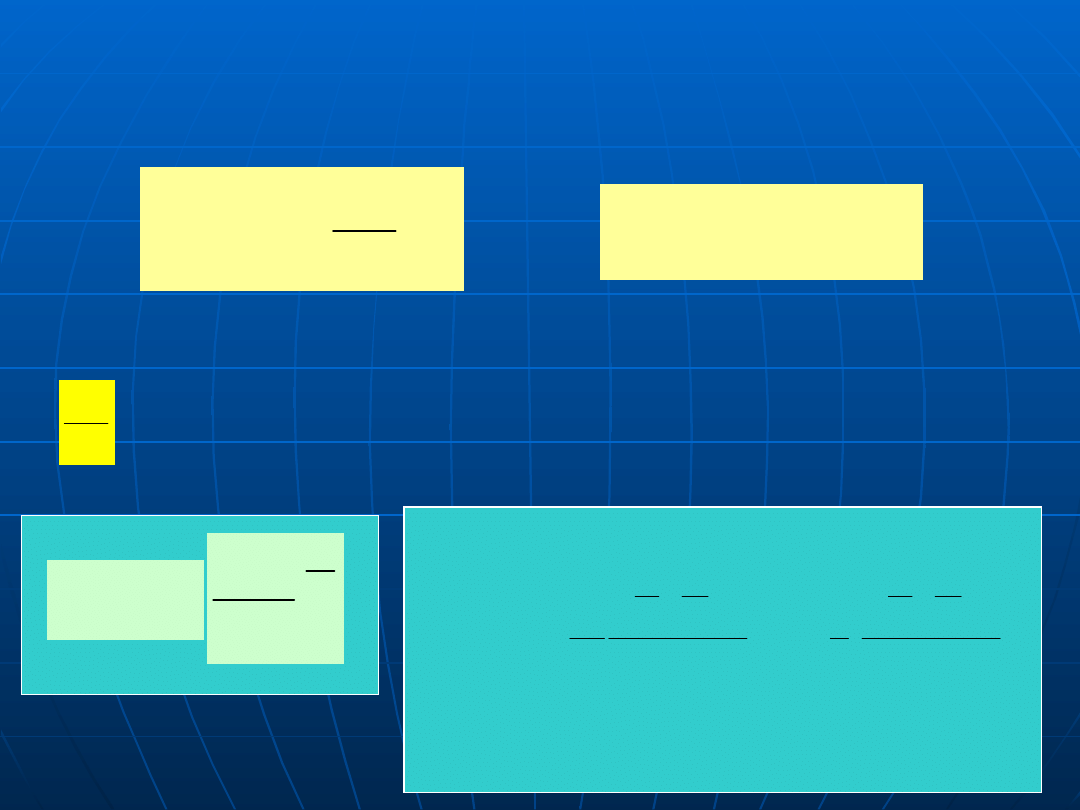
Promień krzywizny powierzchni międzyfazowej

Promień krzywizny powierzchni międzyfazowej

ciecz-ciało stałe można wyznaczyć korzystając z

ciecz-ciało stałe można wyznaczyć korzystając z

warunku

warunku

x

dx

dT

T

T

e

x









T

T

T

e

x







gdzie: T

x

– temperatura powierzchni rozdziału ciecz- ciało stałe,

dx

dT

- gradient temperatury, Δx – przemieszczenie względem izotermy T

e

;

T

e

równowagowa temperatura krystalizacji czystego metalu

Po podstawieniu:





e

x

T

T

H

L

T

e



2





e

x

T

T







































































F

F

e

F

F

e

dF

dF

L

T

dF

dF

L

T

2

1

2

1

1

1

1

1

1















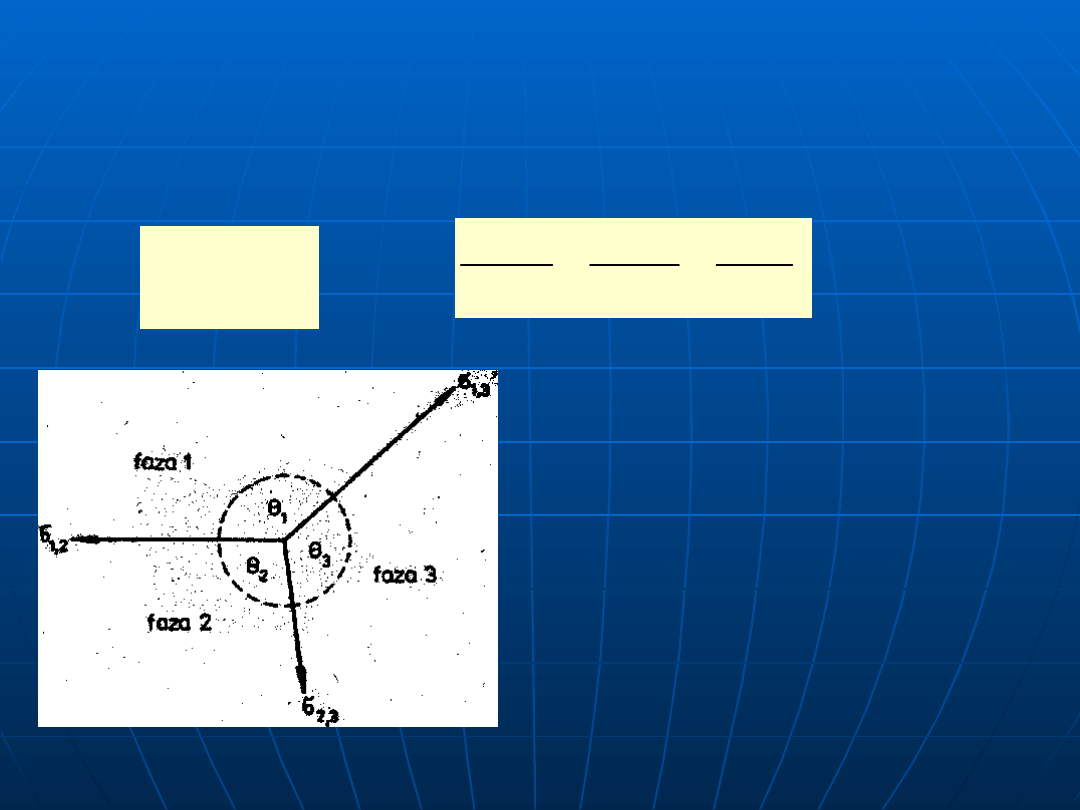
Rozpatrując prosty przypadek równowagi sił

Rozpatrując prosty przypadek równowagi sił

powierzchniowych dwufazowej osnowy i

powierzchniowych dwufazowej osnowy i

cząstki zbrojącej spełniony musi być

cząstki zbrojącej spełniony musi być

warunek Neumana, równości napięć

warunek Neumana, równości napięć

powierzchniowych:

powierzchniowych:

0

1





i



2

31

1

23

3

12

sin

sin

sin

















Równowaga granic rozdziału w

Równowaga granic rozdziału w

układzie trójfazowym

układzie trójfazowym

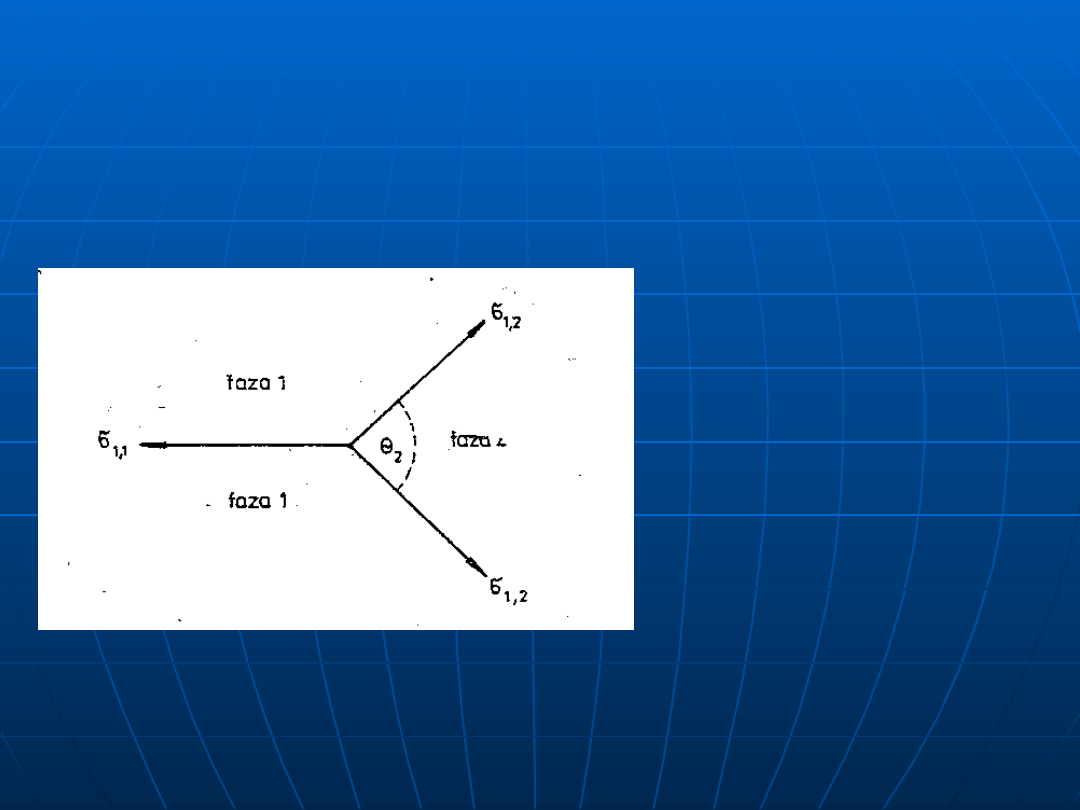
Granice między ziarnami tej samej fazy mają

Granice między ziarnami tej samej fazy mają

jednakowe energie powierzchniowe, natomiast

jednakowe energie powierzchniowe, natomiast

granice między ziarnami różnych faz mają inne

granice między ziarnami różnych faz mają inne

wartości energii powierzchniowych i inne napięcia

wartości energii powierzchniowych i inne napięcia

powierzchniowe

powierzchniowe

Równowagowy dwuścienny kąt zwilżania Θ2 na
styku dwóch ziarn jednej fazy z drugą fazą



Uzyskanie płaskich ścian jest możliwe

Uzyskanie płaskich ścian jest możliwe

tylko wówczas, gdy układ ma

tylko wówczas, gdy układ ma

zrównoważone nadmiary

zrównoważone nadmiary

powierzchniowe energii, czyli jest

powierzchniowe energii, czyli jest

stabilny. Kąty tetraedryczne dążą do

stabilny. Kąty tetraedryczne dążą do

wartości 109,5

wartości 109,5

o

o

. Warunki związane z

. Warunki związane z

wypełnieniem przestrzeni i

wypełnieniem przestrzeni i

równowagi napięć powierzchniowych

równowagi napięć powierzchniowych

spełniają ziarna w postaci

spełniają ziarna w postaci

czternastościanów

czternastościanów

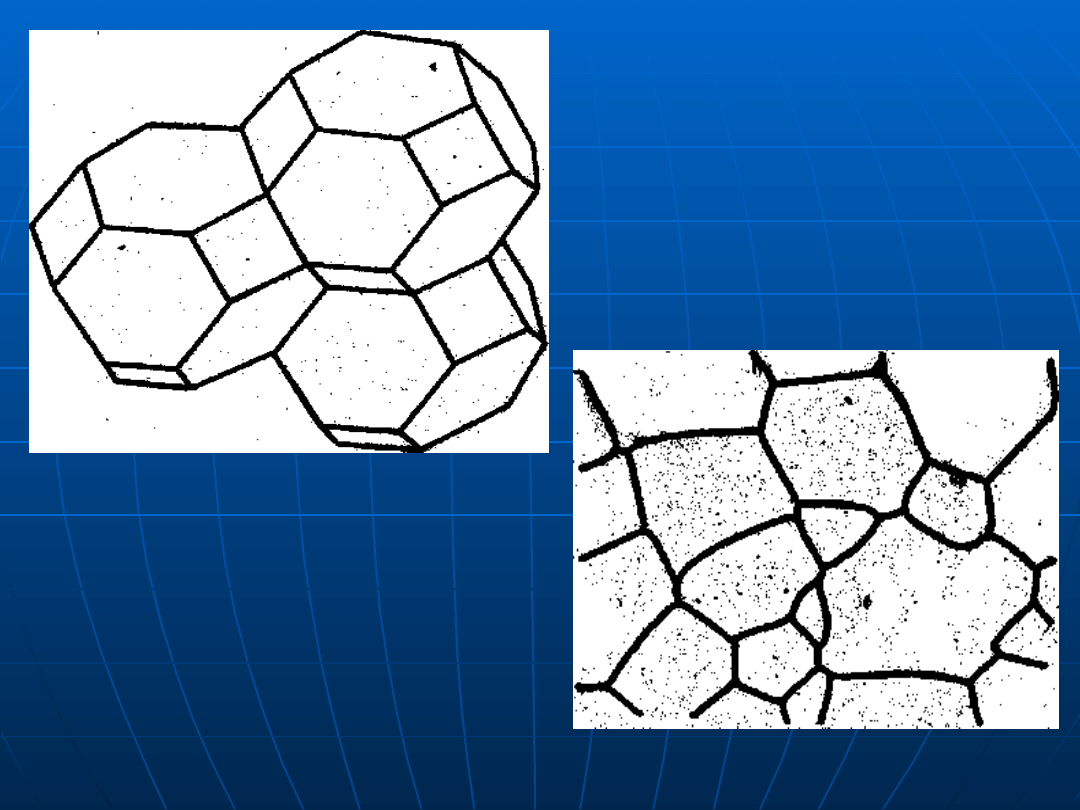
Ułożenie i kształt ziarn
wypełniających przestrzeń w pełni
przy zachowaniu płaskich ścian:

model czternastościany

oraz

powierzchnia odpowiadającego
modelowi zgładu



Przy krystalizacji pojedynczych kryształów

Przy krystalizacji pojedynczych kryształów

równowagowy kształt odpowiada minimalnej

równowagowy kształt odpowiada minimalnej

energii powierzchniowej przy stałej objętości.

energii powierzchniowej przy stałej objętości.

Wynika to z prawa Gibbsa:

Wynika to z prawa Gibbsa:



Kształt kulisty jest uprzywilejowany z

Kształt kulisty jest uprzywilejowany z

założenia w warunkach izotropowego pola

założenia w warunkach izotropowego pola

napięcia powierzchniowego. Przy anizotropii

napięcia powierzchniowego. Przy anizotropii

napięcia powierzchniowego spowodowanego

napięcia powierzchniowego spowodowanego

odmiennością energii powierzchniowych w

odmiennością energii powierzchniowych w

zależności od orientacji krystalograficznej na

zależności od orientacji krystalograficznej na

powierzchnia kryształu wystąpią granice o

powierzchnia kryształu wystąpią granice o

niesferycznych kształtach. Kształt ziarna wg

niesferycznych kształtach. Kształt ziarna wg

Wulfa pokazany na rysunku powiązany z

Wulfa pokazany na rysunku powiązany z

energiami i napięciami powierzchniowymi:

energiami i napięciami powierzchniowymi:





i

i

i

F min



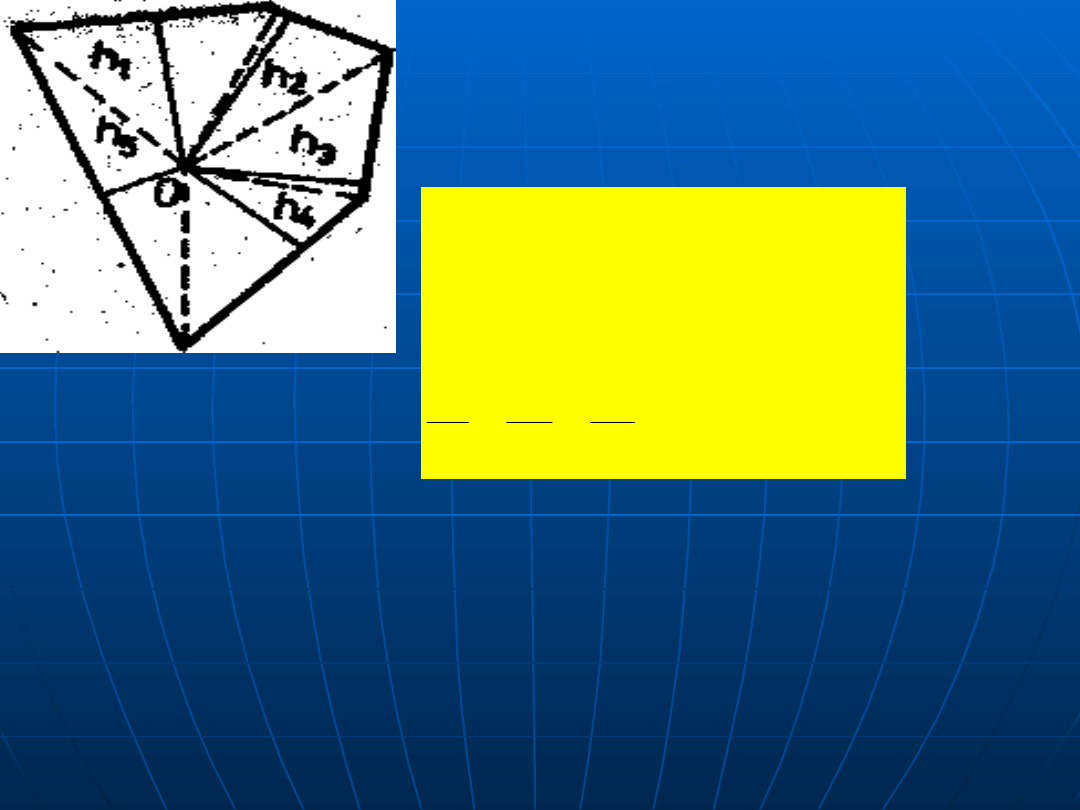
Kryształ Wulfa

Kryształ Wulfa

const

h

h

h

h

h

h

b

E

h

h

h

d

V

h

h

h

b

F

































....

...)

(

...)

(

...)

(

3

3

2

2

1

1

2

3

3

2

2

2

2

1

1

3

3

3

2

3

1

2

3

2

2

2

1















gdzie: F, V, odpowiednio powierzchnia całkowita , objętość
kryształu, b, d – stałe zależne od kształtu, σi napięcie
powierzchniowe na ścianie przy wysokości hi zgodnie z
rysunkiem