Modele obciążeń stawu

biodrowego



Staw biodrowy stanowi niezwykle istotny element łańcucha
kinematycznego kończyny dolnej, poddany stosunkowo dużym
obciążeniom przenoszonym z korpusu na kończynę dolną.
Obciążenia powierzchni stawowych wynikające z aktywności
fizycznej, a w szczególności chodu są wynikiem całego szeregu
oddziaływań zewnętrznych i reakcji pochodzących od współdziałania
elementów układu kostno-stawowego, układu więzadłowego oraz
układu mięśniowego.



Istnieje wiele modeli obciążenia stawu biodrowego , które w sposób
uproszczony opisują zarówno kierunki jak i wartości sił obciążających
poszczególne elementy stawu biodrowego. Biorąc pod uwagę niezwykle
złożony system oddziaływań pomiędzy wszystkimi kośćmi i tkankami
miękkimi zgrupowanymi w rejonie obręczy biodrowej, wprowa dzenie
pewnych uproszczeń w proponowanych modelach jest naturalne i jak
najbardziej uzasadnione, z drugiej jednak strony może to prowadzić do zbyt
jednostronnego spojrzenia na mechanikę stawu biodrowego. Wraz z
rozwojem wiedzy modele stopniowo stają się bardziej złożone, coraz więcej
grup mięśniowych (spośród 30 otaczających staw biodrowy) jest
uwzględnianych w obliczeniach sił obciążających powierzchnie stawowe.

Jeden z pierwszych modeli obciążenia stawu biodrowego to

model Pauwelsa .
Jest to stosunkowo prosty model uwzględniający jedynie dwie grupy
mięśniowe stabilizujące staw w płaszczyźnie czołowej.

Pauwels w swej pracy uznał, że obciążenia powstające w

trakcie stania na jednej kończynie dolnej (np. w fazie podporowej
chodu), są jednymi z największych jakie oddziałują na staw biodrowy
człowieka.

Pauwels rozważał zatem układ równowagi momentów sił wokół

środka głowy kości udowej, który uznał jednocześnie za środek obrotu
stawu.

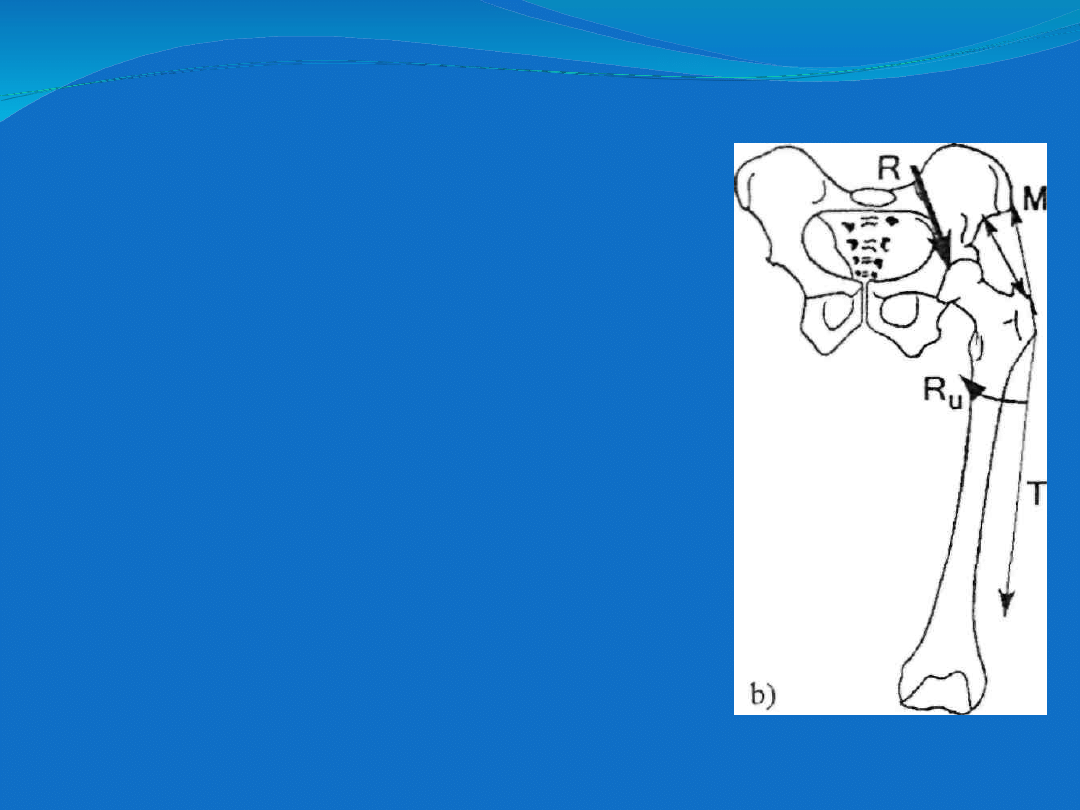
Model obciążenia stawu biodrowego (wg Pauwelsa).

Siły zewnętrzne jakie działają na
staw biodrowy to w tym przypadku
ciężar części ciała znajdującej się
powyżej stawu biodrowego. Jest on
równoważony przez napięcie mięśni
pośladkowych (gluteus mazimus,
gluteus medius).
Reakcja powstająca na powierzchni
stawowej głowy kości udowej jest
wynikiem obu tych oddziaływań.
Pasmo biodrowo-piszczelowe (tractus
iliotibialis) wg Pauwelsa ściśle
połączone z krętarzem większym oraz
stawem kolanowym zapobiega
jedynie nadmiernemu zginaniu kości
udowej.

Pauwels F.:

Biomechanics of the locomotour apparatus, Berlin

1976.

Model obciążenia stawu biodrowego (wg

Maqueta)

Kolejny model został zaproponowana
przez Maqueta, który odmiennie
rozumiał oddziaływanie i funkcje pasma
biodrowo-piszczelowego.
W modelu Maqueta przesuwa się ono
swobodnie po powierzchni krętarza
większego powodując powstanie reakcji
zwróconej prostopadle do powierzchni
krętarza w kierunku przyśrodkowym.
Powoduje to zarówno zmianę proporcji
sił powstających wokół stawu biodrowego
jak również kierunek i wartość reakcji
obciążającej głowę kości udowej.

Maquet P.G.J.:

Biomechanics of the hip,

Berlin 1985

Oba wymienione powyżej modele

uwzględniają, jedynie grupy mięśniowe

oddziałujące głównie w płaszczyźnie

czołowej, podczas gdy rzeczywista

Sytuacja jest bardziej złożona i

obejmuje

również oddziaływania w pozostałych

płaszczyznach podstawowego układu

współrzędnych.

Model autorski (powstał w Zakładzie

Doświadczalnej Analizy Konstrukcji

Inżynierskich i Biomechanicznych)

W tym modelu pasmo biodrowo piszczelowe

również

miało

możliwość

przesuwania

się

po

powierzchni

krętarza większego kości udowej.
Na podstawie analizy szeregu prac powstał

również

model uwzględniający inne grupy mięśniowe
(gluteus minimus, iliopsoas), oraz sytuacje

bardziej

złożone niż niesymetryczne stanie na jednej
kończynie dolnej (wchodzenie po schodach,
wstawanie z krzesła) .

Bernakiewicz R

.: Opracowanie kryteriów odkształceniowo-

naprężeniowych doboru implantów stawu biodrowego, Praca doktorska,
Raport Instytutu Konstrukcji i Eksploatacji Maszyn Politechniki Wrocław
skiej Serii PRE-010/98, Wrocław 1998.

''Łuki gotyckie" struktur

kostnych w okolicy panewki

stawu biodro wego.

Również Bombelli w swoich

pracach uznaje istotną rolę

oddziaływania mięśni zginaczy uda jak

iliopsoas w obciążeniu stawu

biodrowego, argumentując

powstawanie pewnych struktur

kostnych (łuki gotyckie) jako rezultatu

oddziaływania sił wzdłuż osi tych

mięśni

Bombelli R.: Structure and function of
normal and abnormal hips, Berlin 1993.

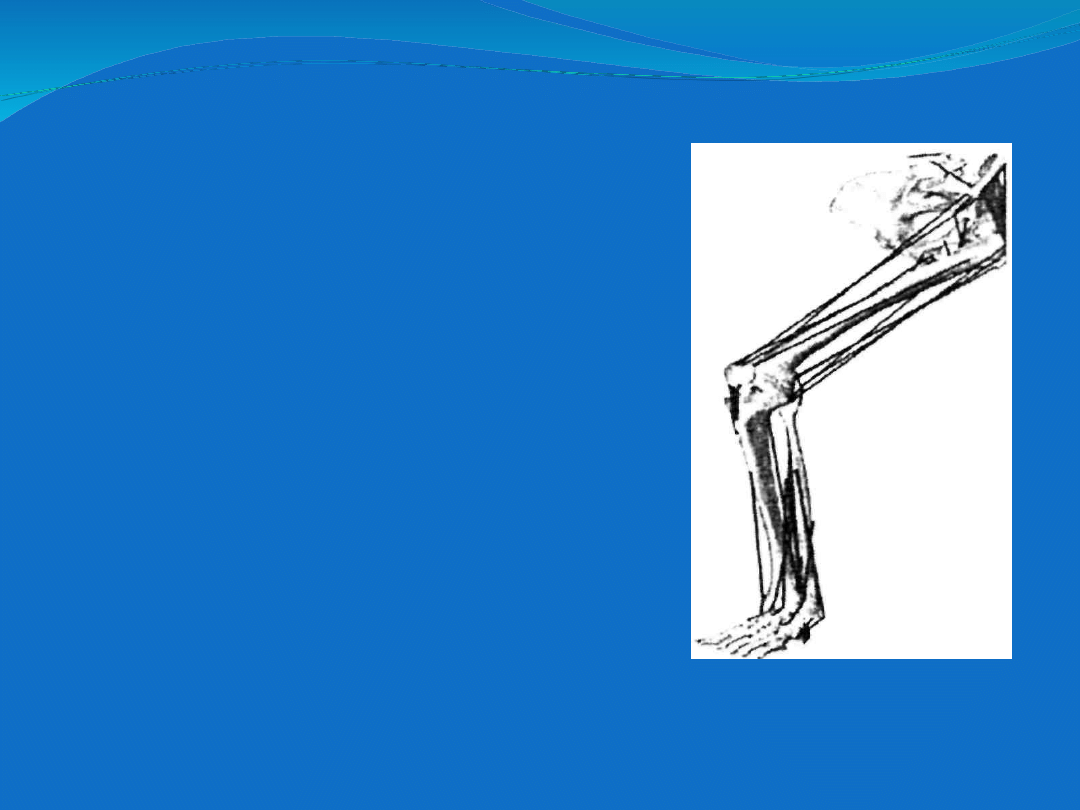
Model układu kostno-stawowego i

mięśniowego

(wg Pohla i Dudy).

Współczesne metody numeryczne
pozwalają na uzyskanie złożonych
modeli obciążenia uwzględniających
większość

grup

mięśniowych

biorących

udział w przenoszeniu obciążenia oraz
ruchu kończyny dolnej.
W pracach Pohla, Dudyinn. , został
opracowany na podstawie danych
Visible Humań Project pełny model
całej kończyny dolnej, który umożliwia
określanie sił mięśniowych oraz
reakcji

w

stawach

zarówno

w

sytuacjach

obciążenia statycznego jak

i dynamicznego

.

Heller M.O., Bergmann G., Deuretzbacher G., Durselen L., Pohl M., Claes L., Haas N.P.,
Duda G

.: Musculo-skeletal loading conditions at the hip during walking and stair climbing, Journal

of Biomechanics, vol.32, str.883-893, 2001.

Pohl M, Duda G., Heller M., Cleas L.:

A realistic model for the simula-tion of loading of the

human lower extremity, Proceedings of the 12th Conference of the European Society of
Biomechanics, Dublin 2000.

Na szczególną uwagę zasługują również prace doświadczalne z zakresu
biomechaniki stawu biodrowego mające na celu dokładne określenie
rzeczywistych obciążeń występujących w stawie biodrowym .

Prace Bergmana i innych – prowadzone przy użyciu specjalnego rodzaju

implantów stawu biodrowego zaopatrzonych w czujniki sił przenoszonych
przez implant oraz oprzyrządowanie telemetryczne umożliwiające
przekazywania sygnałów poza organizm umożliwiły określenie
rzeczywistych sił działających na staw biodrowy w czasie chodu.

Pomiary prowadzone na pacjentach, ze sztucznym stawem biodrowym

nie odpowiadają co prawda w pełni rzeczywistemu obciążeniu stawu
biodrowego zdrowego człowieka, jednakże stanowią ogromny krok naprzód
w tej dziedzinie biomechaniki, a w połączeniu z rozbudowanymi modelami
numerycznymi pozwalają na analizę wielu problemów związanych ze
schorzeniami stawu biodrowego i jego leczeniem (w tym przez
implantacje).

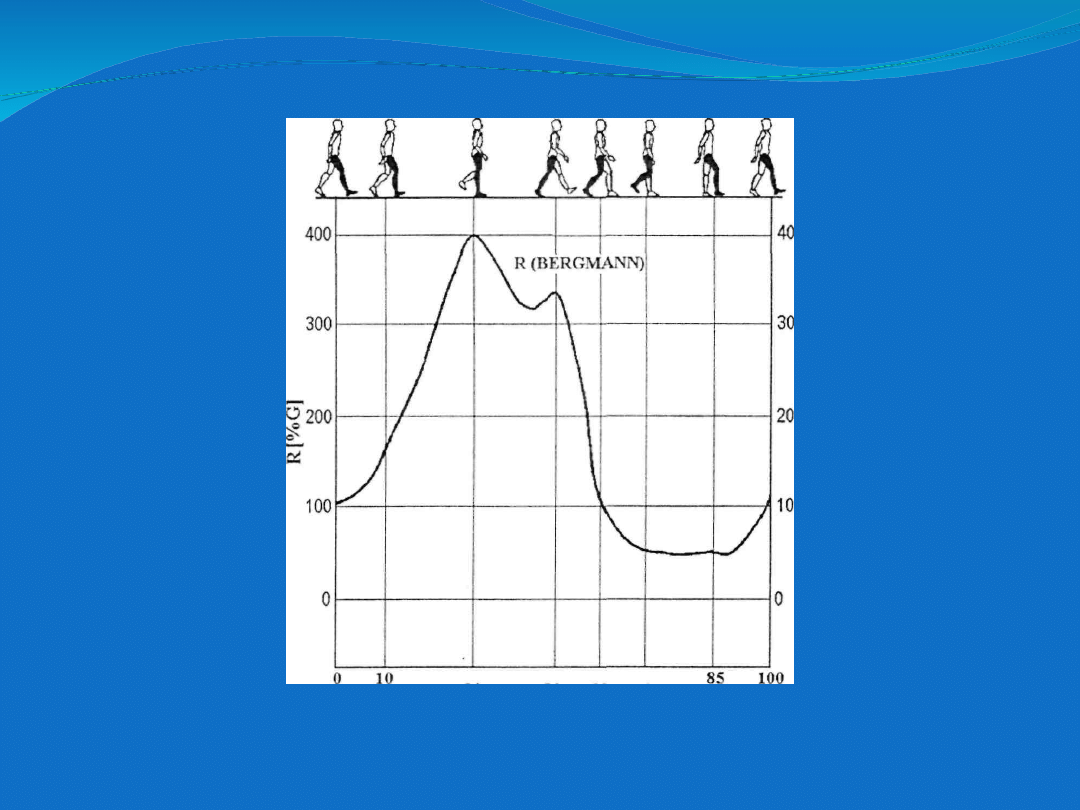
Przebieg sil w stawie biodrowym w jednym cyklu

chodu

(wg Bergmana).

% fazy chodu
(cyklu)

Staw biodrowy przy stosunkowo

dużym obciążeniu jest również

jednym ze stawów najczęściej

narażonych na

zniszczenie lub uszkodzenie .



Będziński R., Bernakiewicz M., Ścigała K.: Biomechanical
aspects of artificial joint implantation in a lower limb, Journal
of Theoretical and Applied Mechanics, Vol,37, Nr 3, str.455-
481, 1999.



Będziński R.: Biomechanika Inżynierska, Zagadnienia
wybrane, Wrocław 1997.



Bernakiewicz R.: Opracowanie kryteriów odkształceniowo-
naprężeniowych doboru implantów stawu biodrowego, Praca
doktorska, Raport Instytutu Konstrukcji i Eksploatacji Maszyn
Politechniki Wrocław skiej Serii PRE-010/98, Wrocław 1998

Skuteczne leczenie zmian degeneracyjnych stawu to jedno z
najważniejszych zadań współczesnej ortopedii.

Co prawda operacyjne metody leczenia schorzeń stawu biodrowego
to jedne z najczęściej i najpowszechniej stosowanych technik
leczenia, jednakże duży odsetek zabiegów wciąż obarczony jest
niepowodzeniem lub powikłaniami. Biorąc pod uwagę, że w wielu
przypadkach jest to jedyna metoda przywrócenia aktywności
fizycznej pacjenta oraz rosnącą ilość zabiegów wykonywanych
rocznie konieczne jest opracowanie lepszych, nowocześniejszych
rozwiązań pozwalających na zapobieganie niepożądanych skutków
zabiegu, zarówno o
podłożu klinicznym jak i mechanicznym i biologicznym.

Konieczne jest również opracowanie zbioru
wytycznych i kryteriów doboru implantu dla
danego przypadku chorobowego nie tylko z
punktu widzenia praktyki klinicznej ale również z
punktu widzenia biomechaniki

.

Tymczasem wiele spośród problemów

dotyczących endoprotezoplastyki stawu

biodrowego wciąż pozostaje

nierozwiązana.

BIOAKCEPTOWALNOŚĆ BIOKOMPATYBILNOŚĆ

PRZEBUDOWA TKANKI KOSTNEJ I STRESS SHIELDING

ZUŻYCIE ZASTĘPCZYCH POWIERZCHNI STAWOWYCH

OBLUZOWANIA PANEWKI

OBLUZOWANIA TRZPIENIA

ZŁAMANIA TRZPIENIA

INFEKCJA

975

1971

1980

1999

2000

Rozwiązania

najbardziej

palących

problemów

protezowania stawu biodrowego poszukuje się zarówno na bazie
badań

klinicznych

jak

i biomechanicznych.

Badania kliniczne koncentrują się wokół zapobiegania

infekcjom oraz powstającym na ich bazie septycznym
obluzowaniom trzpieni endoprotez.

Są one najczęstszą pierwotną przyczyną niepowodzeń

alloplastyki.

Obluzowania

aseptyczne

mają

najczęściej

podłoże

biomechaniczne

związane

z

nieprawidłowymi

relacjami

odkształceniowo-naprężeniowymi
w układzie trzpień-kość, bądź brakiem biozgodności bądź co
najmniej bioakceptowalności materiałów z których wykonane są
endoprotezy.

Zarówno w przypadku endoprotez cementowych jak

i bezcementowych można obserwować w wielu przypadkach
efekty negatywnej przebudowy tkanki kostnej wywołane zmianą
stanu naprężeń i odkształceń tkanki kostnej w wyniku
wprowadzenia metalicznego implantu.

Można w tym przypadku mówić zarówno

o przebudowie tkanki kostnej, zmianie jej
własności
mechanicznych, a nawet kształtu kości
wywołanych nadmiernym wzrostem poziomu
odkształceń, bądź zmianą ich rozkładu
(remodeling) jak i o swoistej osteoporozie
tkanki kostnej (zaniku nośnych struktur
kostnych,

znacznym

spadku

własności

mechanicznych tkanki kostnej) wywołanej
powstaniem naprężeniowych stref ochronnych
(stress shielding).

Badania biomechaniczne stawu

biodrowego koncentrują się zatem wokół

określenia:

1.rozkładów naprężeń i odkształceń tkanki
kostnej
otaczającej implant (zarówno przed jak i po
implantacji),

2. wpływu parametrów konstrukcyjnych
(sztywność
trzpienia, jego długość, wpływ pokryć
warstwy
wierzchniej, wpływ cementu kostnego) na
stan
odkształceń i naprężeń tkanki kostnej,

3. opracowanie nowoczesnych konstrukcji
endoprotez
typu "custom design!”

4. budowy modeli zmian adaptacyjnych
tkanki kostnej
po zabiegu alloplastyki.

Badania eksperymentalne

stawu biodrowego

Badania doświadczalne prowadzone od szeregu
lat w Zakładzie Doświad czalnej Analizy
Konstrukcji Inżynierskich i Biomechanicznych na
Politechnice

Wrocławskiej

z

zakresu

biomechaniki stawu biodrowego mają na celu
wyznaczenie rozkładów naprężeń, odkształceń i
przemieszczeń

kości

udowej

z zaimplantowanymi trzpieniami endoprotez
cementowych i bezcementowych oraz określenie
na ich podstawie zasadniczego zbioru kryteriów
biome chanicznych

doboru

i

stosowania

implantów w alloplastyce stawu biodrowego [4],
[6],[11] .

Obserwując zależności pomiędzy rodzajem użytego do implantacji
trzpienia oraz uzyskanymi rozkładami przemieszczeń kości
w płaszczyźnie czołowej bądź rozkładami naprężeń oraz porównując je
z rozkładami uzyskanymi w badaniach kości zdrowej można
wnioskować na temat wyników prowadzonego zabiegu oraz zasadności
użycia konkretnego implantu w wybranych przypadkach chorobowych.

Badania stanu przemieszczeń kości udowej z implantami cementowymi
i bezcementowymi prowadzono metodą interferometrii holograficznej .

[2] Będziński R., Bernakiewicz M.: A study of stiffness relations in the femur with hip

endoprosthesis, Proc. of 3rd World Congress of Biomechanics, str.388-389, Japan, Sapporo
1998.

[3] Będziński R., Bernakiewicz M.: Experimental analysis of displacements of the femur after

total hip arthroplasty, Medical & Biological Engineering & Computing, str. 264-65, 1999.

[4] Będziński R., Bernakiewicz M., Ścigała K.: Biomechanical aspects of artificial joint

implantation in a lower limb, Journal of Theoretical and Applied Mechanics, Vol,37, Nr 3,
str.455-481, 1999.

[6] Będziński R.: Biomechanika Inżynierska, Zagadnienia wybrane, Wro cław 1997.
[11] Bernakiewicz R.: Opracowanie kryteriów odkształceniowo-naprężeniowych doboru

implantów stawu biodrowego, Praca doktorska, Raport Instytutu Konstrukcji i Eksploatacji
Maszyn Politechniki Wrocław skiej Serii PRE-010/98, Wrocław 1998.

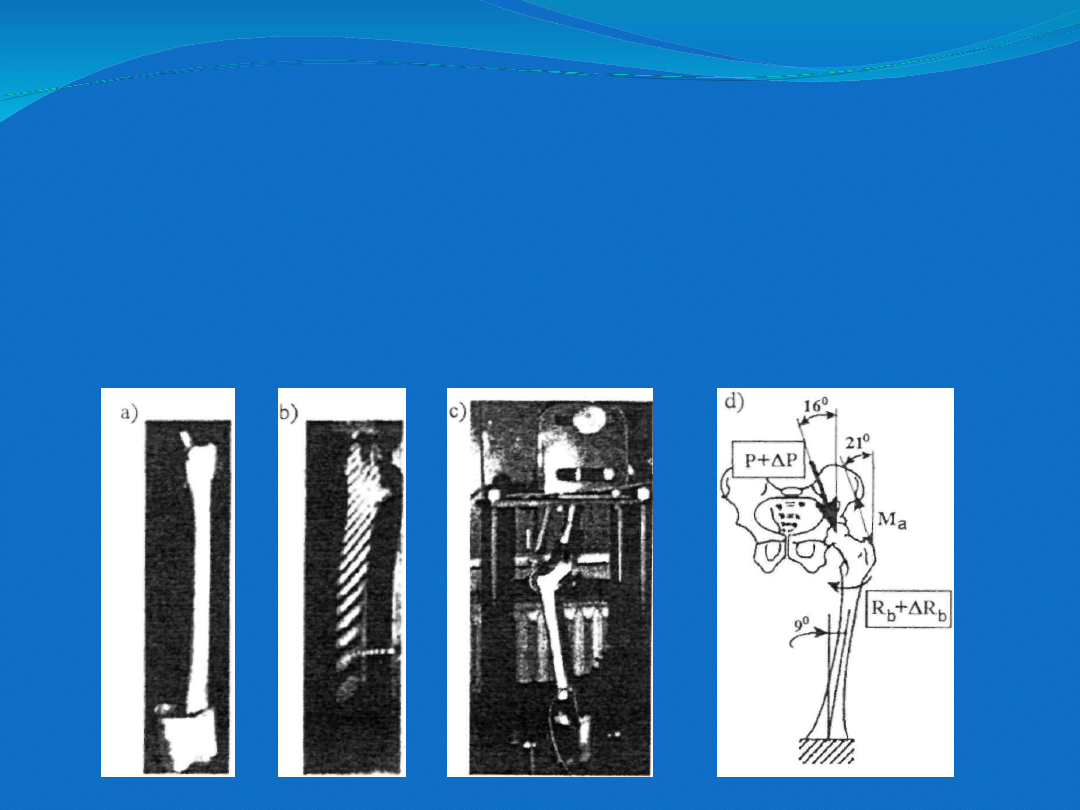
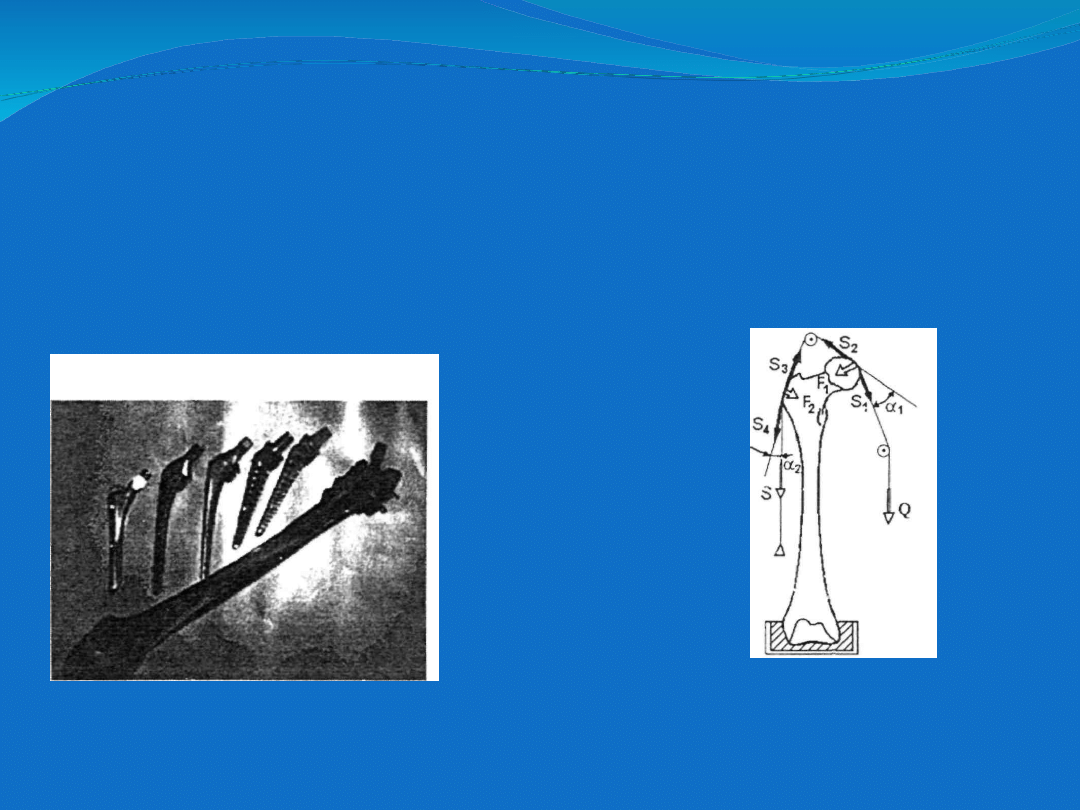
Badania prowadzono na kompozytowych modelach fizycznych kości udowej z
zaimplantowanymi rzeczywistymi trzpieniami endoprotez. Modele poddano
obciążeniu wg modelu przedstawionego na rys. d. Zarejestrowano
interferogramy holograficzne powierzchni bocznej kości udowej
pozwalające

na

analizę

rozkładu

przemieszczeń

kości

w płaszczyźnie czołowej.

Model kompozytowy kości (a) , przykładowy interferogram (b) , stanowisko
obciążające (c) oraz model obciążenia zastosowany w trakcie pomiarów (d).

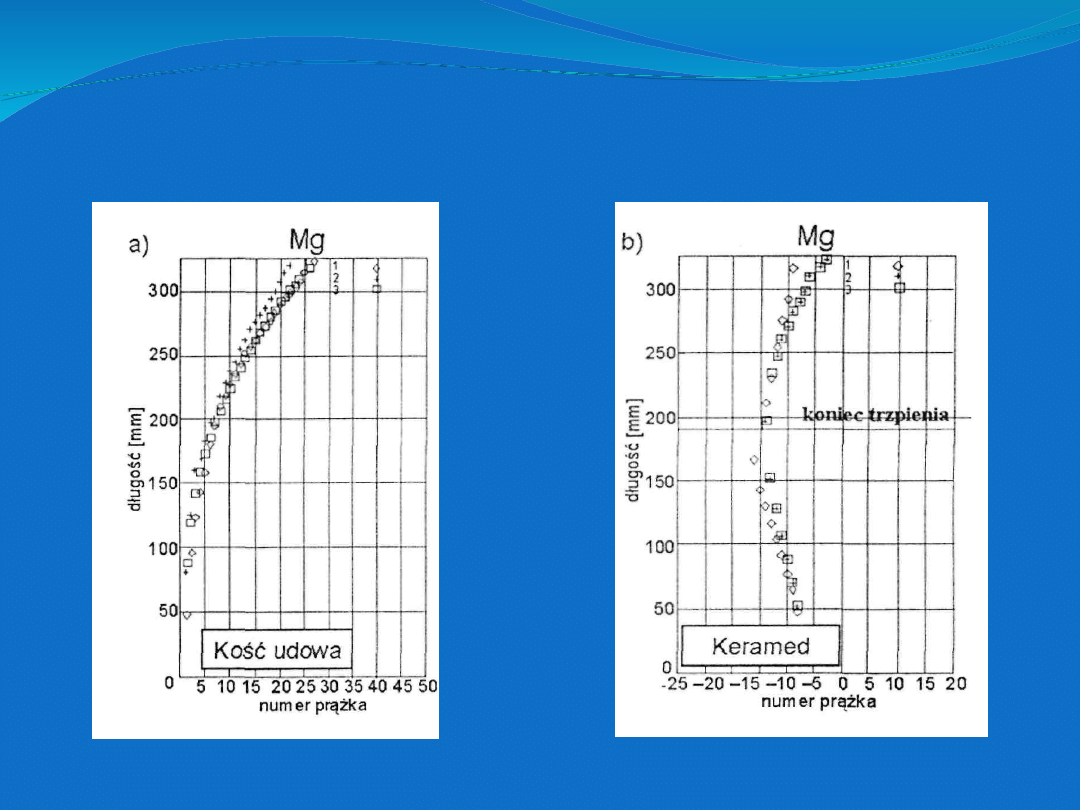
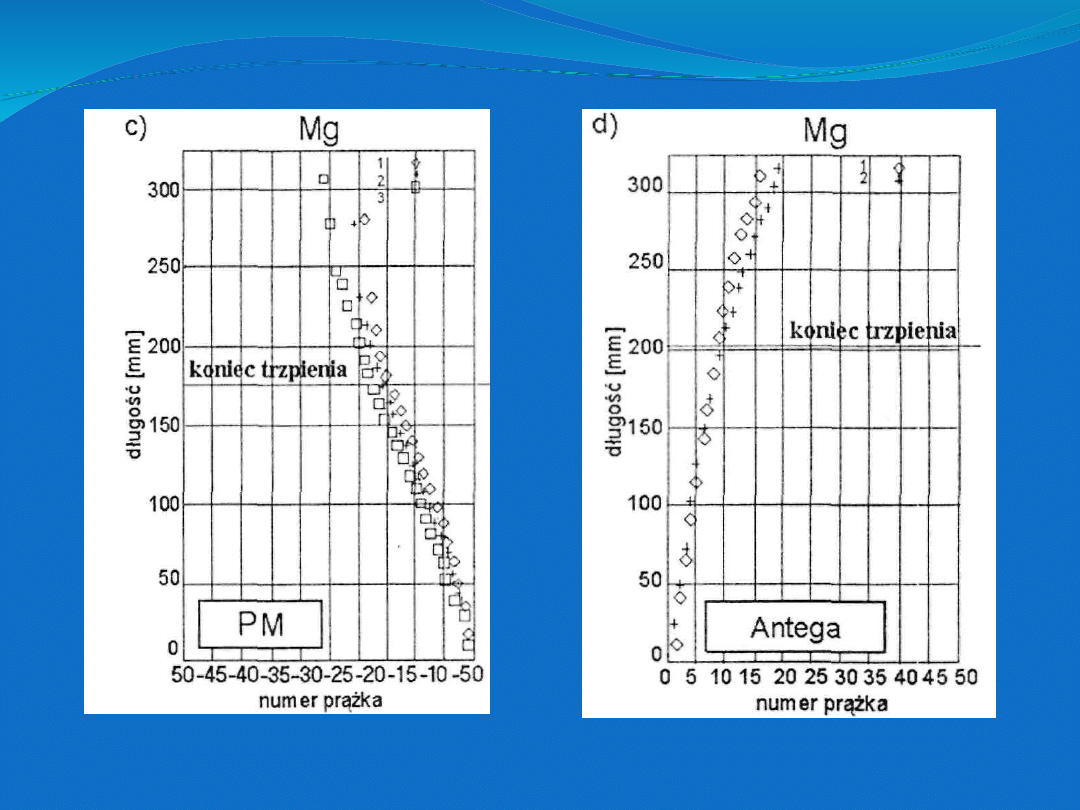
Rozkład przemieszczeń (wyrażonych w numerach prążków
interferencyjnych) modelu zdrowej kości udowej (a) oraz modeli
kości z zaimplantowanymi trzpieniami endoprotez stawu
biodrowego: typu Keramed (b), typu PM (c) oraz typu Antega (d).

Analizując rozkłady przemieszczeń można zauważyć, że kość zdrowa jest

zginana na stronę przyśrodkową, a maksymalne przemieszczenie wynosi
ok..2, 51 · 10

-3

mm .

Rozkłady przemieszczeń dla kości z trzpieniem endoprotezy typu PM oraz

Keramed różnią się zasadniczo od rozkładów zarejes trowanych dla kości
zdrowej.

W przypadku kości z trzpieniem PM kość odchyla się na stronę boczną, przy

czym szczególnie w rejonie bliższej części kości można zaobserwować również
efekt zginania na stronę przyśrodkową. Efekt ten jest jeszcze wyraźniej
widoczny

w

przypadku

kości

z

trzpieniem

protezy

Keramed.

W części dalszej trzon kości udowej odchyla się na stronę boczną,

natomiast w części bliższej kość jest silnie zginana przyśrodkowo.

W obu przypadkach efekt ten jest związany z wprowadzeniem sztywnego

trzpienia w kanał kości udowej. Usztywnienie części kości niweluje

naturalny

efekt związany z przemieszczaniem się całej kości przyśrodkowo .

W przypadku krótszego trzpienia jak Keramed jest to szczególnie

widoczne, gdyż maksymalna wartość przemieszczenia bocznego została
zarejestrowana w okolicy końca trzpienia i wynosi ona ok. 6,42 · 10

-3

mm.

W przypadku dłuższego trzpienia jakim jest trzpień

typu PM, jego koniec znajduje się w stosunkowo sztywnej
części kości (bliższa część trzonu kości) co powoduje że cała
kość odchyla się na stronę boczną, a maksymalne
przemieszczenie zarejestrowane w pobliżu krętarza większego
wynosi około 6.39 · 10

-3

mm.

Rozkład zbliżony do fizjologicznego zarejestrowano dla

kości
z endoprotezą typu Antega, kiedy to kość przemieszcza się w
całości

na

stronę

przyśrodkową,

jednakże

wartość

maksymalnego przemieszczenia jest mniejsza niż w przypadku
fizjologicznym i wynosi ok. 5,14 ·10

-3

mm co również świadczy o

zmianie sztywności w stosunku do kości zdrowej.

Powyższe wyniki świadczą dobitnie o znaczącym

wpływie sztywności giętnej trzpienia na podatność kości
udowej na obciążenie oraz powstawanie zmian rozkładów
przemieszczeń kości, co może spowodować znaczące zmiany w
strukturze tkanki kostnej a tym samym prowadzić do
niepożądanych efektów implantacji.

Badania

trójwymiarowego

stanu

naprężeń

prowadzono

metodą

elastooptyczną

Badania

prowadzono na modelach kości udowej z trzpieniami
endoprotez

stawu

biodrowego

wykonanych

z żywicy epoksydowej.

W celu uzyskania zróżnicowania własności mechanicznych tkanki

kostnej i materiału trzpienia modele kości i trzpienia wykonano z różnych
rodzajów żywicy.

Model poddano obciążeniu wg schematu przedstawionego na rys. a

następnie procesowi "zamrażania naprężeń".

Przykładowy model elastooptyczny kości udowej z trzpieniem
endoprotezy stawu biodrowego oraz zastosowany w trakcie
pomiarów model obciążenia stawu biodrowego.

Kolejnym etapem badań było wycięcie płaskich próbek

równolegle do płaszczyzny czołowej oraz analiza rozkładów izochrom
całkowitych

i

połówkowych

w badanych próbkach. Analiza porównawcza rozkładów naprężeń w
tkance kostnej umożliwia w tym przypadku ocenę zmian stanu
odkształceń tkanki kostnej spowodowanych wprowadzeniem implantu i
pośrednio oszacowanie możliwości powstania niekorzystnych efektów
przebudowy tkanki kostnej prowadzących do obluzowania trzpienia.
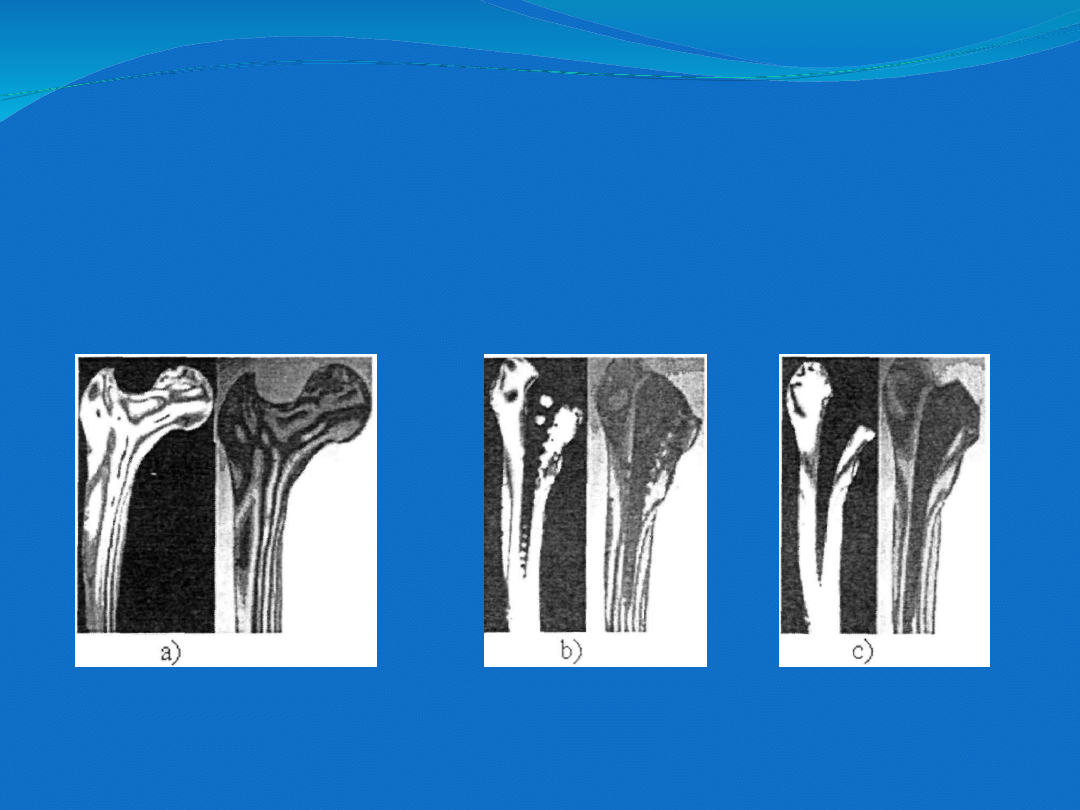
Zarejestrowane obrazy izochrom oraz wykresy naprężeń konturowych dla
kości zdrowej oraz z trzpieniami typu Mittellmeier i PM przedstawia rys.

Obraz izochrom całkowitych i połówkowych dla modelu kości
zdrowej (a),
z trzpieniem endoprotezy typu PM (b) oraz z trzpieniem typy
Mittellmeier (c).

Obraz izochrom dla kości zdrowej wskazuje na zginanie trzonu kości udowej

w płaszczyźnie czołowej połączone z jej ściskaniem, oraz złożony stan naprężeń
w głowie, szyjce kości udowej i jej nasadzie bliższej. Wykres naprężeń
konturowych dla kości zdrowej wskazuje na powstawanie naprężeń o większej
wartości po stronie przyśrodkowej oraz w trzonie kości niż w nasadzie bliższej.

Po stronie przyśrodkowej wartości naprężeń maleją gwałtownie w rejo nie krętarza

mniejszego i szyjki kości udowej utrzymując się na niskim poziomie na dolnej części
powierzchni głowy kości udowej.

Po stronie bocznej stosunkowo niewielkie wartości naprężeń konturowych zwiększają

się w rejonie przynasady bliższej kości udowej, następnie maleją i ponownie rosną
osiągając maksimum lokalne w szczytowym punkcie krętarza większego.

W przypadku modeli kości po zabiegu alloplastyki przy obu rodzajach trzpieni można

zaobserwować zmiany w rozkładzie izochrom całkowitych i połówkowych świadczące
głównie o znacznym spadku wartości naprężeń w nasadzie kości - zarówno w okolicy
krętarza większego jak i w strefie podkołnierzowej.

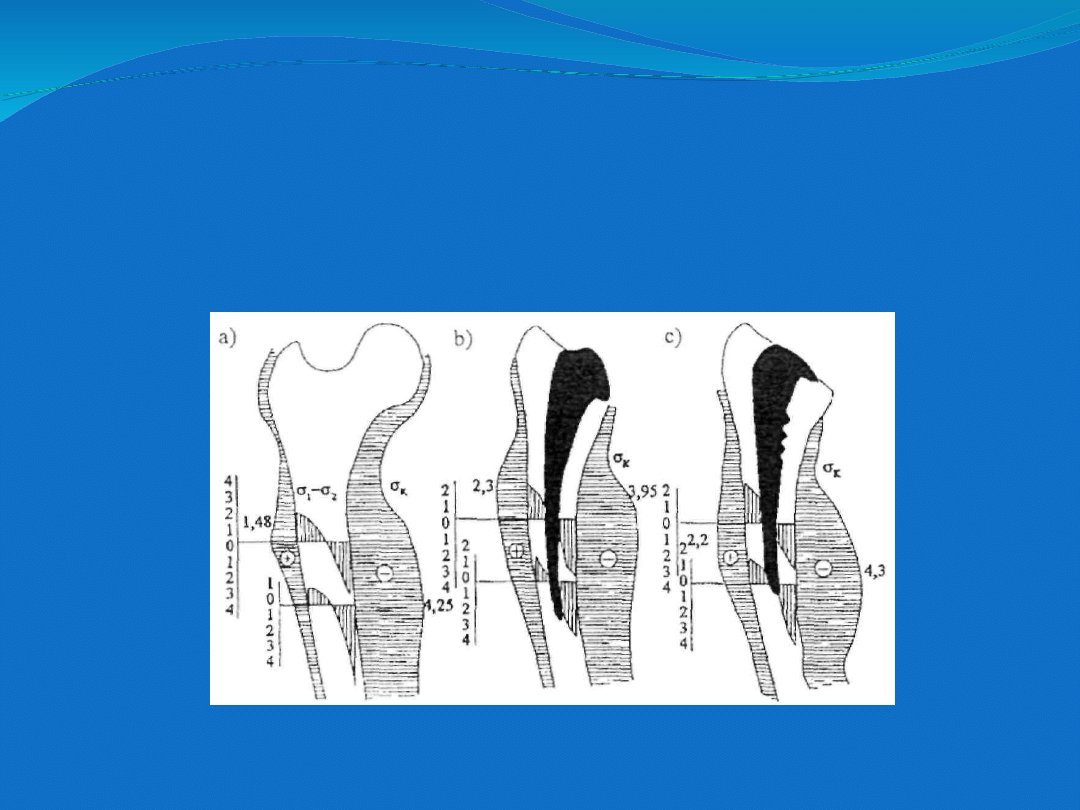
Analizując wykresy naprężeń konturowych można

zauważyć w przypadku protezy typu PM zmniejszenie wartości
naprężeń

konturowych

w okolicy szczytu krętarza większego, w przypadku protezy
Mittellmeier również w strefie podkołnierzowej gdzie wartość
naprężeń konturowych spada do zera.

Zmienił się również charakter rozkładów różnicy

naprężeń głównych dla wybranych przekrojów kości, co
świadczy o zmianie proporcji pomiędzy efektem zginania i
ściskania kości.

Wykresy rozkładu naprężeń konturowych dla modelu kości

zdrowej (a), z trzpieniem endoprotezy typu PM (b) oraz z
trzpieniem typy Mittelmeier (c).

Podsumowując wyniki z otrzymanych rezultatów

badań należy podkreślić, że wprowadzenie implantu
w każdym przypadku prowadzi do znaczących zmian
stanu

naprężeń.

Można

zatem

zaryzykować

stwierdzenie że projektowanie nowoczesnych trzpieni
endoprotez powinno opierać się na zasadzie, iż
zmiany stanu odkształceń i naprężeń spowodowane
wprowadzeniem implantu są nieuniknione, można
jednak tak sterować parametrami konstrukcji i
doboru implantu, aby były one na takim poziomie, że
naturalne procesy adaptacyjne spowodują niewielkie
zmiany

struktury

tkanki

kostnej,

które

nie

doprowadzą do niepowodzenia zabiegu.

Modelowanie MES kości udowej z

trzpieniem endoprotezy stawu

biodrowego

Modelowanie

MES

umożliwia

znacznie

szerszą

analizę

trójwymiarowego stanu naprężeń, odkształceń oraz przemieszczeń
kości udowej niż metody eksperymentalne, należy jednak
podkreślić,

że

w

każdym

przypadku

konieczne

jest

przeprowadzenie doświadczalnej weryfikacji opracowanych modeli.
Zakres prezentowanych prac obejmuje opracowanie modeli kości
udowej wraz z różnego typu trzpieniami endoprotez, analizę stanu
naprężeń i odkształceń tkanki kostnej otaczającej trzpień
endoprotezy oraz opracowanie biomechanicznych kryteriów doboru
implantu dla danego przypadku chorobowego.

Model MES kości udowej (a), schemat zastosowanego modelu
obcią żenia (b).

Modele MES kości udowej powstały na bazie

pomiarów CT kompozytowych modeli fizycznych kości
udowej.

Dokładna

i szczegółowa analiza oraz przetwarzanie danych
wyjściowych

umożliwiło

opracowanie

modelu

geometrycznego

kości

udowej

z dużą dokładnością (maksymalna różnica wymiarów
rzeczywistych
i wymiarów modelu geometrycznego nie przekraczała
0,5

mm).

Do podziału na siatkę elementów .skończonych

użyto elementu typu TETRA, 10-węzłowego o trzech
stopniach

swobody

w każdym węźle. Model zawiera 63312 elementów
skończonych

oraz

113885

węzłów.

W

mo delu

uwzględniono

rozbicie

na

tkankę

zbitą

i gąbczastą, jednakże założono że każda z tkanek
charakteryzuje się liniowymi własnościami sprężystymi
oraz jest materiałem izotropowym.

Wyniki analizy dla kości zdrowej, oraz z trzpieniami
typu PM, Zweimiller oraz Antega są przedstawione na
rysunku

Rozkład odkształceń

zredukowanych w modelu
kości zdrowej (a),

kości z trzpieniem

endoprotezy typu
Zweimiller (b),

kości z trzpieniem

endoprotezy typy PM (c),

kości z trzpieniem

endoprotezy typu Antcga
(d).

Analiza odkształceń zredukowanych według hipotezy Hubera von
Missesa w zdrowej kości udowej wskazuje, że w przypadku
zastosowanego modelu obciążenia mamy do czynienia nie tylko ze
zginaniem w płaszczyźnie czołowej lecz również ze skręcaniem kości
udowej.
Zginanie kości udowej jest nadal dominującym stanem odkształceń,
jednakże wpływ mięśni rotujących jest znaczący. Dodatkowo należy
zwrócić w tym miejscu uwagę na niejednorodny rozkład odkształceń w
rejonie nasady bliższej kości udowej a w szczególności w okolicy krętarza
mniejszego.
W przypadku modelu kości z endoprotezą typu Zweimiller wartości
odkształceń w trzonie kości udowej są mniejsze niż w przypadku modelu
kości z trzpieniem typu PM.
Można jednak zaobserwować znaczne koncentracje odkształceń kości,
zarówno w okolicy końca trzpienia jak i w miejscu styku trzpienia
endoprotezy z tkanką kostną na odcinku ok. 1/3 długości trzpienia po
stronie przyśrodkowej.

Podobnie jak w przypadku modelu kości z

trzpieniem typu PM nasada kości w okolicy krętarza większego jest
odciążona. Podobna sytuacja występuje w przypadku trzpienia typu
Antega,

jednakże

rejon

koncentracji

odkształceń

po

stronie

przyśrodkowej jest znacznie mniejszy, a poziom odkształceń w odciążonej
części nasady bliższej kości udowej niemal dwukrotnie wyższy.

Podsumowując, analiza wyników uzyskanych zarówno na drodze badań

eksperymentalnych jak i symulacji numerycznych wykazała, że starszego typu
trzpienie, a w szczególności trzpienie długie, jak trzpień typu PM są w znacznej
mierze konstrukcjami wywołującymi niepożądane skutki, w postaci
niefizjologicznych rozkładów naprężeń i odkształceń tkanki kostnej, co
wywołane jest nieprawidłową z punktu widzenia biomechaniki konstrukcją a w
szczególności charakterystyką sztywności. Krótsze trzpienie, typu Zweimiller
czy Keramed pozwalają na uzyskanie korzystniejszych rozkładów odkształceń
tkanki kostnej, jednakże wciąż powodują powstawanie rejonów przeciążonych
lub niedociążonych w obrębie tkanki kostnej otaczającej implant.

W badanych przypadkach krótki trzpień anatomiczny Antega, o stosunkowo

niskiej sztywności w porównaniu z masywnymi trzpieniami Zweimiller czy
Keramed, pozwolił na uzyskanie najkorzystniejszych rozkładów odkształceń
tkanki kostnej jednakże nie jest to rezultat w pełni zadowalający. Należy się
zatem spodziewać, że dalszy rozwój konstrukcji trzpieni endoprotez stawu
biodrowego powinien podążać w kierunku trzpieni krótkich o charakterystyce
sztywności, która umożliwi zachowanie poprawnych relacji naprężeniowo-
odkształceniowych w układzie implant-kość.

W tworzeniu modeli obciążenia stawu kolanowego niezwykle istotne jest

uwzględnienie geometrii kończyny dolnej a w szczególności pozycji stawu
kolanowego względem pozostałych stawów kończyny dolnej. Zmiany położenia
stawu kolanowego względem umownych osi kończyny dolnej oraz związane z
tym deformacje powierzchni stawowych i przeciążenie części stawu są
najczęstszą przyczyną interwencji chirurgicznych w obrębie stawu kolanowego.

Geometria kończyny dolnej jest opisana przez oś mechaniczną kończyny

dolnej, oś anatomiczną kości udowej i piszczelowej. Oś mechaniczna kończyny
dolnej jest linią prostą przechodzącą przez środek głowy kości udowej oraz
punkt centralny stawu skokowego leżący pomiędzy jego bloczkami:
piszczelowym i strzałkowym. W prawidłowo zbudowanej kończynie dolnej oś
mechaniczna przechodzi również przez środek stawu kolanowego, czyli punkt
leżący pomiędzy guzkami wyniosłości międzykłykciowej kości piszczelowej.

Modele obciążeń stawu kolanowego

Oś anatomiczna kości piszczelowej to inaczej jej oś długa, w
prawidłowo

zbudowanej kończynie dolnej oś anatomiczna kości piszczelowej

całkowicie

pokrywa się z osią mechaniczną kończyny dolnej.

Oś anatomiczna kości udowej to jednocześnie jej oś długa
rozpoczynająca

się w dole międzykłykciowym i biegnąca centralnie przez trzon

kości udowej.
Określenie sił obciążających powierzchnie stawowe również dla
deformacji

szpotawej oraz koślawej stawu kolanowego jest niezwykle

istotne dla

uzyskania pełnego obrazu obciążeń stawu kolanowego.

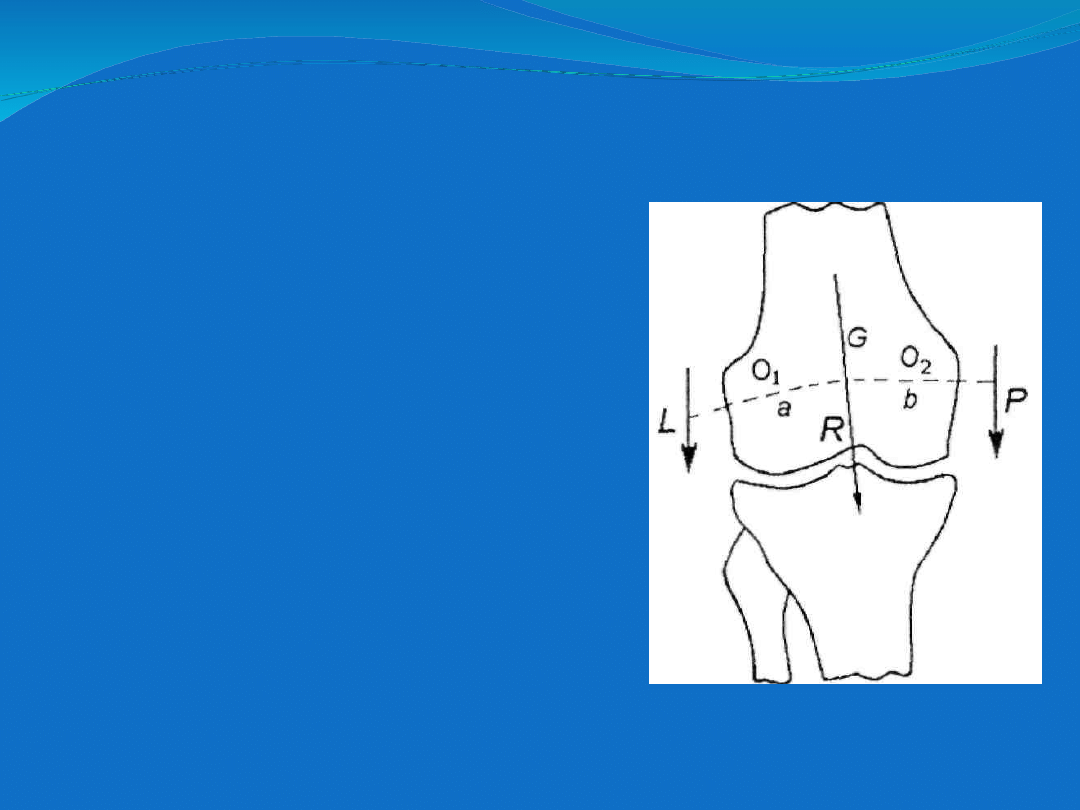
Jednym z podstawowych modeli
obciążenia stawu kolanowego
jest

model

Maqueta.

Dla

sytuacji

niesymetrycznego

stania na jednej kończynie
dolnej, Maquet wyznaczył siłę
reakcji w stawie kolanowym
jako wynik działania ciężaru
części ciała, znajdującej się
powyżej stawu kolanowego oraz
równoważącego go względem
środka stawu, napięcia mięśni
trójkąta miedniczego

Model obciążenia stawu kolanowego (wg

Maqueta).

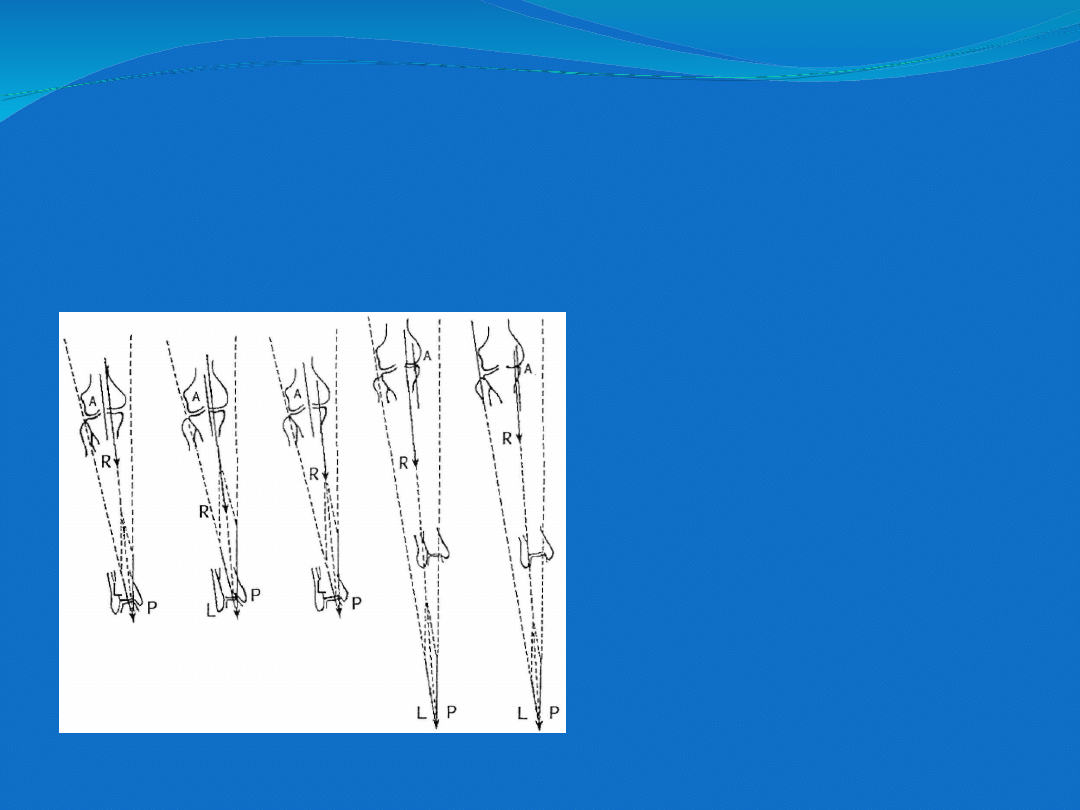
Siła reakcji jest w tym przypadku oczywiście rozłożona na
dwie siły

powstające pomiędzy powierzchniami stawowymi w przedziale
przyśrodkowym i bocznym stawu kolanowego. W przypadku

deformacji

koślawej lub szpotawej stawu kolanowego następuje zaburzenie

proporcji

sił obciążających powierzchnie stawowe oraz wartości napięcia

mięśni

trójkąta miedniczego

.

Maquet P.G.J.: Biomechanics of the knee, Berlin 1983.

Przeciążenie przedziału
przyśrodkowego stawu
kolanowego (wg
Maqueta).

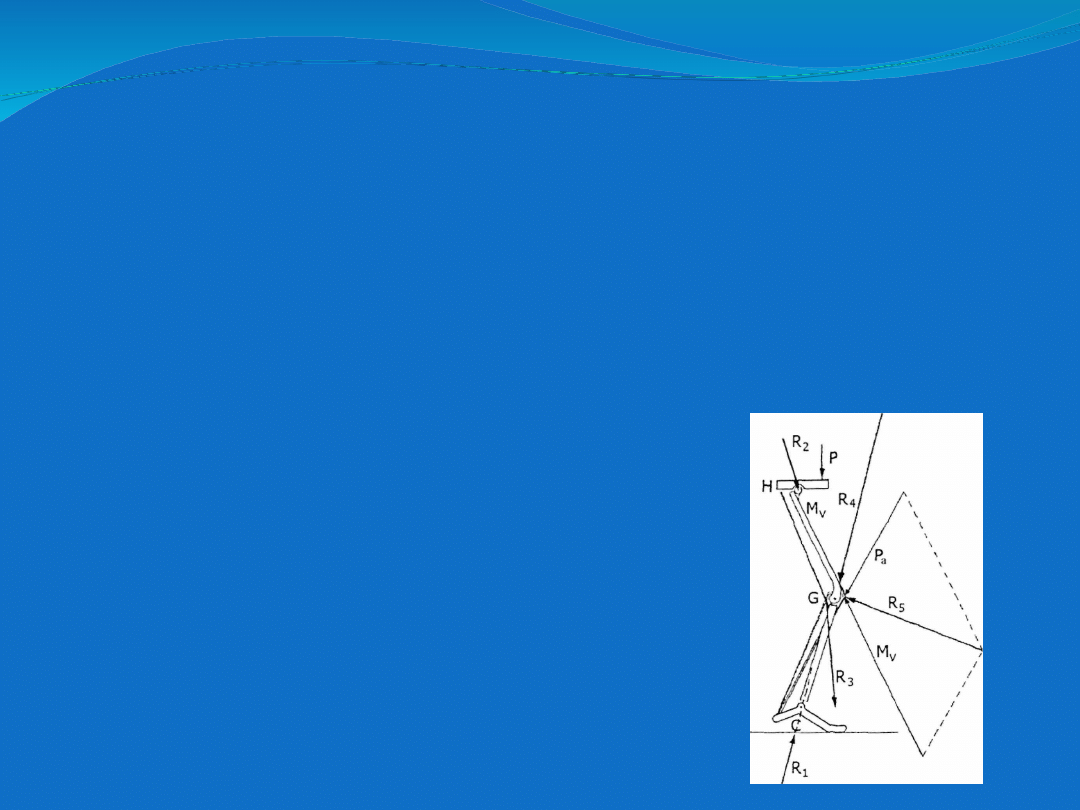
Jeżeli mamy do czynienia z deformacją szpotawa stawu kolanowego
przeciążeniu ulega przedział przyśrodkowy stawu kolanowego,
natomiast w przypadku deformacji koślawej, przeciążony jest przedział
boczny. W stawie zgiętym Maquet określił siły działające na staw
kolanowy na podstawie rozpatrzenia łańcucha kinematycznego
obciążonego dwiema siłami zewnętrznymi (ciężar części ciała powyżej
obręczy biodrowej oraz reakcja podłoża na nacisk stopy), którym
przeciwstawia się napięcie mięśni z podstawowych grup mięśniowych
kończyny dolnej. Wyznaczył w ten sposób dwie reakcje na powierzchnie
stawowe w stawie kolanowym, jedną oddziałującą w przedziale udowo-
piszczelowym i drugą w przedziale udowo-rzepkowym rys.

Obciążenie stawu kolanowego

zgiętego (wg Maqueta).

Nieco odmienny pod tym względem jest model Denhama, który zauważył,
że w części przedniej na nasadę dalszą kości udowej oddziałuje nie tylko
reakcja pochodząca od oddziaływania rzepki lecz
również pasma mięśnia czworogłowego uda powyżej górnej krawędzi
rzepki. Ponadto założył on, że w przedziale udowo-piszczelowym siła
reakcji nie jest prostopadła do powierzchni stawowych, lecz istnieje
również pewna składowa styczna.

Siła napięcia wiązadła rzepki została wyznaczona przez Denhama jako
równoważąca reakcję podłoża na nacisk stopy. Na jej podstawie, znając
kierunki reakcji pomiędzy rzepką i kością udową oraz działania mięśnia
czworogłowego określone zostały wartości tych sił.

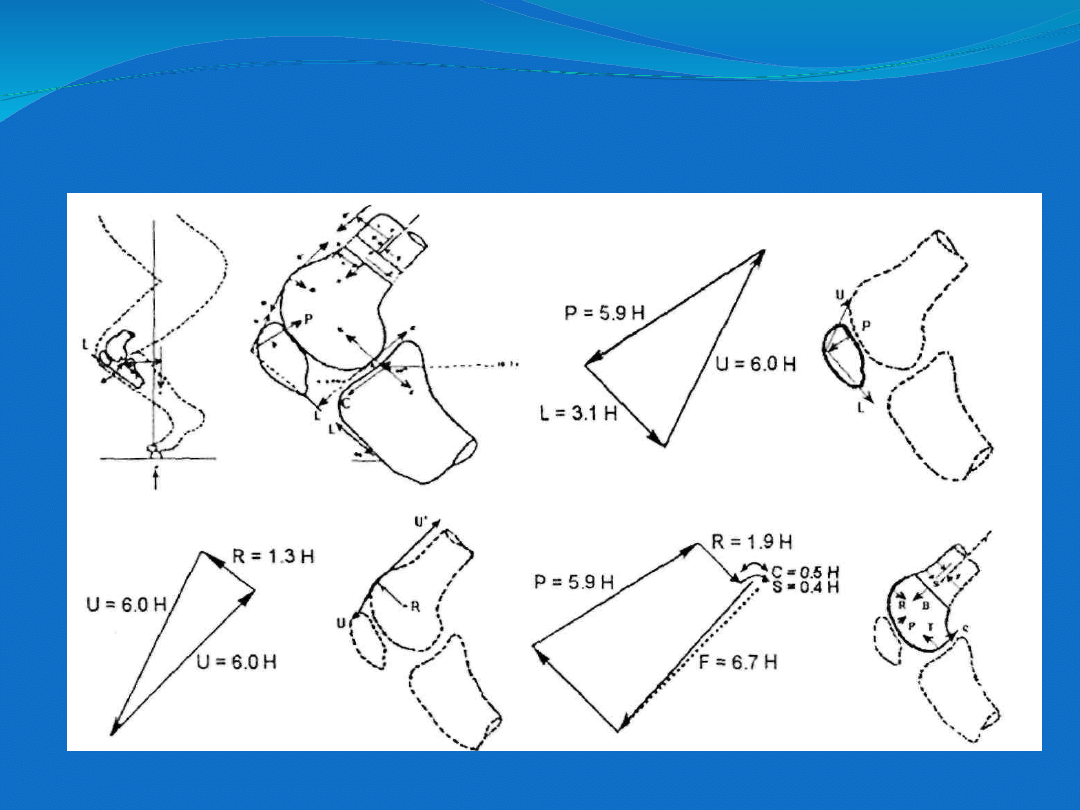
Obciążenie stawu kolanowego zgiętego (wg

Denhama)

W przypadku mięśnia czworogłowego wyznaczono w ten sposób siłę
oddziałującą jedynie w części pomiędzy górną krawędzią rzepki oraz
punktem
w którym ścięgno mięśnia czworogłowego ślizga się po powierzchni kości
udowej rys. Na jej podstawie możliwe było dopiero wyznaczenie
rzeczywistego napięcia mięśnia czworogłowego i reakcji w punkcie styku
z kością udową. Znając dwie siły oddziałujące na kość udową możliwe
było wyznaczenie reakcji na powierzchniach stawowych w stawie
kolanowym i biodrowym. Wartości siły normalnej i stycznej w stawie
kolanowym zostały określone przez Denhama jako

T=3,7H oraz C = 0,6 H

(gdzie H - wartość reakcji podłoża na nacisk

stopy).

Obecnie, w coraz większej ilości prac stopień

złożoności modeli obciążenia stawu kolanowego wciąż
rośnie, przez uwzględnienie dodatkowych grup mięśniowych
oddziałujących na staw, uwzględnienie roli więzadeł,
łękotek czy torebki stawowej.

Wymienione już wcześniej prace Pohla, Dudy i innych

pozwalają na wyznaczenie sił obciążających powierzchnie
stawowe również w stawie kolanowym.

W stawie biodrowym podstawową przyczyną alloplastyki stawu
jest zniszczenie powierzchni stawowych, natomiast w stawie
kolanowym podstawowym wskazaniem do interwencji chirurgicznej
jest powstanie deformacji szpotawej bądź koślawej stawu i
związanego z tym przeciążenia jednego z przedziałów stawu
prowadzącego również do degradacji powierzchni stawowej kości
piszczelowej oraz zmian w warstwie podchrzęstnej [6], [7], W
przypadku

zniekształcenia

o

niewielkim

kącie

deformacji

podstawowym sposobem leczenia stawu kolanowego jest
wykonanie zabiegu korekcji poprzez osteotomię podkolanową
piszczeli techniką "plus" bądź "minus".

Obie techniki mają swoje wady i przeciwwskazania, w przypadku
techniki "minus" w wyniku wycięcia klina kostnego w nasadzie
bliższej kości udowej dochodzi do pewnego skrótu leczonej
kończyny, możliwe jest powstanie tzw. efektu "wiszącego kłykcia"
lub

hyperkorekcji

prowadzącej

do

narastania

deformacji

symetrycznej do leczonej, natomiast w przypadku techniki
"plus„ wstawienie dodatkowego klina kostnego lub ceramicznego
w odcinku międzywięzadłowym może prowadzić do nadmiernego
napięcia więzadeł stawu kolanowego, może również wystąpić
zjawisko degradacji i "zapadania" się klina kostnego jak również
istnieje ryzyko nawrotu deformacji.

Zniekształcenia o większym kącie deformacji oraz takie w
przypadku których doszło do całkowitej degradacji powierzchni
stawowych
i zniszczenia struktur kostnych są leczone przez wykonanie
całkowitej alloplastyki stawu kolanowego. Głównym problemem
protezowania stawu kolanowego są obluzowania komponentu
piszczelowego

endoprotezy

i jego migracja.
Asymetryczne

obciążenie

stawu

kolanowego

powoduje

przeciążenie pewnych stref w tkance kostnej otaczającej implant, a
nawet powstanie warstwy tkanki włóknistej wokół implantu co
prowadzi do stopniowej zmiany pozycji komponentu piszczelowego
względem osi anatomicznej piszczelowej.
Często przyczyną pierwotną tego rodzaju migracji może być
nieprawidłowe osadzenie endoprotezy, w związku z czym proces
prawidłowej implantacji zależy również od opracowania
instrumentarium pozwalającego na precyzyjne określenie pozycji
protezy względem kości udowej i piszczelowej.

Podobnie jak w przypadku alloplastyki stawu biodrowego wciąż
wiele problemów związanych z protezowaniem stawu kolanowego
pozostaje nierozwiązanych.

Problemy alloplastyki stawu

kolanowego.

BIOAKCEPTOWALNOŚĆ BIOKOMPATYBILNOŚĆ

PRZEBUDOWA TKANKI KOSTNEJ I MIGRACJA PROTEZY

ZUŻYCIE ZASTĘPCZYCH POWIERZCHNI

STAWOWYCH

OBLUZOWANIA PROTEZ KŁYKCIOWYCH

OBLUZOWANIA PROTEZ ZAW.

ZŁAMANIA KOŚCI

INFEKCJA

1976 1975 1980 1990
2000

Celem

cyklu

badań

doświadczalnych

było

określenie

stanu

przemieszczeń kości udowej i piszczelowej dla stawu w pozycji
poprawnej, w pozycji szpotawej, po zabiegu osteotomii oraz określenie
rozkładu naprężeń w nasadach kości udowej i piszczelowej dla
wymienionych powyżej konfiguracji stawu.

Badania stanu przemieszczeń kości prowadzono metodą interferometrii
holograficznej [6j, [7], [8]. Badania prowadzono przy użyciu modeli
stawu kolanowego zestawionych z rzeczywistych kości wypreparowanych
ze zwłok. Dla każdej konfiguracji stawu pozycję kości kontrolowano
poprzez porównanie z rentgenogramami pacjentów. Modele stawu
poddano obciążeniu według modelu przedstawionego na rys.

Badania eksperymentalne stawu

kolanowego

Model obciążenia zastosowany w trakcie pomiarów oraz stanowisko
obciążające

Zarejestrowano interferogramy powierzchni przedniej kości
udowej

i

piszczelowej

z

prążkami

interferencyjnymi

informującymi o rozkładzie przemieszczeń w płaszczyźnie
strzałkowej. Możliwe było określenie na ich podstawie zarówno
przemieszczenia kości udowej jako bryły sztywnej na kłykciach
kości piszczelowej, ugięcia kości piszczelowej w płaszczyźnie
czołowej jak również zakresu przemieszczeń związanych z
rotacją kości udowej i skręcaniem kości piszczelowej.

W stawie poprawnym zaobserwowano równomierny rozkład
prążków o poziomym przebiegu zarówno na kości udowej jak i
piszczelowej. Obie kości przemieszczają się więc w płaszczyźnie
strzałkowej, w sposób nie wskazujący na przemieszczenia
rotacyjne.

Wartości

maksymalnych

obserwowanych

przemieszczeń to 2,827 • 10

-3

mm (dla obciążenia 238N).

Analiza wykresów przemieszczeń pozwala na następujące

spostrzeżenia:

1.

kość piszczelowa, sztywno zamocowana w dalszej części, pod
wpływem oddziaływania kości udowej jest ściskana, ale
jednocześnie zginana. Jej bliższa nasada przemieszcza się ku
tyłowi , lecz wartości przemieszczeń są niewielkie (1, 542 •10

-3

mm).

2.

kość udowa przemieszcza się jak bryła sztywna, pod wpływem
przyłożonego obciążenia i reakcji na powierzchniach stawowych,
przesuwając się ku przodowi. Kość udowa była zamocowana w
części bliższej w sposób, który umożliwiał przesunięcie
równoległe
w płaszczyźnie strzałkowej i obrót wokół ustalonej osi obrotu,
umieszczonej na dźwig ni obciążającej. Poprzez takiego typu
mocowanie, kość udowa uzyskała tyle stopni swobody co
w rzeczywistym stawie. Rozkład przemieszczeń pozwala na
stwierdzenie, że kość zarówno przesunęła się do przodu jak
również nastąpił jej niewielki obrót w płaszczyźnie strzałkowej.
Również
w tym przypadku wartości maksymalnych przemieszczeń są
niewielkie (2,83 •10

-3

mm).

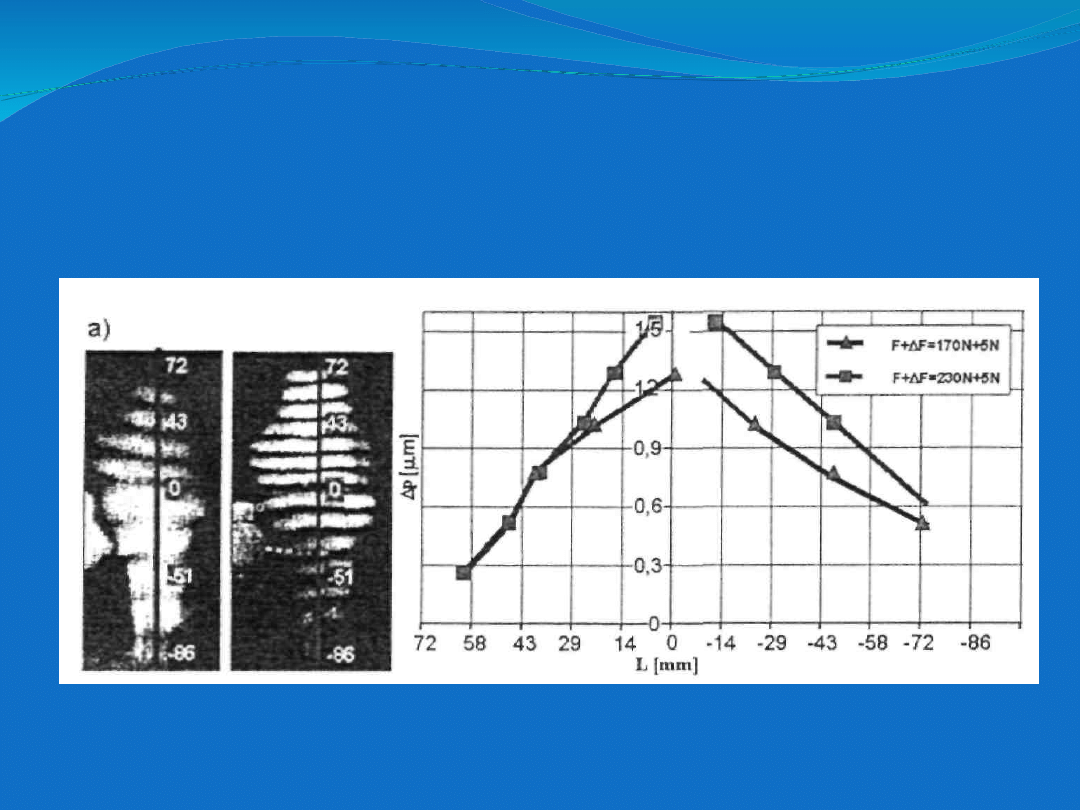
Rozkład przemieszczeń w płaszczyźnie

strzałkowej dla modelu stawu zdrowego (a),

oraz modelu stawu szpotawego (b) i stawu po

korekcji ostotomią podkolanową "minus" (c).

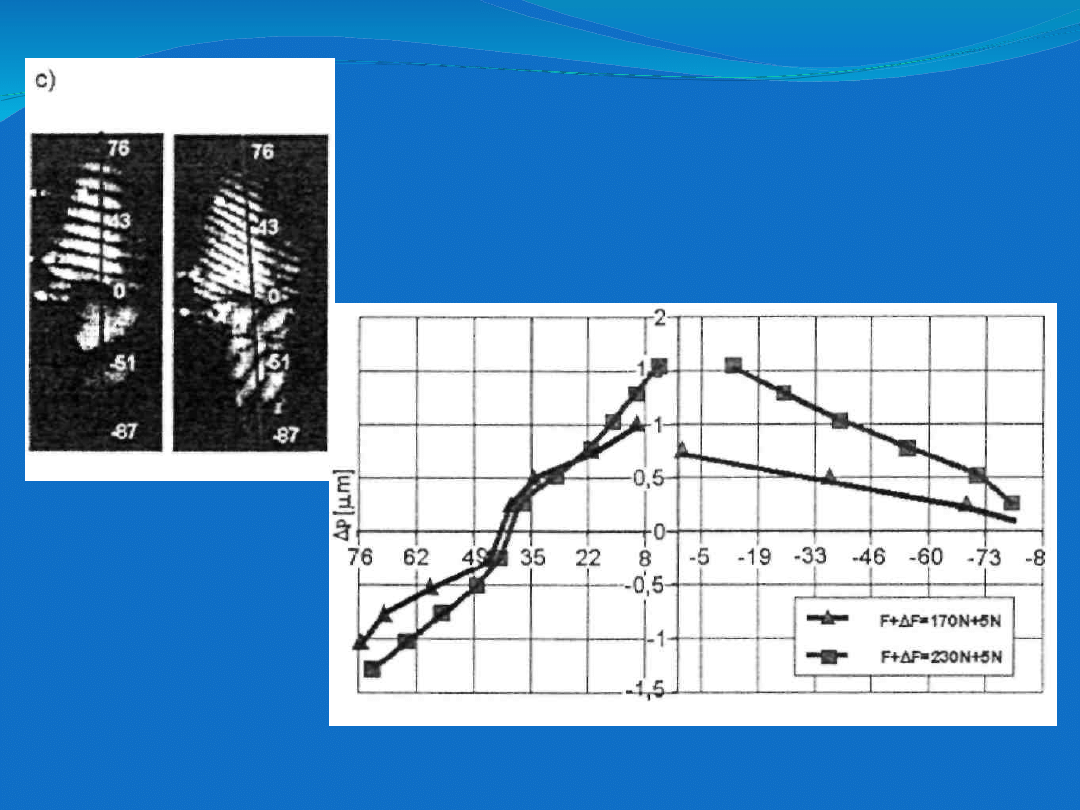
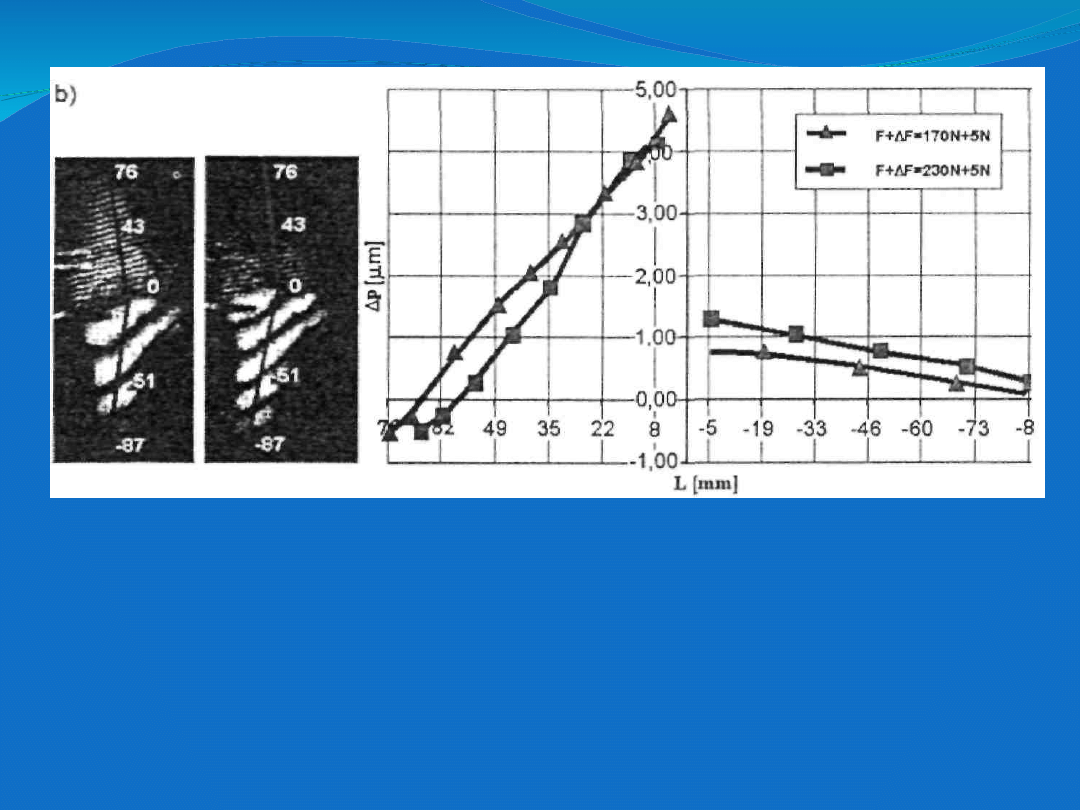
Zbliżone

wartości

przemieszczeń

zarejestrowanych

na

kości

udowej

i

piszczelowej w rejonie szpary stawowej
wskazują na niewielkie ruchy względne. a tym
samym na niewielki poślizg na powierzchniach
stawowych.

Odmienny stan zarejestrowano dla drugiego etapu badań - badania
stawu kończyny zdeformowanej.
W tym przypadku zmienił się w stosunku do etapu zarówno rozkład
zarejestrowanych prążków interferencyjnych jak i ok reślonych na ich
podstawie rozkładów przemieszczeń. Prążki interferencyjne układają
się na kości udowej i piszczelowej w sposób skośny co wskazuje na
przemieszczenia rotacyjne obu kości. Maksymalne przemieszczenie
zarejestrowane na modelu wystąpiło na kości udowej, w rejonie
szpary stawowej, o wartości 3,88 •10-2 mm. Jest ono 15 razy większe
niż maksymalne przemie szczenie zarejestrowane w etapie pierwszym.
Kość udowa przesunęła się w tym przypadku jak bryła sztywna, co
przy podparciu na jednym tylko kłykciu kości spowodowało znaczny
obrót kości względem osi przebiegającej przez kłykieć przyśrodkowy
stawu kolanowego. Kość piszczelowa jest w tym wypadku obciążona
siłą

przechodzącą

przez

powierzchnie

stawową

kłykcia

przyśrodkowego i obraz prążków interferencyjnych wynika ze zginania
w płaszczyźnie czołowej i strzałkowej jak i skręcania kości
piszczelowej wokół osi pionowej. Kość piszczelowa została sztywno
zamocowana,

więc

wartości

maksymalnych

przemieszczeń

obserwowanych na nasadzie bliższej są dużo mniejsze niż na kości
udowej. Przemieszczenia wzajemne powierzchni stawowych (które
można w tym wypadku uznać za poślizg na powierzchniach
stawowych) znacznie wzrosły w stosunku do etapu pierwszego.

Etap trzeci obejmował badania przemieszczeń stawu poddanego
korekcji osi mechanicznej kończyny klasyczną techniką operacyjną
Coventry.
Wyniki badań wskazują na znaczący wpływ korekcji chirurgicznej
zarówno na rozkład prążków interferencyjnych, jak i rozkład
przemieszczeń.
W stosunku do wyników etapu II, odchylenie od poziomu prążków
interferencyjnych obserwowanych na kości piszczelowej jak i udowej
uległo zmianie. Zmieniła się również gęstość prążków. Wskazuje to na
zmianę sposobu przenoszenia obciążeń przez staw kolanowy, a w
szczególności

na

zmianę

w

sposobie

współpracy

pomiędzy

powierzchniami stawowymi kości udowej i piszczelowej. W modelu,
dzięki korekcji osi uzyskano kontakt pomiędzy powierzchniami
stawowymi

zarówno

po

stronie

przyśrodkowej

jak

i bocznej, jednakże rozkład prążków wskazuje, że oś obrotu kości
udowej nadal przebiega po stronie przyśrodkowej, chociaż z całą
pewnością zmieniło się położenie tej osi w stosunku do osi obrotu kości
stawu zdeformowanego jak i zmienił się zakres rotacji kości udowej i
piszczelowej. Wskazuje to na wciąż istniejące przeciążenie jednego z
przedziałów stawu, pomimo korekcji chirurgicznej. Maksymalne
przemieszczenie kości udowej wynosi dla tego przypadku 1,73 •10-3
mm.
Maksymalne przemieszczenie zarejestrowane dla kości piszczelowej
wynosi 1,54 • 10-3 mm. Kość piszczelowa nadal jest zginana ku
przodowi, co wynika z oddziaływania kłykci kości udowej.

Modelowanie MES kości

piszczelowej z komponentem protezy

stawu kolanowego

Podstawowym celem tego etapu badań było szczegółowe
określenie zależności pomiędzy obciążeniem zewnętrznym (w tym
przypadku obciążeniem stawu kolanowego) a stanem odkształceń
tkanki kostnej.
Obliczenia prowadzono na modelach przestrzennych kości
piszczelowej opracowanych na podstawie jej modeli fizycznych
(Sawbones) [9], [10].
Dokonano pomiarów zewnętrznej powierzchni modeli kości
piszczelowej za pomocą skanowania współrzędnych punktów przy
pomocy skanera trójwymiarowego Digiboot.
Wewnętrzna powierzchnia kości zbitej powstała na podstawie
analizy tomogramów komputerowych powstałych w wyniku
prześwietlenia tych samych modeli fizycznych kości. Do utworzenia
siatki elementów skończonych użyto elementu bryłowego o 12
węzłach i trzech stopniach swobody w każdym węźle.
W przypadku modelowania tkanek miękkich elementem użytym do
modelowania był element cięgnowy o dwóch węzłach i trzech
stopniach swobody w każdym węźle.

Model kości piszczelowej szpotawej powstał w wyniku
zdeformowania nasady bliższej kości piszczelowej oraz zmiany jej
położenia względem osi mechanicznej kończyny dolnej (w tym
przypadku przez odchylenie na stronę zewnętrzną nasady
bliższej kości piszczelowej względem jej nasady dalszej). Model
kości został odchylony na zewnątrz o żądany kąt szpotawości, a
następnie dokonywano zmian w nasadzie bliższej kości w celu
uzyskania efektu "zapadania się" kłykcia przyśrodkowego pod
wpływem przeciążenia. Modele kości piszczelowej po zabiegu
osteotomii powstały poprzez wstawienie lub usunięcie klina o
kącie wierzchołkowym równym kątowi deformacji na wysokości
połowy odcinka między-więzadłowego.
W modelu kości po zabiegu alloplastyki stawu kolanowego
odwzorowano komponent piszczelowy protezy stawu kolanowego
typu "Search" mocowanej przy użyciu cementu kostnego.
Wszystkie materiały w modelu były odwzorowane jako liniowo-
sprężyste.
Symulacje prowadzono, odtwarzając sytuację niesymetrycznego

stania na jednej kończynie dolnej. Wartości obciążeń stawu

kolanowego

określono na podstawie modelu Maquet`a.

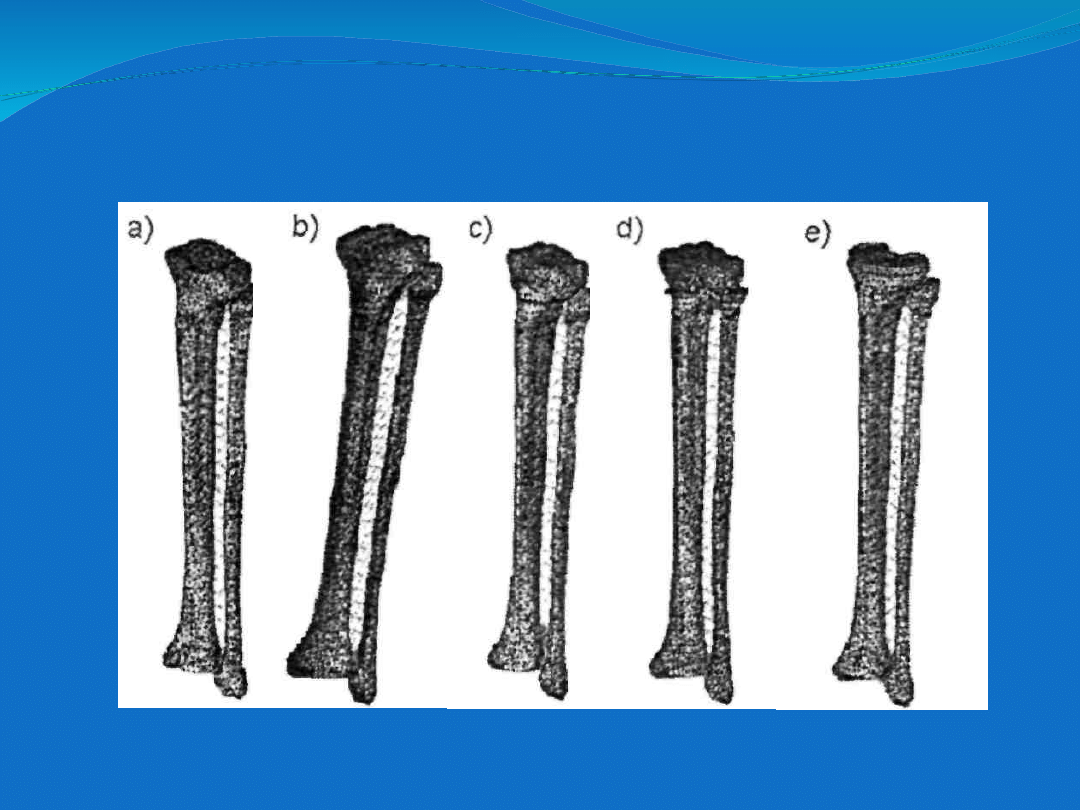
Model MES kompleksu kości podudzia zdrowych

(a) szpotawych (b), po osteotomii "plus" (c), po

osteotomii "minus" (d), po alloplastyce stawu

kolanowego (e).

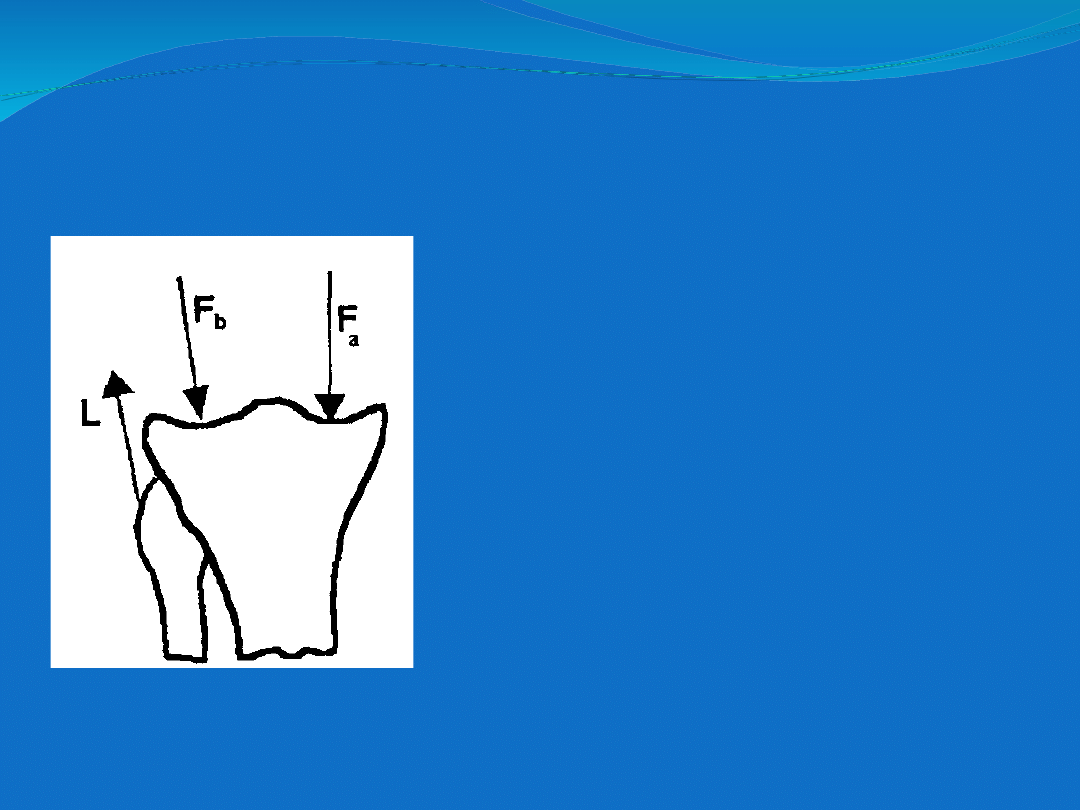
Schemat modelu obciążenia modelu MES

kompleksu kości podudzia.

Fa , Fb - reakcje
powstające w
przedziałach
przyśrodkowym i
bocznym

L -siła napięcia
mięśni trójkąta
miedniczego

Wstępna analiza wyników wykazała, że w kości piszczelowej obciążenie w

sposób fizjologiczny powoduje powstanie złożonego stanu naprężeń i
odkształceń, zbliżonego do przypadku zginanie + ściskanie, lub jego
przypadku szczególnego — ściskanie mimośrodowe. Oczywiście efekt
zginania kości jest tu znacząca mniejszy niż w przypadku kości udowej,
jednakże jest wyraźny, szczególnie w rejonie trzonu kości. Analiza stanu
odkształceń kości kompleksu kości podudzia została przeprowadzona dla
wszystkich wymienionych wcześniej modeli kości, tzn. dla modelu kości
piszczelowej poprawnej, kości szpotawej oraz kości po zabiegu osteotomii

typu

"plus" i "minus" oraz po zabiegu alloplastyki stawu kolanowego.

We wszystkich modelach analizowano rozkład odkształceń e

z

(wzdłuż osi

pionowej, pokrywającej się z osią długą kości piszczelowej). Największe
wartości odkształceń e

z

uzyskano na bocznych powierzchniach trzonu kości

w

jego części dalszej.

Rozkłady odkształceń e

z

na powierzchni kości

piszczelowej a) kość piszczelowa poprawna, b)

kość szpotawa, c) kość po oteotomii typu "plus",

d) kość po oteotomii typu "minus", e) kość po

zabiegu alloplastyki stawu kolanowego.

Rozkłady zarejestrowane na powierzchni kości są w tym przypadku

wyznacznikiem zmian globalnego stanu odkształceń całej kości
piszczelowej wynikającymi z jej obciążenia oraz położenia.

Dla kości poprawnej, której oś anatomiczna jest położona pionowo

można zaobserwować koncentrację odkształceń ściskających po stronie
przyśrodkowo-tylnej, natomiast rozciągających po stronie boczno-przedniej.

Kość piszczelowa jest w tym przypadku zginana na stronę

przyśrodkową i do tyłu. Efekt przemieszczania się nasady bliższej kości
piszczelowej do przodu pod wpływem obciążenia uzyskano również w

badaniach

doświadczalnych.

Charakterystyczne jest to, że wartość maksymalnego odkształcenia

ściskającego po stronie przyśrodkowej jest ponad dwukrotnie większa od
wartości maksymalnego odkształcenia rozciągającego po stronie bocznej.

Dla kości o deformacji szpotawej po stronie przyśrodkowej możemy

obserwować odkształcenia rozciągające, natomiast ściskające po stronie

bocznej.

Punkt, w którym występują maksy malne wartości odkształceń

rozciągających na ściance przyśrodkowej trzonu położony jest w przedniej
części tej powierzchni, natomiast punkt występowania maksymalnych
odkształceń ściskających na ściance bocznej trzonu położony jest w części
tylnej. Kość jest zatem zginana na stronę boczną i do tyłu. Wartość
odkształceń rozciągających wzrosła niemal siedmiokrotnie, natomiast
wartość maksymalnych odkształceń ściskających dwukrotnie stosunku do
wartości uzyskanych dla modelu kości poprawnej.

Można również zaobserwować zmianę położenia obszaru występowania

znacznych odkształceń ściskających i rozciągających w dół w stronę nasady
dalszej kości piszczelowej co można tłumaczyć znacznym odchyleniem
kości piszczelowej od osi mechanicznej kończyny dolnej na stronę boczną.

W przypadku modelu kości po zabiegu osteotomii "plus" można

zaobserwować maksymalne wartości odkształceń ściskających na przedniej
stronie ścianki przyśrodkowej trzonu kości a w części dalszej nawet na
przedniej krawędzi trzonu.

Maksymalne odkształcenia rozciągające występują na tylnej części ścianki

bocznej a w pobliżu nasady na ściance tylnej. Świadczy to o tym że kość w tym
przypadku jest silnie zginana w płaszczyźnie strzałkowej i efekt ten dominuje
nad efektem zginania w płaszczyźnie czołowej. Świadczy o tym również fakt, że
wartość maksymalnych odkształceń ściskających spadła w stosunku do kości
zdrowej, natomiast odkształceń rozciągających jest na porównywalnym
poziomie.

W tym wypadku, nie uzyskano zatem stanu odkształceń identycznego z

uzyskanym w modelu kości poprawnej, pomimo zastosowania poprawnej
procedury korygującej. Zmiany kształtu nasady bliższej kości spowodowały w
tym przypadku zmiany w sposobie przenoszenia obciążeń, szczególnie po
stronie przyśrodkowej nasady kości. Sztywny klin o znacznej grubości po
stronie przyśrodkowej (korekcja 12) spowodował znaczne zmniejszenie
tendencji nasady kości do przemieszcza nia się względem trzonu na stronę
przyśrodkową.

Można zatem twierdzić, że w przypadku korekcji osi za pomocą osteotomii

podkolanowej typu "plus" ryzyko użycia zbyt małego klina oraz tzw.
"hyperkorekcji" jest stosunkowo niewielkie. Natomiast użycie zbyt dużego klina
kostnego może spowodować ponowne powstanie deformacji szpotawej stawu
kolanowego.

W przypadku modelu kości piszczelowej po korekcji osi za pomocą

osteotomii podkolanowej typu "minus" maksymalne odkształcenia
ściskające występują po stronie przyśrodkowej, natomiast maksymalne
odkształcenia rozciągające po stronie bocznej trzonu. W stosunku do
modelu kości poprawnej zaobserwowano przesunięcie punktu występowania
maksymalnych odkształceń ściskających do przodu.

Świadczy to o tym że w stosunku do kości poprawnej zwiększył się udział

zginania w płaszczyźnie czołowej w stosunku do efektu zginania w płaszczyźnie
strzałkowej. Zatem w tym przypadku nadmierna korekcja jest znacznie bardziej
prawdopodobna niż w przypadku zastosowania techniki "plus". Również w tym
przypadku zaobserwowano spadek wartości odkształceń w stosunku do
uzyskanych w modelu kości poprawnej.

Biorąc pod uwagę, że tkanka zbita w znacznie
mniejszym stopniu reaguje na bodźce pobudzające
ją do przebudowy, niż tkanka gąbczasta, oraz to, że
w obserwacjach klinicznych wiąże się kolejne stopnie
zaawansowania

zmian

chorobowych

stawu

kolanowego

ze

zmianą

gęstości

warstwy

podchrzęstnej tkanki kostnej w kłykciu bocznym i
przyśrodkowym,

konieczne

jest

również

przeprowadzenie analizy stanu odkształceń tej
części kości pi szczelowej. Analizę prowadzono dla
przekroju czołowego kości piszczelowej obserwując
rozkłady odkształceń e

z

w kłykciu przyśrodkowym i

bocznym. Pobieżna nawet ocena stanu odkształceń
pozwala stwierdzić, że nawet nie wielkie zmiany
kształtu i położenia kości piszczelowej znacząco
wpływają na stan odkształceń tkanki gąbczastej
kości.

Rozkłady odkształceń e

z

w płaszczyźnie czołowej kości

piszczelowej a) kość piszczelowa poprawna, b) kość szpotawa, c)
kość po ostetomii "plus", d) kość po ostetomii "minus", e) kość po
zabiegu alloplastyki stawu kolanowego.

W modelu kości poprawnej można zaobserwować dwie
koncentracje odkształceń pod powierzchniami stawowymi
kłykcia przyśrodkowego i bocznego. Należy jednak zauważyć, że
koncentracja pod kłykciem bocznym jest większa, a wartości
maksymalnych odkształceń w tej części są większe niż w kłykciu
przyśrodkowym. Część centralna kości oraz rejon zewnętrznych
krawędzi powierzchni stawowych są obciążone w znacznie
mniejszym stopniu a wartości odkształceń są mniejsze. Dla kości
szpotawej wartości odkształceń osiągają najwyższy poziom po
stronie przyśrodkowej, natomiast koncentracja po stronie
bocznej całkowicie zanika, a wartości odkształceń są zbliżone do
obserwowanych w części centralnej kości lub w części oddalonej
od powierzchni stawowych. Na zewnętrznej ściance nasady kości
oraz w rejonie między-kłykciowym pojawiają się znaczne obszary
w których odkształcenia osiągają wartości minimalne. Dla kości
po zabiegach osteotomi podkolanowej można zaobserwować
dwie koncentracje pod powierzchniami stawowymi kłykci,
jednak różnią się one wartościami maksymalnymi odkształceń
od wartości obserwowanych w modelu kości zdrowej.
W przypadki; zastosowania osteotomii podkolanowej typu "plus"
koncentracja odkształceń w warstwie podchrzęstnej kłykcia
bocznego jest większa niż w kłykciu przyśrodkowym, jednakże
można

zaobserwować

spadek

maksymalnych

wartości

odkształceń w obu kłykciach w stosunku do wartości uzyskanych
w modelu kości poprawnej. Odmienna sytuacja występuje w
osteotomii podkolanowej "minus".

W przypadku zastosowania tego typu techniki większa
koncentracja odkształceń występuje po stronie przyśrodkowej,
można za tem zauważyć, iż pomimo że efekt deformacji szpotawej
został w znacznym stopniu skorygowany, to pewne przeciążenie
kłykcia przyśrodkowego wciąż istnieje, podobnie jak efekt zbyt
niskiego obciążenia w kłykciu bocznym Ponadto w rejonie
gwałtownej zmiany przekroju nasady wywołanego resekcją klina
kostnego w tkance gąbczastej kości występują koncentracje od
kształceń rozciągających wynikające z "odrywania" odłamu
górnego kość od powierzchni łączącej w wyniku oddziaływania
siły mięśniowej po stronie bocznej, skierowanej ku górze.
Oczywiście w sytuacji rzeczywistej tegf rodzaju koncentracje
powstaną dopiero na pewnym etapie zrostu kostnego kiedy
powstanie trwałe połączenie pomiędzy odłamami kostnymi.
Możni zatem wnioskować, że po stronie bocznej kości procesy
przebudowy i zrost t kości przebiegać będą w sposób utrudniony,
ze

względu

na

występowano

niefizjologicznego

stanu

odkształceń tkanki kostnej. Wartości maksymalne odkształceń
ściskających w warstwie podchrzęstnej są mniejsze niż
obserwowane w modelu kości poprawnej. W modelu kości po
zabiegu alloplastyki zaobserwowano koncentracji odkształceń
ściskających zarówno pod powierzchnią płytki kłykciowej
protezy, jak i w okolicy końca trzpienia komponenty piszczelowej
protezy. Również w okolicy powierzchni styku płytki protezy z
tkanką korową kości można zauważyć znaczne zwiększenie
wartości odkształceń kości wywołaną efektem bezpośredniego
oddziaływania metalicznego implantu na tkankę kostną.

Wartości odkształceń w obu przedziałach

stawu są zbliżone, jednak są wyższe niż w
modelu kości poprawnej.

Dodatkowo, koncentracja odkształceń o

dużej wartości występująca w okolicy końca
kłykcia również może spowodować dodatkowe
efekty przebudowy tkanki kostnej.

Słownik

alloplastyka

stawu biodrowego (kolanowego) - zabieg

wszczepienia endoprotezy stawu biodrowego (kolanowego),
endoprotezoplastyka

deformacja

koślawa (szpotawa) stawu kolanowego -

zmiana geometrii kończyny dolnej oraz kształtu nasady
dalszej

kości

udowej

i nasady bliższej kości piszczelowej. Staw kolanowy zmienia
położenie względem osi mechanicznej kości kończyny dolnej
przesuwając się na stronę wewnętrzną (zewnętrzną).
Przeciążeniu ulega w tym przypadku przedział boczny
(przyśrodkowy)

stawu

kolanowego

oraz

więzadła

stabilizujące w płaszczyźnie czołowej.

elastooptyka

- doświadczalna metoda modelowa analizy

stanu naprężeń. W metodzie tej wykorzystuje się zjawisko
dwójłomności wymuszonej występujące w niektórych
materiałach (żywice epoksydowe, poliure tanowe). W trakcie
obserwacji

modeli

obiektu

badanego

w

świetle

spolaryzowanym możliwe jest zarejestrowanie rozkładów
charakterystycznych linii (izochrom, izoklin) i na ich
podstawie analiza stanu naprężeń w modelu.

endoproteza

stawu biodrowego - sztuczny staw

biodrowy,

wszczepiany

na

drodze

zabiegu

ortopedycznego do organizmu pacjenta w miejsce
uszkodzonego

stawu

naturalnego.

Endoproteza

znajduje się całkowicie wewnątrz organizmu człowieka
(proteza wewnętrzna), wszystkie elementy protezy
bezpośrednio kontaktują się ze środowiskiem tkanek
organizmu. Typowa endoproteza stawu biodrowego
składa się z trzpienia endoprotezy mocowanego w
kanale kości udowej, zaopatrzonego w główkę oraz
współpracującej z głowicą panewki endoprotezy stawu
biodrowego mocowanej w kości miednicy

interferometria

holograficzna - metoda pomiaru

przemieszczeń badanego obiektu. W trakcie pomiaru
realizuje się rejestracje frontu falowego fali świetlnej
odbitej od badanego obiektu w trakcie pomiaru.
Rejestracja przemieszczeń odbywa się na drodze
interferencji frontów falowych uzyskanych dla różnych
położeń punktów na powierzchni obiektu. Rozkład
prążków interferencyjnych na obrazie obiektu niesie
informację o rozkładzie i wartościach przemieszczeń
punktów na po wierzchni obiektu.

"łuki gotyckie"

- układ beleczek kostnych istoty gąbczastej

powstający powyżej panewki kości miednicy, dobrze
widoczny na obrazach rentgenowskich stawu biodrowego i
kości miednicy. Układ podstawowych włókien tworzących
strukturę kości, pokrywających się z kierunkami przebiegu
obciążeń wewnętrznych kości.

obluzowanie endoprotezy

-

jedno

z

najczęściej

występujących

powikłań

zabiegu

wszczepiania

endoprotezy stawu biodrowego. Objawem obluzowania
endoprotezy jest utrata trwałego połączenia pomiędzy
jednym z elementów endoprotezy a otaczającą tkanką
kostną, wzrost wartości obserwowanych mikroruchów
pomiędzy częścią endoprotezy i tkanką kostną oraz
towarzyszące objawy kliniczne. Obluzowanie endoprotezy
jest najczęściej wynikiem zmian własności i struktury
tkanki kostnej otaczającej implant

osteotomia podkolanowa

-

zabieg chirurgiczny mający na

celu

korekcję

geometrii

kończyny

dolnej

i

przywrócenie

odpowiednich

proporcji

obciążenia

przedziałów

przyśrodkowego

i

bocznego

stawu

kolanowego. W trakcie zabiegu w nasadzie bliższej kości

piszczelowej

jest wycinany (technika "minus'') lub

wszczepiany

dodatkowy (technika

"plus") klin

kostny korygujący położenie

powierzchni stawowych

względem osi anatomicznej kości

piszczelowej

Bibliografia
[1| Będziński R.: An attempt at determining the stresses of human
femur with endoprosthesis, Recent Advances in Experimental
Mechanics pod red. J.F. Silva Gomes. Vol.2, str.1369-1374, Rotterdam
1994.
[2] Będziński R., Bernakiewicz M.: A study of st.iffness relations in the
femur with lup endoprosthesis, Proc. of 3rd World Congress of Biome-
chanics, str.388-389, Japan, Sapporo 1998.
[3] Będziński R., Bernakiewicz M.: Ezperimental analysis of displace-
ments of the femur after total hip arthroplasty, Medical & Biological
Engineering & Computing, str. 264-65, 1999.
[4] Będziński R., Bernakiewicz M., Ścigała K.: Biomechanical aspects of
artificial joint implantation in a lower limb, Journal of Theoretical and
Applied Mechanics, Vol,37, Nr 3, str.455-481, 1999.
[5] Będziński R.. Bernakiewicz M., Ścigała K.: Strain analysis in the hu
man femur after total hip arthroplasty under eztremal oad conditions,
Medical & Biological Engineering & Computing, str.312-313, 1999.

[6] Będziński R.: Biomechanika Inżynierska, Zagadnienia wybrane, Wro
cław 1997.
[7] Będziński R., Pozowski A., Ścigała K.: Ezperimental Verification of
Tibial Osteotomy using Different Technięues, Zsterreiche Ingenieur und
Architekten Zeitschrift, No.6, 1998.

[

8] Będziński R., Ścigała K.: Eipermierital analysis of surgical corrected

knee, Strain - Journal of British Society of Experimental Mechanics,
str.188-194, 1999.

[9] Będziński R., Ścigała K.: FEM analysis of strain distribution in tibia
bonę and relationship between strains and adaptation of bonę tissue,
Proceedings of 2nd European Conference on Computational Mecha nics,
Kraków 2001.
[10] Będziński R., Ścigała K.: Physical and numerical models of tibia
bonę, Proceedings of the 12th Conference of the European Society of
Biome-chanics, Dublin 2000.

[11] Bernakiewicz R.: Opracowanie kryteriów odkształceniowo-
naprężenio-wych doboru implantów stawu biodrowego, Praca doktorska,
Raport Instytutu Konstrukcji i Eksploatacji Maszyn Politechniki Wrocław
skiej Serii PRE-010/98, Wrocław 1998.
[12] Bombelli R.: Structure and function of normal and abnormal hips,
Berlin 1993.
[13] Chao E.: Orthopaedic Biomechanics, The past, present and futurę,
International Orthopaedics, Nr 20, str.239-243, 1996.
[14] Denham R.A., Bishop R.E.D.: Mechanics of the knee and problems in
reconstructive surgery, Journal of Biomechnics, str.372-384, 1978.
[15] Heller M.O., Bergmann G., Deuretzbacher G., Durselen L., Pohl M.,
Claes L., Haas N.P., Duda G.: Musculo-skeletal loading conditions at the
hip during walking and stair climbing, Journal of Biomechanics, vol.32,
str.883-893, 2001.
[16] Huiskes R.: Bonę remodelling around implants can be explained as
ana effect of mechanical adaptation, Total Hip Revision Surgery pod.
red. O. Galante, G. Resenberga i J. Callaghana, Nowy Jork 1995.
[17] Maąuet P.G.J.: Biomechanics of the knee, Berlin 1983.
[18] Maąuet P.G.J.: Biomechanics of the hip, Berlin 1985.
[19] Pauwels F.: Biomechanics of the locomotour apparatus, Berlin 1976.
[20] Pohl M, Duda G., Heller M., Cleas L.: A realistic model for the
simula-tion of loading of the human lower eztremity, Proceedings of the
12th Conference of the European Society of Biomechanics, Dublin 2000.