Elementy wnioskowania

statystycznego

PRAWDOPODOBIEŃSTWO

Zmienna losowa

Jeżeli każdemu zdarzeniu

elementarnemu przyporządkujemy

liczbę rzeczywistą, to mówimy,

że została określona zmienna

losowa jednowymiarowa.

Zmienna losowa Y

• P(Y = -1) = P({: Y() = -1}) = P({

1

, 

2

, 

3

}) =

• P(Y = 0) = P({: Y() = 0}) = P({

4

}) =

• P(Y = 1) = P({: Y() = 1}) = P({

5

, 

6

}) =

2

1

6

3



6

1

3

1

6

2



Rozkład

prawdopodobieństwa

zmiennej losowej X

jest funkcją, która każdemu

podzbiorowi

możliwych

wartości

tej zmiennej przypisuje liczbę

z domkniętego przedziału [0,1]

Najczęściej spotykanym

rozkładem jest rozkład normalny.
Według jego postaci kształtują
się rozkłady większości zjawisk
ekonomicznych, przyrodniczych i
społecznych. Zadany jest on
funkcją uzależnioną od dwóch
parametrów: średniej

i odchylenia standardowego.

Pojęcia podstawowe

• Populacja

• Próba losowa (reprezentatywność

próby)

• Błąd z próby (odchylenie

charakterystyk z próby w stosunku do
charakterystyk z populacji)

• Charakterystyki próby ~ statystyki próby
• Charakterystyki populacji ~ parametry

populacji

Parametry populacji są stałe. Statystyki mają

charakter losowy i zmieniają się z próby na

próbę.

Testy statystycznej

istotności

• Badając różnice między

statystykami jednej próby a
parametrami populacji stosujemy
test dla jednej próby

• Badając statystyki z dwóch prób

stosujemy test dla dwóch prób
(test chi-kwadrat)

Przykład

•Kolokwium ze statystyki pisało

17 osób. Można było uzyskać od
0 do 30 punktów.Średnia
arytmetyczna dla grupy
wyniosła 20 punktów

a odchylenie standardowe 3,5

punktu (µ = 20, σ = 3,5).

Próba

• Wylosowane do próby cztery osoby

uzyskały następującą liczbę punktów
z kolokwium:

18, 21, 22, 25

.

5

,

21



X

Hipotezy

• Hipoteza zerowa

H

0

:

• Hipoteza alternatywna

H

1

:





X





X

Weryfikacja hipotezy

zerowej

•Błąd I rodzaju-błąd

odrzucenie hipotezy zerowej chociaż jest

prawdziwa

•Błąd II rodzaju-błąd

przyjęcie hipotezy zerowej chociaż jest fałszywa





Poziom istotności testu

• Prawdopodobieństwo popełnienia błędu

I rodzaju przyjmuje się arbitralnie

przed przystąpieniem do badań.

Ustalając ryzyko odrzucenia hipotezy

zerowej

chociaż jest ona prawdziwa ustalamy

poziom istotności testu.

Poziomy istotności testu

Poziom

istotności 

Obszar

krytyczny od z



0,05

1,96

0,01

2,58

0,001

3,29

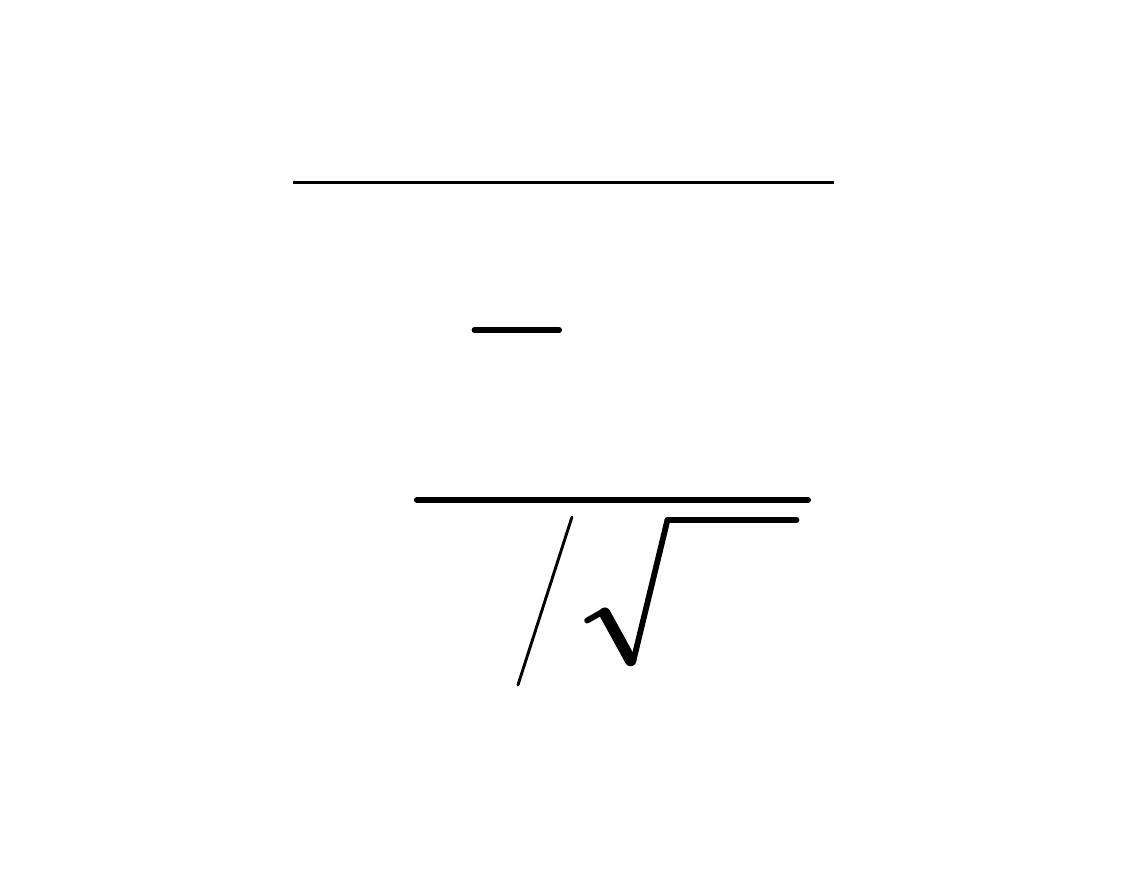
Statystyka testu

N

X

z









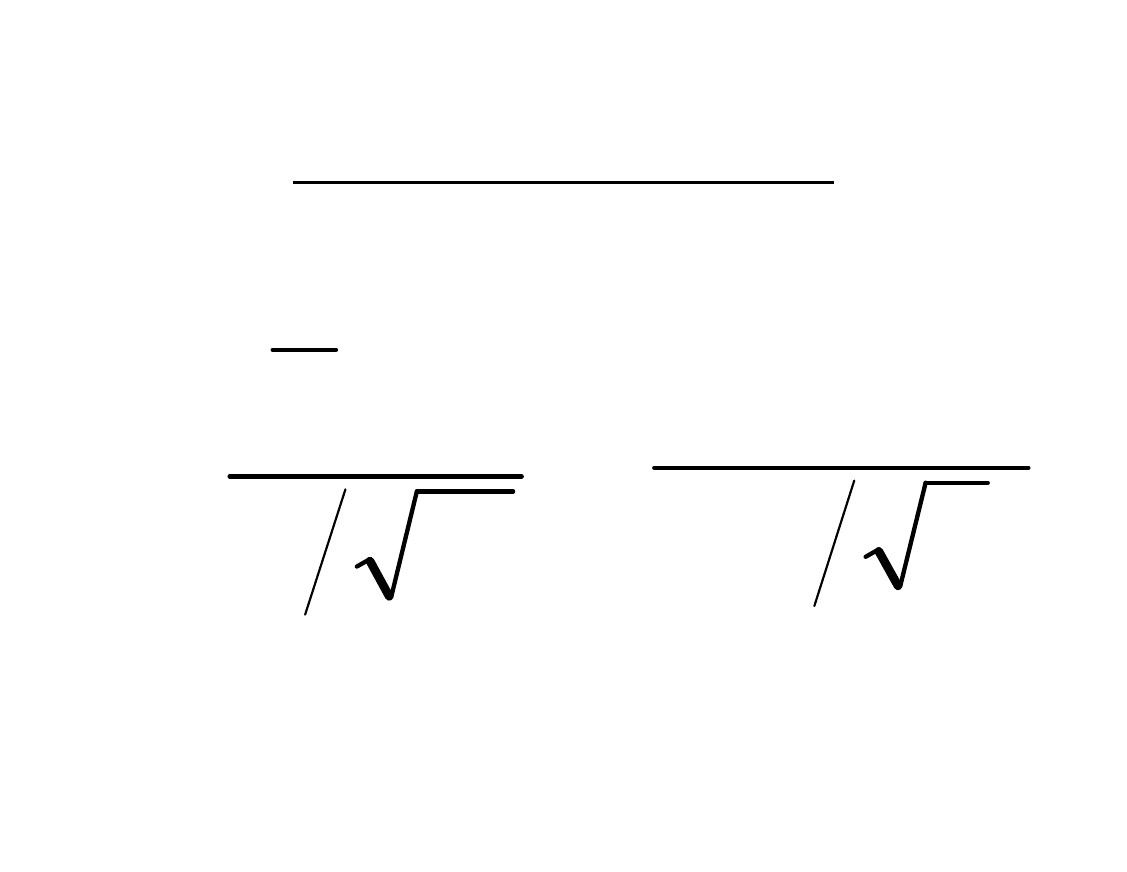
Statystyka testu

N

X

z









4

5

,

3

20

5

,

21 



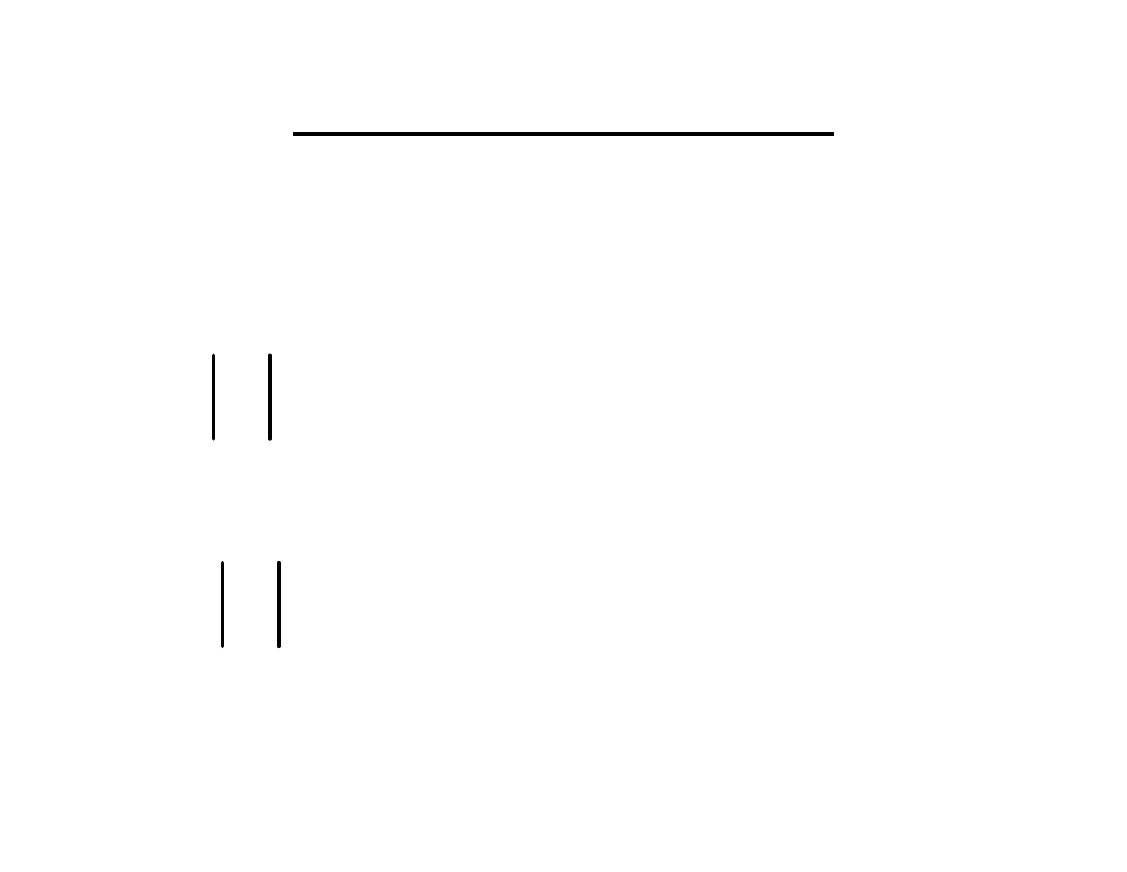
Statystyka testu

86

,

0



z

• jeżeli < z

α

, to nie ma podstaw do

odrzucenia

hipotezy zerowej

• jeżeli z

α

, wówczas odrzucamy

hipotezę zerową

z



z

Wniosek

•0,86 < 1,96

•Przyjmujemy, że różnica

pomiędzy wielkością statystyki
próby (21,5)

a wielkością parametru (20)

wynika z błędu próby.

Rozkład

Normalny

Rozkład normalny jest charakterystyczny dla
dowolnego zbioru wartości, na które działa wiele
niezależnych i jednakowo ważnych czynników
przypadkowych, z których żaden nie jest
dominujący.

Rozkład normalny

Rozkład zwany rozkładem Gaussa-Laplace'a jest
najczęściej spotykanym rozkładem zmiennej
losowej ciągłej.

Mówimy, że zmienna losowa ciągła X ma
rozkład normalny o wartości oczekiwanej
μ i odchyleniu standardowym σ









,

~N

X

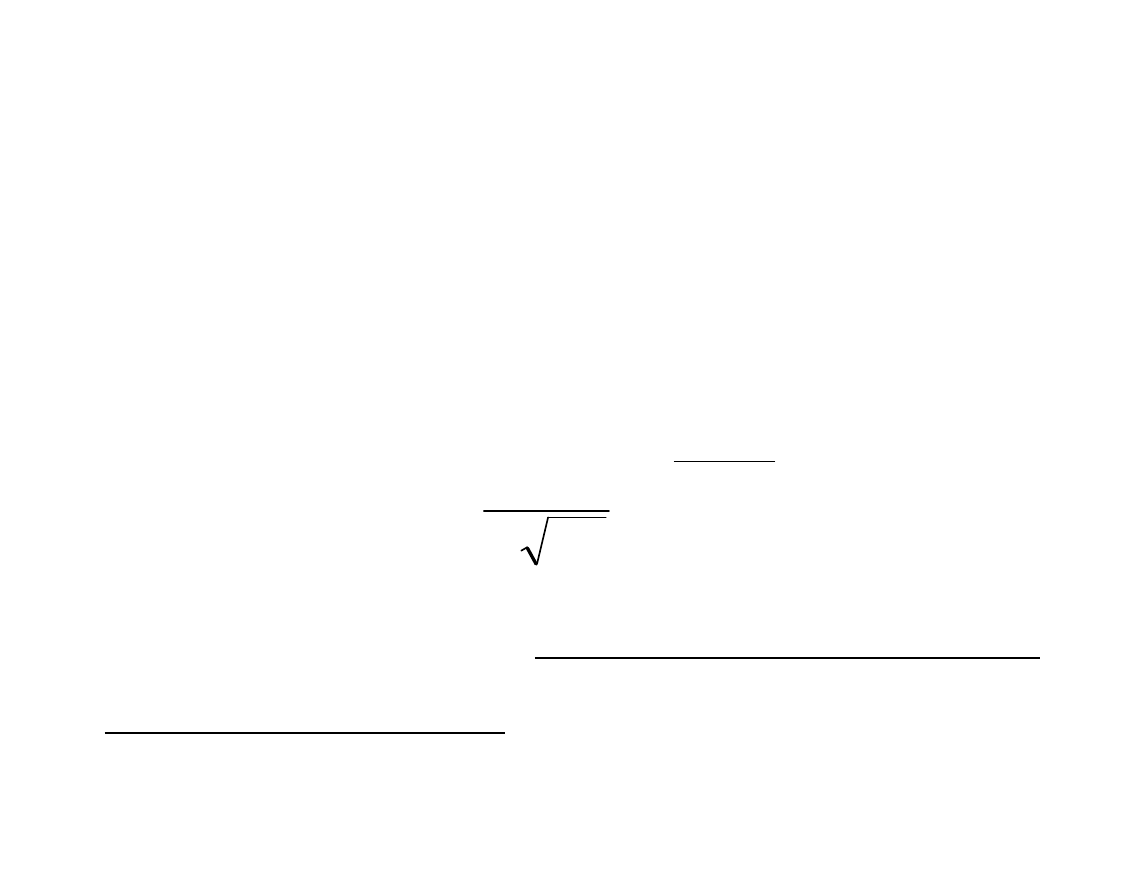
Rozkład prawdopodobieństwa w przypadku
zmiennej losowej ciągłej nosi nazwę rozkładu
(funkcji) gęstości.























2

2

2

2

1

)

(









x

e

x

f

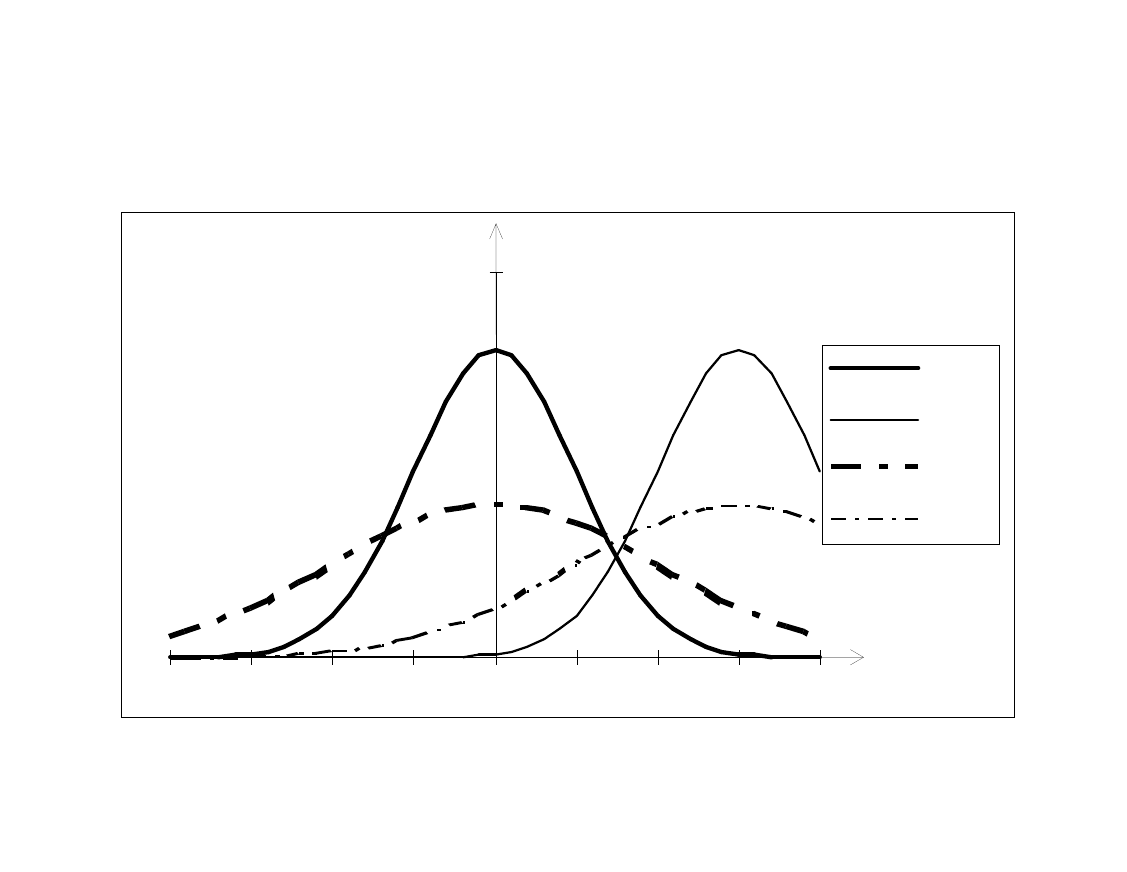
Funkcja gęstości w rozkładzie normalnym

postaci:

określona została dla wszystkich rzeczywistych

wartości zmiennej X, gdzie e = 2,72…, π =

3,14…

0

0,5

-4

-3

-2

-1

0

1

2

3

4

N(0,1)
N(3,1)
N(0,2)
N(3,2)

Przykładowe rozkłady funkcji gęstości dla
danych μ i σ

Funkcja gęstości w rozkładzie
normalnym:

- jest symetryczna względem prostej x
=



- w punkcie x =



osiąga wartość

maksymalną
- kształt funkcji gęstości zależy od

wartości
parametrów:



i σ. Parametr



decyduje o
przesunięciu krzywej, natomiast

parametr σ
decyduje o „smukłości” krzywej.

Reguła „trzech sigm” - jeżeli zmienna losowa ma
rozkład normalny to:

- 68,3 % populacji mieści się w przedziale (



- σ;



+ σ)

- 95,5 % populacji mieści się w przedziale (



- 2σ;



+ 2σ)

- 99,7 % populacji mieści się w przedziale (



- 3σ;



+ 3σ)

W celu obliczenia

prawdopodobieństwa

zmiennej X w rozkładzie

normalnym

o dowolnej wartości oczekiwanej μ

i odchyleniu standardowym σ

dokonuje się standaryzacji.

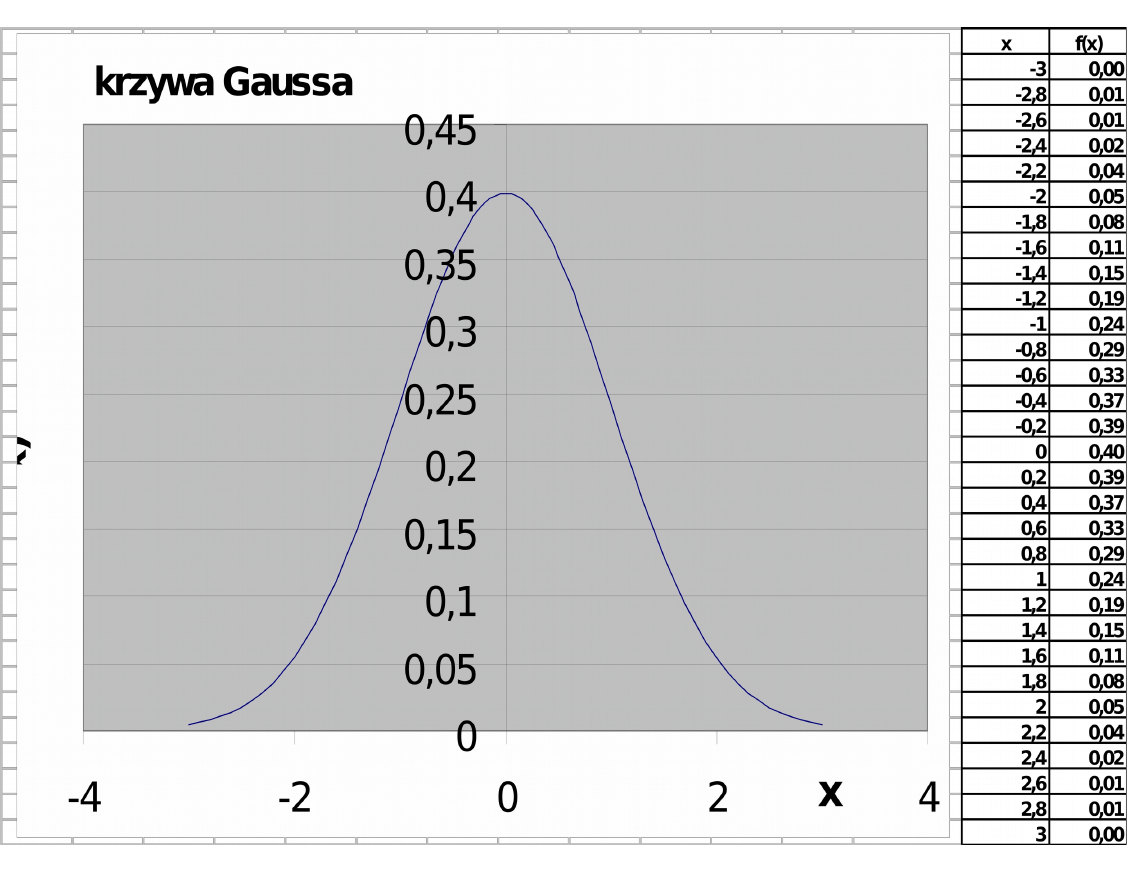
Zmienną losową X zastępujemy zmienną

standaryzowaną Z, która ma rozkład N(0,1)









x

z

Standaryzacja polega na sprowadzeniu

dowolnego rozkładu normalnego o danych

parametrach



i σ do rozkładu

standaryzowanego (modelowego) o wartości

oczekiwanej



= 0 i odchyleniu standardowym σ

= 1.

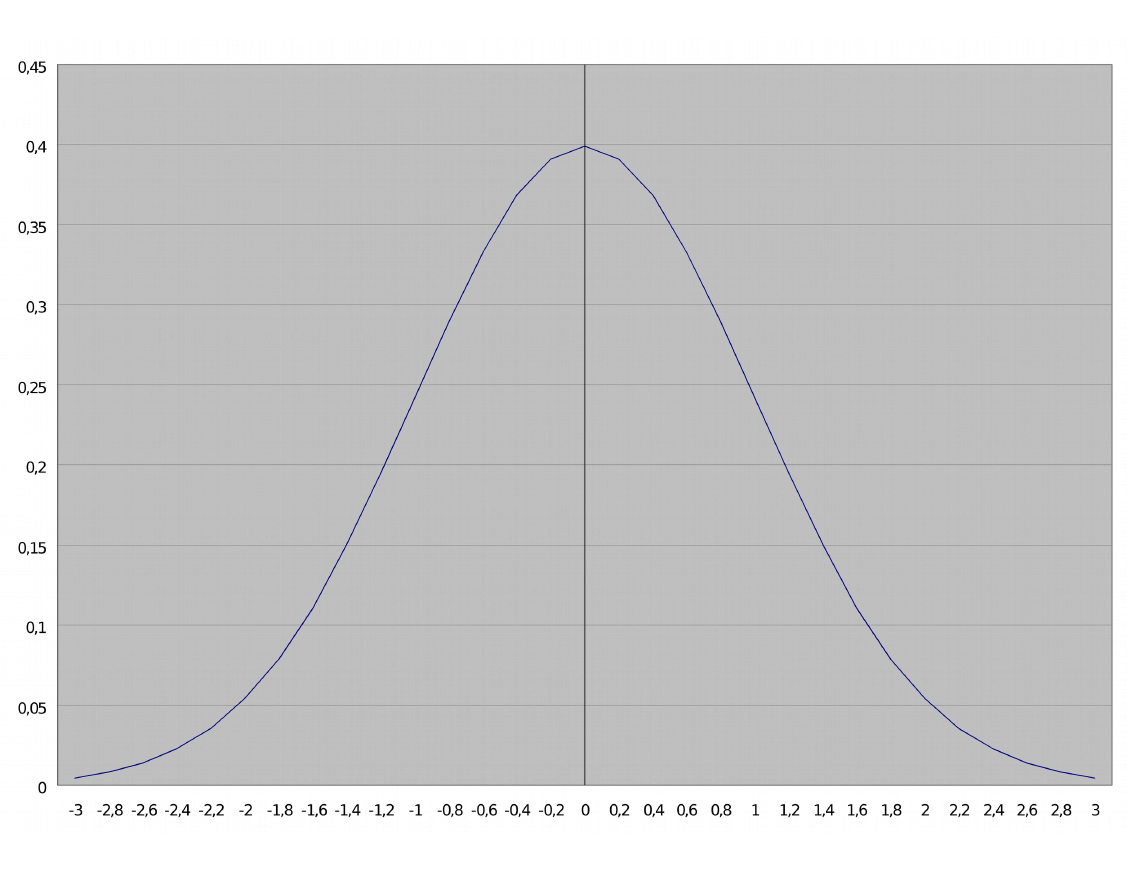
Wartości dystrybuanty

standaryzowanego rozkładu

normalnego zostały

stablicowane

Przykład

Poziom inteligencji mierzony jako współczynnik
inteligencji IQ jest zmienną o rozkładzie normalnym.
Zmienna ta jest mierzona w skali od 0 do 200,
ze średnią równą 100 i odchyleniem standardowym
13 lub 14 w zależności od wieku.

Student A uzyskał 115 punktów, dla uproszczenia

przyjmujemy odchylenie standardowe równe 10

punktów.

Ile osób ma szansę uzyskać lepszy wynik, a ile osób

gorszy ?

Własności rozkładu

normalnego

• Pole pod krzywą normalną jest równe

1,0 (odpowiada wszystkim osobom o

określonej charakterystyce)

• Rozkład normalny jest rozkładem

symetrycznym (prawdopodobieństwo

wylosowania osoby,
której IQ jest niższe od średniej wynosi 0,5,
tyle samo co prawdopodobieństwo

wylosowania osoby o IQ wyższym od

średniej).

Student A uzyskał 115
punktów

• 115 – 100 = 15

• Standaryzacja

• Uzyskany wynik znajduje się na prawo

od średniej arytmetycznej, w odległości
1,5 odchylenia standardowego od tej
średniej.







x

5

,

1

10

15











x

Student A wyniki

•0,5 + 0,4332 = 0,9332

93,32 %

•0,0668

6,68

%

Student B uzyskał 80
punktów

• 80 – 100 = -20

• Standaryzacja

• Uzyskany wynik znajduje się na lewo

od średniej arytmetycznej, w odległości
dwóch odchyleń standardowych od tej
średniej.







x

0

,

2

10

20















x

Student B wyniki

•0,0223 2,23 %

•0,4772 + 0,5 = 0,9772

97,72 %

Obszar krytyczny

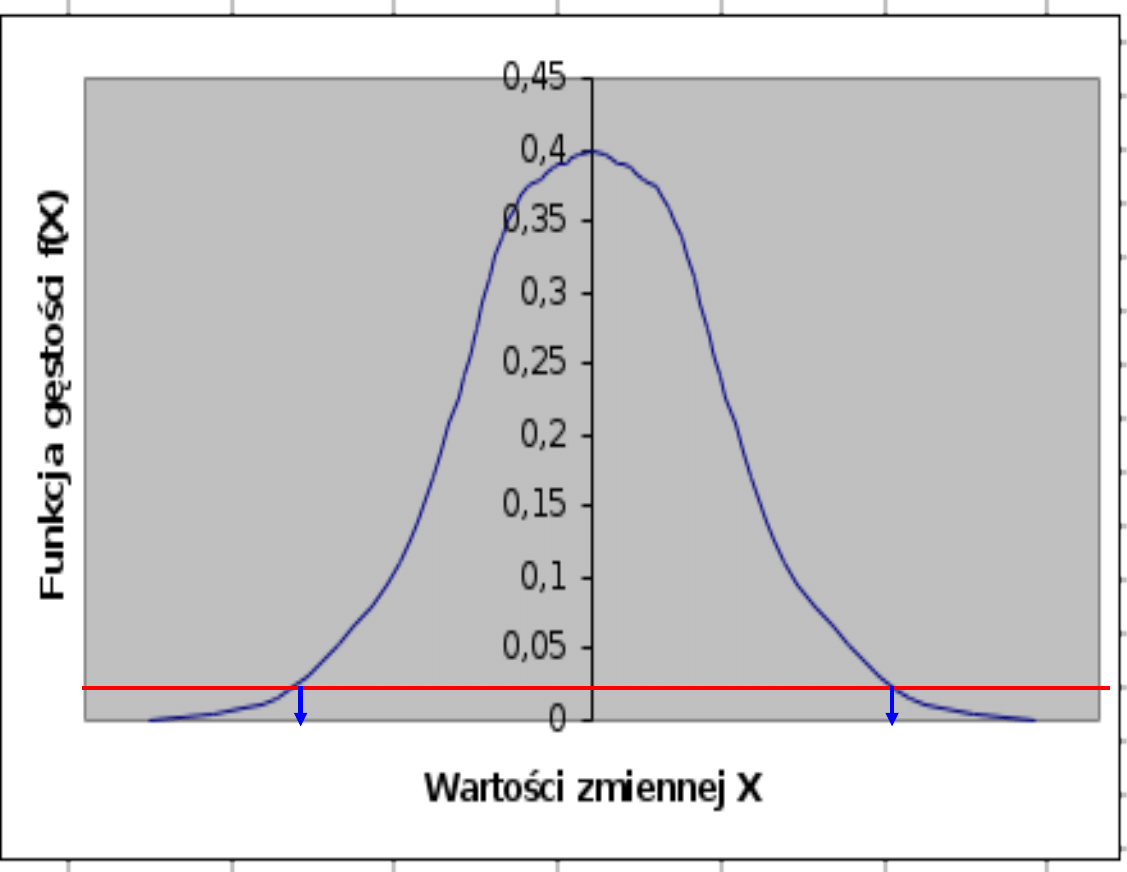
- z





z



Test dwustronny

• - z



< z < z



nie ma podstaw do odrzucenia hipotezy H

0

• z < - z



lub z > z



odrzucamy H

0



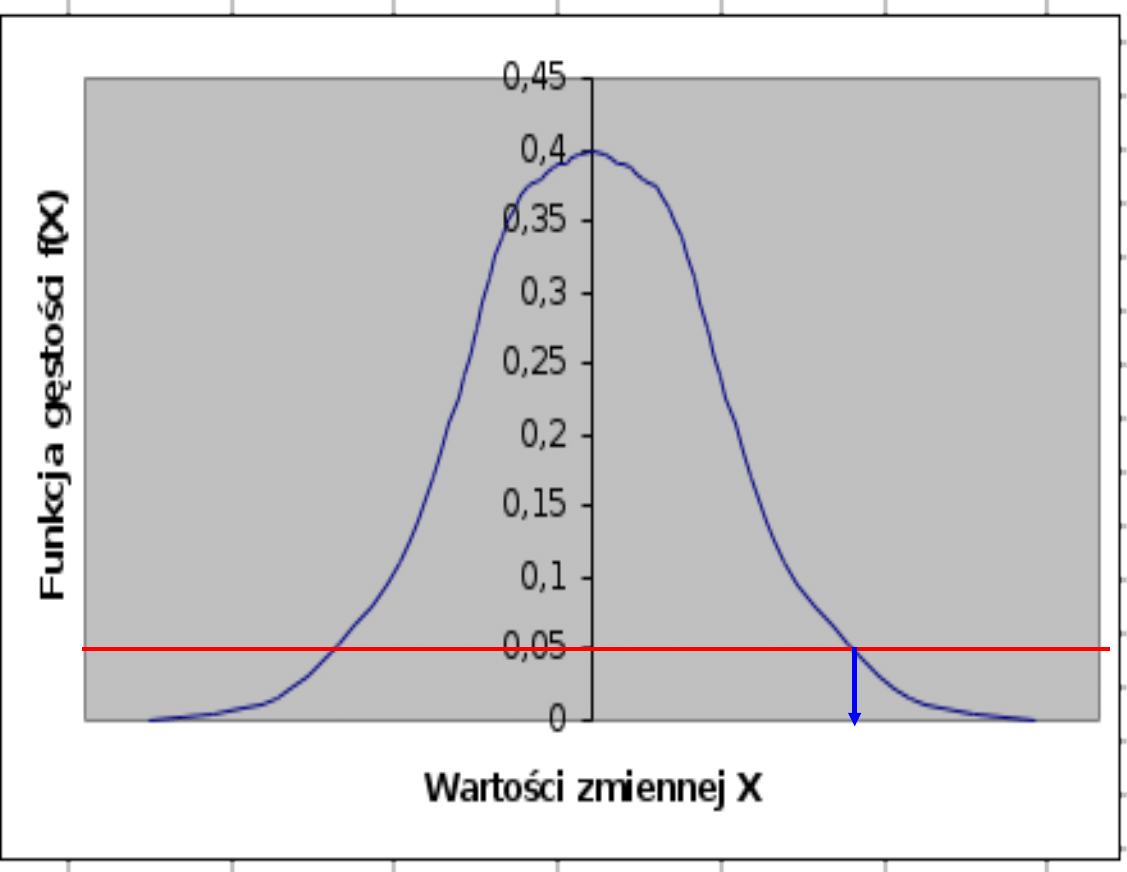
z



Test prawostronny

•

z < z



nie ma podstaw do odrzucenia hipotezy H

0

• z  z



odrzucamy H

0



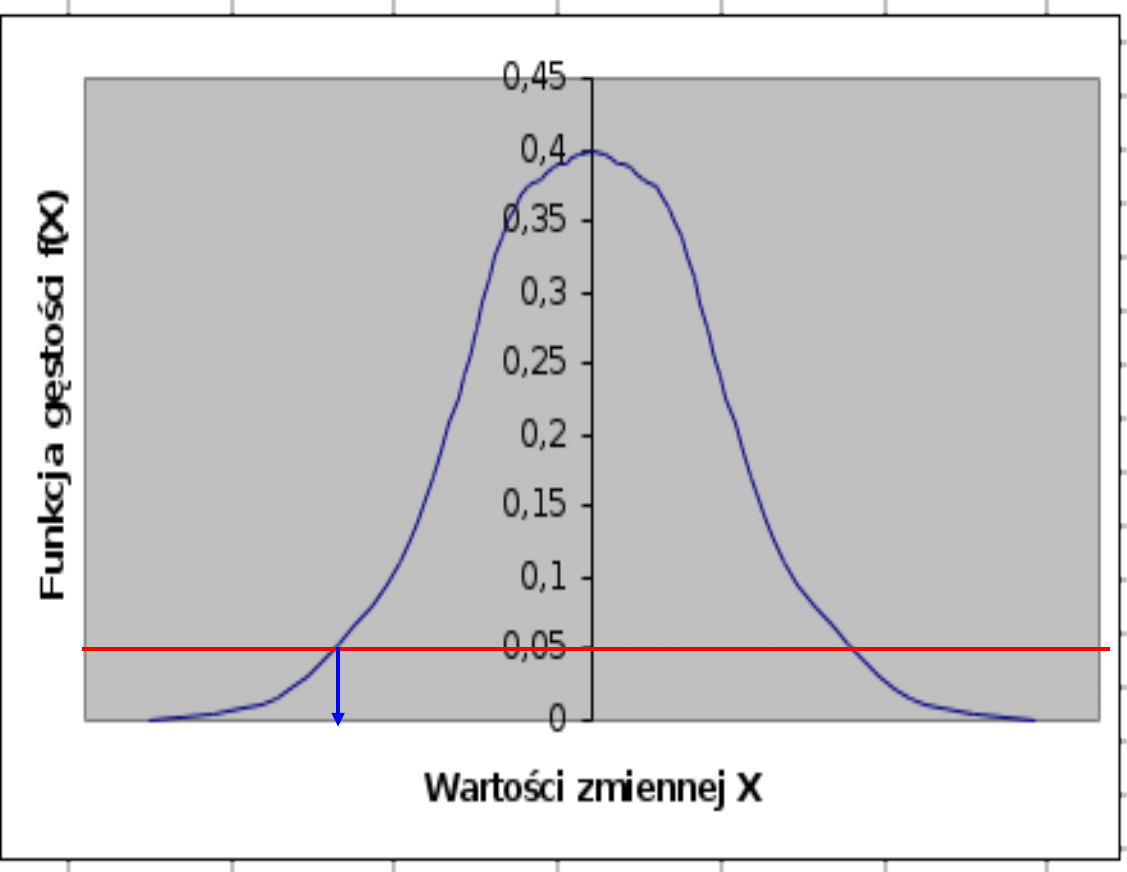
-z



Test lewostronny

•

z > -z



nie ma podstaw do odrzucenia hipotezy H

0

• z  -z



odrzucamy H

0

Rozkład średnich z próby

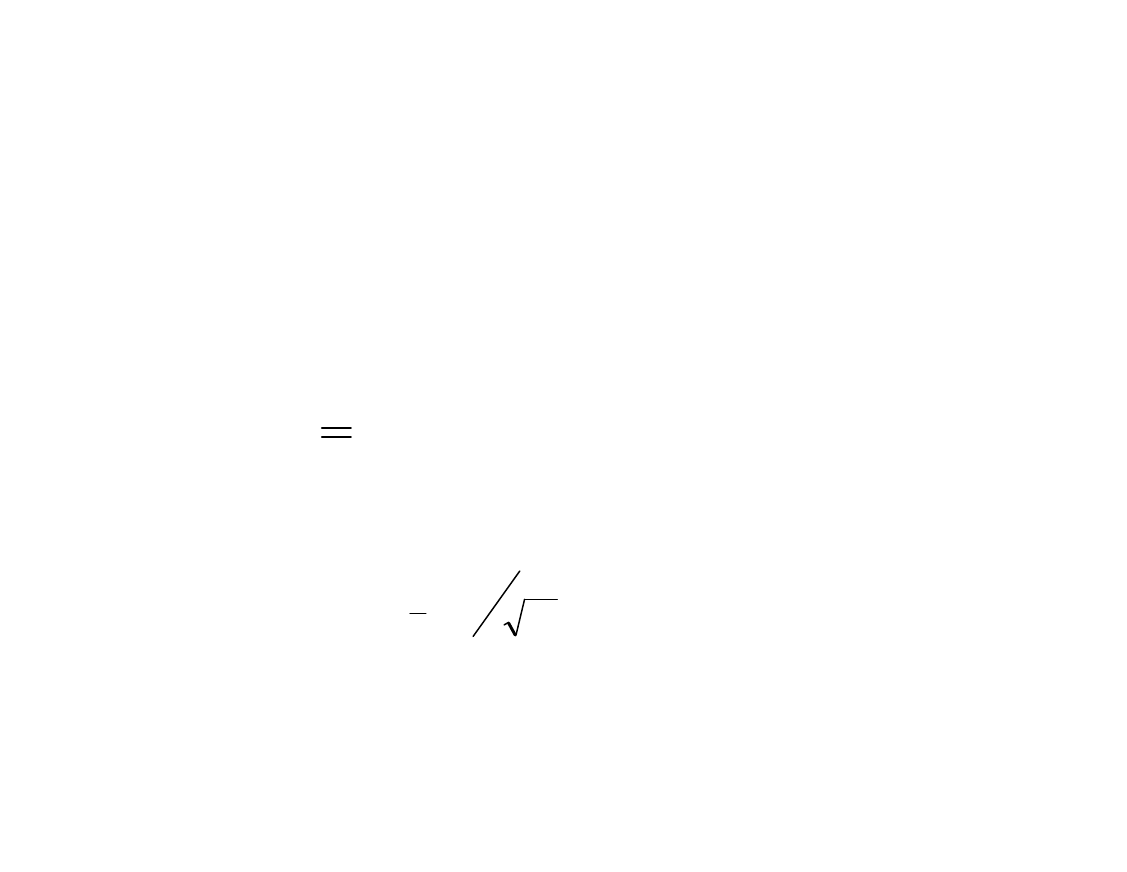
Jeżeli jakaś zmienna (x) ma rozkład normalny w

populacji,

z której dobieramy szereg prób o tej samej

liczebności (N), to:

• rozkład średnich z próby będzie rozkładem

normalnym;

• średnia rozkładu średnich z próby, czyli

średnia średnich , będzie równa średniej z

populacji ,

z której te próby zostały dobrane;
• odchylenie standardowe rozkładu średnich z

próby
będzie równe  =

(błąd standardowy średniej)

X

x

N



Centralne twierdzenie

graniczne

Jeżeli dobieramy próby losowe o
liczebności N z populacji o dowolnym
rozkładzie o parametrach µ i , to

wraz ze wzrostem N, rozkład średnich
dąży
do rozkładu normalnego o średniej µ

i odchyleniu standardowym .

N



Jeżeli liczebność

próby jest

dostatecznie duża,

możemy pominąć

założenie o

normalności rozkładu

w populacji.

•N ≥ 100 –zawsze można znieść

założenie normalności

rozkładu

;

•50 ≤ N < 100 - prawie zawsze;

•30 ≤ N < 50 – z wielką

ostrożnością;

• N < 30 - nigdy