Zginanie walcowe płyt

Zginanie walcowe płyt

prostokątnych

prostokątnych

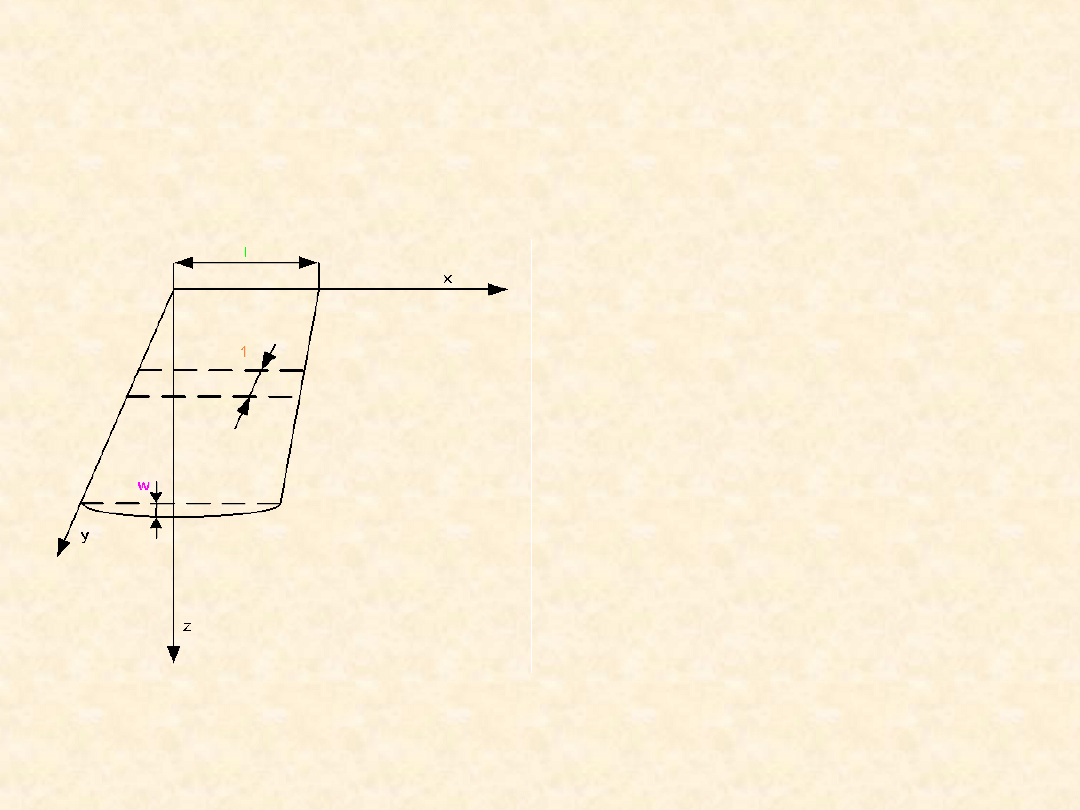
Podstawowe założenia:

Podstawowe założenia:

gdzie:

1

– szerokość płyty,

l

– długość jednostkowa

płyty,

Elementarne pasemko
traktujemy jako belkę o
prostokątnym przekroju
poprzecznym, gdzie
długość l, wysokość h.

Rys. 1.

a) płyta długa prostokątna pod wpływem obciążenia

poprzecznego i stałego na całej długości (rys. 1.);

b)

rozważamy płytę o stałej grubości h i założeniu, że

płaszczyzna płyty leżąca pod obciążeniem pośrodku

pomiędzy zewnętrznymi powierzchniami jako płaszczyzna

„xy”. Oś y pokrywa się z podłużną krawędzią płyty, oś z

skierowana jest ku dołowi. Natomiast „

1

” jest szerokością

płyty (elementarne pasemko, które uważamy jako belkę o

przekroju prostokątnym o długości „

l

”);

c)

ugięcie płyty opisano równaniem różniczkowym (dla

pasemka płyty), które podobne jest do równania ugięcia

belki zginanej;

d)

przekrój poprzeczny belki pozostaje podczas zginania

płaski i ulega obrotowi względem osi obojętnej;

e)

do końcowych przekrojów belki nie są przełożone siły

osiowe, to powierzchnia obojętna belki pokrywa się ze

środkową powierzchnią płyty, a jednostkowe wydłużenie

włókna równoległego do osi „x” jest proporcjonalne do

jego długości „z” od powierzchni środkowej;

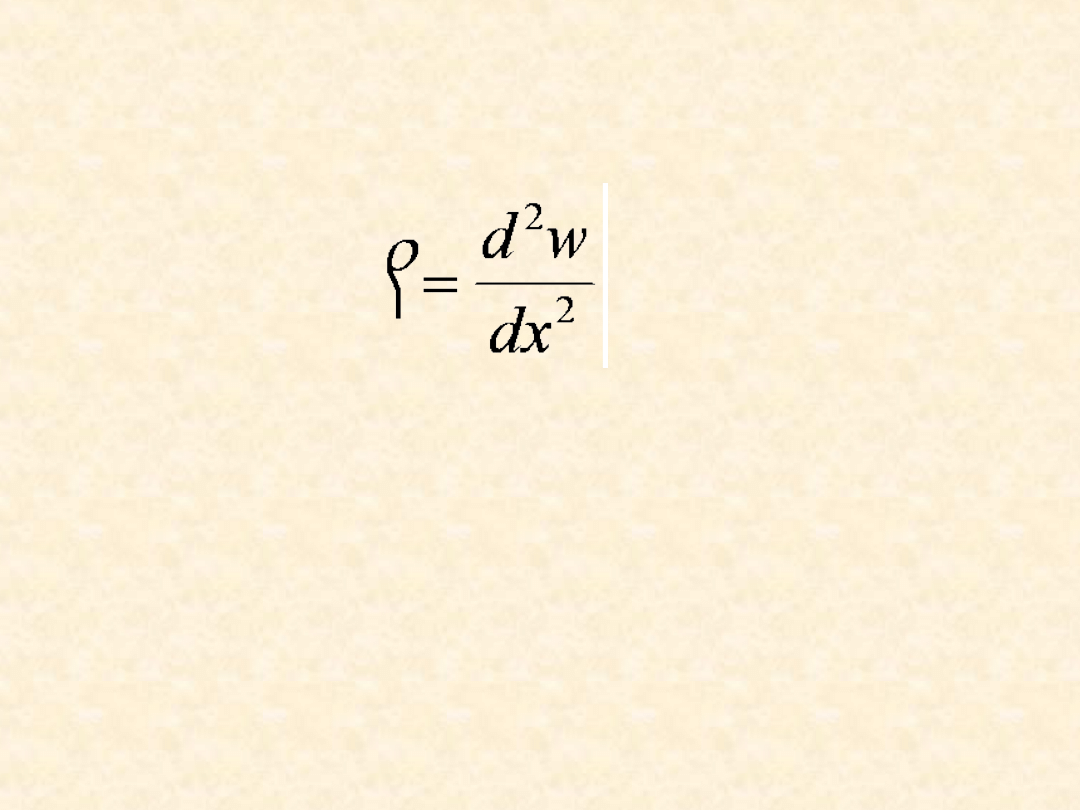
f)

krzywizna odkształconej belki przyjęto wg wzoru:

gdzie:

wgięcie płyty (belki) w kierunku osi „z” jest małe w porównaniu z
długością belki „l”

(1
)

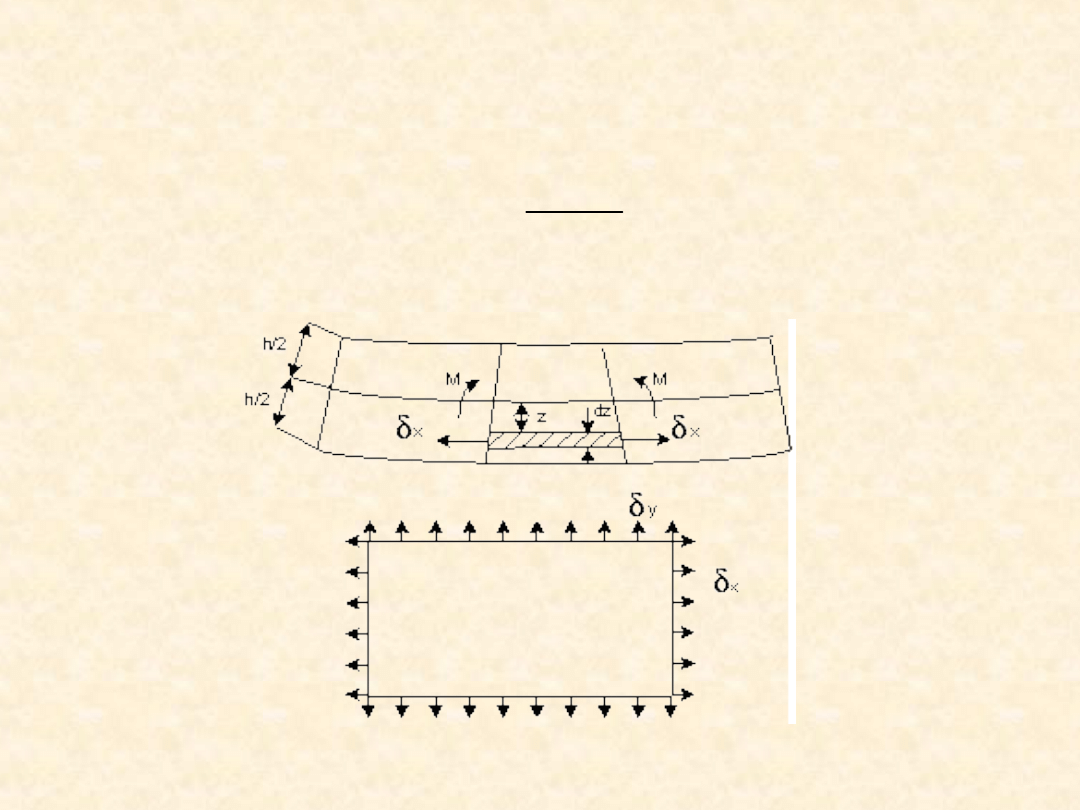
g) jednostkowe wydłużenie włókna, które znajduje się w

odległości „z” od powierzchni środkowej (rys. 2.) określono
wzorem:

2

2

dx

w

d

z

x







rys.
2.

(2
)

Podstawy teoretyczne

Podstawy teoretyczne

• Przy wykorzystaniu prawa Hooke’a określono jednostkowe

wydłużenie:

E

E

y

x

x













0







E

E

x

y

y







(3
)



– współczynnik
Poissona.

gdzie:

E

– moduł sprężystości

materiału,

• Odkształcenie poprzeczne płyty w kierunku osi „y” jest

równe zeru. W związku z zachowaniem warunku ciągłości
płyty przy zginaniu otrzymano następujące zależności:

x

y







(4
)

• Po podstawieniu (4) do (1) otrzymano:

E

x

x







)

1

(

2





2

2

2

2

1

1

dx

w

d

Ez

E

x

x



















(5)

• Moment zginający określono całką:

2

2

2

3

2

2

2

2

2

2

2

2

)

1

(

12

1

dx

w

d

Eh

dz

dx

w

d

Ez

zdz

M

h

h

h

h

x





























(6)

gdzie
:

)

1

(

12

2

3







Eh

D

• Krzywa odkształconego elementarnego pasemka

przedstawiono w następującej postaci różniczkowej:

2

2

dx

w

d

D

M 



gdzie
:

D

– jest sztywnością zginania płyty, która jest odpowiednikiem „EJ

z

”

sztywności belki,

w

– ugięcie płyty (belki) przedstawiono w formacie całkowej (równanie

analogiczne jak dla belki.

(7
)