Równowagi

Równowagi

chemiczne

chemiczne

Rozpatrujemy

układ zamknięty

, w którym

zachodzi reakcja chemiczna :

aA bB

rR qQ

+

�

+

oraz ciśnienie i temperatura są stałe.

p,T = const

Entalpia swobodna takiego układu zależy
od składu układu. Zmieniające się w
trakcie przebiegu reakcji liczby moli
poszczególnych składników możemy
powiązać razem liczbą postępu reakcji



(ksi).

q

dn

r

dn

b

dn

a

dn

dn

d

Q

R

B

A

i

i





















W układzie zamkniętym entalpia swobodna
jest funkcją ciśnienia, temperatury i składu,
który można opisać jedną zmienną – liczbą
postępu reakcji.

(

)

p

p T

T

p

p T

T

G G p T

G

G

G

dG

dT

dp

d

T

p

G

G

G

S

V

T

p

,

,

,

,

,

,

, ,

?

x

x

x

x

=

x

� �

� �

�

�

�

� �

=

+

+

x

� �

� �

� �

�

�

�

x

� �

� �

� �

� �

� �

�

�

�

� � =-

=

=

� �

� �

� �

�

�

�

x

� �

� �

� �

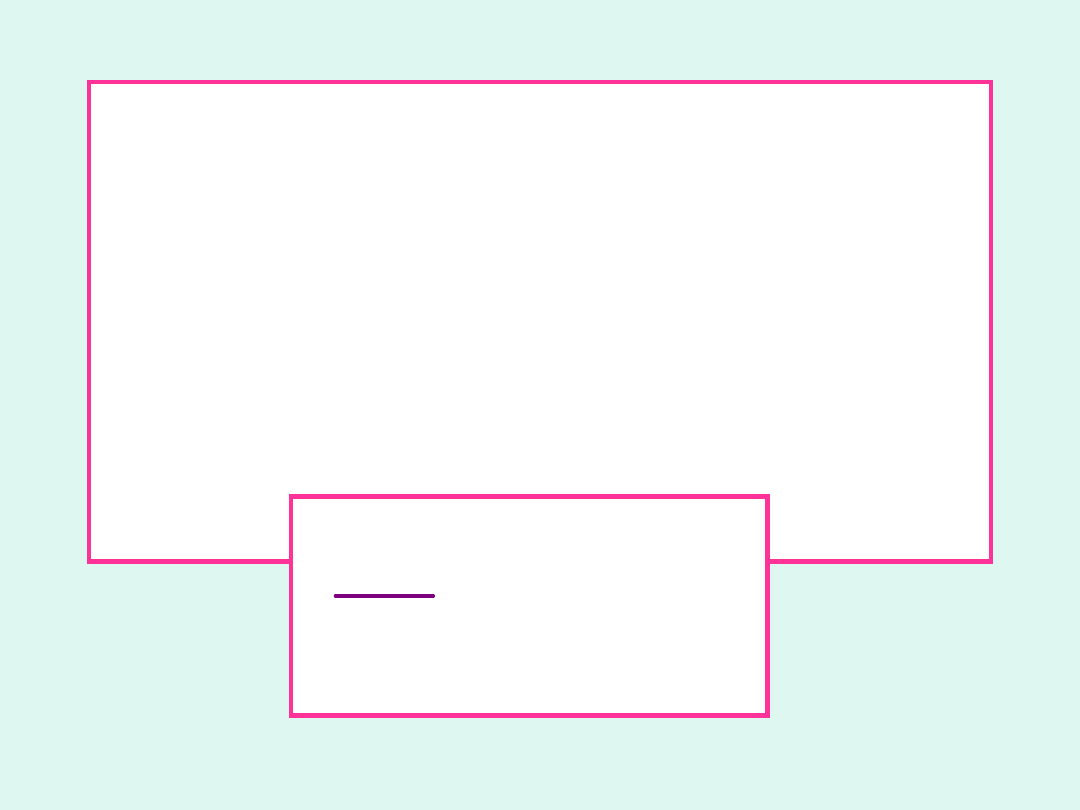
Entalpia

swobodna

reakcji

chemicznej 

r

G

to zmiana entalpii

swobodnej układu zamkniętego o
nieskończenie

dużej

ilości,

w

którym zachodzi reakcja chemiczna
w

warunkach

izotermiczno-

izobarycznych, gdy liczba postępu
reakcji zmienia się o jeden.

r

T,p

G

G

� �

�

=D

� �

�

x

� �

G

0  →

1

p,T = const



r

G<0



r

G=0



r

G>0

G









sub

o

G









prod

o

G

o

r

G



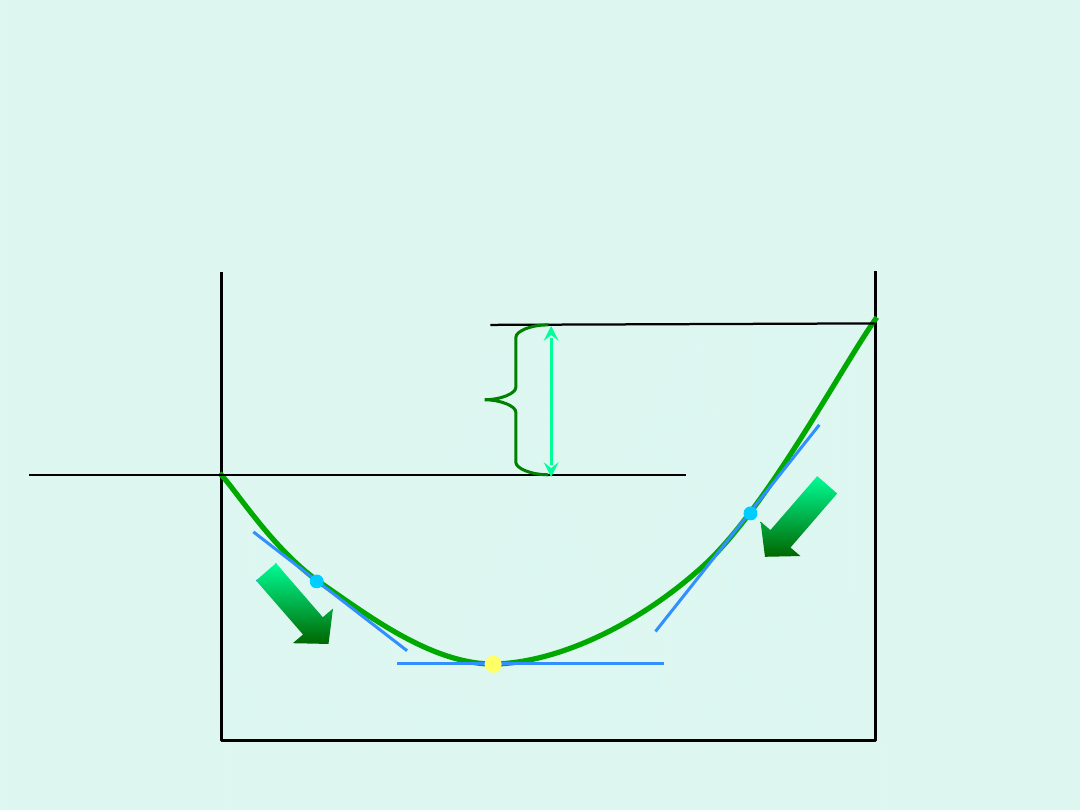
Zmiany entalpii swobodnej układu,

w którym zachodzi reakcja

chemiczna w funkcji liczby postępu

reakcji 



r

G

1

0



r

G

T,p = const

reakcja

egzergonic

zna

reakcja

endergonic

zna

→

stan

równowa

gi

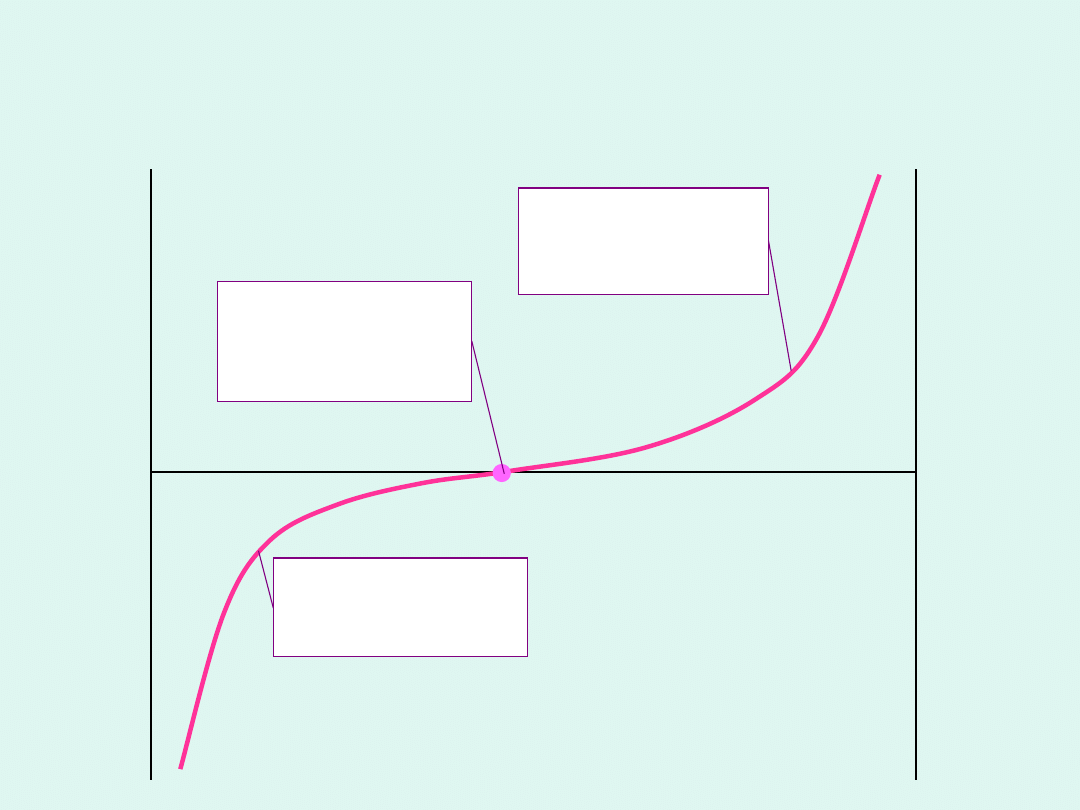
Zależność entalpii swobodnej

reakcji od liczby postępu reakcji

Reakcja egzergoniczna

to taka,

w wyniku której uzyskujemy
pracę użyteczną.

Reakcja endergoniczna

to taka,

która do zajścia w określonym
kierunku wymaga nakładu pracy z
zewnątrz.

0

1



G

T,p=const

1

2

3

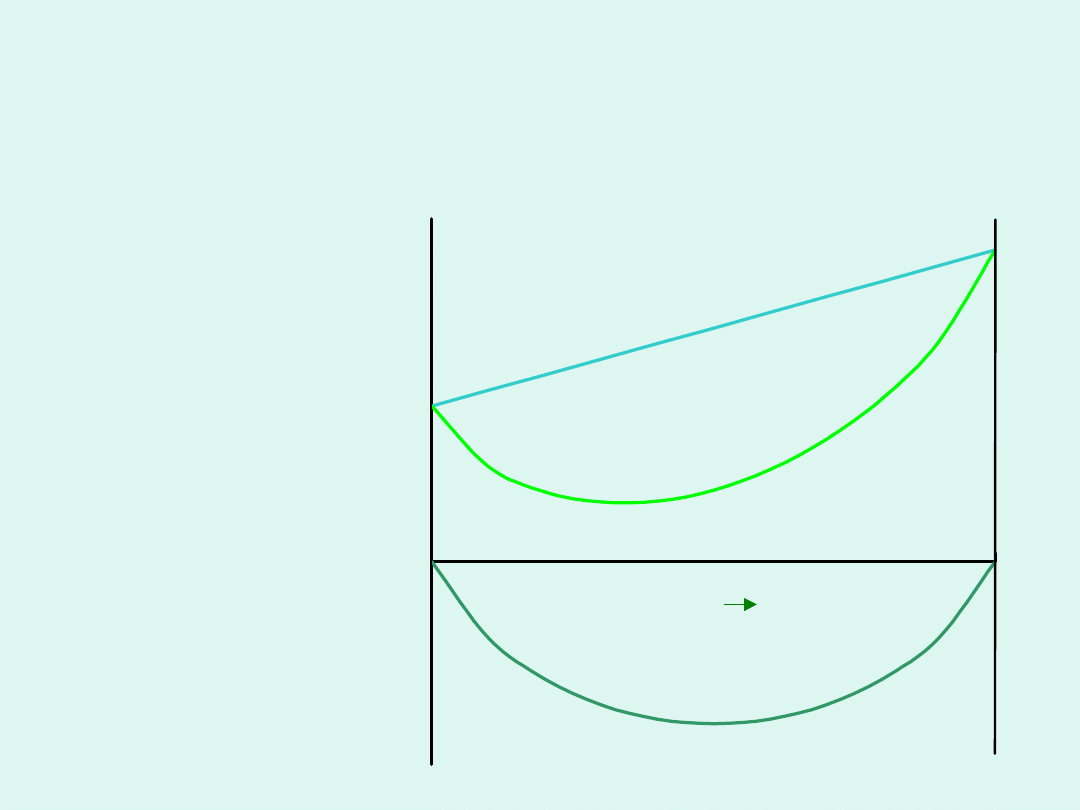
Co powoduje, że na krzywej zależności
entalpii swobodnej układu, w którym
zachodzi reakcja chemiczna, od liczby
postępu reakcji, pojawia się minimum ?

1

– zmiany

entalpii
swobodnej
układu
wynikające tylko
ze zmiany liczby
moli reagentów

2

– zmiany

entalpii
swobodnej
układu
wynikające tylko
z mieszania się
różnej liczby moli
reagentów

3 =1+2

Gdy

T,p = const

, to :













































i

i

i

r

i

i

i

i

i

i

i

i

i

i

i

p

,

T

r

p

,

T

G

d

dn

d

dn

dn

dG

d

G

dG

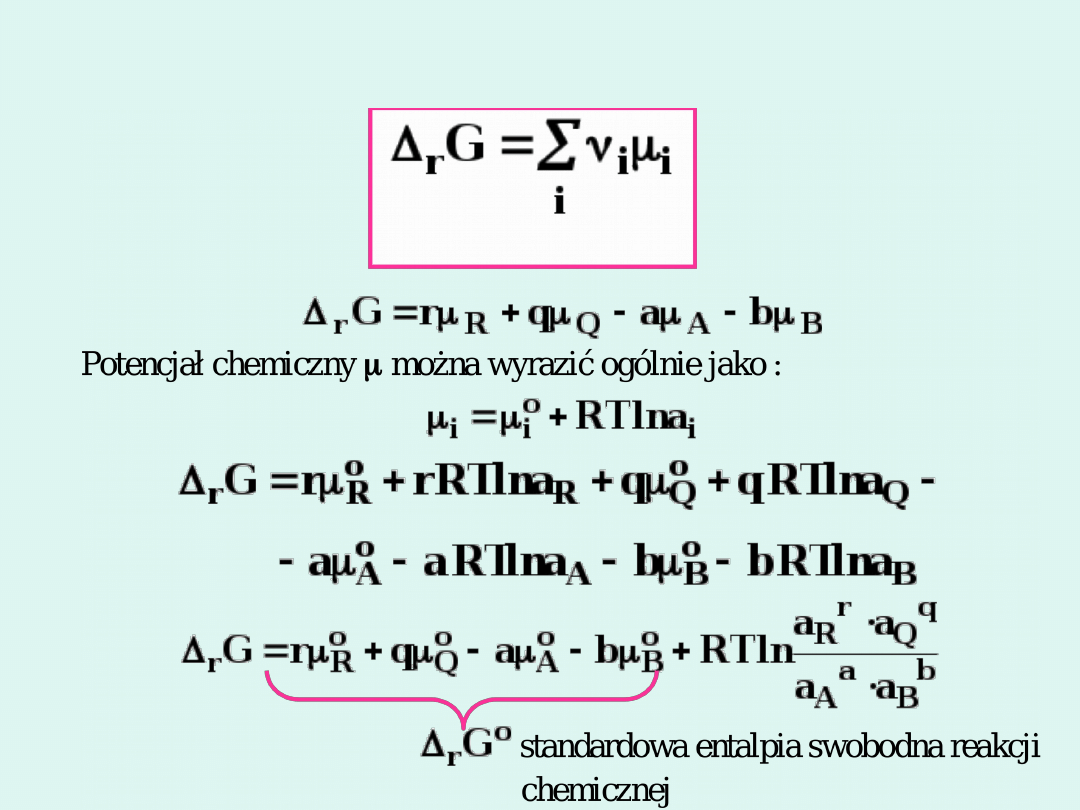
aA bB

rR qQ

+

�

+

Izoterma van’t Hoffa

Jeżeli



r

G < 0

, to reakcja przebiera

samorzutnie z lewa na prawo.

Jeżeli



r

G > 0

, to reakcja przebiera

samorzutnie z prawa na lewo.

Jeżeli



r

G = 0

, to reakcja osiągnęła

stan równowagi.

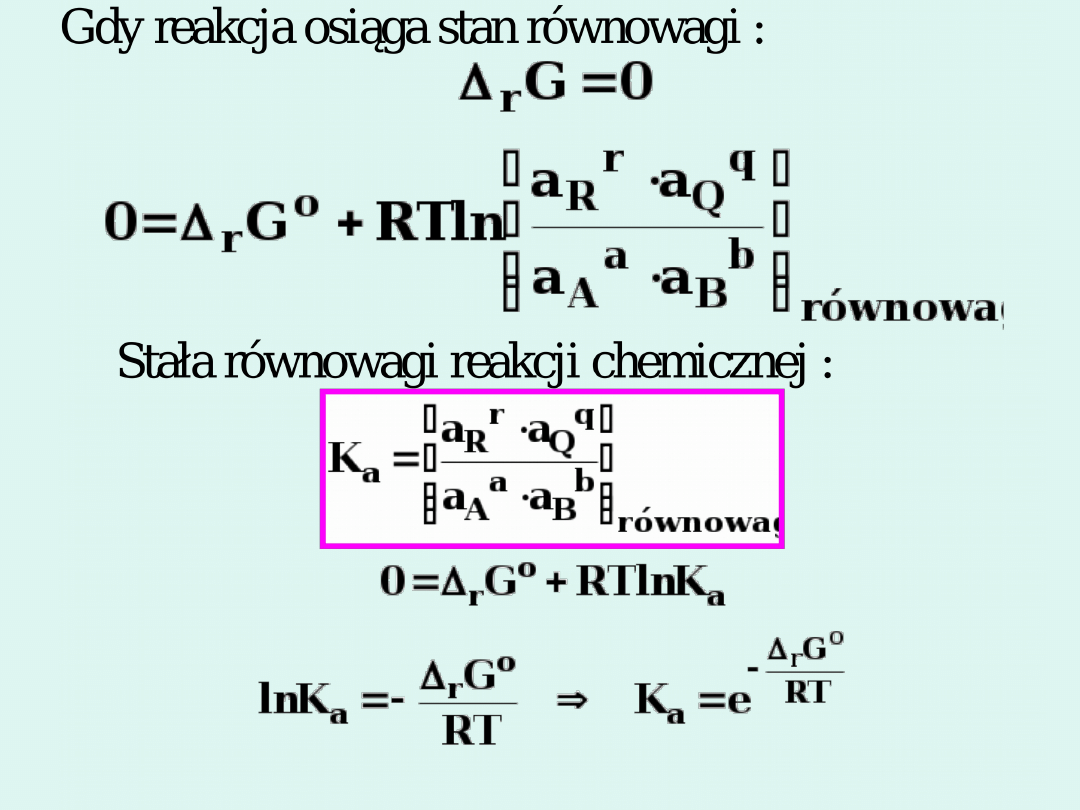
RT

G

a

o

r

e

K







Jeżeli



r

G

o

< 0

, to

K

p

> 1

.

Jeżeli



r

G

o

> 0

, to

K

p

< 1

.

Jeżeli



r

G

o

= 0

, to

K

p

= 1

.

Reakcje w fazie gazowej, gdy

reagenty traktujemy jako gazy

doskonałe

Q

R

o

o

A

B

o

o

q

r

p

a

b

p

p

p

p

K

p

p

p

p

� �

� �

� � � �

� � � �

� � � �

� � � �

� � � �

�

=

�

Stała równowagi ciśnieniowa

K

p

i

o

i

i

o

p

RT

p

ln

m =m +

Stała równowagi ciśnieniowa zależy tylko od
temperatury !

Reakcje w fazie gazowej, gdy

reagenty traktujemy jako gazy

doskonałe

( )

( )

( ) ( )

q

r

R

Q

x

a

b

A

B

x

x

K

x

x

�

=

�

Stała równowagi

K

x

wyrażona przez

ułamki molowe

i

i

i

RT

x

*

ln

m =m +

Stała równowagi

K

x

zależy od temperatury i

ciśnienia !

Związek pomiędzy K

p

i K

x

( )

( )

( ) ( )

( )

( )

( )

( )

Q

R

Q

R

o

o

o

o

A

B

A

B

o

o

o

o

r

g

i

i

q

r

q

r

p

a

b

a

b

q

r

r q a b

R

Q

a

b

o

A

B

p

x

o

r

g

i g prod

i g sub

prod

sub

p

x P

x

x

P

p

x

x

P

K

K

p

x P

x P

p

p

p

p

p

p

K

p

p

x P

x P

p

p

p

p

Kp

,

,

+ - -

D n

= �

�

�

�

�

� �

� �

�

�

�

�

� � � �

�

�

�

�

� � � �

�

�

� � � �

�

� �

�

� � � �

�

� �

�

� � � �

�

� �

�

�

� �

�

� �

� �

�

� �

=

�

� �

� �

D n

=

n

-

n

�

�

�

� �

�

=

=

�

�

�

�

=

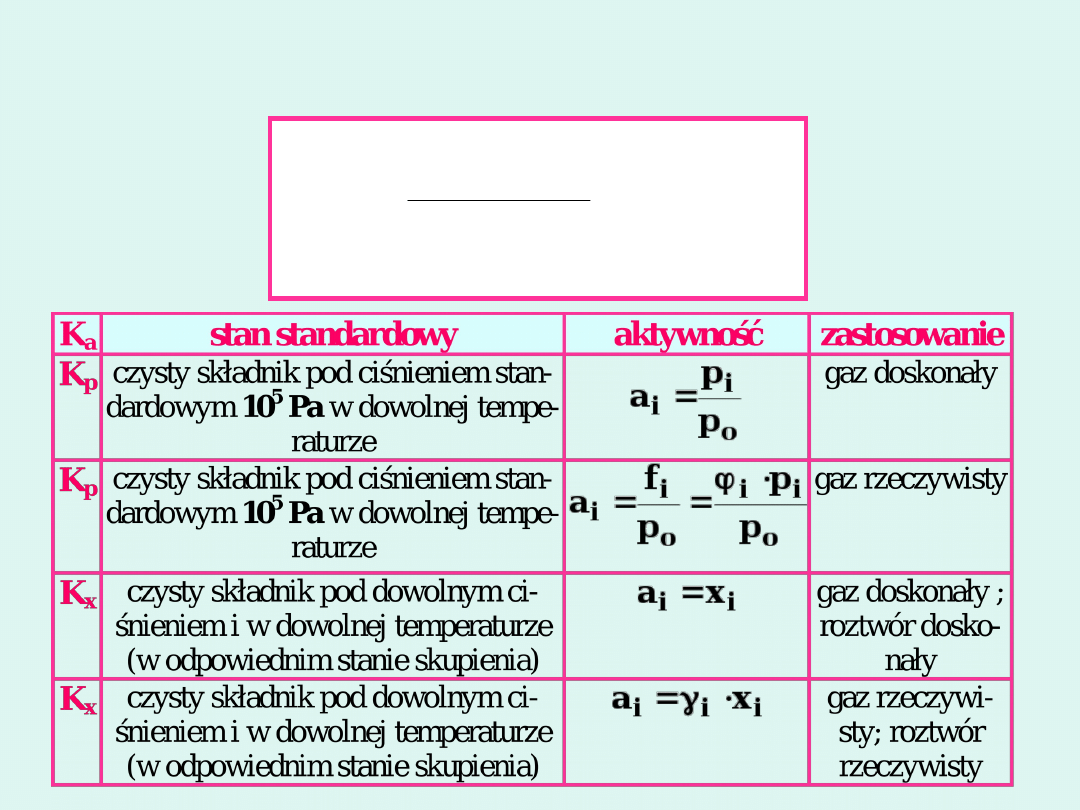
Sposoby wyrażania stałych

równowagi i ich zastosowanie

równowaga

b

B

a

A

q

Q

r

R

a

a

a

a

a

K





















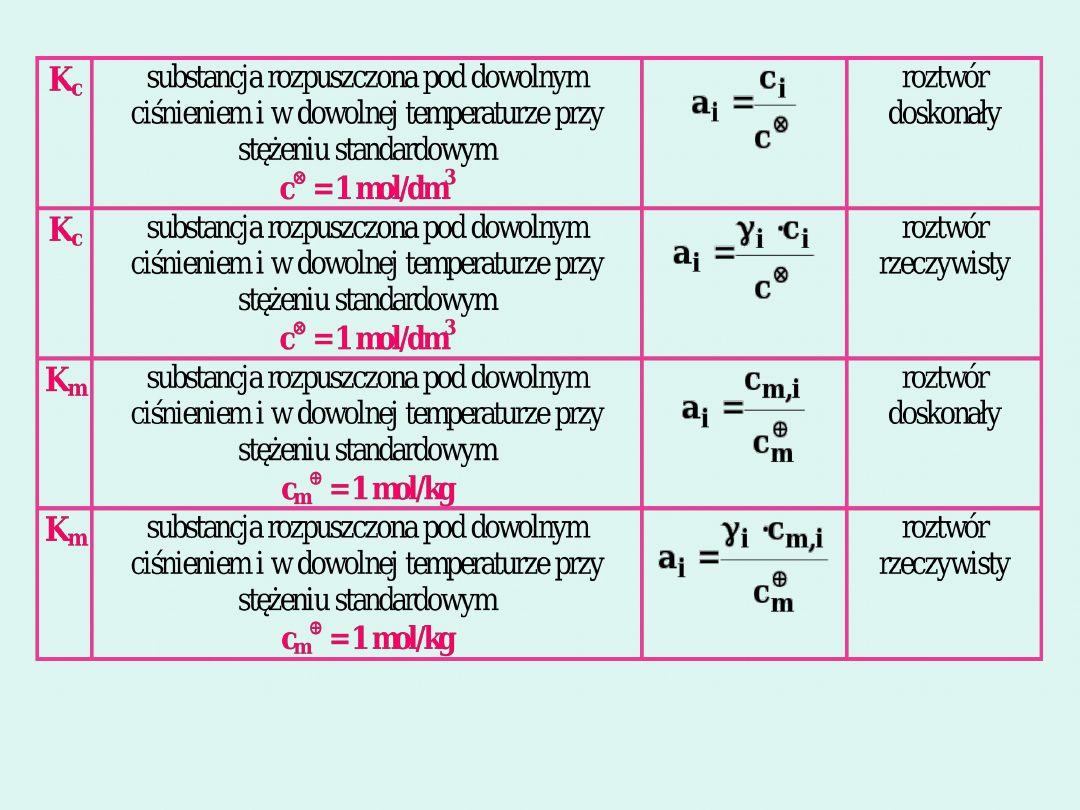
Wpływ temperatury i

ciśnienia na stan

równowagi reakcji

chemicznej

Wpływ temperatury na stan

równowagi reakcji chemicznej

Zakładamy, że ciśnienie jest stałe

p = const.

Korzystamy z równania

Gibbsa-Helmholtza

:

2

o

r

p

a

p

a

p

T

K

RT

a

o

r

2

o

r

p

T

G

T

H

T

K

R

T

K

R

T

K

RT

G

T

H

T

a

o

r









































































































ln

ln

ln

ln

Izobara van’t Hoffa

a 2

2

a 1

1

2

a 2

a 1

1

o

a

r

2

p

o

r

a

2

K

T

o

r

a

2

K

T

T

o

K

r

K

2

T

K

H

T

RT

H

d

K

dT

RT

H

d

K

dT

RT

H

dT

RT

,

,

,

,

ln

ln

ln

ln

�

D

�

�

=

�

�

�

�

�

D

=

D

=

D

=

�

�

�

Jeżeli przedział temperatur, w którym
wykonujemy całkowanie jest niewielki,
możemy przyjąć, że



r

H

o

jest stała.

Wówczas :

2

2

2

a 2

a 1

1

1

1

a 2

a 1

a 2

a 1

a 2

a 1

T

T

o

o

o

T

K

r

r

r

K

2

2

T

T

T

o

o

K

r

r

K

2

1

1

2

o

K

r

2

1

K

2 1

K

1 2

K

o

r

2

1

H

H

H

dT

1

T

dT

R

R

T

RT

T

H

H

1

1

1

1

R

T

T

R

T

T

H T

T

R

T T

RT T

H

T

T

,

,

,

,

,

,

,

,

ln

ln

ln

ln

D

D

D

� �

=

=

=

-

� �

� �

D

D

�

�

�

�

=

-

+

=

-

�

�

�

�

�

�

�

�

D

-

=

�

D

=

-

�

�

o

o

r

r

a

2

2

o

r

a

H

H

dT

d K

dT

R

RT

T

H

1

K

C

R

T

ln

ln

D

D

=

=

D

=-

� +

�

�

�

Możemy też założyć, że entalpia reakcji jest
stała w szerokim zakresie temperatur i
scałkować bez granic :

  

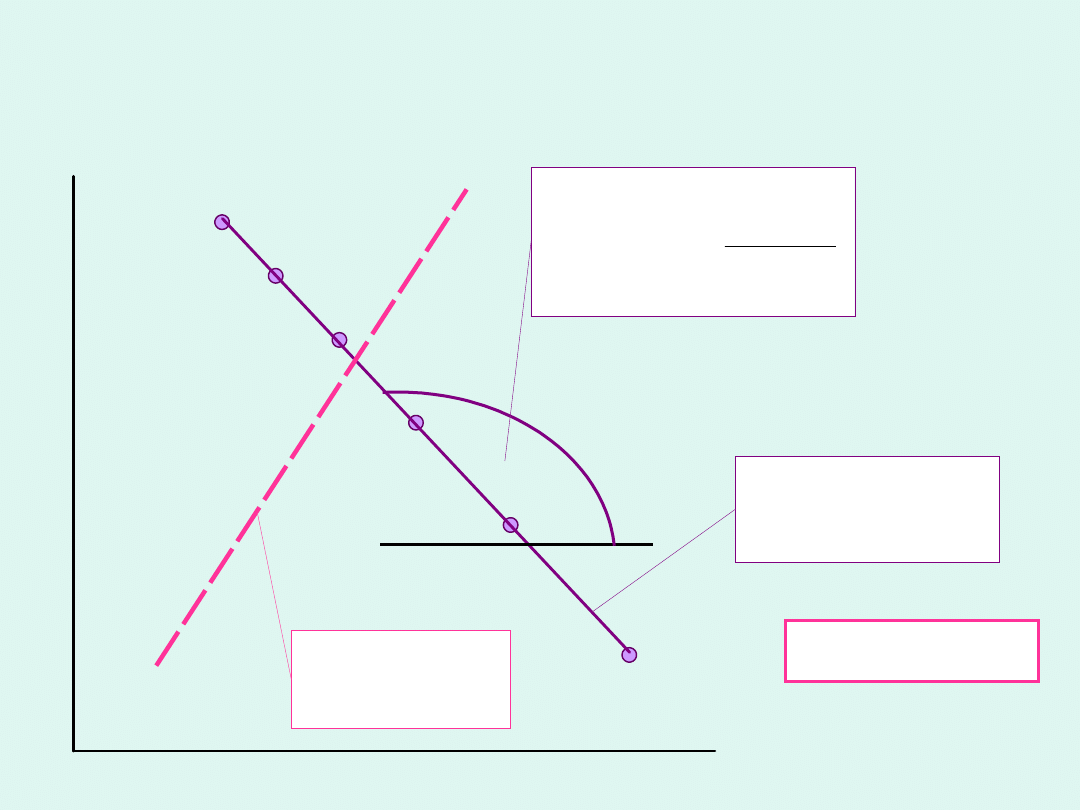
lnK

p



reakcja

endotermiczn

a

reakcja

egzotermic

zna

R

H

tg

a

o

r











a

R

H

o

r









Wyznaczanie entalpii reakcji na

podstawie zależności stałej równowagi od

temperatury

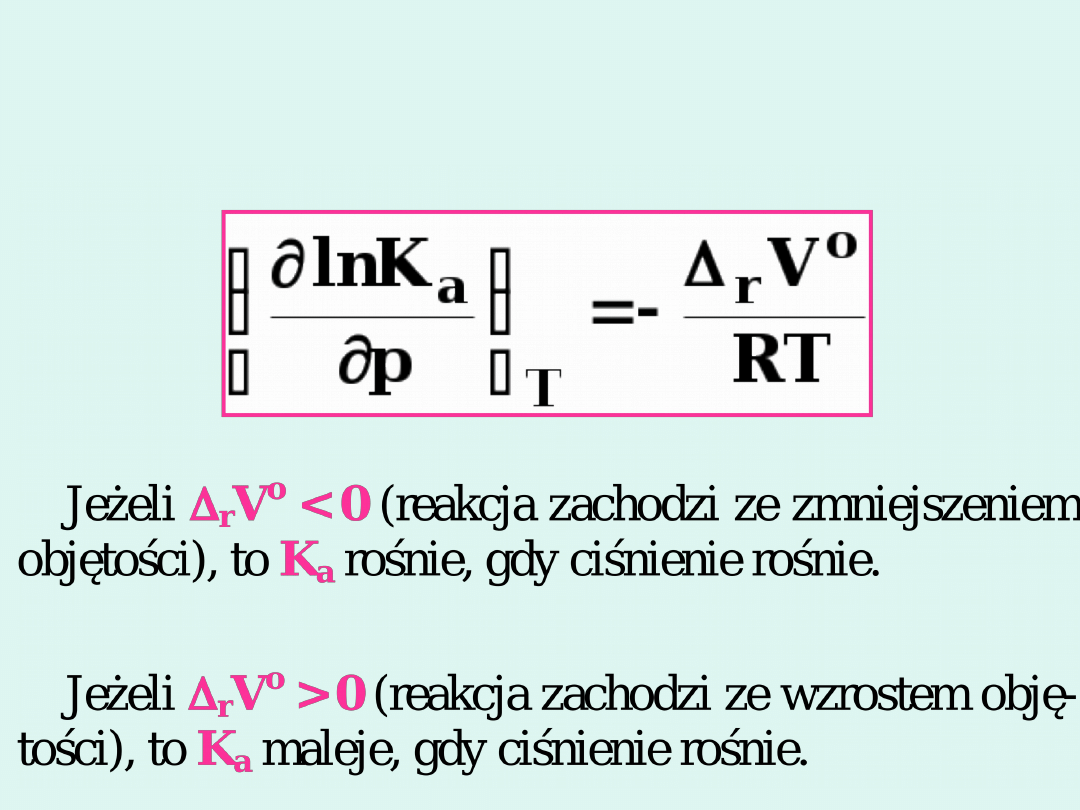
Wpływ ciśnienia na stałą

równowagi chemicznej

Rozpatrujemy układ w stałej temperaturze.

Od ciśnienia zależą stałe równowagi

K

x

,

K

m

i

K

c

.

Stała równowagi

K

p

nie zależy od ciśnienia

!

o

r

T

o

r

V

p

G



























r

V

o

– standardowa zmiana objętości w reakcji

chemicznej czyli różnica objętości czystych,
rozdzielonych produktów i substratów w stanie
standardowym.























substr

substr

o

i

,

m

i

prod

prod

o

i

.

m

i

o

r

V

V

V

(

)

o

r

a

a

a

T

T

a

o

r

T

G

RT

K

RT

K

K

RT

p

p

K

RT

V

p

ln

ln

ln

ln

D

=-

�

�

�-

�

�

�

=-

�

�

�

�

�

�

�

�

�

�

�

�

�

�

�

-

=D

�

�

�

�

�

Izoterma van Laara-

Plancka

RT

V

p

K

ln

*

r

T

x























RT

V

p

K

ln

r

T

c

























RT

V

p

K

ln

r

T

m

























Dla reakcji przebiegających w fazie
gazowej uwzględniamy tylko reagenty
gazowe i w pierwszym przybliżeniu
traktujemy je jak gazy doskonałe.

RT

V

p

K

ln

*

r

T

x























 

 





 



















substr

substr

g

*

i

,

m

i

prod

prod

g

*

i

,

m

i

g

*

r

V

V

V

 

 

 

 

 

 

 

 

g

i

r

g

*

substr

substr

g

i

prod

prod

g

i

g

*

g

*

i

,

m

p

RT

V

p

RT

p

RT

V

p

RT

V



























r

r

 

p

p

K

ln

g

i

r

T

x

























 

p

p

K

ln

g

i

r

T

x

























 

 

 

 

g

i

r

2

1

2

x

1

x

1

2

1

x

2

x

1

2

g

i

r

1

x

2

x

p

p

g

i

r

K

K

x

g

i

r

x

p

p

K

K

p

p

K

K

p

dp

K

d

dp

p

K

d

















































,

,

,

,

ln

ln

ln

ln

,

,

Reakcje w fazach

skondensowanych

W tym wypadku zmiany objętości są bardzo
małe, rzędu cm

3.

Powoduje to, że wpływ

ciśnienia na stan równowagi takich reakcji
jest nieznaczny. Aby stała równowagi
zmieniła się w zauważalny sposób ciśnienie
musi się zmienić o kilka rzędów wielkości.

RT

V

p

K

ln

r

T

m





























1

2

r

1

m

2

m

p

p

r

K

K

m

r

m

p

p

RT

V

K

K

dp

RT

V

K

d

dp

RT

V

K

d

2

1

2

m

1

m































,

,

ln

ln

ln

,

,

Jeśli założymy, ze zmiana objętości jest
stała (nie zależy od ciśnienia) to możemy
uzyskać scałkowana postać izotermy van
Laara-Plancka.