Indeksy statystyczne

Janusz Górczyński

2

Rodzaje danych
liczbowych

Absolutne (mianowane), np. wynagrodzenie pracowników w

złotych, wydajność pracy mierzona w sztukach danego produktu

na godzinę pracy, zużycie paliwa w litrach na 100 km itd .

Jak pamiętamy ze statystyki takie miary położenia jak średnia,

mediana czy kwartyle są liczbami mianowanymi. Podobnie takie

miary rozrzutu jak wariancja czy odchylenie standardowe również

są liczbami mianowanymi

Względnymi (niemianowanymi), które powstają

poprzez porównanie dwóch liczb mianowanych. Również
ze statystyki pamiętamy takie miary względne jak choćby
współczynnik zmienności, czy współczynnik korelacji lub
determinacji.

Miary

tego

typu

pozwalają

na

porównywanie zmienności różnych cech (o różnych
miarach) lub siły związku różnych par zmiennych.

3

Rodzaje danych liczbowych (c.d)

Liczby względne odgrywają szczególnie ważną rolę w

analizie rozwoju zjawisk w czasie, pozwalają bowiem na
porównanie właśnie cech (zjawisk) bezpośrednio
nieporównywalnych.

Przykładowo, jeżeli w pewnym zakładzie w badanym

okresie czasu wartość produkcji wzrosła ze 150 mln zł do
180 mln zł, a wielkość zatrudnienia w tym samym okresie
wzrosła z 1000 osób do 1100 osób, to bezpośrednie
porównanie tych dwóch zjawisk jest niemożliwe (różne
jednostki). Jeżeli jednak przejdziemy na wartości
procentowe dla obu zjawisk, to ich porównanie jest już
możliwe. Widzimy bowiem, że wartość produkcji wzrosła
w badanym okresie o 20 %, a wielkość zatrudnienia o 10
%, tym samym rosła wydajność pracy (ze 150 tys. zł na 1
zatrudnionego w pierwszym okresie do 163,6 tys. zł
w drugim okresie).

4

Podstawowe mierniki dynamiki

oznacza wartość danego zjawiska w chwili t.

Podstawowymi miernikami dynamiki są:

)

1

...,

,

2

,

1

,

0

(





n

t

y

t

Niec
h

Absolutne przyrosty wartości y

t

w okresie

czasu t-1, t:

)

1

...,

,

2

,

1

(

1













n

t

y

y

t

t

t

Względne przyrosty wartości y

t

w okresie

czasu t-1, t:

gdzie y

t*

oznacza wartość danego zjawiska

w dowolnie wybranej chwili t*

)

1

...,

,

2

,

1

(

*









n

t

y

t

t

t



5

Podstawowe mierniki dynamiki
(c.d)

Wskaźniki (indeksy) dynamiki wartości y

t

:

)

1

...,

,

2

,

1

,

0

(

*

*







n

t

y

y

i

t

t

t

t

gdzie y

t*

oznacza wartość danego zjawiska w

dowolnie wybranej chwili t*

6

Podstawowe mierniki dynamiki
(c.d)

W przypadku gdy punktem odniesienia w każdym

momencie czasowym jest wartość zjawiska w
poprzednim okresie, to takie przyrosty względne
nazywamy

łańcuchowymi

:

)

1

...,

,

2

,

1

(

1











n

t

y

t

t

t



Jeśli zaś punkt odniesienia jest stały dla

wszystkich momentów czasowych, to takie
przyrosty

względne

nazywamy

jednopodstawowymi

.

7

Podstawowe mierniki dynamiki
(c.d)

Analogiczne uwagi można sformułować także w

odniesieniu do indeksów.

W przypadku, gdy punktem odniesienia jest

wartość zjawiska w poprzednim okresie, to
mówimy o indeksach

łańcuchowych

.

W tych zaś przypadkach, gdy punktem

odniesienia jest wartość zjawiska w jakimś
ustalonym momencie czasowym, to mówimy o
indeksach

jednopodstawowych

.

8

Wybór podstawy

Wybór stałej podstawy (w indeksach i

względnych przy-rostach) zależy od celu badań.

Może to być wartość pierwszego okresu lub

dowolnego innego, ale w każdym przypadku
wybór

podstawy

musi

być

uzasadniony

przesłankami ekonomicznymi. Powinien to być
taki

moment

czasowy,

który

jest

charakterystyczny dla badanego zjawiska.
Porównanie innych wartości badanego zjawiska w
odniesieniu do poprawnie wybranego okresu
podstawowego daje szansę na poznanie istoty
zachodzących zmian.

Z kolei wybór jako stałej podstawy takiej

wartości danego zjawiska, która jest wyjątkowo
unikalna nie daje takiej szansy, a wręcz prowadzi
do fałszywych wniosków.

9

Interpretacja przyrostów i
indeksów

Przyrosty absolutne 

t

są miarą

bezwzględnych

zmian

w

poziomie

analizowanego zjawiska w czasie.

Przyrosty względne 

t

są miarą tempa

zmian.

Wskaźniki łańcuchowe (przyrosty względne i

indeksy) dają możliwość uchwycenia okresów
o szczególnie dużym lub szczególnie małym
przyroście poziomu danego zjawiska

10

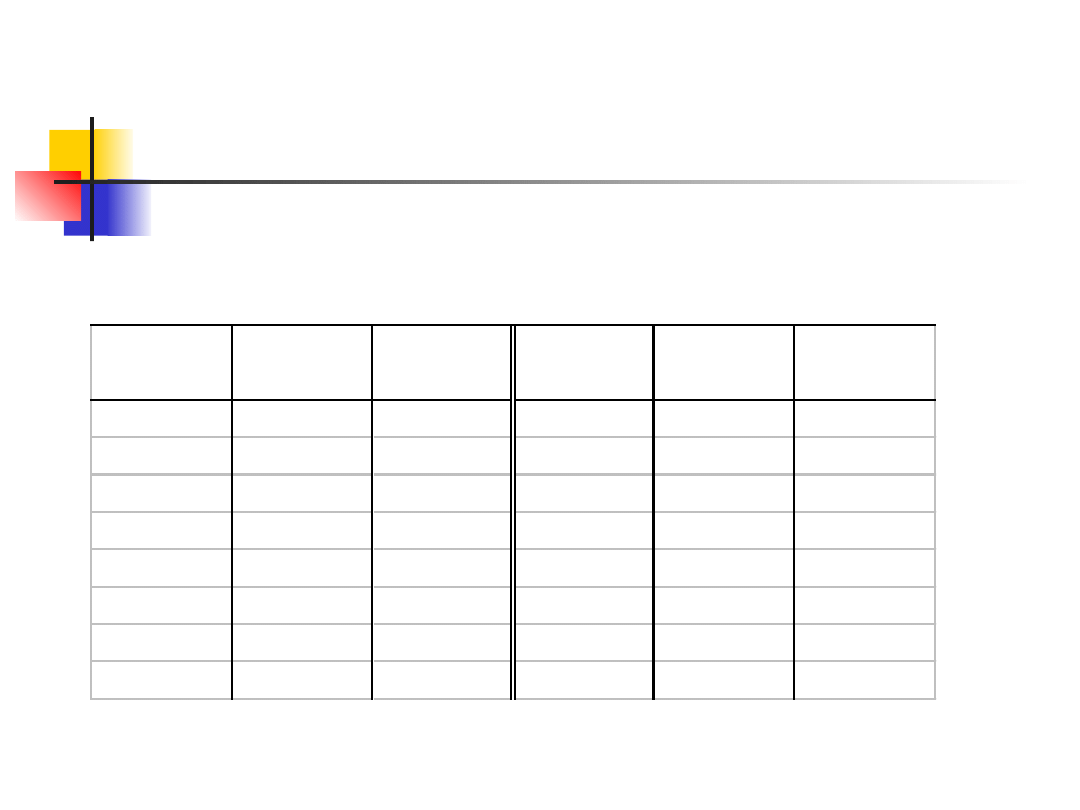
Przykład liczbowy 1

Wyznaczmy przyrosty absolutne i względne
oraz indeksy dynamiki liczby ciągników
w rolnictwie w latach 1968-1983 na podstawie
poniższych danych GUS.

Czas

Rok

Liczba
ciągników

Czas

Rok

Liczba
ciągników

0

1968

180 500

8

1976

434 000

1

1969

202 700

9

1977

472 600

2

1970

224 531

10

1978

514 460

3

1971

248 400

11

1979

573 100

4

1972

278 800

12

1980

619 353

5

1973

319 200

13

1981

669 671

6

1974

364 800

14

1982

710 199

7

1975

401 200

15

1983

757 283

11

Przykład 1, rozwiązanie

1

2

3

4

5

6

7

8

Czas

Rok

Liczba
ciągników

0

1968

180 500

-

-

-

1,00

1

1969

202 700

22 200

12,30%

12,30%

1,12

1,12

2

1970

224 531

21 831

10,77%

12,09%

1,11

1,24

3

1971

248 400

23 869

10,63%

13,22%

1,11

1,38

4

1972

278 800

30 400

12,24%

16,84%

1,12

1,54

5

1973

319 200

40 400

14,49%

22,38%

1,14

1,77

6

1974

364 800

45 600

14,29%

25,26%

1,14

2,02

7

1975

401 200

36 400

9,98%

20,17%

1,10

2,22

8

1976

434 000

32 800

8,18%

18,17%

1,08

2,40

9

1977

472 600

38 600

8,89%

21,39%

1,09

2,62

10

1978

514 460

41 860

8,86%

23,19%

1,09

2,85

11

1979

573 100

58 640

11,40%

32,49%

1,11

3,18

12

1980

619 353

46 253

8,07%

25,62%

1,08

3,43

13

1981

669 671

50 318

8,12%

27,88%

1,08

3,71

14

1982

710 199

40 528

6,05%

22,45%

1,06

3,93

15

1983

757 283

47 084

6,63%

26,09%

1,07

4,20

t



1







t

t

t

y



0

y

t

t







1



t

t

i

0

t

i

12

Przykład liczbowy, opis

Oryginalne dane są podane w kolumnie

drugiej i trzeciej, w kolumnie pierwszej podano
(pomocniczo) wartości zmiennej czasowej.

W kolumnie czwartej wyznaczono absolutne

przyrosty liczby ciągników, z danych tych wynika,
że największy przyrost ciągników był w 1979 roku,
a najmniejszy w 1970.

W kolumnie piątej wyznaczono względne

przyrosty łańcuchowe, z ich analizy wynika, że
okresami o szczególnie dużym tempie przyrostu
liczby ciągników były lata 1972-74 oraz rok 1979.
Z kolei w latach 1982‑83 obserwujemy szczególnie
małe tempo przyrostu ciągników.

13

Przykład liczbowy, opis (c.d)

W

kolumnie

szóstej

wyznaczono

względne

przyrosty jedno-podstawowe przyjmując jako
podstawę liczbę ciągników w 1968 roku. Z analizy
tego wskaźnika wynika, że w 1979 roku rolnictwo
zostało zasilone liczbą ciągników rzędu 1/3 ich
stanu z roku 1968. przyrost liczby ciągników w
1979 roku był największy

W kolumnie siódmej zamieszczono indeksy
łańcuchowe,

ich

analiza

potwierdza

nasze

wcześniejsze wnioski: lata 1972-74 i rok 1979 to
te, w których obserwowaliśmy największe zmiany
w liczbie ciągników w rolnictwie. Podobnie lata
1982-83 to te, w których obserwujemy szczególnie
mały przyrost liczby ciągników.

14

Przykład liczbowy, opis (c.d)

Kolumna ostatnia zawiera indeksy o stałej

podstawie (rok 1968).

Z ich analizy wynika, że w 1979 roku

w rolnictwie było ponad trzykrotnie więcej
ciągników niż w roku podstawowym, a w 1983
liczba ciągników była 4,2 raza większa niż w
okresie podstawowym.

15

Przeliczanie indeksów

16

Zmiana podstawy indeksu

Z definicji indeksów wynika, że mając indeks

jednopodsta-wowy możemy w łatwy sposób zmienić
podstawę indeksu:

*

'

*

*

'

*

'

'

:

:

t

t

t

t

t

t

t

t

t

t

t

t

i

i

y

y

y

y

y

y

i







gdzie t’ jest czasem nowej podstawy.

Z powyższego wzoru wynika, że w celu zmiany

podstawy indeksu z czasu t* na czas t’ musimy
każdy dotychczasowy indeks podzielić przez
indeks wyliczony dla czasu t’.

17

Przykład liczbowy 2, przeliczanie
indeksów jednopodstawowych

W przykładzie 1 wyznaczyliśmy indeksy przy

podstawie t*=0 (rok 1968). Chcemy zmienić
podstawę indeksu na rok 1979, czyli t’=11.

32

,

1

18

,

3

:

20

,

4

:

..

..........

..........

..........

..........

..........

00

,

1

18

,

3

:

18

,

3

:

.

..........

..........

..........

..........

..........

35

,

0

18

,

3

:

12

,

1

:

31

,

0

18

,

3

:

00

,

1

:

0

11

0

15

11

15

0

11

0

11

11

11

0

11

0

1

11

1

0

11

0

0

11

0

























i

i

i

i

i

i

i

i

i

i

i

i

18

Przeliczanie indeksów (c.d)

Mając wyznaczone indeksy jednopodstawowe

przy

dowolnej

podstawie

t*

możemy,

korzystając z ogólnej definicji indeksów, przejść
do indeksów łańcuchowych:

*

1

*

*

1

*

1

:

:

t

t

t

t

t

t

t

t

t

t

i

i

y

y

y

y

i











Zgodnie z powyższym wzorem indeksy

łańcuchowe

otrzymamy,

jeżeli

indeksy

jednopodstawowe dla chwili t podzielimy
przez indeksy dla chwili t-1.

19

Przykład liczbowy 3, przeliczanie
indeksów

07

,

1

93

,

3

:

20

,

4

:

...

..........

..........

..........

..........

..........

11

,

1

12

,

1

:

24

,

1

:

12

,

1

00

,

1

:

12

,

1

:

0

14

0

15

14

15

0

1

0

2

1

2

0

0

0

1

0

1



















i

i

i

i

i

i

i

i

i

Przykładowo, na podstawie danych z

przykładu 1 prze-śledzimy przeliczanie
indeksów jednopodstawowych na indeksy
łańcuchowe.

20

Przeliczanie indeksów (c.d)

Problem przeliczania indeksów zakończymy

przeliczeniem

indeksów

łańcuchowych

na

indeksy

jednopodstawowe

przyjmując

jako

podstawę wartość zjawiska w chwili t*. Zgodnie z
ogólną definicją indeksów mamy:













































*

*

1

*

1

1

*

1

*

1

1

*

t

t

dla

i

t

t

dla

t

t

dla

i

i

t

t

i

i

i

t

t

i

i

i

t

t

21

Przykład liczbowy 4, przeliczanie
indeksów

Ponownie

skorzystajmy

z

danych

zamieszczonych przykładzie 1. W kolumnie 7
mamy

zamieszczone

indeksy

łańcuchowe,

przeliczymy je na indeksy jednopodstawowe
przyjmując za podstawę rok 1979 (t*=11).
Zgodnie z wzorem (slajd 20) mamy kolejno:

dla t = 1 (rok
1969):

35

,

0

11

,

1

12

,

1

11

,

1

11

,

1

1

1

10

11

3

4

2

3

1

2

11

1



























i

i

i

i

i

dla t = 2 (rok
1970):

39

,

0

11

,

1

14

,

1

12

,

1

11

,

1

1

1

10

11

4

5

3

4

2

3

11

2



























i

i

i

i

i

22

Przykład liczbowy 4 (c.d)

dla t = 10 (rok
1978):

90

,

0

11

,

1

1

1

10

11

11

10







i

i

dla t = 12 (rok
1980):

08

,

1

11

12

11

12



i

i

dla t = 13 (rok
1981):

17

,

1

08

,

1

08

,

1

12

13

11

12

11

13











i

i

i

32

,

1

07

,

1

06

,

1

08

,

1

08

,

1

14

15

13

14

12

13

11

12

11

15



















i

i

i

i

i

dla t = 15 (rok
1983):

23

Inne wskaźniki dynamiki

Poza omówionymi wcześniej wskaźnikami

opisującymi dynamikę badanego zjawiska
w analizie szeregów czasowych wykorzystuje się
jeszcze dwa wskaźniki opisujące:

średni poziom zjawiska,
średnie tempo zmian zjawiska.

Kolejno

zajmiemy

się

tymi

dwoma

wskaźnikami.

24

Przeciętny poziom zjawiska

Przeciętny poziom zjawiska może być

określany dwojako, zależnie od charakteru
zjawiska. Jeśli szereg czasowy jest szeregiem
okresów,

czyli

wartości

zjawiska

mają

charakter

strumieni

i

tym

samym

są

sumowalne, to miarą przeciętnego poziomu
zjawiska jest zwykła średnia arytmetyczna:

n

y

y

n

t

t









1

0

25

Przeciętny poziom zjawiska
(c.d)

W sytuacji, gdy szereg czasowy jest

szeregiem

momentów,

czyli

wartości

zasobów

w ustalonych

momentach

czasowych, to miarą przeciętnego poziomu
zjawiska jest tzw. średnia chronologiczna:

1

)

(

5

,

0

2

1

1

0



















n

y

y

y

y

n

t

t

n

26

Przykład liczbowy 5

W przykładzie 1 rozpatrywaliśmy szereg

czasowy liczby ciągników w rolnictwie
w latach 1968-83. Szereg ten ma charakter
szeregu momentów (łączna suma ciągników
w badanych latach nie ma interpretacji), tym
samym miarą przeciętnego stanu ciągników
w tym okresie będzie średnia chronologiczna
wyznaczona zgodnie z wzorem podanym na
slajdzie 25:

4

,

433460

15

)

710199

202700

(

)

757283

180500

(

5

,

0





















y

27

Przykład liczbowy 6

W kolumnie czwartej w tym samym

przykładzie wyliczono przyrosty absolutne
liczby ciągników w latach 1969-83, dane te
maja charakter szeregu okresów (ich suma
ma logiczną interpretację), tym samym miarą
przeciętnej

liczby

ciągników

zasilających

rolnictwo w badanych latach będzie zwykła
średnia arytmetyczna:

38452,2

15

47084

21831

22200

















y

28

Inne przykłady

Inne przykłady szeregu okresów to: liczba

wyprodukowanych

samochodów,

ilość

wydobytego węgla, ilość zebranych owoców,
wyprodukowanych zbóż, liczba absolwentów
szkół średnich itd.

Przykładami szeregu momentów (zasobów)

może być np. liczba ludności na określony dzień
roku, areał uprawy pszenicy itd.

29

Tempo (stopa wzrostu)

Przez tempo lub inaczej stopę wzrostu

rozumie się względny przyrost wartości
zjawiska w danym momencie czasowym do
jego wartości w poprzednim okresie.

Tempo jest wyrażane przez różnicę

miedzy indeksem łańcuchowym a jednością:

1

1

1

;









t

t

t

t

i

r

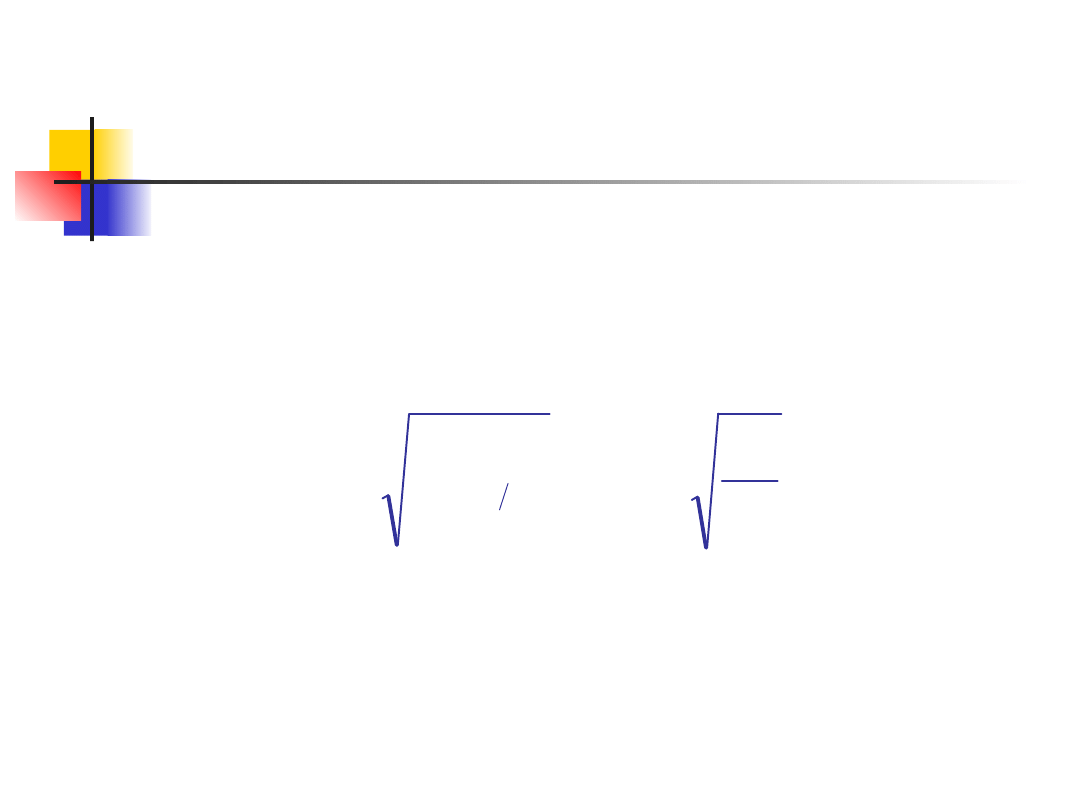
30

Średnie tempo

Miarą średniego tempa (średniej stopy

wzrostu) w badanym okresie (t

0

, t

1

) będzie

różnica miedzy średnim indeksem łańcuchowym

z tego okresu a jednością:

1

1

0

1

0

1

0

1

1

0

1

0

1

1

;





















t

t

t

t

t

t

t

t

i

i

i

t

t

y

y

i

r

31

Przykład liczbowy 7

Na podstawie danych z przykładu 1

wyznaczmy średnioroczne tempo przyrostu
liczby ciągników w latach 1968-75, 1975-83
oraz 1968-83 .

Na podstawie danych z kolumny trzeciej
mamy:

Dla okresu 1968-75

%

09

,

12

1209

,

0

1

1209

,

1

1

2,222715

1

180500

401200

7

7

7

;

0

















r

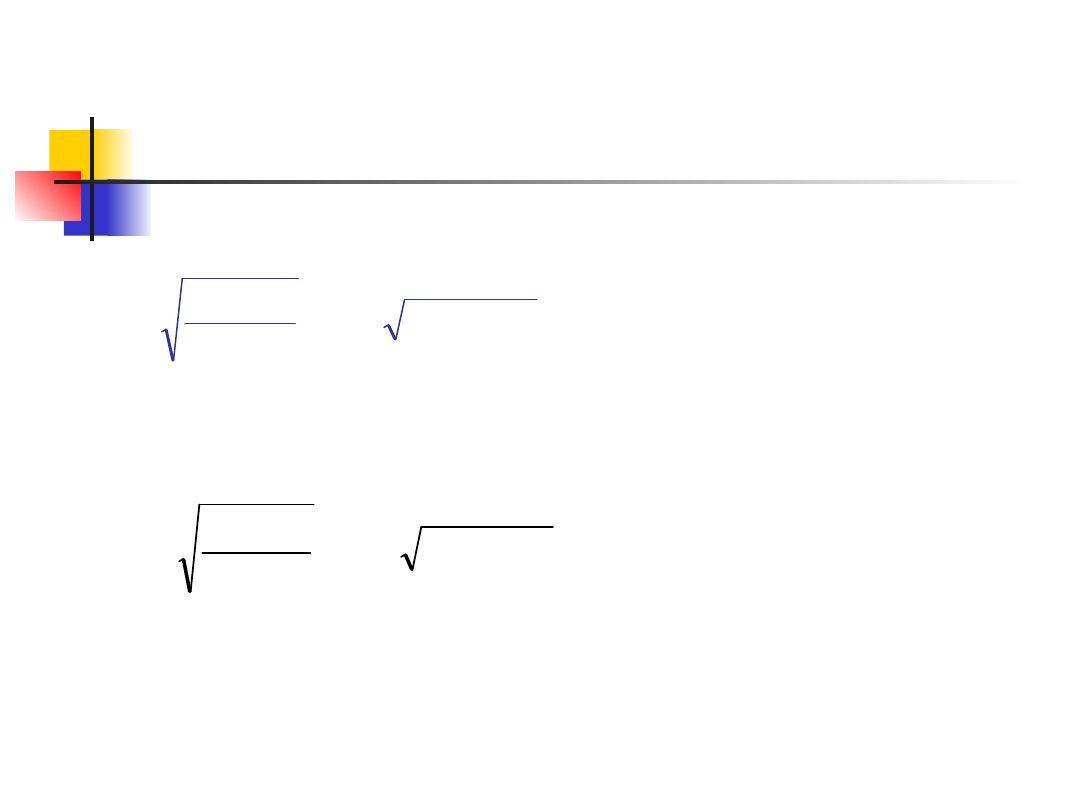
32

Przykład liczbowy 7 (c.d)

Dla okresu 1975-83 mamy:

%

26

,

8

0826

,

0

1

0826

,

1

1

1,887545

1

401200

757283

8

8

15

;

7

















r

Dla okresu 1968-83 średnioroczne tempo
wynosi:

%

03

,

10

1003

,

0

1

1003

,

1

1

195474

,

4

1

180500

757283

15

15

15

;

0

















r

33

Przykład liczbowy 7,
interpretacja

W latach 1968-75 średnioroczny przyrost

liczby ciągników wynosił 12,09%, a w latach
1975-83 odpowiednio 8,26%.

W całym badanym okresie lat 1968-83

średnioroczne

tempo

przyrostu

liczby

ciągników było równe 10,03%.

Widzimy z powyższego, że w okresie

pierwszych siedmiu lat przyrost liczby
ciągników był zdecydowanie szybszy niż w
drugiej części tego okresu.

34

Dziękuję za uwagę