UNIWERSYTET BYDGOSKI

IM. KAZIMIERZA WIELKIEGO

W BYDGOSZCZY

Wydział Matematyki, Fizyki i Techniki

ANALIZA WYBOCZENIA UKŁADU KONSTRUKCYJNEGO

ZŁOŻONEGO Z PRĘTA SCISKANEGO SIŁĄ OSIOWĄ .

Kamiński Paweł

2007

Multimedialna

pomoc

dydaktyczna

- instrukcja do ćwiczeń z

mechaniki technicznej :

wyboczenie prętów prostych –

teoria i przykłady zadań

Część I

TEORIA

ŚCISKANIE SŁUPÓW PROSTYCH

Ważnym zagadnieniem w wytrzymałości materiałów,
oprócz obliczeń wytrzymałościowych, odkształcalności
jest stateczność układu. Równowaga jest stateczna, jeżeli
dowolnie niewielkie odkształcenie układu wywołuje siły
przywracające mu postać pierwotną. Jeżeli siła ściskająca
P pręt będzie wzrastać, to przy pewnej jej wartości P

kr

minimalny impuls (Q = 0) spowoduje, że pręt nie wróci
do prostoliniowego stanu równowagi lecz pozostanie w
stanie równowagi przy krzywoliniowej postaci pręta

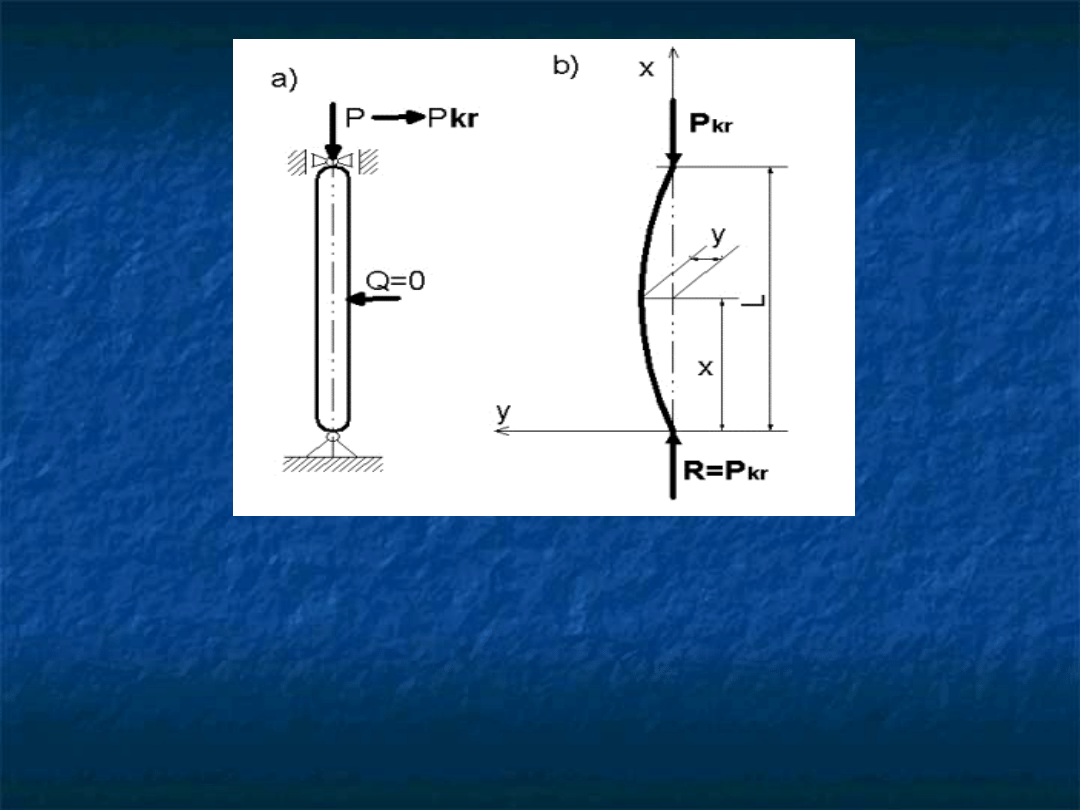
Jest to stan, gdzie oprócz ściskania siłą P , powstaje również
zginanie pręta momentem Mg = P

kr

, co może spowodować

zniszczenie pręta nawet przy niewielkim wzroście siły
ściskającej. Przejście układu ze stanu równowagi chwiejnej lub
obojętnej (krzywoliniowa postać równowagi pręta) nazywamy
utratą stateczności układu, a siłę powodującą zmianę stanu
równowagi nazywamy siłą krytyczną P

Wykorzystując równanie różniczkowe linii
ugięcia można uzyskać równanie linii
ugięcia pręta ściskanego siłą krytyczną, a
stąd najmniejszą wartość siły krytycznej,
która dla pręta ściskanego między dwoma
przegubami wynosi:

2

min

2

l

J

P

kr





NAPRĘŻENIA KRYTYCZNE

Jeżeli wyznaczymy siłę krytyczną, to oczywiście uzyskamy naprężenia krytyczne

F

P

kr

kr

/





przy których następuje utrata stateczności pręta ściskanego.

Wprowadzając pojęcie minimalnego promienia bezwładności przekroju:

F

I

i

min

min



zwaną smukłością pręta, otrzymamy wzór na naprężenia

krytyczne zwane wzorem Eulera:

2

2

s

E

kr







a następnie wielkość charakteryzującą wymiary pręta:

min

i

l

s

w



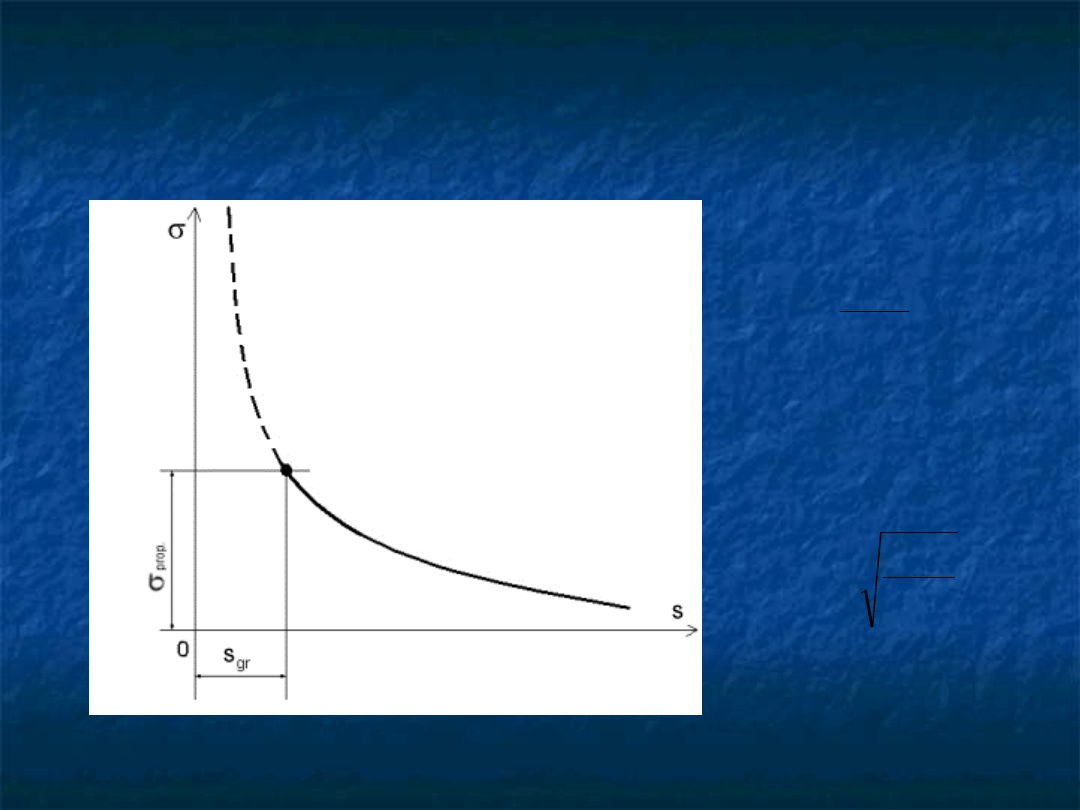
KRZYWA EULERA DLA PRĘTÓW ŚCISKANYCH

prop

gr

kr

s

R











2

2

prop

gr

s









stąd :

RÓWNANIE PRĘTÓW ŚCISKANYCH OSIOWO

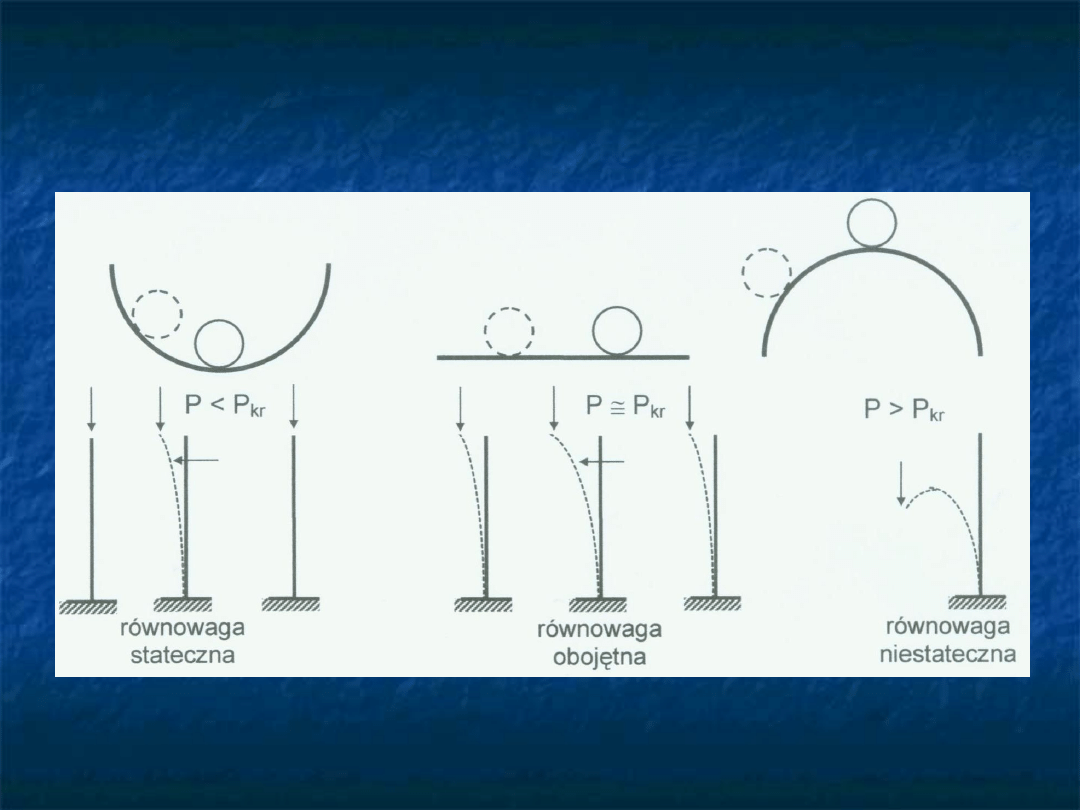
Równowaga nosi nazwę statecznej w przypadku
gdy po dowolnie małym początkowym wychyleniu
z

położenia

równowagi,

ruch

układu

mechanicznego jest taki, że wychylenia żadnego
punktu nie są większe od początkowych.
W przeciwnym przypadku równowaga jest
niestateczna.

• stateczny

• niestateczny

DŁUGOŚCI WYBOCZENIOWE DLA ŚCISKANYCH PRĘTÓW.

W układach sztywnych wartości występujących sił nie mają
wpływu na rodzaj równowagi.
W układach odkształcalnych do pewnej wartości obciążenia
układ

znajduje

się

w

równowadze statecznej,

po

przekroczeniu tej wartości przechodzi w stan równowagi
niestatecznej.

Zjawisko to zwane jest wyboczeniem i występuje przy:

• Ściskaniu
• Zginaniu
• Skręcaniu i innych kombinacjach obciążeń

Przypadek najprostszego wyboczenia występuje przy
zwykłym osiowym ściskaniu pręta prostego. Wyboczeniu
podlegają pręty smukłe, cienkie płyty i powłoki.

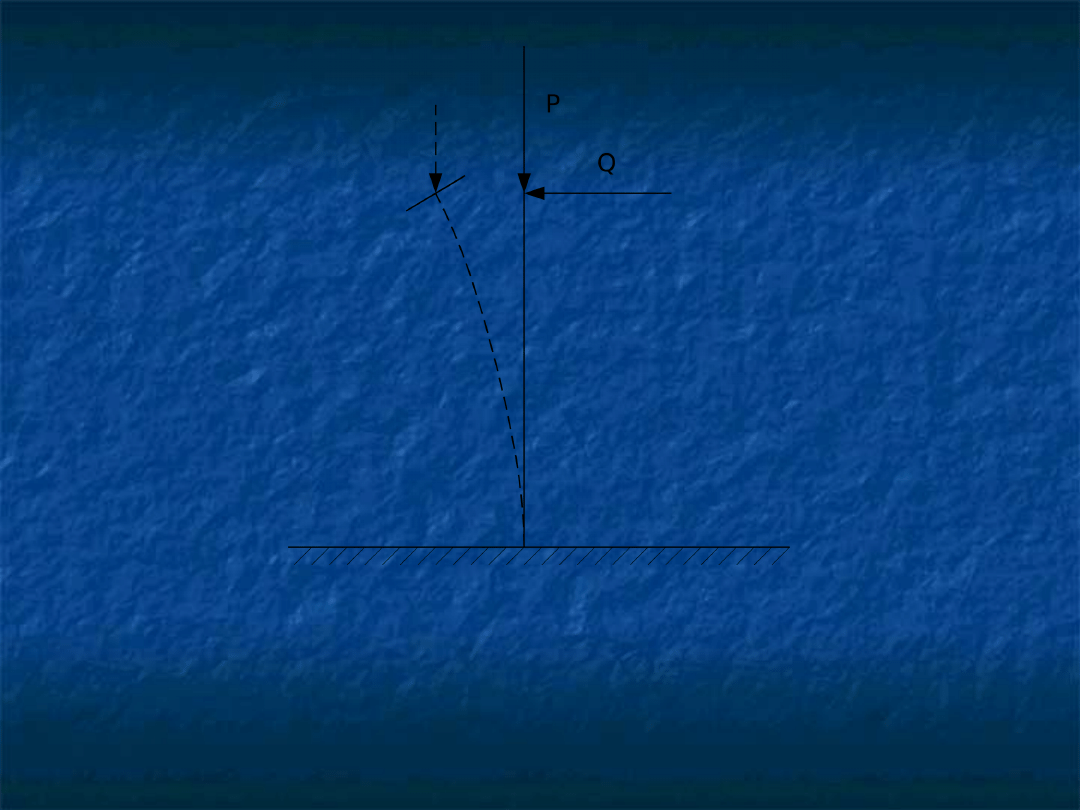
Jeżeli na pręt działa stosunkowa niewielka siła P , to po usunięciu
poprzecznej zginającej siły Q = 0 pręt powróci do postaci
prostoliniowej . W przeciwnym wypadku po przekroczeniu wartości
siły, zwaną krytyczną P

kr

, po usunięciu siły Q pręt pozostanie w

postaci krzywej.

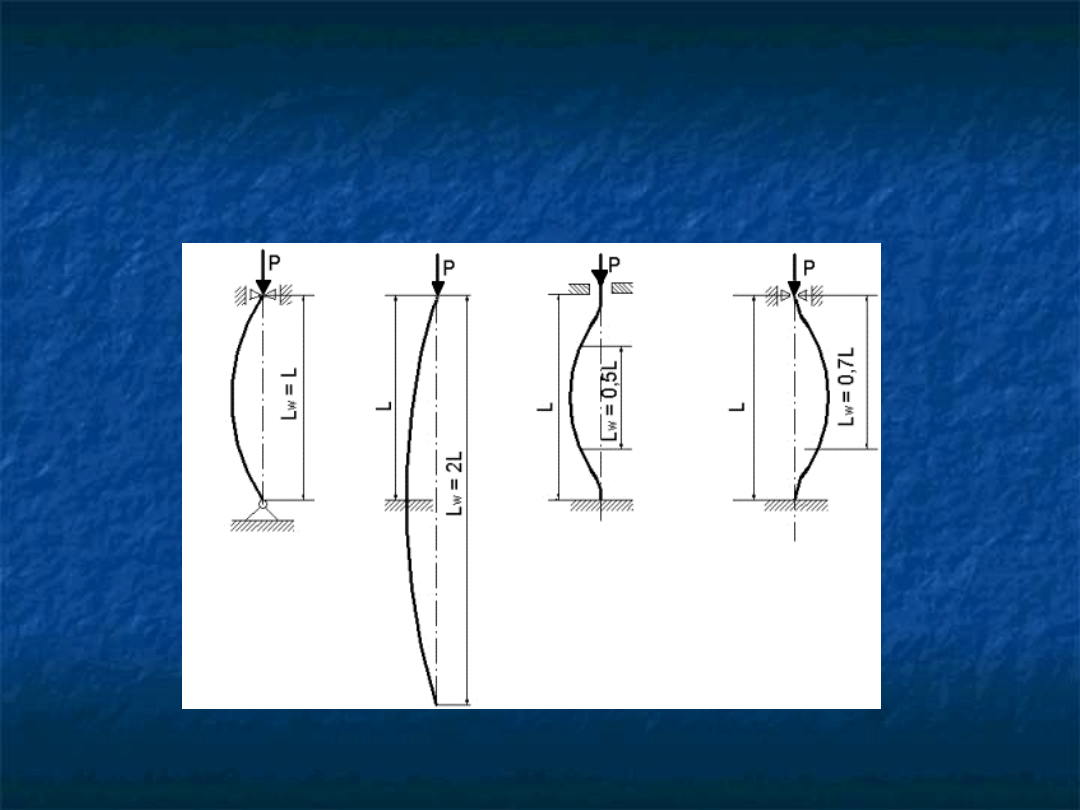
WYBOCZENIA, KTÓRE ZALEŻĄ OD WARTOŚCI SIŁY
KRYTYCZNEJ ORAZ OD WYMIARÓW PRĘTA I SPOSOBU JEGO
ZAMOCOWANIA.

WYBOCZENIE SPRĘŻYSTE PRĘTÓW PROSTYCH

Mx

dx

y

d

EJ





2

2

y

x

P

M 

Równanie różniczkowe osi ugiętego pręta określono

wzorem :

Moment zginający, który spowodowany jest

przemieszczaniem środkowych przekrojów pręta

wynosi :

Po dokończeniu przekształceń algebraicznych otrzymano:

0

2

2

2





y

k

dx

y

d

gdzie
:

z

z

EJ

P

K

EJ

P

K





,

2

MODEL FIZYCZNY

Rozważmy warunki równowagi konieczne dla zachowania
równowagi

ściskanego

pręta

w

postaci

wygiętej

( wyboczeniowej). Decydujący wpływ na stateczność pręta na
zginanie tzn. na wyboczenie, wystąpi w płaszczyźnie
najmniejszej sztywności na zginanie EJ.

Całkę ogólną równania określono następującą zależnością :

kx

B

kx

A

y

cos

sin 



A i B – stałe całkowanie

gdzie :

Stałe całkowanie wyznaczono z następujących warunków brzegowych :

0

0





x

y

0



l

x

y

kx

A

y

sin



Dla B=0 mamy :

Po wykorzystaniu otrzymujemy :









n

kl

kl

A

0

sin

,..

3

,

2

,

1

,

0



n

...



w

n

gdzie:

Po uwzględnieniu otrzymujemy :

z

EJ

l

n

P

n

l

EJ

P

2

2

2











Dla n=1 równanie przedstawia wzór na siłę krytyczną P

kr

:

2

2

l

EJ

P

z

kr





ODKSZTAŁCENIA SPRĘŻYSTE WEDŁUG EULERA

w

w

z

w

kr

dop

n

l

I

E

n

P

P

2

2





















2

2

s

n

E

n

k

w

w

kr

w

lub

P

dop

- dopuszczalne naprężenie wybaczające,

gdzie:

n

w

- współczynnik bezpieczeństwa na

wyboczenie

ODKSZTAŁCENIA SPRĘŻYSTE – PLASTYCZNE

WEDŁUG TETMAJERA













w

w

kr

w

n

bs

a

n

k

gdzie:



- naprężenia, które są ilorazem siły ściskającej
przez pole przekroju poprzecznego pręta,

n

w

- współczynnik bezpieczeństwa na

wyboczenie

k

w

– dopuszczalne naprężenia wybaczające

Część II

Przykład zadania z

odkształceń

sprężystych według

Eulera i sprężysto –

plastycznych według

Tetmajera

Przykład 1

Stalowy pręt wykonany ze stali miękkiej o przekroju
kołowym zamocowano przegubowo na obu końcach,
ściskany jest osiowo działającą siła P.
Określić graniczne wymiary przekroju poprzecznego pręta
przy danej długości „ ”, dla których można jeszcze
stosować wzór Eulera. Znaleźć wartość siły ściskającej
pręt.

l

cm

m

l

120

2

,

1





2

7

/

10

1

,

2

cm

N

E





M

2

/

19000 cm

N



w





9

5

,

1 



Długość pręta:

R

M

Dane:

n

w

2



w

n

105



gr

s

Przyjmuję współczynnik pewności na wyboczenie :

.

Smukłość graniczna :

- z tabeli.

Dopuszczalne naprężenia wybaczające

w

k













2

2

s

n

E

n

k

w

w

kr

w

to

2

2

7

2

2

/

2

,

18780

11025

/

10

1

,

2

8596

,

9

cm

N

cm

N

s

E

kr















Średnica przekroju „d” wyliczona ze wzoru :

2

2

2

2

2

2

2

16

16

l

R

E

d

E

l

R

d

i

M

M























cm

cm

N

cm

cm

N

E

l

R

d

M

6

,

4

/

10

1

,

2

8596

,

9

14400

/

1900

16

16

2

7

2

2

2

2





















lub

16

2

2

d

i 

4

d

i 

i

l

s 

to

oraz

podstawiając , mamy :

cm

s

l

d

l

s

d

d

l

s

6

,

4

105

480

105

120

4

4

4

4





















Przekrój poprzeczny „F” :

2

2

2

61

,

16

4

16

,

21

14

,

3

4

cm

cm

d

F











2

61

,

16 cm

F 

cm

d

6

,

4



m

l

2

,

1



Graniczne

wymiary

przekroju to :

- przekrój poprzeczny

- średnica przekroju

- długość pręta

Wartość siły ściskającej „ P ”

w

z

n

E

l

P

I











2

2

4

4

2

22

64

75

,

447

14

,

3

64

cm

cm

d

I

z











Po przekształceniu :

kN

N

cm

cm

N

cm

n

l

E

I

P

n

l

P

E

I

w

z

16

,

158

42

,

158164

2

14400

/

10

1

,

2

8596

,

9

22

2

2

7

4

2

2

2

2

2

2







































cm

d 3



2

,

1



w

l

8

,

0

w

l

2

7

/

10

1

,

2

cm

N

E





M

2

/

19000 cm

N



w





9

5

,

1 



w

m

l

2

,

1



Dla danych :

;

0,7

przyjmę n

w

= 2 Obliczam dla:

;

w

l

R

M

n

w

Obliczam przekrój poprzeczny pręta „F”

2

2

2

1

,

7

4

9

14

,

3

4

cm

cm

d

F











Promień
bezwładności

:

i

16

2

2

d

i 

to

cm

cm

d

i

75

,

0

4

3

4







Smukłość s:

i

l

s 

160

3

120

4

4









cm

cm

d

l

s

to

Smukłość graniczna :

105



gr

s

Spełniony jest więc warunek, że

:

gr

s

s 

,
bo

105

160

Stosujemy więc wzór Eulera :

w

w

z

w

kr

dop

n

l

I

E

n

P

P

2

2











lub











2

2

s

n

E

n

k

w

w

kr

w

Minimalny moment bezwładności

:

:

z

I

4

4

2

4

64

81

14

,

3

64

cm

cm

d

I

z











Siłę ściskającą „P”

w

w

z

n

l

P

E

I













2

2

kN

N

cm

cm

N

cm

m

N

cm

n

l

E

I

P

w

w

z

76

,

28

2

,

28757

28800

828206400

2

14400

/

10

1

,

2

896

,

9

4

2

2

2

2

7

4

2

2





























Ściskająca wartość krytyczna :

kr

P

kr

P

w

dop

kr

w

kr

dop

n

P

P

n

P

P









Dopuszczalne naprężenie wybaczające

:

w

k













2

2

s

n

E

n

k

w

w

kr

w

2

2

2

7

2

2

/

4044

51200

/

207051600

25600

2

/

10

1

,

2

8596

,

9

cm

N

cm

N

cm

N

s

n

E

k

w

w

















kr



w

kr

w

n

k





Naprężenie krytyczne ze wzoru :

2

2

2

/

8088

2

/

4044

1

,

7

2

,

28757

cm

N

cm

N

cm

N

F

P

kr













Przykład 2

Rozważania odkształceń sprężysto – plastycznych.

Dla stali miękkiej ST 3 musi być warunek :

gr

s

s 

Dla stali miękkiej ST 3 wg tabeli mamy:

105



gr

s

2

/

3100

310

cm

N

MPa

a





2

/

4

,

11

14

,

1

cm

N

MPa

b





122



gr

s

2

/

2800

280

cm

N

MPa

A





2

/

0937

,

0

0094

,

0

cm

N

MPa

B





Wg Tetmajera :

Wg Ostenfelda :

bs

a

kr







2

Bs

A

kr







Funkcje aproksymujące :

- prosta określona wzorem Tetmajera – Jasińskiego

- prosta określona wzorem Ostenfelda

gdzie:
a, b, A, B to stałe materiałowe

gr

kr

s

b

a









2

/

1903

105

4

,

11

3100

cm

N

kr











Wg Tetmajera :

2

gr

kr

Bs

A





2

2

/

4

,

1405

122

0937

,

0

2800

cm

N

kr











Wg Ostenfelda :

2

/

20000 cm

N

R

M



2

6

/

10

0

,

2

cm

N

E





cm

d 5



w

l

m

l



 2

,

1





9

5

,

1 



w

n

2



w

n

105



gr

s

1





Przeanalizujmy zadanie o danych :

Stal miękka ST 3

, przyjmuje

Smukłość graniczna

II sposób mocowania

- z tabeli

Przekrój poprzeczny „F”

2

2

2

6

,

19

4

25

14

,

3

4

cm

cm

d

F









z

I

4

4

4

7

,

30

64

625

14

,

3

64

cm

cm

d

I

z









Minimalny moment bezwładności

i

l

s

w



cm

cm

cm

F

I

i

z

6

,

1

6

,

19

7

,

30

2

4







Smukłość „s”

gdzie :

gr

s

s

cm

cm

s







75

6

,

1

120

Poza zakresem ważności wzoru Eulera do obliczeń zastosujemy

wzór Tetmajera – Jasińskiego przyjmując wartości dla a ,

b z tabeli.













w

w

kr

w

n

bs

a

n

k

Krytyczne naprężenia ściskające:

2

/

2245

75

4

,

11

3100

cm

N

bs

a

kr















Siła ściskająca ze wzoru

:

w

w

z

n

E

l

P

I









2

2

2

/

2245

75

4

,

11

3100

cm

N

bs

a

kr















kN

N

cm

cm

N

cm

n

l

E

I

P

n

l

P

E

I

w

w

z

w

w

z

21

21020

2

14400

/

10

2

7

,

30

8596

,

9

2

2

6

4

2

2

2







































Po przekształceniu

:

2

2

/

5

,

1072

6

,

19

21020

cm

N

cm

N

F

P















2

2

/

5

,

1072

/

2245

cm

N

cm

N



Rzeczywiste naprężenia ściskające :

Dany pręt spełnia wymagane

warunki na odkształcenia

sprężysto – plastyczne !!!

Wnioski

• Stosowanie wzoru Eulera do wyznaczenia
naprężeń krytycznych ogranicza się wyłącznie do
prętów o smukłości większej od smukłości
granicznej

gr

s

s 

• Wyboczenie prętów o smukłości mniejszej od
granicznej zachodzi przy naprężeniach określonych
wzorem Eulera, co wynika z przeprowadzonych
zadań.

• Wyboczenie pręta nie musi koniecznie
doprowadzić go do zniszczenia, lecz skutki
jakie spowodują w całej konstrukcji będą
zależne od jej rodzaju i od charakteru
samego wyboczenia ( sprężyste, plastyczne).

• Pręt wyboczony nie jako „wyczerpuje” swą
sztywność,

po

nie

znacznym

nawet

przekroczeniu siły krytycznej w prętach
smukłych

przemieszczenia

gwałtownie

wzrastają , co powoduje znaczny wzrost
naprężeń.

•

pręt w konstrukcji złożonej traci swą

nośność, co powoduje najczęściej utratę
nośności całej konstrukcji

KONIEC