
Politechnika Śląska, Wydział
Politechnika Śląska, Wydział
Elektryczny
Elektryczny
KATEDRA MECHATRONIKI
KATEDRA MECHATRONIKI
Sterowanie i
Sterowanie i
Programowanie Robotów
Programowanie Robotów
Wykład nr 01 i 02
Wykład nr 01 i 02
dr inż. Tomasz Trawiński
Przykłady rozwiązywania zagadnienia kinematyki
prostej
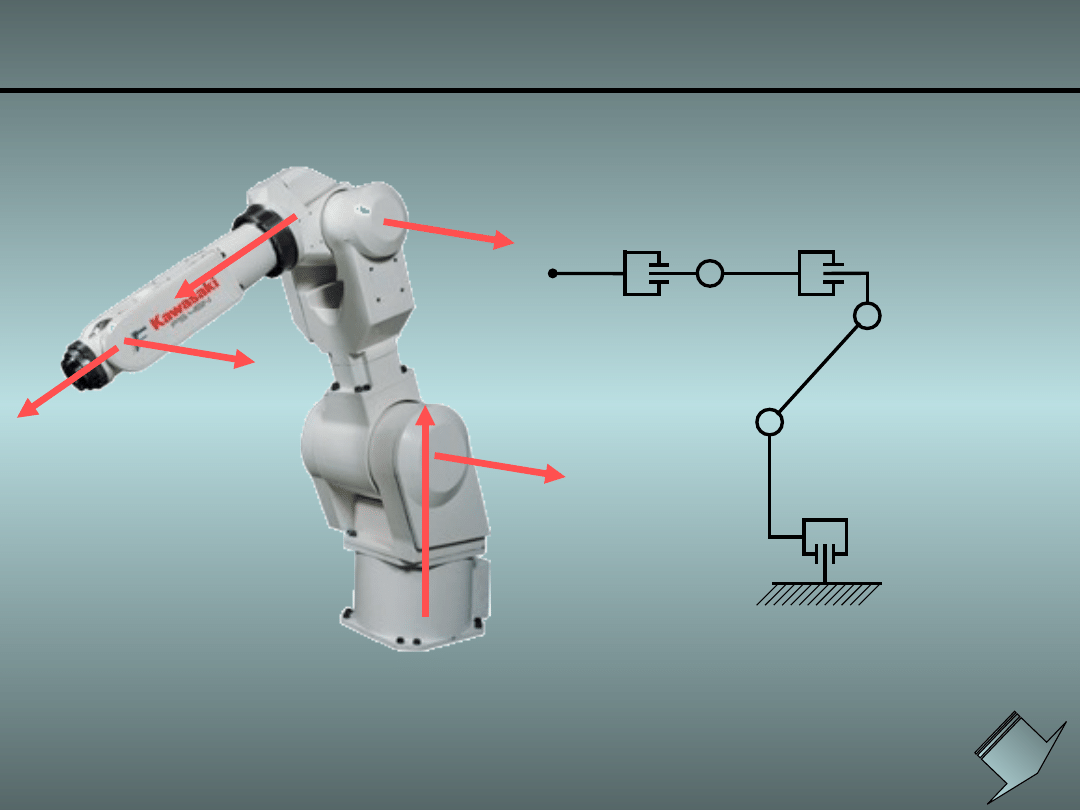
Łańcuchy kinematyczne robotów
Łańcuchy kinematyczne robotów
przemysłowych
przemysłowych
Narysować łańcuch
kinematyczny
Kawasaki
Kawasaki
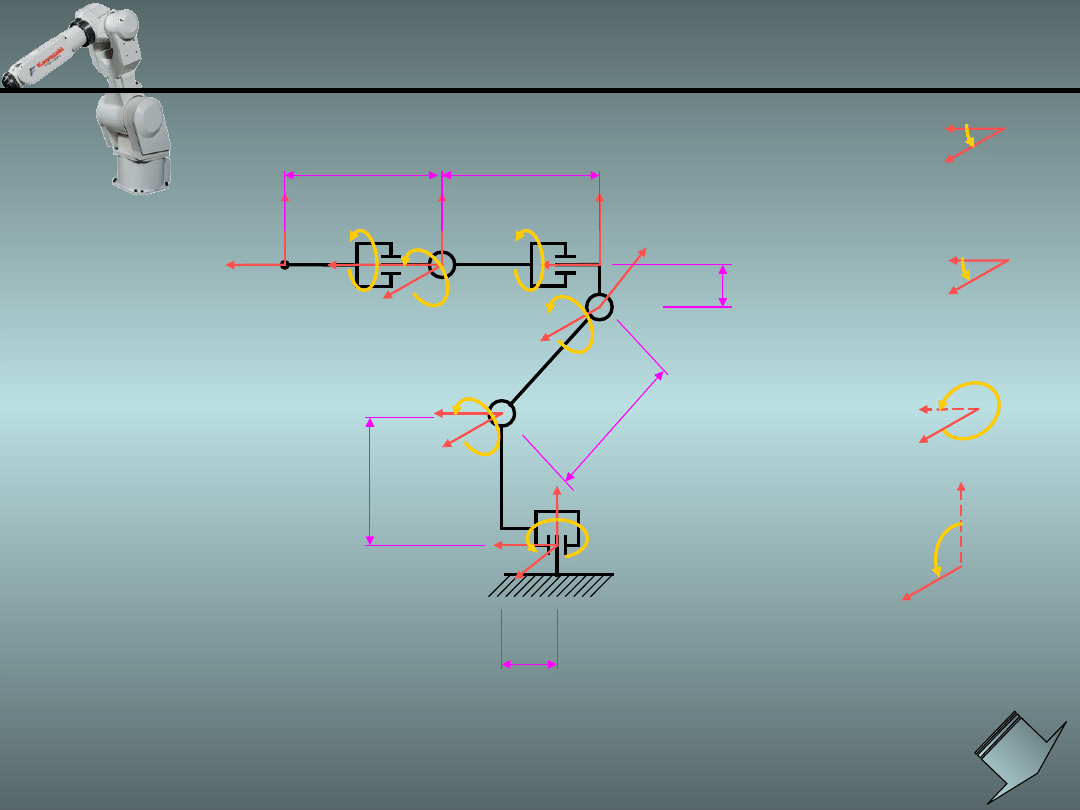
Przykład 3.
Przykład 3.
Kawasaki
Kawasaki
z
z
0
0
z
z
1
1
1
1
z
z
1
1
x
x
1
1
z
z
2
2
x
x
2
2
z
z
3
3
x
x
3
3
d
d
1
1
a
a
1
1
a
a
2
2
x
x
0
0
z
z
0
0
y
y
0
0
1
1
2
2
3
3
z
z
4
4
x
x
4
4
z
z
5
5
x
x
5
5
z
z
6
6
x
x
6
6
a
a
3
3
d
d
4
4
d
d
6
6
4
4
5
5
6
6
z
z
2
2
z
z
3
3
3
3
z
z
3
3
z
z
4
4
4
4
z
z
4
4
z
z
5
5
5
5
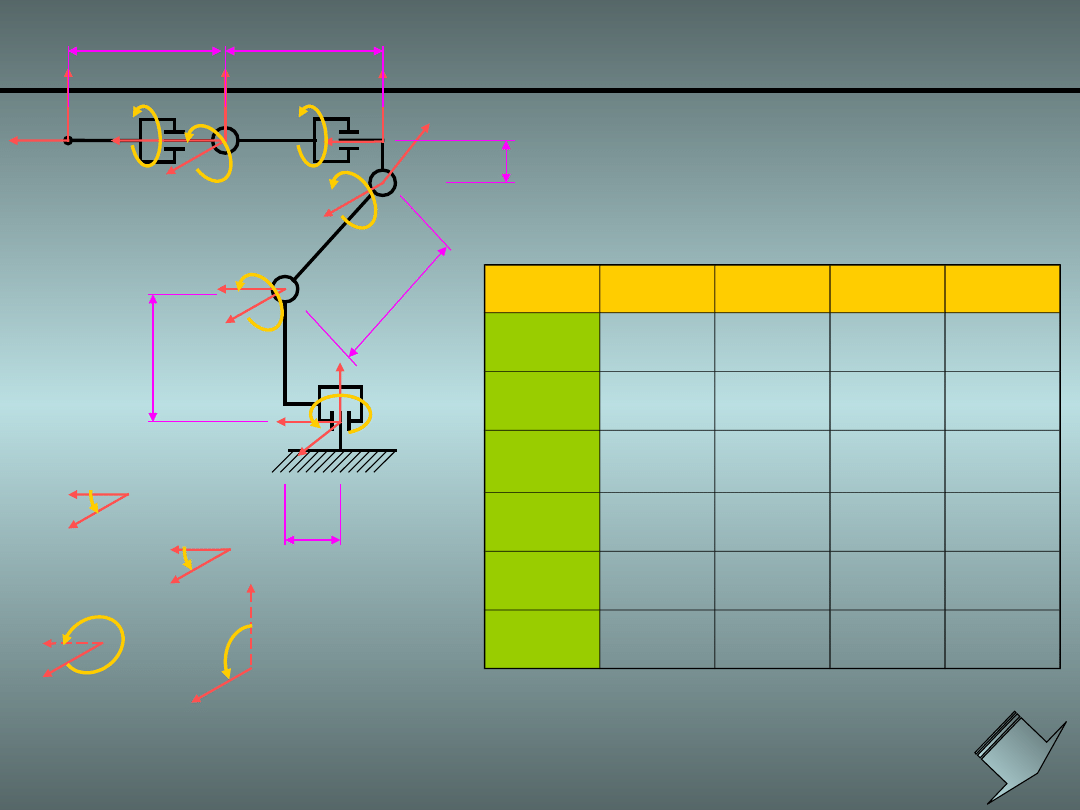
Przykład 3.
Przykład 3.
z
z
0
0
z
z
1
1
1
1
z
z
2
2
z
z
3
3
3
3
z
z
3
3
z
z
4
4
4
4
z
z
4
4
z
z
5
5
5
5
Człon
Człon
a
a
i
i
i
i
d
d
i
i
i
i
1
1
a
1
/2
d
1
1
2
2
a
2
0
0
2
3
3
a
3
/2
0
3
4
4
0
/2
d
4
4
5
5
0
/2
0
5
6
6
0
0
d
6
6
z
z
1
1
x
x
1
1
z
z
2
2
x
x
2
2
z
z
3
3
x
x
3
3
d
d
1
1
a
a
1
1
a
a
2
2
x
x
0
0
z
z
0
0
y
y
0
0
1
1
2
2
3
3
z
z
4
4
x
x
4
4
z
z
5
5
x
x
5
5
z
z
6
6
x
x
6
6
a
a
3
3
d
d
4
4
d
d
6
6
4
4
5
5
6
6
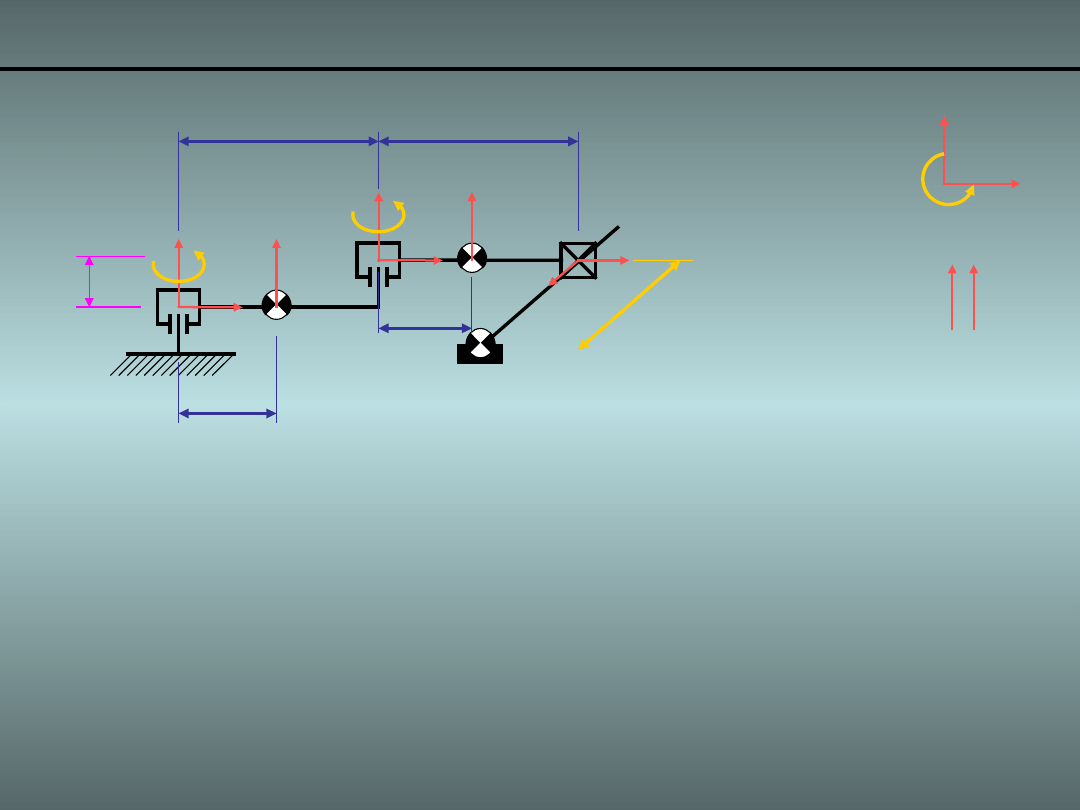
Przykład 4.
Przykład 4.
z
z
1
1
z
z
2
2
2
2
z
z
0
0
z
z
1
1
z
z
0
0
x
x
0
0
x
x
1
1
z
z
1
1
z
z
2
2
a
a
c1
c1
1
1
2
2
z
z
c1
c1
z
z
c2
c2
m
m
1
1
m
m
2
2
x
x
2
2
m
m
3
3
a
a
c
c
2
2
d
d
3
3
a
a
1
1
a
a
2
2
d
d
1
1
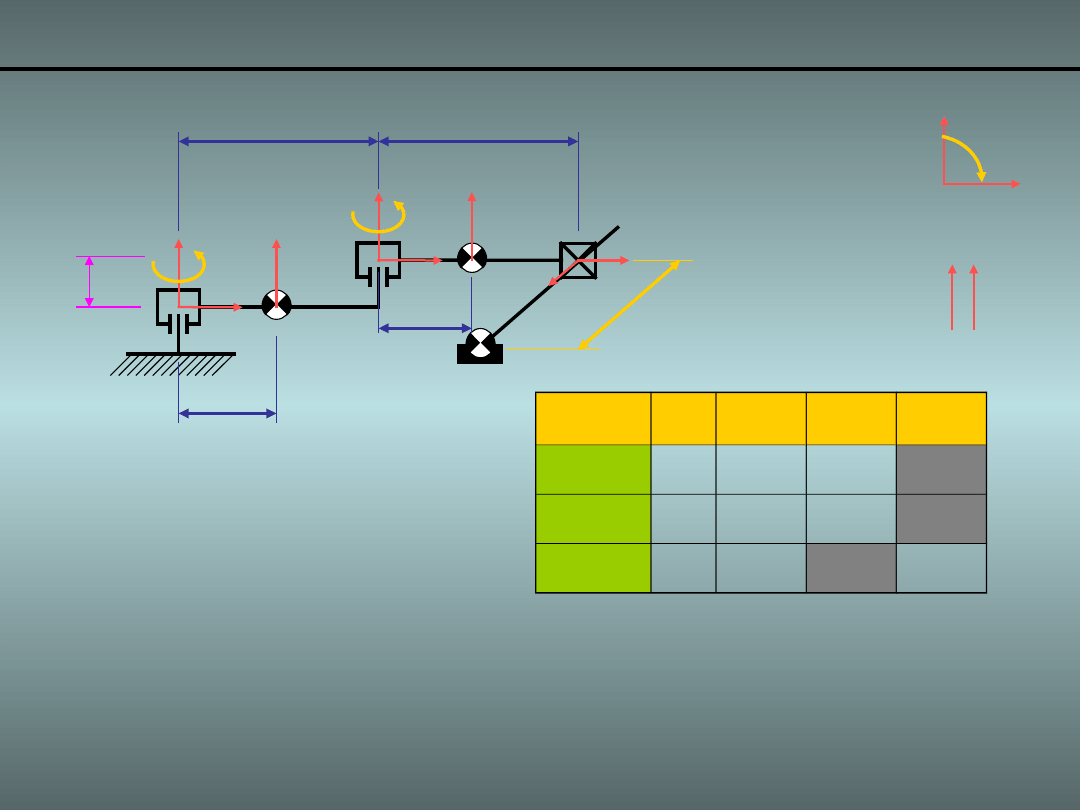
Przykład 4.
Przykład 4.
z
z
1
1
z
z
2
2
2
2
z
z
0
0
z
z
1
1
z
z
0
0
x
x
0
0
x
x
1
1
z
z
1
1
z
z
2
2
a
a
c1
c1
1
1
2
2
z
z
c1
c1
z
z
c2
c2
m
m
1
1
m
m
2
2
x
x
2
2
m
m
3
3
a
a
c
c
2
2
d
d
3
3
a
a
1
1
a
a
2
2
Człon
Człon
a
a
i
i
i
i
d
d
i
i
i
i
1
1
a
1
0
d
1
1
2
2
a
2
pi/2
0
2
3
3
0
0
d
3
0
d
d
1
1
Przykład 5.
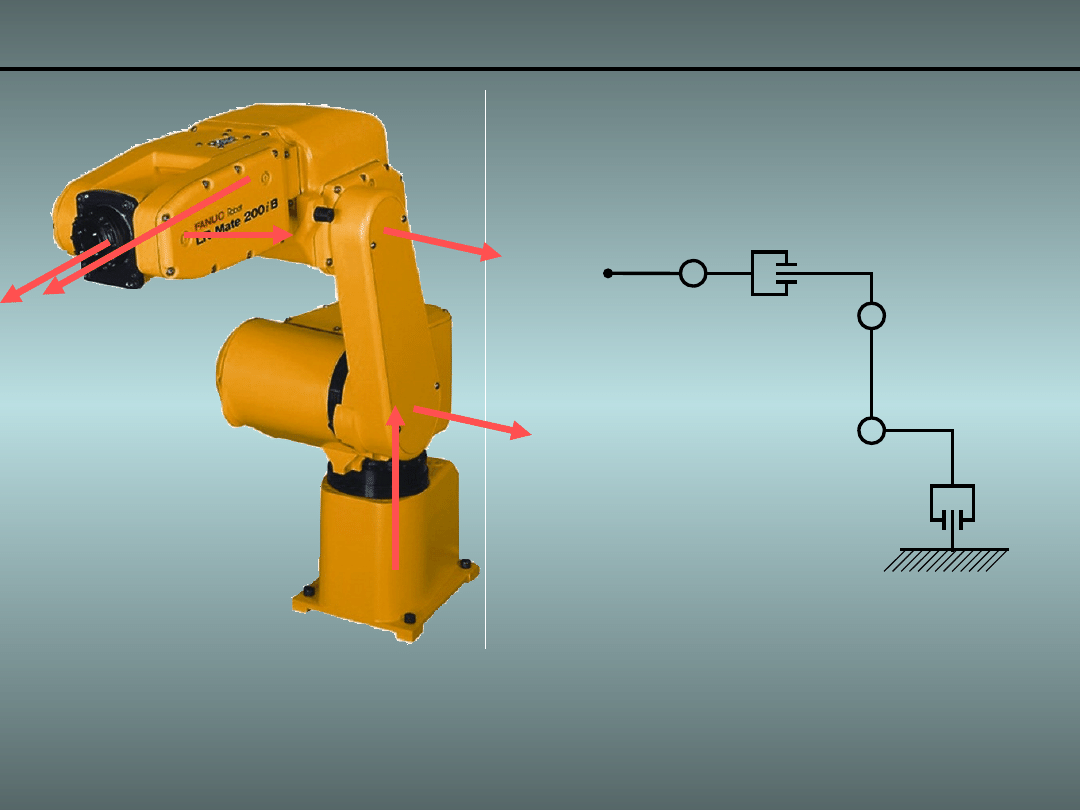
Przykład 5.
FANUC
FANUC
Przykład 5.
Przykład 5.
z
z
1
1
d
d
1
1
a
a
1
1
x
x
0
0
z
z
0
0
y
y
0
0
1
1
2
2
z
z
2
2
z
z
4
4
x
x
1
1
x
x
2
2
x
x
4
4
z
z
3
3
x
x
3
3
z
z
5
5
x
x
5
5
a
a
2
2
a
a
3
3
d
d
4
4
a
a
5
5
3
3
4
4
5
5
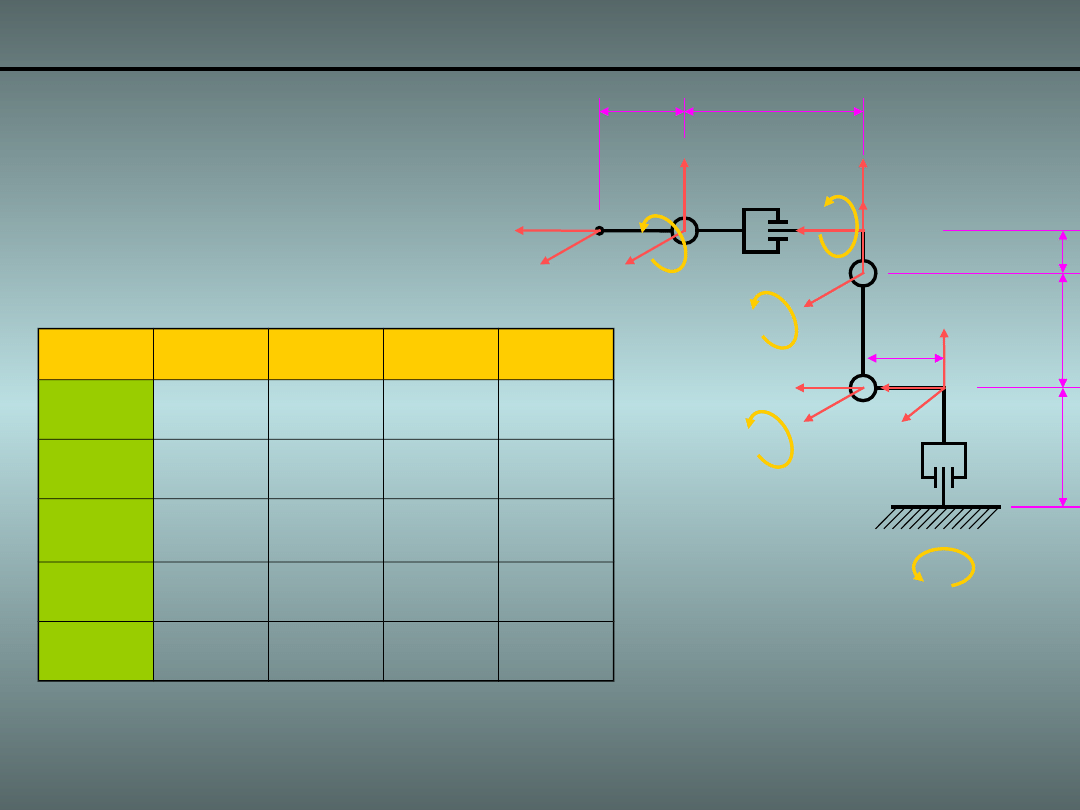
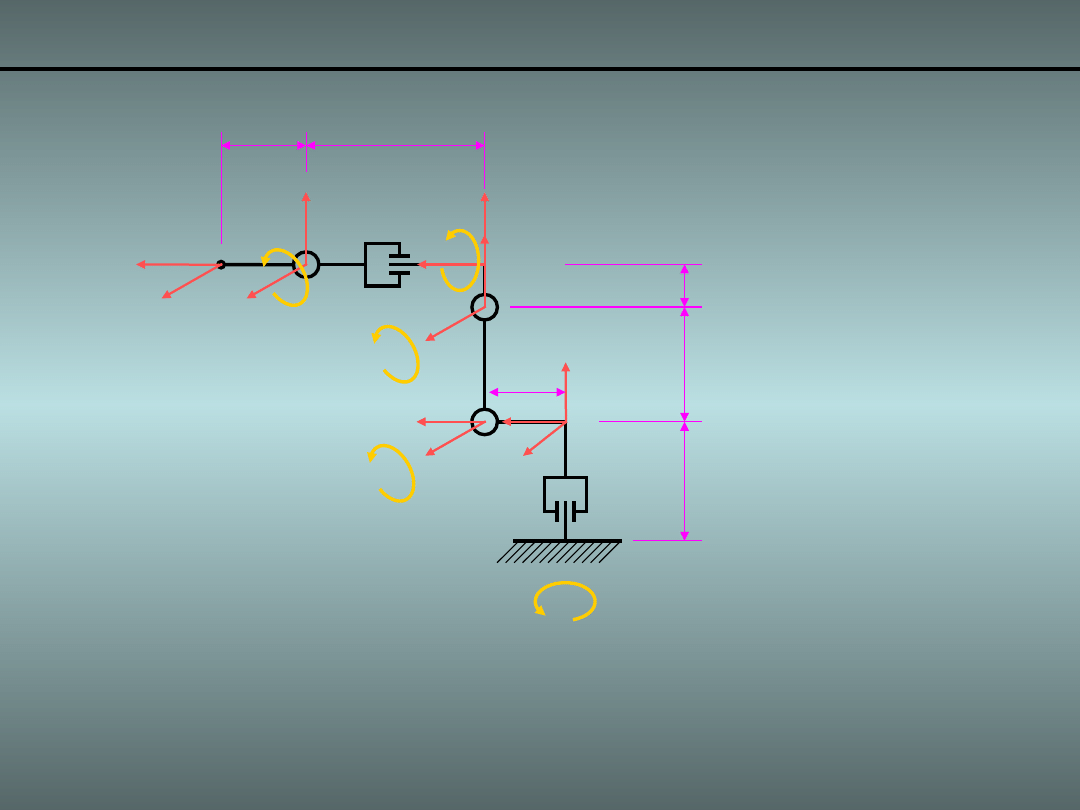
Przykład 5.
Przykład 5.
z
z
1
1
d
d
1
1
a
a
1
1
x
x
0
0
z
z
0
0
y
y
0
0
1
1
2
2
z
z
2
2
z
z
4
4
x
x
1
1
x
x
2
2
x
x
4
4
z
z
3
3
x
x
3
3
z
z
5
5
x
x
5
5
a
a
2
2
a
a
3
3
d
d
4
4
a
a
5
5
3
3
4
4
5
5
Człon
Człon
a
a
i
i
i
i
d
d
i
i
i
i
1
1
a
1
/2
0
1
2
2
a
2
0
0
2
3
3
a
3
/2
0
3
4
4
0
/2
d
4
4
5
5
0
/2
0
5
Document Outline
Wyszukiwarka
Podobne podstrony:
wykład 5 +matlab, W SPR nr 03 04 Kinematyka Odwrotna
7 Wykład 13 CHRONOMETRAŻ przyklad
Matlab T Twardowski ,,Wprowadzenie Do Matlaba Na Przykładach''
Metodologia badań z logiką dr Karyłowski wykład 13 Dodatkowe przykłady schematów quasiekspe
MATLAB zestaw przykladowe zadania
Wykład 6 informacja dodatkowa (przykładowa firma)
ściąga z prawa - wykład, Różne Spr(1)(4)
TI MATLAB zestaw przykladowe zadania
7.Wykład 13 CHRONOMETRAŻ przyklad
edukacja społeczno- przyrodnicza z metodyką- wykłady, Różne Spr(1)(4)
2)WYKŁAD 3 WYKAZ SPR DOT ODPADÓW
Wykład 3 Analiza spr fin
IMIR przyklady kinematyka id 21 Nieznany
WYKŁADY Zadania na przykładowy egzamin
matlab2, wojtek studia, Automatyka, studia 2010, Matlab spr
PROP 2 (4 wykład) Bazy Rodzaje Przykłady
matlab spr
7 Wykład 13 CHRONOMETRAŻ przyklad
więcej podobnych podstron