KONCYPOWANIE I

KONCYPOWANIE I

OPTYMALIZACJA

OPTYMALIZACJA

Piotr

Piotr

GENDARZ

GENDARZ

Wydział Mechaniczny Technologiczny

Instytut Automatyzacji Procesów Technologicznych

i Zintegrowanych Systemów Wytwarzania

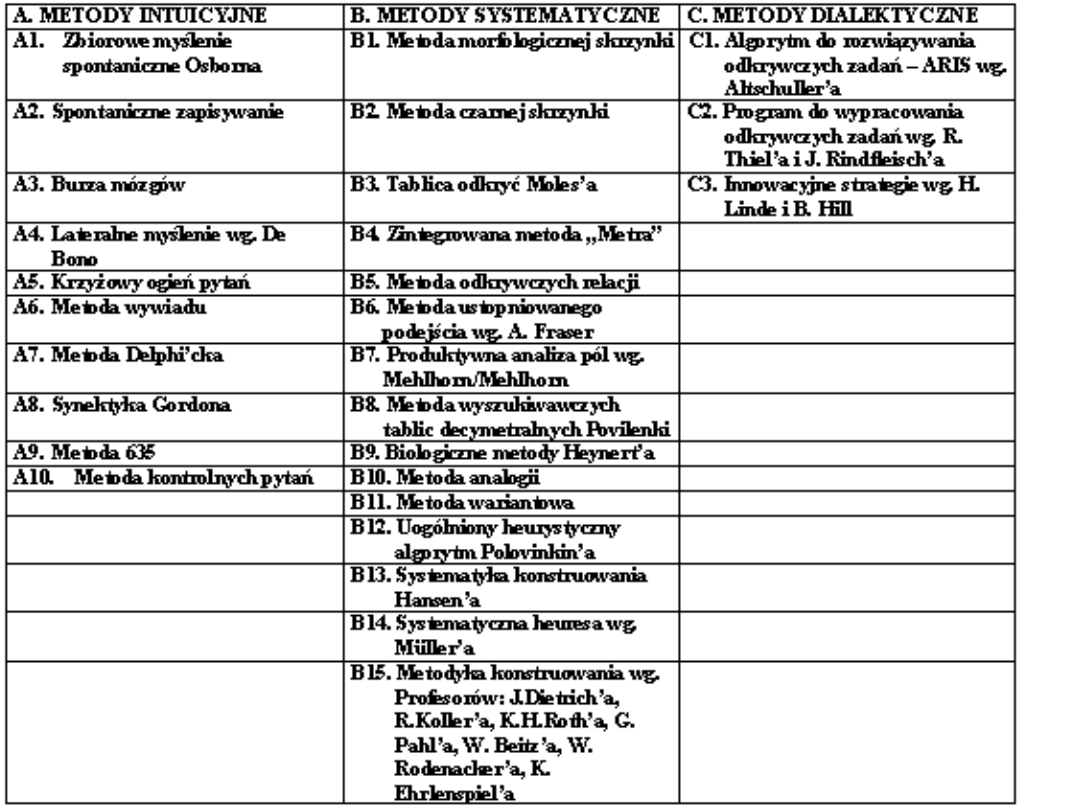
METODY KONCYPOWANIA

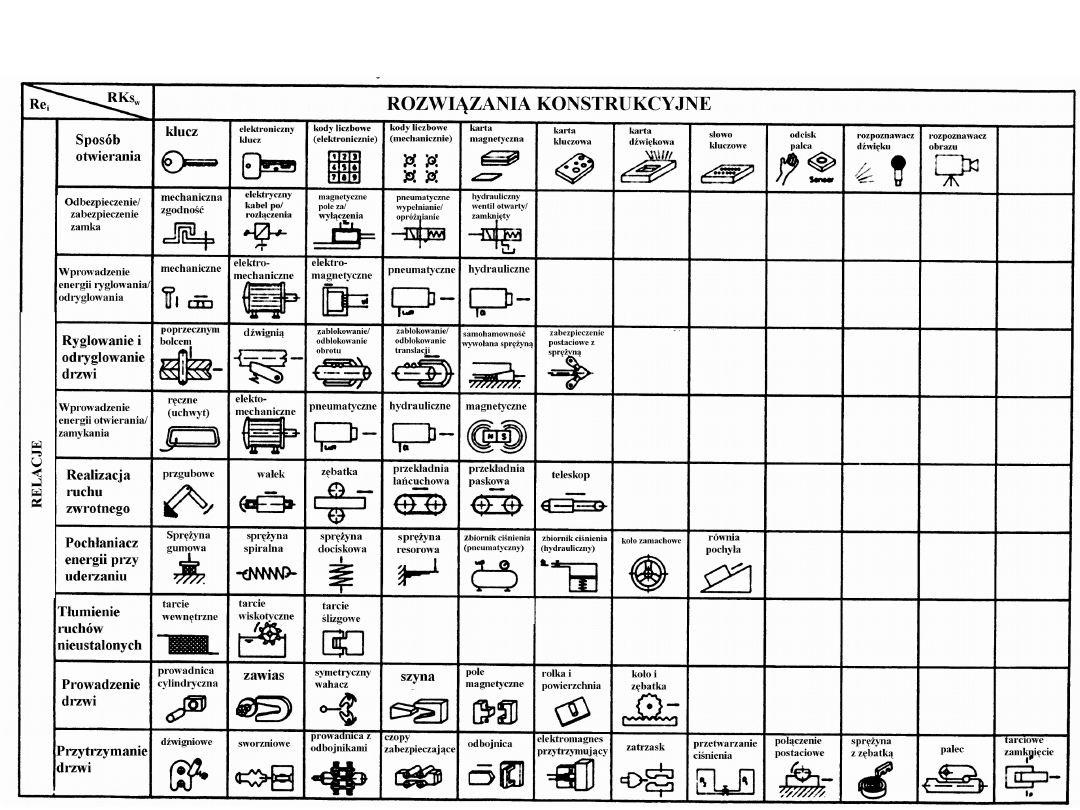
METODA MORFOLOGICZNEJ
SKRZYNKI

ALGORYTM JONESA

1. ANALIZA

1.1.   Zebranie wykazu danych, wśród których znajdują się
również wiadomości
przypadkowe.
1.2.   Klasyfikacja danych.
1.3.   Sporządzenie wykazu źródeł informacji.
1.4.   Analiza danych i rozpoznanie współzależności między
danymi.
1.5.   Opracowanie wykazu kryteriów działania (osiągów).
1.6. Uwzględnienie obowiązujących kryteriów.

2. SYNTEZA

2.1.   Przeprowadzenie procesu obmyślania twórczego.
2.2.   Opracowanie części całości.
2.3.   Wyznaczenie rozkładów struktur tych części
(elementów).
2.4.   Rozpatrzenie różnych kombinacji rozwiązań części.
Tzw. ukartowanie uzyskanych rozwiązań
(systematyczne
uporządkowanie umożliwiające łatwy wgląd w wynik
opracowań).

3. OCENA

3.1.   Dobranie metody oceny.
3.2. Przeprowadzenie oceny ze względu na działanie,

wytwarzanie i

zbyt.

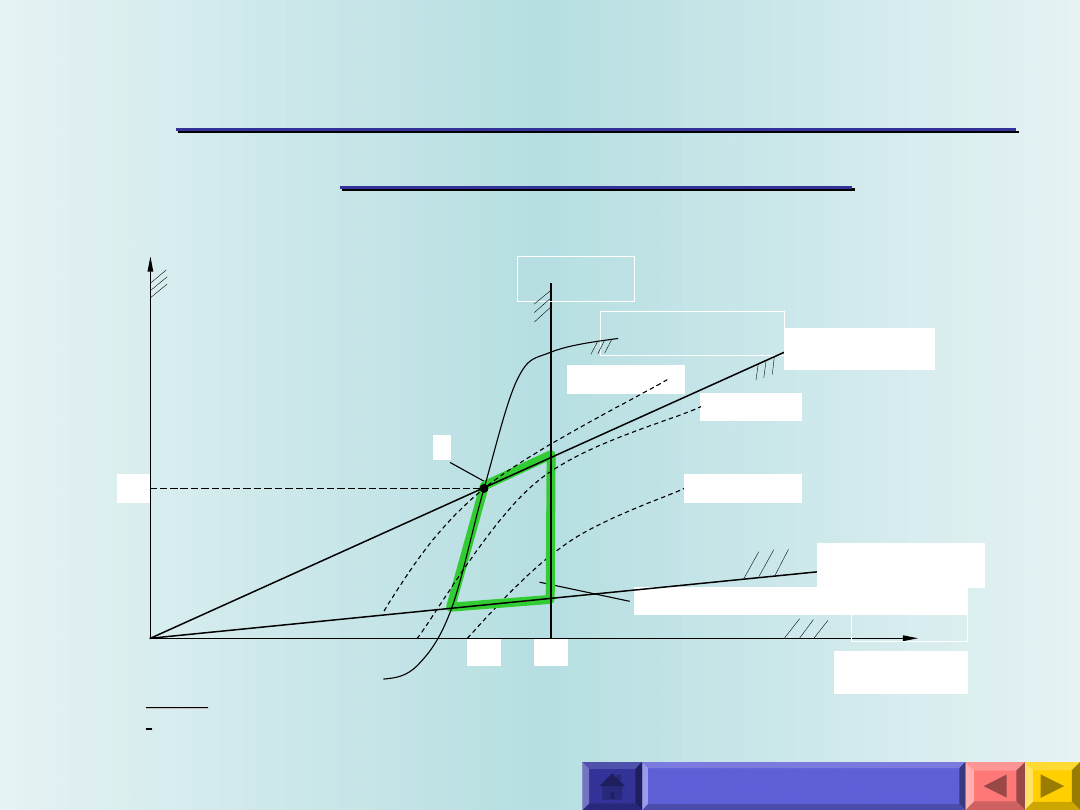
OPTYMALIZACJA W PROCESIE

OPTYMALIZACJA W PROCESIE

KONSTRUOWANIA

KONSTRUOWANIA

Rodzaje optymalizacji

A

D

4

-51D-d

4

0

q=5,25*10

-4

q=7,8*10

-4

3,5

5

D*10

-2

[m]

d*10

-2

[m]

4,4

 - zbiór dopuszczalnych rozwiązań

d-0,2D0

q=10,6*10

-3

5-D0

0,8D-d

d>0

D>0

Wynik

Wynik

:

:

[m]

10

*

3,5

d

ˆ

[m]

10

*

4,4

D

ˆ

2

2









OPTYMALIZACJA W PROCESIE KONSTRUOWANIA

OPTYMALIZACJA W PROCESIE KONSTRUOWANIA

4. Optymalizacja punktowa

4. Optymalizacja punktowa

SStadia metody:

SStadia metody:

1.    ocena kryteriów g

1.    ocena kryteriów g

n

n

, (n=1,n

, (n=1,n

z

z

),

),

2.    ocena rozwiązań konstrukcyjnych względem układu kryteriów w

2.    ocena rozwiązań konstrukcyjnych względem układu kryteriów w

nl

nl

,

,

(n=1,n

(n=1,n

z

z

, l=1,l

, l=1,l

z

z

),

),

3.  wybór na podstawie wartości znaczenia rozwiązania z

3.  wybór na podstawie wartości znaczenia rozwiązania z

l

l

, (l=1,l

, (l=1,l

z

z

)

)

rozwiązań konstrukcyjnych

rozwiązań konstrukcyjnych

najlepiej spełniających układ

najlepiej spełniających układ

kryteriów.

kryteriów.

Rodzaje optymalizacji

Podstawowe metody polioptymalizacji

OPTYMALIZACJA W PROCESIE

OPTYMALIZACJA W PROCESIE

KONSTRUOWANIA

KONSTRUOWANIA

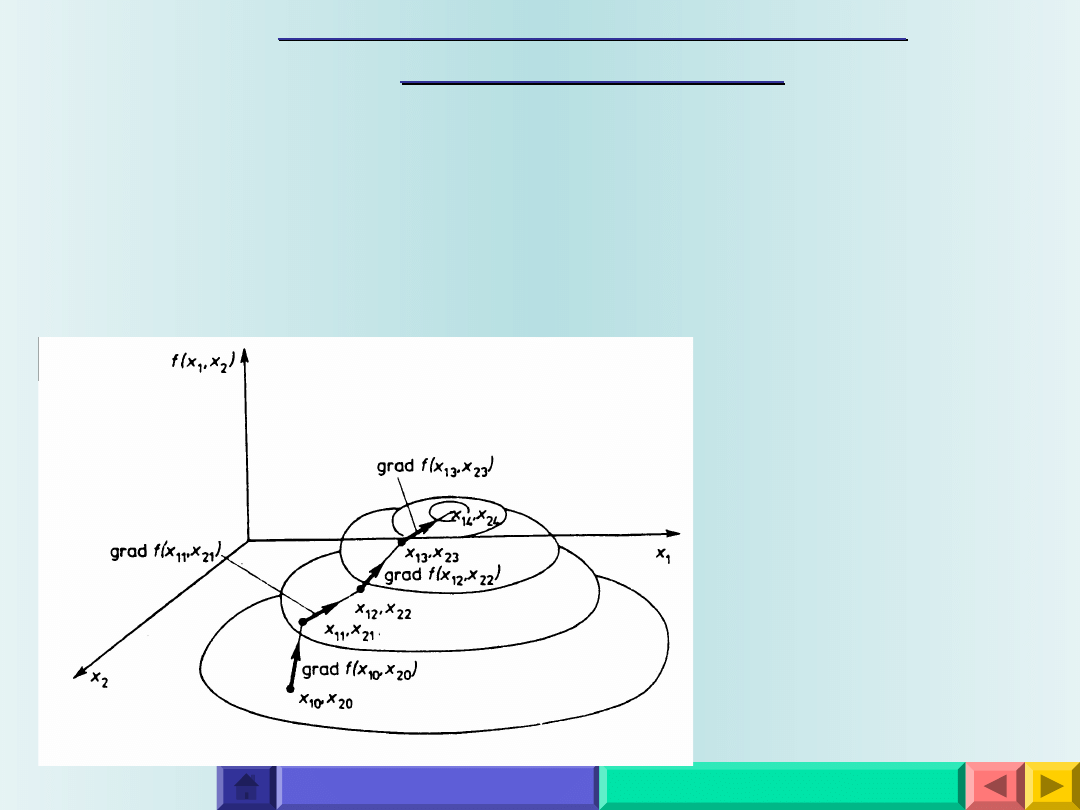
8. Metoda gradientowa

8. Metoda gradientowa

Rodzaje optymalizacji

Podstawowe metody polioptymalizacji

Wśród metod sekwencyjnego badania wielowymiarowych przestrzeni zmiennych decyzyjnych najbardziej
rozpowszechnione są metody polegające na postępowaniu wzdłuż największego wznoszenia się funkcji celu,
czyli tzw. metody gradientowe.

Stosując prostą metodę gradientową, wybiera się początkowy punkt poszukiwań XΩ, a następnie wyznacza się gradient

funkcji celu w tym punkcie: grad ƒ(X

0

, P). Kierunek i zwrot tego gradientu wskazują kierunek największego wznoszenia się funkcji

celu. Posuwając się w tym kierunku o pewien krok, wyznacza się nowy punkt X

1

, w którym wartość funkcji celu jest większa niż

wartość w punkcie X

0

.

ƒ(X

1

, P)> ƒ(X

0

, P)

Następnie wyznacza się znowu kierunek i zwrot gradientu i posuwa się w kierunku zgodnym z tym nowym wektorem o następny
krok do punktu X

2

. Tak postępując, wyznacza się kolejne punkty. Postępowanie prowadzi się tak długo, aż wartości funkcji celu

przestaną rosnąć bądź do momentu, w którym osiągnie się brzeg obszaru decyzji dopuszczalnych.

Algorytmy genetyczne

Operuje się podobnymi pojęciami jak w samej

genetyce. Istnieją chromosomy – populacje

abstrakcyjnych osobników, które pretendują

do stania się rozwiązaniami – osobnikami.

Łączenie oraz podział chromosomów zgodnie

z zasadami występującymi w naturze zmierza

do uzyskania rozwiązania optymalnego.
Proces ewolucji zaczyna się od utworzenia

losowej populacji osobników i zdarzeń w

generacji. W każdej generacji, dla całej

populacji obliczana jest funkcja dopasowania.

Mnożone

osobniki

są

stochastycznie

wybierane

spośród

obecnej

populacji,

modyfikowane

(mutowane

lub

rekombinowane)

do

postaci

nowych

osobników, w nowej populacji, która stanie

się bieżącą w następnej iteracji algorytmu.