Instrumenty zarządzania

jakością

• Służą realizacji zadań i osiągania celów

wyznaczonych przez przedsiębiorstwo
(zawartych np. w księdze jakości,
strategii TQM)

• Pomagają kształtować jakość wyrobu na

wszystkich etapach w cyklu jego
istnienia (projektowanie, wytwarzanie,
…)

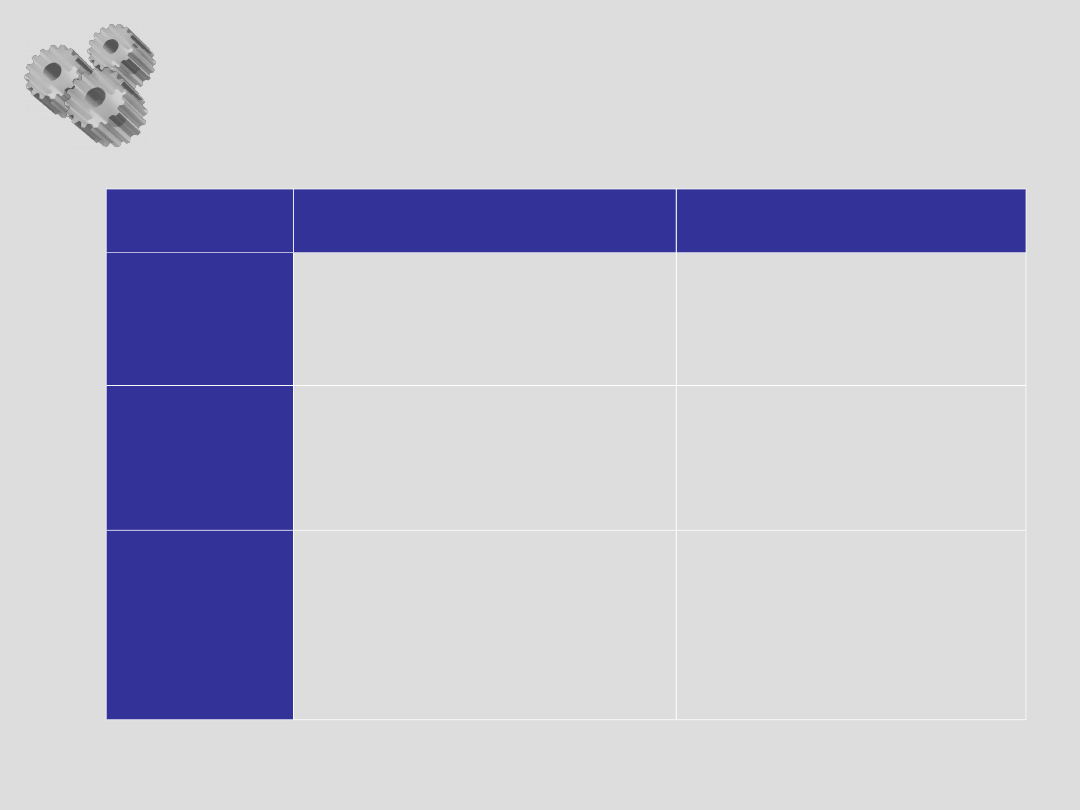
Podział instrumentów ZJ

CECHY I SPOSÓB ODDZIAŁYWANIA

NA JAKOŚĆ

PRZYKŁADY

ZASADY

Określają stosunek przedsiębiorstwa i

jego pracowników do ogólnie

rozumianych problemów jakości

Określają strategię przedsiębiorstwa

Nie dają wytycznych operacyjnych

•Zasady Deminga
•Zasada ciągłego doskonalenia procesów

(Kaizen)
•Zasada „zero defektów”
•Zasada pracy zespołowej

METODY

Charakteryzują się planowym,

powtarzalnym i opartym na naukowych

podstawach sposobem postępowania

przy realizacji zadań związanych z

zarządzaniem jakością

Oddziaływanie „średnioterminowe”

•QFD
•FMEA
•SKO
•SPC
•DOE

NARZĘDZIA

Służą do zbierania i przetwarzania

danych związanych z różnymi

aspektami zarządzania jakością

Mają charakter krótkotrwały

(operacyjny)

•Schemat blokowy
•Diagram Ishikawy
•Diagram Pareto
•Histogram
•Arkusze kontrolne
•Wykresy korelacji
•Karta kontrolna
•„nowe” narzędzia

Narzędzia jakości

Cechy:
- zbieranie i przetwarzanie danych
- wizualizacja danych
- odkrywanie danych
- są instrumentami monitorowania i

diagnozowania procesów
- umożliwiają podejmowanie decyzji
- umożliwiają analizowanie rezultatów

podjętych działań
- ułatwiają doskonalenie produktów /usług

/procesów

Podstawowe narzędzia (7

tools)

1) schemat blokowy

2) arkusze kontrolne

3) diagram przyczynowo – skutkowy

(Ishikawy, „rybia ość”)

4) analiza Pareto (Lorenza)

5) histogram

6) wykresy rozrzutu (korelacja)

7) karty kontrolne

„Nowe” narzędzia (new 7

tools)

1) diagram relacji

2) macierzowa analiza danych

3) diagram pokrewieństwa

4) diagram procesu podejmowania decyzji

5) diagram systematyki

6) diagram strzałkowy

7) diagram macierzowy

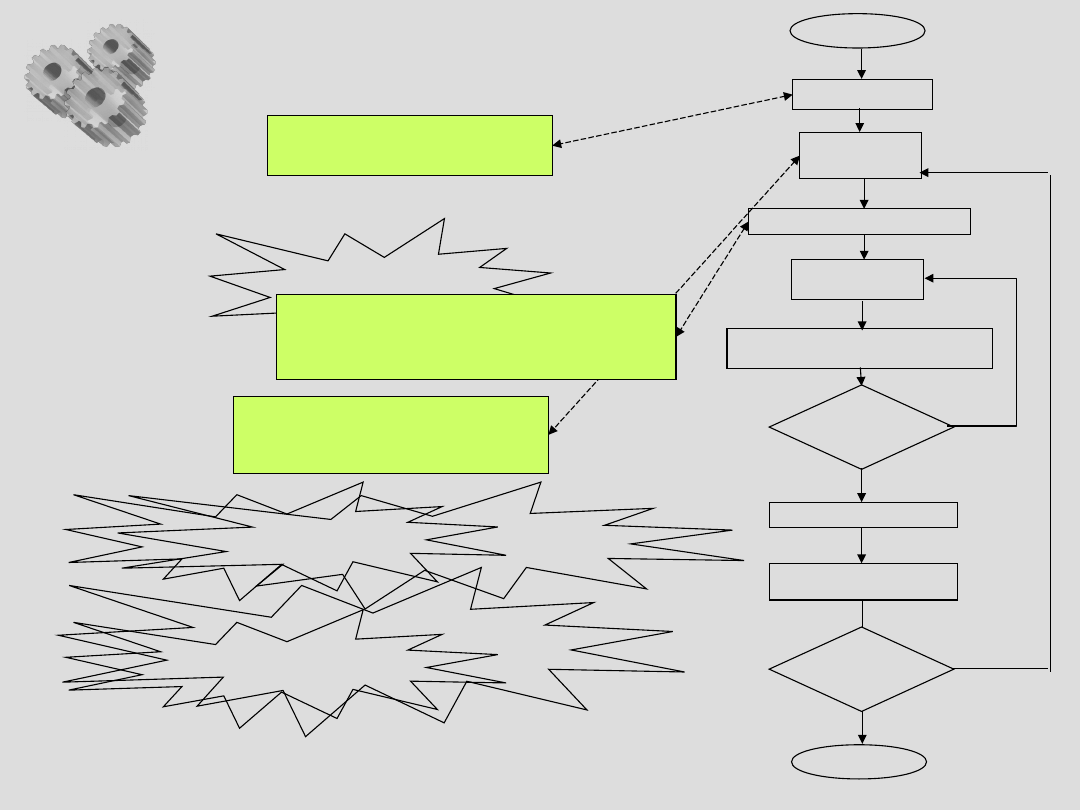
Określenie problemu

START

Zbieranie danych i

informacji o

problemie

nie

tak

STOP

tak

nie

Systematyzowanie informacji

Określenie problemu

Analiza Pareto

Zbieranie danych

i informacji o

problemie

Arkusz
kontrolny

Diagram
Ishikawy

Systematyzowanie

informacji

Schemat blokowy

Histogram

Poszukiwanie

rozwiązań

Analiza wprowadzenia rozwiązań w

kontekście przyjętych kryteriów

Wdrożenie rozwiązania

Czy

rozwiązania

zostały

zaakceptowan

e?

Weryfikacja rezultatów

wprowadzenia zmian

Czy osiągnięto

zamierzony

cel?

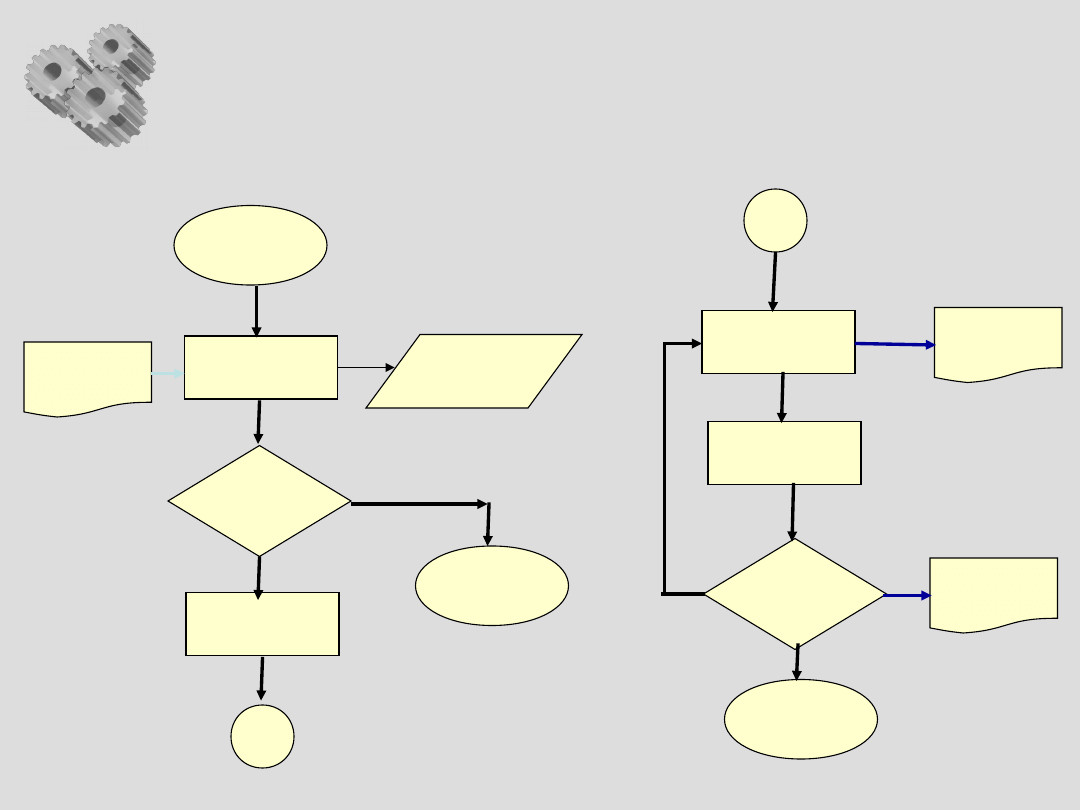
1. Schemat blokowy

Start

działanie

blok

informacyjny

dokument

A

A

blok

decyzyjny

Koniec

działanie

działanie

blok

decyzyjny

działanie

dokument

Koniec

T

N

N

dokument

2. Arkusz kontrolny

• stosowane do gromadzenia danych z

jednoczesnym ich porządkowaniem

• dotyczą najczęściej wad, zdarzeń, dat
• karty projektuje się indywidualnie dla

problemów

• powinniśmy określić:

– co chcemy wiedzieć
– jak będziemy zbierać dane

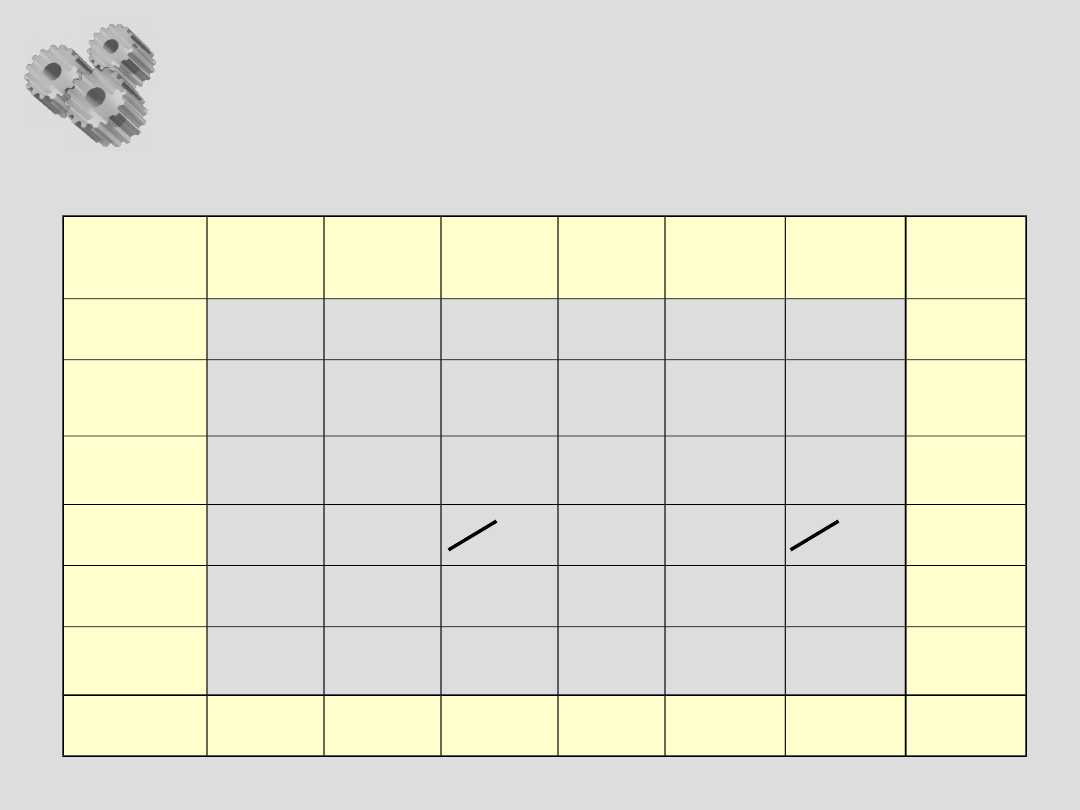
Arkusz kontrolny - przykład

Rodzaj

wady

sty

luty

mar

kwie

maj

cze

Suma

silnik

I

III

I

II

7

wyciek

oleju

II

II

IIII

I

I

II

12

układ

sterowania

III

II

III

I

I

10

narzędzie

IIII

III

IIII

III

II

IIII

22

zła obsługa

III

II

IIII I

I

II

III

16

pasek

klinowy

II

I

III

IIII

I

I

12

Suma

14

11

20

12

8

14

79

Przyczyny awarii maszyn na Wydziale W-2

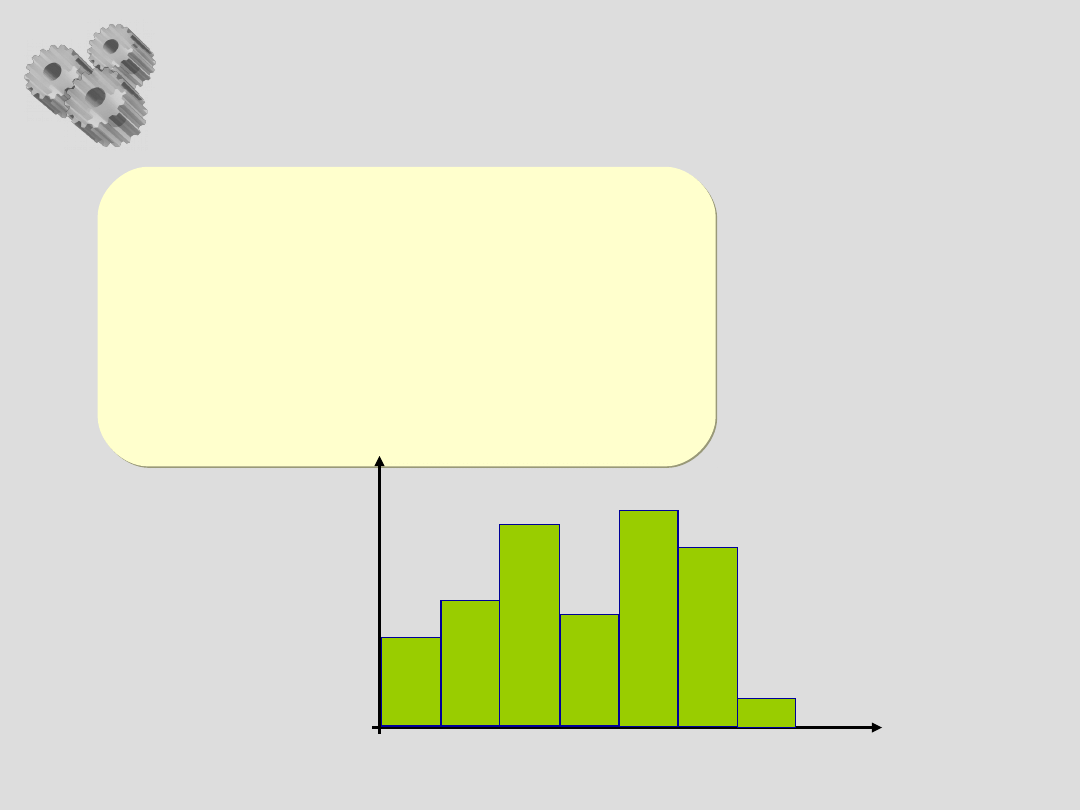
3. Histogram

Co to jest?
Specjalny typ wykresu
słupkowego, pokazujący
rozkład pewnej cechy
(częstotliwość występowania
poszczególnych jej wartości)

Co to jest?
Specjalny typ wykresu
słupkowego, pokazujący
rozkład pewnej cechy
(częstotliwość występowania
poszczególnych jej wartości)

x

1….

x

2 …

x

3 …

x

4 …

x

5 …

x

6 …

x

7 …

x

8

y

Histogram

Liczność próbki

n

Ilość przedziałów

k

30  50

6  10

51  100

7  11

101  200

8  12

201  500

9  15

• szerokość przedziałów powinna być „naturalna” (np. co 0,02 mm a nie

co 0,0167)

• klasy muszą się wykluczać! (np.:

1,25 < x  1,30 albo 1,25  x <

1,30)

• można podać granice tolerancji
• unikać przedziałów pustych

Histogram c.d.

Kiedy korzystamy?

• prezentacja wyników

potrzebnych do analizy
problemu

• identyfikacja rozkładu

• prezentacji danych

obrazujących efektywność
rozwiązań

Kiedy korzystamy?

• prezentacja wyników

potrzebnych do analizy
problemu

• identyfikacja rozkładu

• prezentacji danych

obrazujących efektywność
rozwiązań

4. Wykres przyczynowo –

skutkowy (Ishikawy, „rybiej

ości”)

Co to jest?

Sposób porządkowania
umożliwiający wizualizację
powiązań pomiędzy czynnikami
(przyczynami) a wynikiem
(problemem)

Cel:

Diagnoza przyczyn (po
fakcie dla działań
korygujących lub przed
dla zapobiegawczych)

Wykres przyczynowo – skutkowy

Jak to się robi?

dla problemów technicznych

(5M+E)

•człowiek (man),
•maszyna (machine),
•materiał (material)
•metoda (method)
•zarządzanie (management)

•pomiar (measurement)

•środowisko (environment)

dla usług(5P)

•ludzie (people)
•wyrób (produkt)
•cena (price)
•promocja (promotion)
•miejsce (place)

•sposób sprzedaży

•...

Sporządzić wykaz możliwych

kryteriów przyczyn (przyczyn

głównych), np:

Sporządzić wykaz możliwych

kryteriów przyczyn (przyczyn

głównych), np:

Określić rozważany problem

Określić rozważany problem

Określać czynniki (szczegółowe)

w każdej z przyczyn głównych

Określać czynniki (szczegółowe)

w każdej z przyczyn głównych

N

a

w

y

kr

e

si

e

N

a

w

y

kr

e

si

e

Wybrać czynnik(i) krytyczne

Wybrać czynnik(i) krytyczne

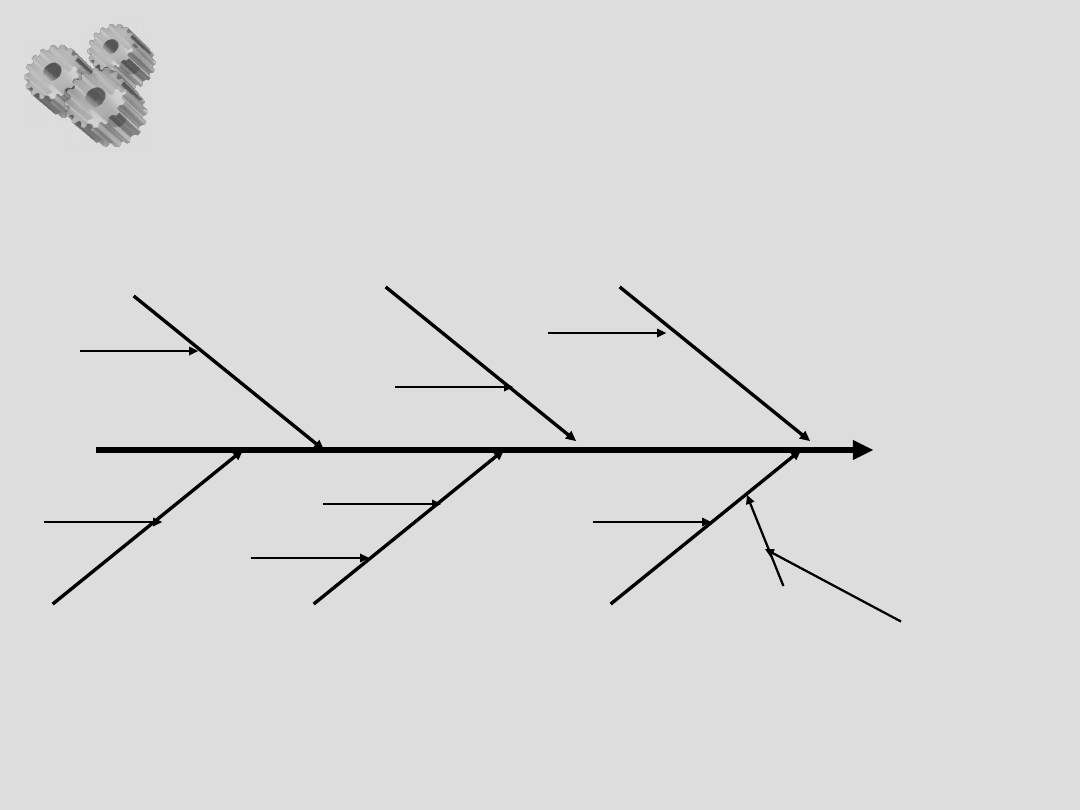
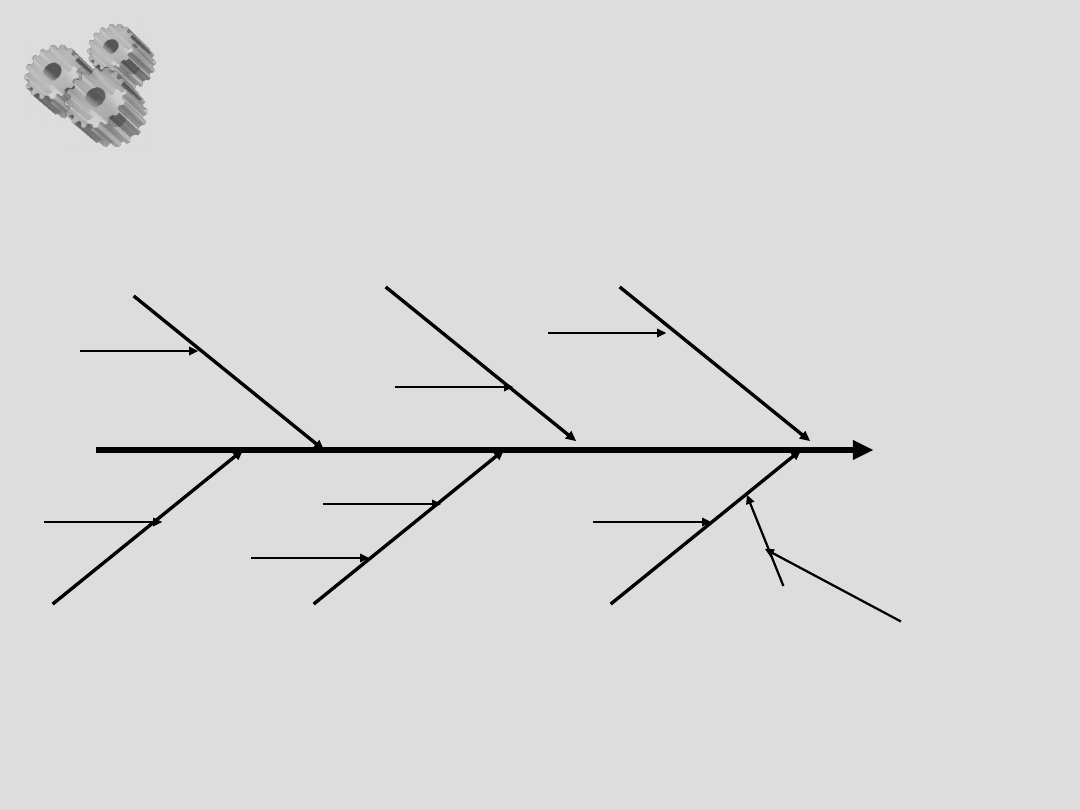
Wykres przyczynowo –

skutkowy c.d.

Proble
m

Człowiek

Metoda

Środowisk
o

Materiał

Maszyna

Zarządzani
e

Wykres przyczynowo –

skutkowy c.d.

Proble
m

ludzie

wyrób

cena

promocja

miejsce

sposób
sprzedaży

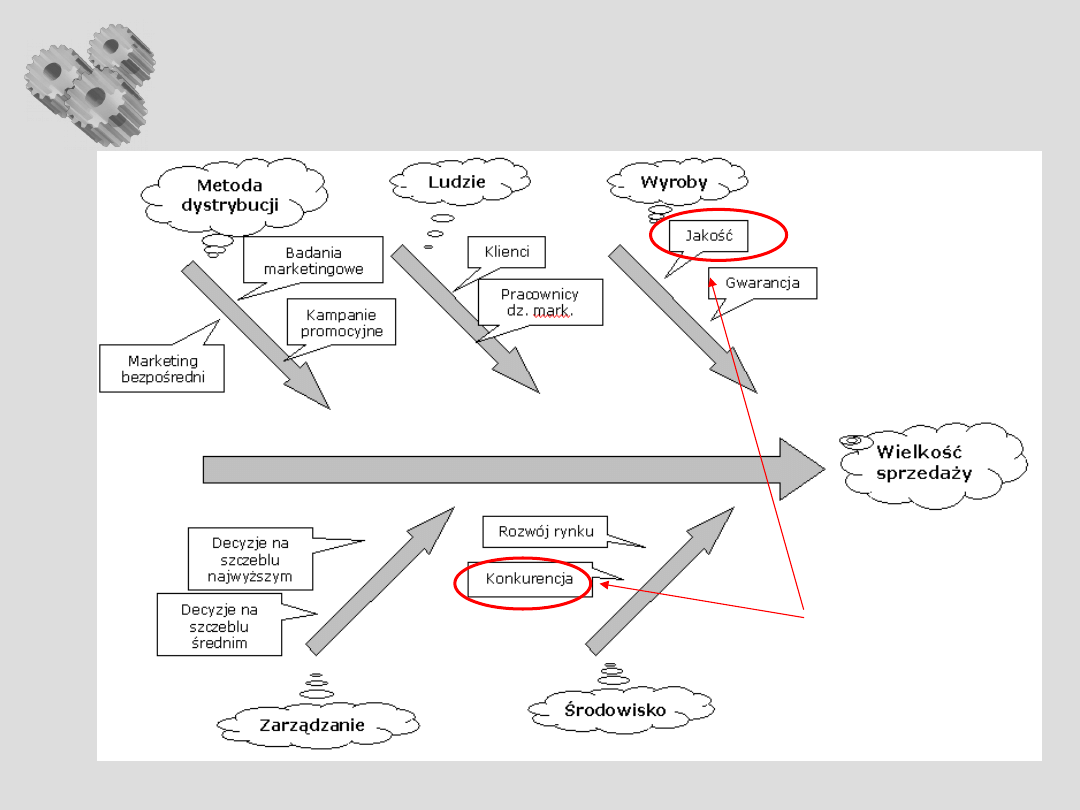
Przykład diagramu

czynniki
krytyczne

5. Analiza Pareto

Co to jest?

Technika oddzielania przyczyn
istotnych od błahych

Co to jest?

Technika oddzielania przyczyn
istotnych od błahych

Zasada empiryczna:

„80 – 20”

80 % problemów spowodowane

jest

20 % przyczyn

Czasami stosuje się dodatkowo

zasadę „95 – 50”

Zasada empiryczna:

„80 – 20”

80 % problemów spowodowane

jest

20 % przyczyn

Czasami stosuje się dodatkowo

zasadę „95 – 50”

Analiza Pareto – c.d.

 Określić cechę danego problemu (czas,

koszty, częstość występowania)



Określić cechę danego problemu (czas,
koszty, częstość występowania)

Zaprojektować formularze (np: arkusz kontrolny)



Zaprojektować formularze (np: arkusz kontrolny)

Zebrać dane



Zebrać dane

Uporządkować dane
malejąco



Uporządkować dane

malejąco

Obliczyć wartości
skumulowane



Obliczyć wartości

skumulowane

Przeliczyć wartości
skumulowane na procenty



Przeliczyć wartości

skumulowane na procenty

Określić obszar „80 – 20” {„95 –
50”}



Określić obszar „80 – 20” {„95 –

50”}

Sporządzić wykres
(procentowy)



Sporządzić wykres

(procentowy)

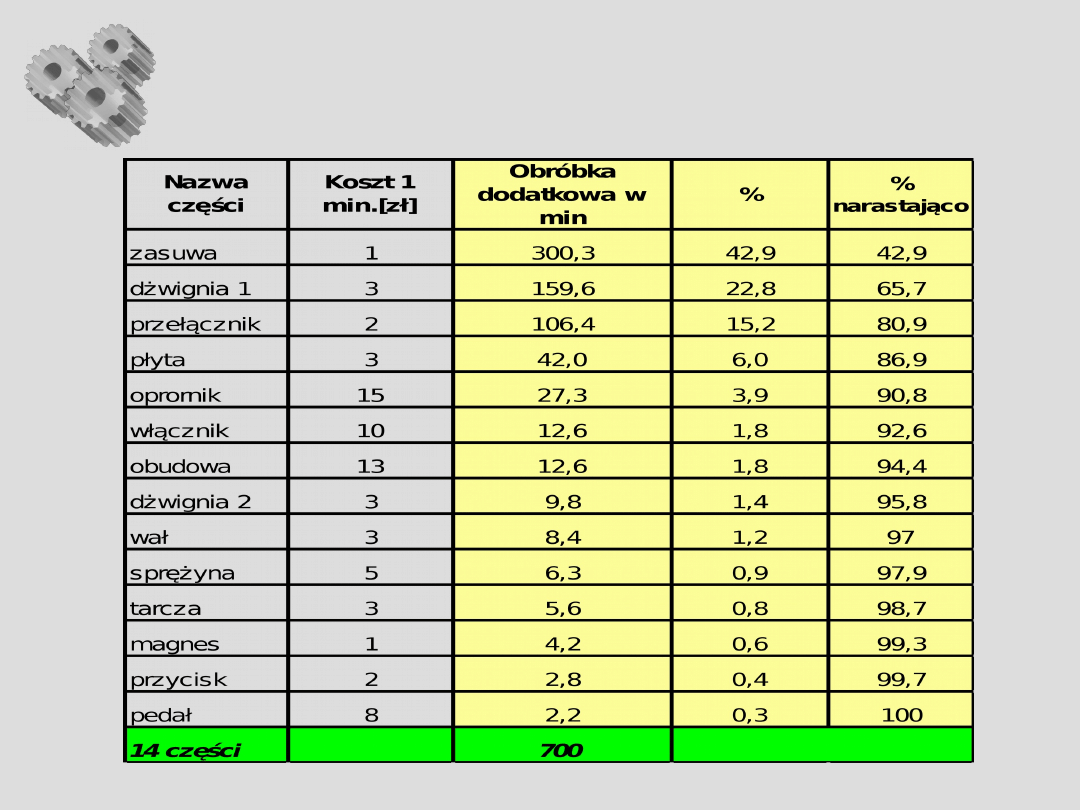
Analiza Pareto – c.d.

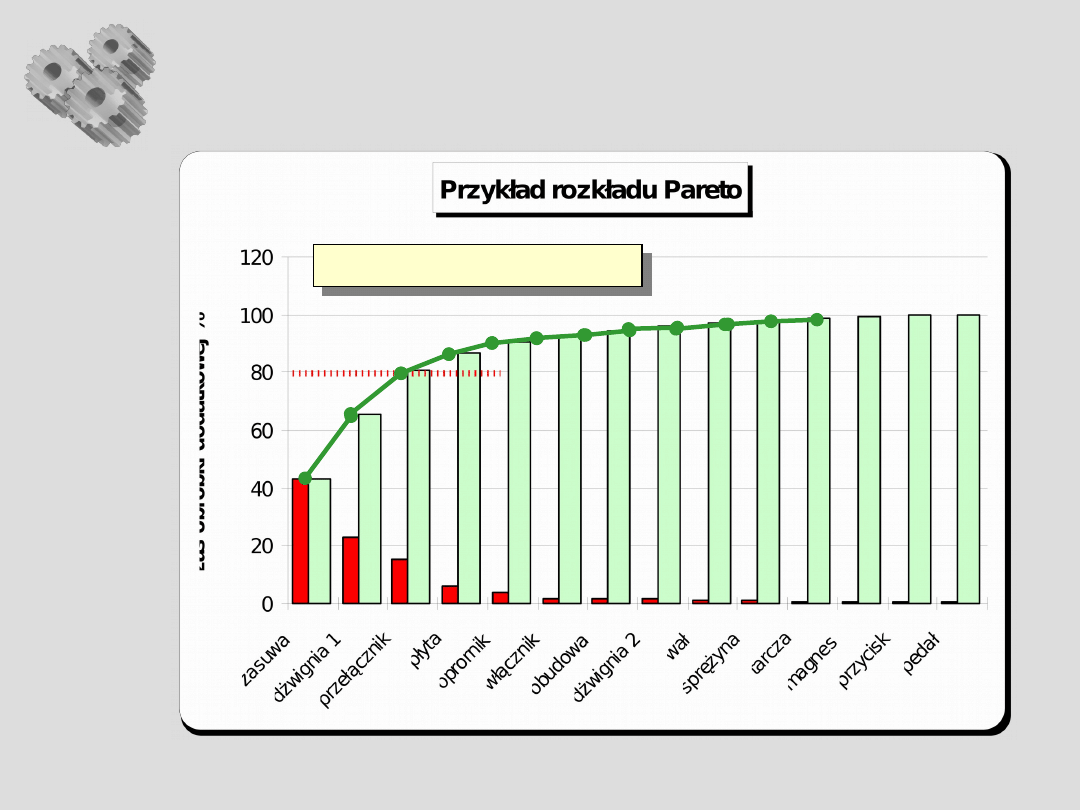
Analiza Pareto - c.d.

Cecha: strata czasu

Cecha: strata czasu

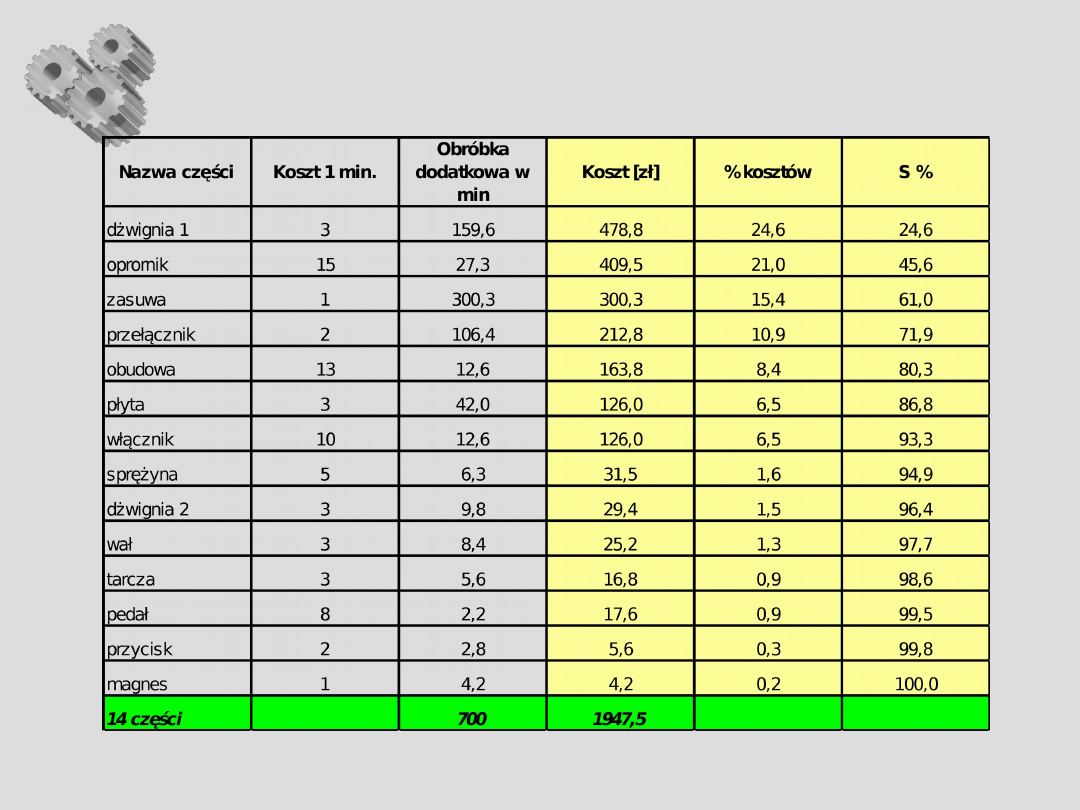
Analiza Pareto – c.d.

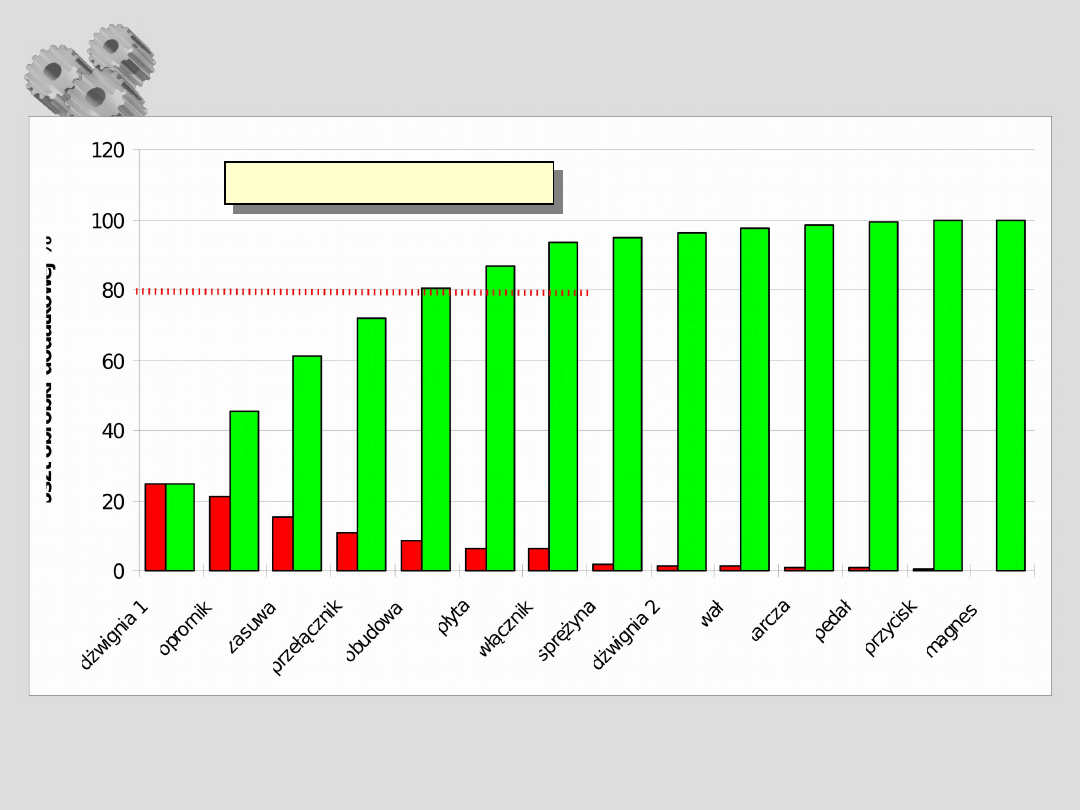
Analiza Pareto – c.d.

Cecha: koszty

Cecha: koszty

Przykład projektu studentów Koła
QC w mieście OSAKA w Japonii

[Donald J. Wheeler, Making Sense of
Data, 2003]

• Straty w klubie studenckim

• Po przeanalizowaniu listy dostaw i sprzedaży dla

poszczególnych miesięcy skonstruowano tabelę:

Co?

Koszt

Butelki
Zamówienia
dodatkowe
Sake
Opóźnienia
Piwo
Inne

7 380

18 900
81 180

7 920

59 400

5 220

• Po przeanalizowaniu listy dostaw i sprzedaży dla

poszczególnych miesięcy skonstruowano tabelę:

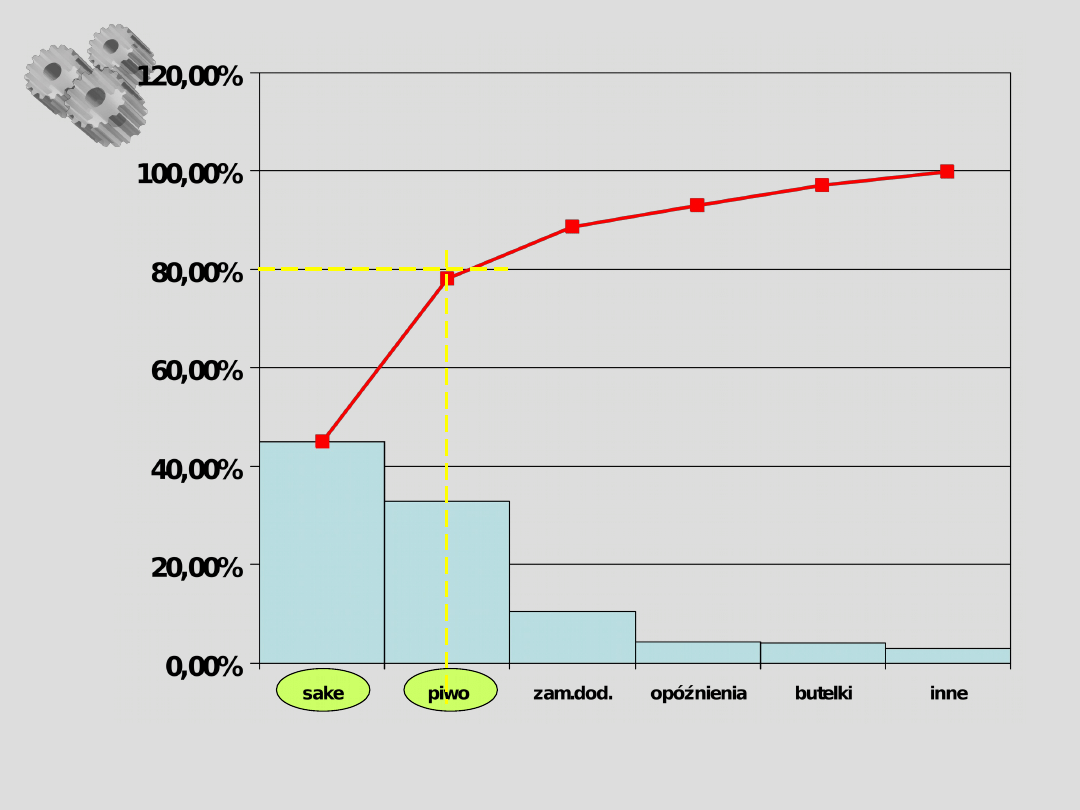
Co?

Koszt

Koszt

w %

Skum.

koszt

Sake
Piwo
Zamówienia

dodatkowe
Opóźnienia
Butelki
inne

81 180
59 400
18 900

7 920
7 380
5 220

45,1%

33%

10,5%

4,4%
4,1%
2,9%

45,1%
78,1%
88,6%
93,0%
97,1%
100%

180
000

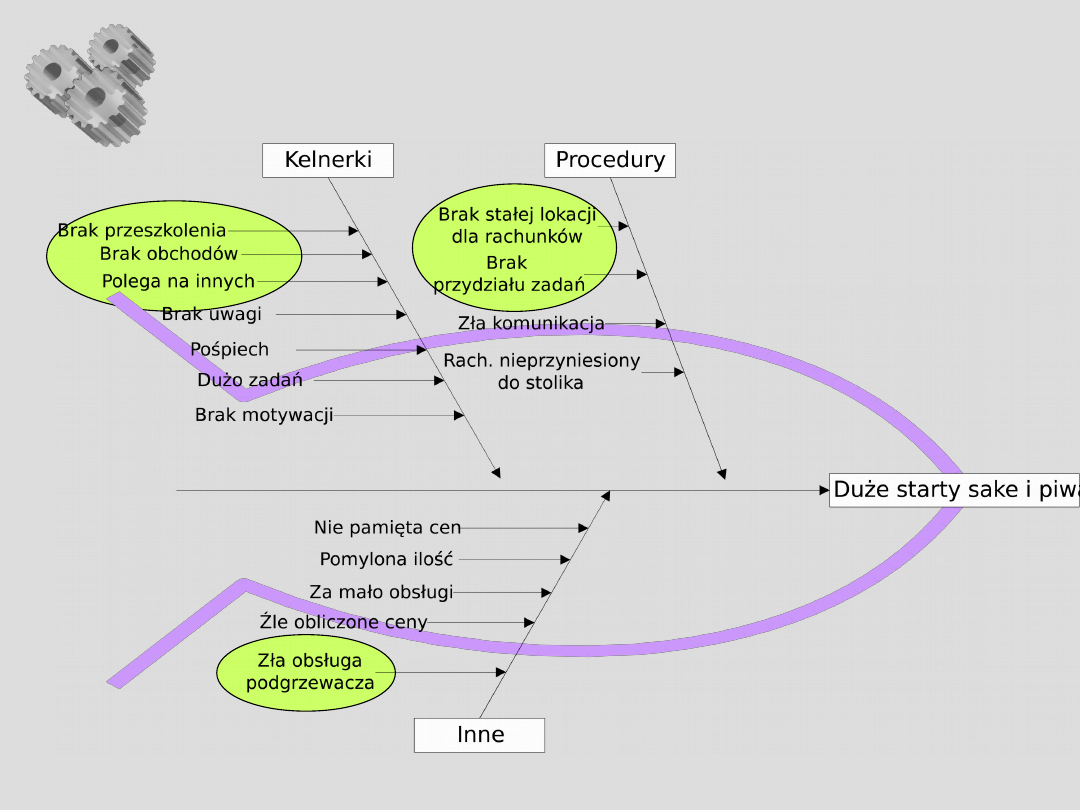
Wyodrębniono najbardziej

istotne przyczyny:

• Brak wyznaczonego miejsca na rachunek
• Poleganie na innych
• Nieumiejętna obsługa pogrzewacza
• Pomyłki w sumowaniu cen
• Niewłaściwe przydzielenie zadań
• Brak szkoleń
• Brak regularnych obchodów po sali

Działania w celu

wyeliminowania problemów:

• Upewnij się czy rach. pozostawiono na stoliku
• W czasie dużego ruchu zaznaczać podawaną

wodę, sake, piwo na kartce dołączonej do

rachunku

• Co godzinę osoba odpowiedzialna za dany rejon

klubu powinna sprawdzić wszystkie rachunki

• Osoba, która zajmuje się „oshibori” (parujący

ręcznik do rąk) ma być odpowiedzialna za

dopisanie do listy nowych gości, którzy pojawili

się na przyjęciach firmowych

• Kierownik powinien zapewnić szkolenie dla

nowych pracowników

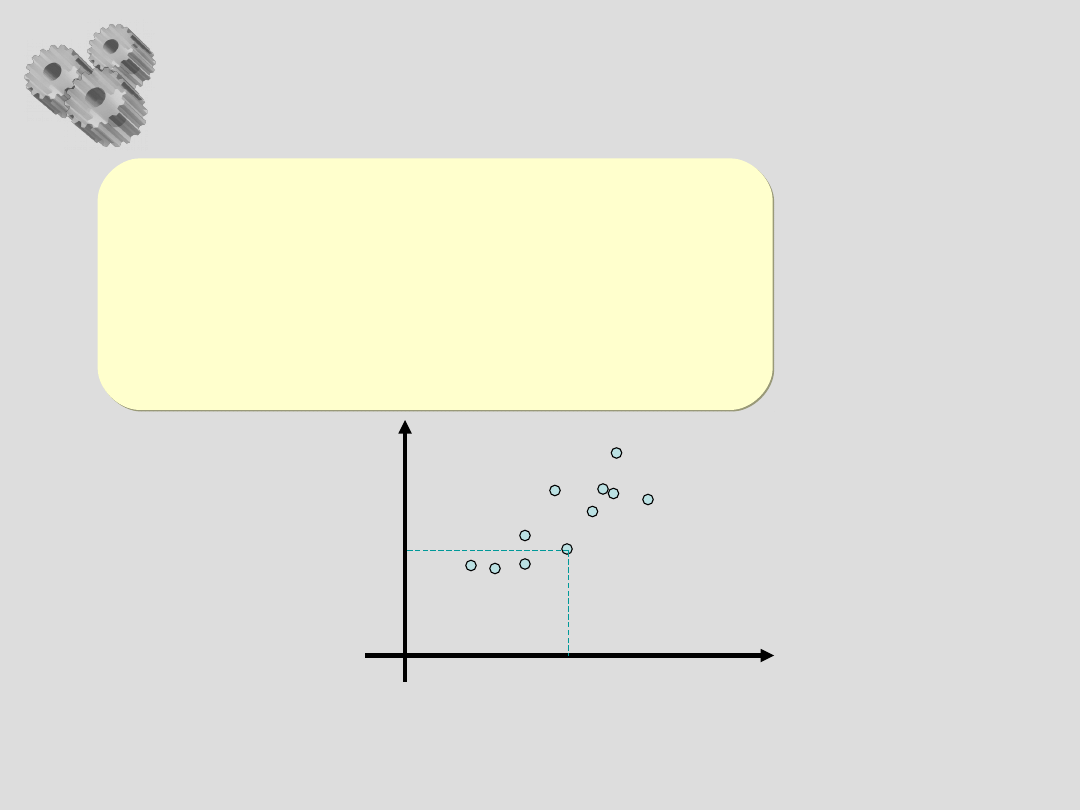
6. Wykres rozrzutu

(scatter diagram)

Co to jest?
Wykres, na którym wartości
jednego czynnika X wykreślane są
w odniesieniu do zbadanych
wartości drugiego Y

Co to jest?
Wykres, na którym wartości
jednego czynnika X wykreślane są
w odniesieniu do zbadanych
wartości drugiego Y

X

Y

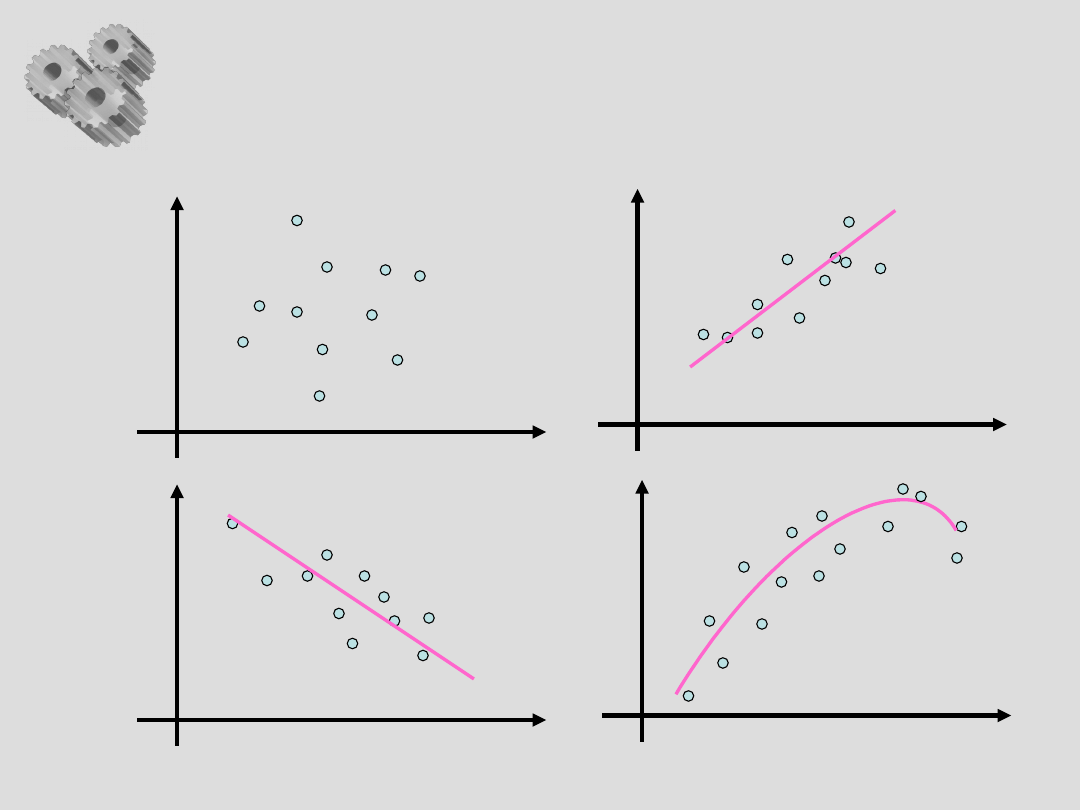
Wykres rozrzutu – c.d.

X

Y

X

Y

X

Y

X

Y

brak

korelacji

r  0

korelacja

dodatnia

0 < r  1

korelacja

ujemna

-1  r < 0

funkcja

nieliniowa

r > 0

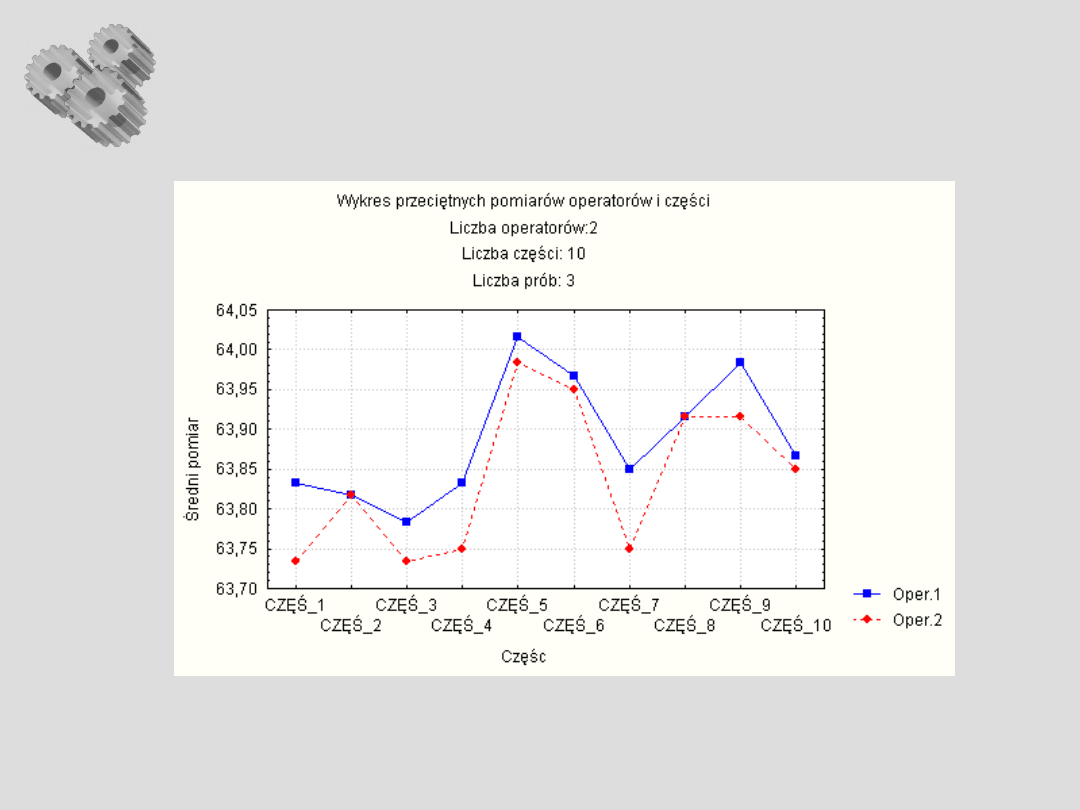
7. Karty kontrolne

(wykresy przebiegu)

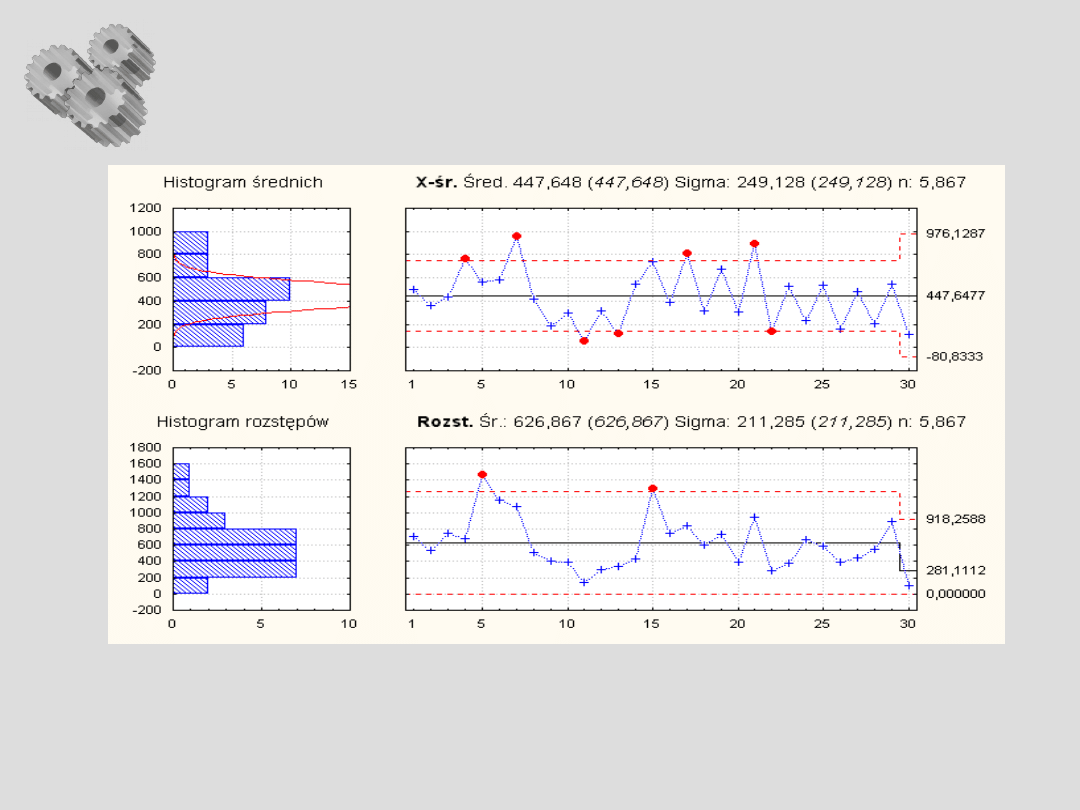
Karty kontrolne (SPC)

Zrozumienie

świadomoś

ć

świadomoś

ć

Narzędzia i metody