
ZPT
1
Dekompozycja polegająca na zastosowaniu
twierdzenia Curtisa jest absolutnie nieprzydatna
w automatycznych obliczeniach komputerowych.
Znacznie skuteczniejsza jest metoda dekompozycji, w
której obliczenia są wykonywane przy pomocy
rachunku podziałów
ZPT
2
V
U
G
H
Y = F(X)
W
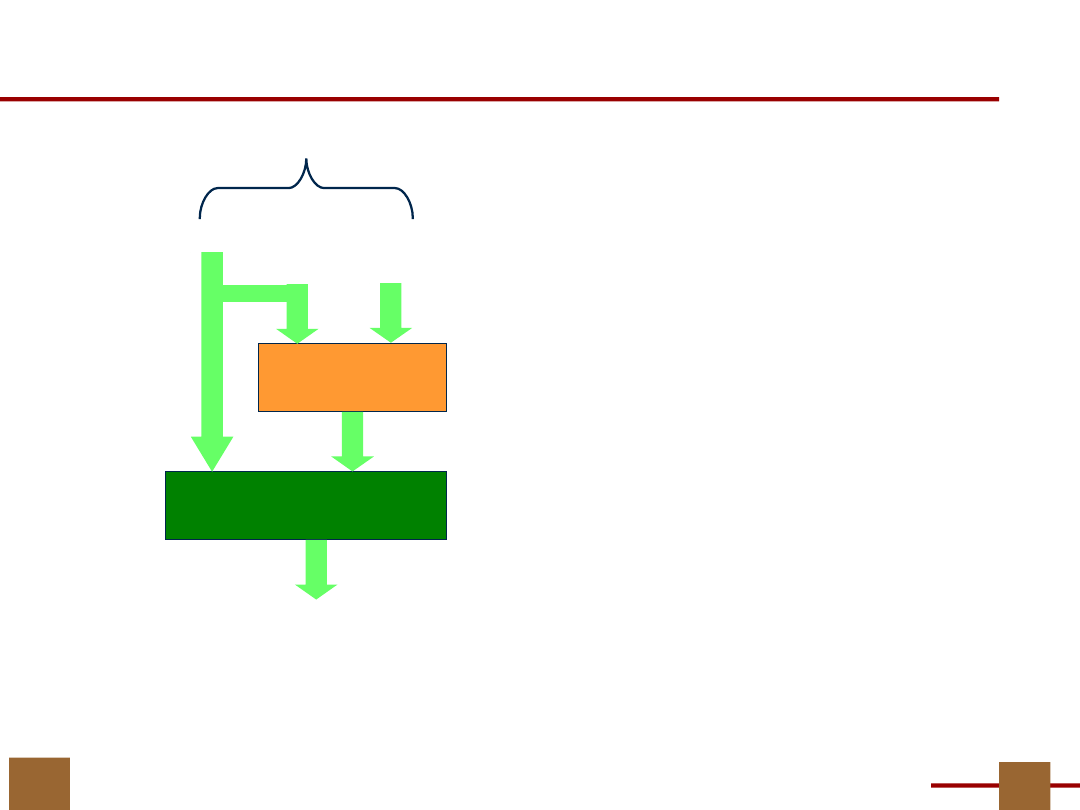
czyli U V X
Nowy model
dekompozycji
X
Ponadto dopuszczamy powiększenie
zbioru argumentów bloku G
U, V są rozłącznymi podzbiorami
X,
ale U V niekoniecznie = X
W jest podzbiorem właściwym U
W U

ZPT
Rachunek podziałów (przypomnienie)
Podziałem na zbiorze S jest system zbiorów P = {
B
i
},
którego bloki są rozłączne, czyli
B
i
B
j
=, jeśli tylko i j.
Dla S = {1,2,3,4,5,6}, P = {{1,2}, {3,5}, {4,6} } jest
podziałem na S.
P =
)
4,6
5;
3,
;
1,2
(
Iloczyn podziałów oraz relacja .

ZPT
Rachunek podziałów (przypomnienie)
Powiemy, że podział P
a
jest nie większy od P
b
(co oznaczamy: P
a
P
b
), jeśli każdy blok z P
a
jest zawarty w pewnym bloku z P
b
.
P
b
=
Iloczynem podziałów P
a
•
P
b
nazywamy największy
(względem relacji ) podział, który jest nie większy od
P
a
oraz P
b
.
)
3,5
;
2,6
;
1,4
(
)
3,5,6
;
1,2,4
(
)
3,5
;
6
;
4
;
1,2
(
P
a
=
P
c
=
P
a
• P
b
=
)
3,5
;
6
;
2
;
1,4
(
P
c
≤ P
a
Tak
P
c
P
b
NIE!

ZPT
4,5
;
2,3,8
;
1,6,7
P
a
(4,5)
;
(3)(2,8)
;
(1)(6,7)
P
|
P
b
a
6,7
;
4,5
;
3
;
2,8
;
1
P
b
Rachunek podziałów (przypomnienie)
Podział ilorazowy
Niech P
a
i P
b
są podziałami na S. Podział P
a
| P
b
jest
podziałem ilorazowym P
a
i P
b
, jeżeli jego elementy są
blokami P
a
·
P
b
,
a bloki są blokami P
a
. Na przykład:
ZPT
6
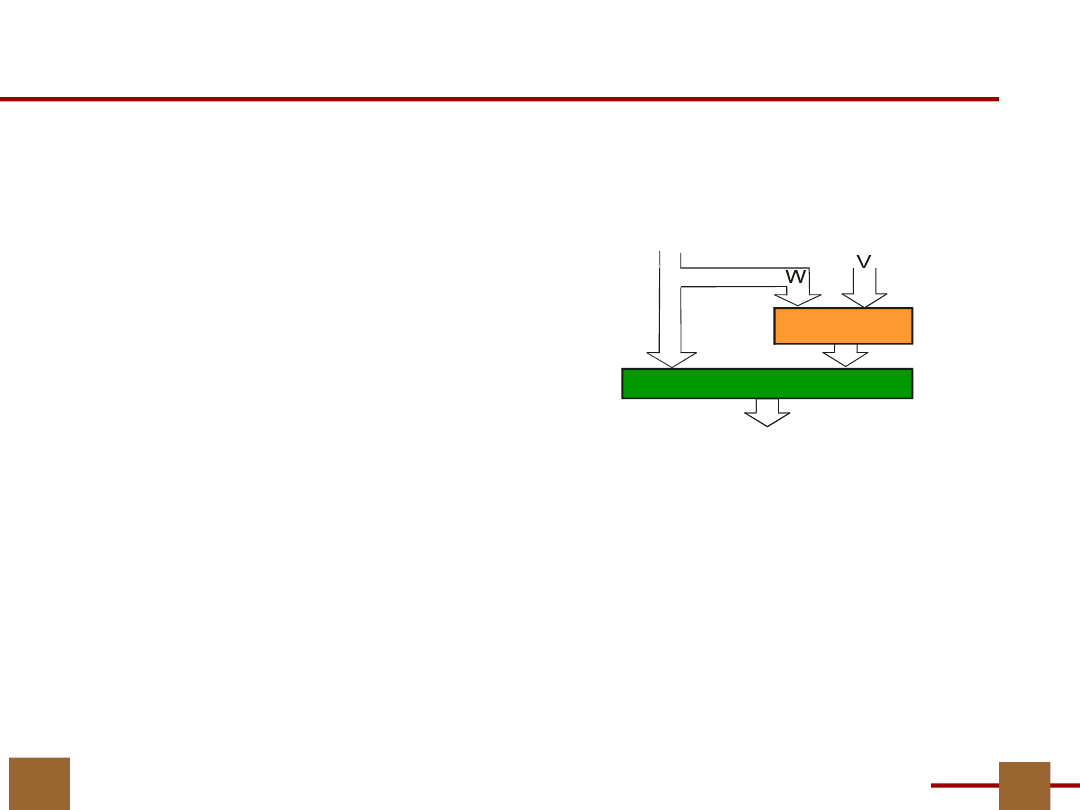
… w ujęciu rachunku podziałów
Funkcję F: B
n
{0,1}
m
można zrealizować w
strukturze:
F = H(U,G(V,W))
Twierdzenie o dekompozycji
U
G
H
G
P
F
wtedy i tylko wtedy, gdy istnieje podział
G
P
VW
taki,
że:
P
U
·
G
P
F
ZPT
7
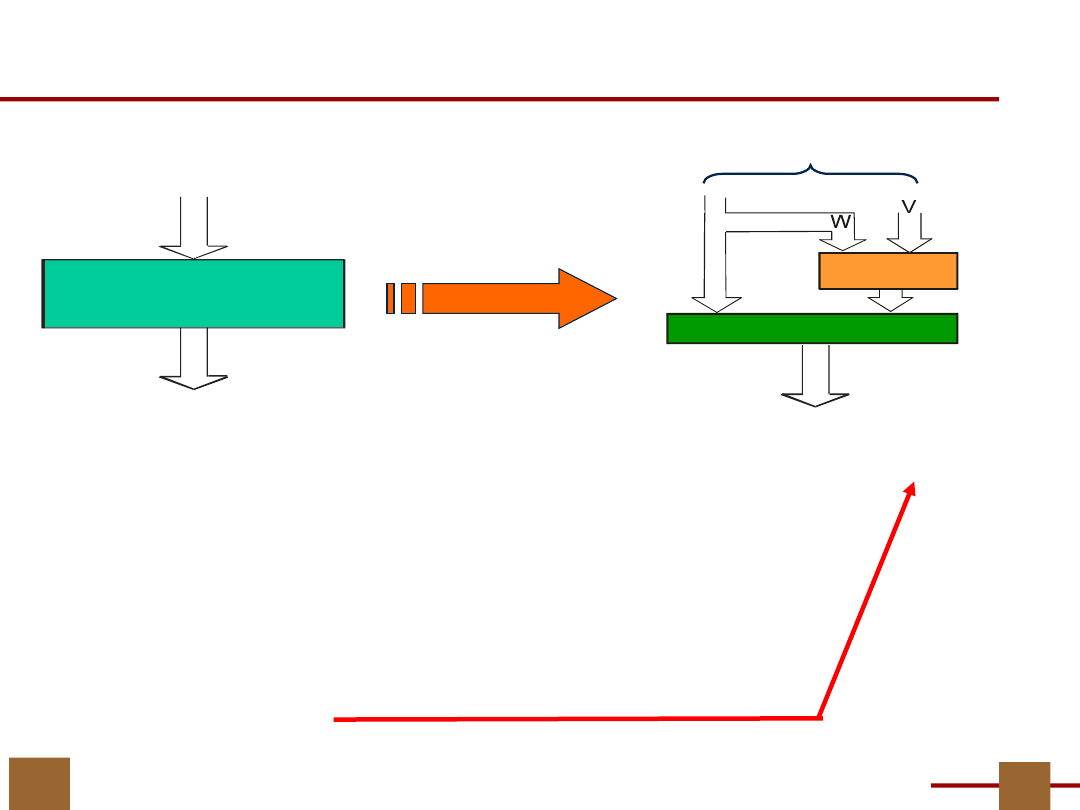
Twierdzenie o dekompozycji -
interpretacja
G
P
VW
taki, że: P
U
·
G
P
F
F
Y = F(X)
X
Y = H(U,G(V,W))
U
G
H
G
X
G
P
U
P
VW
(P
V
)
P
F
to podziały indukowane przez
argumenty zbiorów U, V W,
(V)
Podział wyjściowy funkcji F
Trzeba obliczyć!!!
ZPT
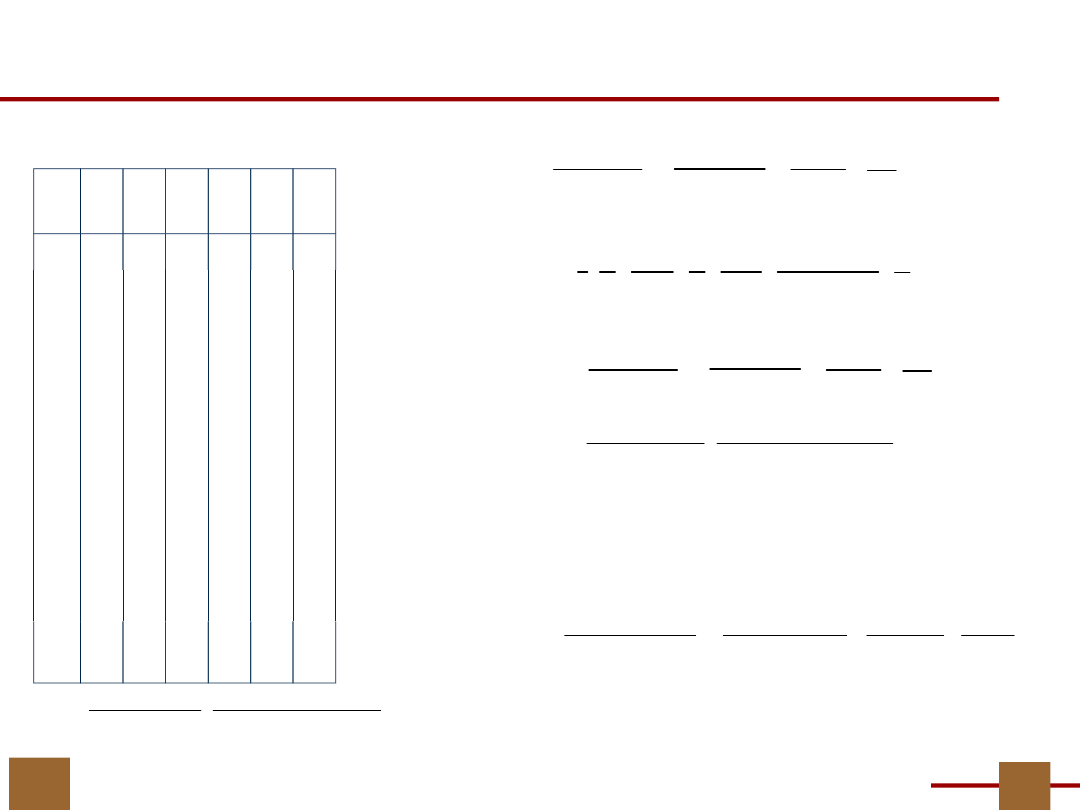
8
Przykład ilustrujący metodę
dekompozycji
Obliczyć dekompozycję
dla U = {x
1
,x
2
}, V =
{x
3
,x
4
,x
5
}
)
,11
6,7,8,9,10
;
1,2,3,4,5
(
P
f
=
Funkcja f:
G
H
x
1
x
2
x
3
f
x
5
x
4
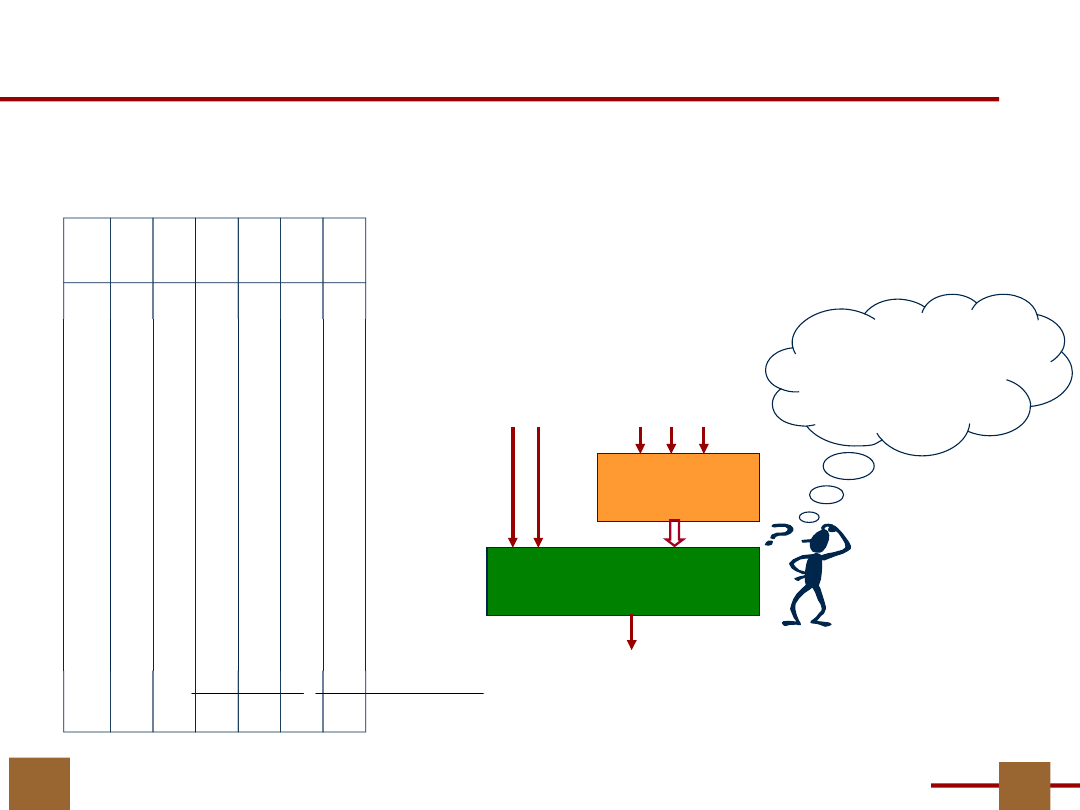
Nie wiemy
ile jest wyjść
z bloku G
x
1
x
2
x
3
x
4
x
5
f
1
0
0
0
0
0
0
2
0
1
0
1
1
0
3
0
0
1
0
1
0
4
0
1
1
1
1
0
5
0
0
1
1
0
0
6
0
1
0
0
1
1
7
0
0
1
0
0
1
8
0
1
1
1
0
1
9
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
1
1
0
0
0
1
1
ZPT
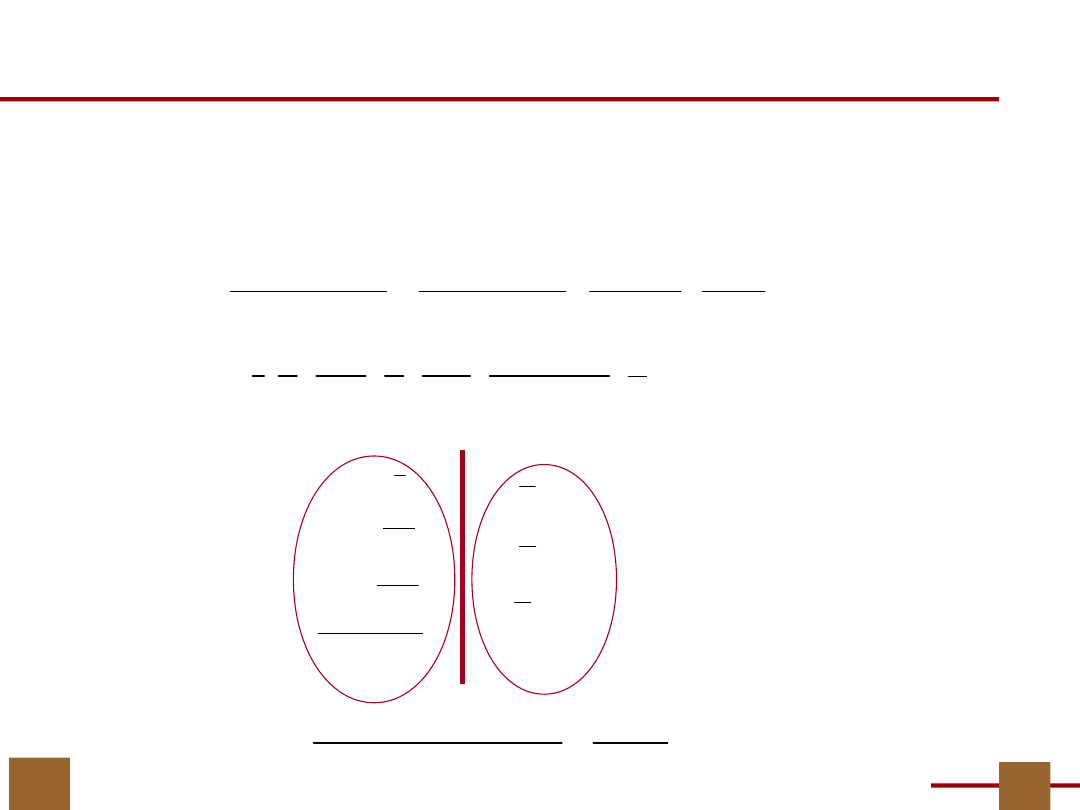
9
Przykład…obliczanie podziałów P
U
,
P
V
)
,11
6,7,8,9,10
;
1,2,3,4,5
(
P
f
=
P
U
|P
U
·
P
f
=
P
U
=
;
1,3,5,7
(
P
V
=
)
7
;
6,10,11
;
5,8
;
4
;
3,9
;
2
;
1
(
U =
{x
1
,x
2
}
Bardzo ważny w dalszych obliczeniach
jest…
;
2,4,6,8
)
10
;
9,11
)
,11
6,7,8,9,10
;
1,2,3,4,5
(
P
f
=
;
(1,3,5)(7)
(
;
(2,4)(6,8)
)
(10)
;
(9,11)
x
1
x
2
x
3
x
4
x
5
f
1
0
0
0
0
0
0
2
0
1
0
1
1
0
3
0
0
1
0
1
0
4
0
1
1
1
1
0
5
0
0
1
1
0
0
6
0
1
0
0
1
1
7
0
0
1
0
0
1
8
0
1
1
1
0
1
9
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
1
1
0
0
0
1
1
P
U
=
;
1,3,5,7
(
;
2,4,6,8
)
10
;
9,11
V = {x
3
,x
4
,
x
5
}
ZPT
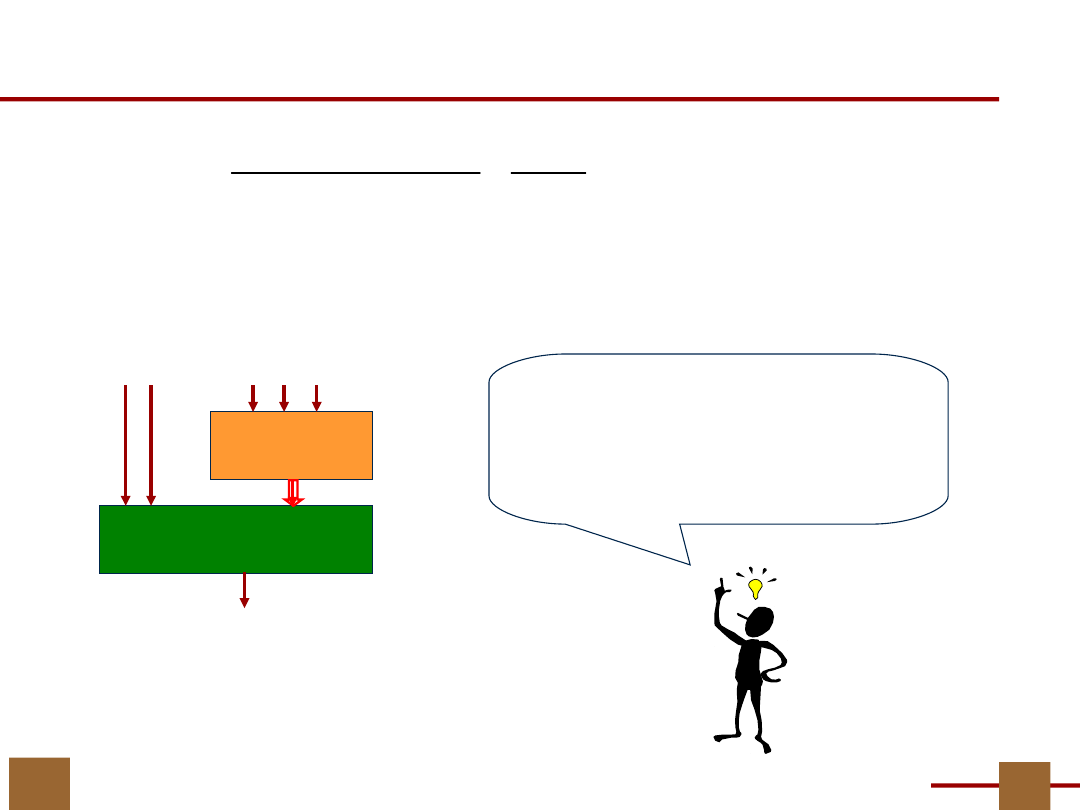
10
Przykład…obliczanie П
G
1
3,9
П
G
=
P
V
=
)
7
;
6,10,11
;
5,8
;
4
;
3,9
;
2
;
1
(
5,8
6,10,11
7
2
4
;
9,10,11
1,3,5,6,8,
(
;
(1,3,5)(7)
(
;
(2,4)(6,8)
)
(10)
;
(9,11)
P
U
|P
U
·
P
f
=
G
P
V
P
U
·
G
P
F
Podział
G
składamy z bloków podziału
P
V
, ale tak aby zapewnić warunki
„rozdziału” zapisane w podziale
P
U
|
P
U
·P
f
G
:
)
2,4,7
ZPT
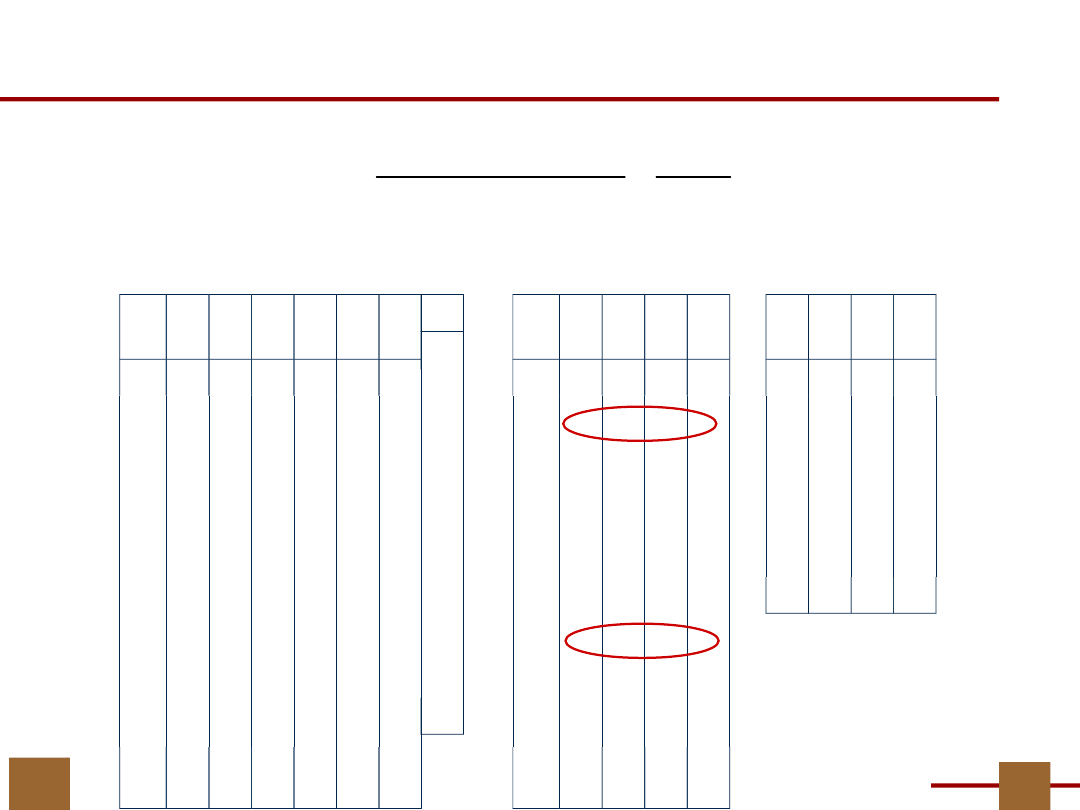
11
Komentarz
H
x
1
x
2
x
3
f
x
5
x
4
П
G
=
;
9,10,11
1,3,5,6,8,
(
)
2,4,7
G
Zatem dopiero teraz wiemy ile jest
wyjść z bloku G.
Tylko jedno wyjście!
Obliczony Π
G
jest
dwublokowy…
ZPT
12
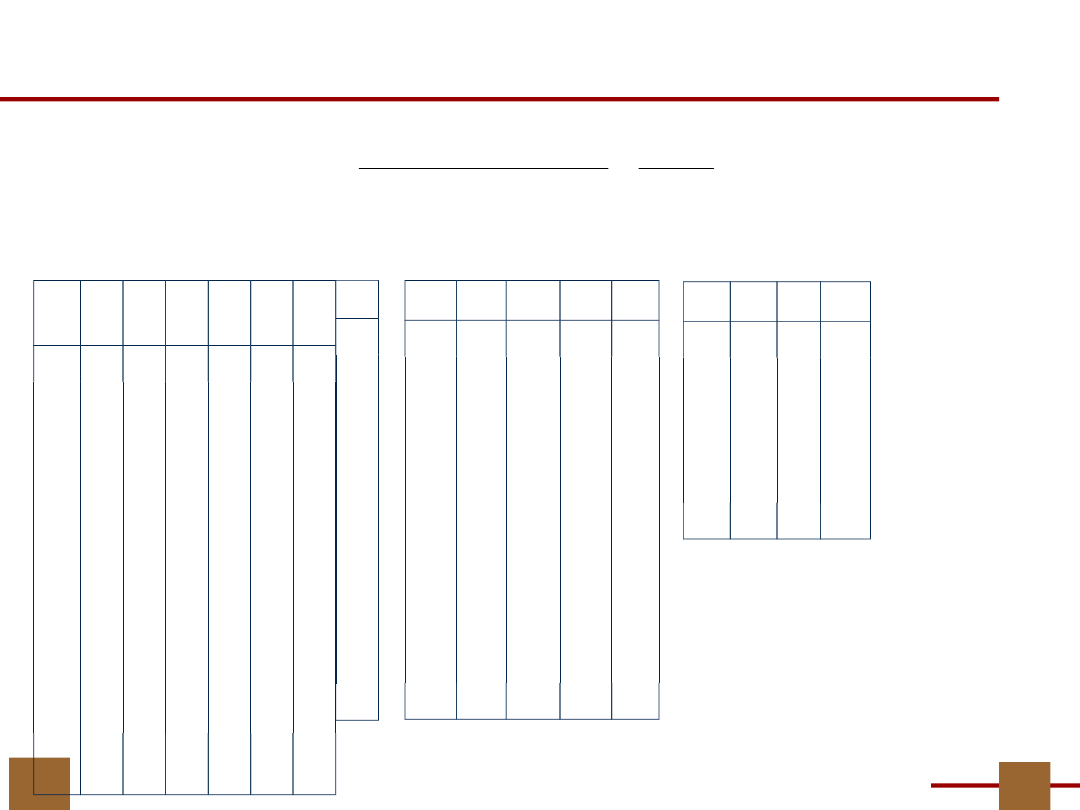
Przykład…tworzenie tablicy funkcji
g
x
1
x
2
x
3
x
4
x
5
f
1
0
0
0
0
0
0
2
0
1
0
1
1
0
3
0
0
1
0
1
0
4
0
1
1
1
1
0
5
0
0
1
1
0
0
6
0
1
0
0
1
1
7
0
0
1
0
0
1
8
0
1
1
1
0
1
9
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
1
1
0
0
0
1
1
x
3
x
4
x
5
g
1
0
0
0
0
2
0
1
1
1
3
1
0
1
0
4
1
1
1
1
5
1
1
0
0
6
0
0
1
0
7
1
0
0
1
8
1
1
0
0
9
1
0
1
0
1
0
0
0
1
0
1
1
0
0
1
0
x
3
x
4
x
5
g
0
0
0
0
0
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
1
0
1
0
0
1
П
G
=
;
9,10,11
1,3,5,6,8,
(
)
2,4,7
g
0
1
0
1
0
0
1
0
0
0
0
ZPT
13
x
1
x
2
x
3
x
4
x
5
f
1
0
0
0
0
0
0
2
0
1
0
1
1
0
3
0
0
1
0
1
0
4
0
1
1
1
1
0
5
0
0
1
1
0
0
6
0
1
0
0
1
1
7
0
0
1
0
0
1
8
0
1
1
1
0
1
9
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
1
1
0
0
0
1
1
x
1
x
2
g
h
1
0
0
0
0
2
0
1
1
0
3
0
0
0
0
4
0
1
1
0
5
0
0
0
0
6
0
1
0
1
7
0
0
1
1
8
0
1
0
1
9
1
0
0
1
10
1
1
0
1
11
1
0
0
1
x
1
x
2
g
h
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
1
0
1
П
G
=
;
9,10,11
1,3,5,6,8,
(
)
2,4,7
g
0
1
0
1
0
0
1
0
0
0
0
Przykład…tworzenie tablicy funkcji
h

ZPT
14
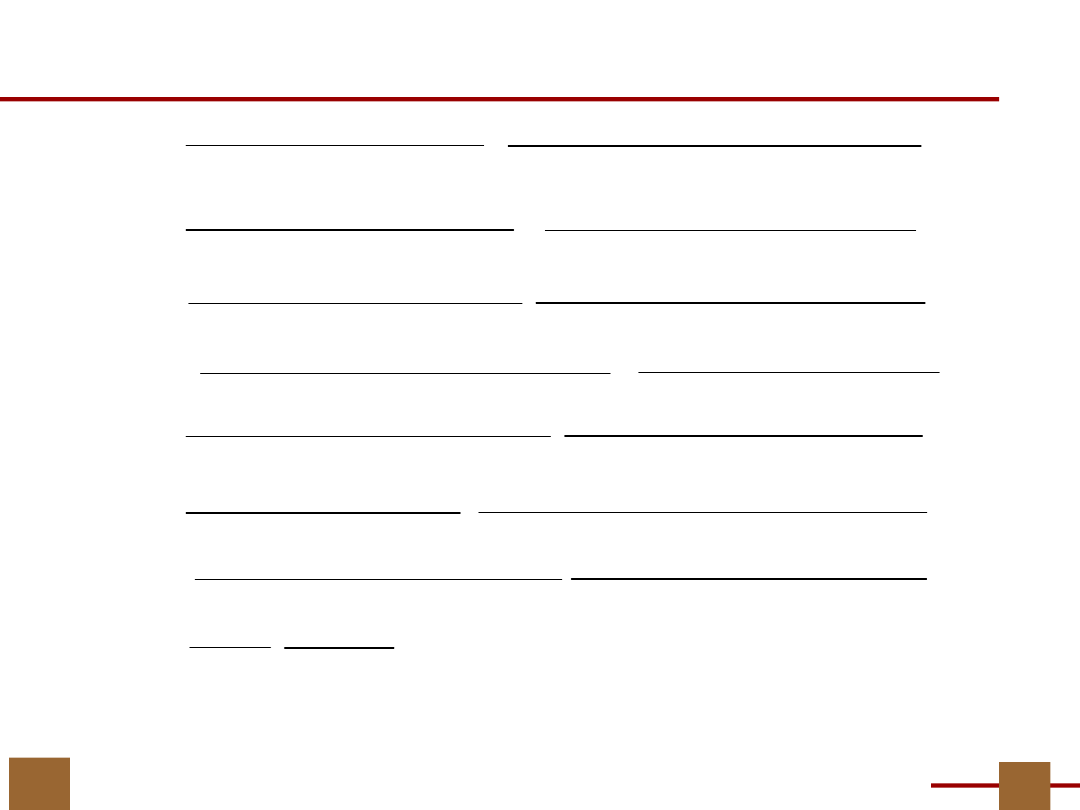
Przykład ilustrujący skuteczność
dekompozycji
.type fr
.i 10
.o 1
.p 25
0010111010
0
1010010100
0
0100011110
0
1011101011
0
1100010011
0
0100010110
0
1110100110
0
0100110000
0
0101000010
0
0111111011
1
0000010100
1
1101110011
1
0100100000
1
0100011111
1
0010000110
1
1111010001
1
1111101001
1
1111111111
1
0010000000
1
1101100111
1
0010001111
1
1111100010
1
1010111101
1
0110000110
1
0100111000
1
.e
Można wykazać, że funkcja ta
jest zależna od
7 argumentów
X = {x
3
, x
5
, x
6
, x
7
, x
8
, x
9
,
x
10
}
Synteza układów logicznych str. 65
Dalej wszystkie obliczenia będą wykonywane na podziałach
P
3
, P
5
, P
6
, P
7
, P
8
, P
9
, P
10
Celem przykładu jest pokazanie, że cały proces
dekompozycji (łącznie z obliczeniem tablic prawdy)
można wykonać wyłącznie na podziałach
Są to podziały na zbiorze ponumerowanych
wektorów 1,…,25
ZPT
15
Specyfikacja funkcji – podziałami
P
3
=
;
25
,
20
,
14
,
13
,
12
,
11
,
9
,
8
,
6
,
5
,
3
{
}
24
,
23
,
22
,
21
,
19
,
18
,
17
,
16
,
15
,
10
,
7
,
4
,
2
,
1
P
5
=
;
24
,
21
,
19
,
16
,
15
,
14
,
11
,
9
,
6
,
5
,
3
,
2
{
}
25
,
23
,
22
,
20
,
18
,
17
,
13
,
12
,
10
,
8
,
7
,
4
,
1
P
6
=
;
24
,
22
,
21
,
20
,
19
,
17
,
15
,
13
,
9
,
7
,
4
{
}
25
,
23
,
18
,
16
,
14
,
12
,
11
,
10
,
8
,
6
,
5
,
3
,
2
,
1
P
f
=
;
9
,...,
2
,
1
{
}
25
,...,
10
P
7
=
;
24
,
22
,
20
,
19
,
16
,
15
,
13
,
12
,
11
,
9
,
8
,
7
,
6
,
5
,
2
{
}
25
,
23
,
21
,
18
,
17
,
14
,
10
,
4
,
3
,
1
P
8
=
;
25
,
22
,
19
,
17
,
16
,
13
,
12
,
10
,
9
,
8
,
5
,
4
,
1
{
}
24
,
23
,
21
,
20
,
18
,
15
,
14
,
11
,
7
,
6
,
3
,
2
P
9
=
;
25
,
23
,
19
,
17
,
16
,
13
,
11
,
8
,
2
{
}
24
,
22
,
21
,
20
,
18
,
15
,
14
,
12
,
10
,
9
,
7
,
6
,
5
,
4
,
3
,
1
P
10
=
;
25
,
24
,
22
,
19
,
15
,
13
,
11
,
9
,
8
,
7
,
6
,
3
,
2
,
1
{
}
23
,
21
,
20
,
18
,
17
,
16
,
14
,
12
,
10
,
5
,
4
ZPT
16
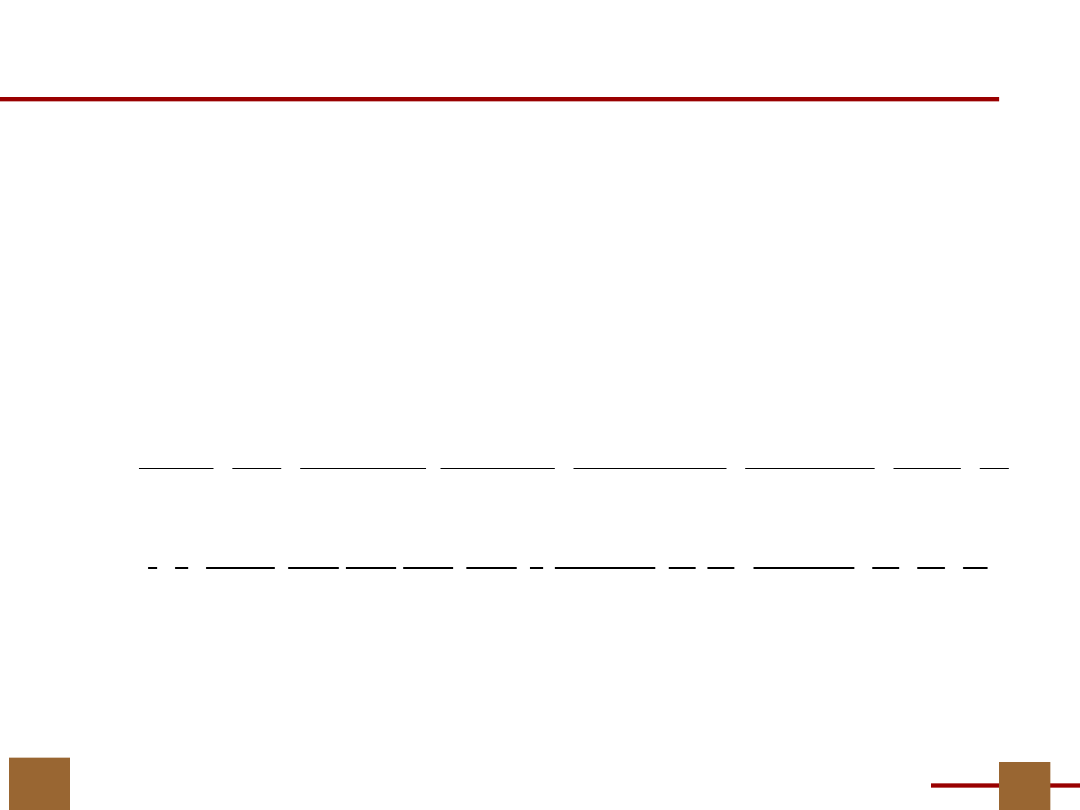
Ustalenie zbiorów U i V
X = {x
3
, x
5
, x
6
, x
7
, x
8
, x
9
,
x
10
}
Ile wyjść z bloku G???
U = {x
7
, x
8
,
x
9
}
V = {x
3
, x
5
, x
6
,
x
10
}
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
Przyjmujemy
arbitralnie…
ZPT
17
Obliczenie podziałów P
U
, P
V
)
23
;
17,25
;
8,13,16,19
;
24
6,7,15,20,
;
5,9,12,22
;
3,14,18,21
;
2,11
;
1,4,10
(
P
V
=
)
21
;
20
;
16
;
15,19,24
;
13
;
12
;
10,18,23
;
9
;
8,25
;
7,22
;
5,14
;
4,17
;
3,6,11
;
2
;
1
(
P
U
=
P
U
=P
7
•P
8
•P
9
P
V
=P
3
•P
5
•P
6
•P
10
Można je wyznaczyć bezpośrednio z tablicy
funkcji, ale tym razem przy zastosowaniu
rachunku podziałów:

ZPT
18
)
23
;
17,25
;
8,13,16,19
;
24
6,7,15,20,
;
5,9,12,22
;
3,14,18,21
;
2,11
;
1,4,10
(
((1,4)
(10)
P
U
=
P
f
=
;
1,2,...,9
{
10,...,25}
Podział ilorazowy
P
u
|P
u
•
P
F
; (2)
(11)
(6,7)(15,20,24) ; (8)(13,16,19) ;
(17,25) ; (23))
; (3)
(14,18,21)
; (5,9)
(12,22)
P
u
|P
u
•
P
f
=
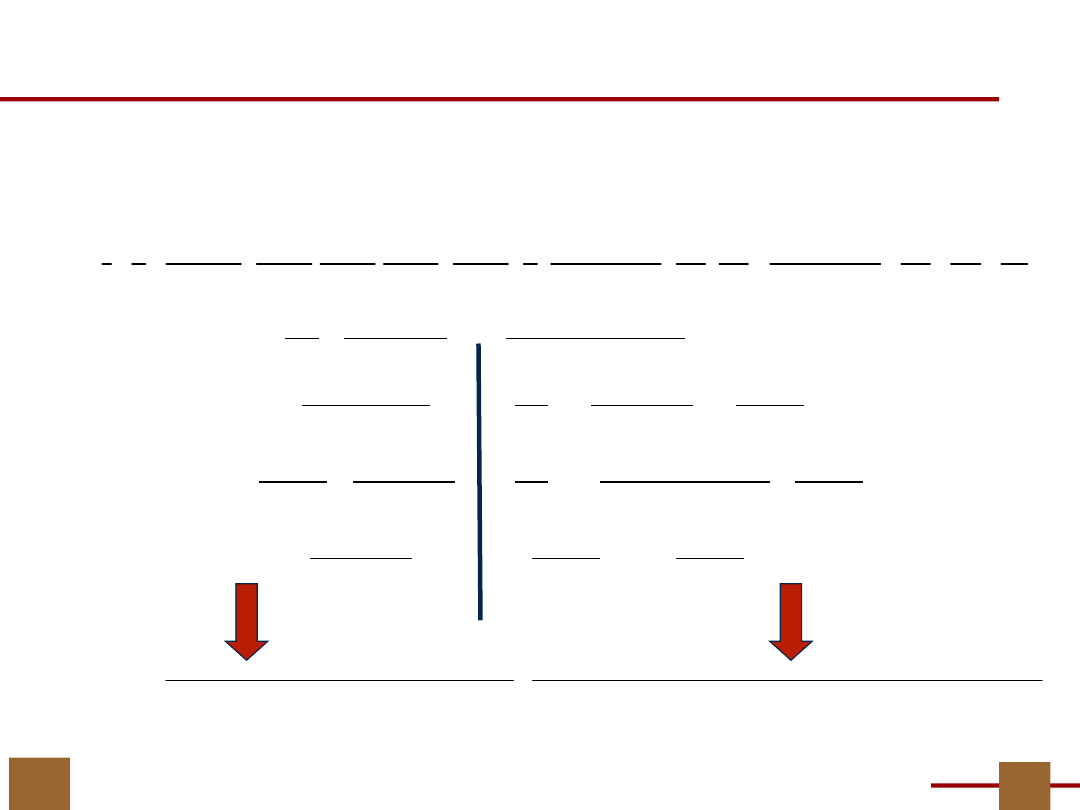
Przy liczeniu podziału ilorazowego po prostu
rozdzielamy elementy bloków P
U
między różne bloki
podziału P
f
W każdym bloku P
u
|P
u
• P
f
są co najwyżej dwa elementy
(nawiasy), zatem liczba bloków podziału Π
G
musi być co
najmniej dwa.
ZPT
19
Obliczenie Π
G
)
24
23,
21,
20,
19,
18,
4,15,16,
13,1
10,
2,5,9,
;
25
22,
17,
11,12,
7,8,
6,
1,3,4,
(
Π
g
P
u
|P
u
· P
f
= ((1,4)(10) ; (2)(11) ; (3)(14,18,21) ; (5,9)(12,22) ;
(6,7)(15,20,24) ; (8)(13,16,19) ; (17,25) ; (23))
P
V
=
)
21
;
20
;
16
;
15,19,24
;
13
;
12
;
10,18,23
;
9
;
8,25
;
7,22
;
5,14
;
4,17
;
3,6,11
;
2
;
1
(
4,1
7
1
10,18,2
3
3,6,1
1
2
5,1
4
1
2
7,2
2
8,2
5
9
15,19,
24
2
0
1
3
1
6
2
1
ZPT
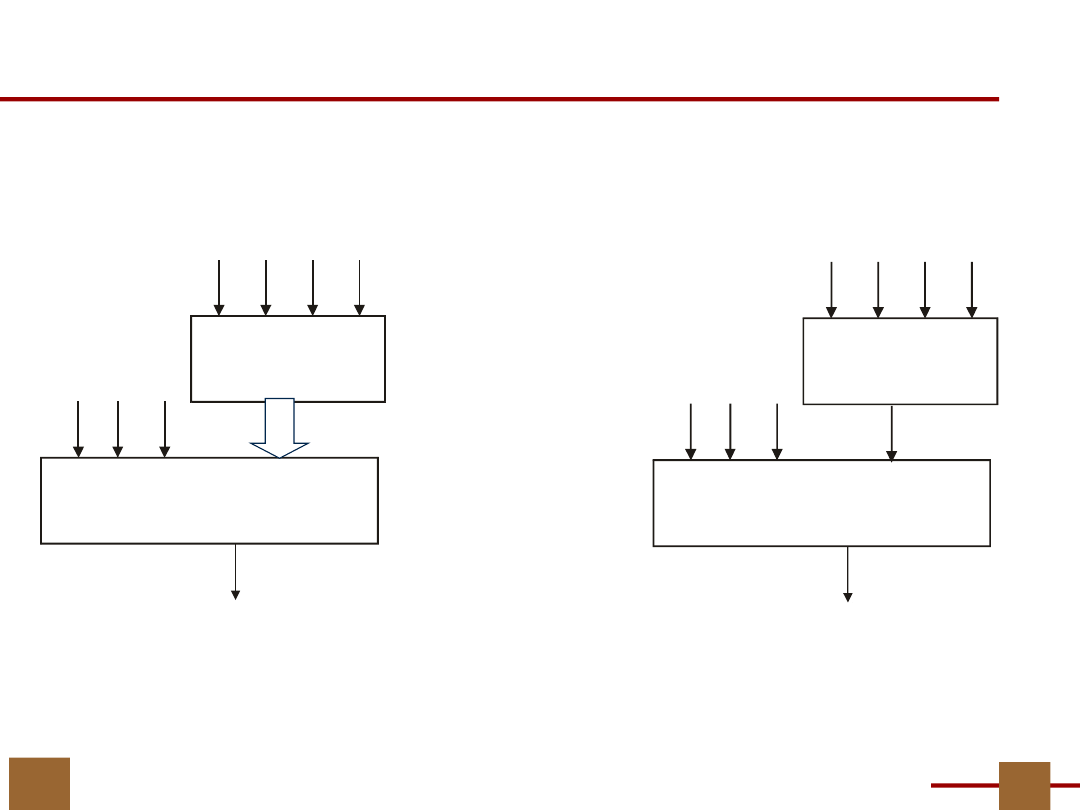
20
Liczba wyjść bloku G
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
1 0
Liczba wyjść z bloku G = 1
Skoro Π
G
jest
dwublokowy
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
ZPT
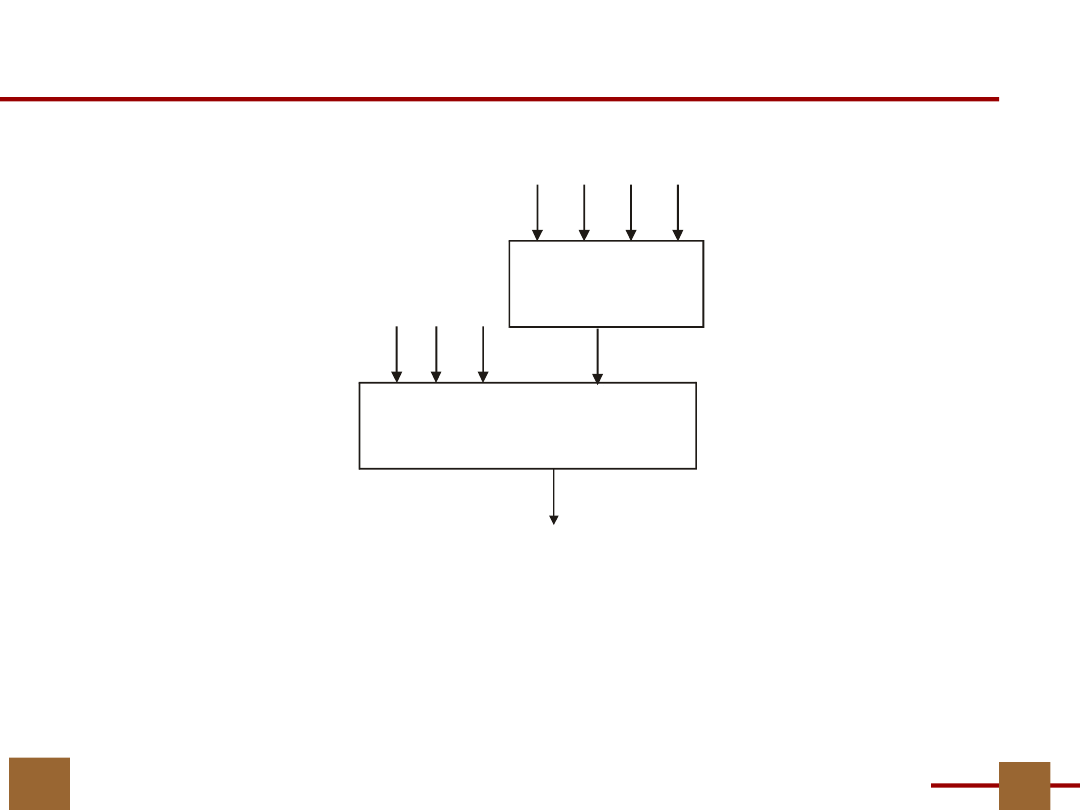
21
Co dalej …
Zawartość bloków G i H, czyli tablice
prawdy funkcji G i H
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
10
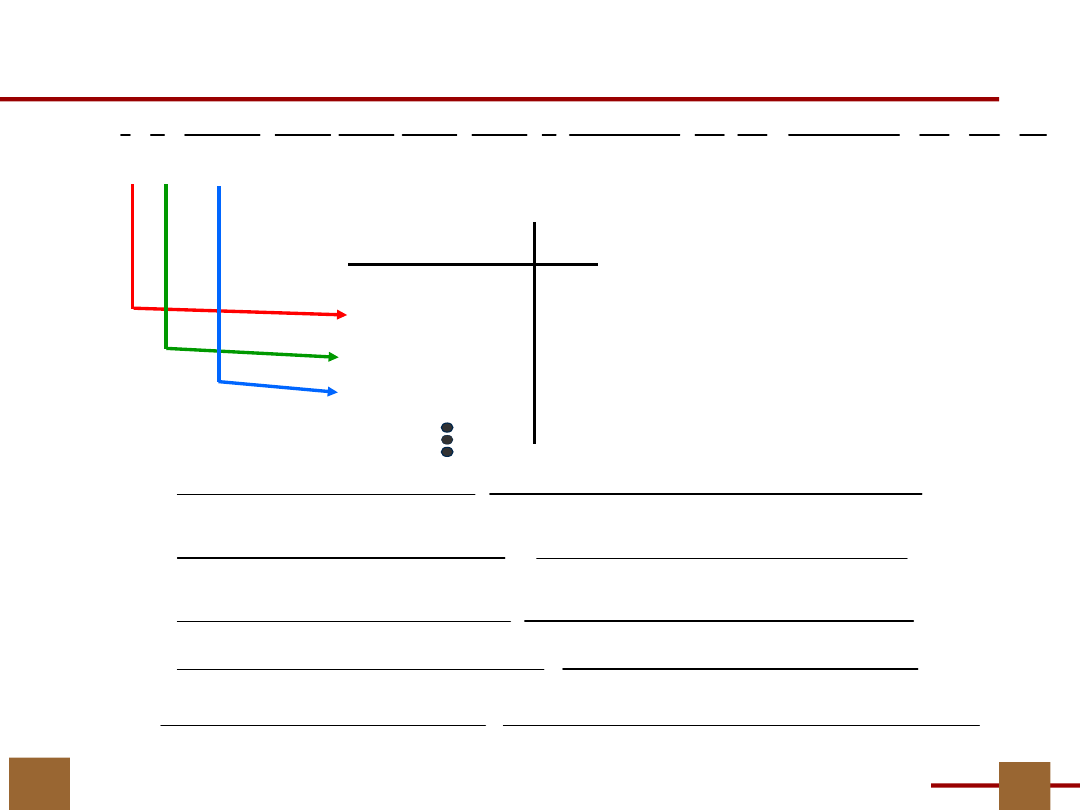
ZPT
22
Funkcja G
x
3
x
5
x
6
x
10
g
P
V
=
)
21
;
20
;
16
;
15,19,24
;
13
;
12
;
10,18,23
;
9
;
8,25
;
7,22
;
5,14
;
4,17
;
3,6,11
;
2
;
1
(
1 1 1
0
0
1 0 1
0
1
0 0 1
0
0
)
24
23,
21,
20,
19,
18,
4,15,16,
13,1
10,
2,5,9,
;
25
22,
17,
11,12,
7,8,
6,
1,3,4,
(
Π
g
P
3
=
;
25
,
20
,
14
,
13
,
12
,
11
,
9
,
8
,
6
,
5
,
3
{
}
24
,
23
,
22
,
21
,
19
,
18
,
17
,
16
,
15
.
10
,
7
,
4
,
2
,
1
P
5
=
;
24
,
21
,
19
,
16
,
15
,
14
,
11
,
9
,
6
,
5
,
3
,
2
{
}
25
,
23
,
22
,
20
,
18
,
17
,
13
,
12
,
10
,
8
,
7
,
4
,
1
P
6
=
;
24
,
22
,
21
,
20
,
19
,
17
,
15
,
13
,
9
,
7
,
4
{
}
25
,
23
,
18
,
16
,
14
,
12
,
11
,
10
,
8
,
6
,
5
,
3
,
2
,
1
P
10
=
;
25
,
24
,
22
,
19
,
15
,
13
,
11
,
9
,
8
,
7
,
6
,
3
,
2
,
1
{
}
23
,
21
,
20
,
18
,
17
,
16
,
14
,
12
,
10
,
5
,
4
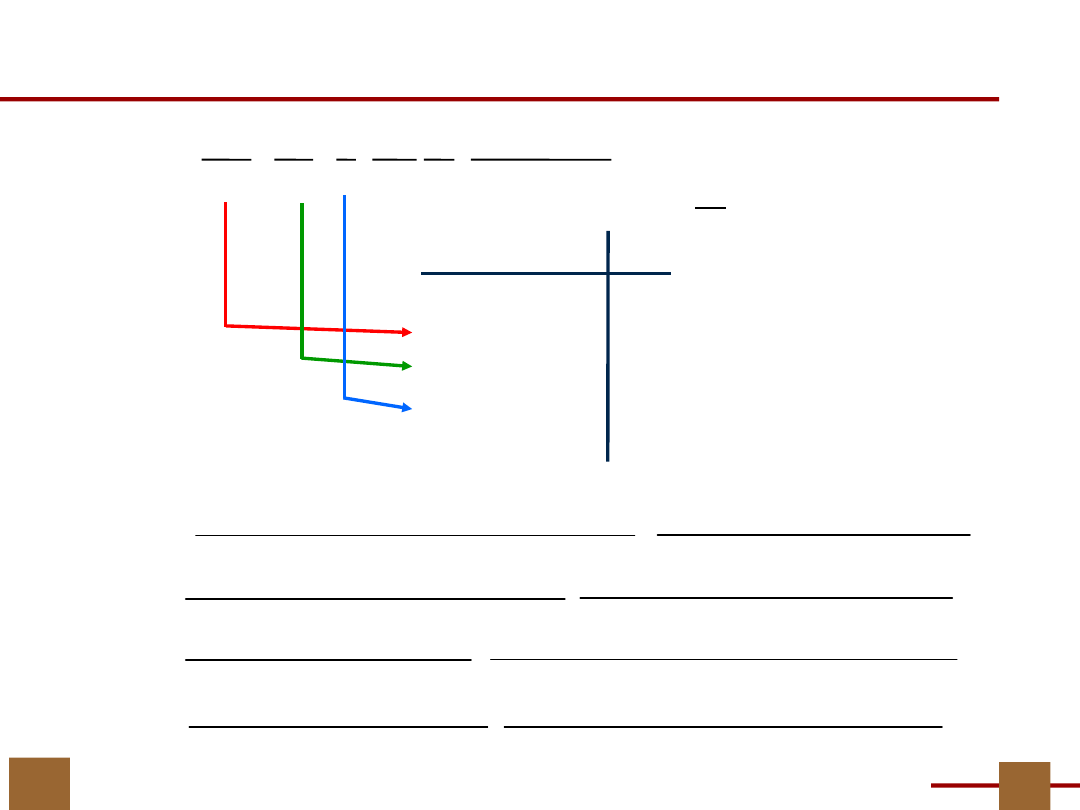
Wektory (wiersze) tablicy funkcji g
są wyznaczane przez bloki P
V
,
a wartości tej funkcji przez bloki Π
G
ZPT
23
Funkcja H
x
7
x
8
x
9
g
h
...)
14,18,21
;
3
;
11
;
2
;
10
;
1,4
(
P
U
G
< P
F
1 0 1
0
0
1 0 1
1
1
0 1 0
1
0
…
P
7
=
;
24
,
22
,
20
,
19
,
16
,
15
,
13
,
12
,
11
,
9
,
8
,
7
,
6
,
5
,
2
{
}
25
,
23
,
21
,
18
,
17
,
14
,
10
,
4
,
3
,
1
P
8
=
;
25
,
22
,
19
,
17
,
16
,
13
,
12
,
10
,
9
,
8
,
5
,
4
,
1
{
}
24
,
23
,
21
,
20
,
18
,
15
,
14
,
11
,
7
,
6
,
3
,
2
P
9
=
;
25
,
23
,
19
,
17
,
16
,
13
,
11
,
8
,
2
{
}
24
,
22
,
21
,
20
,
18
,
15
,
14
,
12
,
10
,
9
,
7
,
6
,
5
,
4
,
3
,
1
)
24
23,
21,
20,
19,
18,
4,15,16,
13,1
10,
2,5,9,
;
25
22,
17,
11,12,
7,8,
6,
1,3,4,
(
Π
g
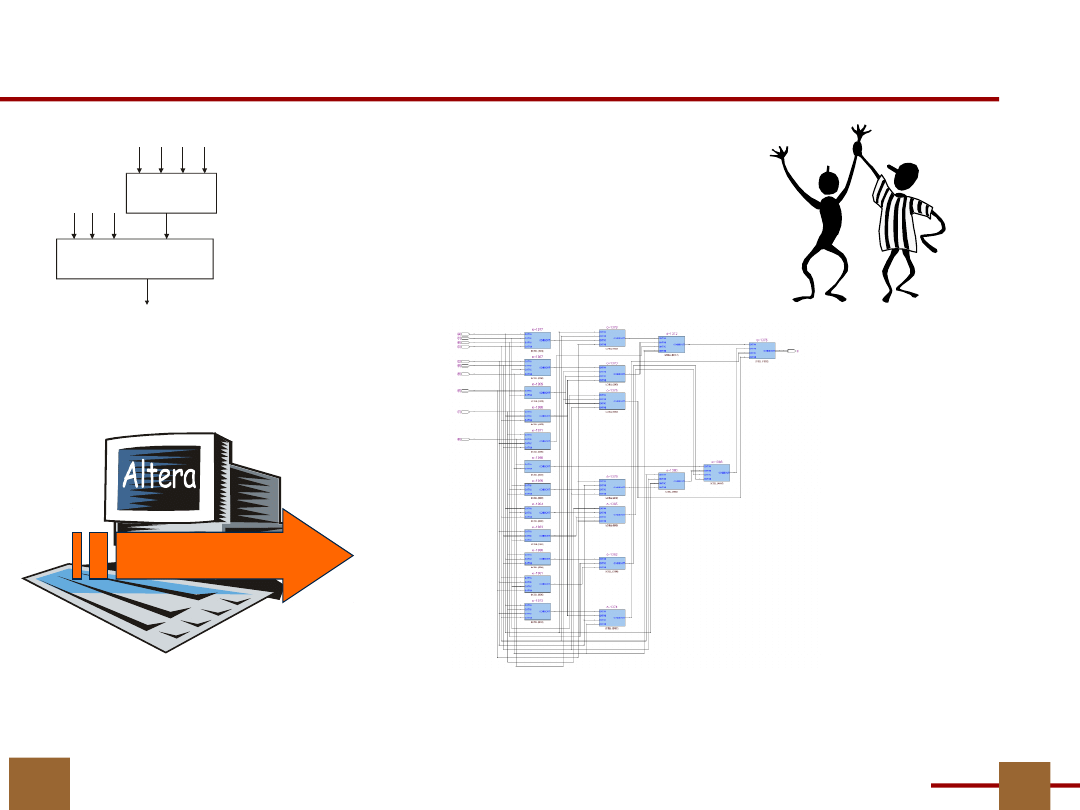
Wektory (wiersze) tablicy
funkcji h są wyznaczane
przez bloki P
U
G
, a wartości
tej funkcji przez bloki P
F
ZPT
24
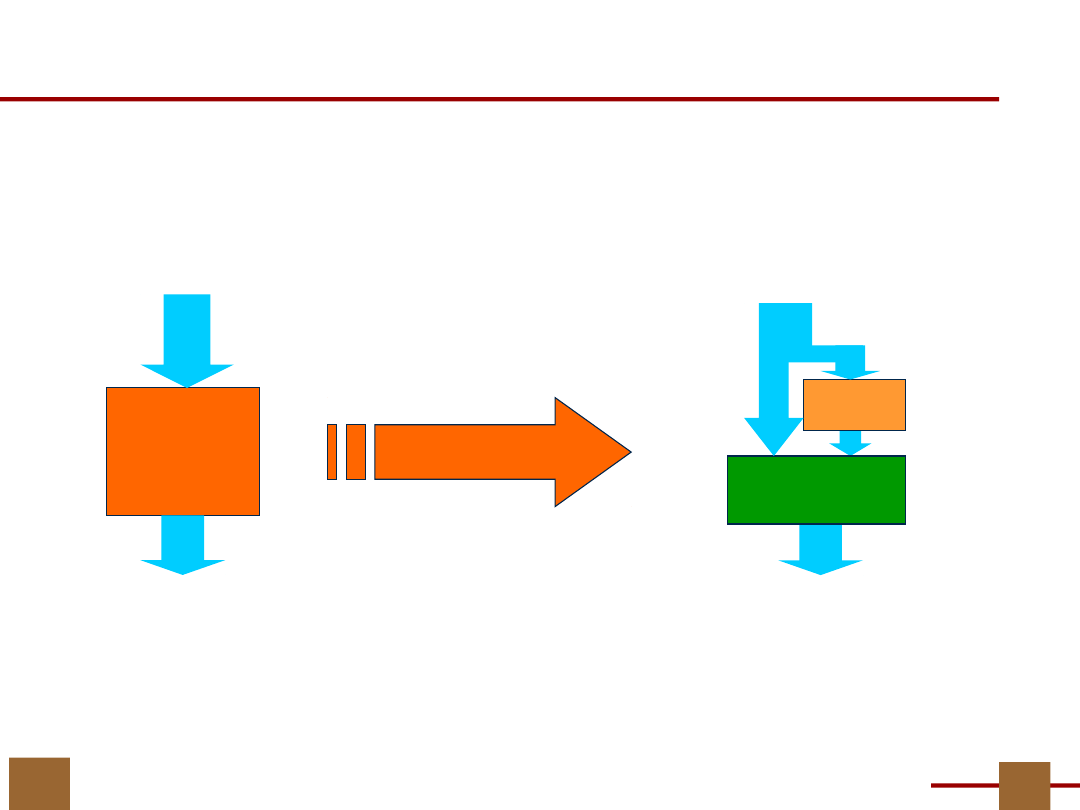
Co uzyskaliśmy…
f
G
H
x
7
x
8
x
9
x
3
x
5
x
6
x
1 0
Tylko 2 komórki
typowej struktury
FPGA
QUARTU
S
Uzyskaliśmy wynik dziesięciokrotnie razy
lepszy od wyniku systemu Quartus
amerykańskiej firmy Altera
23 kom.
ZPT
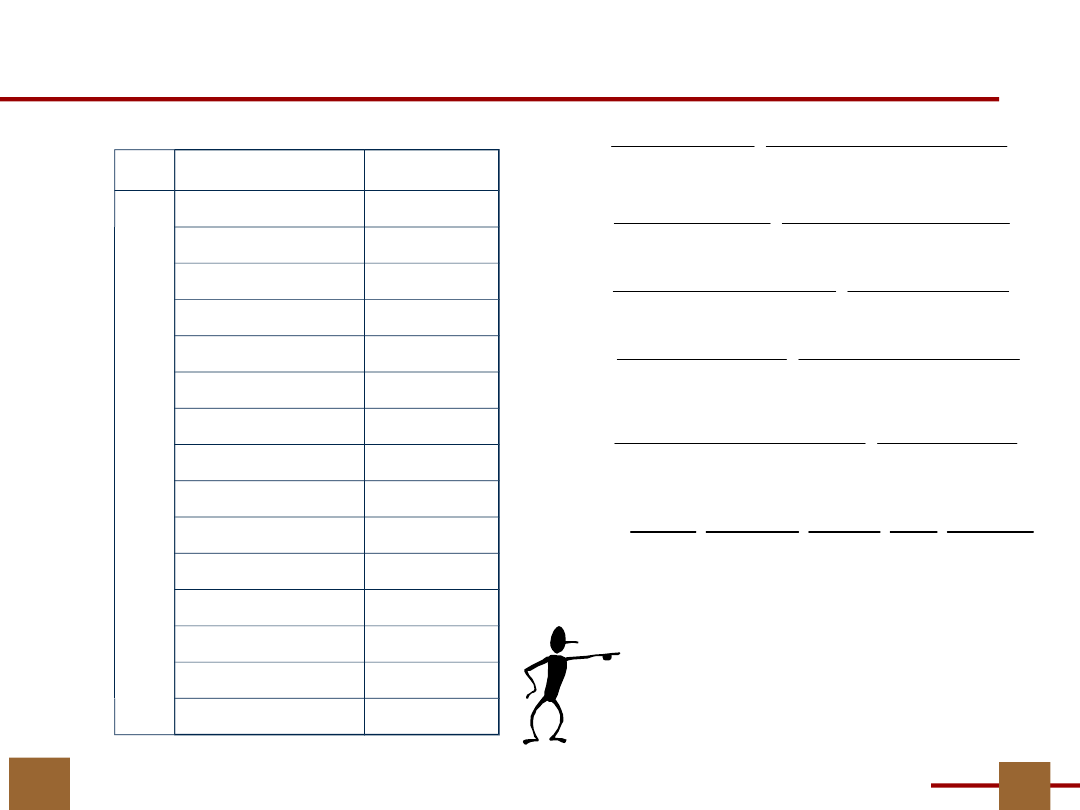
25
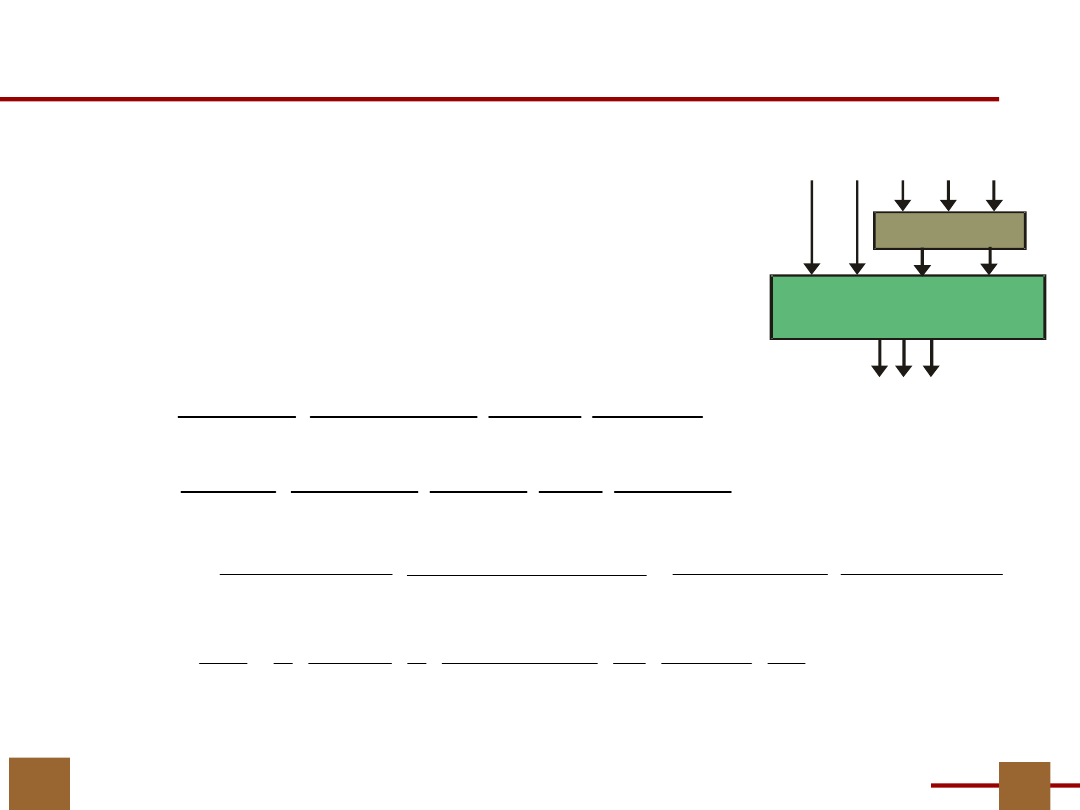
Dekompozycja zespołu funkcji
X
F
X
G
H
Y
U
V
Y = y
1
, y
2
,…, y
m
Twierdzenie w ujęciu rachunku podziałów jest ogólne,
obliczenia są niezależne od liczby wyjść funkcji F.
Dekompozycj
a
ZPT
26
x
1
x
2
x
3
x
4
x
5
y
1
y
2
y
3
1
0 0 0 0 0
0 0 0
2
0 0 0 1 1
0 1 0
3
0 0 0 1 0
1 0 0
4
0 1 1 0 0
0 1 1
5
0 1 1 0 1
0 0 1
6
0 1 1 1 0
0 1 0
7
0 1 0 0 0
0 0 1
8
1 1 0 0 0
0 0 1
9
1 1 0 1 0
0 0 0
10
1 1 1 0 0
1 0 0
11
1 1 1 1 1
0 1 1
12
1 1 1 1 0
0 1 0
13
1 0 0 0 1
0 0 1
14
1 0 0 1 1
0 0 0
15
1 0 0 1 0
1 0 0
)
15
,
14
,
13
,
12
,
11
,
10
,
9
,
8
;
7
,
6
,
5
,
4
,
3
,
2
,
1
(
1
P
)
15
,
10
,
3
;
11
,
4
;
12
,
6
,
2
;
13
,
8
,
7
,
5
;
14
,
9
,
1
(
F
P
Przykład dekompozycji zespołu funkcji (SUL
Przykład 8.4)
)
12
,
11
,
10
,
9
,
8
,
7
,
6
,
5
,
4
;
15
,
14
,
13
,
3
,
2
,
1
(
2
P
)
12
,
11
,
10
,
6
,
5
,
4
;
15
,
14
,
13
,
9
,
8
,
7
,
3
,
2
,
1
(
3
P
)
15
,
14
,
12
,
11
,
9
,
6
,
3
,
2
;
13
,
10
,
8
,
7
,
5
,
4
,
1
(
4
P
)
14
,
13
,
11
,
5
,
2
;
15
,
12
,
10
,
9
,
8
,
7
,
6
,
4
,
3
,
1
(
5
P
Niezależnie od
liczby
funkcji wszystkie
wyjścia opisujemy
jednym! podziałem
ZPT
27
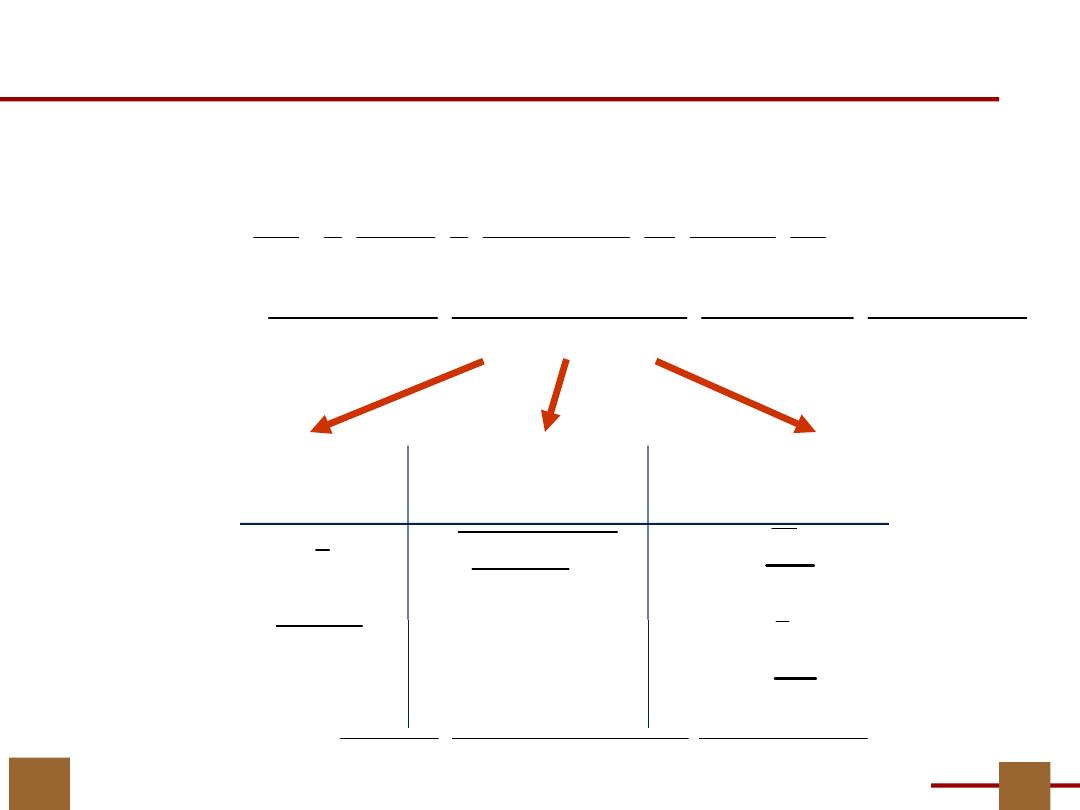
Przykład…wyznaczanie podziałów
P
U
,
P
V
U = {x
3
,x
4
} V = {x
1
,x
2
,x
5
}
6,11,12
;
4,5,10
;
5
2,3,9,14,1
;
1,7,8,13
P
U
3,10,15
;
4,11
;
2,6,12
;
5,7,8,13
;
1,9,14
P
F
;
)
(1)(7,8,13
P
U
= P
3
•
P
4
P
V
=P
1
•
P
2
•
P
5
F
U
U
P
P
|
P
;
3,15)
(2)(9,14)(
(11)(6,12)
;
(4)(5)(10)
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
x
3
x
4
x
1
x
2
x
5
g
h
•
•
•
Szukamy dekompozycji
ZPT
28
Przykład…obliczanie
G
(2)
(9,14)
(3,15)
2
12
,
10
,
9
,
8
14
,
13
3
,
1
15
7
,
6
,
4
5
11
5
1,3,5,11,1
;
13,14
8,9,10,12,
;
2,4,6,7
Π
G
(11)(6,12)
;
(4)(5)(10)
;
3,15)
(2)(9,14)(
;
)
(1)(7,8,13
P
|
P
F
U
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
Jak wyznaczyć
G
???

ZPT
29
Przykład…kodowanie
Π
G
5
1,3,5,11,1
;
;
13,14
8,9,10,12,
2,4,6,7
G
Należy zakodować bloki Π
G
01
10
00
Kodowanie jest dowolne
Aktualna teoria nie podaje rozwiązania
problemu kodowania
W przypadku zespołu funkcji liczba bloków podziału Π
G
jest większa.
Kodowanie jest potrzebne do wyznaczenia tablic prawdy funkcji G i H

ZPT
30
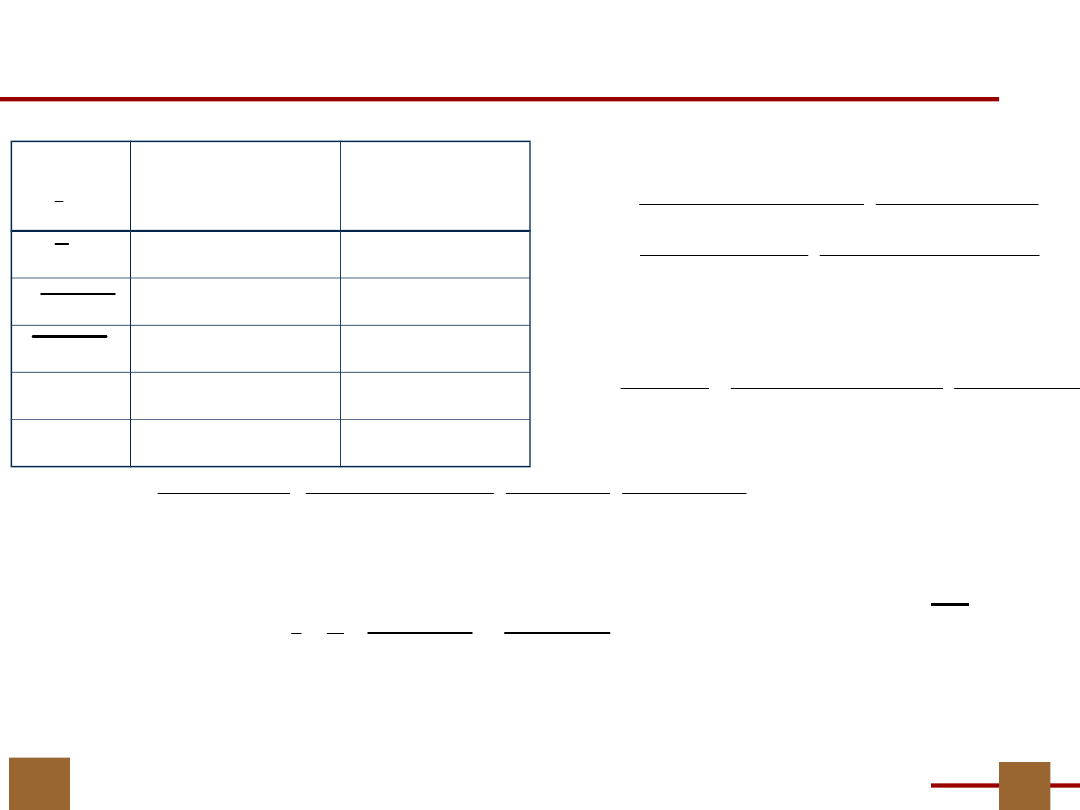
Tablica prawdy G
)
14
,
13
,
11
,
5
,
2
;
15
,
12
,
10
,
9
,
8
,
7
,
6
,
4
,
3
,
1
(
)
12
,
11
,
10
,
9
,
8
,
7
,
6
,
5
,
4
;
15
,
14
,
13
,
3
,
2
,
1
(
)
15
,
14
,
13
,
12
,
11
,
10
,
9
,
8
;
7
,
6
,
5
,
4
,
3
,
2
,
1
(
5
2
1
P
P
P
x
1
x
2
x
5
g
1
g
2
. . .
. . .
3
,
1
2
7
,
6
,
4
5
1,3,5,11,1
;
;
13,14
8,9,10,12,
2,4,6,7
G
01
10
00
0 0 0
0 0 1
0 1 0
0
0
0
1
0
1
5
0 1 1
0
0
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
ZPT
31
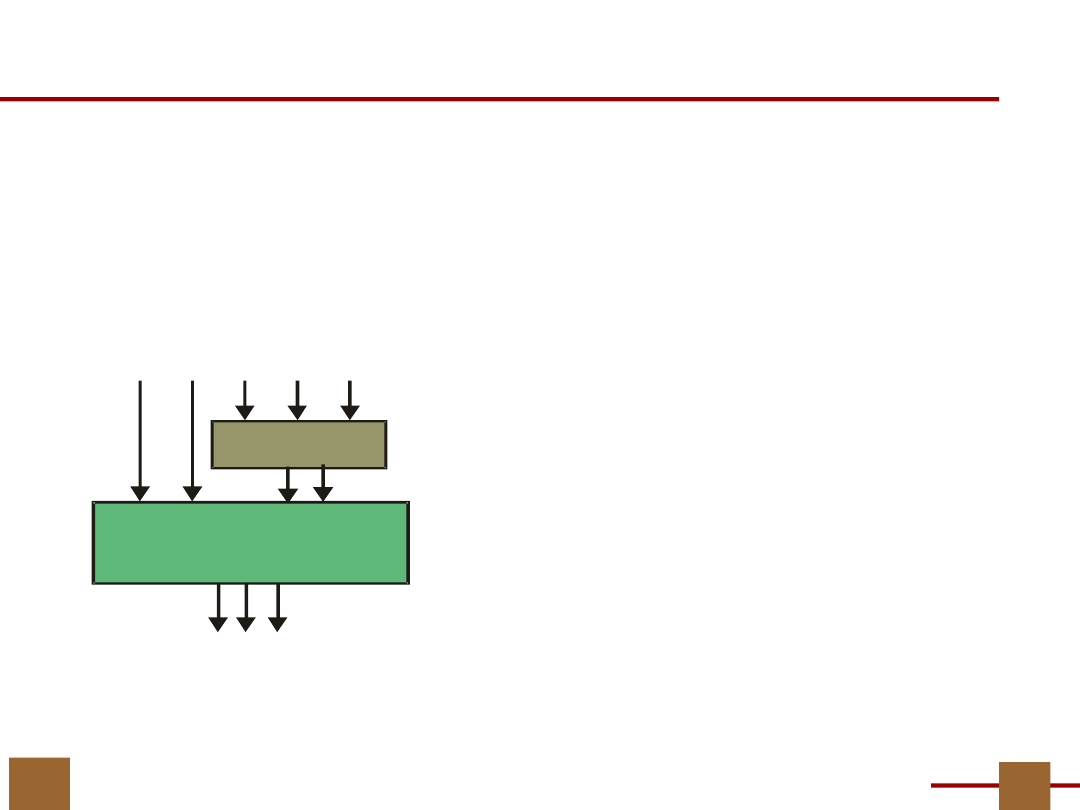
Tablica prawdy H
x
3
x
4
g
1
g
2
y
1
y
2
y
3
. . .
. . .
1
7
13
,
8
15
,
3
)
15
,
14
,
12
,
11
,
9
,
6
,
3
,
2
;
13
,
10
,
8
,
7
,
5
,
4
,
1
(
)
12
,
11
,
10
,
6
,
5
,
4
;
15
,
14
,
13
,
9
,
8
,
7
,
3
,
2
,
1
(
4
3
P
P
P
U
G
=
5
1,3,5,11,1
;
;
13,14
8,9,10,12,
2,4,6,7
G
01
10
00
0 0 0
0
0 0 0
1
0 0 1
0
0 1 0
0
0 0
0
1 0
0
0 0
1
0 0
1
;
7
;
13
,
8
;
15
,
3
…
;
1
(
P
U
G
< P
F
6,11,12
;
4,5,10
;
5
2,3,9,14,1
;
1,7,8,13
P
U
ZPT
32
Co uzyskaliśmy…
Ale dla struktur FPGA
wystarczy schemat
dekompozycji i
tablice prawdy.
Funkcje g i h można obliczyć jawnie…z tablic prawdy
można uzyskać realizacje na bramkach.
x
3
x
4
x
1
x
2
x
5
g
h
Proces
minimalizacji jest
niepotrzebny!!!

ZPT
33
Obliczanie podziału Π
G
metodą
przenoszenia bloków P
V
na
podstawie podziału ilorazowego
P
U
│P
U
•
Π
G
jest trudne do
zalgorytmizowania.
Szczęśliwie jednak algorytm
obliczania Π
G
można sprowadzić do
algorytmu obliczania MKZ.
Systematyczny algorytm
dekompozycji

ZPT
34
Systematyczny algorytm
dekompozycji
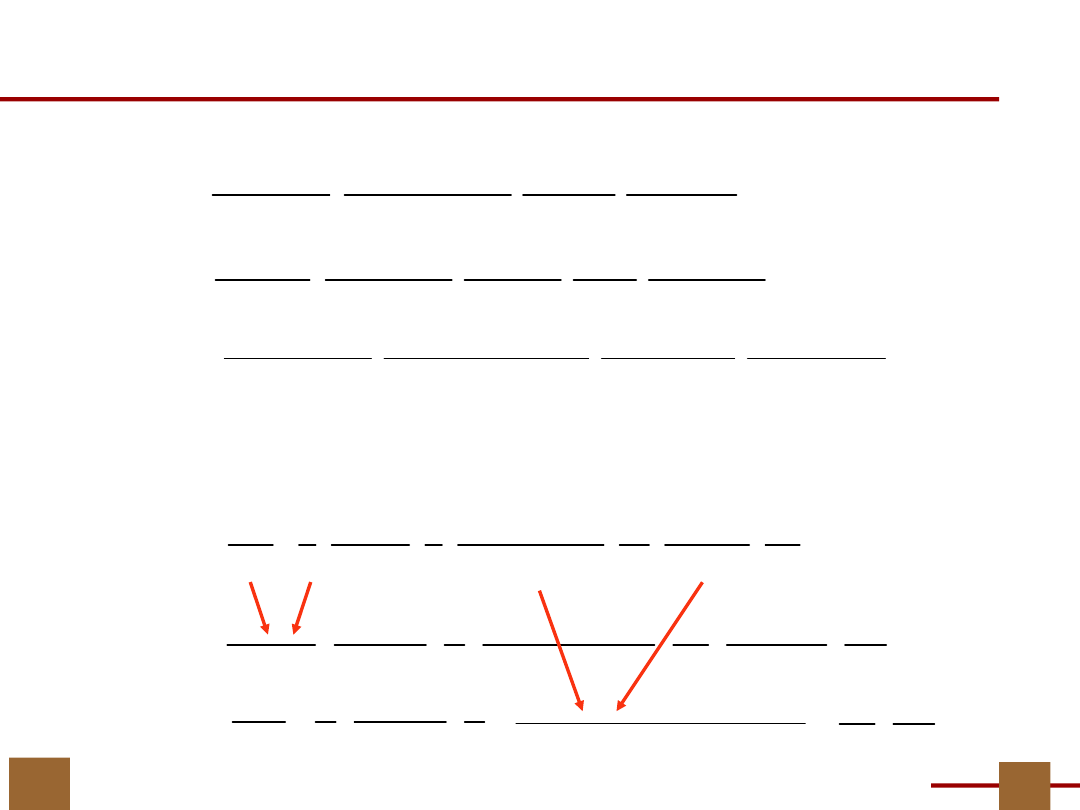
Dwa bloki B
i
i B
j
podziału P
V
są zgodne, jeśli podział
ij
uzyskany z P
V
przez sklejenie B
i
oraz B
j
w jeden blok i
pozostawienie pozostałych bloków bez zmiany
W przeciwnym przypadku B
i
oraz B
j
są niezgodne.
P
V
=( B
1
,…,B
i
,…,B
j
,…,B
N
)
ij
=( B
1
,…,B
i
B
j
,…,B
N
)
spełnia warunek Twierdzenia o dekompozycji: P
U
ij
P
F
.
ZPT
35
Przykład (ten sam co poprzednio)
6,11,12
;
4,5,10
;
5
2,3,9,14,1
;
1,7,8,13
P
U
3,10,15
;
4,11
;
2,6,12
;
5,7,8,13
;
1,9,14
P
F
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
B
1
B
2
B
3
B
4
B
5
B
6
B
7
B
8
(11)(6,12)
;
(4)(5)(10)
;
3,15)
(2)(9,14)(
;
)
(1)(7,8,13
P
P
|
P
F
U
U
57
=
12
=
;
1,2,3
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
13,14
8,9,10,12,
;
5
;
4,6,7
;
2
;
1,3
15
;
11
U = {x
3
,x
4
} oraz V = {x
1
,x
2
,x
5
}
Numerujemy bloki P
V

ZPT
36
Przykład …
Ale do wyznaczenia zgodnych (lub sprzecznych) par (B
i
, B
j
)
niekoniecznie musimy się posługiwać skomplikowaną
nierównością P
U
ij
P
F
Można sprawdzić, że
P
U
12
P
F
,
P
U
57
P
F
(B
1
, B
2
) jest
sprzeczna
(B
5
, B
7
) jest
zgodna
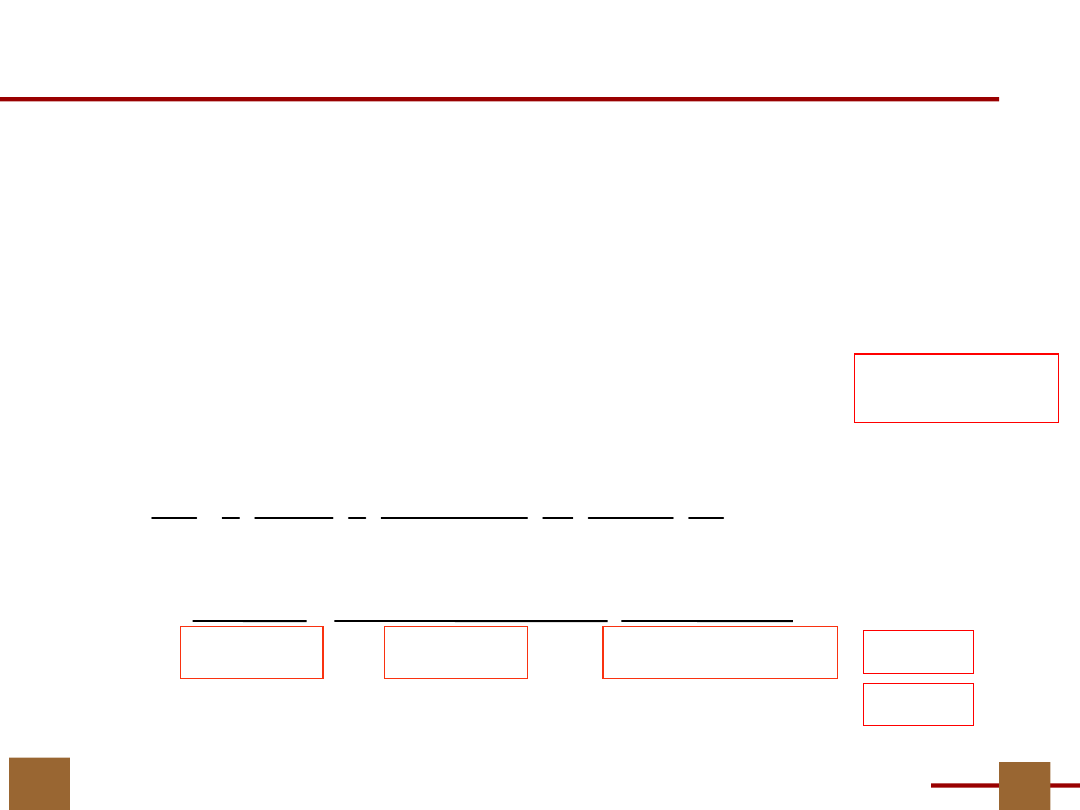
Wystarczy w tym celu obliczyć iloczyn zbioru
B
i
B
j
z blokami podziału
P
U
i sprawdzić, czy każdy
„niepusty iloczyn” jest zawarty w jakimś
bloku P
F

ZPT
37
Przykład …
6,11,12
;
4,5,10
;
5
2,3,9,14,1
;
1,7,8,13
P
U
3,10,15
;
4,11
;
2,6,12
;
5,7,8,13
;
1,9,14
P
F
B
1
B
2
B
3
B
4
B
5
B
6
B
7
B
8
(B
1
,B
2
) jest sprzeczna
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
B
1
B
2
=
1,2,3
1,2,3
P
U
)
( 2,3
;
1
P
F
B
5
B
7
=
13,14
8,9,10,12,
13,14
8,9,10,12,
P
U
12
;
10
;
9,14
;
8,13
P
F
(B
5
, B
7
) jest
zgodna
ZPT
38
Przykład c.d.
Pary zgodne: (B
1
,B
4
), (B
1
,B
6
), (B
1
,B
8
), (B
2
,B
3
), (B
2
,B
4
), (B
2
,B
6
),
(B
3
,B
7
), (B
3,
B
8
), (B
4
,B
6
), (B
4
,B
7
), (B
4
,B
8
), (B
5
,B
7
), (B
6
,B
7
), (B
6
,B
8
).
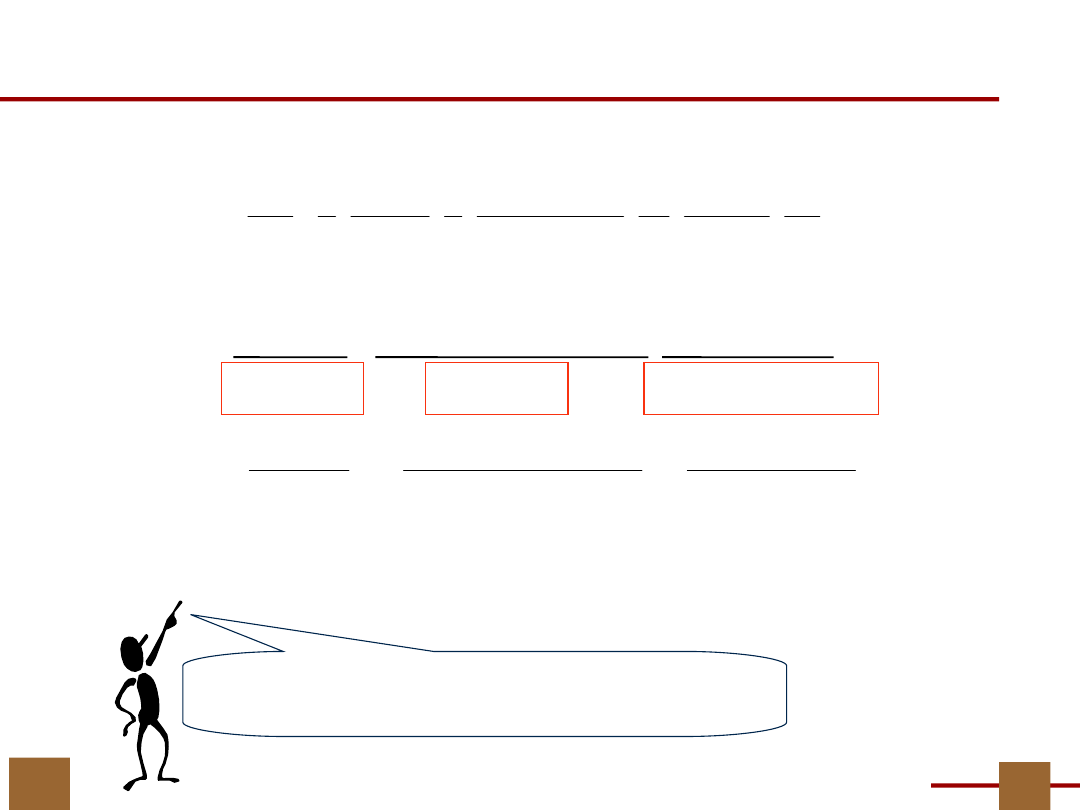
Doskonale wiemy jak obliczać
Maksymalne Klasy Zgodne
MKZ
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
B
1
B
2
B
3
B
4
B
5
B
6
B
7
B
8
G
;
{B
1
,B
4
, B
6
, B
8
}
;
{B
2
, B
3
}
{B
5
, B
7
}
Klasy maksymalne:
{B
1
,B
4
, B
6
, B
8
}
{B
4
, B
6
, B
7
}
{B
2
, B
4
, B
6
}
{B
3
, B
7
}
{B
3
, B
8
}
{B
2
, B
3
}
{B
5
, B
7
}
ZPT
39
Przykład c.d.
5
1,3,5,11,1
;
13,14
8,9,10,12,
;
2,4,6,7
G
15
;
13,14
;
11
;
8,9,10,12
;
5
;
4,6,7
;
2
;
1,3
P
V
B
1
B
2
B
3
B
4
B
5
B
6
B
7
B
8
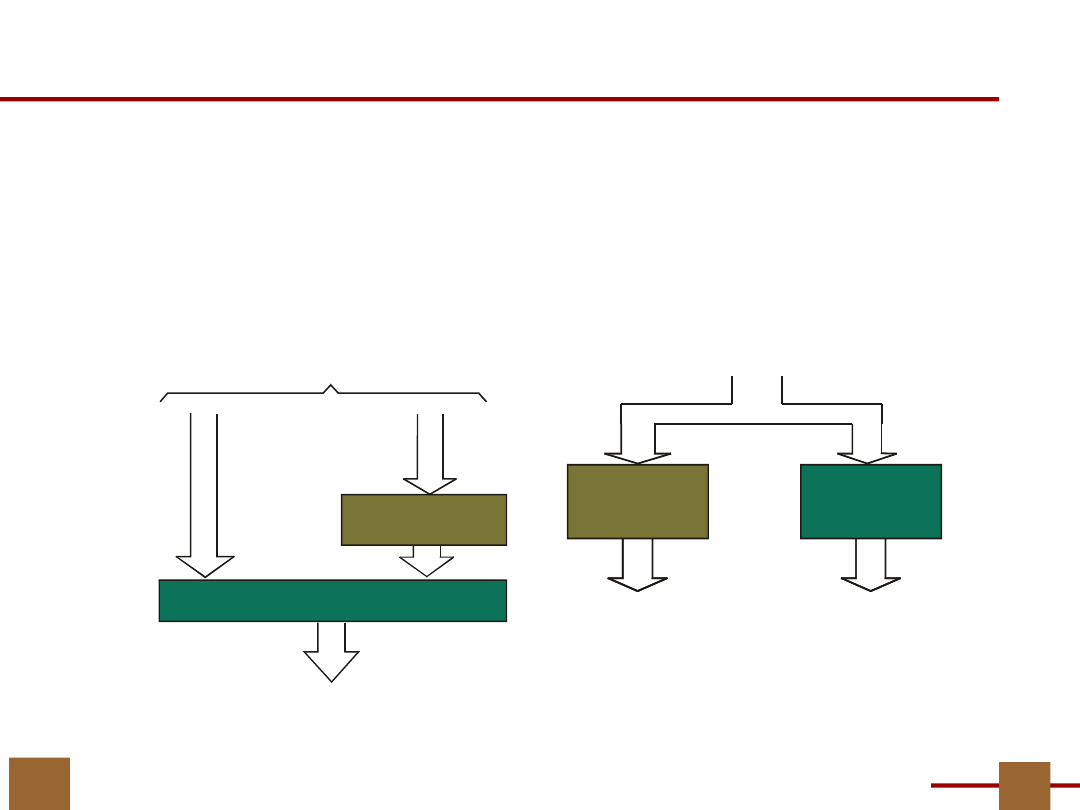
Ten sam rezultat co poprzednio
G
;
{B
1
,B
4
, B
6
, B
8
}
;
{B
2
, B
3
}
{B
5
, B
7
}
ZPT
40
Komentarz: algorytmy
dekompozycji
Y
A
B
X
G
H
Szeregowa
X
Y g
Y h
G
H
Równoległa
Dekompozycję funkcjonalną nazywać będziemy szeregową, dla
odróżnienia od równoległej

Życzą: Grzegorz Borowik
i Paweł Tomaszewicz
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
Wyszukiwarka
Podobne podstrony:
W09 Ja wstep ROZ
164 ROZ M G w sprawie prowadzeniea prac z materiałami wybu
124 ROZ stwierdzania posiadania kwalifikacji [M G P P S
013 ROZ M T G M w sprawie warunków technicznych, jakim pow
4 ROZ w sprawie warunkow techn Nieznany (2)
16 ROZ w sprawie warunkow tec Nieznany
18 ROZ warunki tech teleko Nieznany (2)
034 ROZ M I w sprawie wzoru protokołu obowiązkowej kontroli
5 ROZ w sprawie warunkow tech Nieznany (2)
123 roz uprawnienia D20140176id Nieznany
bio gle srod roz
133 ROZ bhp i p poz w zakla Nieznany
hej mam bardzo fajna zagadke dla ciebie jak bedziesz miał chwile to sobie zobacz, ■RÓŻNOŚCI, MOŻNA S
rr RĂłznice Indywidualne Wszytskie pytania, Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Psy
teorie roz reg, ściągi 2 rok ekonomia 1 sem
Roz 4 Pedagogika egzystencjalna[1]
tc spr 3
więcej podobnych podstron