Monografia Liczby

Monografia Liczby

Agata Iglewska

Agata Iglewska

PWP 22

PWP 22

Pojęcie liczby jest pojęciem

Pojęcie liczby jest pojęciem

abstrakcyjnym. Liczba

abstrakcyjnym. Liczba

bowiem sama w sobie nie

bowiem sama w sobie nie

istnieje realnie.

istnieje realnie.

Liczba

Liczba

określa

określa

pewną ilość lub wielkość.

pewną ilość lub wielkość.

Cyfry

Cyfry

są znakami graficznymi

są znakami graficznymi

służącymi do zapisywania

służącymi do zapisywania

liczb.

liczb.

Monografia liczb 0-10

Monografia liczb 0-10



Etap1 Wprowadzenie do zajęć

Etap1 Wprowadzenie do zajęć

Przypomnienie poprzedniej liczby we

Przypomnienie poprzedniej liczby we

wszystkich aspektach (kardynalnym -

wszystkich aspektach (kardynalnym -

umiem określić moc zbioru;

umiem określić moc zbioru;

porządkowym - umiem odp. na pyt.

porządkowym - umiem odp. na pyt.

który z kolei; miarowym - jaka jest

który z kolei; miarowym - jaka jest

długość)

długość)

-przelicza elementy

-przelicza elementy

(niezależność liczby od

(niezależność liczby od

sposobu liczenia).

sposobu liczenia).

- dziecko pamięta liczbę sąsiednią

- dziecko pamięta liczbę sąsiednią

nowej liczby,

nowej liczby,

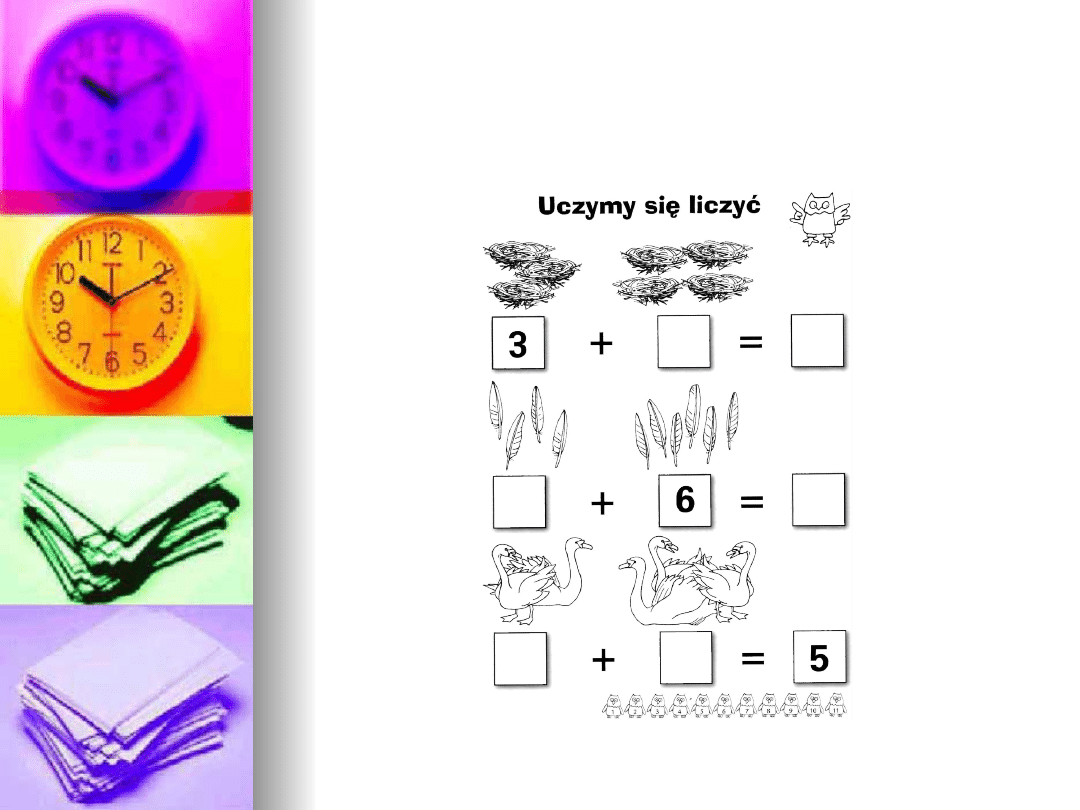
-potrafi rozłożyć liczbę

-potrafi rozłożyć liczbę

sąsiednią na składniki,

sąsiednią na składniki,

•

Tworzenie nowego zbioru

Tworzenie nowego zbioru

poprzez dodanie jednego

poprzez dodanie jednego

elementu (dopełnianie) i

elementu (dopełnianie) i

czynność odwrotna,

czynność odwrotna,

przeliczanie nowego zbioru;

przeliczanie nowego zbioru;

POLICZ ILE JEST

POLICZ ILE JEST

KACZEK

KACZEK

Ile jest kaczek teraz?

Ile jest kaczek teraz?

Etap2 Część główna

Etap2 Część główna

- budowanie zbiorów

- budowanie zbiorów

równolicznych; dodawanie i

równolicznych; dodawanie i

odejmowanie w ramach

odejmowanie w ramach

nowej liczby;

nowej liczby;

- wprowadzenie aspektów

- wprowadzenie aspektów

liczby;

liczby;

ASPEKT KARDYNALNY

ASPEKT KARDYNALNY

W tym aspekcie liczba związana jest z liczebnością

W tym aspekcie liczba związana jest z liczebnością

zbiorów, określa ile elementów ma dany zbiór.

zbiorów, określa ile elementów ma dany zbiór.

W tym ujęciu liczba jest wspólną własnością

W tym ujęciu liczba jest wspólną własnością

wszystkich zbiorów między sobą równolicznych.

wszystkich zbiorów między sobą równolicznych.

Zbiorom równolicznym przyporządkowuje się tę

Zbiorom równolicznym przyporządkowuje się tę

samą liczbę elementów.

samą liczbę elementów. Liczba kardynalna

Liczba kardynalna

odpowiada na pytanie: ile? Ile jest

odpowiada na pytanie: ile? Ile jest

elementów w zbiorze?

elementów w zbiorze?

Na jej określenie używamy liczebników głównych.

Na jej określenie używamy liczebników głównych.

Zatem, gdy na zajęciach wprowadzamy np.

Zatem, gdy na zajęciach wprowadzamy np.

liczbę 7, dobrze jest zgromadzić na stole różne

liczbę 7, dobrze jest zgromadzić na stole różne

przedmioty pogrupowane po 7. Prosimy dzieci,

przedmioty pogrupowane po 7. Prosimy dzieci,

aby je obejrzały i zastanowiły się:

aby je obejrzały i zastanowiły się:

Co wspólnego możemy o nich wszystkich

Co wspólnego możemy o nich wszystkich

powiedzieć?

powiedzieć?

Uczniowie powinni odpowiedzieć, że ich wspólną

Uczniowie powinni odpowiedzieć, że ich wspólną

cechą jest to, że jest ich 7.

cechą jest to, że jest ich 7.

Dla kształtowania pojęcia

Dla kształtowania pojęcia

liczby w aspekcie

liczby w aspekcie

kardynalnym można stosować

kardynalnym można stosować

takie ćwiczenia jak:

takie ćwiczenia jak:



Liczenie przedmiotów. Na przykład na stole jest 5 kulek.

Liczenie przedmiotów. Na przykład na stole jest 5 kulek.

Do uczniów zwracamy się: Policz, ile ich jest?.

Do uczniów zwracamy się: Policz, ile ich jest?.



Ćwiczenia manipulacyjne. Układanie przedmiotów, tyle,

Ćwiczenia manipulacyjne. Układanie przedmiotów, tyle,

ile wskazuje liczba, np. pokazujemy uczniom kartonik z

ile wskazuje liczba, np. pokazujemy uczniom kartonik z

cyfrą 5 mówiąc: Ułóż przed sobą tyle patyczków, ile

cyfrą 5 mówiąc: Ułóż przed sobą tyle patyczków, ile

wskazuje ta liczba., oraz inne typu:

wskazuje ta liczba., oraz inne typu:



- Włóż do każdej pętli po 3 kasztany.

- Włóż do każdej pętli po 3 kasztany.



- Wskaż w klasie zbiory dwuelementowe.

- Wskaż w klasie zbiory dwuelementowe.



- Sprawdź, czy w dwóch zbiorach jest po 6 elementów.

- Sprawdź, czy w dwóch zbiorach jest po 6 elementów.



- Włóż do pętli 5 kasztanów, połóż obok pętli kartonik z

- Włóż do pętli 5 kasztanów, połóż obok pętli kartonik z

odpowiednią cyfrą.

odpowiednią cyfrą.



Ćwiczenia związane z rysowaniem, np.

Ćwiczenia związane z rysowaniem, np.



- Zamaluj 4 piłki.

- Zamaluj 4 piłki.



- Obrysuj pętlami po 5 grzybów.

- Obrysuj pętlami po 5 grzybów.



- Narysuj tyle kółek, ile widzisz balonów.

- Narysuj tyle kółek, ile widzisz balonów.



- Narysuj w koszyku tyle jabłek, ile wskazuje cyfra

- Narysuj w koszyku tyle jabłek, ile wskazuje cyfra

napisana przy koszyku.

napisana przy koszyku.

ASPEKT PORZĄDKOWY.

ASPEKT PORZĄDKOWY.

Liczba w aspekcie porządkowym oznacza miejsce danego

Liczba w aspekcie porządkowym oznacza miejsce danego

elementu w uporządkowanym zbiorze przedmiotów.

elementu w uporządkowanym zbiorze przedmiotów.

Wszelkie liczenie, ustawianie po kolei, umieszczanie, itp.

Wszelkie liczenie, ustawianie po kolei, umieszczanie, itp.

wiąże się z aspektem porządkowym liczby naturalnej. Liczba

wiąże się z aspektem porządkowym liczby naturalnej. Liczba

porządkowa mówi, o który z kolei element zbioru chodzi,

porządkowa mówi, o który z kolei element zbioru chodzi,

który z kolei element danego zbioru właśnie rozpatrujemy.

który z kolei element danego zbioru właśnie rozpatrujemy.

Odpowiada na pytanie: który z kolei? Na jej określenie

Odpowiada na pytanie: który z kolei? Na jej określenie

używamy liczebników porządkowych, np. Pomaluj pierwszy

używamy liczebników porządkowych, np. Pomaluj pierwszy

koralik na czerwono a szósty na niebiesko.

koralik na czerwono a szósty na niebiesko.

Pomiędzy aspektem kardynalnym a porządkowym liczby istnieje

Pomiędzy aspektem kardynalnym a porządkowym liczby istnieje

ścisły związek. Na przykład podczas kolejnego przeliczania

ścisły związek. Na przykład podczas kolejnego przeliczania

żetonów od pierwszego do szóstego należy zwrócić uczniom

żetonów od pierwszego do szóstego należy zwrócić uczniom

uwagę, że ważny przy tym przeliczaniu jest ostatni

uwagę, że ważny przy tym przeliczaniu jest ostatni

wypowiadany liczebnik, bo on oznacza liczbę kardynalną,

wypowiadany liczebnik, bo on oznacza liczbę kardynalną,

czyli szósty ostatni żeton oznacza, że żetonów jest 6. Gdy

czyli szósty ostatni żeton oznacza, że żetonów jest 6. Gdy

dziecko liczy kasztany: jeden, dwa, trzy, to choć wypowiada

dziecko liczy kasztany: jeden, dwa, trzy, to choć wypowiada

liczebniki główne, to określone nimi liczby mają wyraźny

liczebniki główne, to określone nimi liczby mają wyraźny

aspekt porządkowy: określają, który z kolei jest dany żeton.

aspekt porządkowy: określają, który z kolei jest dany żeton.

Dla kształtowania pojęcia liczby w aspekcie porządkowym

Dla kształtowania pojęcia liczby w aspekcie porządkowym

można stosować takie ćwiczenia jak:

można stosować takie ćwiczenia jak:



- Podaj mi trzeci lizak od prawej strony.

- Podaj mi trzeci lizak od prawej strony.



- Pomaluj czwartą piłkę w rzędzie licząc od strony lewej.

- Pomaluj czwartą piłkę w rzędzie licząc od strony lewej.



- Ponumeruj kubeczki, do szóstego od prawej włóż łyżeczkę.

- Ponumeruj kubeczki, do szóstego od prawej włóż łyżeczkę.



- Pod piątą choinką narysuj grzybka.

- Pod piątą choinką narysuj grzybka.



- W szóstym pudełku narysuj trzy guziki.

- W szóstym pudełku narysuj trzy guziki.



- Stań na trzecim schodku.

- Stań na trzecim schodku.



- Weź do ręki czwartą od dołu książkę.

- Weź do ręki czwartą od dołu książkę.

ASPEKT KARDYNALNY

ASPEKT KARDYNALNY

ASPEKT MIAROWY

ASPEKT MIAROWY

Liczba w aspekcie miarowym określa, ile razy

Liczba w aspekcie miarowym określa, ile razy

w danej wielkości mieści się wielkość

w danej wielkości mieści się wielkość

jednostkowa. Wynik pomiaru zależy od

jednostkowa. Wynik pomiaru zależy od

wyboru jednostki; przy zmianie jednostki

wyboru jednostki; przy zmianie jednostki

zmienia się wartość liczbowa wyniku, choć

zmienia się wartość liczbowa wyniku, choć

wielkość mierzona jest ta sama.

wielkość mierzona jest ta sama.

Ćwiczenia kształtujące pojęcie liczby w tym

Ćwiczenia kształtujące pojęcie liczby w tym

aspekcie to np.

aspekcie to np.

- Zmierz przy pomocy ołówka szerokość ławki.

- Zmierz przy pomocy ołówka szerokość ławki.

- Zmierz krokami długość klasy.

- Zmierz krokami długość klasy.

- Sprawdź ile patyczków potrzeba do zmierzenia

- Sprawdź ile patyczków potrzeba do zmierzenia

długości książki.

długości książki.

- Zmierz długość swojej ręki przy pomocy

- Zmierz długość swojej ręki przy pomocy

ołówka.

ołówka.

- Zmierz stopami długość swojego skoku.

- Zmierz stopami długość swojego skoku.

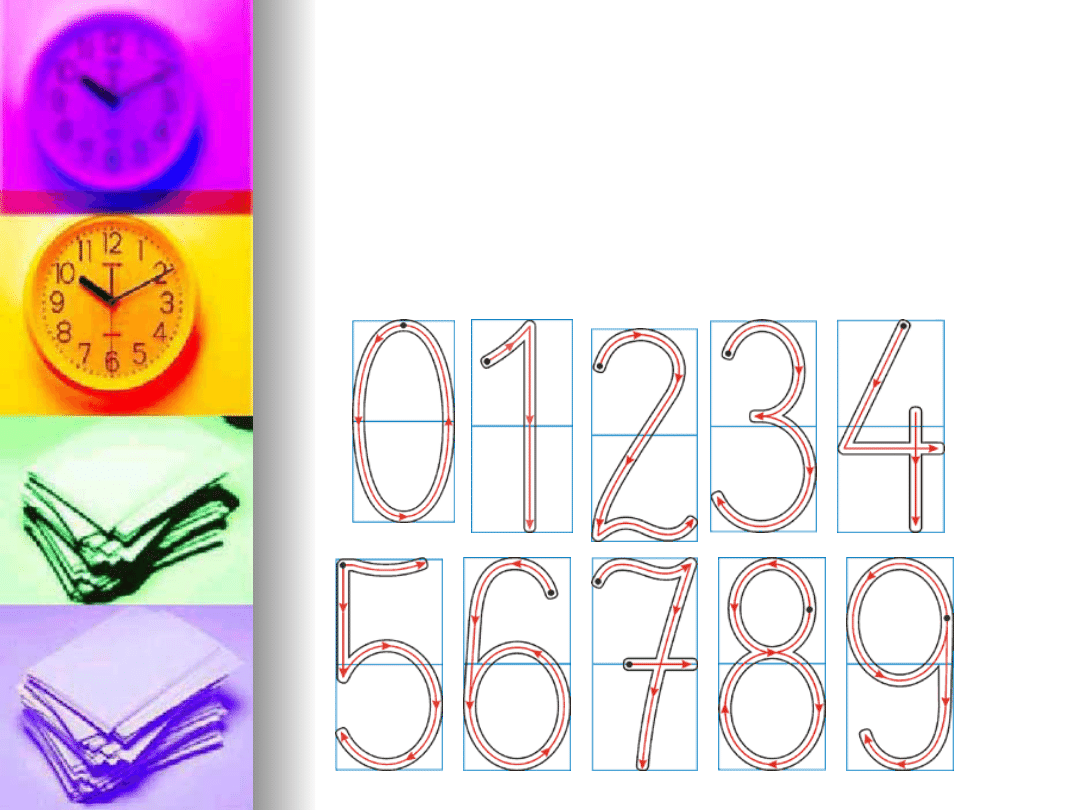
Etap3 Używanie liczby w

Etap3 Używanie liczby w

zabawie, np.

zabawie, np.

- pisanie cyfry po śladzie, w

- pisanie cyfry po śladzie, w

grysiku itp;

grysiku itp;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

Znak liczby, pisanie liczby za

Znak liczby, pisanie liczby za

pomocą cyfry;

pomocą cyfry;

-

układanie dywaników

układanie dywaników

liczbowych;

liczbowych;

-

- rzucanie kostkami do gry;

- rzucanie kostkami do gry;

-

- zab. dyd. Pociągi wg

- zab. dyd. Pociągi wg

Bogdanowicz itd itp

Bogdanowicz itd itp

Monografia liczby siedem –

Monografia liczby siedem –

konspekt zajęć w klasie

konspekt zajęć w klasie

pierwszej. KONSPEKT

pierwszej. KONSPEKT

1. Czas trwania: 1 jednostka lekcyjna.

1. Czas trwania: 1 jednostka lekcyjna.

2. Ośrodek tematyczny: Zwierzęta wokół

2. Ośrodek tematyczny: Zwierzęta wokół

nas.

nas.

3. Temat dnia: Pomagamy ptakom.

3. Temat dnia: Pomagamy ptakom.

4. Temat zajęć: Monografia liczby siedem.

4. Temat zajęć: Monografia liczby siedem.

5. Cele ogólne:

5. Cele ogólne:



kształtowanie pojęcia liczby naturalnej.

kształtowanie pojęcia liczby naturalnej.



rozwijanie myślenia matematycznego

rozwijanie myślenia matematycznego

poprzez rozwiązywanie zadań

poprzez rozwiązywanie zadań

tekstowych.

tekstowych.

6. Cele szczegółowe:

6. Cele szczegółowe:



Uczeń:

Uczeń:

- rozumie pojęcie liczby siedem we

- rozumie pojęcie liczby siedem we

wszystkich jej aspektach

wszystkich jej aspektach

- pisze cyfrę 7

- pisze cyfrę 7

- układa treść zadania do formuły

- układa treść zadania do formuły

matematycznej

matematycznej

- zna dni tygodni i ich kolejność

- zna dni tygodni i ich kolejność

- porównuje liczby w zakresie 7

- porównuje liczby w zakresie 7

7. Metody: samodzielnych

7. Metody: samodzielnych

doświadczeń, pokaz.

doświadczeń, pokaz.

8. Formy: indywidualna, zbiorowa

8. Formy: indywidualna, zbiorowa

jednolita.

jednolita.

9. Środki dydaktyczne: M. A.

9. Środki dydaktyczne: M. A.

Szymańska ,,Już w szkole’’ –

Szymańska ,,Już w szkole’’ –

ćwiczenia do kształcenia

ćwiczenia do kształcenia

zintegrowanego, kaseta

zintegrowanego, kaseta

magnetofonowa z muzyką do

magnetofonowa z muzyką do

zabaw ruchowych – U. Bissinger

zabaw ruchowych – U. Bissinger

– Ćwierz ,,Muzyka i ruch dla

– Ćwierz ,,Muzyka i ruch dla

każdego’’ wyd. Klanza, liczby w

każdego’’ wyd. Klanza, liczby w

kolorach, kartoniki z liczbami,

kolorach, kartoniki z liczbami,

tekst wiersza J. Brzechwy ,,

tekst wiersza J. Brzechwy ,,

Tydzień’’

Tydzień’’

Przebieg zajęć:

Przebieg zajęć:



Powitanie.

Powitanie.



Sprawdzenie pracy domowej.

Sprawdzenie pracy domowej.



Rachunek pamięciowy:

Rachunek pamięciowy:

- nauczyciel podaje działania na

- nauczyciel podaje działania na

dodawanie i odejmowanie w zakresie

dodawanie i odejmowanie w zakresie

6 np. 3+1, a uczniowie pokazują

6 np. 3+1, a uczniowie pokazują

kartoniki z wynikiem

kartoniki z wynikiem

- nauczyciel pokazuje kartonik z liczbą 6,

- nauczyciel pokazuje kartonik z liczbą 6,

5, 4. Uczniowie pokazują przykładowe

5, 4. Uczniowie pokazują przykładowe

składniki tych liczb. Rozkładają liczby

składniki tych liczb. Rozkładają liczby

na 2 i 3 składniki.

na 2 i 3 składniki.

- nauczyciel pokazuje kartonik z liczbą 3,

- nauczyciel pokazuje kartonik z liczbą 3,

2, 4 uczniowie podnoszą kartoniki z

2, 4 uczniowie podnoszą kartoniki z

liczbą o 2 większą lub mniejszą.

liczbą o 2 większą lub mniejszą.

4. Monografia liczby 7

4. Monografia liczby 7



Nauczyciel przypina na tablicy 6

Nauczyciel przypina na tablicy 6

sylwetek ptaków, uczniowie liczą głośno

sylwetek ptaków, uczniowie liczą głośno

1,2,3,4 itd.

1,2,3,4 itd.



Nauczyciel pyta:

Nauczyciel pyta:



Ile jest ptaków?

Ile jest ptaków?



Nauczyciel dokłada jeszcze jedną

Nauczyciel dokłada jeszcze jedną

sylwetkę i pyta:

sylwetkę i pyta:



Ile ptaków jest teraz?

Ile ptaków jest teraz?



O ile więcej niż na początku?

O ile więcej niż na początku?



Uczniowie układają 6 białych klocków,

Uczniowie układają 6 białych klocków,

następnie poszukują jednego, który

następnie poszukują jednego, który

będzie miał długość 6.

będzie miał długość 6.



Jaki ma kolor?

Jaki ma kolor?



Uczniowie dokładają do niego 1 biały

Uczniowie dokładają do niego 1 biały

klocek i sprawdzają jaki kolor ma klocek

klocek i sprawdzają jaki kolor ma klocek

długości 7.

długości 7.



Nauczyciel pokazuje planszę z cyfrą 7.

Nauczyciel pokazuje planszę z cyfrą 7.

5.Ćwiczenia w pisaniu cyfry 7.

5.Ćwiczenia w pisaniu cyfry 7.



Nauczyciel rozdaje kartonik

Nauczyciel rozdaje kartonik

z cyfrą 7, dzieci wkładają

z cyfrą 7, dzieci wkładają

do foliowych koszulek i

do foliowych koszulek i

ćwiczą pisanie na folii.

ćwiczą pisanie na folii.

6. Utrwalanie nazw i kolejności dni tygodnia.

6. Utrwalanie nazw i kolejności dni tygodnia.

- nauczyciel czyta wiersz pt. ,,Tydzień’’

- nauczyciel czyta wiersz pt. ,,Tydzień’’

- dzieci wymieniają dni tygodnia i czynności, jakie

- dzieci wymieniają dni tygodnia i czynności, jakie

te dni wykonywały

te dni wykonywały

- nauczyciel układa na tablicy kartoniki z cyframi

- nauczyciel układa na tablicy kartoniki z cyframi

o 1 do 7

o 1 do 7

1.-------------------------

1.-------------------------

2.-------------------------

2.-------------------------

3.-------------------------

3.-------------------------

4.-------------------------

4.-------------------------

5.-------------------------

5.-------------------------

6.-------------------------

6.-------------------------

7.-------------------------

7.-------------------------

Uczniowie wymieniają dni tygodnia i umieszczają

Uczniowie wymieniają dni tygodnia i umieszczają

kartoniki z nazwą we właściwe miejsce.

kartoniki z nazwą we właściwe miejsce.

Nauczyciel pyta:

Nauczyciel pyta:

- Jak nazywa się drugi dzień tygodnia, jak

- Jak nazywa się drugi dzień tygodnia, jak

czwarty, jak piąty itd.

czwarty, jak piąty itd.

- Którym dniem tygodnia jest niedziela, środa,

- Którym dniem tygodnia jest niedziela, środa,

poniedziałek itd.

poniedziałek itd.

7. Wykonanie ćwiczenia 3 str. 48

7. Wykonanie ćwiczenia 3 str. 48

8. Zabawa ruchowa: ,,Czy znasz

8. Zabawa ruchowa: ,,Czy znasz

magiczną liczbę 7 ?’’ Urszula

magiczną liczbę 7 ?’’ Urszula

Bissinger – Ćwierz ,,Muzyka i

Bissinger – Ćwierz ,,Muzyka i

ruch dla każdego’’ wyd. Klauza

ruch dla każdego’’ wyd. Klauza

9. Układanie treści zadania do

9. Układanie treści zadania do

ilustracji

ilustracji

Ćwiczenie 1 i 2 str. 48

Ćwiczenie 1 i 2 str. 48

10. Zabawa ,,Głoskomania’’

10. Zabawa ,,Głoskomania’’

Siedzimy w kręgu. Uczniowie

Siedzimy w kręgu. Uczniowie

otrzymują kartoniki z nazwami

otrzymują kartoniki z nazwami

dni tygodnia. Jedna osoba stoi w

dni tygodnia. Jedna osoba stoi w

środku i głosuje nazwę jednego z

środku i głosuje nazwę jednego z

dni tygodnia wypowiadając

dni tygodnia wypowiadając

pierwszą głoskę wskazuje na

pierwszą głoskę wskazuje na

siebie, a potem kolejne osoby w

siebie, a potem kolejne osoby w

kręgu. Osoba na którą wypadnie

kręgu. Osoba na którą wypadnie

ostatnia głoska wstaje i

ostatnia głoska wstaje i

kontynuuje zabawę, a osoba ze

kontynuuje zabawę, a osoba ze

środka zajmuje miejsce w kręgu.

środka zajmuje miejsce w kręgu.

Dziękuję za uwagę

Dziękuję za uwagę