Druga zasada 

Druga zasada 

termodynamiki

termodynamiki

                   Trzecia 

                   Trzecia 

zasada

zasada

                   

                   

termodynamiki

termodynamiki

Warunki 

Warunki 

samorzutności 

samorzutności 

procesów

procesów

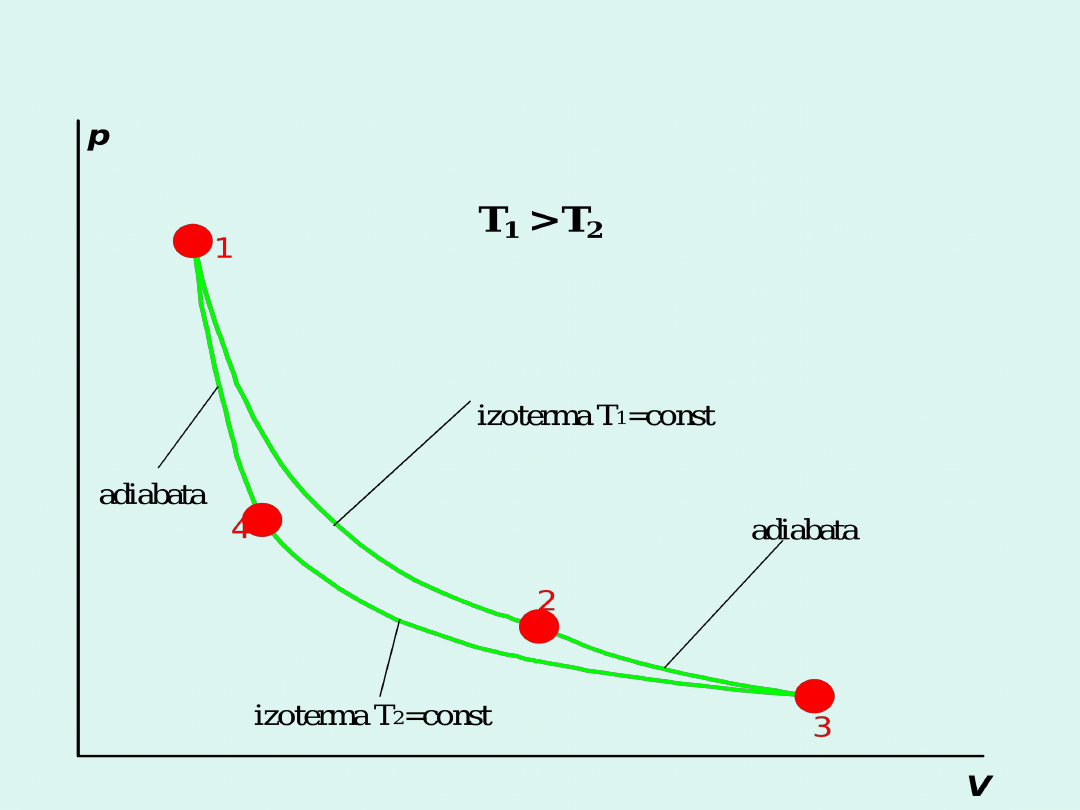
Cykl Carnota

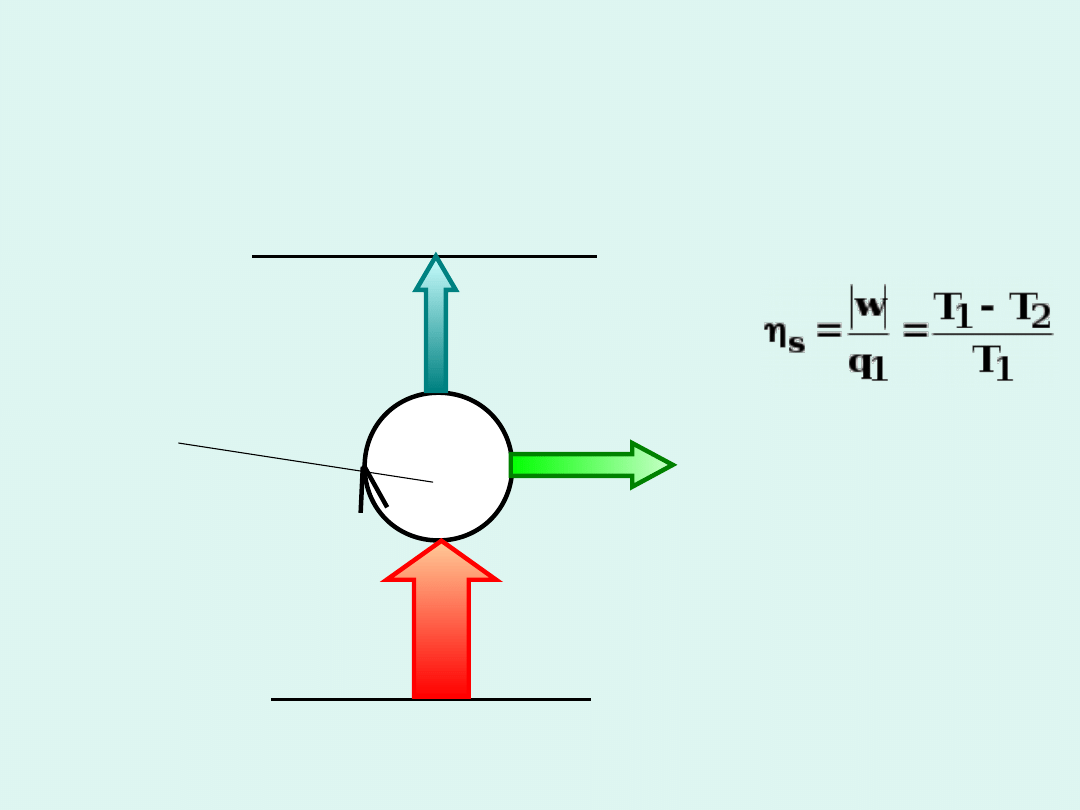
źródło ciepła 

T

1

chłodnica 

T

2

pracujący układ

q

1

q

2

w

T

1

 > 

T

2

           

Schemat silnika 

cieplnego

Wydajność 

silnika 

cieplnego

Słuszne, gdy 
silnik pracuje w 
sposób 
odwracalny.

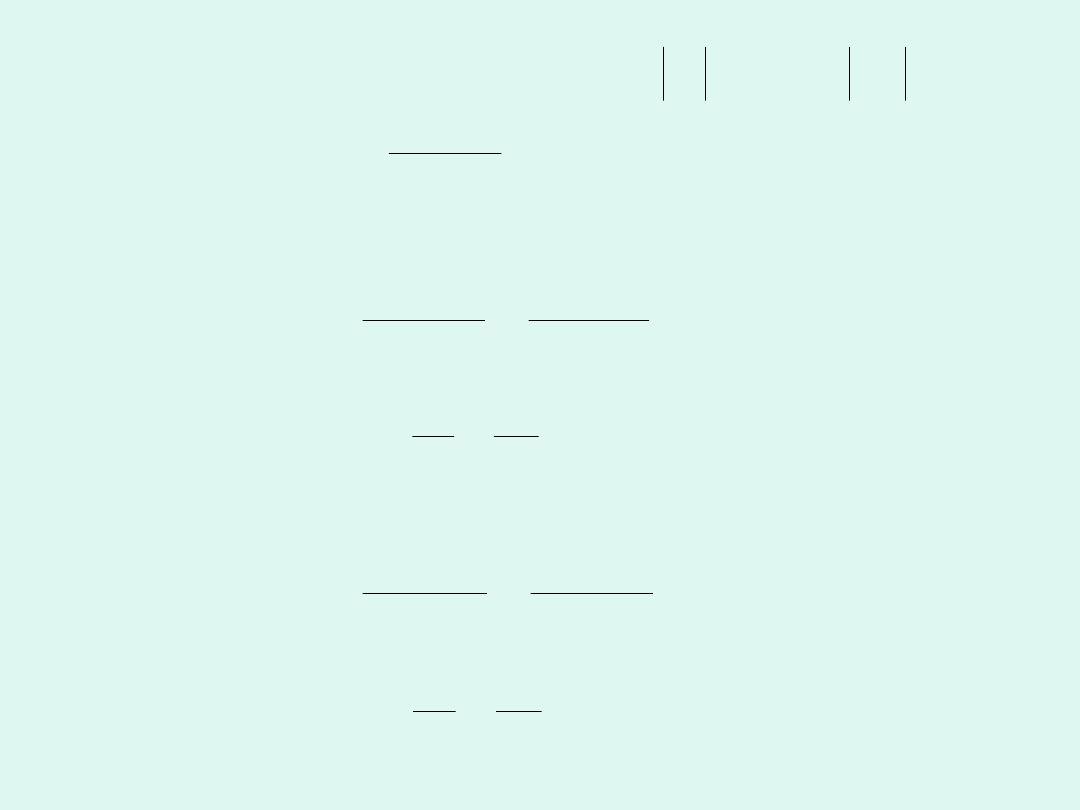
1

2

1

lny

nieodwraca

odwracalny

lny

nieodwraca

T

T

T 











0

T

q

T

q

T

T

T

q

q

q

2

2

1

1

1

2

1

1

2

1











0

T

q

T

q

T

T

T

q

q

q

2

2

1

1

1

2

1

1

2

1











Dla procesu 
odwracalnego

Dla procesu 
nieodwracalne
go

2

1

2

1

q

q

w

q

q

w











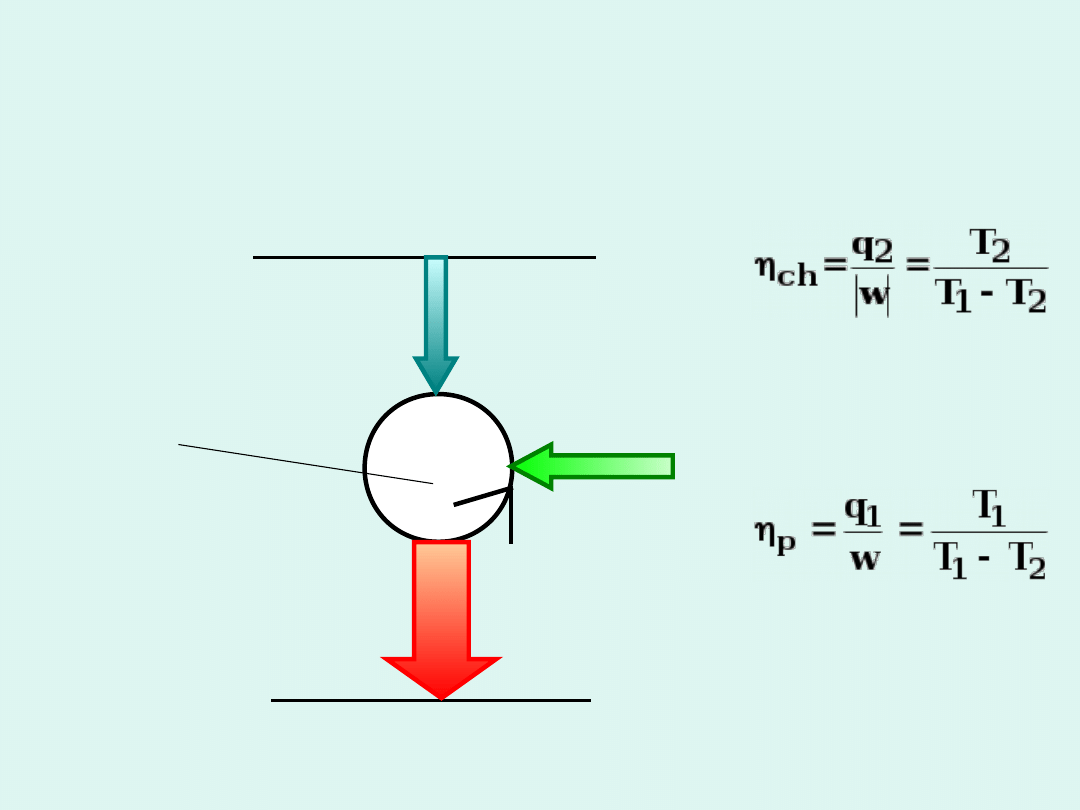
zbiornik ciepła 

T

1

ciało ochładzane 

T

2

pracujący układ

q

1

q

2

w

T

1

 > 

T

2

           

Schemat lodówki lub pompy 

cieplnej

wydajność 
lodówki 
idealnej

wydajność 
pompy 
cieplnej

Słuszne, gdy 
przemiany 
zachodzą w 
sposób 
odwracalny.

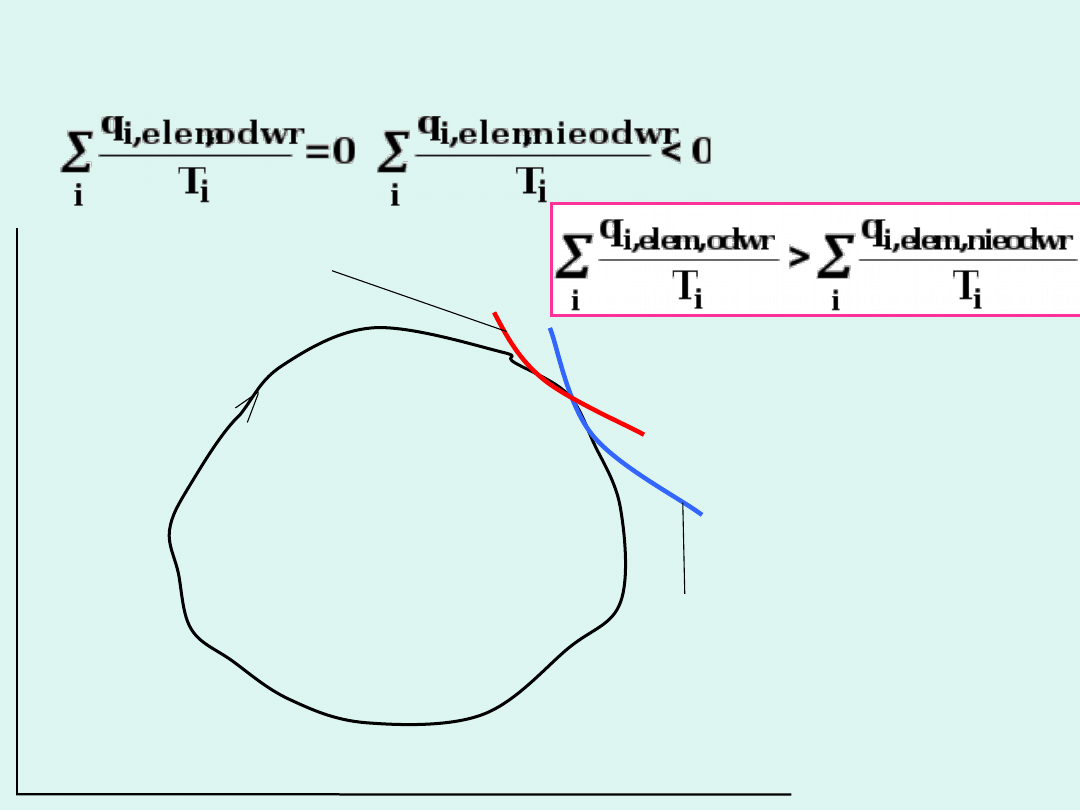
p

V

izoterma T

i

 = const ; q

i,elementarne

adiabata

           

Karnotyzacja dowolnego cyklu

Definicja entropii

Różniczka 

entropii

 

to 

stosunek 

elementarnego ciepła (różniczki ciepła) 
wymienionego  z  otoczeniem  w  sposób 
odwracalny do temperatury, w której ta 
wymiana nastąpiła.

def

odwracalne

dq

dS

T

�

Entropia jest funkcją stanu.

Jest miarą uporządkowania układu.

Matematyczny zapis drugiej 

zasady termodynamiki przy 

użyciu entropii

ukladu

otoczenia

ukladu

otoczenia

dS

dS

0

S

S

0

+

�

D

+D

�

ukladu

otoczenia

ukladu

otoczenia

ukladu

otoczenia

gdy  dS

dS

0

gdy  dS

dS

0

gdy  dS

dS

0

+

>

+

=

+

<

Proces samorzutny, 
nieodwracalny

Stan równowagi, 
proces odwracalny

Proces niesamorzutny 
(samorzutnie 
zachodziłby w 
przeciwnym kierunku)

Entropia i druga zasada 

termodynamiki

dq

dS

T

�

dq

gdy  dS

T

dq

gdy  dS

T

dq

gdy  dS

T

>

=

<

Proces samorzutny, 
nieodwracalny

Stan równowagi, 
proces odwracalny

Proces niesamorzutny 
(samorzutnie 
zachodziłby w 
przeciwnym kierunku)

Nierówność 
Clausiusa

Z pierwszej zasady termodynamiki

'

'

dw

Vdp

dH

dq

dw

pdV

dU

dq













T

dw

Vdp

dH

dS

T

dw

pdV

dU

dS

'

'













dq

dS

T

�

Połączony zapis 
pierwszej i drugiej 
zasady 
termodynamiki

Jeśli w układzie zachodzi proces odwracalny, i 
brak jest pracy nieobjętościowej, to :

T

Vdp

dH

dS

T

pdV

dU

dS



























2

1

2

1

2

1

T

Vdp

dH

T

pdV

dU

dS

S

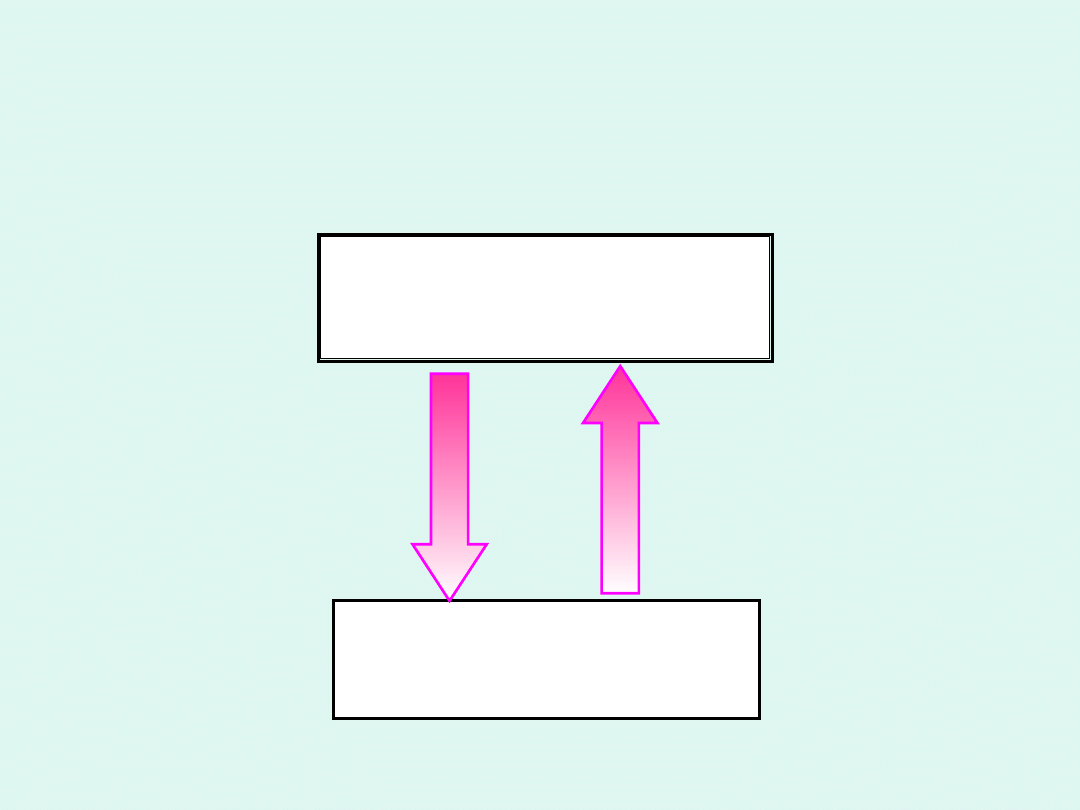
Molekularna interpretacja 

entropii

Entropia  jest  miarą  uporządkowania 
układu. 

W 

miarę 

wzrostu 

nieuporządkowania entropia rośnie.

proces 

samorzutny

S > 0

stan 

nieuporządkowany

proces wymuszony, 

niesamorzutny

S < 0

 

stan uporządkowany

 

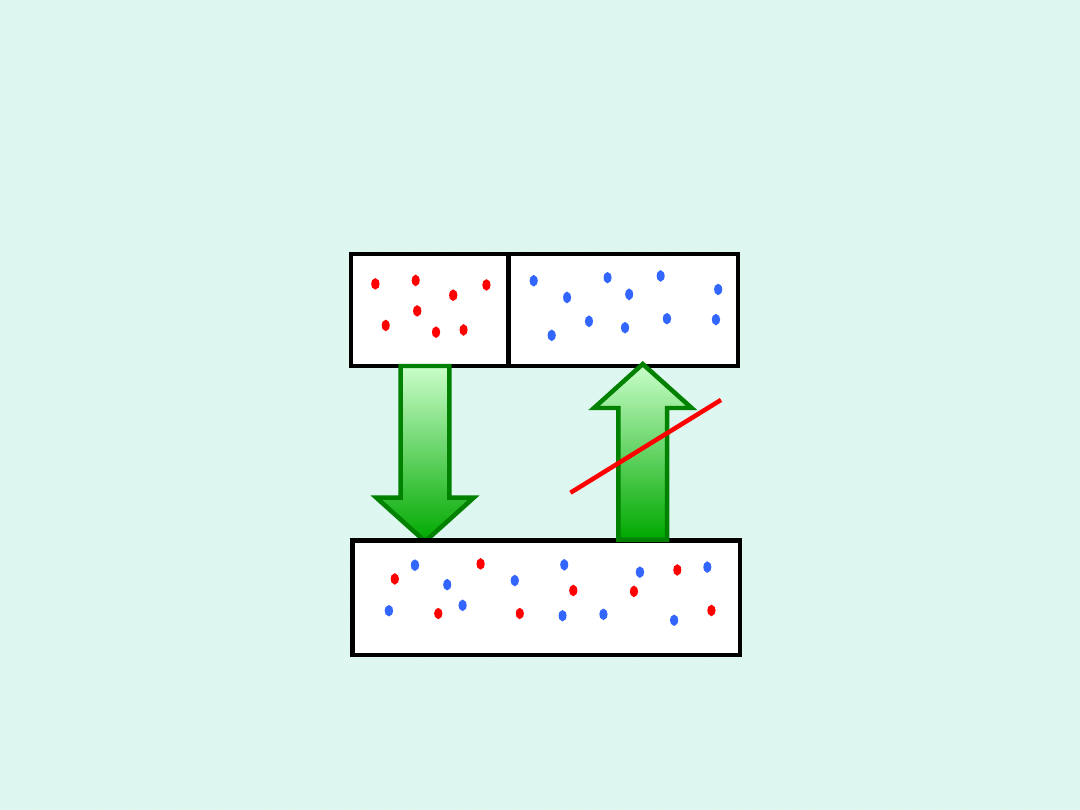
samorzutne 
mieszanie 



mix

S > 

0

gaz A

n

A

 , V

A

gaz B

n

B

 , V

B

mieszanina

n

A

+n

B

 , V

A

+V

B

-

mix

S

rozdzieleni
e 
mieszaniny

Mieszanie izotermiczno-izobaryczne gazów 

doskonałych

T = const   p = const

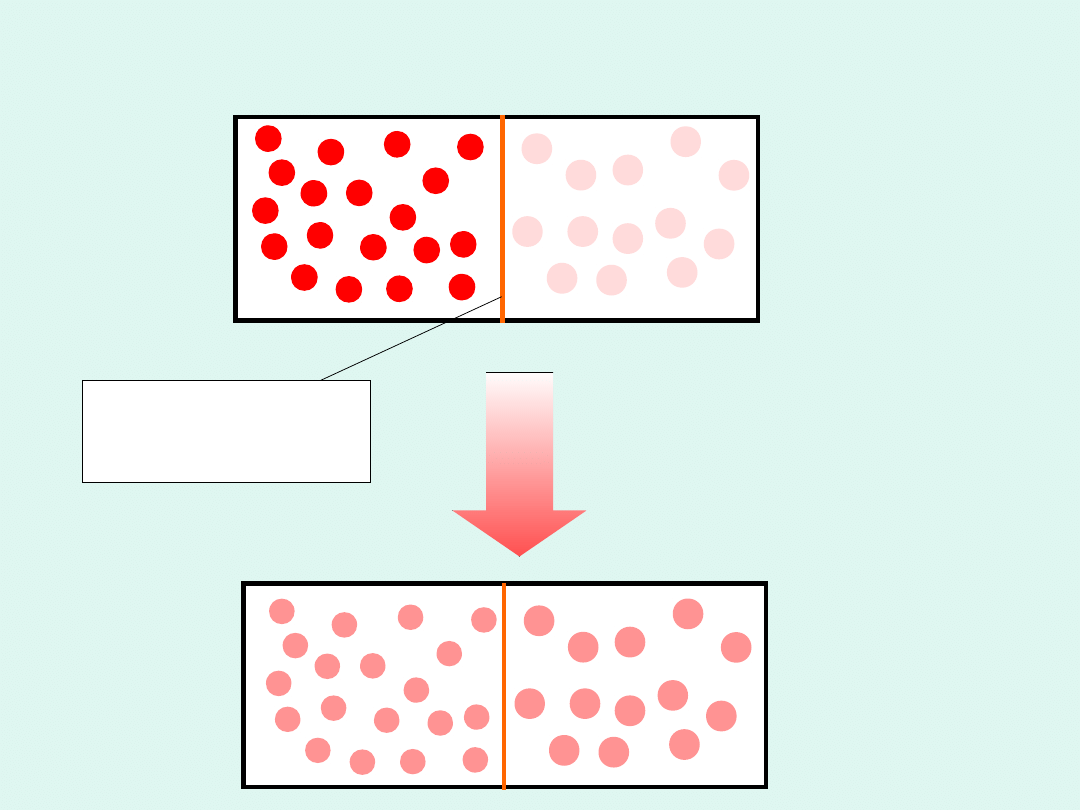
przegroda 

diatermiczna

T

1

  >  

T

2

Wyrównywanie 
temperatur - energie 
kinetyczne cząsteczek 
wyrównują się - 
proces samorzutny 

S 

> 0

Adiabatyczne wyrównywanie temperatur

Teoremat cieplny Nernsta

Zmiana entropii towarzysząca dowolnej 
przemianie fizycznej lub chemicznej dąży do 0, 
gdy temperatura dąży do 0 K.

0

T

as

0

S













Wynika z niego niemożność osiągnięcia 
temperatury zera bezwzględnego (0 K).

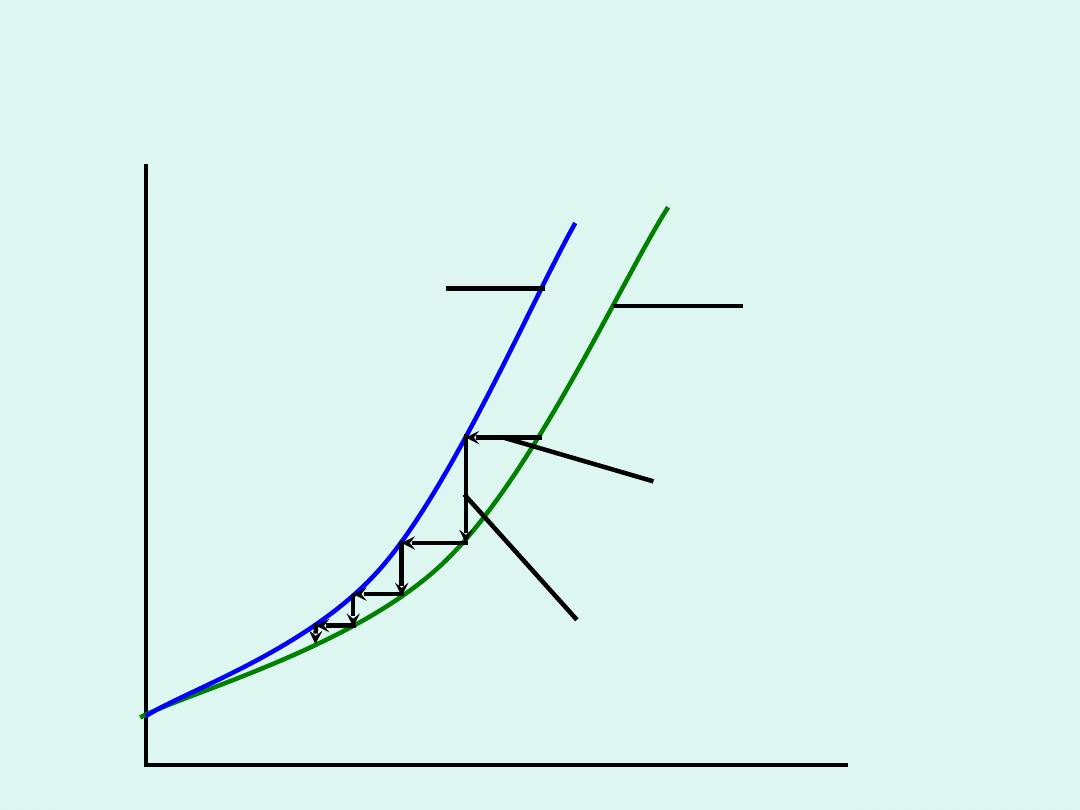
S

T

stan 

stan 

przemiana 
adiabatyczna 

S 

=0

przemiana 
izotermiczna

S = 

S



 

- 

S



Nieosiągalność temperatury 0 K

Wnioski z trzeciej zasady 

termodynamiki

Dla 1 mola substancji, gdy p = const

0

m

T

m

T

K

 

0

m

m

S

S

dS

S

,

,











Na mocy trzeciej zasady termodynamiki 

S

m,0

 

= 0

Wobec tego możemy określić bezwzględną 
wartość entropii molowej substancji. 
Podawane są one dla ciśnienia 
standardowego 

p

o

 = 10

5

 Pa

. Są to 

standardowe entropie.  





K

mol

J

  

S

o

m



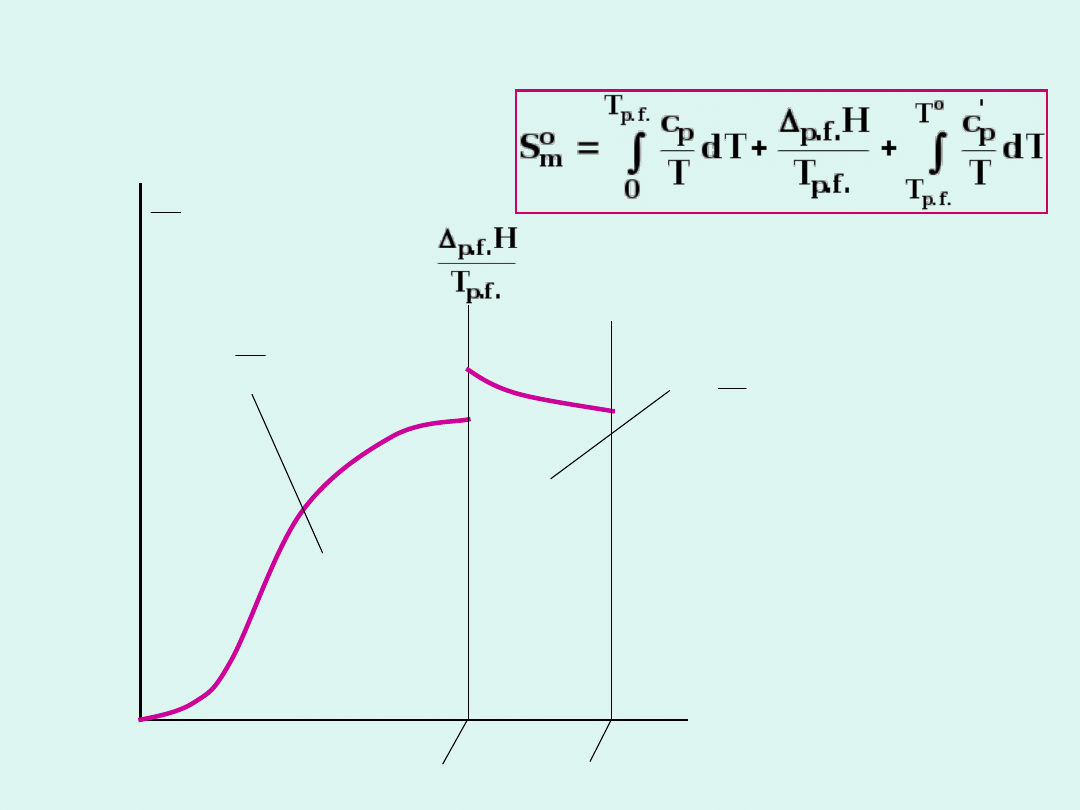
T

T

p.f

.

T

o

0



o

.

f

.

p

T

T

dT

T

p

c



o

f

p

T

T

p

dT

T

c

.

.

'

T

p

c

Wyznaczanie entropii standardowej

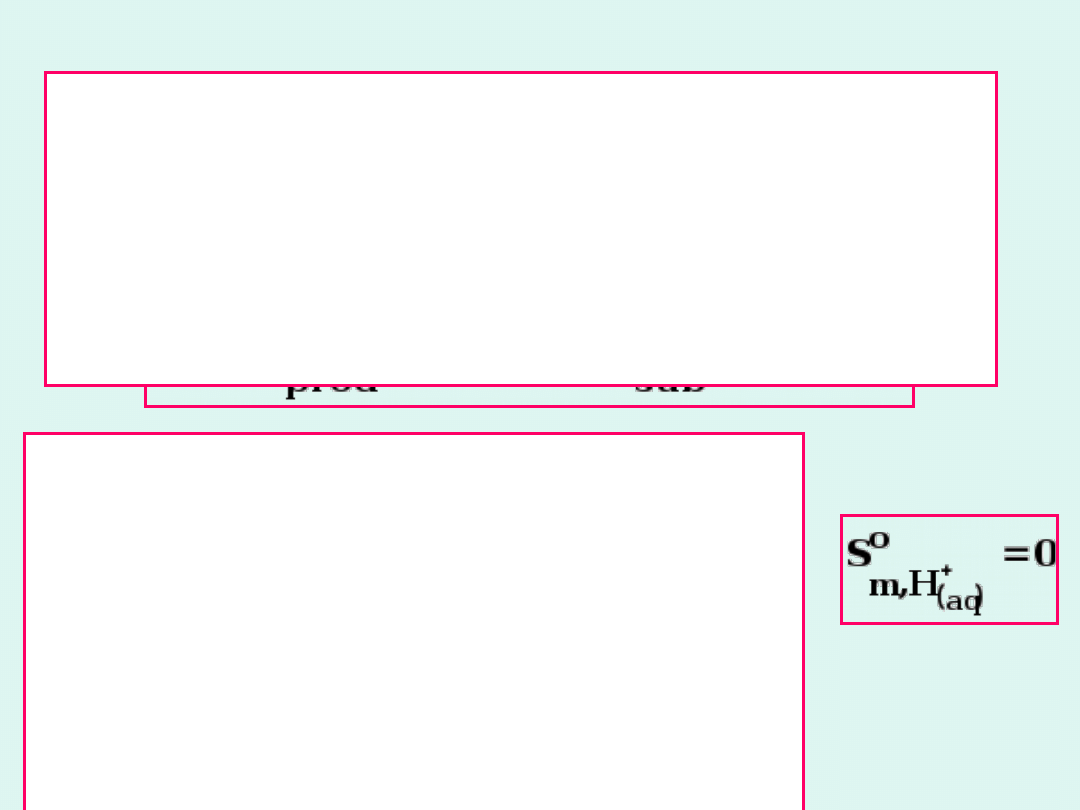
Standardowe 

entropie

 

Standardowa  entropia  reakcji

  jest 

różnicą  entropii  standardowych  czystych 
rozdzielonych 

produktów 

i 

czystych, 

rozdzielonych  substratów,  pomnożonych 
przez 

odpowiednie 

współczynniki 

stechiometryczne. 

Dla 

jonów 

definiuje 

się 

standardowe  entropie  jonu

  jako 

entropie  tworzenia  jednego  mola 

całkowicie  zsolwatowanych  jonów 

w 

rozcieńczeniu 

nieskończenie 

wielkim  z  czystych,  rozdzielonych 

pierwiastków, 

przy 

czym 

standardowa 

entropia 

uwodnionego  jonu  wodorowego  w 

dowolnej 

temperaturze 

wynosi 

zero. 

Wnioski z drugiej zasady 

termodynamiki

dq

dS

T

�

Dla procesów adiabatycznych   

q = 0   đq = 0

0

S

    

0

dS

adiab

adiab







0

S

    

0

dS

0

S

    

0

dS

0

S

    

0

dS

adiab

adiab

adiab

adiab

adiab

adiab



















Proces samorzutny

Stan równowagi 
(proces odwracalny)

Proces 
niesamorzutny 
(zachodziłby 
samorzutnie w 
odwrotnym 
kierunku)

Aby zastosować drugą zasadę termodynamiki do 
typowych warunków, w jakich zachodzą procesy 
fizyczne (np. przemiany fazowe) i reakcji 
chemicznych trzeba zdefiniować dwie nowe 
funkcje termodynamiczne.

Energia 
swobodna 
Helmholtza

Entalpia 
swobodna 
Gibbsa

TS

U

F





TS

H

G





Energia swobodna i entalpia swobodna są 
funkcjami stanu.

 

1

dw

Vdp

SdT

dG

dw

Vdp

SdT

TdS

dG

TdS

SdT

TdS

dG

dH

  

  

SdT

TdS

dH

dG

dw

Vdp

dH

TdS

T

dw

Vdp

dH

dS

















































/

'

'

'

'

'

dw

Vdp

SdT

dG









Jeżeli proces przebiega w stałej temperaturze i 

pod stałym ciśnieniem, to :

p = const  dp =0

 i 

T = const  dT = 0

'

,

dw

dG

T

p



Proces samorzutny

Stan równowagi 
(proces odwracalny)

Proces 
niesamorzutny 
(zachodziłby 
samorzutnie w 
odwrotnym 
kierunku)

'

'

'

'

'

'

,

,

,

w

G

   

dw

dG

w

G

   

dw

dG

w

G

   

dw

dG

T

p,

T

p

T

p,

T

p

T

p,

T

p



















Jeżeli proces przebiega w stałej temperaturze i 

pod stałym ciśnieniem i dodatkowo nie ma pracy 

nieobjętościowej, to :

p = const  dp =0

 i 

T = const  dT = 0 dw’ = 0

0

dG

T

p



,

Proces samorzutny

Stan równowagi 
(proces odwracalny)

Proces niesamorzutny 
(zachodziłby 
samorzutnie w 
odwrotnym kierunku)

0

G

   

0

dG

0

G

   

0

dG

0

G

   

0

dG

T

p,

T

p

T

p,

T

p

T

p,

T

p



















,

,

,

Proces izotermiczno- izobaryczny przebiega w sposób 
samorzutny przy braku pracy nieobjętościowej, wtedy 
i tylko wtedy, gdy entalpia swobodna układu maleje.

Jeżeli proces przebiega w stałej temperaturze i w 

stałej objętości, to :

V = const  dV =0

 i 

T = const  dT = 0

'

,

dw

dF

T

V



Można wykazać, że :

'

dw

pdV

SdT

dF









Jeżeli dodatkowo nie ma pracy 
nieobjętościowej  

dw’ = 0

0

dF

T

V



,

Proces izotermiczno- izochoryczny przebiega w 
sposób samorzutny przy braku pracy 
nieobjętościowej, wtedy i tylko wtedy, gdy energia 
swobodna układu maleje.

'

dw

Vdp

SdT

dG









Jeżeli proces zachodzi w sposób odwracalny, 
bez wykonywania pracy nieobjętościowej, 
to :

Vdp

SdT

dG







Entalpia swobodna jest funkcją temperatury i 
ciśnienia 

G(T,p)

.

dp

p

G

dT

T

G

dG

T

p





































V

p

G

  

i

  

S

T

G

T

p







































Entalpia swobodna jest funkcją stanu. 
Wobec tego jej różniczka jest różniczką 
zupełną. Wynika stąd, że drugie pochodne 
mieszane entalpii swobodnej muszą być 
sobie równe.

p

T

p

T

2

T

p

2

T

V

p

S

T

p

G

p

T

G















































































,

,

Relacja 

Maxwella

Zależności pomiędzy funkcjami 

termodynamicznymi

Standardowa 

entalpia 

swobodna 

tworzenia 

związku 

chemicznego

 

to 

zmiana  entalpii  swobodnej  towarzysząca 
utworzeniu  1  mola  związku  z  czystych, 
rozdzielonych  pierwiastków  w  warunkach 
standardowych,  przy  czym  powstający 
związek  jak  i  pierwiastki  muszą  być  w 
najtrwalszej  w  tych  warunkach  odmianie 
termodynamicznej.  Standardowa  entalpia 
swobodna  tworzenia  pierwiastków  w  ich 
najtrwalszej  odmianie  termodynamicznej 
wynosi zero.

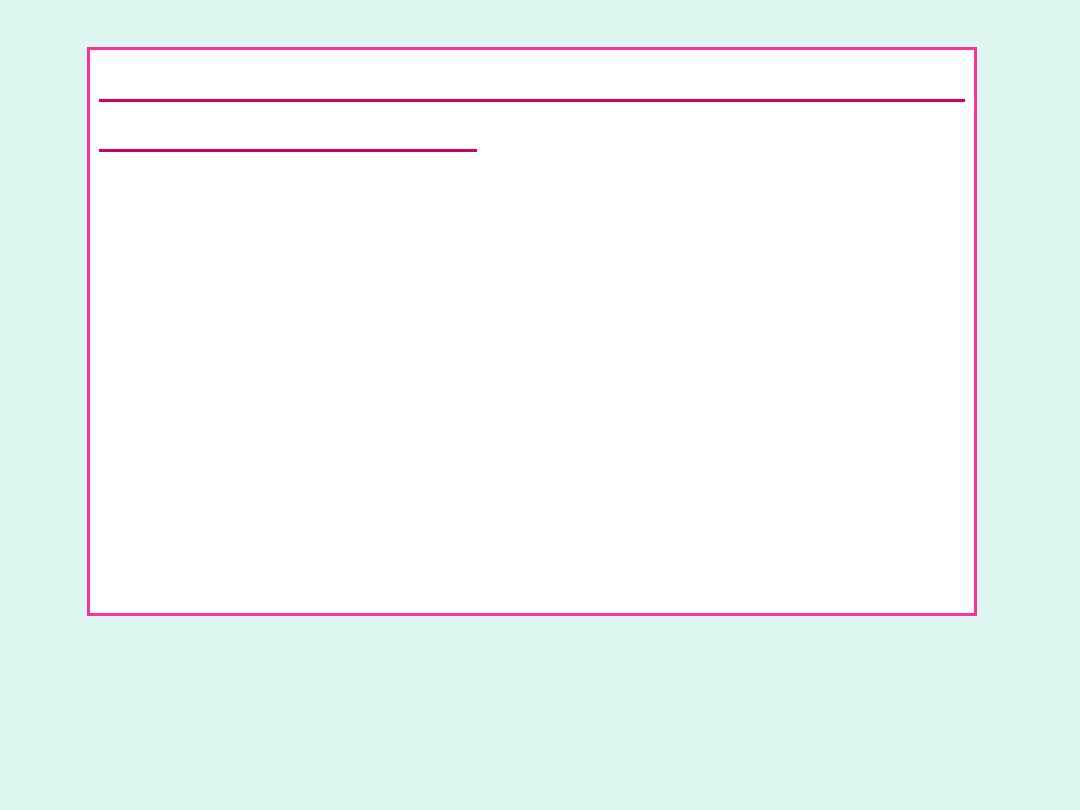
Standardowa 

entalpia 

swobodna 

tworzenia  jonu

  to  zmiana  entalpii 

swobodnej  towarzysząca  powstaniu  1 
mola 

solwatowanych 

jonów 

w 

rozcieńczeniu  nieskończenie  wielkim  z 
czystych,  rozdzielonych  pierwiastków  w 
warunkach 

standardowych. 

Standardowa 

entalpia 

swobodna 

tworzenia 

uwodnionego 

jonu 

wodorowego  w  dowolnej  temperaturze 
wynosi zero. 

 

0

G

o

H

tw

aq





































sub

sub

o

tw

i

prod

prod

o

tw

i

o

r

G

G

G

Standardowa 

entalpia 

swobodna 

reakcji

  (standardowa  zmiana  entalpii 

swobodnej  reakcji)  bądź  przemiany 
fizycznej  to  różnica  entalpii  swobodnych 
czystych,  rozdzielonych  produktów  i 
czystych,  rozdzielonych  substratów  w 
stanie  standardowym  w  tej  samej, 
określonej temperaturze. 

S

T

H

G













Udziały decydujące o samorzutności 

procesów       przy p = const i T = 

const

0

G

 

T

p,





Zależność entalpii swobodnej 

od temperatury

V

p

G

   

S

T

G

Vdp

SdT

dG

T

p













































Gdy ciśnienie jest 
stałe, to :

SdT

dG

p





Ponieważ entropia ma zawsze wartość dodatnią, 
to wraz ze wzrostem temperatury, entalpia 
swobodna maleje.

p

p

p

T

G

T

G

H

T

G

T

H

G

S

T

G

TS

H

G

































































T

H

G

T

G

p





















Równanie Gibbsa-

Helmholtza

 

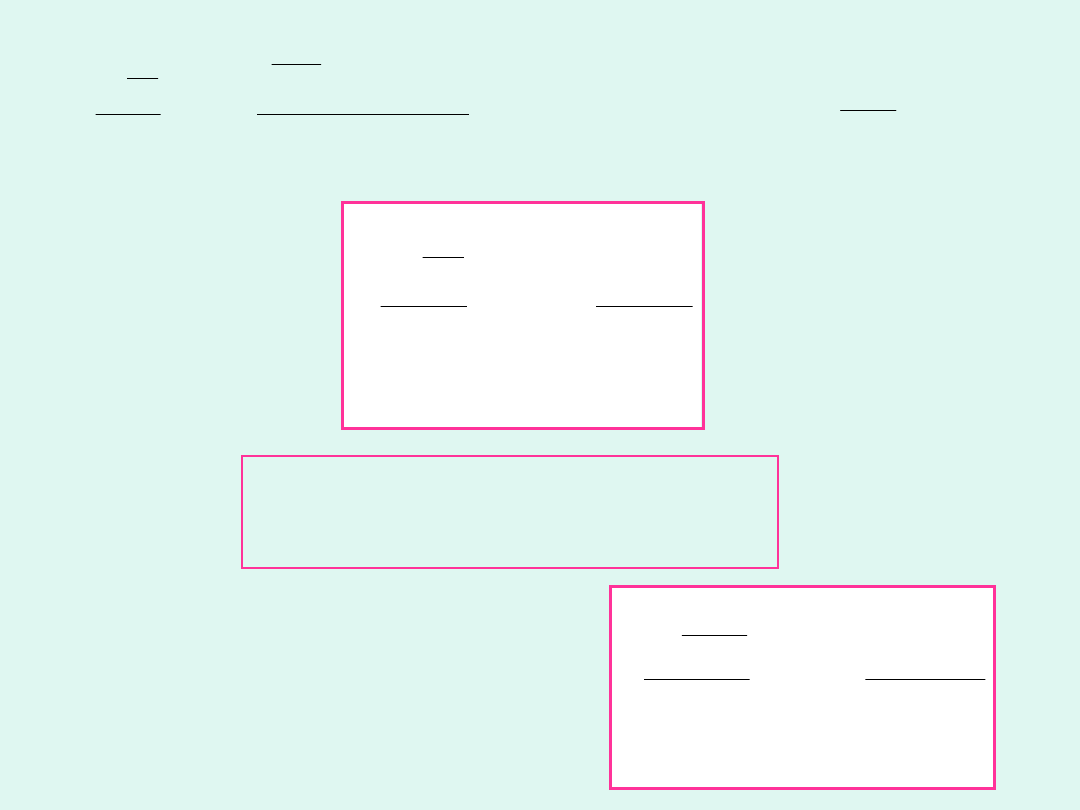
2

p

T

G

p

T

G

T

G

T

T



























p

T

G

T

H

G





















2

p

T

G

T

H

T























Równanie Gibbsa-

Helmholtza

2

p

T

G

T

H

T



























Dla procesu 
izobarycznego :

Zależność entalpii swobodnej 

od ciśnienia

V

p

G

   

S

T

G

Vdp

SdT

dG

T

p













































Gdy temperatura jest 
stała, to :

p

dG

Vdp

=

Ponieważ objętość ma zawsze wartość dodatnią, 
to wraz ze wzrostem ciśnienia, entalpia 
swobodna rośnie.

Załóżmy, że mamy 1 mol gazu doskonałego.

o

p

p

p

RT

o

m

m

p

p

m

G

G

m

m

m

m

p

p

RT

dp

G

G

dp

V

dG

p

RT

V

     

dp

V

dG

o

o

m

o

m

ln



















o

o

m

m

p

p

RT

G

G

ln





o

m

G

Standardowa molowa entalpia swobodna. 
Jest funkcją temperatury.

Dla gazu doskonałego stanem 
standardowym jest stan czystego gazu 
pod ciśnieniem standardowym 

p

o

 = 10

5

 Pa

 i w dowolnej, ustalonej 

temperaturze.

Gaz 

rzeczywisty

o

o

m

m

p

f

RT

G

G

ln





f 

– lotność

Lotność jest to funkcja termodynamiczna, zależna od 
ciśnienia i temperatury, dobierana tak, aby spełnione 
było powyższe równanie.

1

p

f

0

p

   

gdy

   

p

f

lim

0

p









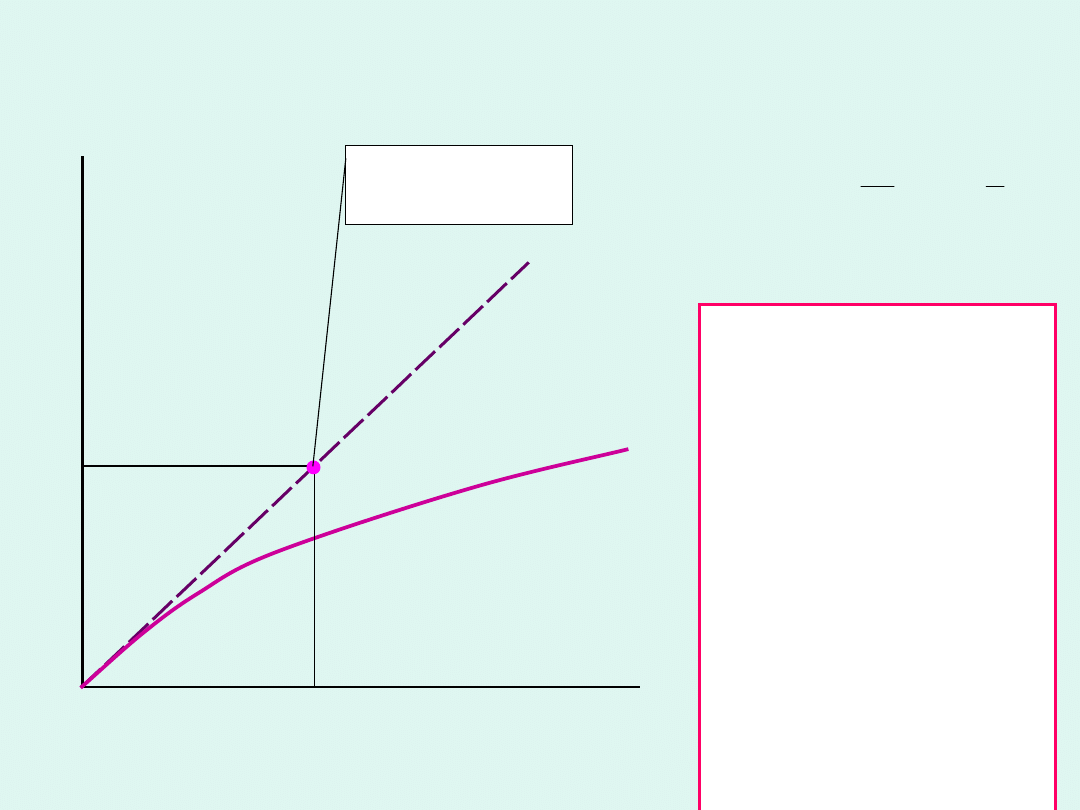
gaz 
doskona
ły

gaz 
rzeczywis
ty

hipotetyczny 
stan 
standardowy

l
o
t
n
o
ś
ć

ciśnienie

p

o

f

o

0

1

p

f

     

p

f

ln

RT

G

G

lim

0

p

o

o

m

m









Stan  standardowy

 

dla 

gazu 

rzeczywistego to stan 
gazu rzeczywistego w 
hipotetycznym  stanie 
pod 

ciśnieniem 

standardowym 

(10

5

 

Pa), 

w 

określonej 

temperaturze,  gdyby 
zachowywał  się  on 
jak 

przy 

bardzo 

niskich 

ciśnieniach 

(przy 

ciśnieniu 

dążącym do zera). 

Sposób przyjęcia stanu standardowego dla 

gazu rzeczywistego

o

o

m

m

p

p

RT

G

G









ln

1

0

p

   

gdy

   

1

lim

0

p













p

f







 



 - współczynnik lotności