GEODEZJA

Wiadomości podstawowe

Zadania geodezji

Geodezja jest nauką zajmującą się określaniem wielkości i
kształtu Ziemi (lub też jej części) oraz tworzeniem
konstrukcji potrzebnych do pomiaru a następnie do
rysunkowego zobrazowania jej fizycznej powierzchni.
Ostatecznym więc wynikiem prac geodezyjnych są mapy w
różnych skalach, obrazujące powierzchnię Ziemi zarówno
pod względem sytuacyjnych, jak i wysokościowym,
W geodezji rozróżniamy następujące działy:
1.Geodezja niższa (ogólna) zajmuje się pomiarami
mniejszych
obszarów,

które

można

uważać

za

płaskie,

oraz

sporządzaniem map wielkoskalowych.
2.Topografia zajmuje się pomiarem terenu ze szczególnym
uwzględnieniem jego rzeźby oraz sporządzaniem map w
skalach średnich, przeważnie dla celów wojskowych.
3.Rachunek wyrównawczy zajmuje się matematycznym
ujęciem wyników pomiarów, wyrównaniom nieuniknionych
błędów pomiarowych i oceną dokładności wyników prac
geodezyjnych.
4. Fotogrametria zajmuje się opracowaniem planów i map
na podstawie zdjęć fotograficznych (naziemnych i
lotniczych).

Zadania geodezji c.d.

5.Kartografia zajmuje się zagadnieniem odwzorowania
krzywej
powierzchni Ziemi na płaszczyznę, opracowaniem map oraz
ich reprodukcją,
6.Geodezja wyższa zajmuje się triangulacją podstawową i
niwelacją precyzyjną kraju lub kontynentu oraz. wszelkimi
obliczeniami geodezyjnymi, gdy powierzchnią odniesienia
jest kula lub spłaszczona elipsoida obrotowa .
7.Grawimetria zajmuje się zagadnieniami wyznaczenia
kształtu bryły ziemskiej z pomiarów przyspieszenia siły
ciężkości na jej powierzchni.
8. Astronomia geodezyjna zajmuje się określaniem
położenia punktów na Ziemi na podstawie obserwacji ciał
niebieskich,
9. Geodezja jest stosowana w różnych dziedzinach
gospodarki narodowej tworząc dział zwany geodezją
gospodarczą. Obejmuje on geodezję w zastosowaniu do
prac inżynieryjno-budowlanych (geodezja inżynieryjna),
górniczych (geodezja górnicza), urządzenioworołnych,
leśnych itp

.

 

Układy współrzędnych

W zależności od przyjętej powierzchni odniesienia stosowane są
różne układy współrzędnych do określania położenia punktów.
Jeżeli za powierzchnię odniesienia przyjmiemy elipsoidę lub
kulę, wówczas stosujemy układ współrzędnych geograficznych
 i )

Położenie

dowolnego

punktu

P

na

powierzchni kuli o znanym promieniu R
jest określone jednoznacznie przez dwa
kąty zwane szerokością i długością
geograficzną. Szerokość geograficzna 

jest to kąt zawarty miedzy promieniem kuli
w punkcie P a płaszczyzną równika. Kąt
ten uważamy za dodatni, jeżeli P leży na
północ od równika, a ujemny, gdy P leży na
południe

od

równika.

Szerokość

geograficzną liczymy od równika w
kierunku

biegunów.

Szerokość

geograficzna  zmienia się od 0° do +90°

dla półkuli północnej i od 0° do -90° dla
półkuli południowej. Wszystkie punkty
położone na danym równoleżniku mają
jednakową szerokość geograficzną

Układy współrzędnych c.d.

Długość geograficzna  jest to kąt zawarty

między południkiem początkowym, który
nazywamy południkiem zerowym, a
południkiem przechodzącym przez punkt P.
Długość geograficzna liczy się od 0° do
360° lub też od południka zerowego na
wschód - od 0° do +180° i na zachód - od
0° do -180°. Punkty położone na kuli
między biegunami i znajdujące się na tej
samej połowie łuku południka mają
jednakową długość geograficzną

.

Południki i równoleżniki tworzą na powierzchni kuli siatkę

geograficzną, która jest siatką ortogonalną, ponieważ
południki i równoleżniki przecinają się pod kątem prostym.

Jeżeli przyjmiemy elipsoidę obrotową za powierzchnię

odniesienia, określenie położenia dowolnego punktu P jest
podobne jak na kuli.

Szerokością geograficzną punktu P na elipsoidzie obrotowej
oznaczonej symbolem B jest kąt zawarty. między normalną do
elipsoidy w punkcie P a płaszczyzną równika

.

Układy współrzędnych c.d.

Normalna ta nie przechodzi przez środek elipsoidy, z wyjątkiem
punktów leżących na równiku i na biegunach. Szerokość
geograficzną na elipsoidzie liczymy podobnie jak na kuli.
Długość geograficzną na elipsoidzie oznacza się symbolem - L i
liczy się tak samo jak w przypadku kuli . Współrzędną B

nazywamy szerokością geodezyjną, a współrzędną L długością
geograficzną. Siatka południków i równoleżników tworzy na
powierzchni elipsoidy siatkę geograficzną ortogonalną

.

Przyjmując płaszczyznę za powierzchnię odniesienia, położenie
punktów może być określone za pomocą układu współrzędnych
prostokątnych lub układu współrzędnych biegunowych Układ
współrzędnych prostokątnych składa się z dwu prostych
przecinających się pod kątem prostym. Proste te noszą nazwę osi
współrzędnych, a punkt przecięcia prostych jest początkiem
układu. Oś współrzędnych x, zwana osią odciętych, jest
skierowana na północ, zaś oś współrzędnych y, zwana osią
rzędnych, jest skierowana na wschód.

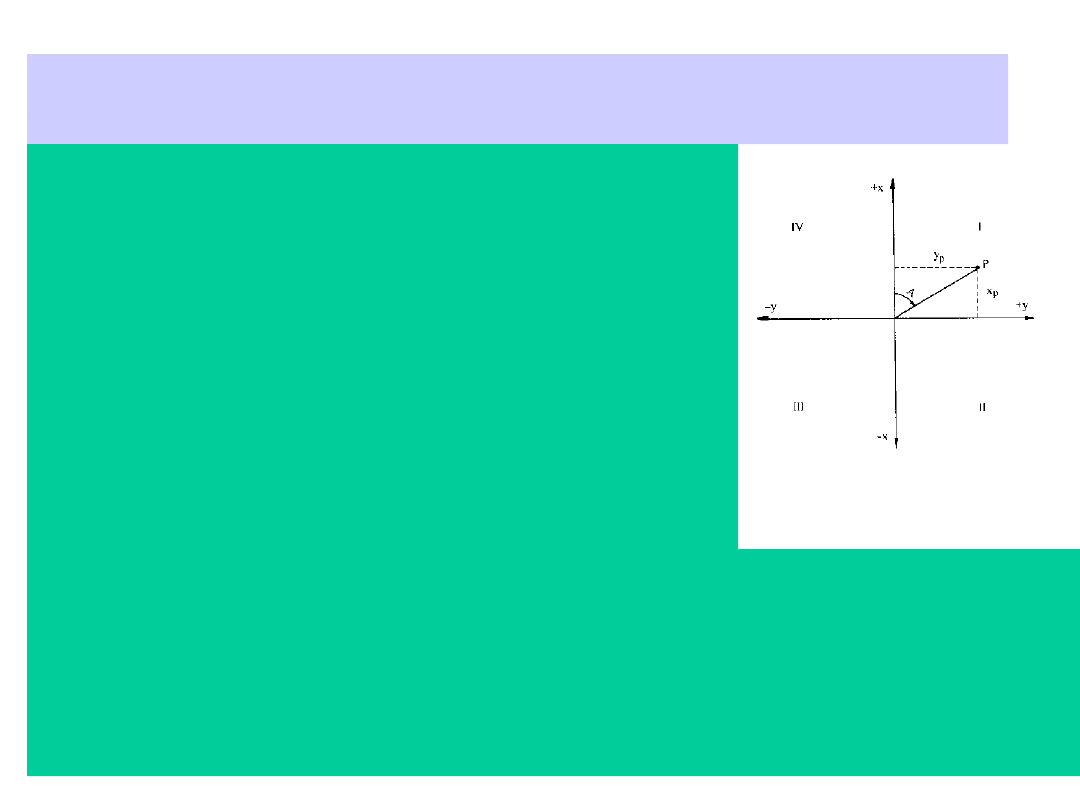
Układy współrzędnych c.d.

Kierunek północny osi x i wschodni osi y

przyjmujemy jako dodatnie. Kąt zawarty
między dodatnim kierunkiem osi x a danym
kierunkiem, liczony od osi x w prawo
(zgodnie z kierunkiem wskazówek zegara),
nazywamy azymutem i oznaczamy symbolem
A Należy zwrócić uwagę, że oznaczenie osi
współrzędnych jest odwrotne niż w układzie
przyjętym w matematyce. Osie układu
współrzędnych dzielą płaszczyznę na cztery
ćwiartki. W układzie geodezyjnym ćwiartki
te oznacza się w przeciwnym kierunku niż w
układzie matematycznym.

Osie układu współrzędnych dzielą płaszczyznę na cztery

ćwiartki. W układzie geodezyjnym ćwiartki te oznacza się w
przeciwnym kierunku niż w układzie matematycznym. Położenie
punktu P na płaszczyźnie określone jest przez dwie współrzędne
prostokątne, odciętą i rzędną. Odcięta x stanowi odległość
punktu P od osi y, a rzędna y stanowi odległość punktu P od osi x.

Układy współrzędnych c.d.

Znaki współrzędnych w poszczególnych ćwiartkach są

następujące: w pierwszej ćwiartce x dodatnie i y dodatnie, w
drugiej ćwiartce x ujemne, a y dodatnie, w trzeciej ćwiartce x
ujemne y ujemne, w czwartej ćwiartce x dodatnie, y ujemne.

Punkty położone pod lub nad płaszczyzną xy otrzymują

trzecią współrzędną, z która jest odległością punktu od
płaszczyzny xy.

Drugim sposobem określania położenia punktu jest

układ wspó

ł

rzędnych biegunowych, składający się ze

sta

ł

ego punktu początkowego B zwanego biegunem

oraz z kier

u

nku

ł

ączącego punkt B z dowolnym

stałym punktem Z. Kierunek ten nazywany je

s

t osią

biegunową. Kierunek osi biegunowej obiera się
dowolnie, w ramach istniejących możliwości.

Położenie punktu w układzie biegunowym określają

dwie współrzędne: odległość od bieguna r zwana
promieniem wodzącym oraz kąt a zawarty miedzy
osią biegunową a promieniem wodzącym .

Osnowa geodezyjna

Pomiary geodezyjne wykonuje się w oparciu o punkty o znanych
współrzędnych x, y i wysokości H. Punkty te nazywamy osnową
geodezyjną.
Osnowy geodezyjne stanowią usystematyzowany zbiór punktów
geodezyjnych, dla których określono matematycznie ich
wzajemne położenie.
Ze względu na sposób przedstawienia wzajemnego położenia
punktów osnowy geodezyjne dzieła się na:
a/ osnowy poziome, w której wzajemne położenie punktów na
powierzchni odniesienia zostało określone w przyjętym układzie
współrzędnych geodezyjnych,
b/ osnowę wysokościowa w której wysokości punktów zostały
określone względem przyjętego poziomu odniesienia. Ze
względu na rolę i znaczenie dla prac geodezyjnych osnowy
geodezyjne dziele się na :
a/ osnowy podstawowe,
b/ osnowy szczegółowe
c/ osnowy pomiarowe,

Osnowa geodezyjna c.d.

Osnowy podstawowe są zbiorami punktów geodezyjnych
wyznaczanych w poszczególnych sieciach w celu .
a/ badania kształtu i wymiarów Ziemi,
b/ nawiązania i wyrównania osnów szczegółowych w
państwowym układzie współrzędnych i państwowym układzie
wysokości.
Osnowy szczegółowe są zbiorami punktów geodezyjnych
wyznaczanych w poszczególnych sieciach w celu:
a/nawiązania, i wyrównania osnów pomiarowych w
państwowym układzie współrzędnych i państwowym układzie
wysokości,
b/ nawiązania do państwowego układu współrzędnych i
państwowego układu wysokości zdjęć fotogrametrycznych i
numerycznych modeli terenu.
Osnowy pomiarowe są zbiorami punktów geodezyjnych
wyznaczanych w poszczególnych sieciach w celu:
a/ oparcia pomiarów sytuacyjnych i rzeźby terenu,
b/ wyznaczania projektów na gruncie,
c/ wykonywania pomiarów realizacyjnych przy obsłudze
inwestycji / osnowa realizacyjna/,
d/ badania i określania przemieszczeń lub odkształceń obiektów
budowlanych i podłoża gruntowego

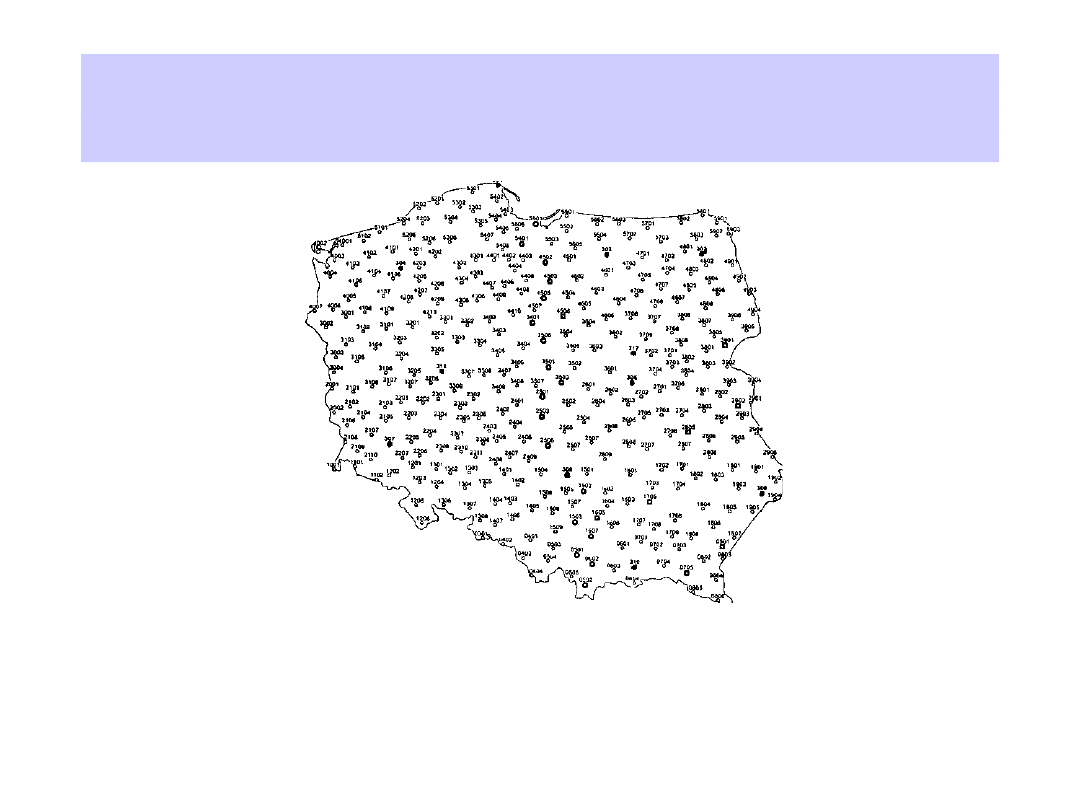
Osnowa geodezyjna c.d.

Sieć punktów osnowy I klasy założonych metodą

satelitarną GPS - POLREF

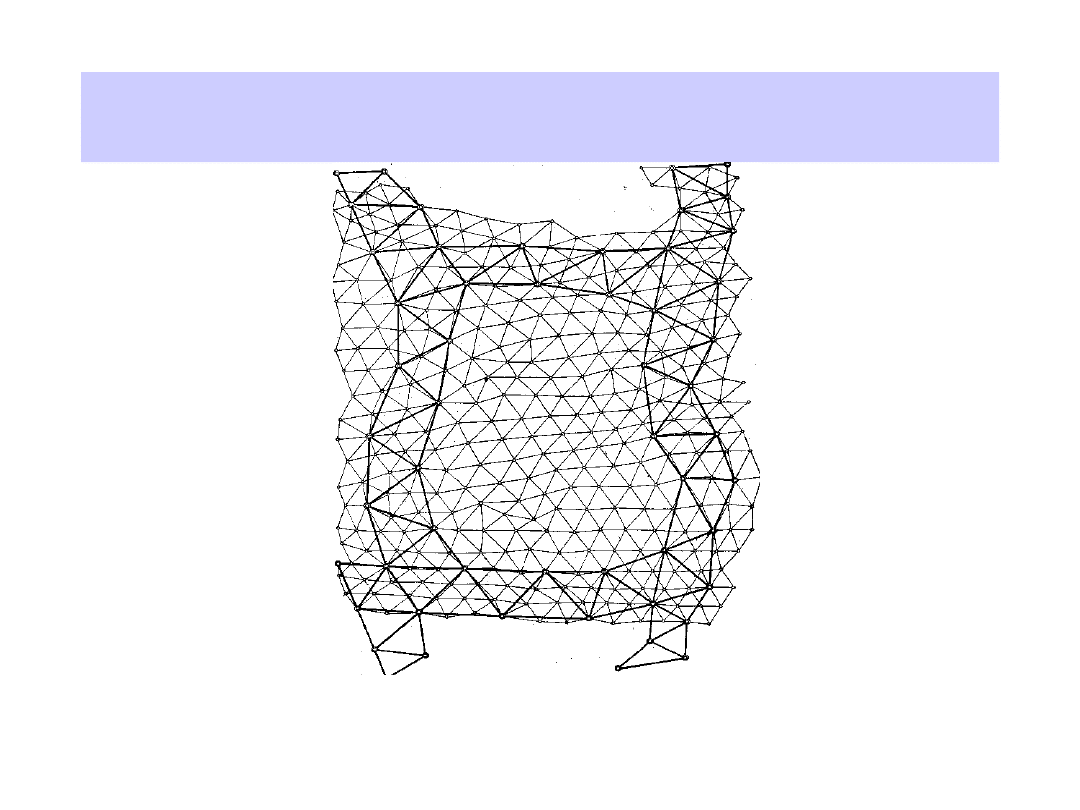
Osnowa geodezyjna c.d.

Sieć punktów triangulacyjnych

Osnowa pozioma

Klasyfikacja poziomej osnowy geodezyjnej
Podstawowa i szczegółowa geodezyjna osnowa pozioma dzieli
się na trzy klasy oznaczane cyframi rzymskimi Punkty osnowy
pomiarowej nie są dzielone na klasy
Miarą dokładności podstawowej osnowy jest błąd względny
długości boku po wyrównaniu, który powinien być mniejszy od
5x10

-6

/1:200 000/

przeciętna gęstość punktów osnowy podstawowej powinna
wynosić 1 punkt na około 50 km

2

.

Szczegółowa osnowa pozioma jest zbiorem punktów II i III
klasy, których średni błąd położenia punktu po wyrównaniu
powinien być mniejszy od 0.10 m.
Szczegółowa osnowa II klasy jest rozwinięciem osnowy l klasy.
Miara dokładności szczegółowej osnowy II klasy jest średni błąd
położenia punktu po wyrównaniu., który powinien być mniejszy
od 0.05 m.

Osnowa pozioma c.d.

Szczegółowa osnowa III klasy jest rozwinięciem osnowy I i II
klasy
Szczegółowa osnowa III klasy jest zbiorem punktów sieci w
których kąty, kierunki, boki i azymuty pomierzono metodami
geodezyjnymi bezpośrednio w terenie, bądź pomiary terenowe
zastąpiono obserwacjami z opracowań fotogrametrycznych
zdjęć lotniczych metodami aerotriangulacji analitycznej.
Miarę dokładności szczegółowej osnowy III klasy jest średni
błąd położenia punktu po wyrównaniu, który powinien być
mniejszy od 0,10 m.
Pomiarowa osnowa jest zbiorem punktów geodezyjnych
założonych w terenie tak aby służyły celom określonym powyżej

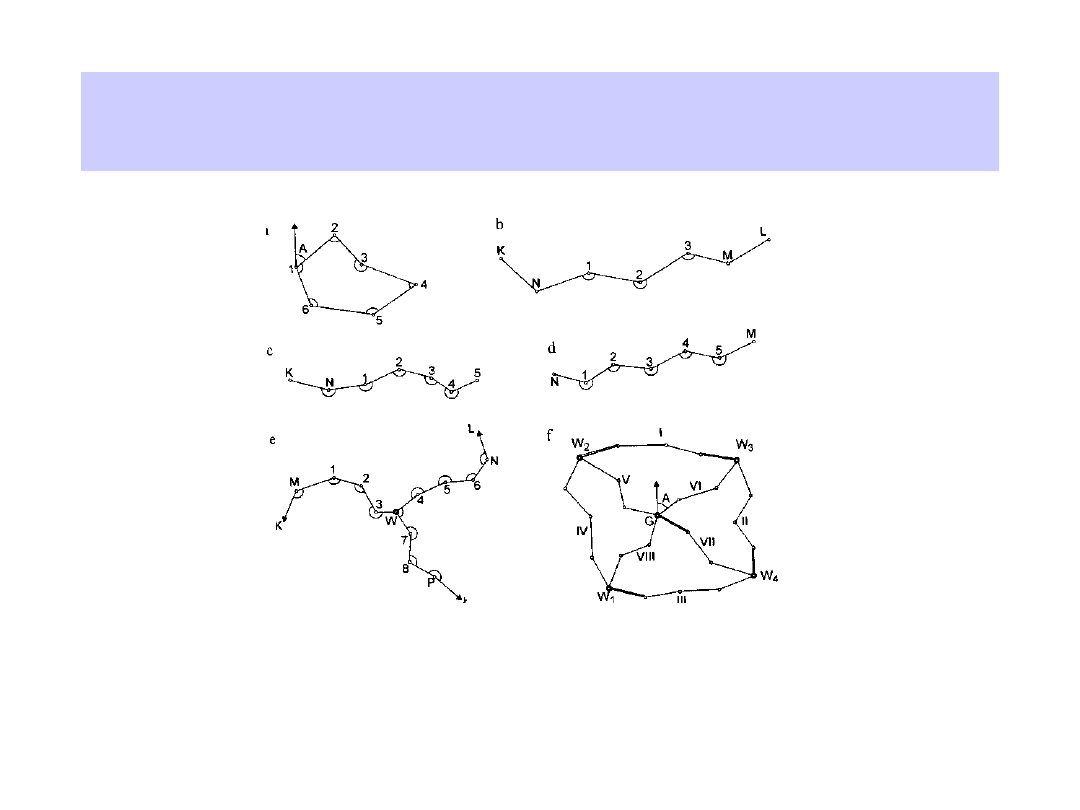
Osnowa pozioma c.d.

Przykłady sieci poligonowych – klasa III

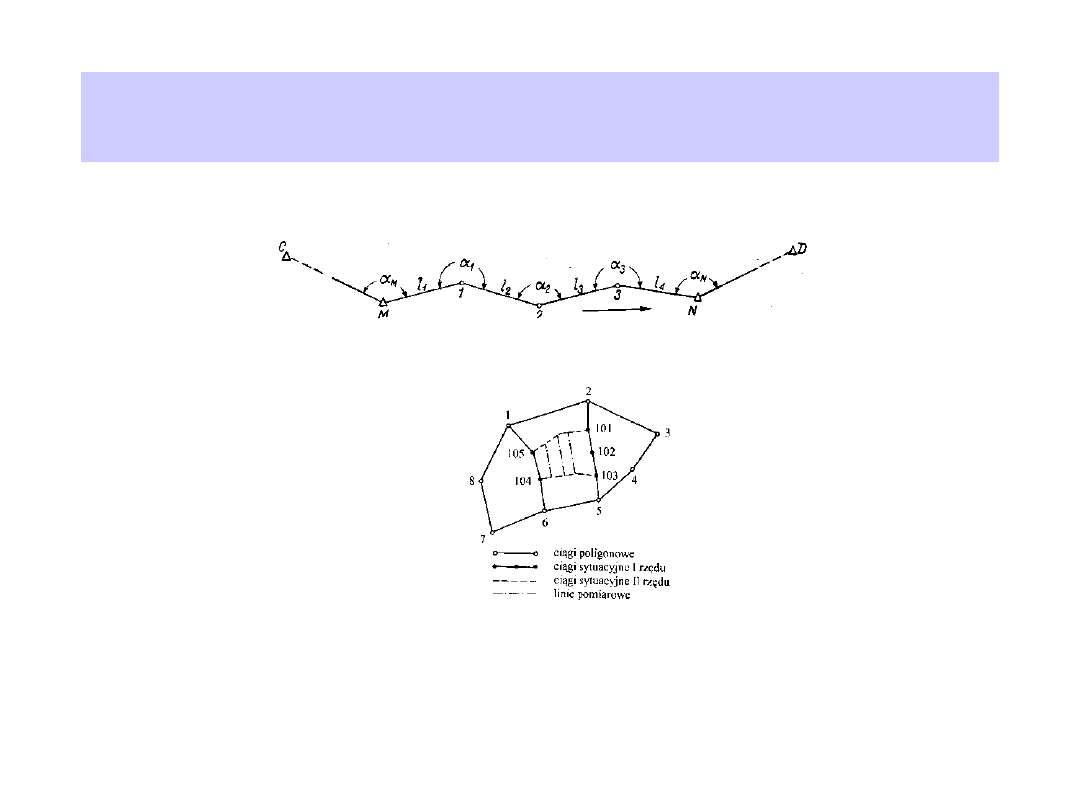
Osnowa pozioma c.d.

Ciąg poligonowy

Sieć pomiarowa

Osnowa geodezyjna

Osnowa wysokościowa

Podstawowa i szczegółowa wysokościowa osnowa geodezyjna
dzieli się na cztery klasy oznaczane cyframi rzymskimi.
Punkty osnowy pomiarowej nie są dzielone na klasy.
Standardowe cechy geodezyjnych osnów wysokościowych
zawiera tablica:

Klasa i nazwa

Punkty

nawiązania

Średni błąd

niwelacji (po

wyrównaniu)

Średni błąd

wysokości

punktu

I podstawowa

1 mm/km

II podstawowa

I kl,

2 mm/km

-

III

szczegółowa

I i lI kl

4 mm/km

0,01 m

IV

szczegółowa

I-III kl.

10 mm/km

 0,02 m

Pomiarowa

l-IVkl

20 mm/km

 0,10m

Jedną z najczęstszych form opracowań pomiarów geodezyjnych

są mapy.

Mapa jest odtworzeniem w odpowiednim zmniejszeniu

trójwymiarowej przestrzeni całej Ziemi lub jej mniejszych
obszarów na dwuwymiarowej płaszczyźnie przy zastosowaniu
odpowiednich reguł matematycznych oraz przy wykorzystaniu
umownych znaków graficznych.

Powierzchnia kuli lub elipsoidy, ze względu na zakrzywienie, nie

da się ułożyć na płaszczyźnie bez rozciągania lub zgniatania,
czyli bez zniekształceń..

Przekształcenie obszaru kulistego na obraz płaski nazywamy

odwzorowaniem kartograficznym.

Obraz powierzchni kuli przedstawiony na płaszczyźnie będzie

zawsze zniekształcony, ale w zależności od przyjętego
rozwiązania zniekształcenia te mogą być różne. Zniekształceniu
ulegają takie elementy terenu, jak długości linii, kąty i
powierzchnie. Można jednak dobrać takie odwzorowanie, aby nie
wszystkie elementy zostały zniekształcone.

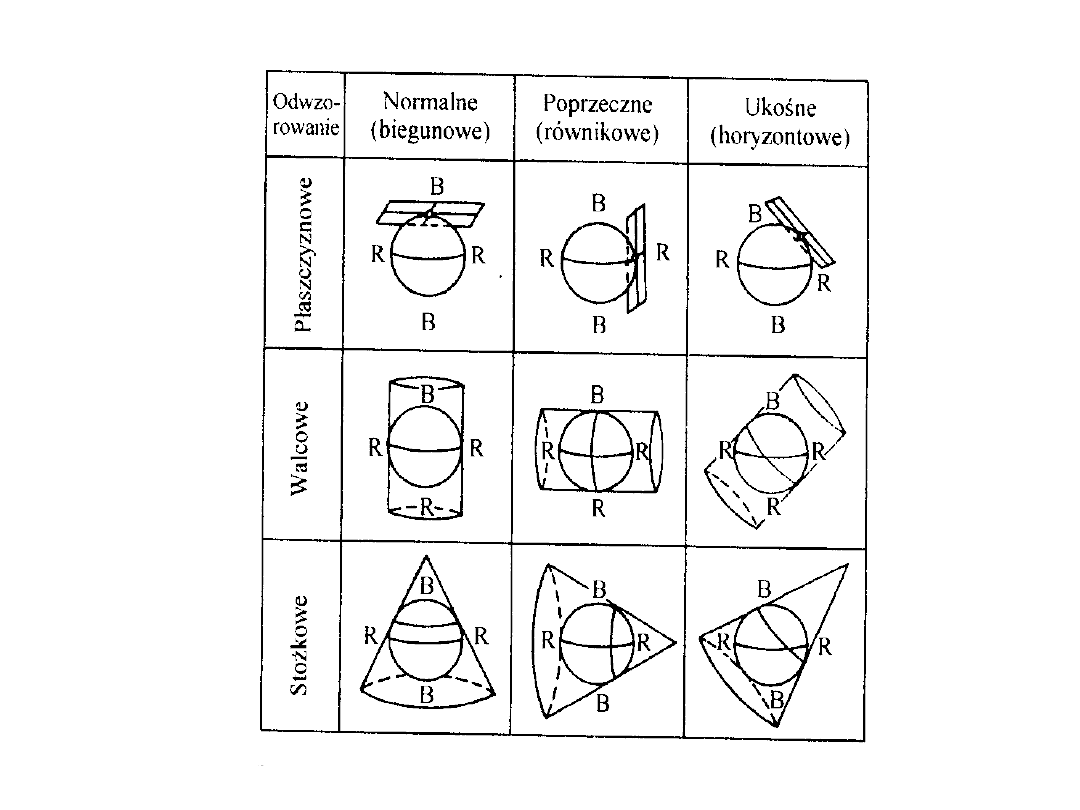
ODWZOROWANIA

Ze względu na rodzaj zniekształceń odwzorowania dzielimy na
cztery grupy:
• równokątne, konforemne, kąty na mapach są równe
odpowiednim kątom w terenie; stosowane przy opracowywaniu
map topograficznych i map dla marynarki, lotnictwa oraz dla
wojska;
•wiernopowierzchniowe, powierzchnie na mapie odpowiadają
(proporcjonalnie do skali) powierzchniom w terenie; stosowane
są przy opracowywaniu map gospodarczych, np. dla
zobrazowania gęstości zaludnienia, ilości opadów, pokładów
bogactw naturalnych
• wiernoodleglościowe, mierzone odcinki wzdłuż pewnych
kierunków, np.
wzdłuż południka lub wzdłuż równoleżnika nie są
zniekształcane; wykorzystywane przy opracowywaniu niektórych
map specjalnych, np. map łączności radiowej;
• dowolne, występują wszystkie trzy rodzaje zniekształceń

Ze względu na rodzaj powierzchni, na której odtwarza się

powierzchnię

oryginału,

rozróżnia

się

następujące

odwzorowania:

• płaszczyznowe, polegające na bezpośrednim odtworzeniu

na płaszczyźnie powierzchni elipsoidy;

• walcowe, polegające na zastosowaniu powierzchni walca

jako powierzchni pomocniczej do otrzymania obrazu elipsoidy na
płaszczyźnie; najpierw odwzorowuje się powierzchnię elipsoidy
na powierzchni walca, którą następnie po rozcięciu rozwija się
na płaszczyźnie;

• stożkowe, polegające na odwzorowaniu obrazu elipsoidy na

pobocznicy stożka, którą następnie rozwija się na płaszczyznę;

• umowne, do których zalicza się wszystkie pozostałe

odwzorowania nie należące do żadnej z poprzednich trzech
grup.

Przyjęcie danego odwzorowania kartograficznego powierzchni

Ziemi sprowadza się do dwóch zasadniczych zadań:

• utworzenia obrazu siatki geograficznej - południków i

równoleżników na płaszczyźnie mapy, czyli wyrysowanie tzw. siatki
kartograficznej, na którą następnie wnosi się treść mapy,

• wyprowadzenia wzorów matematycznych do przeliczenia

współrzędnych

geograficznych

punktów

geodezyjnych

znajdujących się na powierzchni Ziemi na współrzędne
prostokątne płaskie w danym odwzorowaniu.

Następstwem tego jest utworzenie układu współrzędnych

prostokątnych płaskich i obliczenie w tym układzie współrzędnych
wszystkich punktów geodezyjnych oraz w miarę potrzeb innych
punktów terenowych.

Najczęściej stosuje się współcześnie dla celów geodezyjnych i

kartograficznych odwzorowanie Gaussa-Kriigera, stosowane
również w Polsce. Jest to odwzorowanie równokątne, walcowe
poprzeczne. Przy czym południk środkowy obszaru odwzorowuje
się wiernie. Całej powierzchni elipsoidy ziemskiej nie można
odwzorować bez dużych zniekształceń, dlatego obszar Ziemi dzieli
się na wąskie pasy południkowe i każdy z takich pasów
odwzorowuje

się

oddzielnie,

w

oddzielnym

układzie

współrzędnych prostokątnych płaskich.

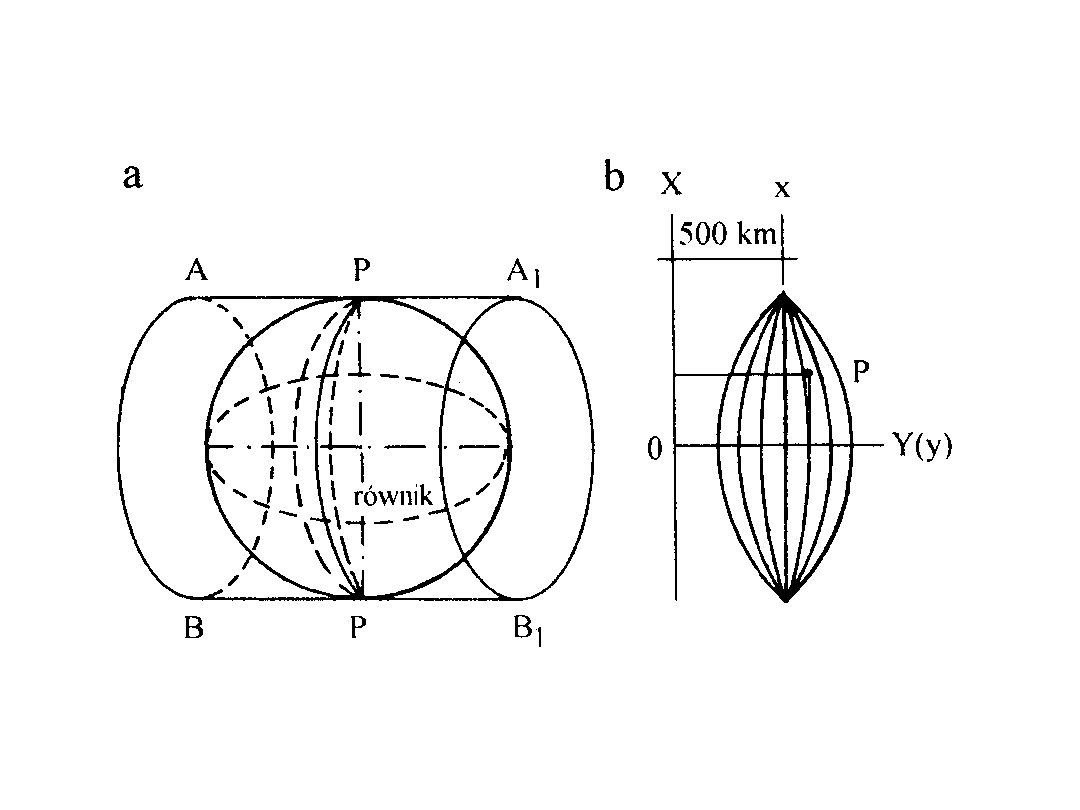
Szerokość pasów ustalono tak, aby każdy z nich można było

rozwinąć na płaszczyźnie i przedstawić na mapie bez
praktycznie odczuwalnych zniekształceń, przekraczających
stopień dokładności map. W tym celu powierzchnię elipsoidy
dzieli się na 60 pasów południkowych po 6° każdy lub 120
pasów, po 3° każdy.

Południk środkowy w każdym pasie nazywa się południkiem

osiowym. Dzieli on pas na dwie równe części - zachodnią i
wschodnią. Pasy liczy się od południka Greenwich na wschód.

Obraz płaski każdego pasa dzieli się za pomocą siatki

kartograficznej na oddzielne arkusze mapy według ustalonych
rozmiarów. W każdym pasie obrazem południka osiowego i
równika będą odcinki prostoliniowe, prostopadłe do siebie.
Wszystkie inne południki odwzorowują się jako linie krzywe,
dłuższe od południka osiowego, są więc zniekształcone.
Wszystkie równoleżniki odwzorowują się również jako krzywe,
dlatego są w pewnym stopniu zniekształcone. Nie ma natomiast
zniekształceń kątowych w obrębie całego pasa - odwzorowanie
jest więc wielokątne.

Zniekształcenia liniowe wzrastają wraz z odległością

odwzorowywanego odcinka od południka osiowego.

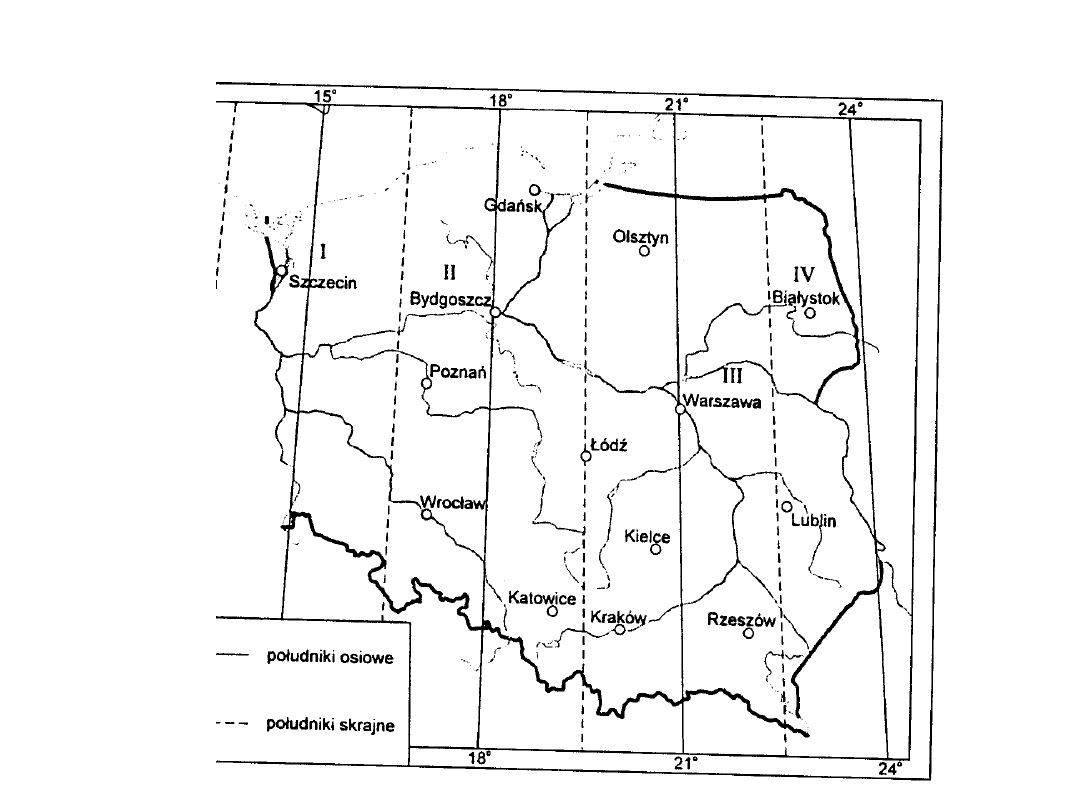
Obecnie w Polsce obowiązuje nowy układu współrzędnych
„1992". Jest to układ wykorzystujący odwzorowanie Gaussa-
Kriigera oraz „nową" elipsoidę obrotową- GRS'80.
Podzielono Polskę na pasy szerokości 3°, jak to już wcześniej
przedstawiono na rysunku. Układ ten stosowany jest do map
wielkoskalowych.

Mapy

Mapa zasadnicza

Mapa zasadnicza zawiera aktualne informacje o

przestrzennym rozmieszczeniu obiektów ogólnogeograficznych

oraz elementy ewidencji gruntów i budynków, a także sieci

uzbrojenia terenu: nadziemnych, naziemnych i podziemnych

Mapę zasadniczą wykonuje się w skali 1:500, 1:1 000, 1:2 000

lub 1:5 000, w zależności od stopnia zagęszczenia terenu

szczegółami stanowiącymi treść mapy oraz zamierzeń

inwestycyjnych. Mapę zasadniczą prowadzi się w formie

numerycznej z możliwością przedstawienia jej treści w formie

analogowej (klasycznej) w podziale sekcyjnym prostokątnym.

Podstawą do określenia formatów i numeracji arkuszy

mapy zasadniczej jest arkusz w skali 1:10 000 o wymiarach 5 km

na 8 km. Schemat podziału arkusza w skali 1:10000 na arkusze

mapy zasadniczej przedstawia rysunek

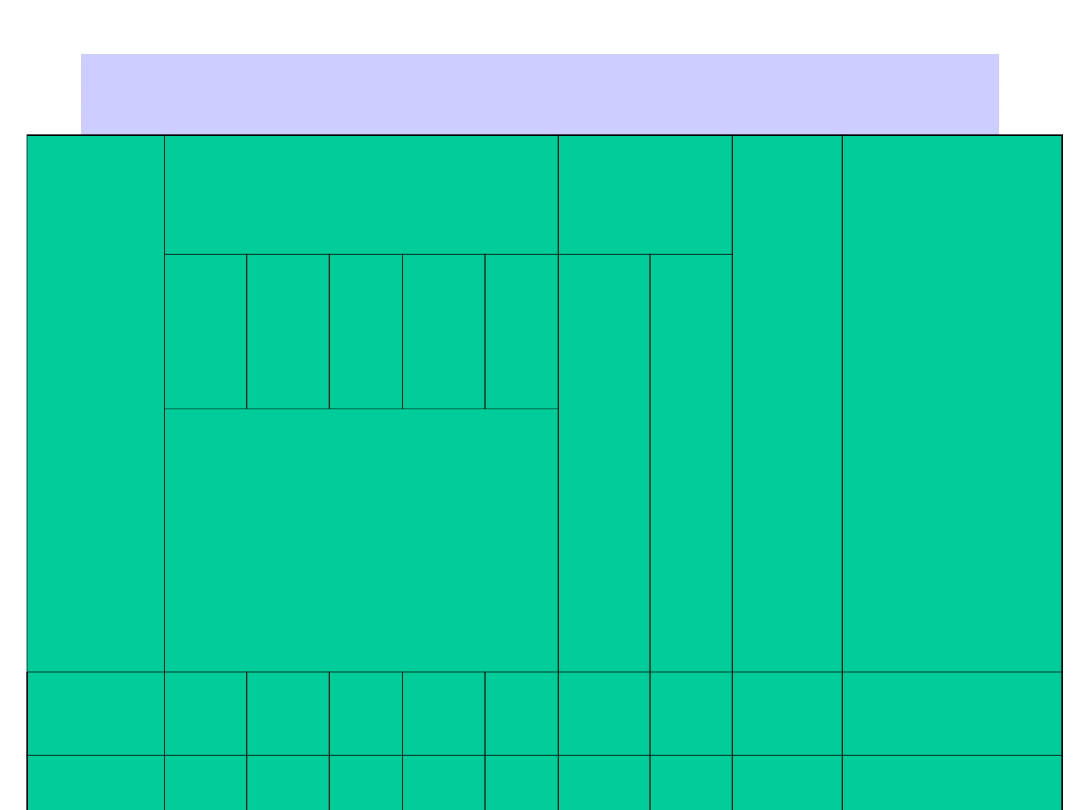
Mapa zasadnicza c.d.

Arkusz

mapy

w skali

Nr arkusza mapy w

skali

Wymiar

arkusza

[km]

Pole

powi

erzch

ni

arkus

za

[ha]

Przykład

godła

1

: 1

0

0

0

0

1

:5

0

0

0

1

: 2

0

0

0

1

: 1

0

0

0

1

: 5

0

0

W

zd

łu

ż o

si

x

W

zd

łu

ż o

si

y

Liczba arkuszy

1: 10

000

1

-

-

-

-

5.0

8.0 4000

6.115.27

1: 5
000

4

1

-

-

-

2.5

4.0 1000

6.115.27.4

1: 2

000

25

6,2

5

1

-

-

1.0

1.6

160

6.115.27.25

1: 1

000

100 25

4

1

-

0.5

0.8

40

6.115.27.25.

4

1: 500 400 100 16

4

1

0.25 0.4

10

6.115.27.25.

4.4.

Mapa zasadnicza c.d.

Schemat podziału arkusza w skali 1: 10 000 na arkusze
mapy zasadniczej
W skalach 1: 5 000, 1: 2 000, 1: 1 000, 1: 500

Mapa zasadnicza

Mapa zasadnicza w skali 1: 1000

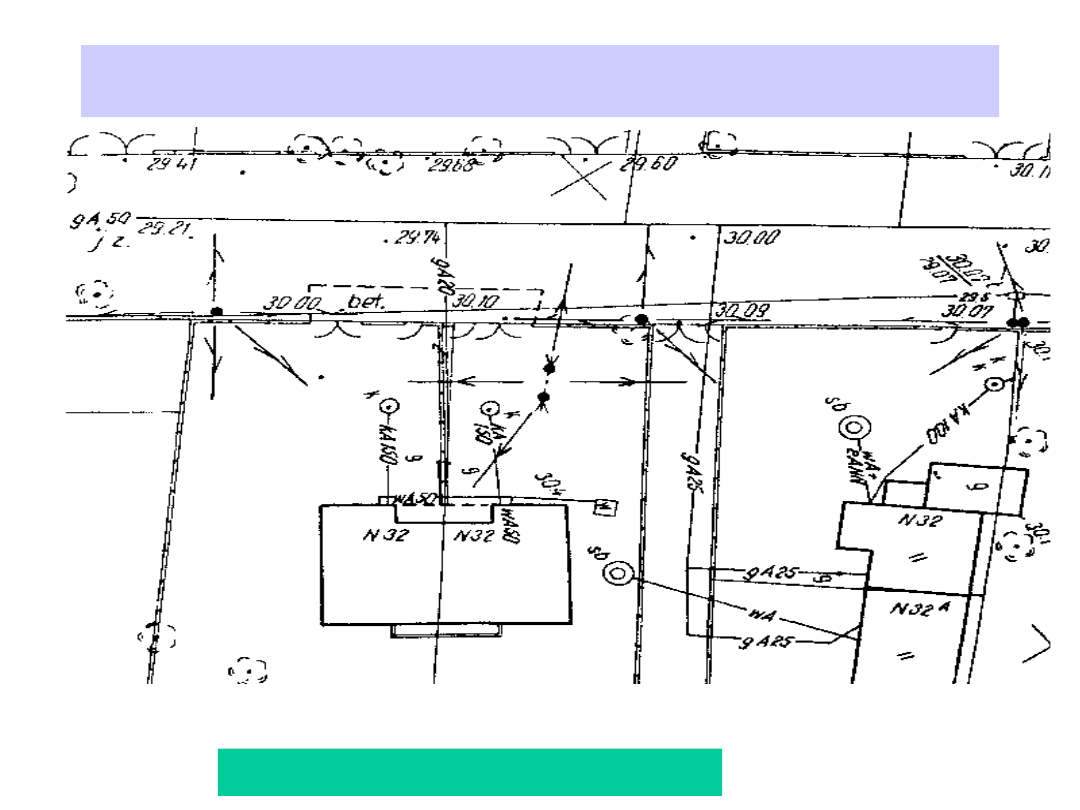
Mapa zasadnicza

Mapa zasadnicza w skali 1: 500

Mapa topograficzna

Mapy topograficzne przedstawiają elementy środowiska

geograficznego
powierzchni Ziemi i ich przestrzenne związki.
Dla obszaru całego kraju sporządza się i aktualizuje mapy
topograficzna w skali
1:10 000 oraz 1:50 000.
Mapa topograficzna w skali 1:10 000 stanowi podstawowy
materiał do redagowania mapy topograficznej w skali 1 :50 000
oraz map topograficznych w innych skalach.
Zasady podziału i oznaczania arkuszy map topograficznych
oraz orientacyjne ich
wymiary i powierzchnie przedstawia tablica i szkic
Wymiary arkuszy map topograficznych wzdłuż szerokości i
długości oraz ich powierzchnie odnoszą się do arkuszy
wypadających w tym samym pasie co arkusze podane w
przykładzie godła. Wymiary i powierzchnie arkuszy maleją ku
północy, natomiast zwiększają się ku południu.

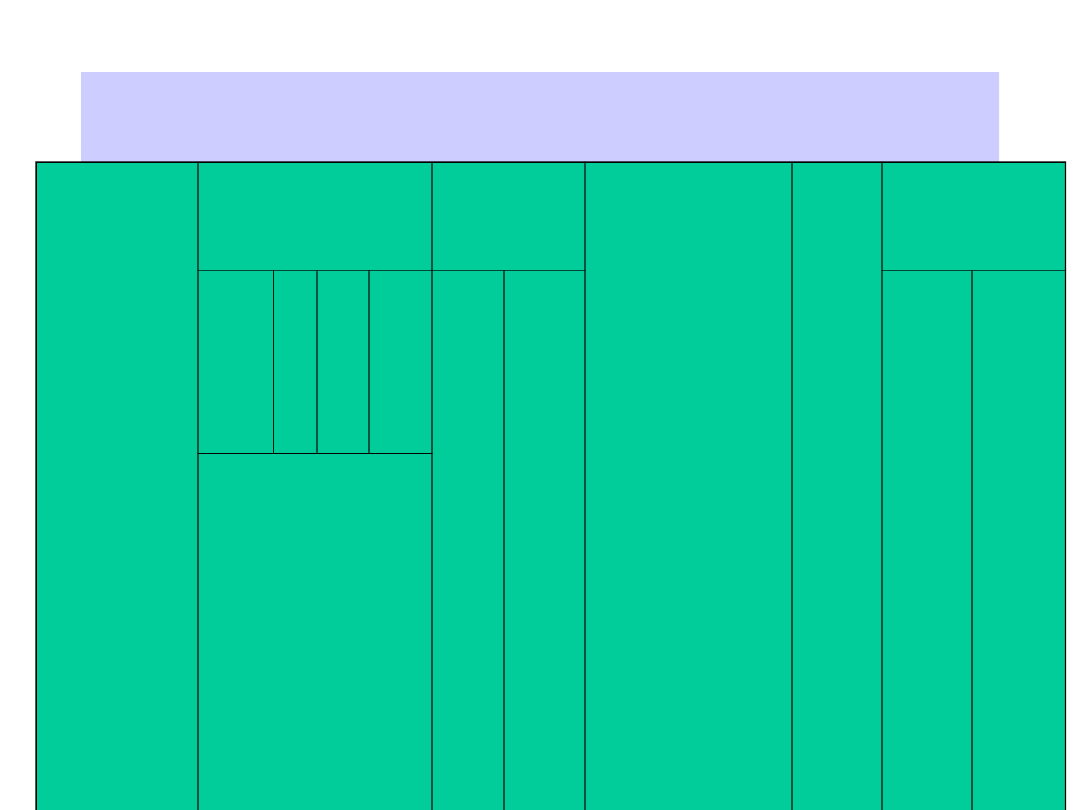
Mapa topograficzna

Arkusz w

skali

Na arkuszu

mapy w skali

Wymiary

arkusza

Przykład

godła

O

d

st

ę

p

y

sia

tk

i k

ilo

m

e

tr

o

w

e

j n

a

m

a

p

ie

Wymiary

arkusza

[km]

1

: 1

0

0

0

0

0

0

1

: 1

0

0

0

0

0

1

: 5

0

0

0

0

1

: 2

5

0

0

0

sz

e

r.

d

łu

g

.

sz

e

ro

k

o

ść

d

łu

g

o

ść

Liczba arkuszy

1: 1 000

000

1

4

6

M-34

430

445

1: 500

000

4

2

3

M-34-D

220

222

1: 200

000

36

40’

1

M-34-XXXVI

2 cm

74

74

1: 100

000

144

20’

30’

M-34-136

2 cm

37

37

1: 50 000

4

10’

15’

M-34-136-B

2 cm 18.5

18.5

1 : 25 000

4

5’

7.5’ M-34-136-C-c 4 cm

9.7

9.7

1: 10 000

4

2.5

’

3.75

’

M-34-136-D-

d-4

10

cm

4.7

4.7

Mapa topograficzna

Schemat podziału arkusza mapy topograficznej w skali 1:
100 000
na arkusze mapy topograficznej w skalach 1: 50 000, 1: 25
000, 1: 10 000,

Mapy tematyczne

Mapy tematyczne opisują wybrane elementy środowiska
geograficznego i
określone procesy lub zjawiska przyrodnicze i społeczno-
gospodarcze.
Do opracowania map tematycznych wykorzystuje się
odpowiednio mapę
zasadniczą oraz mapy topograficzne.

Podstawy jednolitości prac

geodezyjnych

Jednolitość

prac

geodezyjnych

i

kartograficznych

zapewniają:

•jednolity system miar,

•jednolity państwowy system odniesień przestrzennych,
przeliczalny wzajemnie z innymi systemami,

•instrukcje techniczne określające standardowe cechy
produktu
(dokładność, skład, formę).
W pracach geodezyjnych i kartograficznych stosuje się
jednostki

międzynarodowego

systemu

jednostek

(Sl),

obowiązujące oraz dopuszczone do użycia w Rzeczypospolitej
Polskiej.

Podstawy jednolitości prac

geodezyjnych

Instrukcje techniczne dzielą się na grupy oznaczone symbolami

„O", „G" i „K".

Treścią grup są:
1) „O" - ogólne zasady wykonywania prac geodezyjnych i

kartograficznych

(0-1/0-2) zasady kompletowania dokumentacji geodezyjnej i

kartograficznej oraz

prowadzenia państwowego zasobu geodezyjnego i

kartograficznego (0-3/0-4).

2) „G" - zasady wykonywania pomiarów i przetwarzania danych

pomiarowych:

a) osnów geodezyjnych (G-1, G-2, osnów pomiarowych G-4),
b) grawimetrycznych i magnetycznych, związanych z osnowami

geodezyjnymi

lub badaniami Ziemi (G-1),
c) sytuacyjnych i wysokościowych (G-4),
d) realizacyjnych (G-3),
e) dotyczących katastru nieruchomości (G-5),
f) geodezyjnej ewidencji sieci uzbrojenia terenu (G-7),
3) „K" - zasady opracowania i aktualizacji mapy zasadniczej (K-1),

map
topograficznych (K-2) i map tematycznych (K-3), wzory
znaków umownych.

Ogólne zasady

wykonywania pomiarów

Przy wykonywaniu pomiarów geodezyjnych, chcąc uzyskać
zamierzoną

dokład-

ność. należy przestrzegać dwóch podstawowych zasad:
zasada kontrolowania każdego pomiaru.
Należy pamiętać, że przy wykonywaniu każdej czynności pomiarowej
istnieje możliwość popełnienia błędów w pomiarach. Z tego powodu
należy zawsze stworzyć warunki do stwierdzenia, czy wyniki
pomiaru są prawidłowe. Najprostszym sposobem kontroli pomiaru
pewnego elementu jest powtórne wykonanie pomiaru tego elementu.
zasada dokonywania pomiaru od ogółu do szczegółu.
Zasada ta polega na tym, że najpierw trzeba uzyskać ogólne zarysy
obszaru podlegającego pomiarowi, a następnie wykonać pomiary
szczegółów. W związku z tym w pierwszej kolejności trzeba
wyznaczyć na tym obszarze szereg punktów głównych, tworzących
ogólne ramy danego terenu i przez odpowiednie pomiary ustalić
wzajemne
ich położenie względem siebie. Natomiast wszelkie szczegóły
znajdujące się nadanym terenie określamy na podstawie sieci
punktów głównych, wpasowując niejako szczegóły w utworzony
przez punkty główne szkielet.

Pomiary szczegółów

Po założeniu na danym obszarze osnowy pomiarowej i
wykonaniu wszystkich związanych z tym prac pomiarowych i
obliczeniowych oraz po jej odpowiednim zagęszczeniu,
następnym etapem jest pomiar szczegółów sytuacyjnych. Każdy
pomiar szczegółowy polega na tym, że wykorzystując założoną
w terenie osnowę pomiarową, domierzamy do niej punkty
szczegółowe, ustalając ich położenie względem sieci punktów
osnowy.
Istnieje kilka sposobów wykonania pomiaru szczegółowego,
jednak najbardziej popularne i najpowszechniej stosowane są
dwa sposoby:
l) metoda domiarów prostokątnych zwana również metodą
ortogonalną lub metodą rzędnych i odciętych oraz,
2) metoda biegunowa.

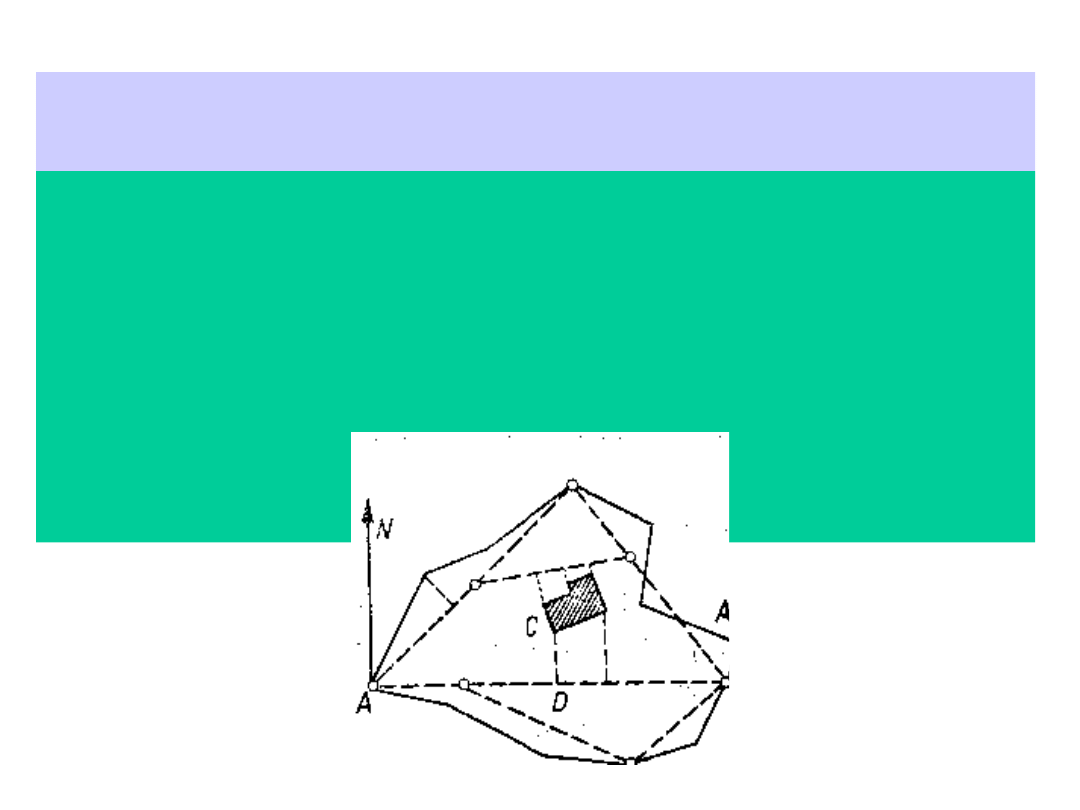
Metoda domiarów

prostokątnych

Sposób ten nazywamy również sposobem rzędnych i odciętych
lub pomiarami
ortogonalnymi. Polega on na tym, że np. położenie punktu C
wyznaczamy przez pomiar odcinka x=AD wzdłuż linii osnowy
pomiarowej (odcięta) i prostopadłego doń odcinka y=DC
(rzędna). Położenie punktu D, który jest rzutem punktu C na
prosta AB, znajdziemy za pomocą węgielnicy Rozpoczynając
układanie taśmy od punktu A wykonamy w punkcie odczyt x
zwany miarą bieżącą, natomiast rzędną y punktu C, zwaną
domiarem, zmierzymy ruletką stalową.

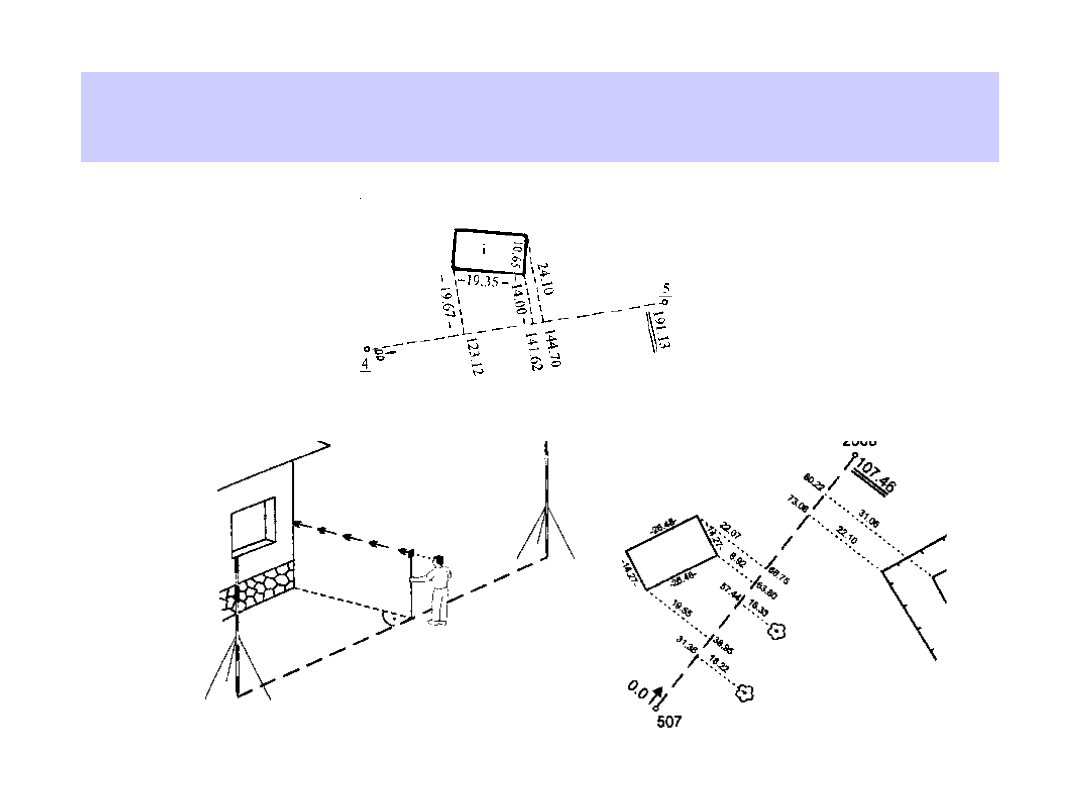
Metoda domiarów

prostokątnych

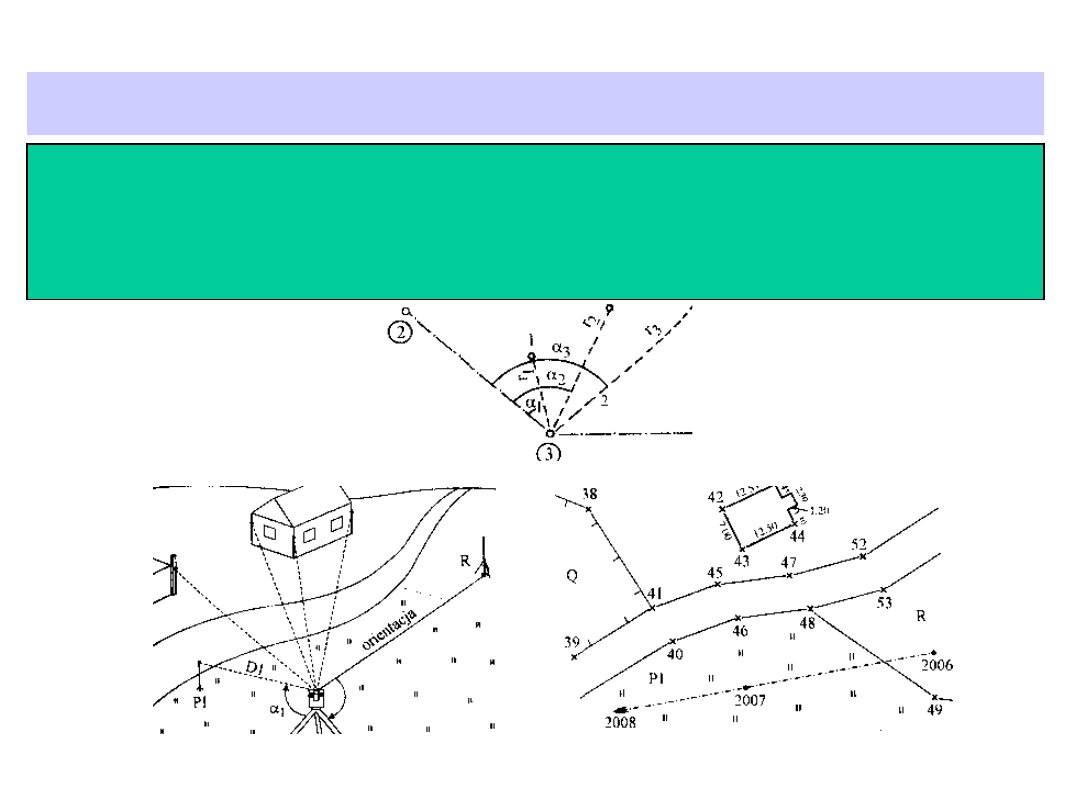
Metoda biegunowa

Metoda biegunowa polega na pomiarze odległości i kątów
biegunowych. Jako stanowiska teodolitu do pomiaru tych kątów
obiera

się

wierzchołki

ciągów poligonowych, głównych i sytuacyjnych

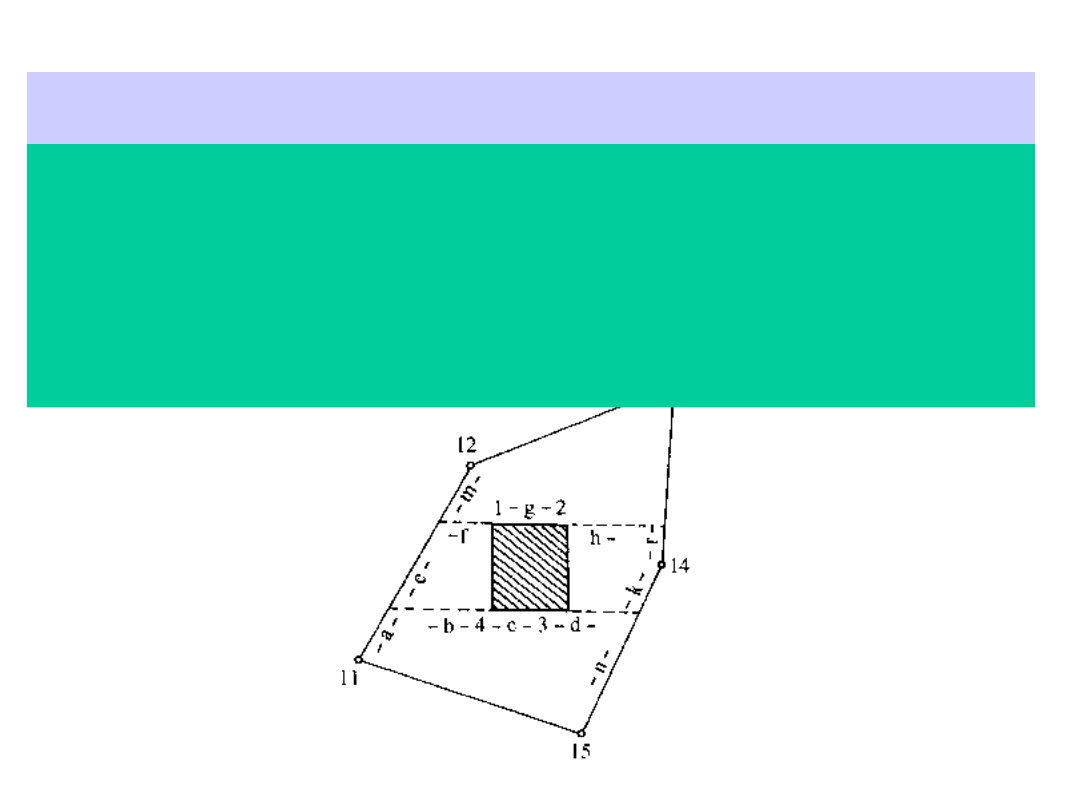
Metoda przedłużeń

Polega ona na przedłużeniu odcinka zdejmowanego do
przecięcia z linią osnowy pomiarowej. Pomiar odcinków a, b, c,
e, f, g. k, r daje dostateczną liczbę danych do określenia
położenia punktów 1,2, 3 i 4,
Pomiar odcinków d, h, n, m pozwoli na skontrolowanie wyników
pomiarów. Dodatkową kontrolą będzie pomiar czołówek, tzn.
odcinków 1-2-3-4-1.

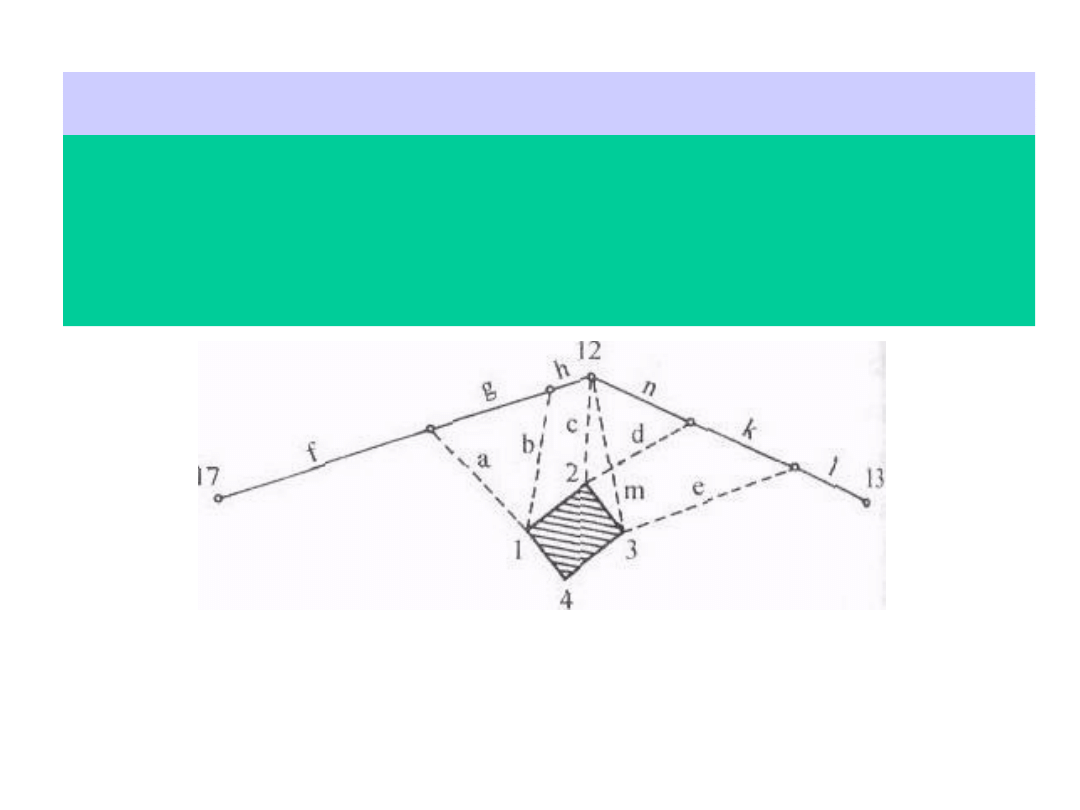
Metoda wcięć liniowych

Metoda wcięć liniowych. Polega ona na pomiarze odległości
od punktu zdejmowanego do dwóch punktów leżących na
liniach osnowy pomiarowej
Pomiar odcinków a, b, c, d, m, e oraz h. g, n, k pozwala
jednoznacznie określić położenie

punktów 1, 2, 3, 4

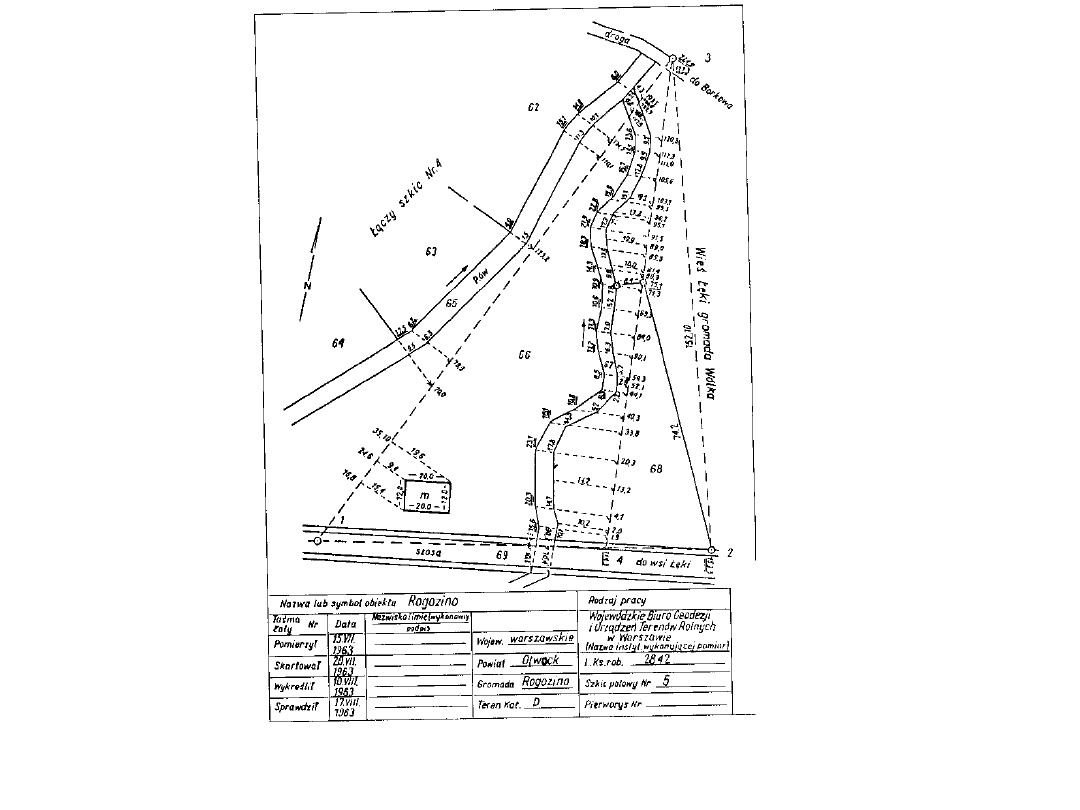
Szkic
polowy