1
Optoelektronika
Dr hab. inż. Jerzy Zieliński
prof. AP
jzielinski@wat.edu.pl
Optoelektronika zaoczny 2011/12
Optoelektronika zaoczny 2011/12
Wykład – 1 -
1
Optoelektronika
Dr hab. inż. Jerzy Zieliński
prof. AP
jzielinski@wat.edu.pl
Optoelektronika zaoczny 2011/12
Optoelektronika zaoczny 2011/12
Wykład – 1 -
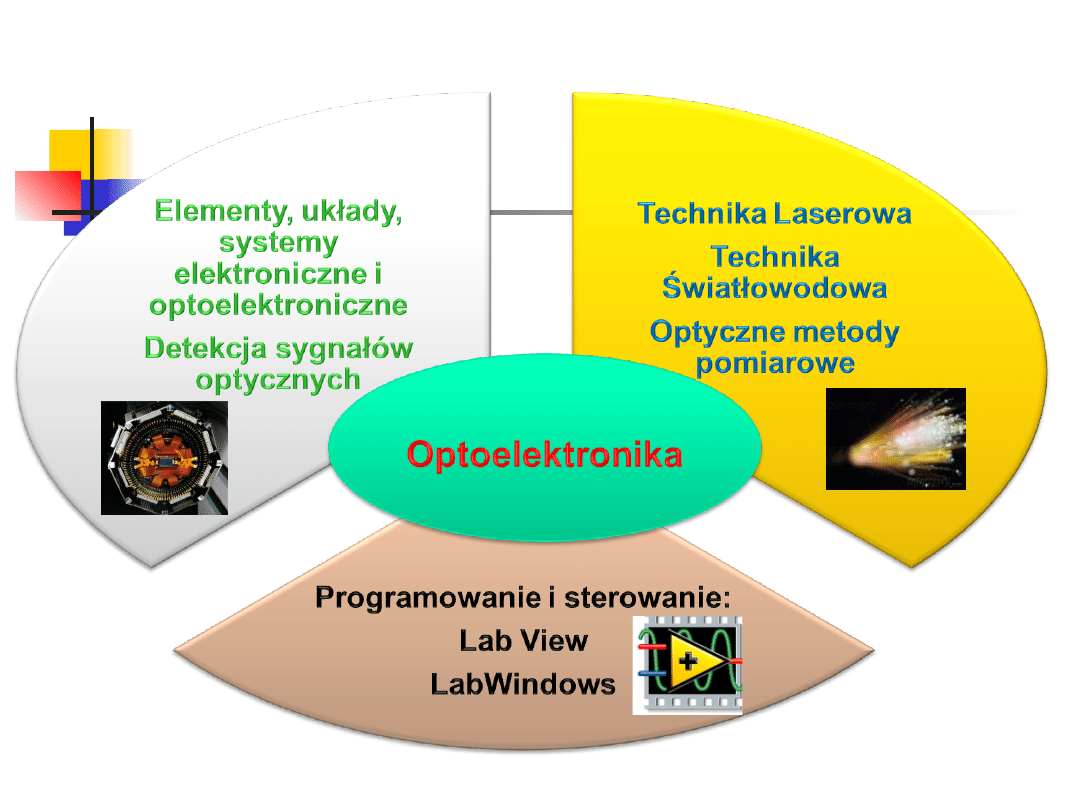
Program przedmiotu
2
1. Źródła i detektory światła -
Podstawy budowy
krystalicznej ciał stałych, podstawy fizyki półprzewodników,
technologie stosowane w fizyce ciała stałego. Elementy
półprzewodnikowe, dioda – budowa, technologie, własności.
Detektory półprzewodnikowe
2. Podstawy techniki laserowej -
podstawy fizyki akcji
laserowej, budowa różnych typów laserów, właściwości
światła laserowego, wybrane zastosowania
3. Światłowody -
podstawy fizyczne, budowa i rodzaje
światłowo-dów, zastosowania telekomunikacyjne i inne.
4. Wybrane
problemy
budowy
systemów
zobrazowania
informacji
-
wyświetlacze
ciekłokrystaliczne,
plazmowe,
elektrolu-minescencyjne,
systemy projekcyjne
3
Terminy spotkań
10.II – 12.II – obecny zjazd(wykład / ćwiczenia)
30.03 – 1.04 (referaty /wykład /ćwiczenia)
19 maj – zaliczenie
(ew. referaty, ćwiczenia)
Program obejmuje 30 godzin wykładu i 15 godzin
ćwiczeń
4
Zasady zaliczenia
przedmiotu
W ramach ćwiczeń będziemy omawiali wybrane
zagadnienia z wykładu + prezentacje referatów
studenckich na tematy wg. wykazu.
Prezentacja referatu = zaliczenie jednego (lub więcej)
pyta-nia z pracy końcowej.
Praca końcowa na ostatnich zajęciach -> zestaw
będzie zawierał 4 pytania student wybiera trzy z nich
i pisze odpowiedź.
Oceny pozytywne będę wpisywał ???
Jeśli ktoś nie zaliczy to będziemy się dodatkowo
spotykać.
5
Czym zajmuje się optoelektronika –
jaki zakres wiedzy obejmuje?
6
Na pierwszy rzut oka wielu z nas nie odgaduje wielu
informacji z określenia optoelektronika. Jednak w
rzeczywistości z tym terminem wiąże sie niemalże
każdy dzień naszego życia. Optoelektronika jest
dziedzina techniki skupiająca wszelkie za-gadnienia
związane z światłem barwy widzialnej.
Wykorzystuje
ona
przede
Wykorzystuje
ona
przede
wszystkim właściwości światła w celu
wszystkim właściwości światła w celu
zgromadzenia, pozyskania, obróbki i
zgromadzenia, pozyskania, obróbki i
przesyłania
informacji
w
postaci
przesyłania
informacji
w
postaci
widzialnej dla ludzkiego oka.
widzialnej dla ludzkiego oka.
Pasma światła widzialnego charakteryzują
bardzo wysoka częstotliwość oraz długość fal.
Najważniejsza w tym przypadku jest właśnie
długość fal która przy źródłach widzialnych
oscyluje w granicach od 380nm do 780nm.
Gdzie to Opto…
Telekomunikacja
Telekomunikacja
światłowodowa
światłowodowa
Motoryzacja
Motoryzacja
Medycyna
Medycyna
Bezpieczeństw
Bezpieczeństw
o
o
Zabawki
Zabawki
Budowa atomu
9
Aby jednak to wszystko zrozumieć musimy
zacząć od przypomnienia i zrozumienia
podstaw
W 1911 r. E. Rutheford wykonując słynne
eksperymenty nad rozpraszaniem cząstek na bardzo
cienkiej folii złota stwierdził, że atom składa się z
bardzo małego, dodatnio naładowanego jądra oraz z
chmury ujemnie naładowanych elektronów. Rozmiary
jądra są rzędu 10
–14
m, rozmiary atomu – rzędu 10
–10
m. Masa jądra jest tysiące razy większa od masy
elektronu (masa protonu = 1836 mas elektronu
swobodnego).
Aby
w
wyniku
działania
sił
elektrostatycznych elektron nie spadł na jądro, należy
przyjąć, że krąży on po orbicie kołowej. Według
mechaniki
klasycznej
energia
elektronu
może
przyjmować dowolne wartości. Tymczasem analiza
widmowa promieniowania emitowanego przez wodór
wykazuje, że poziomy energetyczne elektronu muszą
mieć nieciągłą strukturę. Również założenie o ruchu
elektronu po orbicie kołowej jest sprzeczne z
elektrodynamiką klasyczną. Wiadomo bowiem, że
ładunek poruszający się ruchem niejednostajnym
promieniuje energię. Elektron więc powinien tracić
energię i poruszając się po spirali spaść na jądro.
10
Postulaty Bohra
Pierwszą
próbą
teoretycznego
opisu
nieciągłości
poziomów energetycznych elektronu w atomie była teoria
atomu Bohra.
Bohr sądził, że możliwe orbity elektronów są analogiczne
do klasycznych kołowych orbit planet i usiłował znaleźć
zasadę, która dopuszczałaby jedynie określone wartości
energii lub promieni orbit. Oparł swój model na
następujących postulatach:
I.
Elektrony poruszają się w atomach nie
promieniując energii, po takich orbitach kołowych, że
moment pędu elektronu jest równy całkowitej wartości
stałej ħ
n = 1, 2, 3, ...
(12.1)
II.
Przejścia elektronu z orbity o energii E
n
na orbitę,
gdzie energia wynosi E
m
, towarzyszy emisja lub absorpcja
fotonu o częstości określonej wzorem
(12.2)
n
mvr
h
m
E
n
E
11
Zwróćmy uwagę, że
model Bohra nie tłumaczy,
dlaczego
elektron
krążący
po
orbicie
nie
promieniuje energii. Jest to przyjmowane jako
postulat, aby wyjaśnić fakty eksperymentalne
.
Z pierwszego postulatu Bohra otrzymujemy wyrażenie na
dopuszczalne poziomy energetyczne elektronu w atomie
wodoru. Ponieważ
więc energia kinetyczna
mr
n
v
r
e
mr
n
m
mv
K
o
8
2
1
2
2
2
2
Ostatnie wyrażenie otrzymano uwzględniając równość siły
elektrostatycznej z siłą odśrodkową. Z wyrażenia (12.3) wyliczymy
dozwolone orbity
2
2
2
2
4
n
r
n
me
r
o
o
n
12
gdzie
5,2910
–11
m
jest
promieniem
Bohra.
Promienie
orbit
są
więc
skwantowane i wynoszą: r
o
, 4r
o
, 9r
o
,..., itd.
Natomiast dopuszczalne wartości energii wynoszą
2
2
4
me
r
o
o
2
2
2
2
4
n
r
n
me
r
o
o
n
r
e
r
e
r
e
U
K
E
o
o
o
8
4
8
2
2
2
2
2
2
2
2
4
1
59
13
1
32
n
,
n
me
E
o
n
[eV]
13
0
- 0 , 5 4
- 0 , 8 5
- 1 , 5 1
- 3 , 3 9
- 1 3 , 5 9
S e r i a
P a s h e n a
S e r i a
B a lm e r a
S e r i a L y m a n a
1
2
3
4
5
n
E
(e
V
)
Rys. 12.1. Schemat poziomów
energetycznych atomu wodoru.
Aby
elektron
przesunąć
do
nieskończoności, gdzie miałby energię
zerową, trzeba dostar-czyć energię
13,59 eV przyjmując, że ele-ktron
znajduje się w stanie podstawowym n
= 1. Jest to
energia jonizacji
atomu,
tzn. energia potrzebna do tego, aby
elektron wyrwać z atomu. Energię
potrzebną do przeniesienia elektronu
ze stanu podsta-wowego do stanu
wyższego (wzbudzonego) nazywamy
energią wzbudzenia
energią wzbudzenia
. Na rys. 12.1
przedstawiono schemat dozwolonych
po-ziomów energetycznych dla atomu
wodoru.
Zauważmy, że gdy n rośnie, poziomy leżą coraz bliżej siebie i różnica
między nimi jest bardzo mała. Kiedy elektron odrywa się od jądra
staje się elektronem swobodnym i może przyjmować dowolną
wartość energii większą od zera.
r
14
Chociaż teoria Bohra jest przestarzała,
jednak jest bardzo prosta. Jej znaczenie
historyczne jest duże i z tego powodu ją
przypomnieliśmy. Symbole teorii bohrowskiej
stosowane są do chwili obecnej.
Współczesny model atomu był zaproponowany
w 1926 r. wkrótce po sformułowaniu równania
Schrödingera. Szczegółowe omówienie teorii
atomu w ujęciu kwantowym jest zagadnieniem
skomplikowa-nym. Z tego powodu nasze
podejście będzie raczej opisowe. Położymy
nacisk na interpretację fizyczną wyników, nie
będziemy natomiast zajmować się trudnymi
obliczeniami matematycznymi.
15
Równanie Schrödingera dla atomu wodoru
Pokażemy
teraz
jak
korzystając
z
równania
Schrödingera można wyznaczyć poziomy energetyczne
elektronu w atomie wodoru.
Energia potencjalna oddziaływania elektron-jądro ma
postać
r
e
r
U
o
4
2
Ponieważ potencjał ma symetrię
sferyczną,
wygodniej
jest
wprowadzić
sferyczny
układ
współrzędnych. W układzie tym
położenie określone jest przez
promień
wodzący
r,
kąt
biegunowy i kąt azymutalny , co
przedstawiono
schematycznie
na rys. 12.4.
x
y
z
r
P
16
Współrzędne sferyczne związane są ze współrzędnymi
kartezjańskimi następującymi związkami
cos
r
z
sin
sin
r
y
cos
sin
r
x
Przypomnijmy, że jądro znajduje się w początku układu
współrzędnych i jest nieruchome (jego masa jest 1836 razy większa
od masy elektronu).
Równanie Schrödingera dla przypadku trójwymiarowego
U
E
m
z
y
x
2
2
2
2
2
2
2
2
należy przekształcić do sferycznego układu współrzędnych.
17
Przejście z równania ze współrzędnymi x, y, z do układu
sferycznego nie jest trudne lecz należy przeprowadzić żmudne
przekształcenia. Dlatego napiszemy końcowy wynik
U
E
m
sin
r
sin
sin
r
r
r
r
r
2
2
2
2
2
2
2
2
2
1
1
1
Wobec tego równanie Schrödingera dla atomu wodoru
posiada następującą postać
r
e
E
m
sin
sin
sin
r
r
r
r
r
o
4
2
1
1
1
1
2
2
2
2
2
2
2
2
12.13
Równanie to jest skomplikowane i spróbujemy je rozwiązać,
a właściwie odgadnąć rozwiązanie tylko w wybranych przypadkach.
18
W ogólnym przypadku , gdy funkcja falowa
zależy nie tylko od r, ale także od φ i . Postępowanie w tym
przypadku jest następujące. Funkcję falową
przedstawiamy w postaci iloczynu trzech funkcji z których każda
zależy od jednej zmiennej
,
,
r
r
R
,
,
r
(12.19)
Podstawiając tak przedstawioną funkcję falową do równania
Schrödingera otrzymujemy wówczas trzy równania, z których każde
opisuje zachowanie się funkcji falowej w zależności od .
Równania te nazywa ją się odpowiednio radialne, biegunowe,
azymutalne. Poniżej w sposób skrótowy to przedstawimy.
Podstawiając funkcję (12.19) do równania (12.12), otrzymujemy
.
,
,
r
19
2
2
2
2
2
2
2
2
1
1
1
2
R
sin
r
R
sin
sin
r
r
R
r
r
r
m
ER
R
r
U
Obliczając odpowiednie pochodne, a następnie
mnożąc ostatnie równanie przez wyrażenie r
2
sin
2
i dzieląc przez
R
otrzymamy po uporządkowaniu
2
2
2
2
2
2
2
1
2
U
E
sin
r
m
sin
sin
R
R
r
r
R
sin
Prawa strona tego równania zależy tylko od
, a lewa tylko od r
i
Stąd też równanie to będzie spełnione, jeżeli obie strony będą
równe jednej i tej samej stałej, którą oznaczamy przez –m
2
. Taki
wybór stałej separacji wynika z ogólnej teorii rozwiązywania tego typu
równań. Zatem równanie dla
przyjmie postać
2
2
2
l
m
d
d
(12.22)
20
Jeżeli teraz do pozostałej części przedostatniego równania w
miejsce prawej strony podstawimy-m
l
2
, to dzieląc równanie przez
sin
2
i porządkując, otrzymamy
sin
sin
sin
m
U
E
mr
r
R
r
r
R
1
2
1
2
2
2
2
2
Również w tym równaniu po obu stronach występują różne
zmienne. Będzie więc ono spełnione tylko wówczas, gdy obie jego
strony będą tożsamościowo równe stałej, którą w tym przypadku
oznaczymy przez l(l+1) (znów powód takiego uzasadnienia jak
powyżej)
1
1
2
2
l
l
d
d
sin
d
d
sin
sin
m
2
2
2
2
1
2
1
r
R
l
l
R
U
E
m
dr
dR
r
dr
d
r
21
W ten sposób udało się rozseparować równanie
W ten sposób udało się rozseparować równanie
Schrödingera
trzech
zmiennych
na
trzy
równania
Schrödingera
trzech
zmiennych
na
trzy
równania
różniczkowe jednej zmiennej
różniczkowe jednej zmiennej. Najprostsze z nich jest
równanie na
znamy jego rozwiązanie opisane równaniem
(12.10).
Z równań
Z równań
w niebieskich ramkach
w niebieskich ramkach
można wyznaczyć
można wyznaczyć
możliwe wartości energii, momentu pędu i jednej jego
możliwe wartości energii, momentu pędu i jednej jego
składowej
składowej
. Wielkości te, jak wiemy, są określone przez
podanie n, l, m
l
. Okazuje się przy tym, że dla danego n,
orbitalna liczba kwantowa może przyjmować wartości: l = 0,
1, 2, ..., n–1.
W ten sposób możemy stwierdzić, że trzy
liczby kwantowe opisujące stan elektronu w atomie
wodoru, są związane ze sobą w następujący sposób
:
główna liczba kwantowa
n = 1, 2, 3,....
orbitalna liczba kwantowa
l = 0, 1, 2, ..., n–1
magnetyczna liczba kwantowa
m
l
= –l, –l+1, ...,
0, ..., l–1, l
22
Oznacza to, że przy określonych
Oznacza to, że przy określonych
n
n
, a więc określonej
, a więc określonej
wartości energii, liczba możliwych wartości
wartości energii, liczba możliwych wartości
l
l
i
i
m
m
l
l
,
,
czyli liczba
czyli liczba
niezależnych rozwiązań równania Schrödingera będzie
niezależnych rozwiązań równania Schrödingera będzie
wynosiła
wynosiła
(12.26)
Jeżeli elektron jest w takim stanie, że jednej wartości
energii odpowiada kilka niezależnych rozwiązań równania
Schrödingera, to mówimy, że stan taki jest n
2
-krotnie
zwyrodniały.
Dla zadanych wartości liczb kwantowych n, l, m
l;
funkcja
falowa ma określoną postać którą oznaczamy symbolem
i nazywamy orbitalem atomowym. Każdy orbital
oznaczony jest tym samym symbolem co odpowiadający
mu stan elektronowy. Istnieją ogólnie przyjęte symbole liczb
kwantowych n i l. Tworzy się je z cyfry oznaczającej główną
liczbę kwantową i litery przyporządkowanej liczbie l w
następujący sposób
l = 0, 1, 2, 3, 4
s, p, d, f, g
2
1
0
1
2
n
l
n
l
l
m
,
l,
n
23
Dla stanu podstawowego atomu wodoru n = 1, a zatem l
= m
l
= 0. Stan ten oznaczamy symbolem 1s.
Dla najniższego stanu wzbudzonego n = 2, a
zatem l = 0 lub l = 1. Dla l = 0 (stan 2s) musi być również
m
l
= 0, natomiast dla l = 1 (stany 2p) możemy mieć m
l
=
–1, 0 lub 1. W celu rozróżnienia stanów 2p o różnej
wartości liczby m
l
stosuje się niekiedy dodatkowy indeks
podający wartości tej liczby.
W tabeli na następnej stronie zestawiono stany kwantowe
atomu wodoru dla pewnych wartości głównej liczby
kwantowej.
24
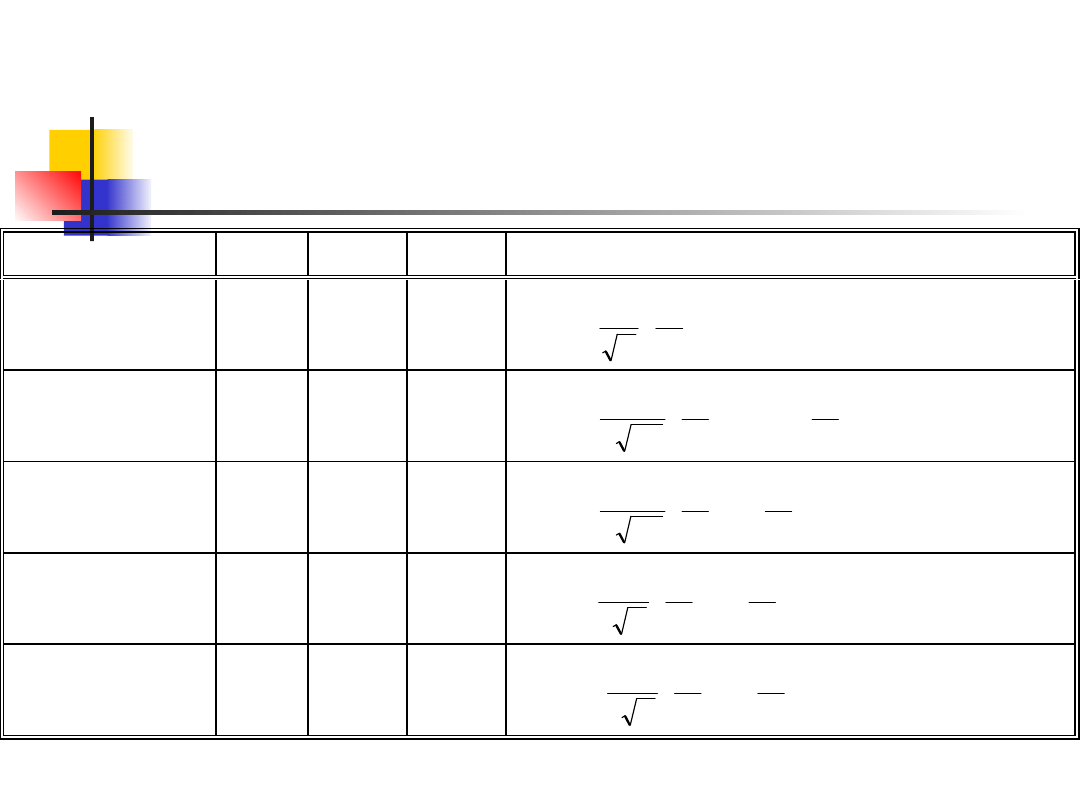
S t a n k w a n t o w y
n
l
m
l
F u n k c j e f a lo w e
1 s
1
0
0
o
r
/
r
/
o
e
r
2
3
100
1
1
2 s
2
0
0
o
r
/
r
o
/
o
e
r
r
r
2
2
3
200
2
1
2
4
1
2 p
0
2
1
0
cos
e
r
r
r
o
r
/
r
o
/
o
2
2
3
210
1
2
4
1
2 p
1
2
1
1
i
r
/
r
o
/
o
e
sin
e
r
r
r
o
2
2
3
211
1
8
1
2 p
– 1
2
1
– 1
i
r
/
r
o
/
o
e
sin
e
r
r
r
o
2
2
3
1
21
1
8
1
Tabela 12.1. Funkcje falowe atomu
wodoru
25
Dokładna analiza funkcji falowych wykazuje, że część
radialna funkcji zależy od n i l, a część kątowa – od l i m
l
. Tak
więc możemy zapisać, że
l
l
l
m
lm
nl
nlm
r
R
(12.27)
Stałe współczynniki występujące w funkcjach zamieszczonych w
tabeli 12.1 są wynikiem ich unormowania. Jako przykład
wyznaczania stałych normujących rozpatrzymy funkcję Ψ
100
w
postaci
. Musi być spełniony warunek
Element objętości we współrzędnych sferycznych wynosi
o
r
r
Ae
1
2
2
2
100
dV
e
A
dV
o
r
/
r
d
d
dr
sin
r
dV
2
Uwzględniając to w powyższym wzorze otrzymujemy
1
2
0
0
0
2
2
2
d
d
sin
dr
e
r
A
o
r
/
r
26
Całkowanie względem jest elementarne, natomiast
Zatem
Stąd wynika, że
Podobnie wyznaczamy stałe w innych przypadkach, choć obliczenia
są bardziej złożone.
Znajomość funkcji falowych pozwala obliczyć prawdopodobieństwo
znalezienia elektronu w określonym elemencie objętości. Wygodnie
jest rozpatrywać prawdopodobieństwo radialne (zależne od r) i
prawdopodobień-stwo kątowe (zależne od φ, θ ).
i
3
0
2
2
2
2
o
r
/
r
r
dr
e
r
o
1
4
2
2
3
2
o
r
A
2
3
1
1
/
o
r
A
27
Prawdopodobieństwo radialne jest zdefiniowane jako
prawdopodobieństwo znalezienia elektronu w warstwie
kulistej o promieniu r i grubości dr. Ponieważ objętość
warstwy kulistej jest proporcjonalna do r
2
, zatem
dr
r
R
dr
r
p
nl
2
2
Stąd
jest gęstością prawdopodobieństwa.
2
2
r
R
r
p
nl
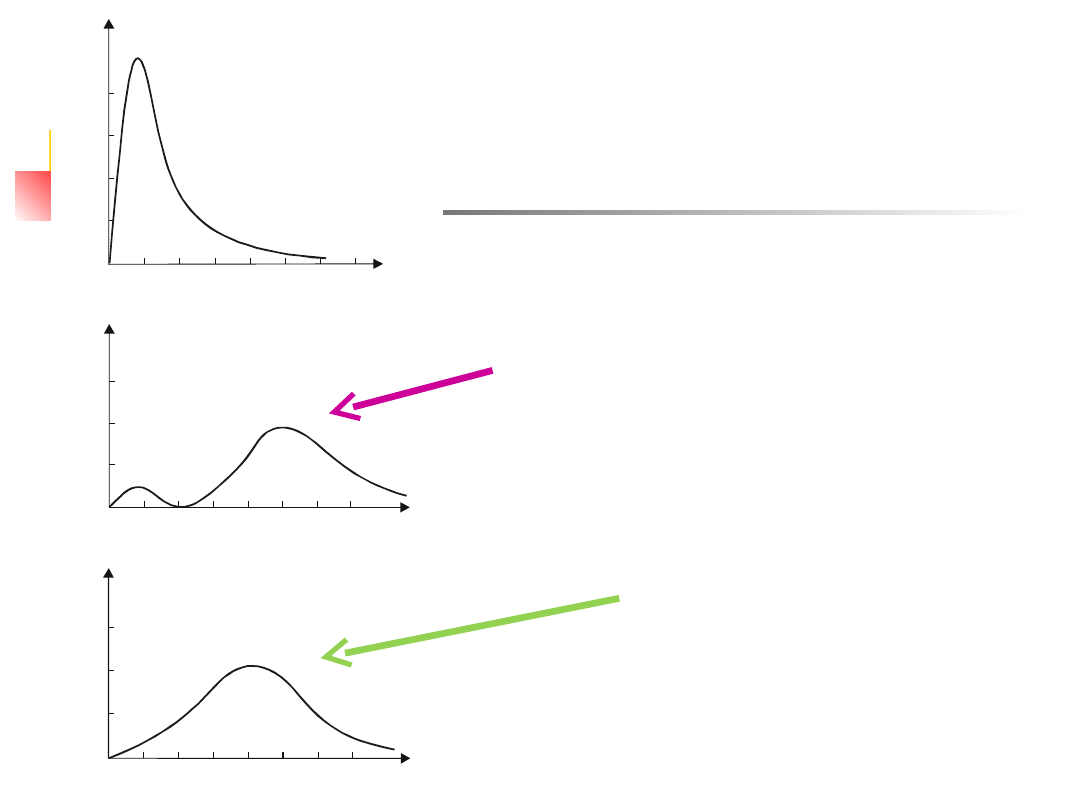
Na rys. 12.5 przedstawiono zależność p(r) dla n = 1 i 2 w
zależności od r/r
o
.
W stanie 1s gęstość prawdopodobieństwa osiąga maksimum
dla r = r
o
. W stanie 2s istnieją dwa maksima: jedno dla r = r
o
, drugie
dla , przy czym to maksimum jest znacznie większe od
pierwszego.
W stanie 2p gęstość prawdopodobieństwa osiąga maksimum
w pobliżu wartości r = 4r
o
.
o
r
r 5
28
2
n l
2
R
r
2
n l
2
R
r
2
n l
2
R
r
1 2 3 4 5 6 7
1 2 3 4 5 6 7
1 2 3 4 5 6 7
n = 1
l= 0
n = 2
l= 0
n = 2
l= 1
0 . 4
0 . 3
0 . 2
0 . 1
0
0 . 3
0 . 2
0 . 1
0
0 . 3
0 . 2
0 . 1
0
r / r
o
r / r
o
r / r
o
29
Na rys. 12.5 przedstawiono
zależność p(r) dla n = 1 i 2 w
zależności od r/r
o
.
W stanie 1s gęstość
prawdopodobieństwa
osiąga
maksi-mum dla r = r
o
. W stanie
2s istnieją dwa maksima: jedno
dla r = r
o
, drugie dla ,
przy czym to maksimum jest
znacznie większe od pierwszego.
W stanie 2p gęstość
prawdopodobieństwa
osiąga
maksi-mum w pobliżu wartości r
= 4r
o
.
o
r
r 5
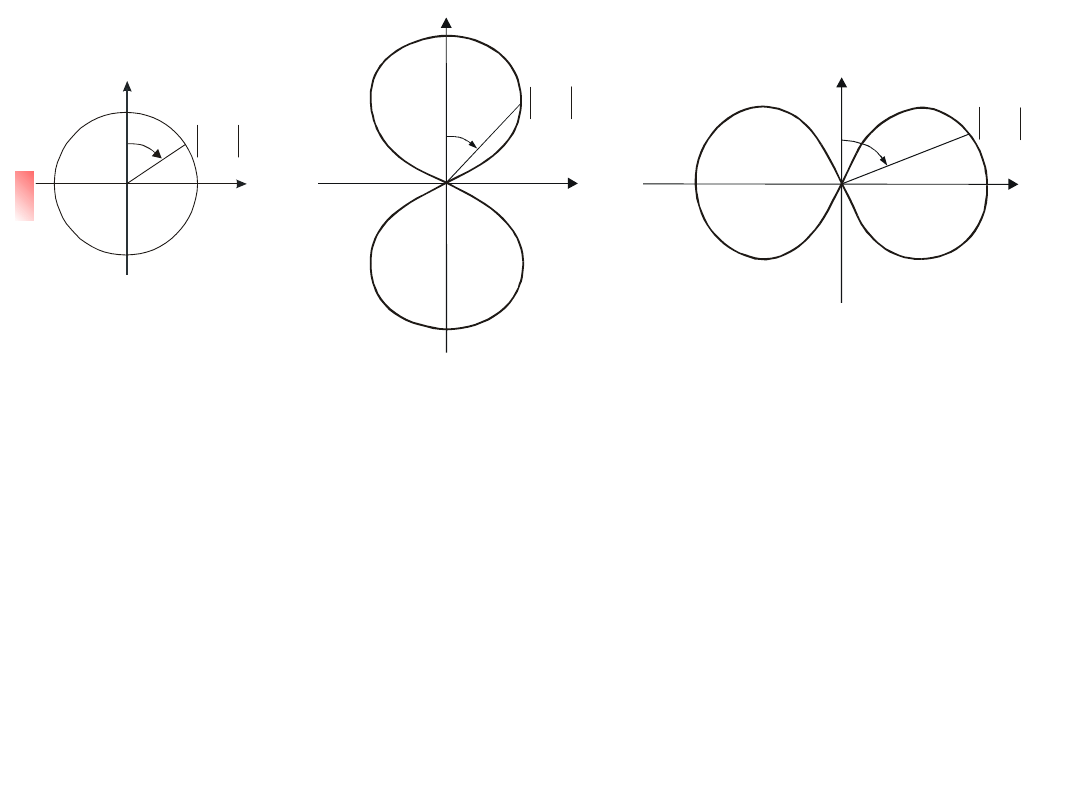
30
l= 0
m = 0
l
y
z
2
lm
l
y
z
2
lm
l
1
m
l
l= 1
l= 1
m = 0
l
y
z
2
l m
l
Analizując część kątową funkcji falowych możemy wyznaczyć
kątową gęstość prawdopodobieństwa . Zauważmy przede
wszystkim, że dla wszystkich stanów zależność funkcji falowych od
kąta φ jest postaci . Zatem gęstość prawdopodobieństwa nie
będzie zależała od φ , gdyż
Na rys. 12.6 przedstawiono zależność p( ) od kąta we
współrzędnych
biegunowych.
Miarą
prawdopodobieństwa
znalezienia elektronu w danym kierunku jest odległość między
początkiem układu współrzędnych i punktem przecięcia prostej
poprowadzonej pod danym kątem, z wykresem funkcji .
,
p
im
e
1
im
im
e
e
2
l
lm
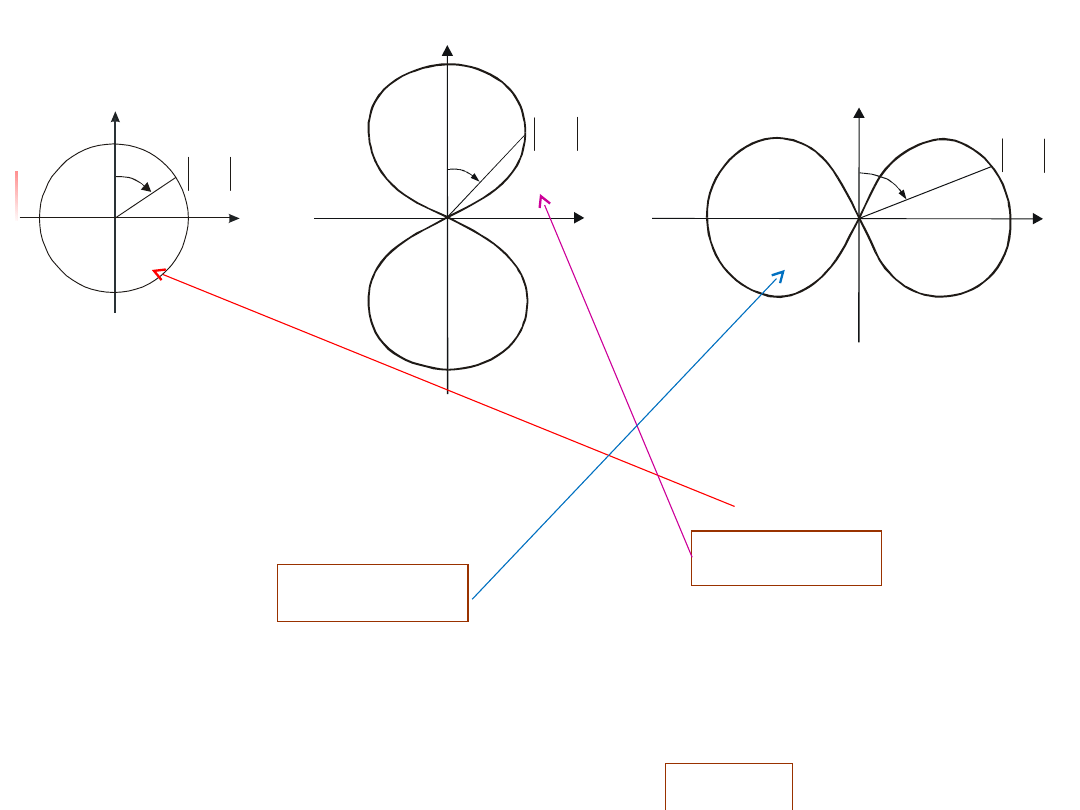
l= 0
m = 0
l
y
z
2
lm
l
y
z
2
lm
l
1
m
l
l= 1
l= 1
m = 0
l
y
z
2
l m
l
Rys. 12.6. Wykresy biegunowe kierunkowej zależności
gęstości prawdopodobieństwa dla atomu wodoru w
przypadku l = 0 i l = 1.
W stanie s (l = 0) gęstość prawdopodobieństwa jest stała. Chmura
elektronowa wykazuje symetrię kulistą. W stanie l= 1 i m = 0,
dla l = 1 i m=±1,
W każdym przypadku gęstość prawdopodobieństwa wykazuje
symetrię obrotową względem osi z.
Funkcja
całkowitej
gęstość
prawdopodobieństwa
znalezienia
elektronu w odległości r od jądra pod kątem jest równa .
2
cos
~
p
2
sin
~
p
p
r
p
31
Spin elektronu - Spinowy moment pędu i spinowy
moment magnetyczny
Precyzyjne pomiary linii widmowych pozwalają stwierdzić,
że
nawet
bez
obecności
zewnętrznego
pola
magnetycznego, składają się one z kilku położonych blisko
siebie linii. Takie rozszczepienie pojedynczej linii widmowej
nazywane jest strukturą subtelną linii widmowych.
Pewnym przypadkiem struktury subtelnej jest oczywiście
zjawisko Zeemana.
Okazuje się, że elektron poza omówionym powyżej
orbitalnym momentem pędu, ma własny moment pędu,
zwany spinowym lub krótko spinem
. Jego istnienie nie jest
. Jego istnienie nie jest
związane z ruchem elektronu lecz jest jego naturalną
związane z ruchem elektronu lecz jest jego naturalną
(wewnętrzną) właściwością
(wewnętrzną) właściwością. Jego istnienie zaproponowali
w 1925 roku Goudsmit i Uhlenbeck w celu wyjaśnienia
struktury subtelnej linii widmowych.
Spinowy moment pędu elektronu wynosi
(12.35)
1
s
s
L
s
32
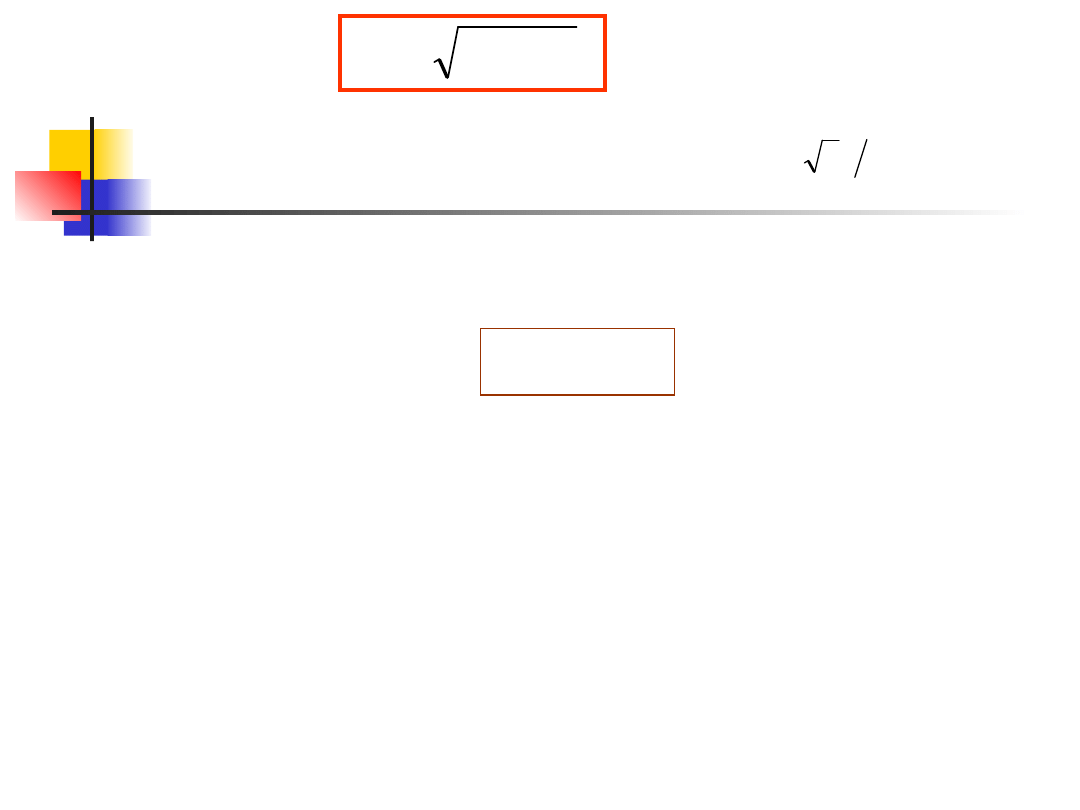
1
s
s
L
s
gdzie spinowa liczba kwantowa s ma tylko jedną wartość
1/2. Wobec tego spin elektronu ma wartość i
jest podstawową właściwością elektronu, taką jak masa i
ładunek.
Rzut spinowego momentu pędu na wyróżniony kierunek,
np. określony zewnętrznym polem magnetycznym, jest
skwantowany i wynosi
(12.36)
gdzie m
s
przyjmuje dwie wartości, 1/2 lub –1/2; i nosi
nazwę magnetycznej spinowej liczby kwantowej. Liczbie
kwantowej m
s
= 1/2 odpowiada spin skierowany w górę, a
m
s
= –1/2 odpowiada spin skierowany w dół (rys. 12.8).
Możliwe kąty między wektorem L
s
a wyróżnionym
kierunkiem w przestrzeni wynoszą 54,7
o
i 125,3
o
.
2
3
s
L
s
sz
m
L
33
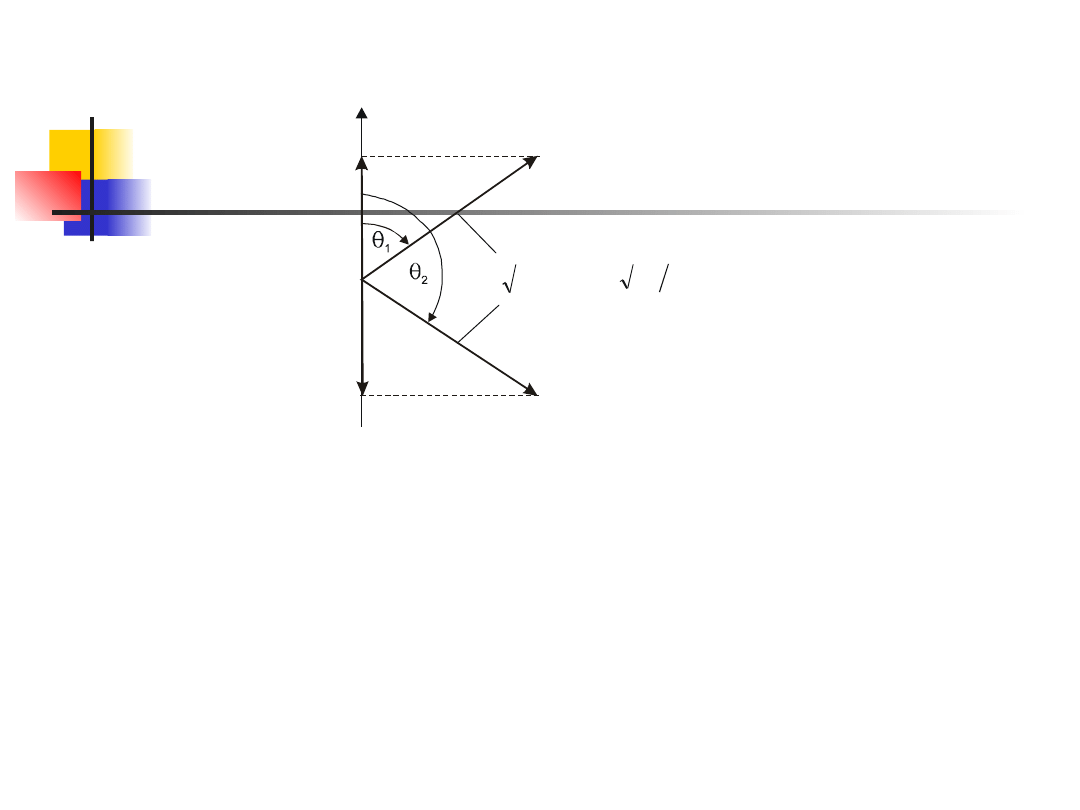
/2
/2
2
3
1
s
s
L
s
z
Rys. 12.8. Spinowy moment pędu elektronu i jego
rzut na określony kierunek w przestrzeni
34
Stan elektronu w atomie będziemy więc opisywać
za pomocą czterech liczb kwantowych: n, l, m
l
i m
s
. Z
poprzednich
rozważań
pamiętamy,
że
liczba
niezależnych stanów związanych z główną liczbą
kwantową wynosi n
2
. Po uwzględnieniu spinu każdy stan
”rozszczepia się” na dwa stany różniące się od siebie
rzutem spinu. Wobec tego całkowita liczba stanów
związanych z daną liczbą kwantową n wynosi 2n
2
.
Ze spinowym momentem pędu L
s
związany jest spinowy
moment magnetyczny μ
s
, który wynosi
1
s
s
m
e
L
m
e
s
s
Rzut spinowego momentu magnetycznego na wyróżniony kierunek
wynosi
B
sz
m
e
cos
s
s
m
e
2
1
a więc μ
sz
może przyjmować dwie wartości różniące się znakiem, co
do modułu równe magnetonowi Bohra.
35
36
Na tej bazie możemy teraz omówić kilka
zagadnień
które będą stanowiły przedmiot
naszego zainteresowania w ramach przedmiotu
optoelektronika
•
Budowę atomów wielo-elektronowych
• Emisję i absorpcję > źródła i detektory światła / emisję
wymuszoną > laser
• Przejścia pomiędzy poziomami > poziomy metastabilne >
laser
• Wiązania > struktura krystaliczna / własności >
półprzewodniki
• Przejścia pomiędzy poziomami > efekty elektrooptyczne >
displeje / techniki zobrazowania
FIZYKA ATOMOWA
Nasze dotychczasowe rozważania dotyczyły głównie
atomu wodoru, gdzie elektron oddziałuje tylko z
jądrem,
a
pole
elektrostatyczne
jest
polem
kulombowskim.
Omówimy
teraz
atomy
wieloelektronowe. Zastanowimy się najpierw, jak są
rozmieszczone elektrony w atomach o liczbie
atomowej Z > 1.
Należałoby oczekiwać, że wszystkie elektrony w
atomie znajdującym się w stanie podstawowym będą
na najniższym poziomie magnetycznym. Tymczasem
fakty
doświadczalne
wskazują,
że
elektrony
rozmieszczają się na różnych poziomach.
37
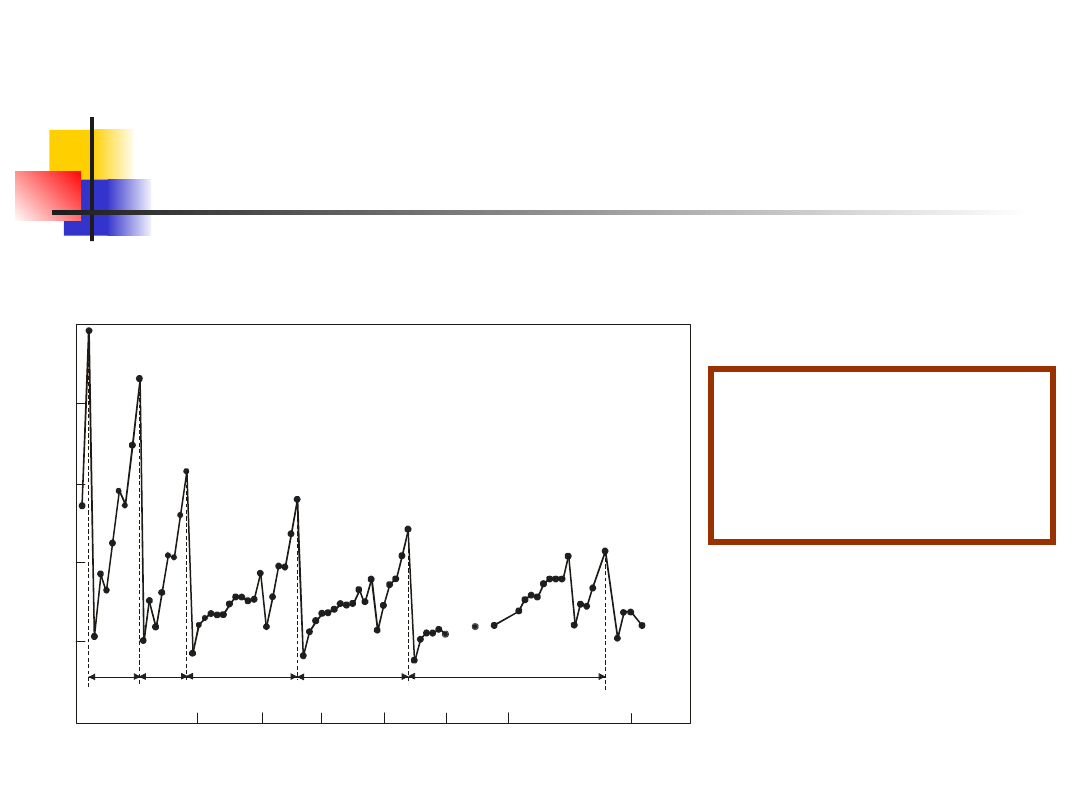
Zakaz Pauliego
Jak wynika z układu okresowego pierwiastków,
okresy zmian właściwości fizycznych i chemicznych
pierwiastków tworzą kolejność liczb 2, 8, 8, 18, 18, 32 (rys.
13.1). W roku 1925 W. Pauli przedstawił prostą regułę która
automatycznie wyjaśnia istnienie grup z 2, 8, 18 i 32
pierwiastkami.
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
5
1 0
1 5
2 0
2 5
H e
N e
N a
A r
L i
X e
H g R n
R b
T l
C s
K r
K
8 8 1 8 1 8 3 2
L ic z b a a to m o w a , Z
P
ot
en
cj
ał
jo
ni
za
cy
jn
y
(e
V
)
Pauli zapostulował,
że jeden orbital ele-
ktronowy mogą zaj-
mować nie więcej
niż dwa elektrony.
38
Pauli zapostulował, że jeden orbital elektronowy
mogą zajmować nie więcej niż dwa elektrony.
Tak
więc w stanie z n = 1 mogą znajdować się dwa elektrony.
Liczbie kwantowej n = 2 odpowiadają 4 orbitale:
(n,l,m
l
) = (2,0,0), (2,1,1), (2,1,0), (2,1,–1).
Wobec tego w stanie z n = 2 może znajdować się 8
elektronów.
W ten sposób otrzymaliśmy liczby 2 i 8.
Liczbę 18 można otrzymać dodając 5 orbitali z l =
2 i 4 orbitale z l = 0. Te dziewięć orbitali może być zajęte
przez 18 elektronów.
Widzimy więc, że liczby 2, 8 i 18 są prostą
konsekwencją zakazu Pauliego, a także zasady kwantowo
mechanicznej zgodnie z którą
i
l
m
l
l
1
0
n
l
39
W chwili pojawienia się zasada Pauliego była
nowym postulatem, którego w tym czasie nie można
było wyprowadzić z ogólnych założeń. Wkrótce po
odkryciu spinu, Pauli i Dirac opracowali relatywistyczną
teorię cząstek o spinie 1/2 i stwierdzili, że warunek
relatywistycznej inwariantności prowa-dzi do funkcji
falowych elektronu, które automatycznie spełnia-ją
zakaz Pauliego. Oznaczało to, że zasada Pauliego nie
była ”wzięta z sufitu”. Dla cząstki o spinie 1/2 rzuty jej
spinu na oś z mogą przyjmować jedną z dwóch
wartości (1/2)lub –(1/2). Zasada zakazu potwierdza, że
w danym stanie określonym czterema liczbami
kwantowymi (n,l,m
l
,s) może znajdować się nie więcej
niż
jeden
elektron.
Jest
to
równorzędne
sformułowaniu zasady Pauliego, że na danym
orbitalu mogą znajdować się nie więcej niż dwa
elektrony.
40
Podsumowując to możemy stwierdzić, że na n-tej
orbicie liczba elektronów może być co najwyżej równa
gdzie czynnik 2 uwzględnia dwie możliwe orientacje
spinu.
Możemy
już
teraz
powiedzieć,
że
rozmieszczenie elektronów w atomie będzie takie, aby
układ miał minimalną energię, ale jednocześnie nie był
naruszony zakaz Pauliego.
1
0
2
2
1
2
2
n
l
n
l
N
41
Atomy wieloelektronowe
Aby wyznaczyć wartości energii elektronów w
atomach wielo-elektronowych należałoby rozwiązać
równanie Schrödingera dla układu złożonego z jądra i
wielu
elektronów.
Jest
to
zadanie
praktycznie
niewykonalne. Jedynie dla atomu helu znaleziono
dokładne rozwiązanie drogą obliczeń numerycznych. Dla
atomów
wielo-elektronowych
stosujemy
na
ogół
przybliżone metody opisu.
W atomach wodoropodobnych, tzn. w atomach (Z–
1)-krotnie zjonizowanych, mamy sytuację podobną do
atomu wodoru. Promienie orbit i poziomy energetyczne
opisujemy wzorami
2
2
2
4
n
mZe
r
o
2
2
2
2
4
2
1
32
n
e
mZ
E
o
42
Dla atomów wielo-elektronowych najprościej jest
przyjąć, że każdy elektron porusza się w polu elektrycznym
o symetrii kuli-stej, która jest wynikiem nałożenia się pola
kulombowskiego jądra z polem elektronów otaczających to
jądro. Tak więc blisko jądra, pole jest w przybliżeniu polem
kulombowskim o potencjale
Powoduje to, że energia wiązania elektronów na pierwszej
orbicie bardzo silnie zależy od Z. Okazuje się, że dla
ciężkich atomów jest ona proporcjonalna do (Z-1)
2
. W
miarę oddalania się od jądra, ekranujący wpływ elektronów
wzrasta i pole przestaje być ku-lombowskie. Można przyjąć,
że jądro ma pewien ładunek efektywny eZ
ef
, przy czym
Z
ef
<Z . Na orbitach najbardziej zewnętrznych wpływ
ekranowania jest tak duży, że energia wiązania nie zależy
praktycznie od Z i jest w przybliżeniu równa energii
wiązania elektronu w atomie wodoru.
r
/
Ze
o
4
43
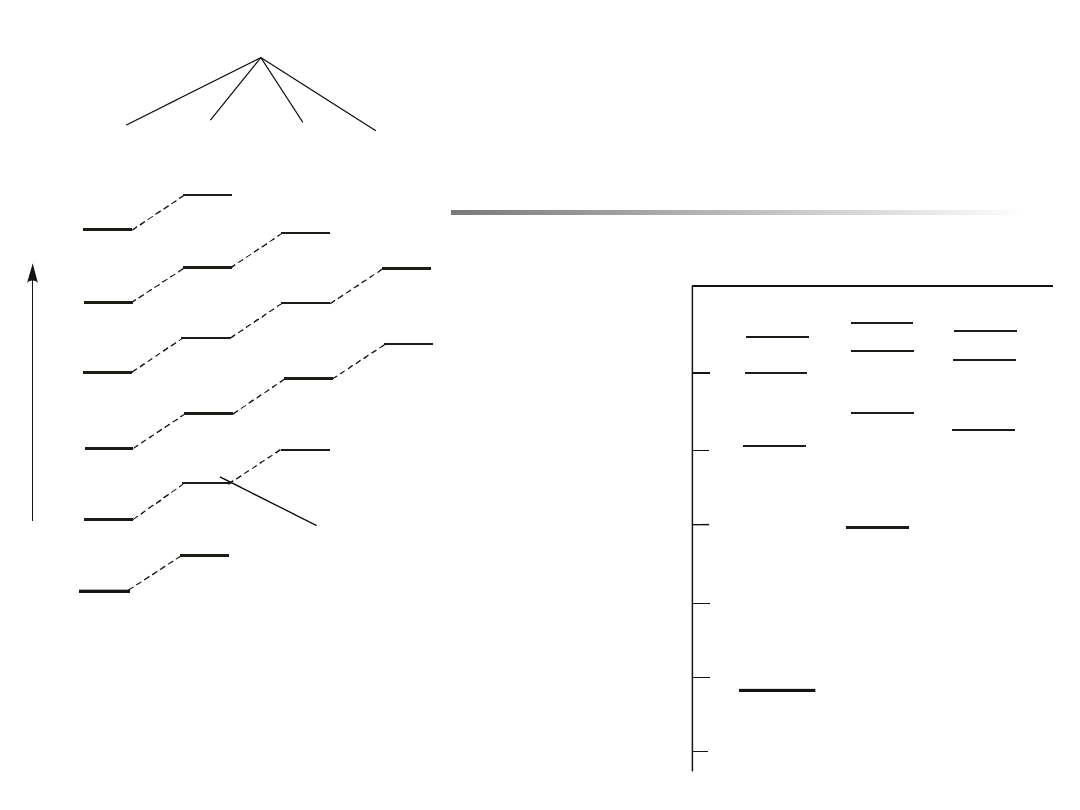
n s p d f
( l= 0 ) ( l= 1 ) ( l= 2 ) ( l= 3 )
S ta n
L i c z b a
e l e k tr o n ó w
6
6
5
4
3
2
1
6
6
6
6
2
2
2
2
2
2
1 0
1 4
1 0
1 0
1 0
E
ne
rg
ia
6 p
6 s
5 p
5 s
5 d
4 p
4 s
4 d
3 p
3 s
3 d
- 1
- 2
- 3
- 4
- 5
- 6
E
ne
rg
ia
(
eV
)
0
Rys.
13.2.
Schematyczne
przedstawienie wpływu orbitalnej liczby
kwantowej l na wartości energii
wiązania elektronu na danej orbicie.
Stany o większej wartości l mają wyżej
położone poziomy energetyczne.
Rys. 13.3. Niektóre poziomy
energetyczne sodu.
44
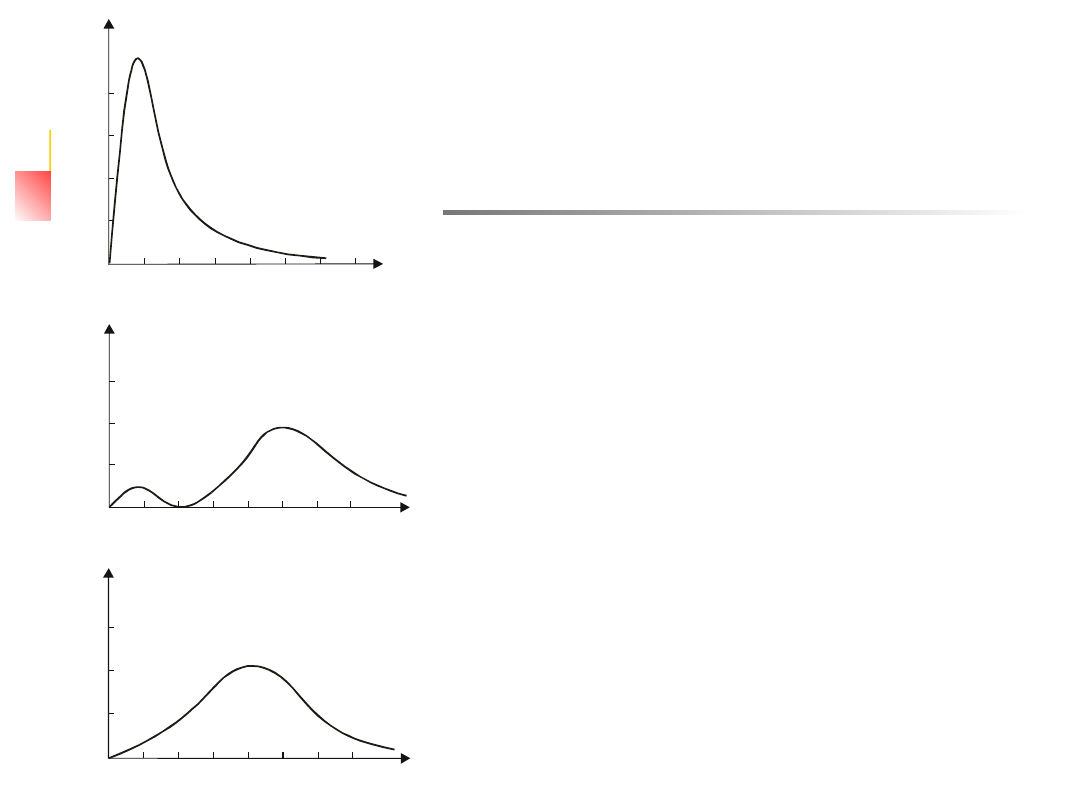
W atomach wielo-elektronowych energia elektronu w
atomie zależy znacznie bardziej od wartości orbitalnej
liczby kwantowej niż w atomie wodoru.
Dla przykładu rozpatrzymy drugą orbitę. W stanie
2s rozkład gęstości prawdopodobieństwa znalezienia
elektronu wykazuje dwa maksima: pierwsze w odległości
około 0.8r
o
od jądra, drugie w odległości 5r
o
od jądra (rys.
12.5). Natomiast w stanie 2p gęstość prawdopodobieństwa
blisko jądra jest mała i występuje tylko jedno maksimum w
odległości 4r
o
od jądra. Oznacza to, że w stanie 2s elektron
będzie często przebywał stosunkowo blisko jądra i w
efekcie będzie bardziej ”odczuwał” ładunek jądra niż w
stanie 2p. Stan 2s będzie stanem silniej związanym. Im
większa wartość głównej liczby kwantowej, tym zależność
energii wiązania elektronu od orbitalnej liczby kwantowej
jest większa (rys. 13.2). Okazuje się również, że
podpoziomy charakteryzujące się dużym l mogą mieć
większe wartości energii niż podpoziomy o małym l, ale o
większej wartości głównej liczby kwantowej. Jako przykład,
na rys. 13.3 pokazano poziomy energetyczne atomu sodu
gdzie stan 3d leży wyżej niż stan 4s, a stan 4f wyżej niż 5p.
45
2
n l
2
R
r
2
n l
2
R
r
2
n l
2
R
r
1 2 3 4 5 6 7
1 2 3 4 5 6 7
1 2 3 4 5 6 7
n = 1
l= 0
n = 2
l= 0
n = 2
l= 1
0 . 4
0 . 3
0 . 2
0 . 1
0
0 . 3
0 . 2
0 . 1
0
0 . 3
0 . 2
0 . 1
0
r / r
o
r / r
o
r / r
o
Układ okresowy pierwiastków
Układ okresowy pierwiastków (patrz Tabele 13.1 i 13.2) przedstawia
takie uporządkowanie pierwiastków według ich liczby atomowej, które
odzwierciedla periodyczność zmian właściwości fizykochemicznych
pierwiastków. Pierwiastki o podobnych właściwościach tworzą grupy, które
w układzie okresowym występują jako kolumny pionowe. Wiersze układu
okresowego nazywamy okresami.
Właściwości pierwiastków uwarunkowane są konfiguracją elektronów w
atomach. Przez konfigurację elektronów rozumiemy określony układ
obsadzeń powłok i podpowłok przez elektrony. Układ ten zapisujemy w
sposób następujący: n, gdzie n, l
k
– odpowiednio główna i orbitalna liczba
kwantowa, k – liczba elektronów na danej podpowłoce.
46
L.
a
Pierwiastek
K
L
M
N
O
P
Z
Nazwa Symb. 1s 2s 2p 3s 3p 3d 4s 4p 4d
4f 5s 5p 5d
5f
6s
1 Wodór
H
1
2 Hel
He
2
3 Lit
Li
2 1
4 Beryl
Be
2 2
5 Bor
B
2 2 1
6 Węgiel
C
2 2 2
7 Azot
N
2 2 3
8 Tlen
O
2 2 4
9 Fluor
F
2 2 5
10 Neon
Ne
2 2 6
11 Sód
Na
2 2 6
1
12 Magnez
Mg 2 2 6
2
13 Glin
Al
2 2 6
2 1
14 Krzem
Si
2 2 6
2 2
15 Fosfor
P
2 2 6
2 3
16 Siarka
S
2 2 6
2 4
17 Chlor
Cl
2 2 6
2 5
18 Argon
Ar
2 2 6
2 6
19 Potas
K
2 2 6
2 6
1
20 Wapń
Ca
2 2 6
2 6
2
47
Promieniowanie
atomów
wzbudzonych
Po
wprowadzeniu
równania
Schrödingera,
mechanikę kwantową zaczęto stosować w teorii
oddziaływań elektroma-gnetycznych, w wyniku czego
powstała
elektrodynamika
kwanto-wa.
Szczegółowe
rozważania tej teorii wychodzą poza ramy nasze-go
wykładu.
Dla nas istotny jest fakt ustanowiony
przez elektrodynamikę kwantową, że
nałado-wana cząstka może pochłonąć lub
emitować pojedyncze fotony
, a teoria
pozwala dokładnie obliczyć odpowiednie
prawdopodobieństwa pochłonięcia lub
emisji fotonu.
48
Widma optyczne
Atomy po zaabsorbowaniu pewnej porcji energii
przechodzą do stanu wzbudzonego. Jeżeli dostarczona
energia wynosi kilka lub kilkanaście elektonowoltów, to
możliwe są jedynie przejścia elektronów walencyjnych na
wyższe poziomy energetyczne. Wiemy bowiem, że energie
wiązania
tych
elektronów
wynoszą
kilka-kilkanaście
elektronowoltów. Takie energie mogą atomy uzyskać
poprzez:
ogrzewanie, przy którym energia jest przekazywana
w wyniku zderzeń w ruchu cieplnym,
wyładowania elektryczne,
oświetlenie promieniowaniem widzialnym i
nadfioletowym,
reakcje chemiczne.
49
Wzbudzone atomy samorzutnie przechodzą do stanu
niższego, a każdemu przejściu towarzyszy emisja kwantu
promieniowania o częstości ν
nm
równej
gdzie E
n
i E
m
– energia elektronu odpowiednio na
wyższym i niższym poziomie energetycznym. Linie
emisyjne promieniowania uwarunkowane tymi przejściami
energetycznymi, nazywamy widmem optycznym, gdyż
widmo to leży w obszarze widzialnym, bliskim nadfiolecie
i bliskiej podczerwieni. Układ linii jest na ogół bardzo
złożony, ale charakterystyczny dla danego pierwiastka.
Fakt ten wykorzystuje się w analizie widmowej do
określania jakościowego i ilościowego składu danej
substancji.
h
E
E
m
n
nm
50
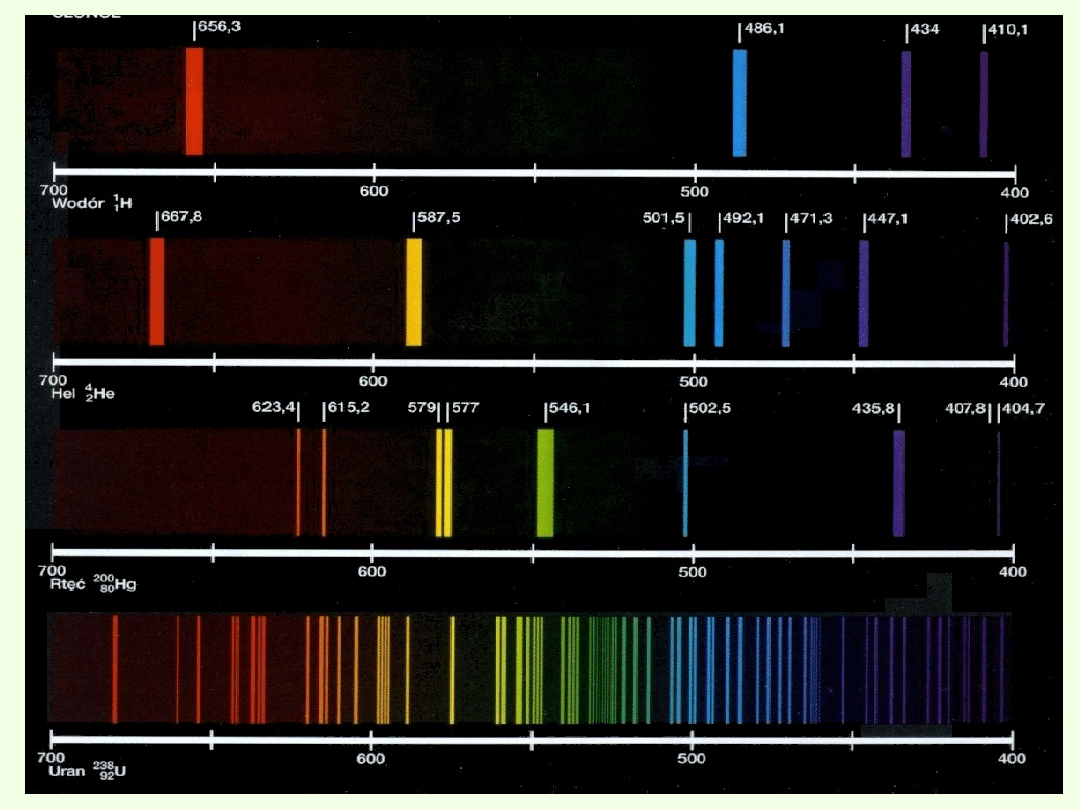
Obserwując widma można stwierdzić, że
nie
zachodzą przejścia między wszystkimi poziomami
energetycznymi
. Okazuje się, że możliwe są tylko
przejścia między takimi poziomami, których liczby
kwantowe l i j spełniają tzw. reguły wyboru
1
l
1
0
,
j
Zatem przejścia zachodzą między poziomami, których liczby
kwantowe l różnią się o jeden, a liczby kwantowe j są jednakowe lub
różnią się o jeden. Mówiąc ściślej,
reguły powyższe nie zabraniają
w sposób bezwzględny innych przejść, lecz mówią tylko, że
przejścia te są mało prawdopodobne.
52
Jeżeli atom jest wzbudzony do wyższego stanu z
którego może powrócić do stanu niżej położonego na
drodze takiego właśnie mało prawdopodobnego przejścia,
to może on pozostać w tym stanie przez bardzo długi
okres czasu.
Poziom taki nazywamy meta-trwałym
(metastabilnym).
O ile typowy czas życia atomu w
stanie wzbudzonym wynosi około 10
–8
s, to poziomy meta-
trwałe charakteryzują się czasami życia rzędu 10
–2
s tzn.
ich czasy życia są miliony razy dłuższe.
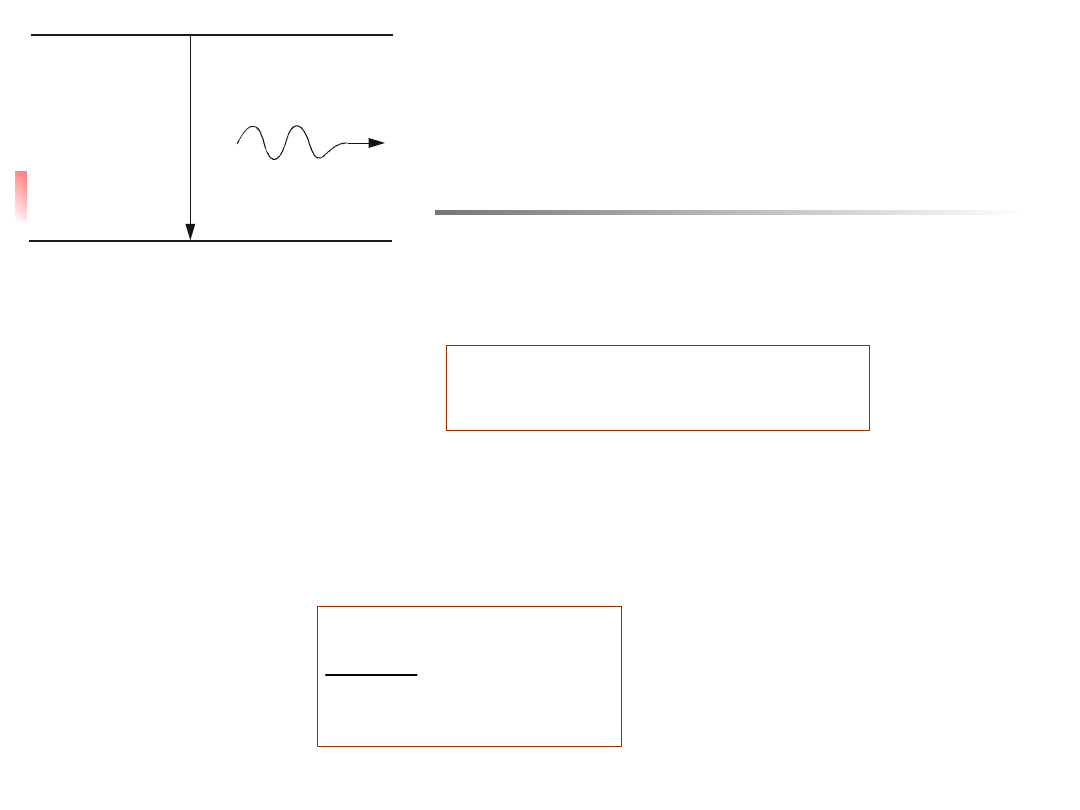
Promieniowanie spontaniczne i wymuszone
Wiemy już, że atom w stanie wzbudzonym przechodzi
samorzutnie do stanu energetycznie niższego, emitując przy tym
kwant promieniowania. Tego rodzaju emisję nazywamy
emisją
spontaniczną (samorzutną).
Przedstawiono ją schematycznie na
rys. 13.4. Omówimy nieco bliżej ten problem.
53
1 sek. >>> 11,5 doby
E
n
E
m
h
n m
Niech
na
wyższym
wzbudzonym
poziomie energetycznym będzie w chwili
początkowej
N
n
(0) atomów. Liczba
przejść spontanicznych w czasie dt
będzie proporcjonalna do N
n
(t)dt. Należy
także oczekiwać, że szybkość przejść
będzie różna dla różnych atomów.
Możemy więc napisać, że na skutek emisji spontanicznej z poziomu n-
tego ubędzie dN
n
atomów, przy czym
(13.1)
gdzie A
nm
jest stałą charakteryzującą szybkość przejść między
poziomem n-tym i m-tym. Jest to współczynnik emisji spontanicznej.
Znak minus występuje dlatego, że na skutek emisji liczba atomów na
poziomie n-tym zmniejsza się. Pisząc wzór (13.1) w postaci
dt
N
A
dN
n
nm
n
dt
A
N
dN
nm
n
n
I całkując otrzymamy
54
C
t
A
N
ln
nm
n
Dla t = 0, N
n
= N
n
(0) , a więc C=lnN
n
(0) . Zatem
Aby bliżej określić stałą A
nm
, obliczamy średni czas życia atomów w
stanie wzbudzonym. Liczba atomów dN
n
, które przeżyły w stanie
wzbudzonym czas t, a następnie w przedziale czasu (t, t + dt)
przeszły do niższego stanu, wynosi
Ponieważ każdy z tych atomów był w stanie wzbudzonym przez czas
t, wobec tego czas życia dN atomów wynosi
t
A
n
n
nm
e
N
t
N
0
dt
A
e
N
dt
A
t
N
dN
nm
t
A
n
nm
n
n
nm
0
tdt
A
e
N
tdN
nm
t
A
n
n
nm
0
55
Całkowity czas życia wszystkich atomów jest równy
A zatem średni czas życia atomów na n-tym poziomie (ze względu
na przejście na poziom m-ty) wynosi
(13.2)
Tak więc współczynnik spontanicznego przejścia, określający
szybkość przejść dla emisji spontanicznej, jest równy odwrotności
średniego czasu życia atomów w stanie wzbudzonym i określa
prawdopodobieństwo przejścia spontanicznego w jednostce czasu
do stanu o niższej energii.
Teoretyczne wyliczenia średniego czasu życia atomu w stanie
wzbudzonym dają wartość około 10
–8
s, tzn. stała emisji
spontanicznej A
nm
wynosi około 10
8
s.
0
0
tdt
A
e
N
T
nm
t
A
n
nm
nm
t
A
nm
n
nm
A
tdt
e
A
N
T
nm
1
0
0
56
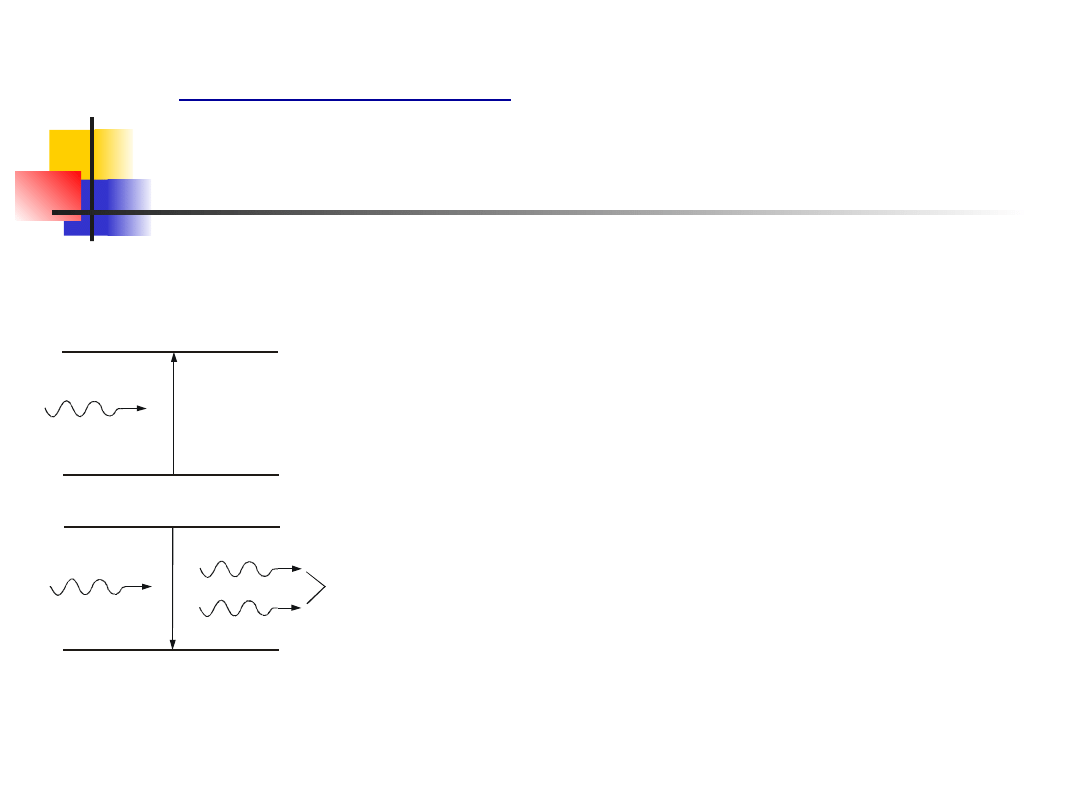
Oprócz emisji spontanicznej występować może także
emisja wymuszona
, co pokazano schematycznie na
rys. 13.5. W procesie absorpcji wymuszonej foton
promieniowania o częstotliwości
nm
powoduje przejście
atomu z poziomu niższego na poziom wyższy, przy czym
foton zostaje zaabsorbowany przez atom.
( a )
( b )
h
n m
h
n m
h
n m
E
n
E
n
E
m
E
m
Rys. 13.5. Absorpcja
(a) i emisja (b)
wymuszona
.
W procesie emisji wymuszonej padający
foton powoduje przejście wzbudzonego
atomu do stanu energetycznie niższego. W
wyniku tego przejścia wzrasta liczba
fotonów, gdyż obok fotonu pada-jącego
pojawia się drugi foton, emitowany przez
atom. Fakt, że foton promieniowania może
spo-wodować przejście z poziomu niższego
na wyższy i odwrotnie ma swoją analogię
klasyczną. Jeżeli na oscylator harmoniczny
działa periodycznie siła zewnętrzna, to
oscylator wykonuje drgania wy-muszone o
częstotliwości siły zewnętrznej.
57
Jeżeli
częstotliwość
ta
jest
równa
częstotliwości
rezonansowej oscylatora, to wówczas opóźnienie fazowe
drgań oscylatora w stosunku do siły wymuszającej wynosi
90 i siła ta przekazuje energię oscylatorowi. Gdyby jednak
oscylator wyprzedzał w fazie siłę zewnętrzną to wówczas
oscylator przekazuje energię na zewnątrz. Traktując atom
jako oscylator, a siłę zewnętrzną jako pole energetyczne
promieniowania, otrzymujemy klasyczne wyjaśnienie
emisji i absorpcji wymuszonej.
Możemy
przyjąć,
że
częstotliwość
przejść
wymuszonych między poziomami n i m będzie
proporcjonalna do gęstości widmowej promieniowania
u(ν
nm
). Gęstość energii promieniowania jest proporcjonalna
do zdolności emisyjnej. Rozważania których nie będziemy
przeprowadzać
prowadzą
do
wniosku,
że
ε(ν,T)=(1/4)cu(ν,T). Czyli
1
1
8
3
3
kT
/
h
exp
c
h
u
nm
nm
nm
58
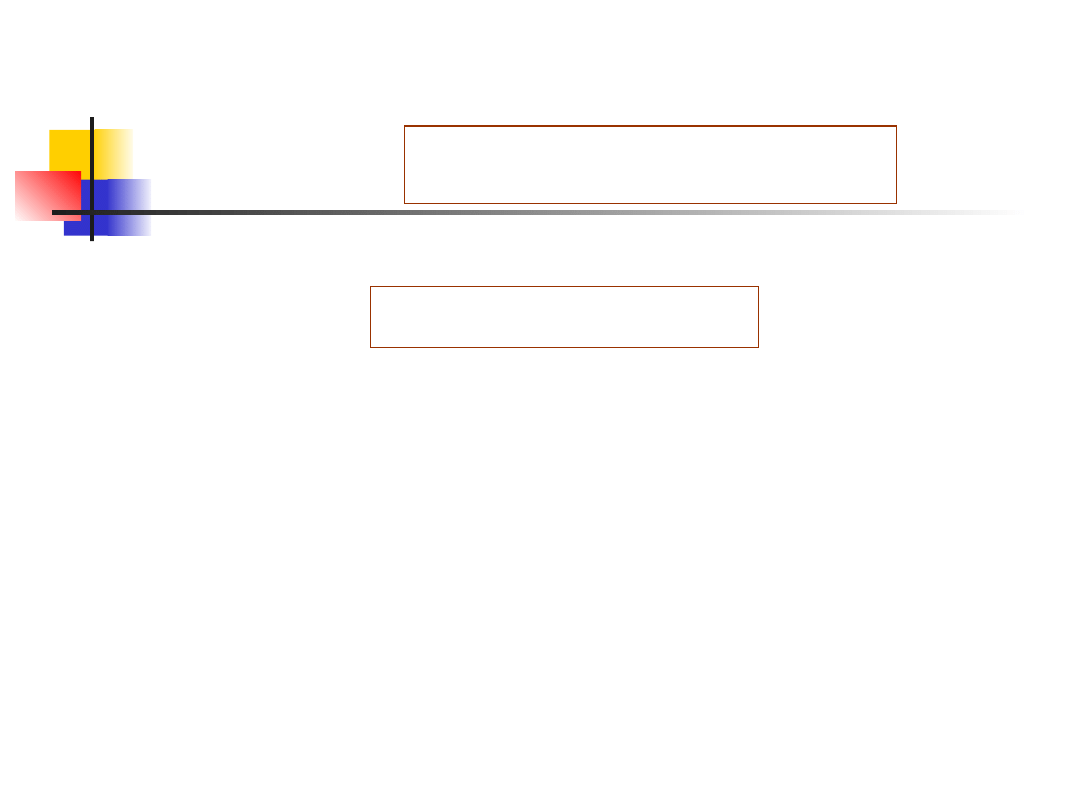
Analogicznie do wzoru (13.1) napiszemy, że ilość przejść
wymuszonych z poziomu n-tego na poziom m-ty w czasie
dt będzie wynosiła
natomiast liczba przejść z poziomu m-tego na n-ty
gdzie B
nm
jest współczynnikiem emisji wymuszonej, a B
mn
– współczynnikiem absorpcji wymuszonej. W wyrażeniach
powyższych opuściliśmy znak minus, gdyż interesuje nas
liczba przejść, a nie zmiana liczby atomów.
Współczynniki A
nm
, B
nm
i B
mn
charakteryzujące procesy
emisji spontanicznej, emisji i absorpcji wymuszonej
nazywamy także współczynnikami Einsteina.
dt
N
u
B
dN
n
nm
nm
n
dt
N
u
B
dN
m
mn
mn
m
59
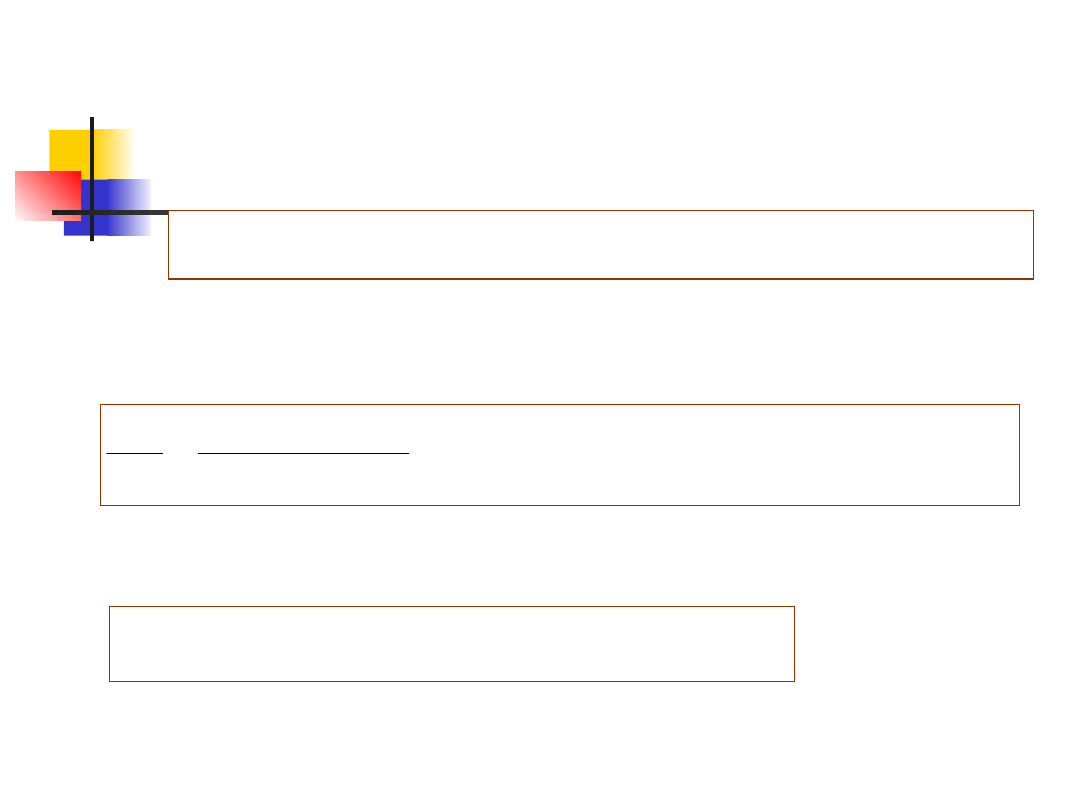
Jeżeli układ składający się z N
n
atomów na poziomie n-tym i
N
m
atomów na poziomie m-tym jest w określonej
temperaturze T w równowadze z promieniowaniem
elektromagnetycznym o gęstości widmowej u(ν
nm
), to liczba
przejść z poziomu wyższego na niższy musi być taka sama
jak z niższego na wyższy. Możemy więc zapisać
Liczby atomów na n-tym i m-tym poziomie możemy wyrazić
przez funkcję rozkładu Boltzmanna . Mamy więc
(13.5)
Po uwzględnieniu tego wzoru, otrzymujemy
(13.6)
dt
N
u
B
dt
N
u
B
dt
N
A
n
nm
mn
n
nm
nm
n
nm
kT
/
h
exp
kT
/
E
E
exp
kT
/
E
exp
kT
/
E
exp
N
N
nm
m
n
m
n
m
n
kT
/
h
nm
mn
nm
nm
nm
nm
e
u
B
u
B
A
60
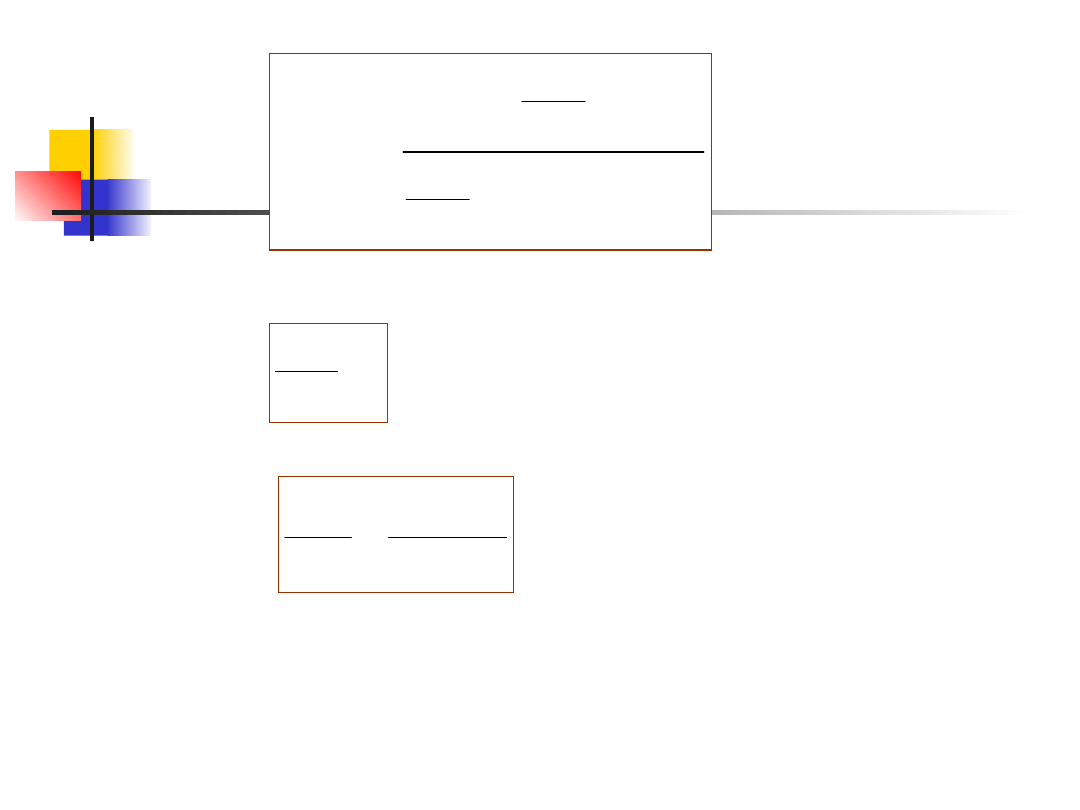
Z ostatniego wzoru obliczymy u(ν
nm
),
Jeżeli porównać powyższe wyrażenie z (13.3), to
otrzymujemy
(13.7)
(13.8)
1
kT
h
exp
B
B
B
A
u
nm
nm
mn
nm
nm
nm
1
mn
nm
B
B
3
3
8
c
h
B
A
nm
nm
nm
61
Z wyrażenia
wynika, że współczynniki emisji i
absorpcji wymuszonej są równe. Ponieważ jednak w stanie
równowagi termodynamicznej N
n
<<N
m
, to absorpcja
wymuszona zdecydowanie przewyższa emisję wymuszoną.
Oznacza to, że promieniowanie elektromagnetyczne jest
absorbowane w układzie. Gdyby jednak doprowadzić do
sytuacji w której N
n
>N
m
, to wówczas promieniowanie
będzie
w
układzie
wzmacniane.
Fakt
ten
jest
wykorzystywany w laserach.
Musimy jednak pamiętać,
że warunek N
n
>N
m
nie może być nigdy spełniony dla
atomów
będących
w
stanie
równowagi
termodynamicznej z otoczeniem
.
1
mn
nm
B
B
62
Powróćmy jeszcze do przypadku, kiedy stosunek N
n
/N
m
jest
dany równaniem (13.5). Wówczas na podstawie zależności
(13.6) możemy wyliczyć stosunek prawdopodobieństwa
A
nm
emisji spontanicznej do prawdopodobieństwa B
nm
u(ν
nm
)
emisji wymuszonej.
Dla promieniowania w obszarze widzialnym
nm
= 510
14
Hz, w temperaturze 300 K otrzymujemy
tzn. emisja spontaniczna jest zdecydowanie bardziej
prawdopodobna niż emisja wymuszona. Mówiąc
inaczej, promieniowanie emitowane przez klasyczne źródła
światła jest promieniowaniem spontanicznym.
1
kT
/
h
exp
u
B
A
nm
nm
nm
nm
1
nm
nm
nm
u
B
A
63
Proponowane tematy referatów
64
1. Wiązania chemiczne i ich wpływ na właściwości
materiałów.
2. Wybrane technologie stosowane w wytwarzaniu
elementów elektronicznych – dyfuzja, epitaksja,
fotolitografia.
3. Tranzystor unipolarny i polowy budowa, zasady
pracy.
4. Półprzewodnikowe elementy fotowoltaiczne.
5. Budowa lasera na ciele stałym – budowa i zasady
pracy.
6. Zastosowanie światła laserowego – omów kilka
wybranych zastosowań.
7. Zastosowanie techniki światłowodowej w
telekomunikacji.
Kolejne tematy
referatów
1. Wyświetlacze ciekłokrystaliczne: efekt TN,
problemy adresowania matrycowego,
budowa kolorowego wyświetlacza video.
2. Wyświetlacze plazmowe: budowa
kolorowego wyświetlacza plazmowego i
technika jego adreso-wania.
3. Wyświetlacze elektroluminescencyjne: EL,
OLED, PLED, LED – budowa, efekt fizyczny,
realizacja zobrazowania barwnego,
zastosowania, kierunki rozwoju.
4. Systemy projekcyjne: historia, współczesne
LCD, DLP, budowa, sposób realizacji
zobrazowania, kino cyfrowe.
5. Wyświetlacze na podłożach giętkich –
problemy budowy i kierunki rozwoju.