ELEKTROTECHNIK

ELEKTROTECHNIK

A II

A II

Obwody rozgałęzione

Obwody rozgałęzione

prądu sinusoidalnego

prądu sinusoidalnego

prof. dr hab. inż. Tadeusz

prof. dr hab. inż. Tadeusz

Niedziela

Niedziela

Równanie macierzowe do

obliczania obwodów prądu

zmiennego metodą oczkową

Z x I

0

= E

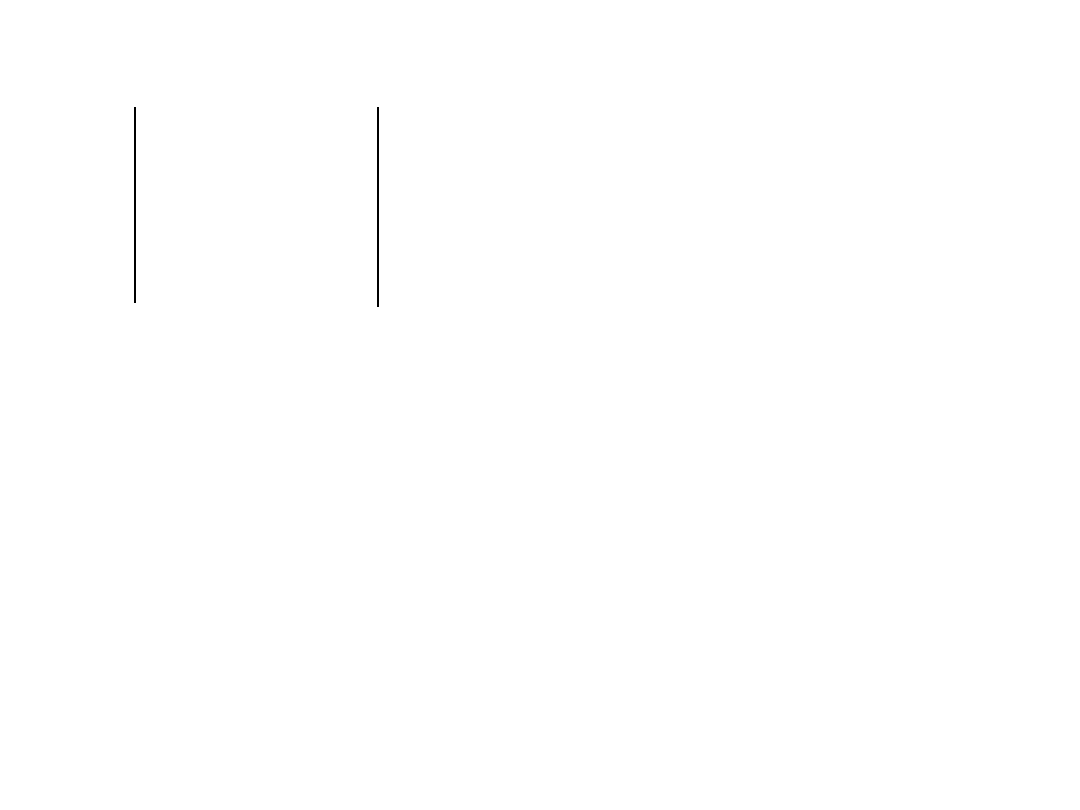
Z

11

, Z

12

, . . . Z

1n

- macierz impedancji własnych i wzajemnych

Z

21

, Z

22

, . . . Z

2n

(macierz kwadratowa symetryczna):

Z= na głównej przekątnej występują impedancje
własne oczkowe (Z

kk

), poza główną przekątną

impedancje wzajemne (Z

kl

)

Z

n1

, Z

n2

, . . . Z

nn

Z

kk

– impedancja własna k-tego oczka jest równa sumie impedancji

wszystkich gałęzi należących do tego oczka.
Impedancje własne oczek przyjmujemy zawsze ze znakiem (+).

Z

kl

– impedancja wzajemna k-tego oczka z oczkiem l-tym jest równa impedancji

gałęzi wspólnej oczka k-tego i l-tego.
Znak impedancji wzajemnej zależy od zwrotów prądów oczkowych w
gałęzi wspólnej.
Jeżeli zwroty prądów oczkowych są zgodne to przyjmujemy znak (+),
jeżeli przeciwne to znak (-).

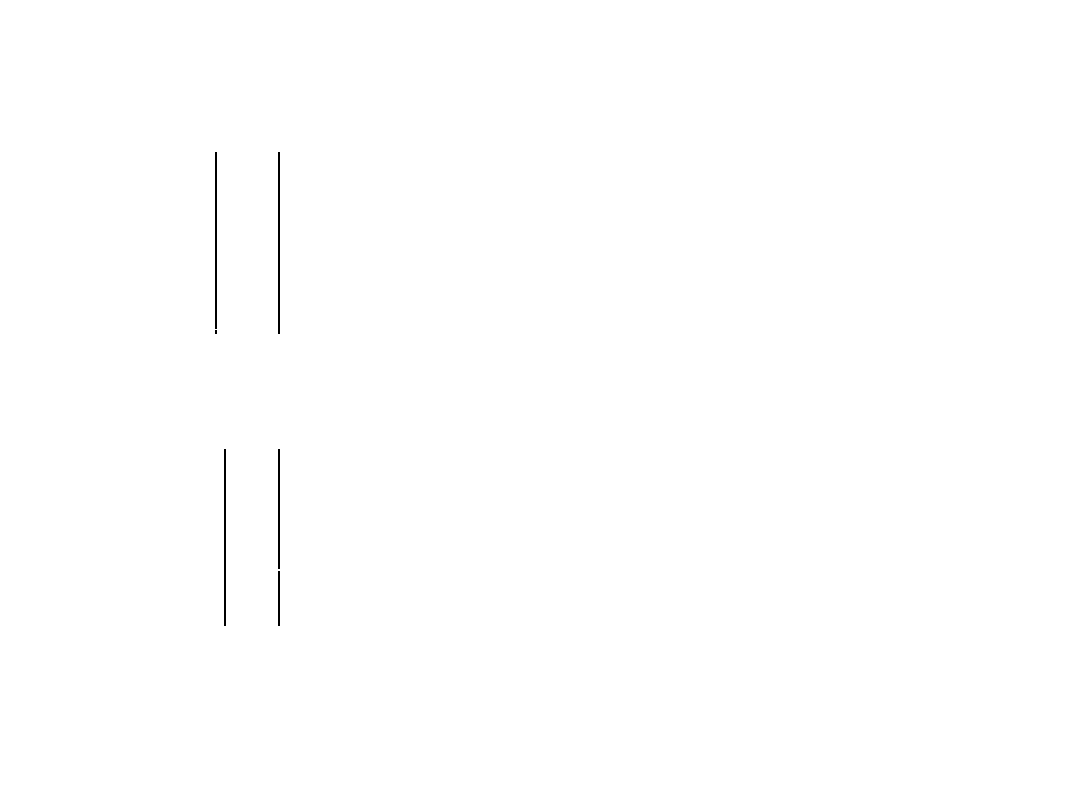
I

01

- macierz prądów oczkowych (macierz kolumnowa)

I

02

o liczbie wierszy n równej liczbie oczek liniowo

I

o

= niezależnych obwodów.

I

on

E

11

- macierz napięć źródłowych oczkowych (macierz kolumnowa)

E

22

o liczbie wierszy n równej liczbie oczek liniowo niezależnych obwodów.

E =
E

kk

– napięcie źródłowe k-tego oczka jest równe sumie napięć

źródłowych gałęzi nieleżących do k-tego oczka.
E

nn

Równanie macierzowe do

obliczania

obwodów prądu zmiennego

metodą

potencjałów węzłowych

Y x V = I

źr

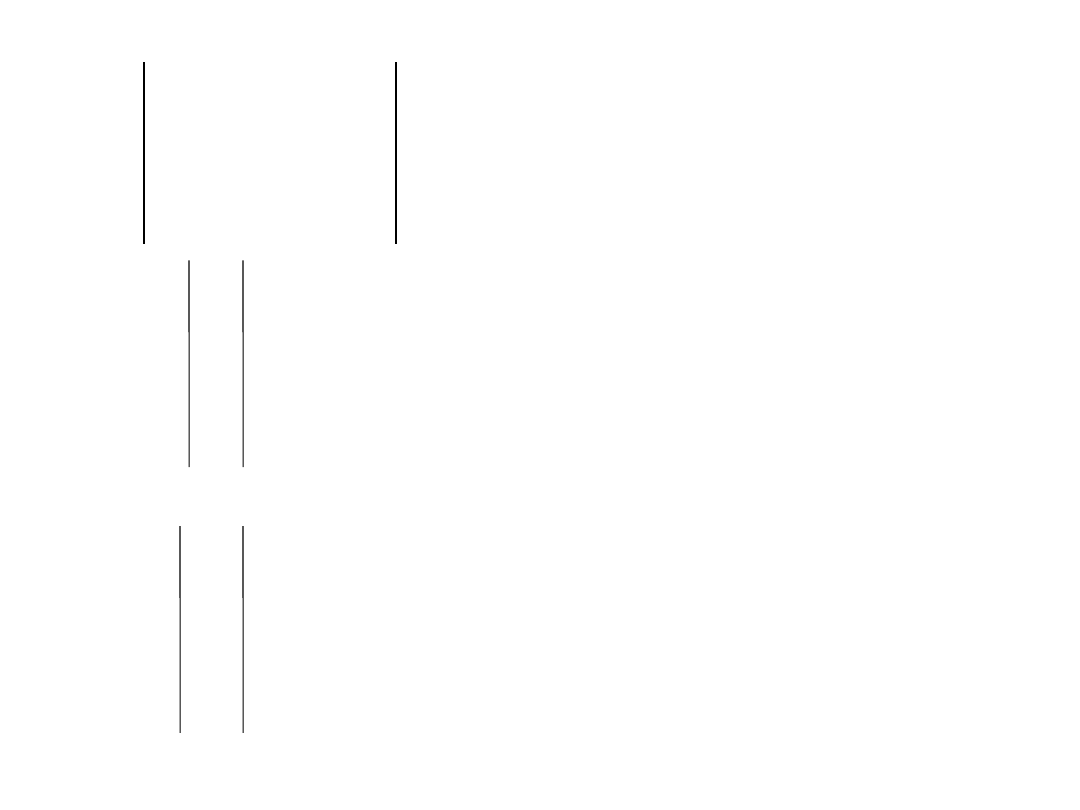
Y

11

, Y

12

, . . . Y

1n

- macierz admitancji własnych i

wzajemnych
Y

21

, Y

22

, . . . Y

2n

(macierz kwadratowa symetryczna): na

głównej
Y = . przekątnej występują admitancje
własne węzłów
ze znakiem (+), poza główną
przekątną (-).
Y

n1

, Y

n2

, . . . Y

n

V

1

V

2

- macierz napięć węzłowych (macierz kolumnowa) o

V =

liczbie wierszy równej n ,

tzn. liczbie n węzłów liniowo niezależnych.
.
V

n

I

źr

1

I

źr

2

- macierz prądów źródłowych wypadkowych w węzłach

I

źr

=

(macierz kolumnowa) o liczbie wierszy n równej liczbie

węzłów liniowo niezależnych.

.

I

źr

n

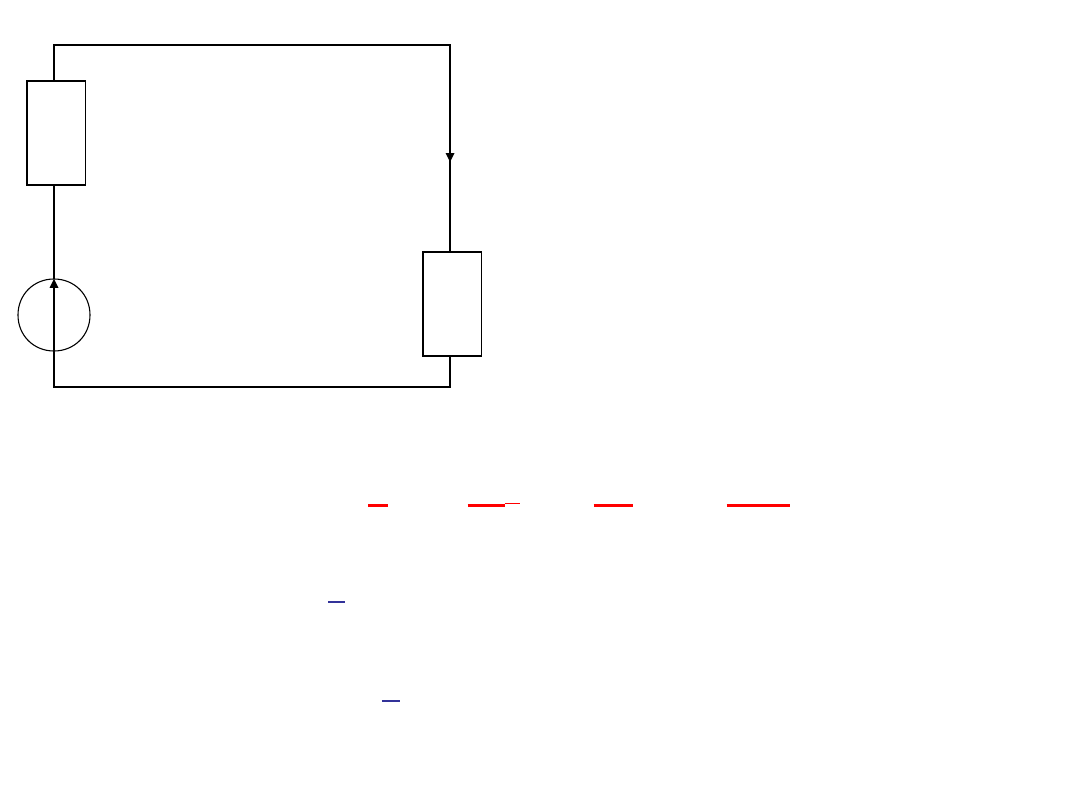
Twierdzenie Thevenina

• Każdy dowolny aktywny obwód

liniowy można od strony wybranych
dwóch zacisków ab zastąpić
obwodem równoważnym złożonym z
połączonego szeregowo jednego
idealnego napięcia E

z

i jednej

idealnej impedancji zastępczej Z

z

.

Z

I = E

z

/ [Z

z

+ Z]

Z – impedancja odbiornika

I

Z

z

E

z

Napięcie zastępcze Ez

jest równe napięciu, jakie wystąpi na

zaciskach ab po odłączeniu odbiornika o impedancji Z , tzn w
stanie jałowym.

Impedancja zastępcza Zz

jest równa impedancji, widzianej z zacisków

ab po zwarciu wszystkich źródeł napięcia i rozwarciu wszystkich źródeł
prądu.

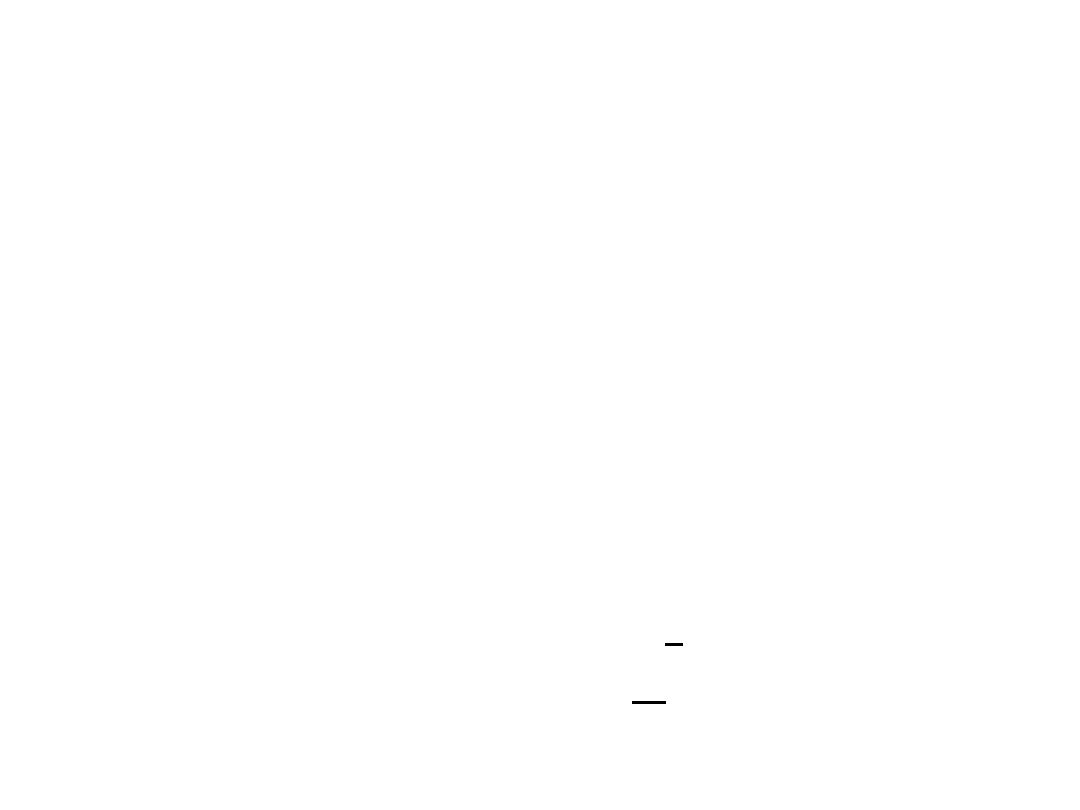
Twierdzenie Nortona

• Każdy dowolny aktywny obwód

liniowy można od strony wybranych
dwóch zacisków ab zastąpić
obwodem równoważnym złożonym z
połączonego równolegle jednego
idealnego źródła prądu I

żr

oraz jednej

admitancji zastępczej Y

z

.

Y

z

= 1 / Z

z

I

źr

= E

z

/ Z

z

Y – admitancja odbiornika

I = {Y / [Y + Y

z

]} I

źr

Y

z

Y

I

źr

I

Prąd źródłowy zastępczego źródła prądu I

źr

jest równy

prądowi
zwarcia I

z

zacisków ab, do których dołączony jest odbiornik.

Admitancja zastępcza Y

z

jest równa admitancji widzianej z zacisków ab

po zwarciu wszystkich źródeł napięcia i rozwarcia wszystkich źródeł prądu.

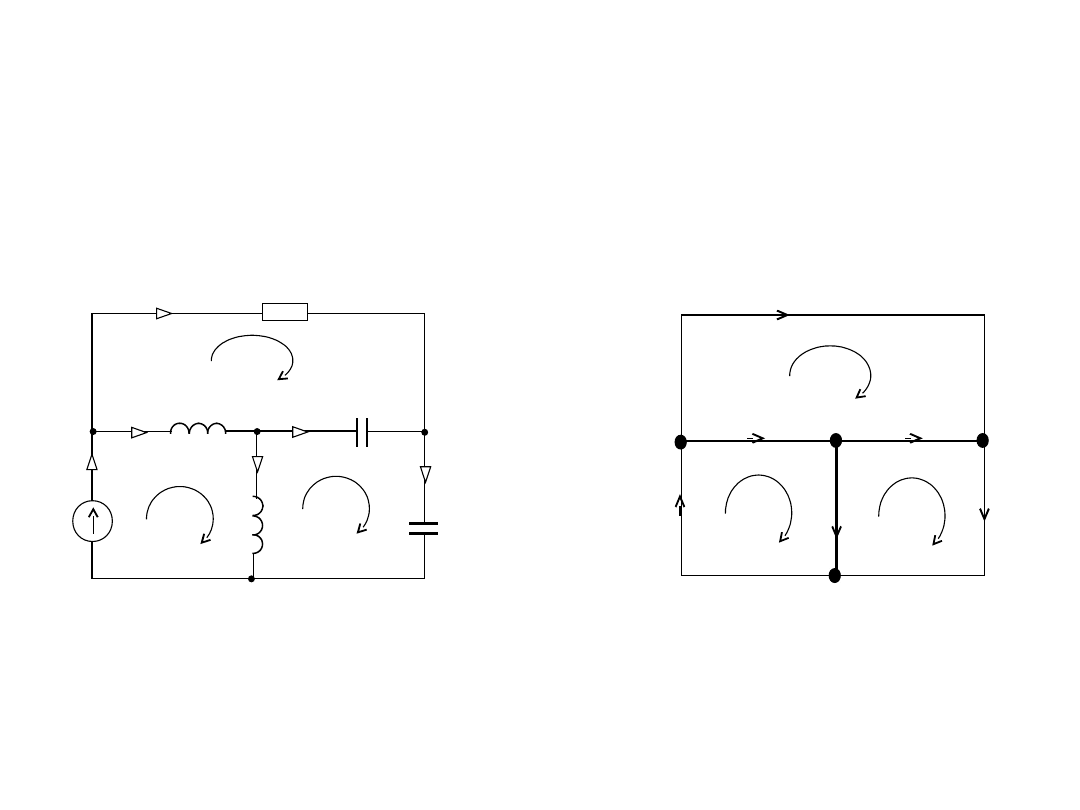
METODA KLASYCZNA

• Zadanie 1

• Oblicz wartości symboliczne prądów gałęziowych w

przedstawionym obwodzie prądu sinusoidalnego stosując metodę
klasyczną

• ( równań Kirchhoffa).

1

2

3

4

U

I

12

I

13

I

23

I

24

R

L

L

C

C

I

34

I

3

1

2

3

1

2

1

2

3

4

Ustalamy liczbę węzłów w = 4.

Ustalamy liczbę niezależnych węzłów m = w – 1 = 4 – 1 = 3.

Wniosek

. Możemy napisać 3 niezależne równania

zgodnie z I prawem Kirchhoffa dla wybranych węzłów (np. 1, 2, 3).

Ustalamy liczbę gałęzi g = 6.
Ustalamy liczbę oczek niezależnych.
n = g – m = 6 – 3 = 3

Wniosek

. Możemy napisać 3 niezależne równania

zgodnie z II prawem Kirchhoffa dla wybranych 3 oczek.

Z I p. Kirchhoffa

Dla 1 węzła I = I

12

+ I

13

-I + I

12

+ I

13

= 0

Dla 2 węzła I

12

= I

23

+ I

24

=> -I

12

+ I

23

+I

24

= 0

Dla 3 węzła I

23

+ I

13

= I

34

-I

13

– I

23

+ I

34

= 0

Z II p. Kirchhoffa

Dla 1 oczka I

12

x Z

L

+ I

24

x Z

L

= U

Dla 2 oczka I

23

x Z

C

+ I

34

x Z

C

– I

24

x Z

L

= 0

Dla 3 oczka I

13

x Z

R

– I

23

x Z

C

– I

12

x Z

L

= 0

Grupujemy odpowiednio 6 równań

-I + I

12

+ I

13

+ 0 x I

23

+ 0 x I

24

+ 0 x I

34

= 0

0 x I - I

12

+ 0 x I

13

+ I

23

+ I

24

+ 0 x I

34

= 0

0 x I + 0 x I

12

- I

13

- I

23

+ 0 x I

24

+ I

34

= 0

0 x I + Z

L

I

12

+ 0 x I

13

+ 0 x I

23

+ Z

L

x I

24

+ 0 x I

34

= U

0 x I + 0 x I

12

+ 0 x I

13

+ Z

C

x I

23

- Z

L

x I

24

+ Z

C

x I

34

= 0

0 x I - Z

L

I

12

+ Z

R

I

13

- Z

C

x I

23

+ 0 x I

24

+ 0 x I

34

= 0

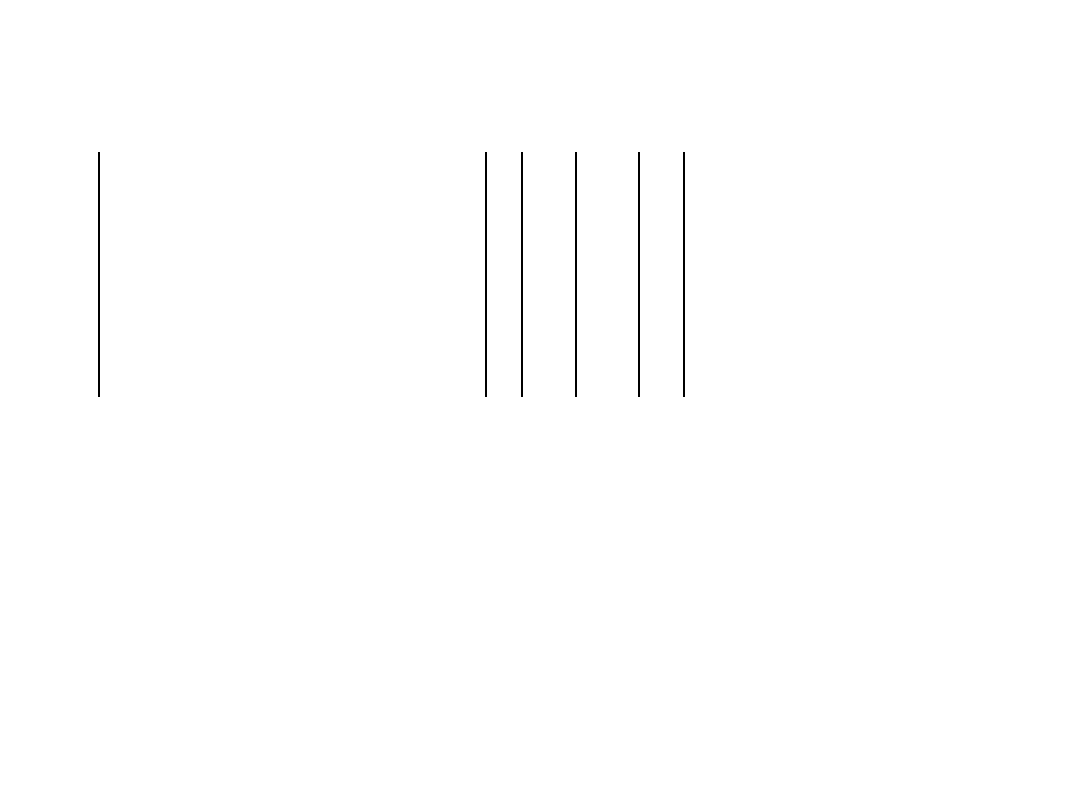
stąd równanie macierzowe

-1 +1 +1 0 0 0 I 0
0 -1 0 1 1 0 I

12

0

0 0 -1 -1 0 1 I

13

= 0

0 Z

L

0 0 Z

L

0 I

23

U

0 0 0 Z

C

– Z

L

Z

C

I

24

0

0 - Z

L

Z

R

– Z

C

0 0 I

34

0

Rozwiązywanie układu 6 równań liniowych z 6-cioma niewiadomymi
dla prądów gałęziowych uzyskamy korzystając z

wzorów Cramera

.

Jednak przy 6 niewiadomych obliczenia są dość pracochłonne.

Pierwsze prawo Kirhoffa

Dla każdego węzła obwodu elektrycznego suma prądów dopływających do węzła

jest równa sumie prądów odpływających od węzła.

I

d

= I

odp

Drugie prawo Kirhoffa

W dowolnym oczku obwodu elektrycznego suma algebraiczna napięć odbiornikowych

oraz suma algebraiczna napięć źródłowych jest równa zero.

Z I + E = 0

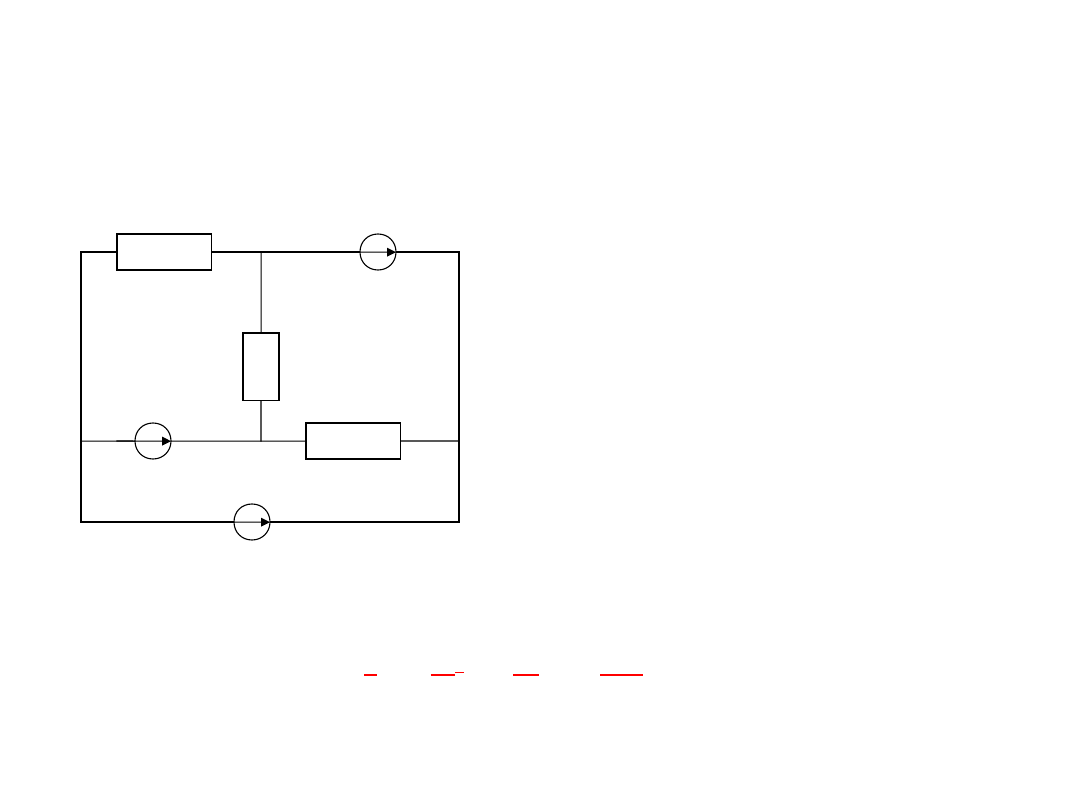
Zadanie 2

Oblicz wartość prądu I płynącego przez odbiornik o impedancji Z w obwodzie
prądu sinusoidalnego stosując

twierdzenie Thevenina oraz zasadę

superpozycji

do obliczania napięcia stanu jałowego Ez

I

E

1

Z

2

Z

1

E

2

I

źr

Z

Dane: E1 = 10V ,
E2 = j20V
Z1 = 5 + j5  ,

Z2 = 5 –j5  ,

Z = 5 

Iźr = 4A

I = E

z

/ [Z

z

+ Z]

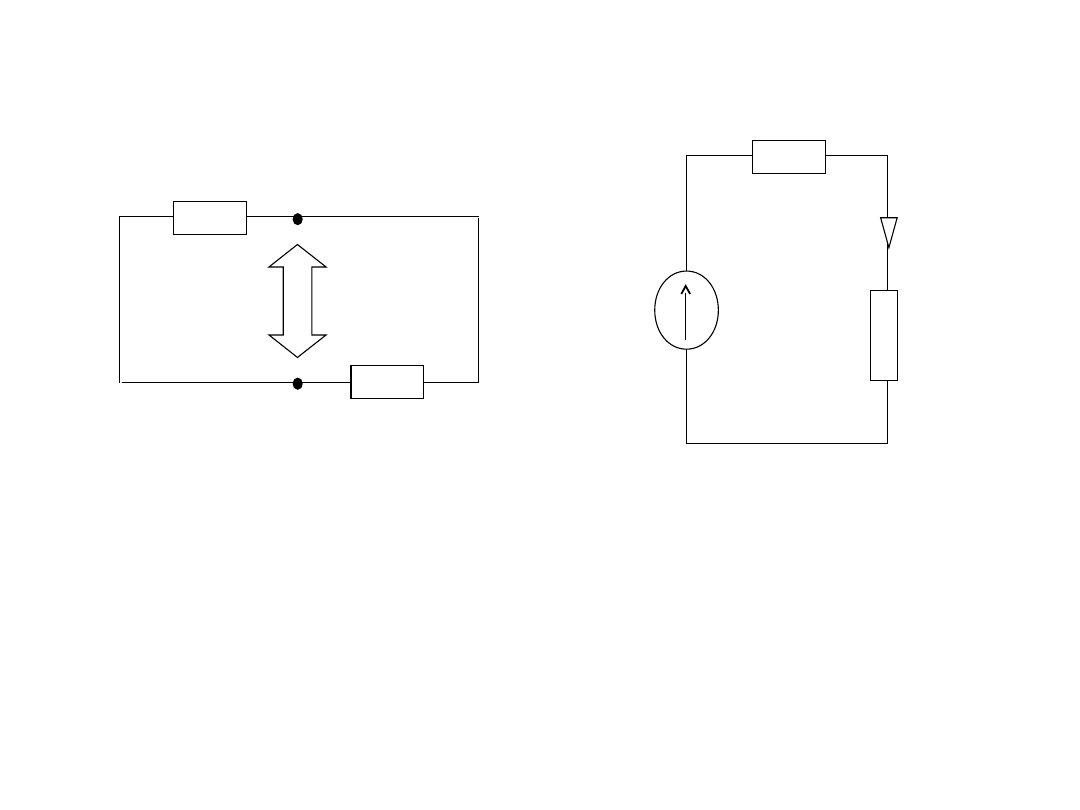
E

z

Z

z

Z

w

Z

2

Z

1

Z

I

1 / Z

z

= 1 / Z

1

+ 1 / Z

2

= [Z

2

+ Z

1

] / Z

1

Z

2

=
[(5 + j5) + (5 - j5)] / [(5 + j5) x (5 - j5)]
=
10 / (25 + 25) = 10 / 50

Z

z

= 5 []

Do wyznaczenia prądu I zastosujemy

twierdzenie Thevenina

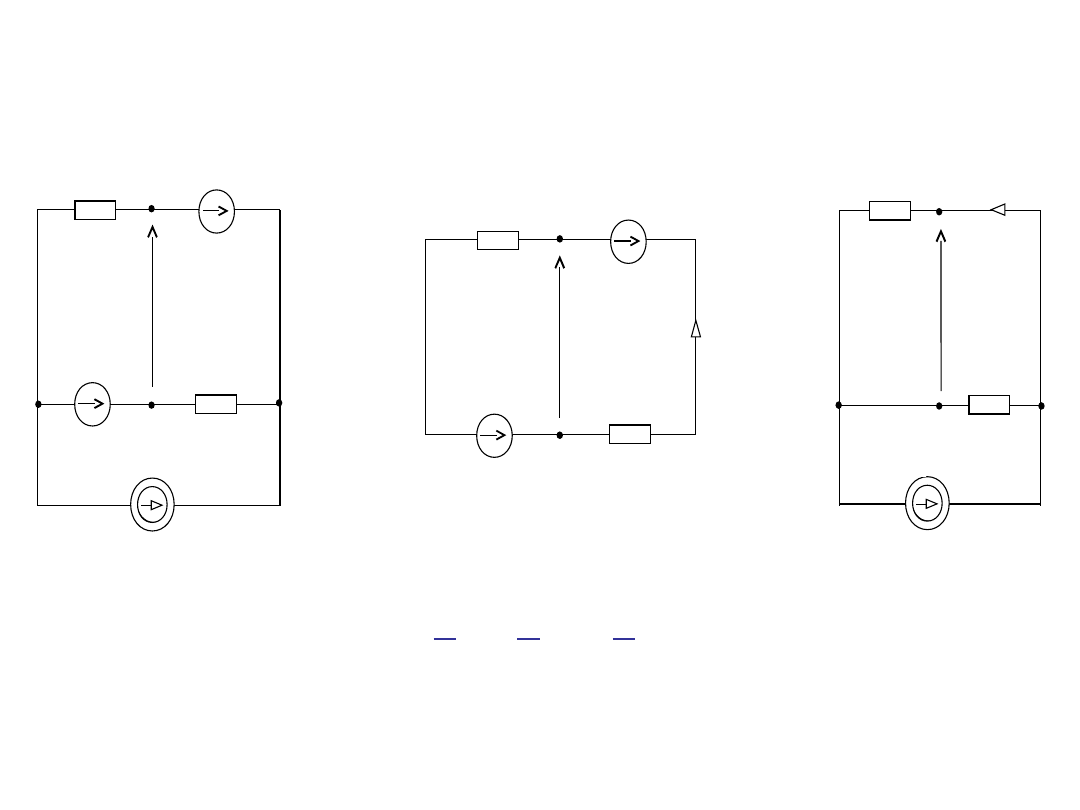
Napięcie zastępcze Ez, napięcie stanu jałowego, obliczymy korzystając z
zasady superpozycji.



+

1

Z

1

E

2

Z

2

E

1

I

źr

E

z

E

1

Z

2

I

0

’

Z

1

E

2

Z

1

I

0

”

E

z

’’

I

źr

Z

2

E

z

’

A

B

E

z

= E

z

’ + E

z

”

Dla schematu

A

:

a)

I

o

’ x Z

1

+ E

2

+ I

o

’ x Z

2

– E

1

= 0

I

0

’(Z

1

+ Z

2

) = - E

2

+ E

1

I

o

‘= [E

1

- E

2

] / [Z

1

+ Z

2

]

= [10 – j20] / {[5+j5] [5-j5]} = [10 - j20] /10

I

0

’ = 1 – 2j [A]

b)

-E

z

’ = E

2

’ + I

0

’ x Z

2

= j20 + (1 - j2) (5 - j5)=

= j20 + 5 – j5 – 10j – 10 = -5 + j5

-

E

z

’ = -5 + j5

czyli: E

z

’ = 5 – j5 [V]

Dla schematu

B

Z

I prawa Kirchoffa

a)

I

x

+ I

źr

= I

0

”

I

x

= I

0

” – I

źr

b)

I

x

Z

2

+ I

0

” Z

1

= 0

(I

0

” – I

źr

) Z

2

+ I

0

” x Z

1

= 0

I

0

” (E

z

Z

2

+ Z

1

) = I

źr

x Z

2

I

0

” = [I

źr

x Z

2

] / [Z

2

+ Z

1

]

=

{ 4 x [5 – j5]} / {[5 – j5] + [5 + j5]} =
= {20 –j20} / 10 = 2 – j2

I

0

” = 2 – 2j [A]

c)

E

z

” = I

0

” x Z

1

= (2 – 2j)(5 + j5) =

= 10 + 10j – 10j + 10 = 20 [V]

E

z

”= 20 [V]

E

z

= E

z

’ + E

z

”

= 5 – j5 + 20 = 25 – j5

[V]

I = E

z

/ [Z

z

+ Z]

= [25 –j5] / [5 + 5] =

[25 – j5] / 10 = 2,5 –j 0,5

I

z

= 2,5 – j0,5 [A]

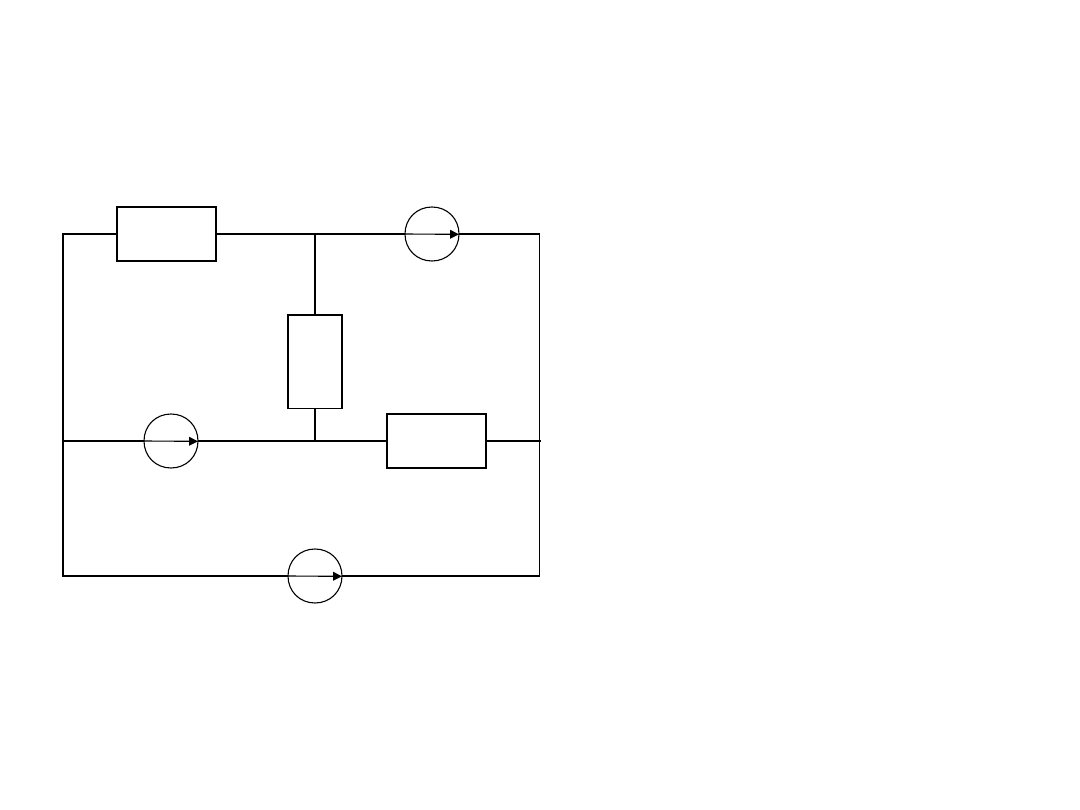
Zadanie 3

Oblicz wartość prądu I płynącego przez odbiornik o impedancji Z w obwodzie prądu
sinusoidalnego stosując

twierdzenie Nortona oraz zasadę superpozycji

do

obliczania prądu zwarcia Iz.

Z

1

E

2

I

żr

I

Z

E

1

Z

2

Dane :E

1

= 10 [V],

E

2

= j20 [V]

Z

1

= 5 + j5 [],

Z

2

= 5 - j5 [],

Z = 5 []

I

źr

= 4 [A]

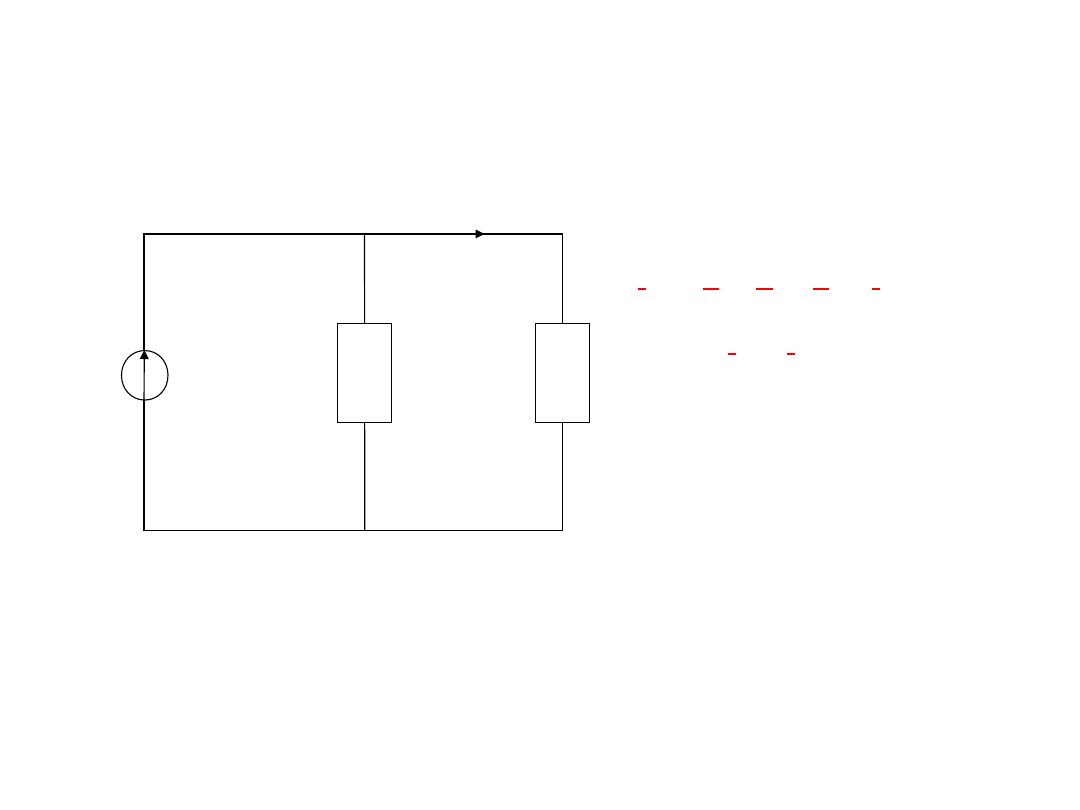
Do wyznaczenia prądu I zastosujemy

twierdzenie Nortona

.

Y

Y

z

I

źr

I = {Y / [Y + Y

z

]} I

źr

I

źr

= I

z

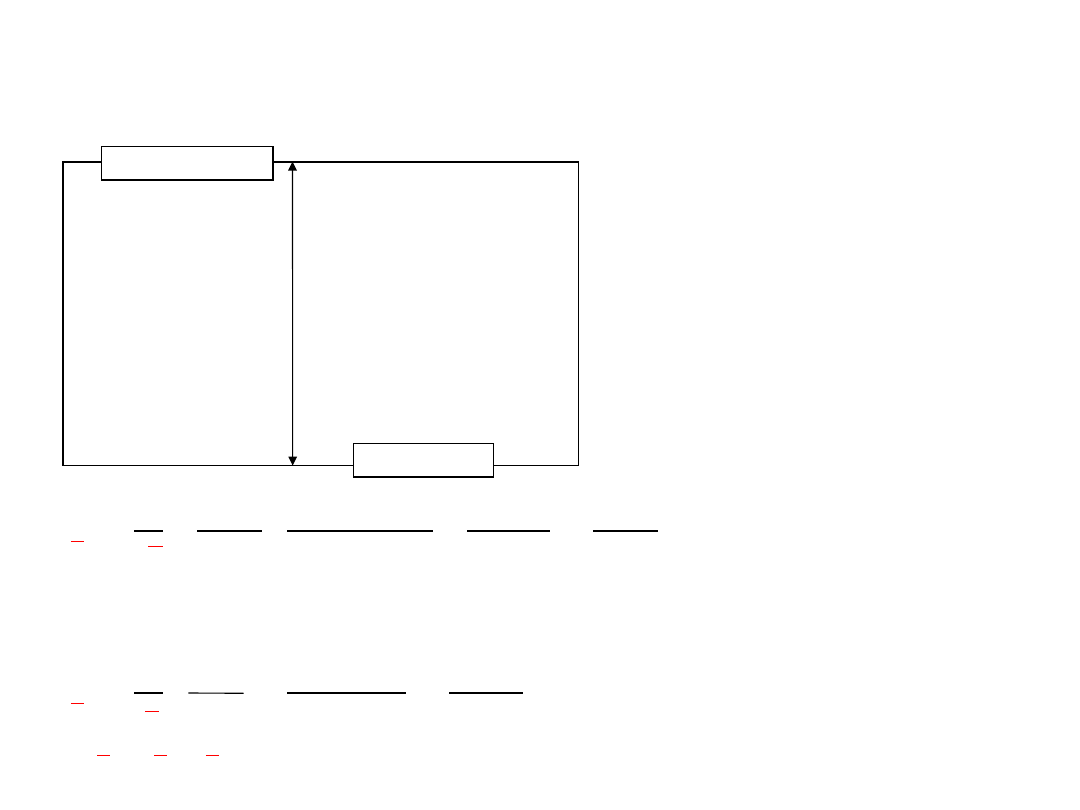
Obliczamy admitację zastępczą Y

z

Y

1

Y

z

Y

2

1

1 5 – j5

5 – j5 5 – j5

Z

1

5 + j5 (5 + j5)(5 – j5) 25 + 25 50

=0,1 – j0,1 [S]

1

1 5 + j5 5 + j5

Z

2

5 - j5 (5 - j5)(5 + j5) 50

Y

z

= Y

1

+ Y

2

= 0,1 – j0,1 + 0,1 + j0,1 = 0,2 [S]

= 0,1 + j0,1 [S]

Y

2

=

=

=

=

=

=

=

=

Y

1

=

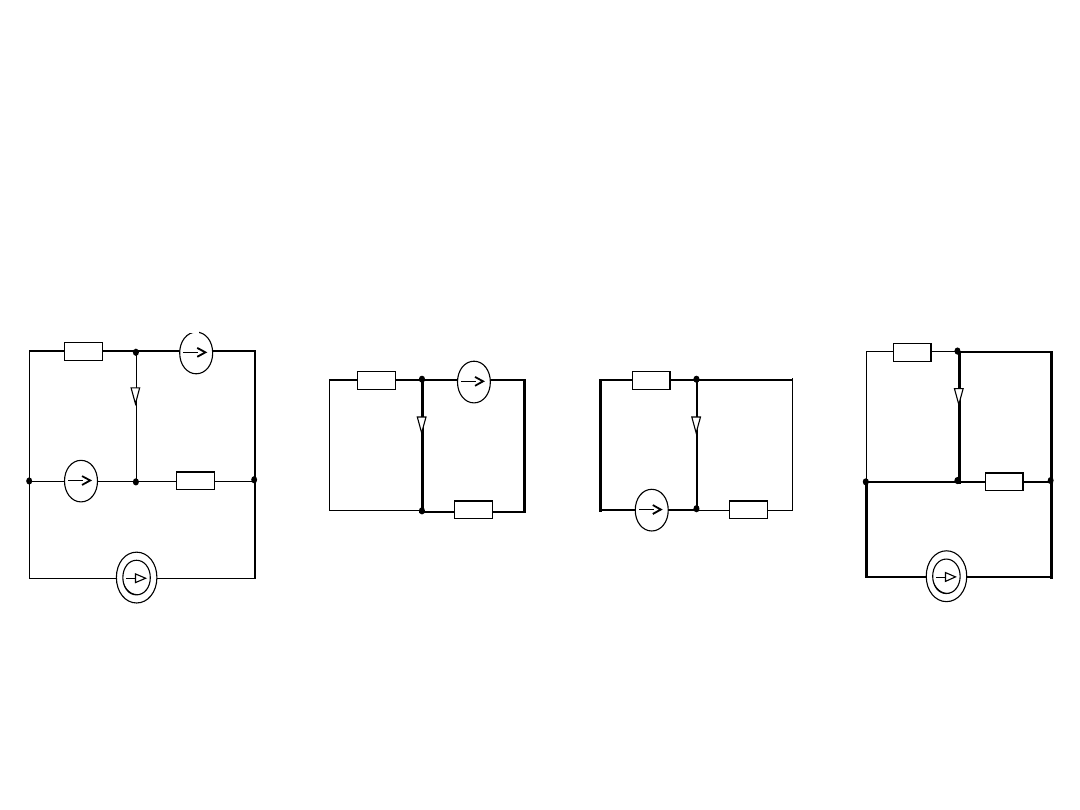
Obliczamy wartości prądu zwarcia Iz korzystając z

zasady superpozycji.

a) b) c)



+

+

I

źr

E

1

Z

1

E

2

I

z

Z

2

Z

1

Z

2

I

z

’

E

2

Z

2

E

1

I

z

’’

Z

1

I

źr

Z

2

I

z

’’’

Z

1

Dla obwodu

a)

E

2

+ I

z

’ Z

2

= 0

I

z

’ = - E

2

/ Z

2

= -j20 / (5 –j5)

= -j20(5 +j5) / {[(5 –j5) (5 +j5)]}
= 2 – j2 [A]

Dla obwodu

b)

E

1

+ I

z

” Z

1

= 0

- E

1

-10 -10(5 – j5)

I

z

” =

Z

1

5 + j5 50

=

(-1 + j) [A]

=

=

Dla obwodu

c)

I

z

”’ = I

źr

= 4[A]

Prąd zwarcia I

z

.

I

z

= I

z

’ + I

z

” + I

z

‘’’

= (2 – 2j) + (-1 + j) + 4 = (5 – j) [A]

Prąd ten przepływa przez gałąź ab w przypadku zwarcia zacisków ab, natomiast
admitancja Y

z

jest admitancją zastępczą sieci pasywnej widzianej z zacisków

ab przy przerwie w gałązi ab.

Prąd Iźr zastępczego źródła prądu jest zatem prądem zwarcia gałęzi ab.
Mając I

z

oraz Y

z

obliczamy prąd I w odbiorniku o admitancji

Y = 1 / Z

I = {Z

z

/ ( Z

z

+ Z)} I

z

= {Y / (Y + Y

z

)} I

z

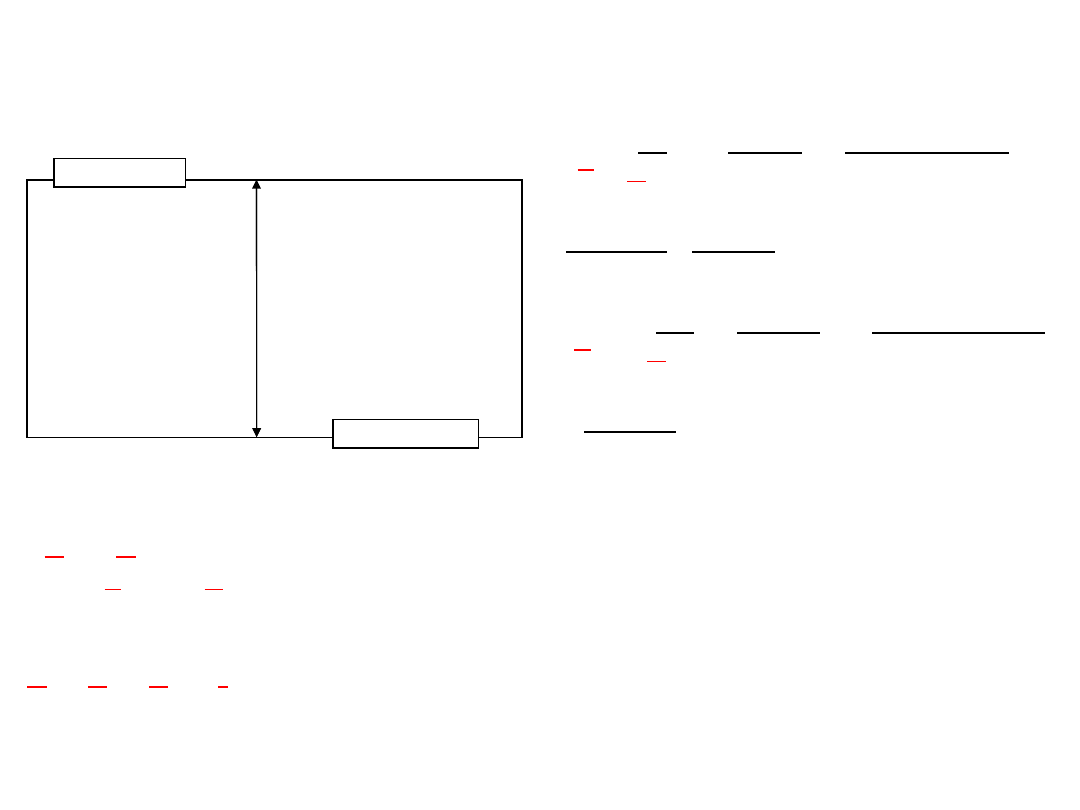
Obliczamy admitancję zastępczą Yz.

Y

1

Y

z

Y

2

1

1

5 – j5

Z

1

5 + j5 (5 + j5)(5 – j5)

5 – j5 5 – j5
25 + 25 50

=

=

=

=

=

=

Y

1

0,1 – j0,1 [S]

1

1 5 + j5

Z

2

5 - j5 (5 - j5)(5 + j5)

5 + j5

50

= 0,1 + j0,1 [S]

Y

2

=

=

=

=

Y

z

= Y

1

+ Y

2

= (0,1 – j0,1) + (0,1 + j0,1) = 0,2 [S]

Y = 1 / Z

= 1/5 = 0,2 [S]

Stąd

I = {Y / [Y + Y

z

]} I

z

= {0,2 / (0,2 + 0,2)} (5 + j) = 0,5 (5 + j) =

= 2,5 + j0,5 [A]

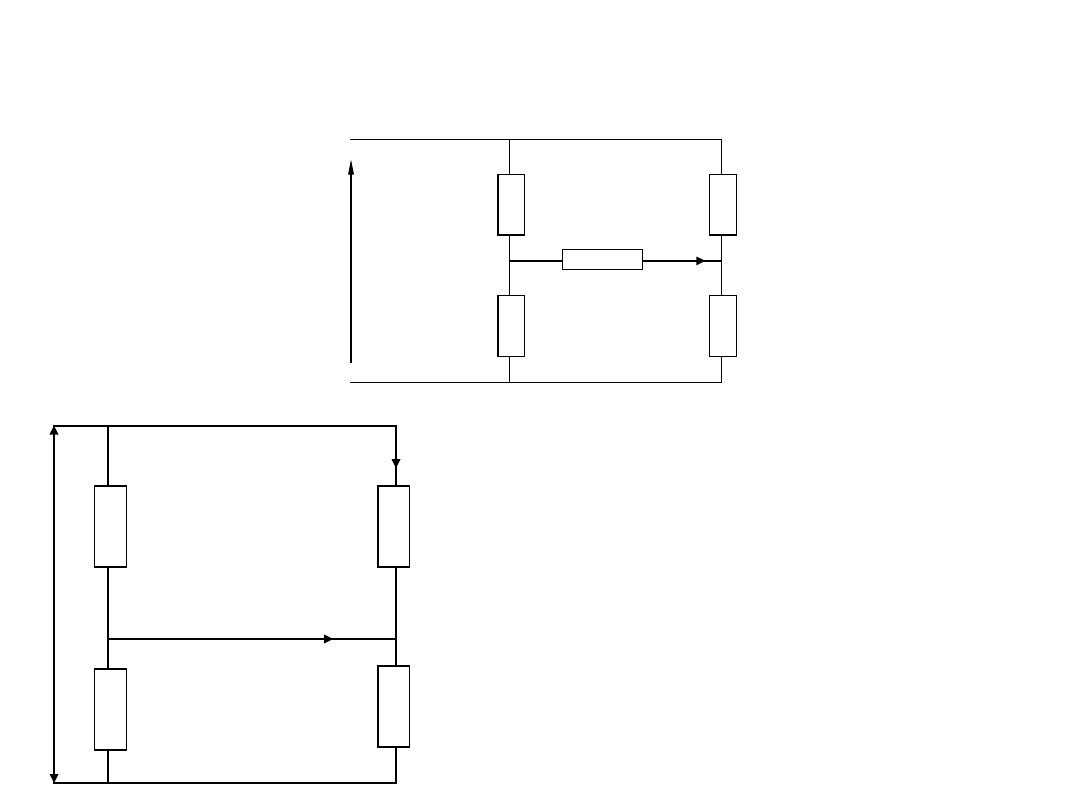
Zadanie 4

Oblicz wartość prądu I płynącego przez amperomierz stosując

twierdzenie Thevenina

.

Z

Z

1

Z

3

Z

4

Z

2

I

a

b

d

c

Dane:

I

1

I

2

Z

2

Z

4

U

4

I

Z

1

Z

3

U

3

Z

3

= 1 – j

U

U = 10V

Z

4

= 2 + j2

Z

2

= 2 – j2

Z

1

= 1 + j

Napięcie zastępcze E

z

obliczamy jako napięcie na zaciskach ab w stanie jałowym,

tzn przy odłączonym amperomierzu

U

10 10 10(3 + j1)

10(3 + j1)

Z

1

+ Z

2

(1 + j)(2 – j2) 3 – j1 (3 – j1)(3 + j1) 10

I

1

=

=

= 3 + j1 =

=

=

=

= (3 + j1) [A]

)

1

3

(

)

1

3

(

10

10

)

1

3

(

)

1

3

(

)

1

3

(

10

1

3

10

)

2

2

(

)

1

(

10

U

1

3

2

j

j

j

j

j

j

j

j

Z

Z









































[A]

)

4

2

(

)

1

3

3

(

)

3

(

)

1

(

1

1

j

j

j

j

j

Z

U





























)

4

2

(

1

j

U





)

4

2

(

)

1

1

3

3

(

)

1

(

)

1

3

(

3

2

3

j

j

j

j

j

Z

U





























)

4

2

(

3

j

U





0

3

1







Z

E

U

U

3

1

U

U

E

Z





j

j

j

8

)

4

2

(

)

4

2

(









 

V

j

E

Z

8



[v]

[v]

[A]

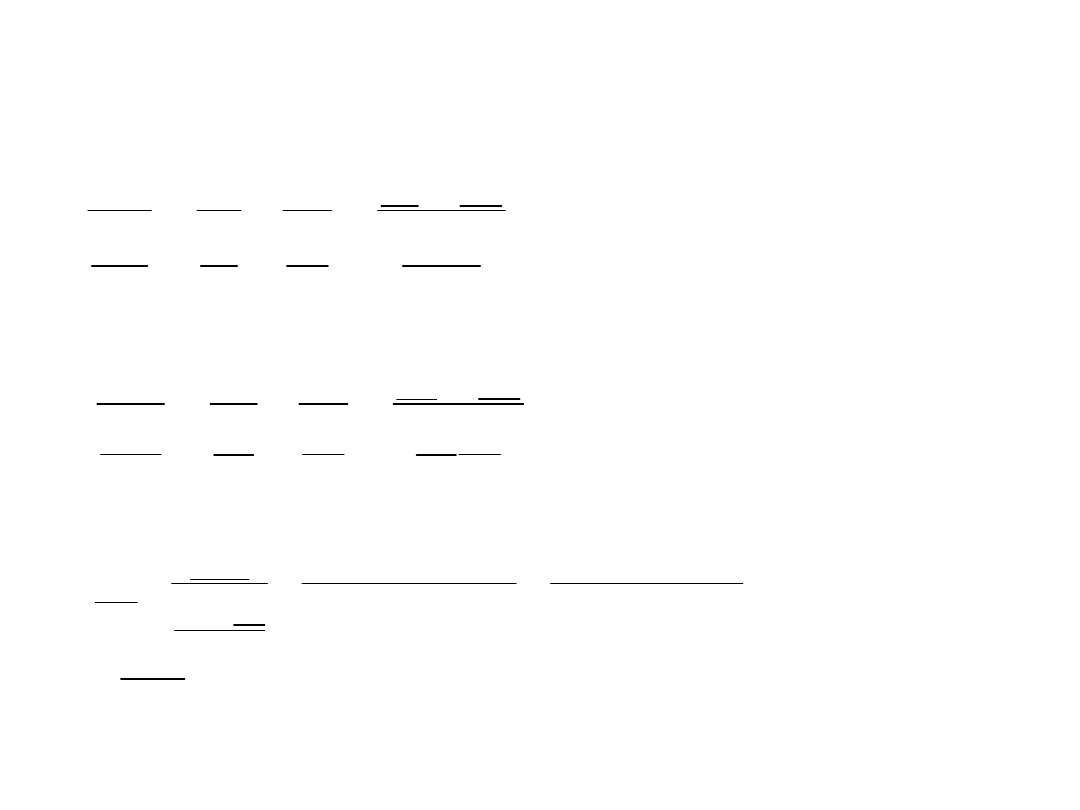
Obliczamy impedancję zastępczą Zz widzianą z zacisków ab przy rozwarciu
źródła zasilania

2

1

2

1

2

1

1

1

1

1

Z

Z

Z

Z

Z

Z

Z

Z









4

3

4

3

4

3

2

1

1

1

Z

Z

Z

Z

Z

Z

Z

Z









j

j

j

j

j

j

j

j

Z

Z

Z

Z

Z

Z

































3

4

3

2

2

2

2

)

2

2

(

)

1

(

)

2

2

)(

1

(

2

1

2

1

1

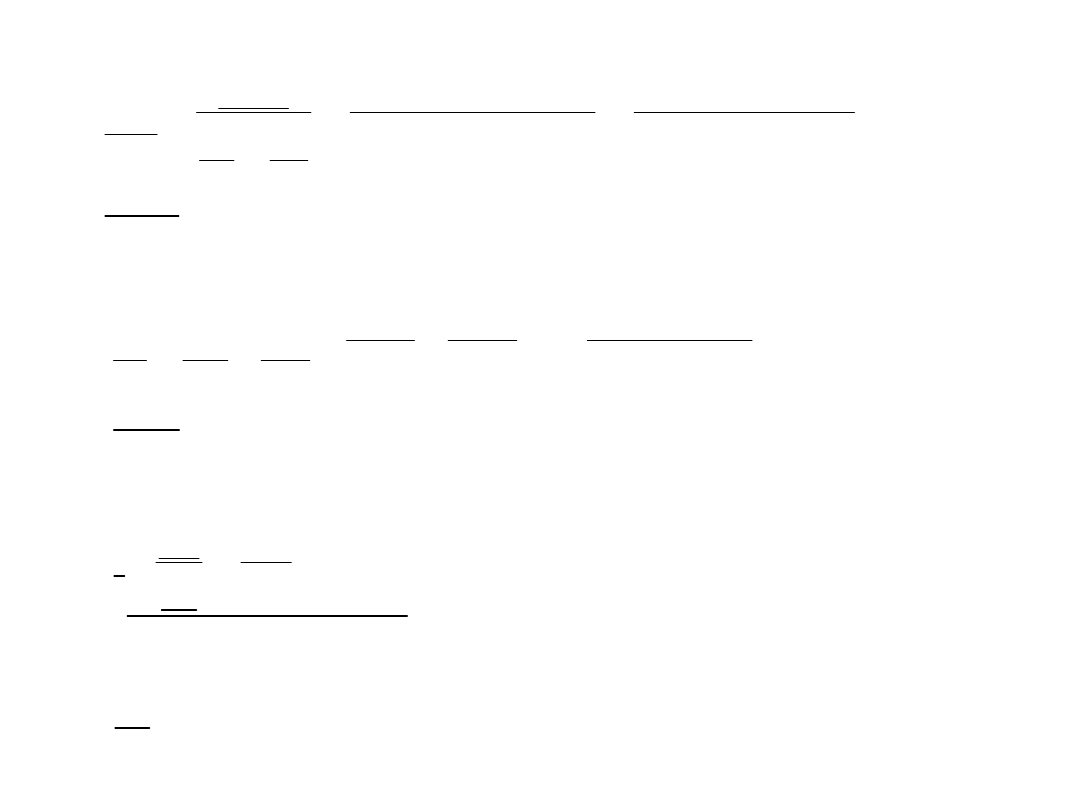
j

j

j

j

j

j

j

j

Z

Z

Z

Z

Z

Z































3

4

3

2

2

2

2

)

2

2

(

)

1

(

)

2

2

)(

1

(

4

3

4

3

2











































4

,

2

10

6

4

1

9

3

3

4

3

4

3

4

2

1

j

j

j

j

Z

Z

Z

Z

Z

z

j

j

Z

E

Z

33

,

3

4

,

2

8

2









[A]

 

A

A

33

,

3





KONIEC .

KONIEC .