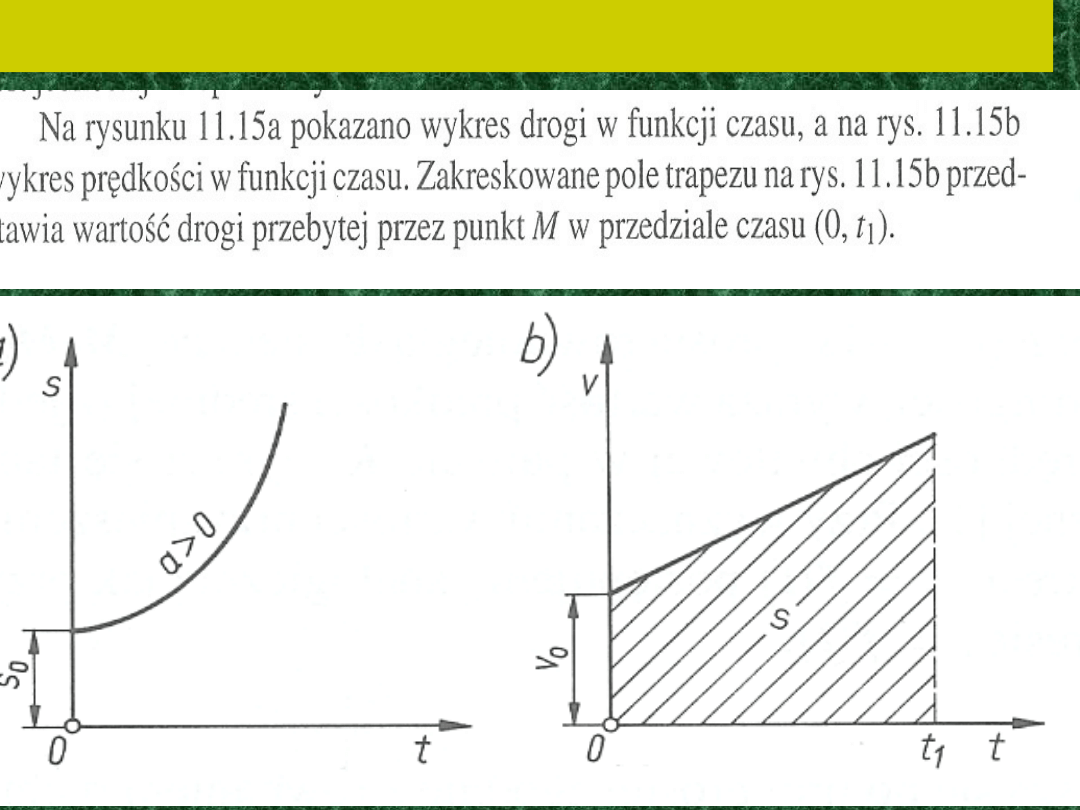
Wykreślny sposób przedstawienia ruchu

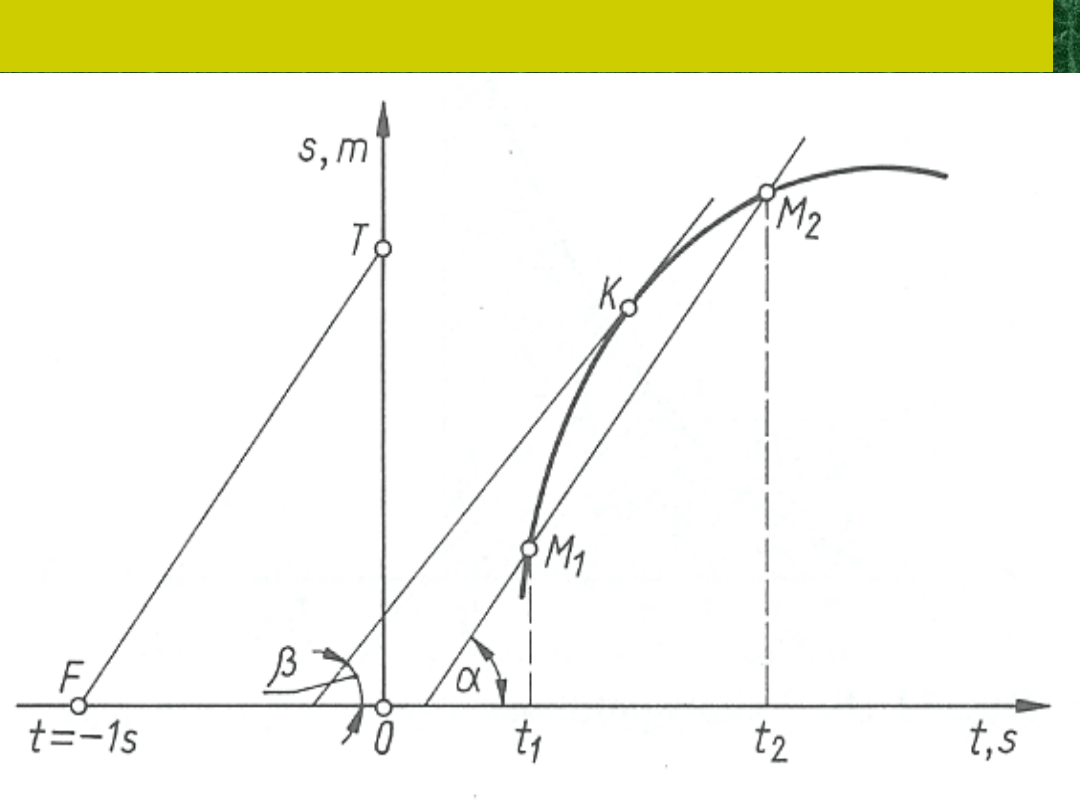
Wykreślny sposób przedstawienia ruchu

Wykreślny sposób przedstawienia ruchu

Ruch harmoniczny prosty

Ruch harmoniczny
prosty punktu

Ruch harmoniczny prosty

Ruch harmoniczny prosty

Ruch harmoniczny prosty

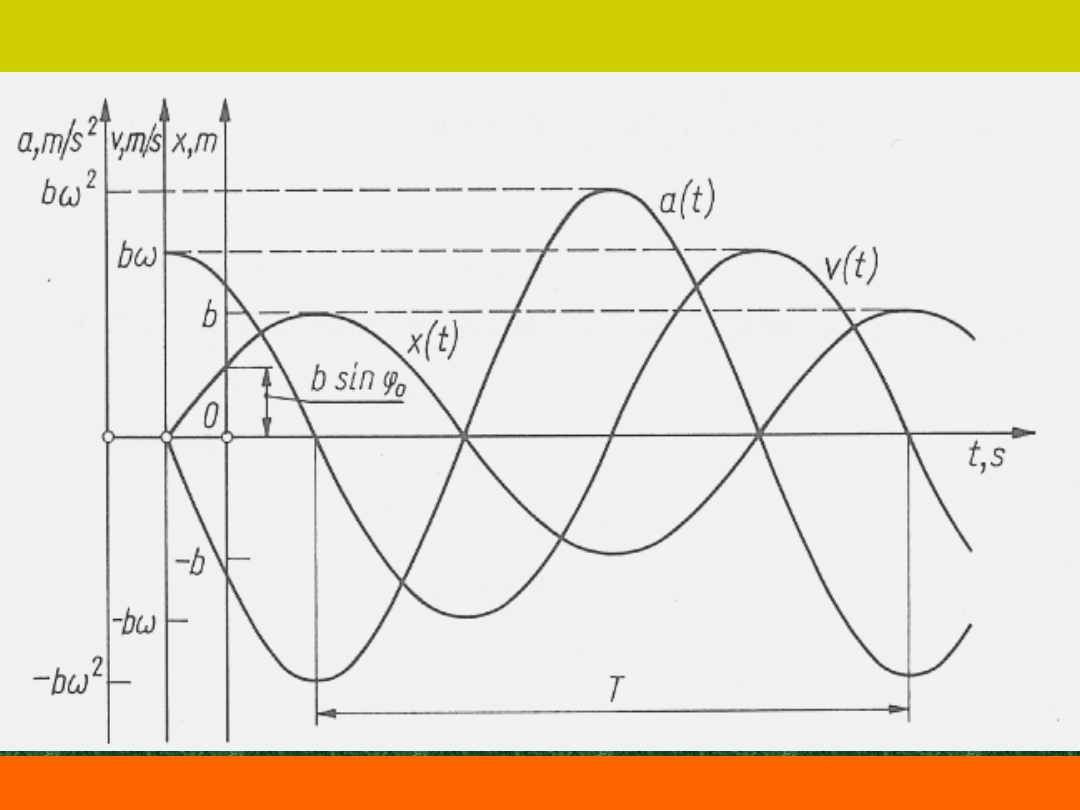
Ruch harmoniczny prosty

Wykresy drogi, prędkości i przyspieszwenia

Wykresy drogi, prędkości i przyspieszwenia

Ruch krzywoliniowy

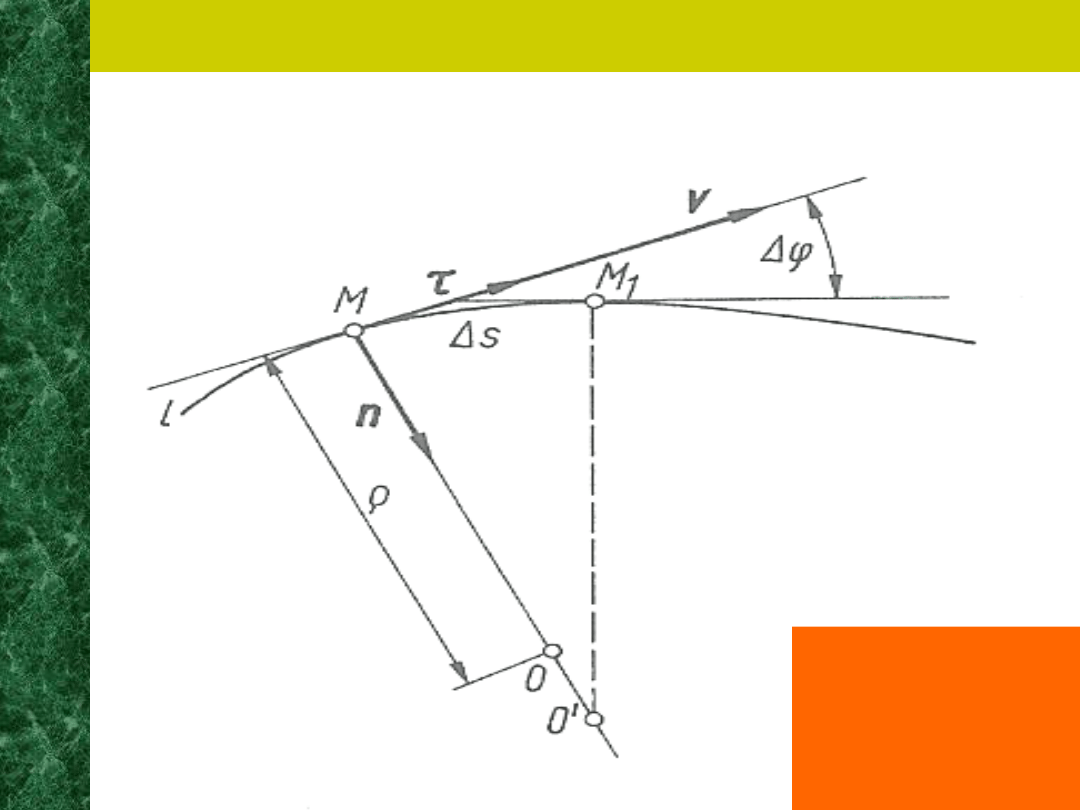
Ruch krzywoliniowy

Ruch

Ruch

krzywoliniow

krzywoliniow

y punktu na

y punktu na

płaszczyźnie

płaszczyźnie

Ruch krzywoliniowy

Ruch
krzywoliniowy

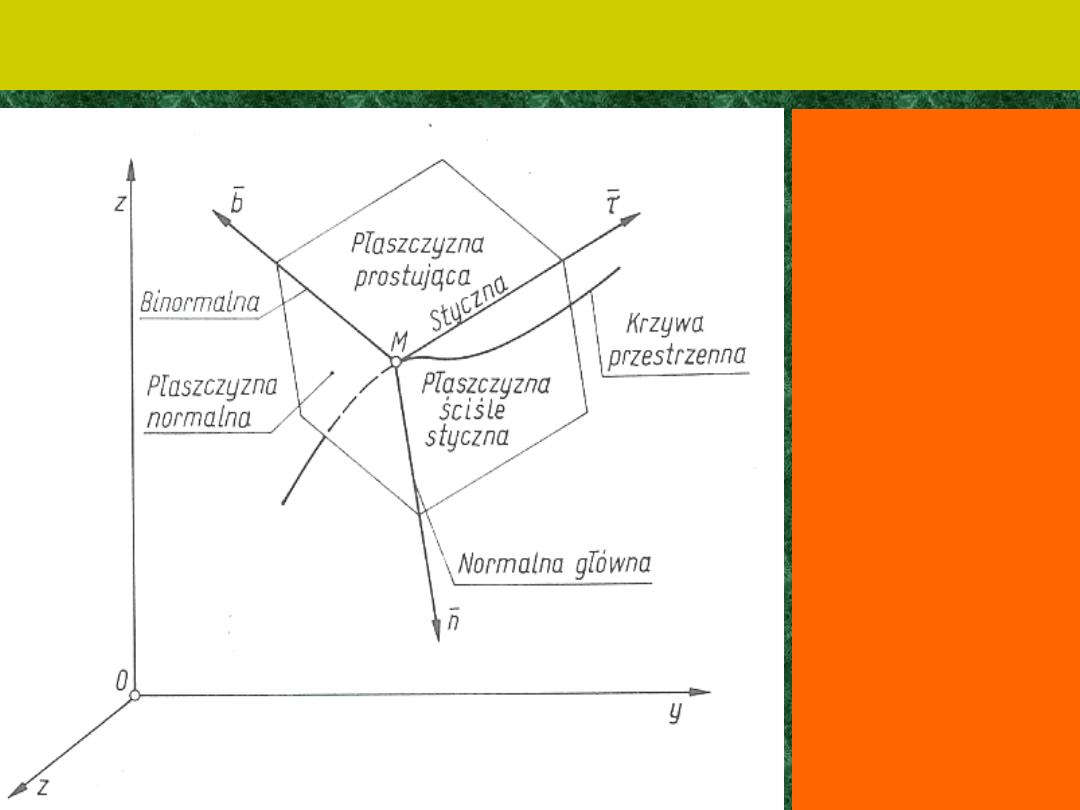
Ruch krzywoliniowy

Ruch
krzywoliniow
y punktu w
przestrzeni
opisany
współrzędny
mi
naturalnymi

Ruch
krzywoliniowy

Przyspieszenia styczne i normalne

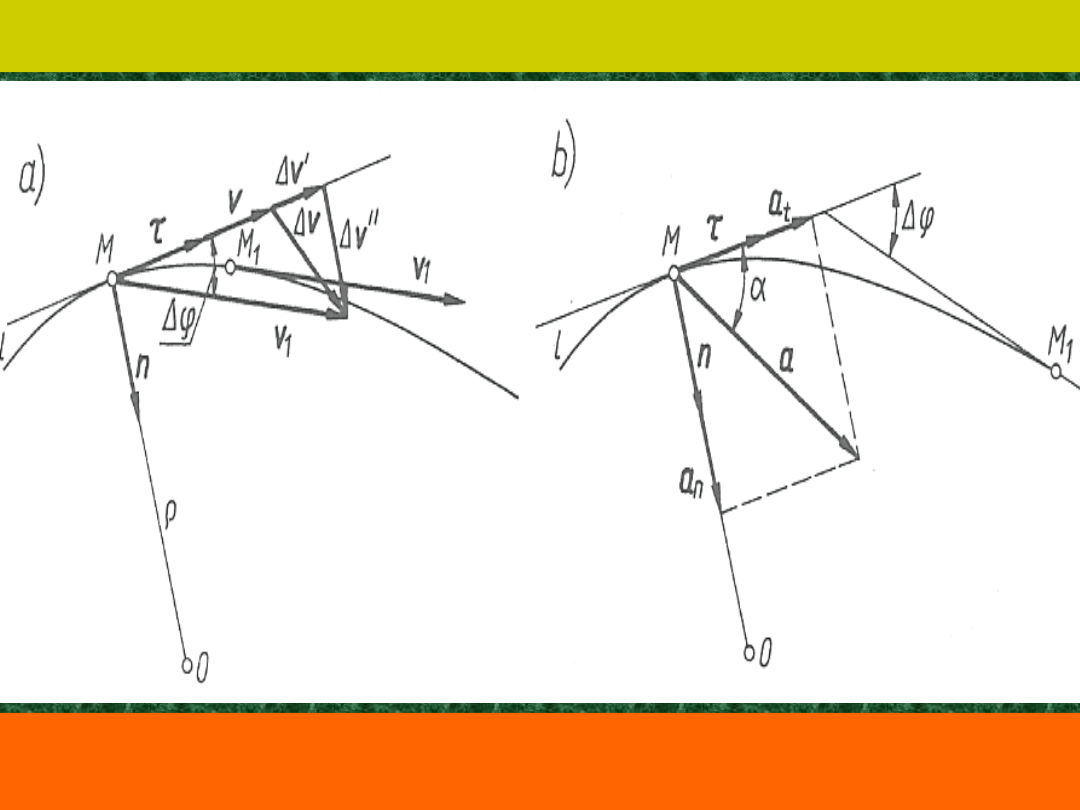
Przyspieszenie styczne i normalne

Przyspieszenie styczne i normalne w ruchu
krzywoliowym punktu na płaszczyźnie

Przyspieszenie styczne i normalne

Przyspieszenie styczne i normalne

Przyspieszenie styczne i normalne

Przyspieszenie styczne i normalne

Przyspieszenie styczne i normalne

Ruch punktu po okręgu

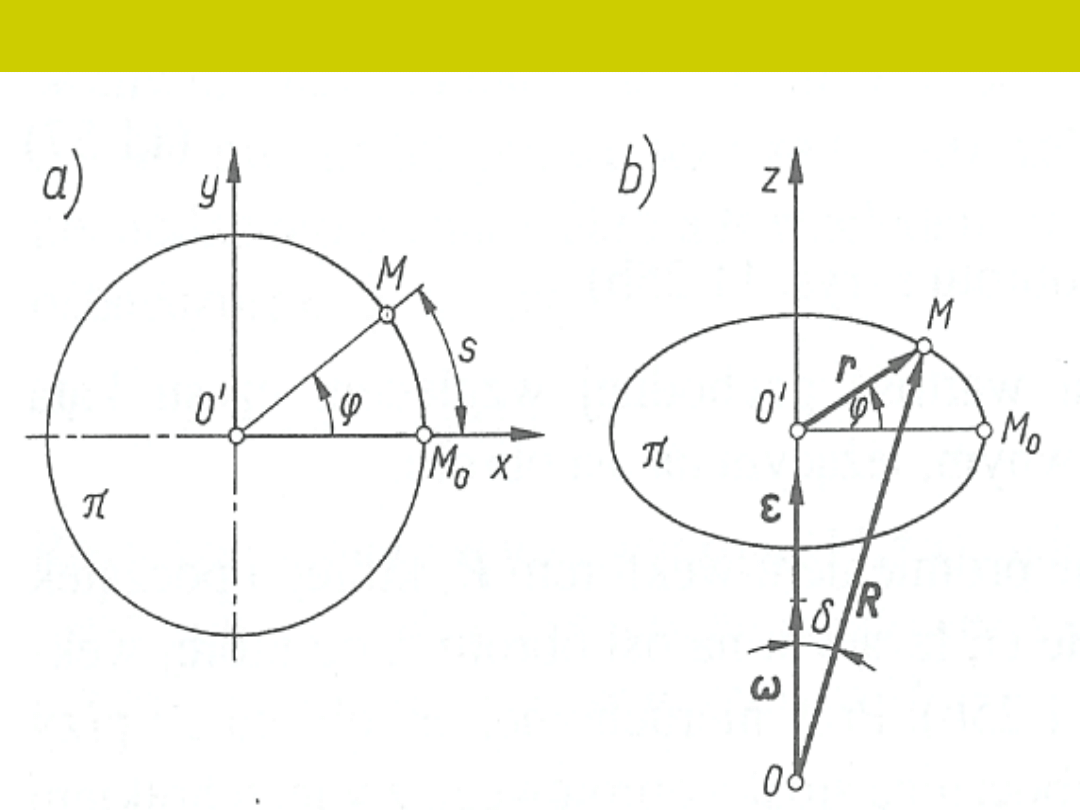
Ruch punktu po okręgu

Ruch punktu po okręgu

Ruch punktu po okręgu

Ruch punktu po okręgu

Ruch punktu po okręgu

Ruch punktu po okręgu

Ruch punktu po okręgu

Prędkość i przyspieszenie
punktu we współrzędnych
prostokątnych, biegunowych i
walcowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych prostokątnych

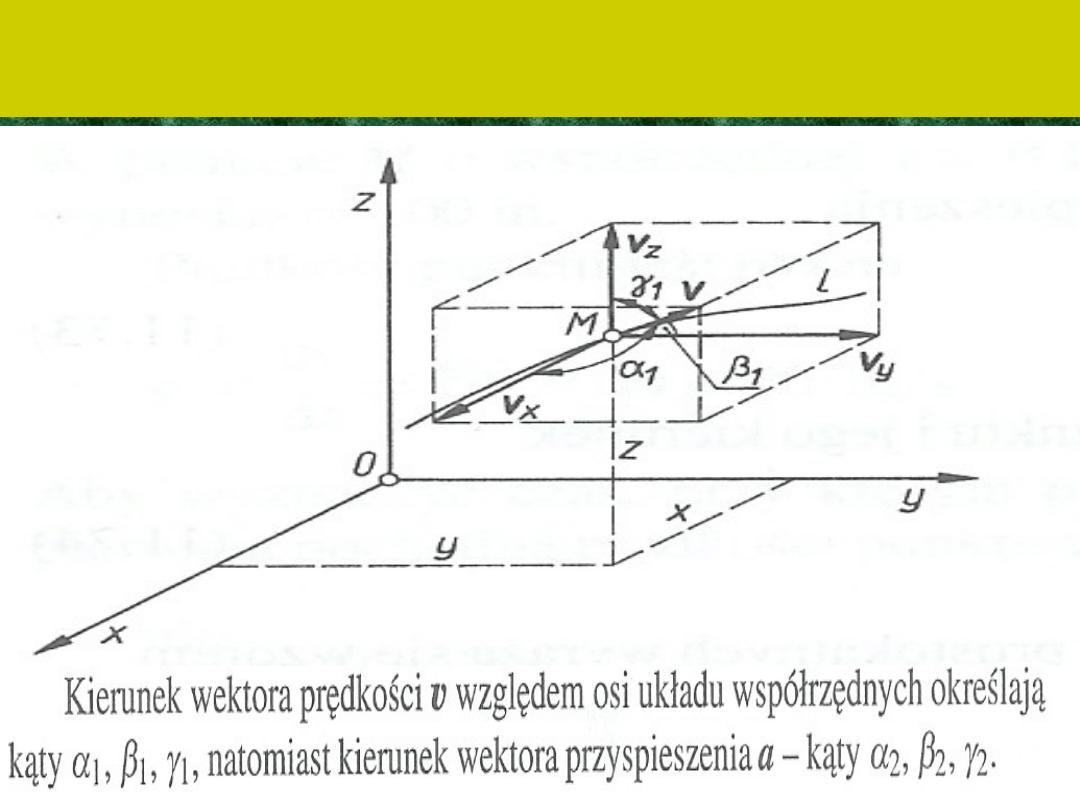
Składowe prędkości i przyspieszenia
punktu we współrzędnych prostokątnych

Składowe prędkości i przyspieszenia
punktu we współrzędnych prostokątnych

Składowe prędkości i przyspieszenia w
płaszczyźnie współrzędnych prostokątnych

Składowe prędkości i przyspieszenia w
płaszczyźnie współrzędnych prostokątnych

Składowe prędkości i
przyspieszenia punktu we
współrzędnych
biegunowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych biegunowych

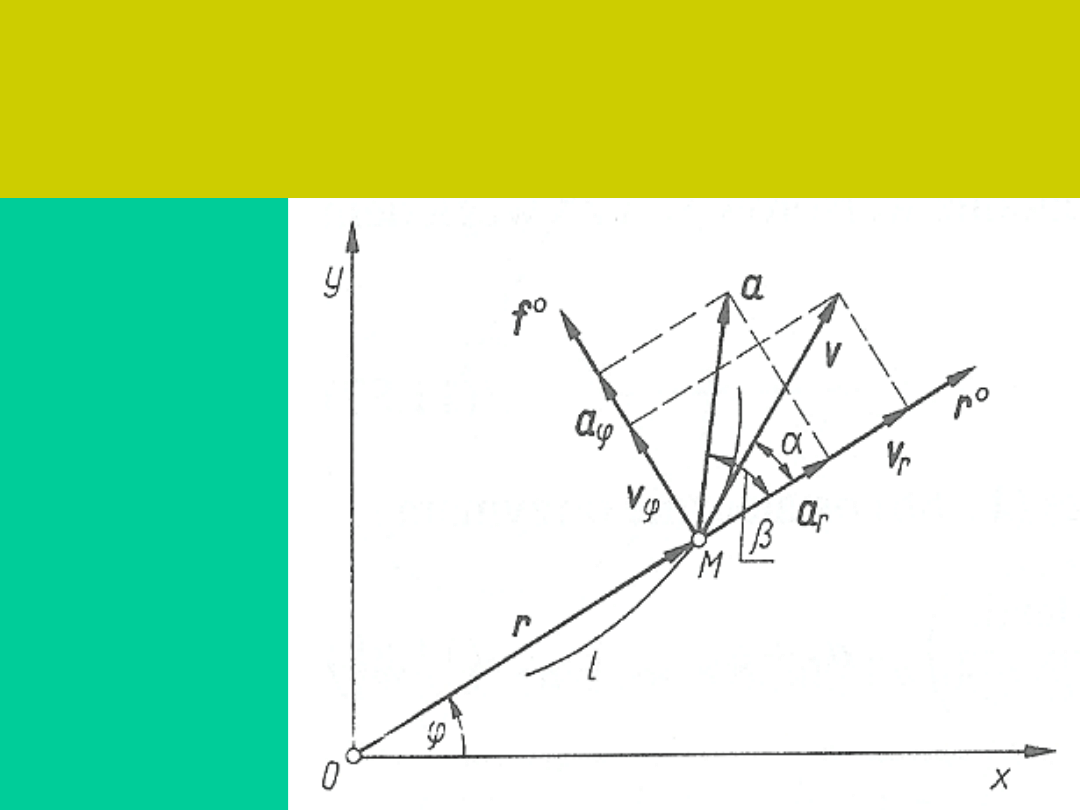
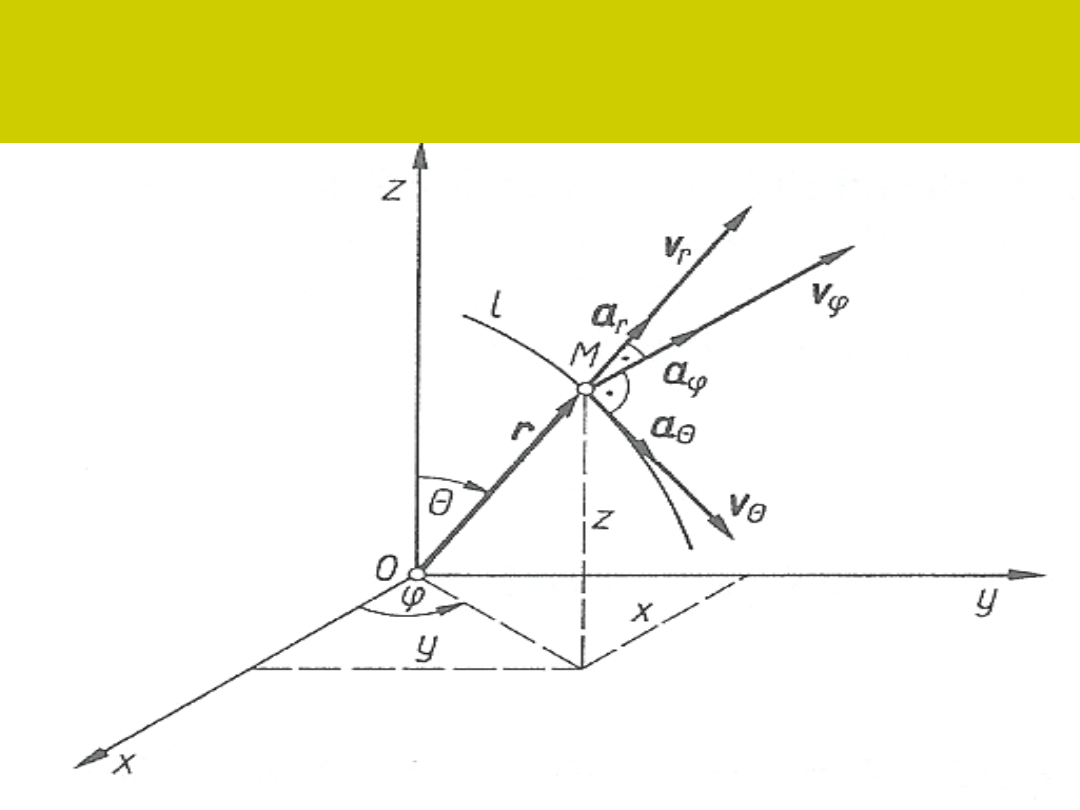
Składowe prędkości i przyspieszenia
punktu w biegunowym układzie
współrzędnych na płaszczyźnie

Położenie
punktu M we
współrzedny
ch
biegunowyc
h określamy
za pomocą
promienia
wodzącego r
i kąta



,

zwanego
argumentem

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

Składowe prędkości i przyspieszenia
punktu we wspólrzędnych biegunowych

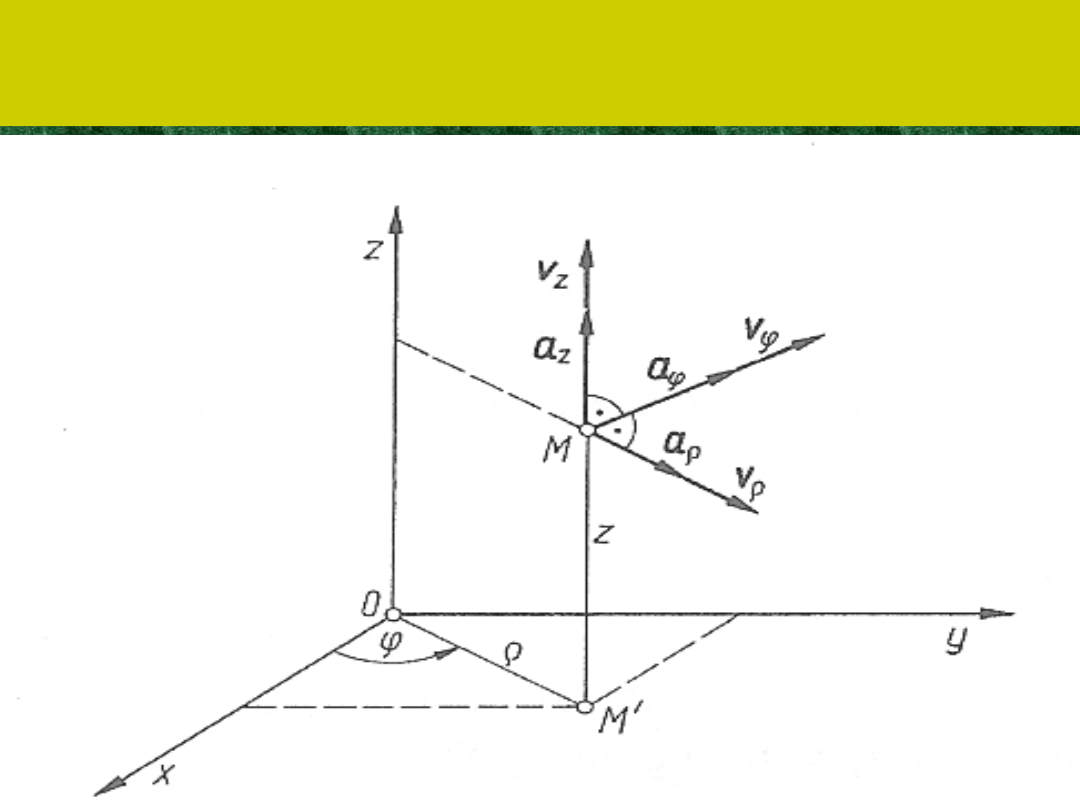
Składowe prędkości i przyspieszenia
punktu we współrzędnych walcowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych walcowych

Składowe prędkości i przyspieszenia
punktu we współrzędnych walcowych

Zależności między składowymi
przyspieszenia punktu we
współrzędnych naturalnych,
biegunowych i prostokątnych

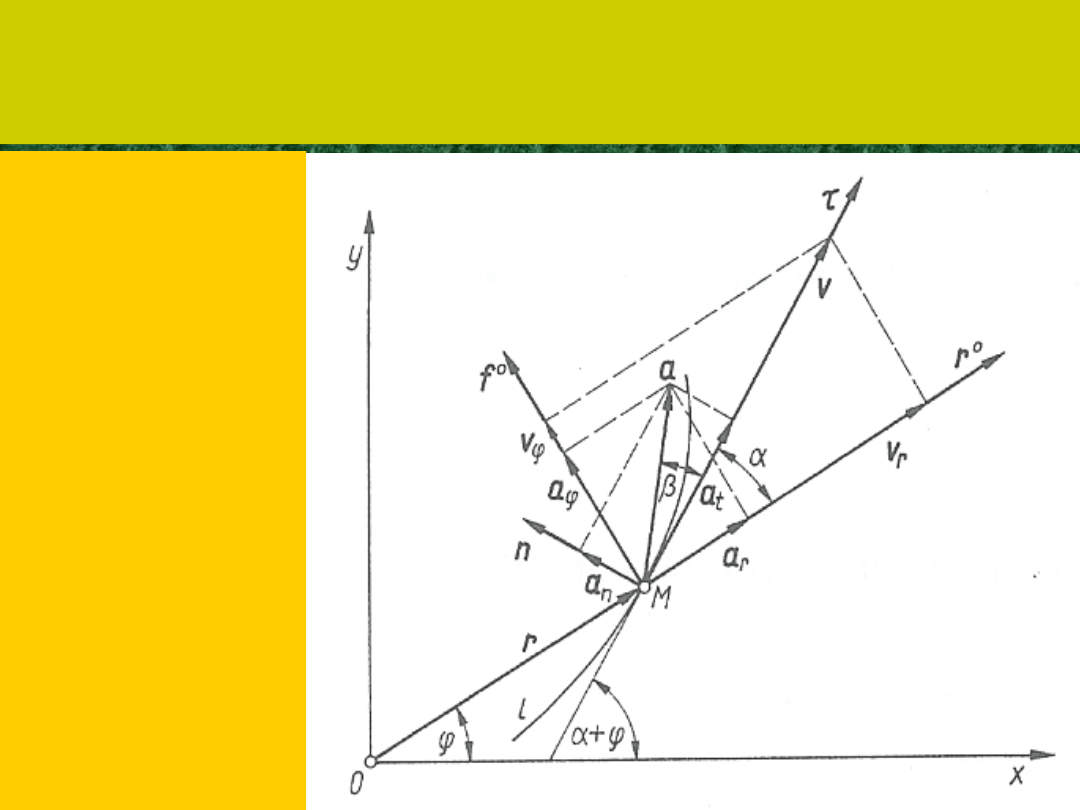
Przejście między układem naturalnym
a biegunowym na płaszczyźnie

W celu
określenia
zależności
między
składowymi
przyspieszenia
we
współrzędnych
naturalnych i
biegunowych
należy wykonać
rzutowanie
przyspieszenia 

na kierunki
stycznej i
normalnej do
toru.

Przejście między układem naturalnym
a biegunowym na płaszczyźnie

Przejście między układem naturalnym
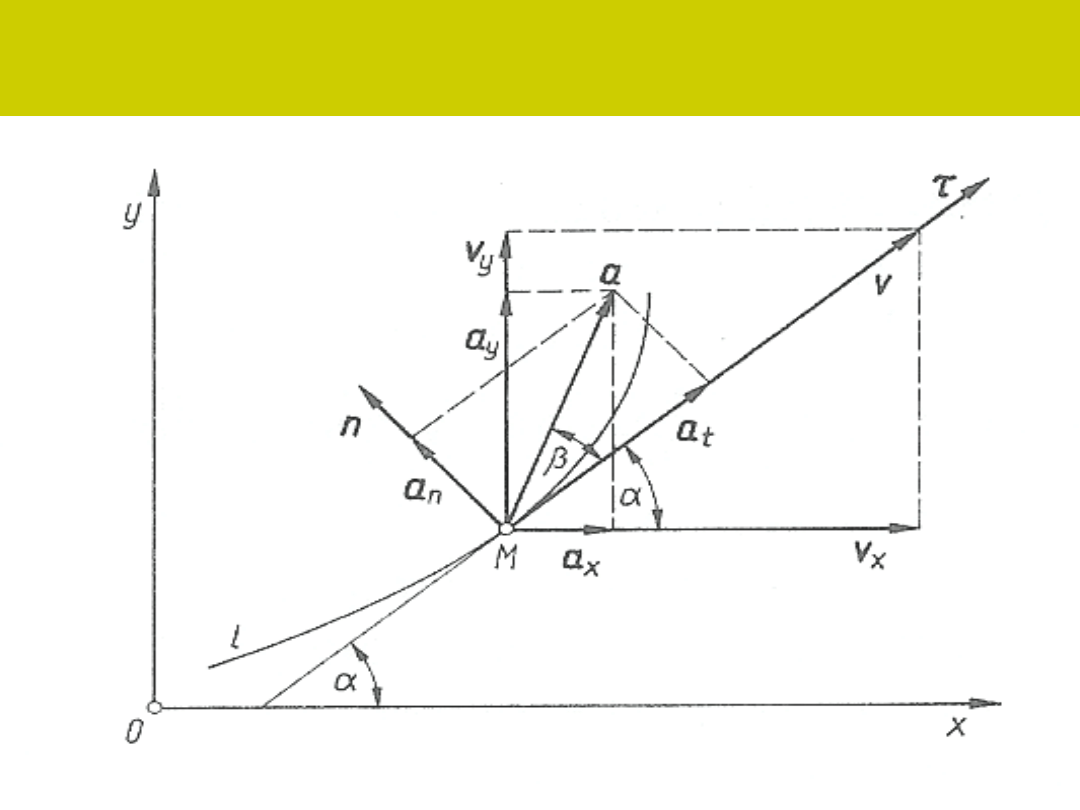
a prostokątnym na płaszczyźnie

Przejście między układem naturalnym a prostokątnym na
płaszczyźnie

DZIĘKUJĘ

DZIĘKUJĘ