TOMOGRAFIA POZYTONOWA

POSITRON EMISSION TOMOGRAPHY 

(PET)

ANIHILACJA POZYTONÓW

 

 

Zjawisko anihilacji pozytonów

W roku 1930 P.A.M.Dirac przewidział istnienie pozytonu, 
natomiast  w  1932  r.  J.Anderson  wykrył  pozytony  w 
promieniowaniu  kosmicznym.  Następnie  J.Curie  i  F.Joliot 
stwierdzili,  że  pozytony  są  emitowane  przez  niektóre 
jądra w procesie rozpadu promieniotwórczego. 
Masa pozytonu równa się masie elektronu :

kg

10

 

 

9.31

m

m

31

-

e

e

-

+







a  ładunek  elektryczny  równy  jest  co  do  wartości 
bezwzględnej ładunkowi elektronu :

C

19

-

e

e

10

 

 

1.6

q

q

-

+







Spin i moment magnetyczny pozytonu i elektronu mają te 
same wartości równe s=1/2     i  = B, z tym, że moment 

magnetyczny  pozytonu  jest  równoległy  do  jego  spinu,  a 
moment magnetyczny elektronu antyrównoległy.

 

 

Jeżeli  pozyton  zderzy  się  ze  swobodnym 
elektronem 

to 

wówczas 

następuje 

anihilacja  tych  cząstek  z  jednoczesną 
emisją    parzystej  lub  nieparzystej  liczby 
kwantów gamma:

e

+

 + e

- 

= 2 n     

e

+

 + e

-

 = (2n + 1) 

 

gdzie n - liczba całkowita; 

 n = 1,2,3....

 

 

Ślad  pozytonu  kosmicznego  o  energii  69  MeV 
otrzymany  przez Andersona  w  komorze  Wilsona: 
w  środku  komory  znajduje  się  płyta  ołowiana  o 
grubości  6  mm,  średnica  komory  16,5  cm,  pole 
magnetyczne o natężeniu 15 kGs.
 

 

 

Tory  pary  pozyton-elektron  otrzymanej  w 
komorze Wilsona przez naświetlanie promieniami 
 o energii 17,6 MeV płytki ołowianej o grubości 

0,33 mm, pole magnetyczne o natężeniu 2,5 kGs.

 

 

Ślady pary elektronowej (negatonu i pozytonu) i 
elektronu odrzutu (fotografia stereoskopowa)

 

 

Jak  się  okazuje  w  wyniku  anihilacji  swobodnej 
pary e+ e

-

  z największym prawdopodobieństwem 

następuje  emisja  dwóch  lub  trzech  kwantów 
gamma.  Obliczone  zostały  przekroje  czynne   
anihilacji  dwu-  i  trójkwantowej  wynoszące 
odpowiednio:

gdzie:

 

r

0 

 = e

2

/ mc

2

 = 2.8 10

-15

 

                -        klasyczny  promień 

elektronu;

c  = 3 x 10

8

 m/  - prędkość światła;

  =  1  /  137      -  stała  struktury 

subtelnej;

v  – prędkość elektronu
Z - liczba atomowa.

v

c

r

2

0

2

















c

r

v

9

3

4

2

0

2

3





 

 

Powyższe  wzory  odnoszą  się  do  pozytonów,  których 
prędkość  jest  dużo  mniejsza  od  prędkości  światła  . 
Stosunek  przekrojów  czynnych  anihilacji  3    i    2   

wynosi:

372

1

3

)

9

(

4

2

2

3





















Powyższy  wynik  wskazuje,  że  w  przypadku  anihilacji 
pozytonów poprzez zderzenia z elektronami swobodnymi, 
spośród 373  pozytonów aż 372 anihiluje dwukwantowo a 
jeden trójkwantowo. 

 

 

W  ośrodkach,  w  których  anihilacja  jest  swobodna 
zdecydowanie przeważa proces anihilacji dwukwantowej. 

Wyznaczono 

wartości 

czasów 

życia 

pozytonów 

swobodnych w próżni i tak dla anihilacji dwukwantowej i 
dla anihilacji trójkwantowej : 



2

 = 4.5 x 10

-10

 s



3

 = 1.7 x 10

-7

 s

 

 

Oprócz anihilacji swobodnej może istnieć także anihilacja 
pozytonu  z  elektronem  w  stanie  związanym.  Następuje 
ona  wtedy,  gdy  pozyton  utworzy  z  elektronem  atom 
wodoropodobny zwany pozytem Ps . 

Istnienie  pozytu  teoretycznie    przewidział  w  1934  r. 
S.Moharovic,  a  eksperymentalnie  stwierdził  istnienie 
pozytu w 1951 r. M.Deutsh. Z przeprowadzonych badań i 
obliczeń  wynika,  że  pozyt  jest  analogiem  atomu  wodoru, 
w którym rolę protonu odgrywa pozyton.

eV

 

6.77

E

Ps
w



Energia wiązania pozytu, jego promień i masa opisane są 
z zadowalającym przybliżeniem, w/g teorii budowy atomu 
Bohra.

Energia  wiązania  pozytu    jest  dwukrotnie  mniejsza  niż 
wodoru.  Natomiast  promień  borowski  pozytu  jest 
dwukrotnie większy niż atomu  wodoru.

 

 

Jeżeli  mamy  do  czynienia  z  oddziaływaniem  powolnych 
pozytonów  z  elektronami,  kiedy  moment  orbitalny  l=0, 
oraz  w  zależności  od  tego  czy  spiny  obu  cząstek  są 
równoległe  czy  antyrównoległe  mamy  do  czynienia  ze 
stanem  tripletowym  3S

1

  (dla  którego  całkowity  mement 

będący sumą momentu orbitalnego i spinowego J=1) lub 
singletowego 1S

0

 (dla którego całkowity moment J=0).

Parytet  ładunkowy  układu  pozyton  -  elektron  Pc  równa 
się:

P

c

 = P

i

 P

l

 P



 

gdzie :

Pi  

- parytet wewnętrzny,

P

l

- parytet przestrzenny,

P 

- parytet spinowy. 

 

 

                                                        

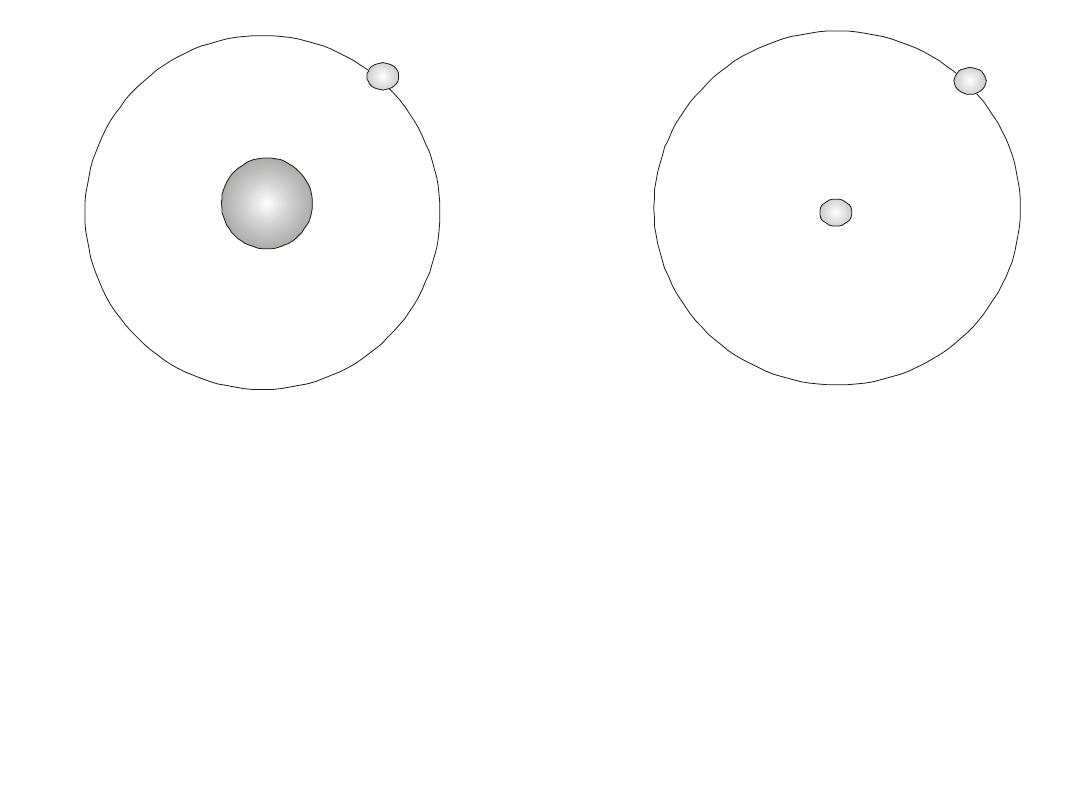
wodór                                              

  pozyt

Masa zredukowana:        ≈ m

e

   

                       

     m

e

/2                                      

Promień Bohra:              0,53Å                            
1,06Å                            
Energia jonizacji:         13,6 eV                          
6,8 eV   

 

 

Dla układu cząstka - antycząstka parytet wewnętrzny  P

i

  

= -1, parytet przestrzenny  P

l

  = (-1)l, parytet spinowy P



 

= -(-1)  . W związku z tym dla stanu tripletowego parytet 

ładunkowy P

c

 będzie:

-1

=

-(-1)

[

(-1)

(-1)

=

P

1

0

c





1

=

[-(-1)

(-1)

(-1)

=

P

0

0

c







Ponieważ  parytet  ładunkowy  n  fotonów  wynosi  Pc=(-1)n 
zatem  z  zasady  zachowania  parytetu  wynika,  że 
anihilacja  ze  stanu  tripletowego 

3

S

1

  zachodzi  na 

nieparzystą 

liczbę 

kwantów 

gamma 

(najbardziej 

prawdopodobna  3  ),  natomiast  dla  stanu  singletowego 

1

S

0

  na  parzystą  liczbę  kwantów  gamma  (najbardziej 

prawdopodobna 2 ).

a dla stanu singletowego:

Ze względu na to, że mamy różne ustawienia spinów pary 
e

+

e

-

 wyróżniamy dwie odmiany pozytu: parapozyt  p-Ps o 

antyrównoległym  ustawieniu  spinów  (stan 

1

S

0

)  oraz 

ortopozyt  o-Ps  o  równoległym  ustawieniu  spinów  (stan 

3

S

1

) .

 

 

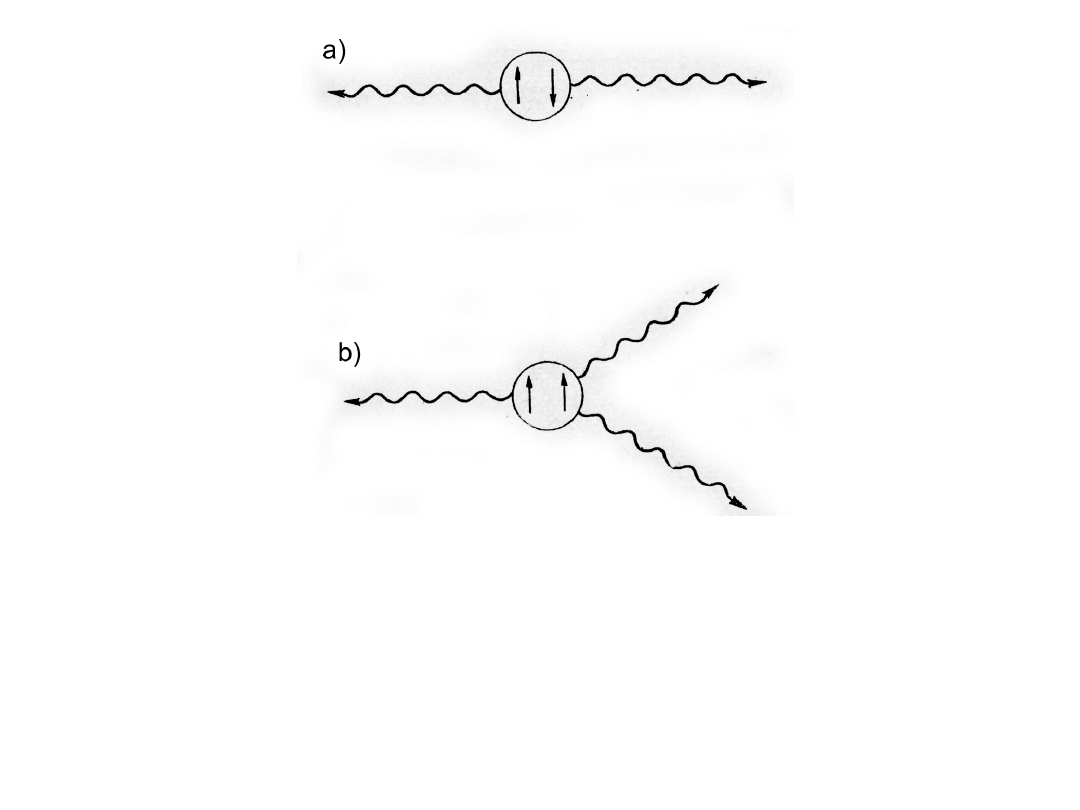
Anihilacja parapozytu (a) i ortopozytu (b)

 

 

Całkowity momement pędu ortopozytu J=1, przy czym są 
możliwe trzy sposoby realizacji tego stanu : a mianowicie 
dla  magnetycznej  liczby  kwantowej  m=0,  m=+1,  m=-1. 
Dla  parapozytu,  gdzie  całkowity  moment  pędu  J=0, 
możliwy  jest  tylko  jeden  przypadek  dla  m=0.  Z  tego 
wynika,  że  w  procesie  tworzenia  się  pozytu  w  75% 
powstaje ortopozyt, a w 25% parapozyt.

2

2

0

s

s

(0)

c

r

4

1











Obliczono teoretyczne wartości stałych rozpadu i czasów 
życia pozytonów ze stanów związanych o-Ps i p-Ps. 

Dla p-Ps stała rozpadu wyraża się wzorem :

gdzie:



s

- średni czas życia p-Ps;

(0 - gęstość funkcji falowej elektronu w obszarze 

zajmowanym przez pozyton w stanie podstawowym 
(n=1).;

r

0

  - klasyczny promień elektronu;       c - prędkość 

światła. 

 

 

gdzie:


t

- średni czas życia o-Ps;



- stała struktury subtelnej;

s

- stała rozpadu p-Ps.

s

t

t

9)

-

(

9

4

=

1

=











s

 

10

1.4

=

  

          

s

 

10

7.14

=

s

 

10

1.25

=

       

          

s

 

10

8

=

7

-

t

1

-

6

t

10

-

s

1

-

9

s

















Dla o-Ps:

Otrzymane stąd wartości stałych rozpadu i średnich 
czasów życia wynoszą odpowiednio:

wartości te są w dobrej zgodności z danymi 
doświadczalnymi dla wielu substancji . 

 

 

Gdy  orientacja  spinów  elektronu  i  pozytonu  jest 
antyrównoległa  to  z  zasady  zachowania  energii,  pędu  i 
parzystości  następuje  emisja  parzystej  liczby  kwantów  o 
energii:  0,51 MeV każdy:



n

2









e

e

przy  czym  najbardziej  prawdopodobna  jest  anihilacja 
dwukwantowa:



2









e

e

Gdy  orientacja  spinów  elektronu  i  pozytonu  jest 
równoległa  to  zasady  zachowania  są  spełnione  tylko  w 
przypadku emisji nieparzystej liczby kwantów zgodnie ze 
wzorem:



)

1

n

2

(











e

e

 

 

przy  czym  najbardziej  prawdopodobna  jest  anihilacja 
trójkwantowa:



3









e

e

Anihilacja  w  której  powstałby  jeden  kwant  jest  możliwa 
jedynie  w  obecności  trzeciego  ciała  przejmującego  pęd 
odwrotny:

M

M

e

e















W 1949 r. A.Ore opracował teorię opisującą 
oddziaływanie pozytonów z gazami.

Jednakże model Ore dotyczący oddziaływania pozytonów 
z gazami nie może być w pełni stosowany w przypadku 
oddziaływania pozytonów z ciałami stałymi i cieczami. 

 

 

Mogensen  założył,  że  pozyton  przy  wytracaniu 
ostatnich  10-50  eV  swojej  energii  przebywa 
drogę tego samego rzędu i wtedy może nastąpić 
reakcja tworzenia pozytu z jednym z uwolnionych 
elektronów towarzyszących niejako pozytonowi.

Dla tych substancji poprawny model przedstawił w 1974 
r. O.E.Mogensen.

Stwierdził  on,  że  pozyton  wytraca  ostatnie  100-200  eV 
swojej  energii  na  jonizację  atomów  ośrodka,  przy  czym 
wytworzone elektrony posiadają energię rzędu 10-50 eV.

Elektrony  te  termalizując  się  (czyli  wytracając  swoją 
energię) przebywają pewną drogę w ośrodku.

 

 

Z  poprzednich  obliczeń  (parytetu  parzystości  i 
momentów  pędu)  wynikało,  że  w  przypadku 
utworzenia 

pozytu 

prawdopodobieństwo 

powstania  ortopozytu  trzykrotnie  przewyższa 
prawdopodobieństwo powstania parapozytu. 

Jednakże  liczne  oddziaływania  pozytu  z  materią 
powodują,  że  stosunek  liczby  atomów  o-Ps  do 
liczby  atomów  p-Ps  w  momencie  anihilacji  może 
być różny od trzech. 

Procesy  prowadzące  do  zmiany  tego  stosunku 
nazywa się procesami gaszenia pozytu . 

 

 

Podstawowym  procesem  gaszącym  jest  proces 
"pick-off". Polega on na tym, że pozyton związany 
z  elektronem  (w  atomie  pozytu)  nie  anihiluje  z 
tym  elektronem,  lecz  z  jednym  z  elektronów 
otoczenia. 

Następuje  tutaj  zerwanie  wiązania  pozytu  i 
natychmiastowa 

anihilacja 

pozytonu 

z 

elektronem  wywołującym  to  zerwanie.  Ze 
względu  na krótki czas życia  parapozytu,  proces 
"pick-off" dotyczy głównie ortopozytu. 

Anihilacja  ortopozytu  poprzez  proces  "pick-off" 
prowadzi  zwykle  do  emisji  dwóch  kwantów 
gamma, jako że anihilacji pozytonu z elektronem 
wywołującym 

ten 

proces 

jest 

anihilacją 

swobodną. 

 

 





-

-

+

-

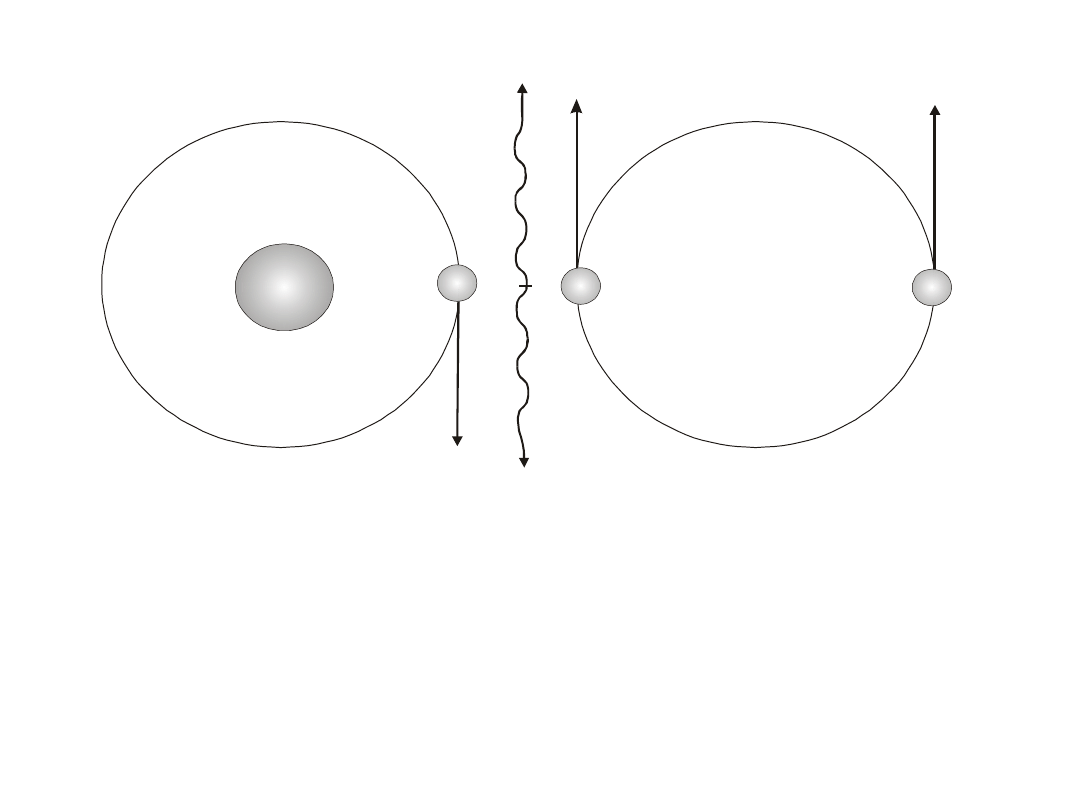
m o l e k u la

p o z y t

Proces pick-off

 

 

 

Konsekwencją  wystąpienia    procesu  "pick-off" 
jest  skróceniem  o-Ps.  Polega  on  na  tym,  że 
pozyton  związany  z  elektronem  (w  atomie 
pozytu) nie anihiluje z czasem życia 
o-Ps. 

Przyjmuje  się  zgodnie  z  pomiarami  czasu  życia 
pozytonów,  że  anihilacja  o-Ps  poprzez  proces 
"pick-off" nastąpi po czasie około 10

-9

 s.  

 

 

Istnieje  szereg  dalszych  procesów  gaszących 
pozyt,  które  jednak  nie  występują  w  przypadku 
stosowania PET :

konwersja wewnętrzna i zewnętrzna występujące 
przy  oddziaływaniu  na  próbkę  silnymi  polami 
magnetycznymi 

i 

elektromagnetycznymi 

i 

paramagnetykami 

oraz 

szereg 

reakcji 

chemicznych  jak:  utlenianie,  reakcje  wymiany  i 
przyłączania. 

Ze  względu  na  bardzo  skomplikowany  charakter 
anihilacji  tych  procesów,  należy  je  rozpatrywać 
dla  indywidualnych  przypadków.  Mogą  tworzyć 
się  pewne  straty  pośrednie,  prowadzące  w 
konsekwencji  do  rozpadu  poprzez  proces    "pick-
off". 

 

 

Czasy  życia  pozytonów    w  próbce  są 

bezpośrednio 

związane 

z 

koncentracją 

elektronów  n

e

  dostępnych  dla  danego  typu 

anihilacji 

(anihilacji 

swobodnej, 

anihilacji 

parapozytu  czy  anihilacji  gaszenia  ortopozytu), 
następującym wzorem:





 

c

r

 

1

 

 

n

2

e



gdzie:

   

n

e

  - koncentracja elektronów dostępnych dla danego 

typu anihilacji,
   
   r

- klasyczny promień elektronów,

   
   c

- prędkość światła,

   
   

- składowa czasu życia pozytonów danego typu 

anihilacji.

 

 

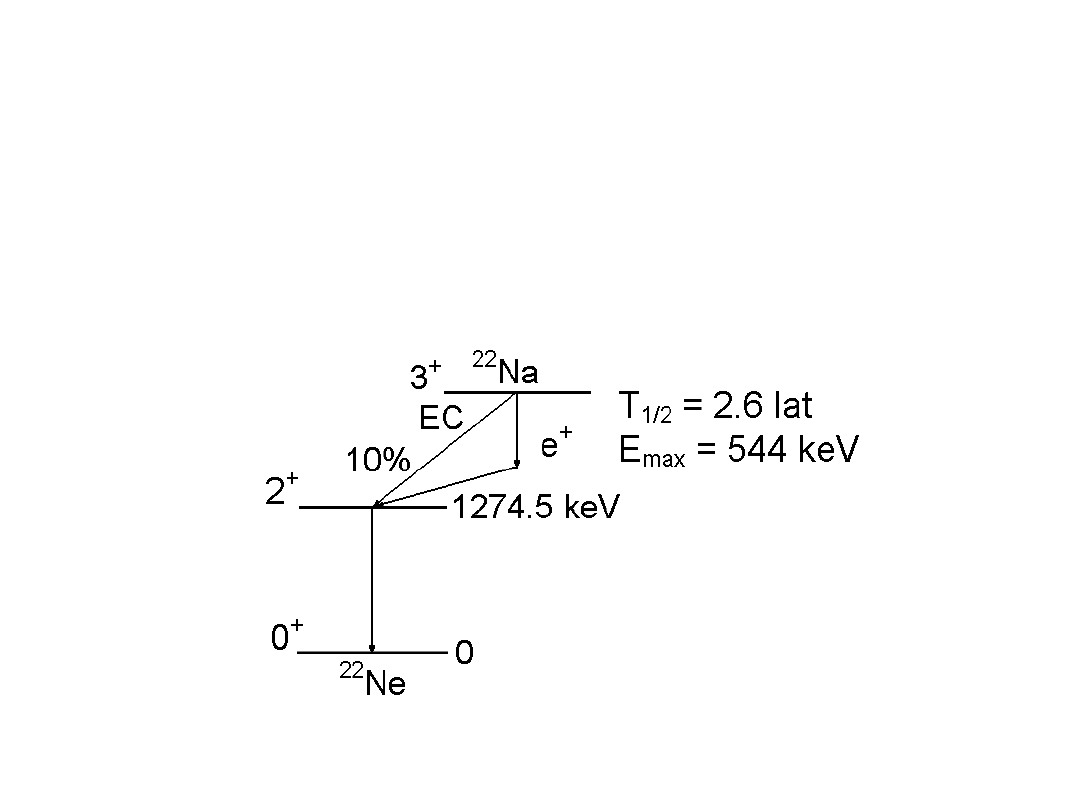
Na

22

  Ne

22

 + 

+

 + 

e