Wiadomości wstępne z
optyki instrumentalnej

•Luneta geodezyjna

•Oś celowa

•Regulacja lunety

•Ogniskowanie obrazu

•Cechy charakterystyczne

lunety

Zasady konstrukcji lunety

Lunety służą do obserwacji obrazów przedmiotów odległych pod

większym kątem widzenia niż ten, pod jakim oglądamy dany przedmiot
okiem nie uzbrojonym.

Luneta skonstruowana przez Schneidera w roku 1615, a opisana

przez Keplera (stąd pochodzi jej nazwa) była powszechnie używana w
instrumentach geodezyjnych produkowanych przed rokiem 1930, a jej
idea konstrukcyjna z kilkoma poprawkami służy do tworzenia
współczesnych instrumentów.

Jest ona zbudowana z dwóch skupiających systemów soczewek:

obiektywu o dużej ogniskowej i okularu o ogniskowej małej. Obraz,
utworzony przez obiektyw i znajdujący się wewnątrz lunety między
obiektywem a okularem, obserwujemy następnie w dużym powiększeniu
przez okular jak przez lupę. Aby obserwatorów zależności od
właściwości swego wzroku i od odległości przedmiotu od lunety, widział
obraz ostro, należy mieć możliwość zmiany położenia okularu wzdłuż osi
lunety.

f

ok

Źrenica
wyjściowa

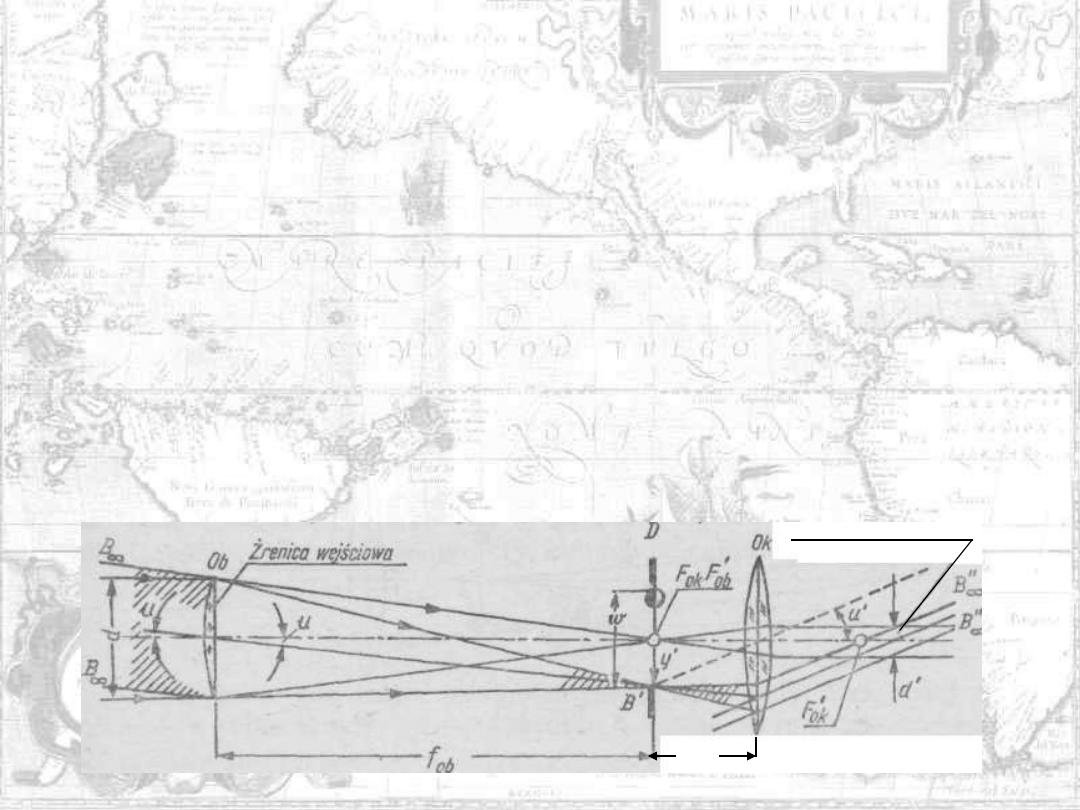
Prześledźmy bieg promieni w lunecie dla przedmiotu bardzo dalekiego i

dla obserwatora o oku miarowym. Z każdego punktu takiego dostatecznie
dalekiego przedmiotu pada na obiektyw pęk promieni równoległych, które
skupiają się i dają obraz w płaszczyźnie ogniskowej obiektywu, należy więc
w celu oglądania tego obrazu w powiększeniu tak przesunąć okular, aby
jego płaszczyzna ogniskowa pokryła się z płaszczyzną ogniskową
obiektywu, gdzie właśnie powstał pierwszy obraz.
Rozpatrzmy bieg dwóch pęków promieni równoległych . Jeden z nich, o
promieniach równoległych do osi układu, skupi się w ognisku obrazowym
obiektywu, a drugi, nachylony do osi pod kątem u, skupi się w obrazowej
płaszczyźnie ogniskowej obiektywu, gdzie powstanie rzeczywisty i
odwrócony obraz obserwowanego przedmiotu. W dalszym swym biegu
pierwszy pęk wyjdzie z okularu znów jako pęk równoległy do osi, a pęk
drugi zostanie przez okular przekształcony na pęk promieni równoległych,
nachylonych do osi układu pod kątem u', większym niż kąt u. Okular,
spełniający tu, jak wspomnieliśmy, rolę lupy da nam obraz urojony i
powiększony, a w stosunku do przedmiotu — odwrócony. Obraz ten,
utworzony przez pęki promieni równoległych, powstaje w nieskończoności,
a więc przez oko miarowe będzie oglądany bez wysiłku akomodacyjnego.

Obiektyw i okular lunety są osadzone w metalowej rurze w ten sposób,

że ich osie optyczne leżą na jednej prostej zwanej osią optyczną lunety,
odległość zaś okularu od obiektywu można w miarę potrzeby zmieniać.
Jeżeli luneta jest ustawiona w położeniu teleskopowym (jak wyżej opisano) ,
to jej długość jest równa sumie ogniskowych obiektywu i okularu.

ok

ob

f

f

l





Jeżeli przedmiot znajduje się blisko lunety, to obraz jego zostanie

utworzony przez obiektyw w odległości większej niż f

ob

. Aby obserwator

mógł zobaczyć ten obraz wyraźnie musimy cofnąć okular tak, aby
płaszczyzna ogniskowa okularu pokryła się z płaszczyzną obrazu
utworzonego przez obiektyw. Jeżeli ponadto obserwator ma wzrok
niemiarowy, to trzeba jeszcze dodatkowo zmienić położenie okularu w
taki sposób, aby oglądany przez niego obraz przedmiotu znalazł się w
punkcie dalekim oka. We wszystkich powyższych wypadkach luneta nie
stanowi już układu teleskopowego,a jej długość nie jest równa sumie
ogniskowych.

Lunety dające obrazy proste bywają nazywane ziemskimi. Luneta

Keplera nosi nazwę astronomicznej, daje bowiem obrazy odwrócone
(góra — dół i prawo — lewo). Aby otrzymywać obrazy proste umieszcza
się między obiektywem a okularem układ soczewkowy skupiający albo
układ pryzmatów, co spowoduje jeszcze jedno odwrócenie obrazu.
Stosowanie takich urządzeń w lunetach geodezyjnych jest obecnie
częste.

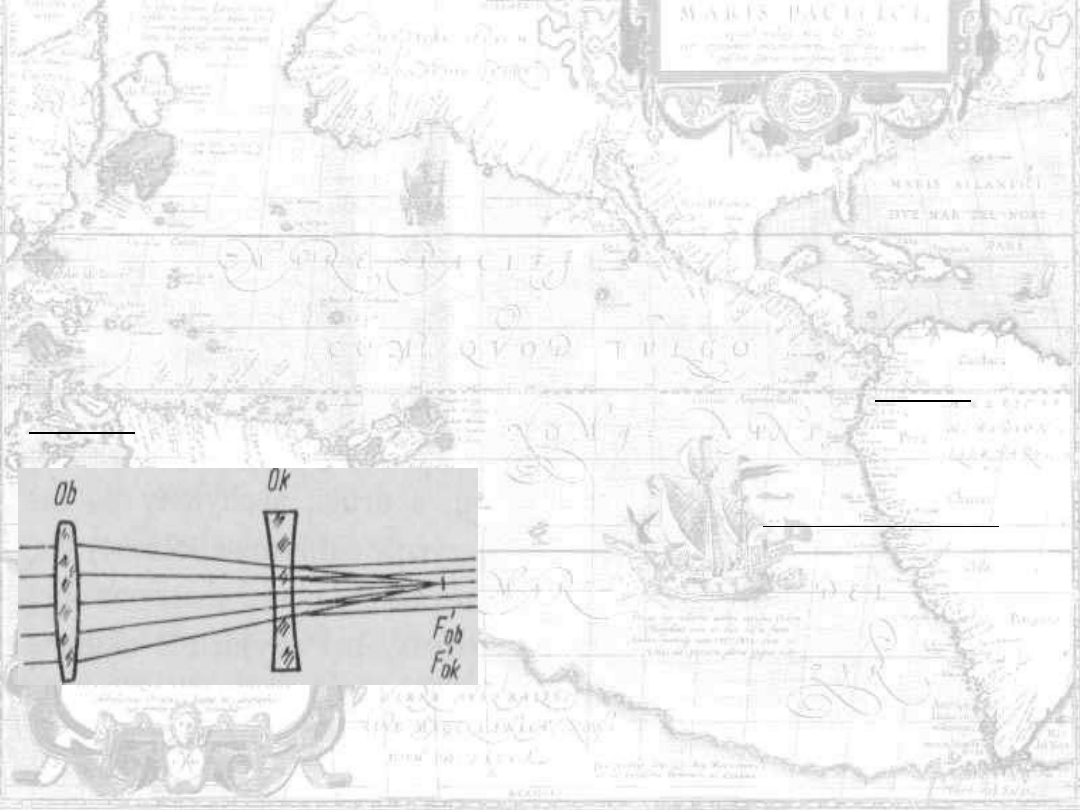
Efekt ten można otrzymać stosując
rozwiązanie znane z lunety Galileusza.
W lunecie tej obiektyw jest soczewką
skupiającą, a okular - rozpraszającą,
układ nie tworzy więc obrazu
rzeczywistego i dlatego nie można tu
umieścić urządzenia celowniczego, co
czyni lunetę nieprzydatną do celów
geodezyjnych.

Długość lunety Galileusza
wynosi:

 

ok

ob

f

f

l





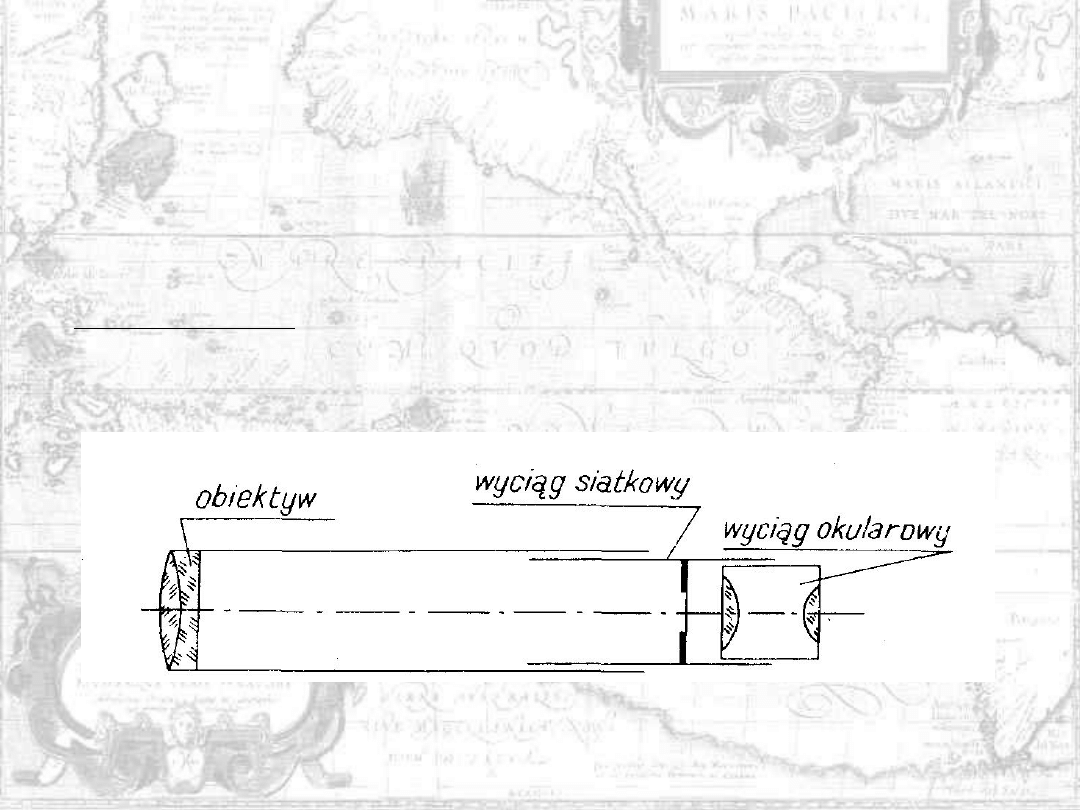
Oś celowa i siatki celownicze

Aby w geodezji wyznaczyć dokładnie kierunek na obserwowany

przedmiot (punkt celowania) za pomocą lunety, należy umieścić w niej
urządzenie celownicze. Jest to tzw. płytka ogniskowa, sporządzona ze
szkła z wytrawioną chemicznie siatką celowniczą zwykle w postaci krzyża
kresek. Środek krzyża staramy się tak umieścić w lunecie, aby pokrywał
się z jej osią optyczną.

OSIĄ CELOWĄ lunety nazywamy prostą przechodzącą przez

obrazowy punkt główny obiektywu i punkt przecięcia się krzyża kresek.
W czasie obserwacji przez lunetę płytkę ustawiamy w takim położeniu,
aby płaszczyzna siatki celowniczej pokryła się dokładnie z płaszczyzną
obrazu rzeczywistego, utworzonego przez obiektyw. Obserwując ten
obraz przez okular lunety obserwujemy jednocześnie w tej samej
płaszczyźnie siatkę celowniczą.

SIATKI CELOWNICZE

wykonywano w dawnych instrumentach z

nitek pajęczych, rozpiętych i zamocowanych na specjalnym pierścieniu
służącym jednocześnie jako diafragma pola. Stąd do dziś jeszcze nazywa
się często urządzenie celownicze krzyżem nitek. Obecnie, jak już
wspomnieliśmy, siatki celownicze są wykonywane na szklanych płytkach
ogniskowych w postaci wytrawionych kresek.
Płytki ogniskowe sporządza się najczęściej z dwóch oddzielnych płytek
szkła złączonych razem, a kreski wykonuje się na wewnętrznej stronie
jednej z nich. Między obu płytkami znajduje się cienka podkładka
pierścieniowa z folii, spełniająca jednocześnie rolę przysłony pola
widzenia lunety. Powierzchnia z naniesionymi kreskami siatki celowniczej
jest w ten sposób zabezpieczona przed osiadaniem pyłu, który
utrudniałby obserwację.
Grubość obu płytek składowych dobiera się w taki sposób, aby okularu
nie można było ustawić na ostre widzenie ani przedniej, ani tylnej
powierzchni tak skonstruowanej łącznej płytki ogniskowej. Obie jej
zewnętrzne powierzchnie będą się więc znajdowały daleko od
płaszczyzny przedmiotowej okularu i dzięki temu nie będą widoczne w
okularze różne zanieczyszczenia i pyłki mogące osiadać na obu tych
powierzchniach.

Grubość b kresek siatki celowniczej powinna być dla danej lunety tak

dobrana, aby nie zakrywały one przedmiotu, na który celujemy, a
jednocześnie kreski nie mogą być cieńsze niż zdolność rozdzielcza oka
podzielona przez powiększenie okularu G

ok

, czyli:

ok

G

b

073

,

0



mm

f

b

ok

250

073

,

0





albo

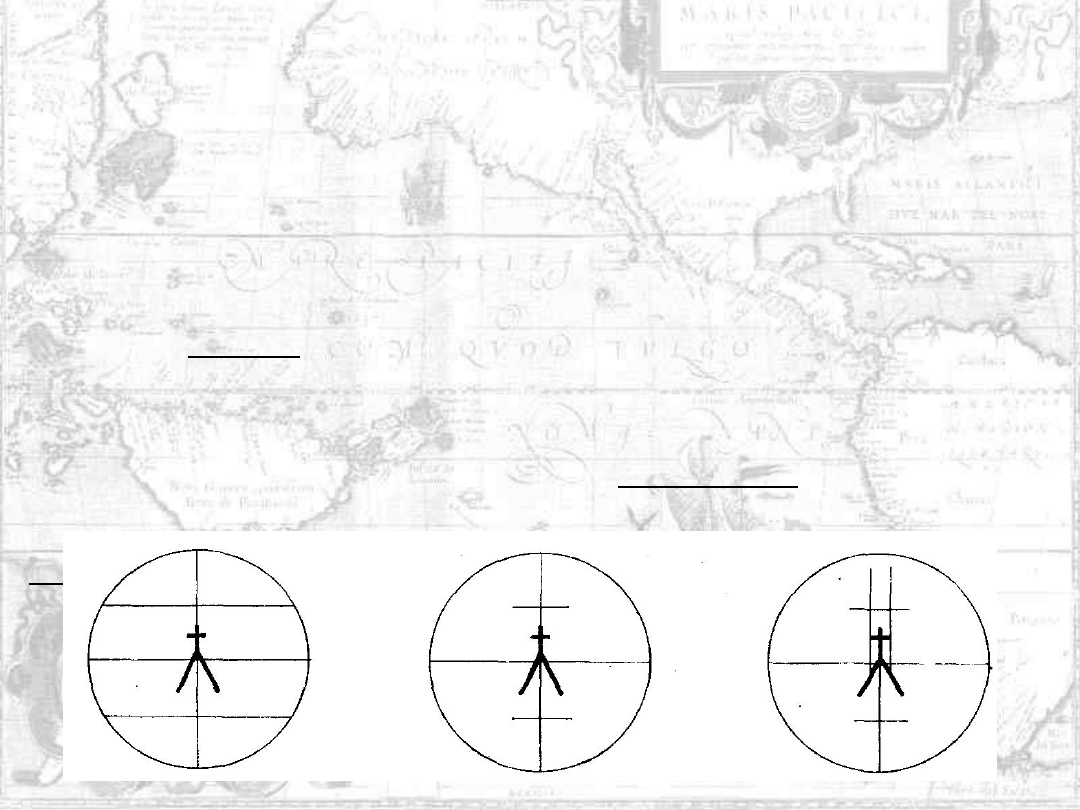
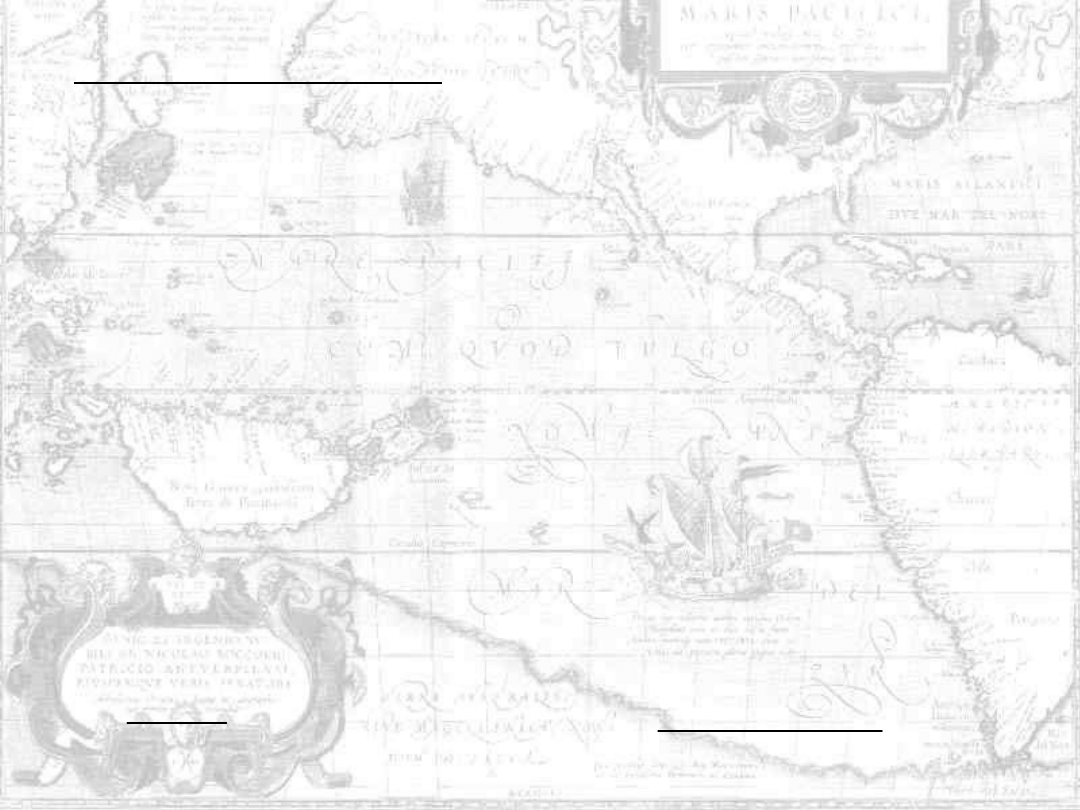
Układ kresek w siatkach celowniczych bywa rozmaity, w zależności od

przeznaczenia lunety. Oprócz krzyża kresek, którego punkt przecięcia leży
na osi celowej i służy do celowania, znajdują się tam zwykle dwie
dodatkowe kreski poziome umożliwiające wyznaczanie odległości lub
podziałki skalowe, diagramy itp., zależnie od przeznaczenia przyrządu.

W teodolitach spotykamy najczęściej układ kresek celowniczych i

dalmierczych pokazany na rysunkach poniżej. W pierwszym z nich kreska
pionowa przecina całe pole widzenia, a więc celowanie może się odbywać
tylko przez bisekcję, czyli podział przedmiotu kreską na dwie części
symetryczne. Jest to najmniej dokładny sposób celowania (jedynie
możliwy przy używanych dawniej krzyżach celowniczych wykonywanych z
nitek pajęczych). Drugi układ z kreską pionową przerwaną w sąsiedztwie
kreski poziomej pozwala celować przez koincydencję, czyli
przedłużenie (zgranie) kreskowego obrazu celu i kreski celowniczej.
Najdokładniejsze celowanie umożliwia trzeci układ kresek przez
symetryczne ustawienie obrazu przedmiotu między dwiema kreskami
siatki.

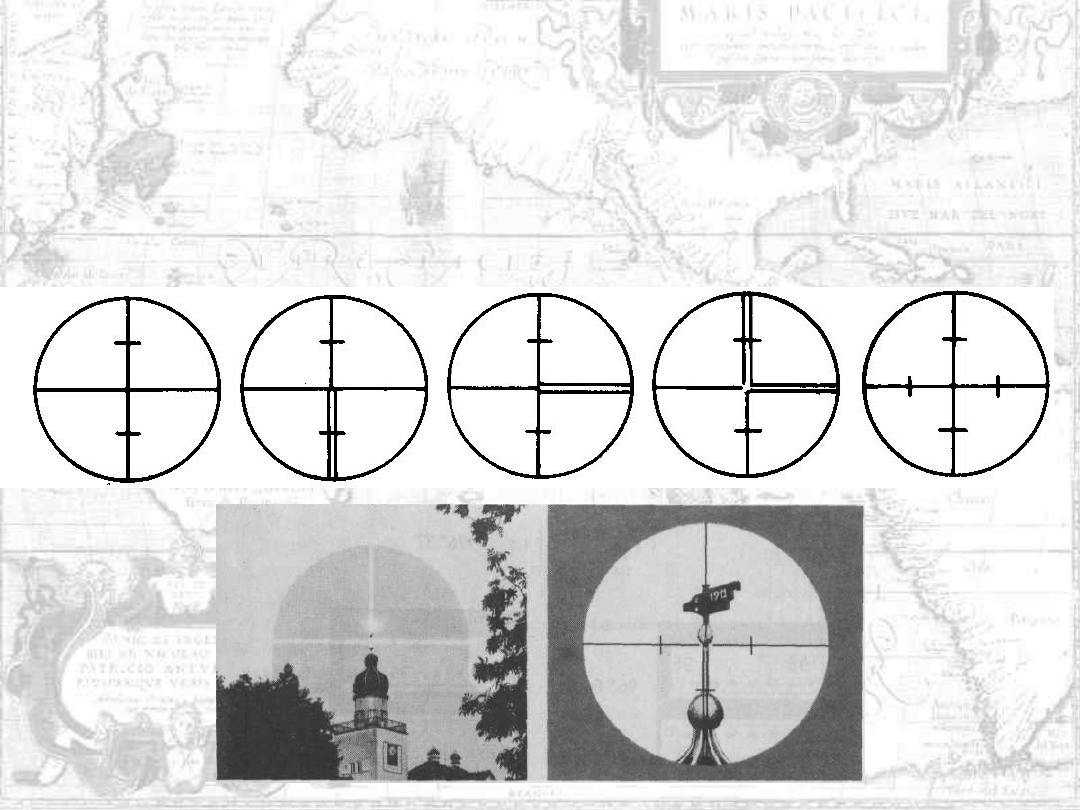
Oko na symetrię jest bardzo czułe i potrafi dokładnie ocenić równość

prześwitów między kreskowym obrazem celu (np. tyczki lub świecy
sygnału triangulacyjnego) a otaczającymi go dwiema bliskimi kreskami.
Mając lunetę o dobrych cechach optycznych można przy sprzyjających,
warunkach polowych i dobrym wzroku osiągnąć w tym wypadku błąd
celowania rzędu 0,2".
Przykłady różnych rozwiązań siatek celowniczych:

REGULACJA LUNETY

Należyta regulacja lunety ma zasadnicze znaczenie dla osiągnięcia

dokładnych wyników w pomiarach geodezyjnych i dla higieny wzroku.
Przed przystąpieniem do obserwacji należy więc wykonać uprzednio
następujące czynności:

 ustawić okular w takim położeniu, aby widzieć ostro siatkę

kresek;

 ustawić lunetę na ostre widzenie obserwowanego przedmiotu;

 sprawdzić, czy na danym stanowisku żadna przeszkoda nie

zasłania części wiązki świetlnej wpadającej do obiektywu.

OGNISKOWANIE OBRAZU

Podczas celowania lunetą obserwator musi widzieć siatkę kresek

ostro, bez żadnego wysiłku akomodacyjnego. Aby to uzyskać kierujemy
lunetę na jasne tło, np. na niebo, i najpierw wykręcamy wyciąg (wkręt)
okularowy całkowicie aż do oporu, tj. oddalamy go od obiektywu, a
następnie powoli wkręcamy dotąd, aż pojawi się pierwszy ostry obraz
siatki kresek. W ten sposób otrzymamy takie nastawienie okularu, że
kreski będą widziane w polu widzenia lunety bez wysiłku
akomodacyjnego mięśni ocznych, gdyż układ optyczny oka jest wtedy
dostosowany do oglądania punktu dali ocznej i to niezależnie od tego,
czy obserwator ma wzrok miarowy, czy też niemiarowy. Gdybyśmy
wkręcali okular w dalszym ciągu, to moglibyśmy nadal widzieć ostro
siatkę kresek, ale już na skutek zwiększonego napięcia oka, co przy
dłuższej pracy spowodowałoby nadmierny wysiłek wzroku, zmęczenie
obserwatora, a więc i obniżenie dokładności pomiaru.

Dla oka miarowego ostre widzenie siatki nastąpi wtedy, gdy znajdzie

się ona w płaszczyźnie ogniskowej okularu. Promienie świetlne po
wyjściu z okularu będą w tym wypadku biegły jako wiązki równoległe.
Dla oka krótkowzrocznego okular należy wkręcić nieco bardziej,
otrzymamy wówczas wpadające do oka wiązki rozbieżne, a dla oka
nadwzrocznego okular należy wkręcić nieco mniej, otrzymamy wówczas
wpadające do oka wiązki zbieżne.

Czynność nastawiania siatki kresek na ostrość wykonuje się tylko raz

dla danego obserwatora przed rozpoczęciem obserwacji.

Następną kolejną czynnością regulacyjną jest nastawienie na ostrość

obrazu przedmiotu oglądanego przez lunetę. Aby otrzymać taki efekt
należy przesunąć siatkę kresek wraz z ustawionym już prawidłowo
okularem aż do uzyskania ostrego obrazu obserwowanego przedmiotu.

Jeżeli dwie te płaszczyzny nie pokrywają się, to przesuwając oko z góry
na dół lub z prawa na lewo zauważymy, że obraz siatki kresek i obraz
przedmiotu przemieszczają się wzajemnie w polu widzenia. Zjawisko to
nazywa się paralaksą instrumentalną i dowodzi, że obraz przedmiotu
utworzony przez obiektyw nie znajduje się w płaszczyźnie siatek
celowniczej, a więc ostrość obrazu nie jest dobrze uregulowana.

Paralaksę usuwamy przesuwając jeszcze nieco wyciąg siatkowy w jedną
lub drugą stronę dotąd, aż stwierdzimy, że przy poruszaniu okiem obrazy
przedmiotu i siatki kresek nie przesuwają się względem siebie.

W lunetach nowoczesnych z teleobiektywem nastawianie na ostrość
obrazu przedmiotu odbywa się za pomocą przesuwania w odpowiednim
kierunku soczewki ogniskującej działanie to nosi nazwę ogniskowaniem
wewnętrznym.

Zakres głębi ostrości ulegnie jednak zmianie, jeżeli część obiektywu

zostanie zasłonięta przez jakąś przeszkodę, co zdarza się często, gdy
celowa przebiega przez szczeliny w płocie lub w pobliżu gałęzi drzew,
ścian domów, słupów telefonicznych itp. Ponieważ luneta jest wtedy
zogniskowana zwykle na cel odległy, więc bliskiej przeszkody nie widać w
lunecie, natomiast obraz przedmiotu będzie jeszcze zupełnie dobrze
widoczny, gdy zostanie zasłonięta połowa, a nawet więcej niż połowa
czynnego otworu obiektywu. Wprawdzie jasność obrazu od strony
przeszkody zmniejszy się, ale nie zawsze w tym stopniu, aby obserwator
zwrócił na to uwagę.
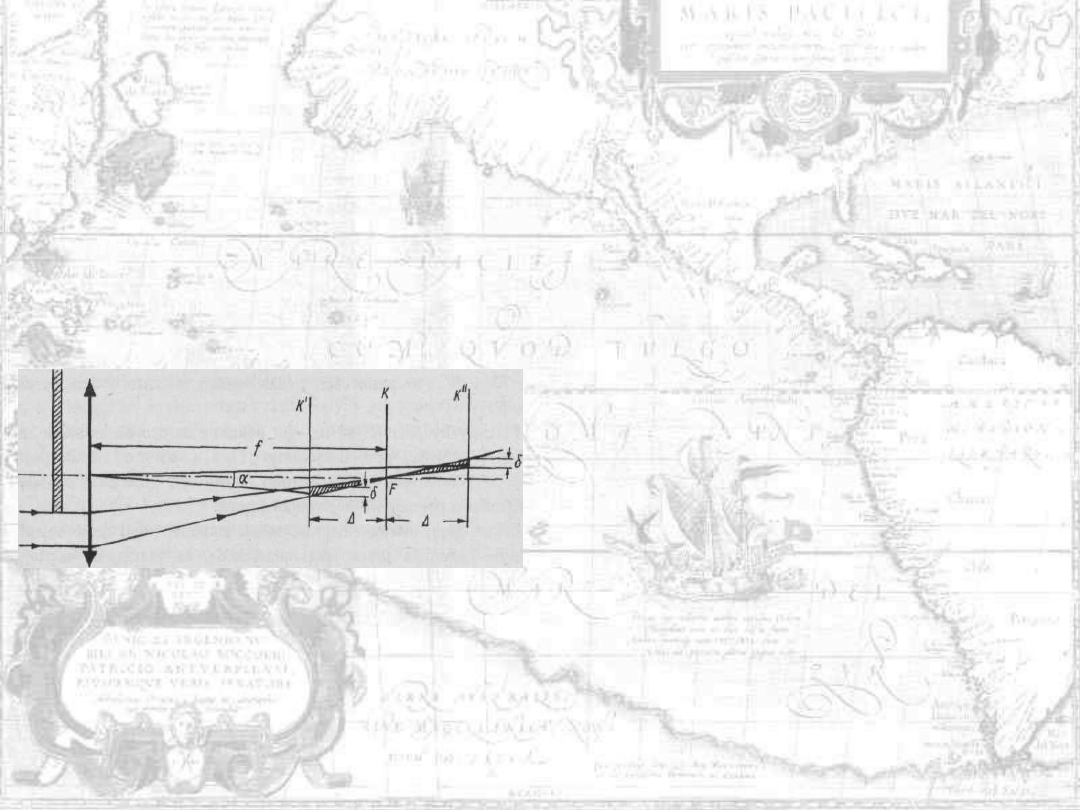
Jeżeli po zasłonięciu części obiektywu będziemy chcieli nastawić na
ostrość obraz przedmiotu, to zajdzie zjawisko zobrazowane na rysunku
poniżej.

Do lunety wpada wtedy tylko wąska
wiązka promieni, a więc płaszczyzny K’
i K’’, między którymi plamka o średnicy
δ będzie przez oko oceniona jako
punkt, znajdą się w znacznie większej
odległości niż wówczas, gdy cały otwór
obiektywu jest czynny.

Głębia ostrości znacznie wzrosła, lecz otrzymane skrajne i ostre jeszcze
obrazy nie będą się znajdowały na osi celowej. Jeżeli przesuwając soczewkę
ogniskującą lub wyciąg siatkowy ustawimy obraz przedmiotu w płaszczyźnie
K’ to będziemy go widzieli ostro z lewej strony pionowej kreski siatki
celowniczej, a jeżeli obraz ustawimy w płaszczyźnie K", to będziemy go
widzieli z prawej strony kreski pionowej. Obraz więc, nic nie tracąc na
ostrości, będzie dla obserwatora przesuwał się o kąt α, a więc błąd, jaki
popełnimy w tych warunkach celując na punkt P, może osiągnąć wartość
0,5α.

Przy zakryciu

1

/

4

otworu czynnego obiektywu, błąd

1

/

2

α nie prze kracza

jeszcze na ogół dokładności pomiaru kąta danym instrumentem, lecz
większe zakrycie może już znacznie zniekształcić wyniki. Przy za kryciu
przekraczającym

1

/

4

otworu czynnego obserwacje są już niemożliwe z

powodu spadku jasności. Przy pomiarach kątów pochylenia lub przy
niwelacji wyniki mogą zostać zniekształcone przez przeszkodę po ziomą,
odcinającą od góry lub od dołu wiązkę promieni wpadających do
obiektywu.

Aby uniknąć omówionych tu błędów obserwacyjnych należy się

upewnić, czy na drodze promieni rzeczywiście znajduje się przeszkoda
ucinająca część wiązki wpadającej do obiektywu. W lunecie nastawionej
na ostre widzenie przedmiotu odległego przeszkoda taka jest w ogóle
niewidoczna, chyba że zasłoni dużą część obiektywu i wywoła wyraźne
zaciemnienie pola widzenia od strony przesłoniętej. Gdy przeszkoda
znajduje się blisko, to wówczas na oko łatwo jest zauważyć, że
przesłania ona obiektyw.

W pomiarach kątowych ucinanie wiązki promieni jest powodem

częstych błędów, niejednokrotnie nie rozpoznanych lub przypisywanych
niesłusznie innym przyczynom, np. refrakcji bocznej.

CHARAKTERYSTYCZNE CECHY

LUNETY

Równoległy pęk promieni, biegnących od odległego punktu B i

nachylonych do osi lunety pod kątem u, będzie po przejściu przez układ
optyczny tej lunety nachylony pod kątem u'. Powiększeniem kątowym
lunety lub wprost powiększeniem nazywamy stosunek tangensów tych
kątów. Obraz B' punktu B, utworzony w obrazowej płaszczyźnie
ogniskowej obiektywu, będzie przesunięty poprzecznie od osi o wielkość
y’ , a więc z odpowiednich trójkątów o kątach przy wierzchołkach u i u'
otrzymamy:

'

'

u

tg

f

u

tg

f

y

ok

ob









Powiększenie lunety γ wynosi więc:

ok

ob

f

f

u

tg

u

tg





'



Dla przedmiotów odległych można długość lunety pominąć i uznać, że

kąt u jest kątem, pod jakim przedmiot byłby widoczny okiem nie
uzbrojonym, umieszczonym za okularem. Ponadto w lunetach używanych
w geodezji kąty u i u’ są małe, a zatem powiększenie możemy wyrazić
wzorem:

ok

ob

f

f

u

u





'



W związku z tym możemy powiedzieć, że powiększenie lunety jest to

stosunek kąta widzenia obrazu utworzonego przez lunetę do kąta
widzenia przedmiotu obserwowanego okiem nie uzbrojonym i równe jest
stosunkowi ogniskowych f

ob

i f

ok

. Jeżeli chcemy, aby powiększenie było

duże, to luneta musi być tak skonstruowana, aby ogniskowa obiektywu
była możliwie duża, a ogniskowa okularu – mała.

Czynny otwór obiektywu o średnicy d ogranicza wiązkę promieni

wpadających do lunety i nazywa się źrenicą wejściową. Rozpatrując pęki
równoległe padające na obiektyw i przekształcone przez lunetę
zauważymy, że wszystkie one przecinają się za okularem w pewnym
ograniczonym obszarze kołowym, gdzie nastąpi największe skupie nie tych
pęków. Jeżeli skierujemy lunetę na jasne tło, a za okularem ustawimy
ekran prostopadle do osi lunety i będziemy go przesuwać, to w miejscu
największego skupienia promieni powstanie na ekranie najmniejszy i
najostrzej zarysowany krążek świetlny, który nazywamy źrenicą wyjściową
lunety i oznaczamy przez d'. Źrenica wyjściowa jest obrazem źrenicy
wejściowej i stanowi najmniejszy przekrój, zbioru promieni padających na
obiektyw.

Rozpatrując ( patrz rysunek slajd 2) dwa trójkąty o podstawach d i d' oraz
wspólnym wierzchołku f

ok

= f'

ob

otrzymamy:

'

d

d

f

f

ok

ob







POLE WIDZENIA

W płaszczyźnie, w której powstaje obraz utworzony przez obiektyw,

znajduje się, jak wiemy, siatka celownicza (krzyż kresek) oprawiona w
kolistą ramkę z okrągłym otworem w środku. Ramka ta ogranicza pole
widzenia lunety i nazywa się diafragmą pola lub przysłoną (ozn. D).
Przez lunetę widoczne są więc tylko przedmioty znajdujące się wewnątrz
pewnej powierzchni stożkowej, której osią jest oś celowa lunety. W
obszarze przedmiotowym kąt przy wierzchołku tego stożka wynosi φ =
2u i nosi nazwę kątowego pola widzenia lunety.
Oznaczając więc przez ω średnicę diafragmy, możemy pole widzenia
lunety φ = 2u wyznaczyć z wzoru :

ob

f

u

tg

2





Pole widzenia lunety nie zależy zatem od średnicy obiektywu, lecz od
średnicy diafragmy. Obserwator patrząc przez okular na obraz utworzony
w płaszczyźnie diafragmy przez obiektyw widzi przedmioty na krańcu pola
widzenia pod kątem równym ψ= 2u. Stosunek

tangensów kątów ψ i φ jest powiększeniem lunety, czyli:





u

tg

u

tg '

u

tg

u

tg





'

zate
m

Z powyższego wzoru wynika, że kąt u' pola widzenia okularu ogranicza
pole widzenia lunety. Jeżeli z danej konstrukcji okularu wynika jego
określony kąt widzenia ψ = 2u , to wówczas iloczyn γ tg u jest wielkością
stałą równą tg u‘, a zatem zwiększając powiększenie lunety γ musimy
zmniejszyć jej pole widzenia φ = 2u, i na odwrót.

W lunetach geodezyjnych, przeznaczonych do obserwacji dokładnych,

a więc mających duże powiększenie, pole widzenia zawiera się zazwyczaj
w granicach od 1° do 1,5°, w lunetach przeznaczonych do pomiarów
mniej dokładnych — nie przekracza kilku stopni

.

Kąt pola widzenia lunety połączonej z urządzeniem kątomierczym

można łatwo zmierzyć. W tym celu obieramy w terenie jakiś odległy,
wyraźny przedmiot, a następnie tak ustawiamy lunetę, abyśmy go widzieli
na samym skraju pola widzenia, i wykonujemy odczyt na podziałce
kątowej. Z kolei przesuwamy lunetę w ten sposób, aby ten sam przedmiot
znalazł się na drugim skraju pola widzenia i znów wykonujemy odczyt.
Różnica odczytów da szukany kąt pola widzenia.
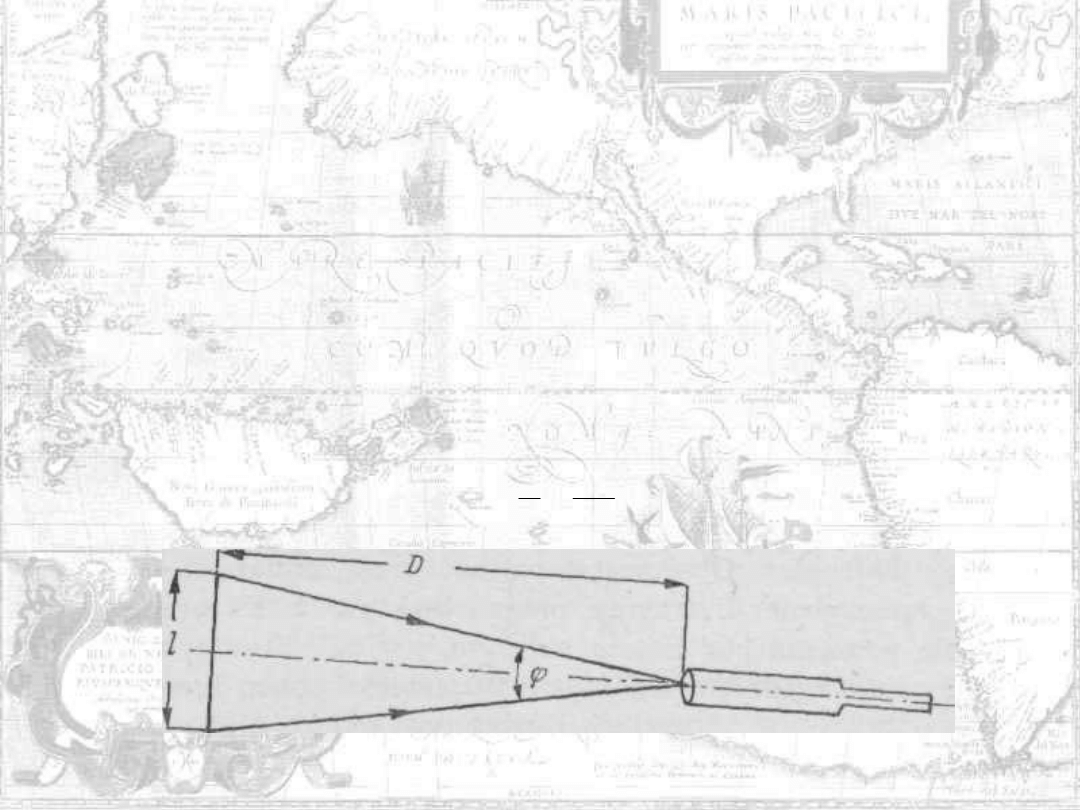
Jeżeli luneta nie jest połączona z przyrządem kątomierczym, to możliwie
daleko ustawiamy w terenie łatę niwelacyjną z podziałką i patrząc przez
lunetę wykonujemy odczyty na krańcach pola widzenia (rys. 5.19). Mając
różnicę odczytów l i znając odległość D łaty od lunety

znajdziemy kąt pola widzenia z wzoru:

D

l

tg

2

2





JASNOŚĆ LUNETY

Jasność fizykalną lunety charakteryzuje stosunek strumienia

świetlnego J

o

który z lunety wychodzi, do strumienia J, który do lunety

wchodzi.

Stosunek ten

J

J

k

0



jest zawsze mniejszy od jedności, ze względu na
straty

strumienia świetlnego z powodu odbicia części światła na powierzchniach
szklanych i z powodu absorpcji, czyli pochłaniania światła w szkle
optycznym.
Ponadto światło odbite od jednych powierzchni szklanych odbija się
ponownie od innych i kierując się ku obrazowi zaciera jego
kontrastowość. Aby temu częściowo za pobiec stosuje się specjalne
powłoki przeciwodblaskowe, którymi pokrywa się powierzchnię szkła
(optyka rozjaśniona). Zwykle stosuje się takie powłoki, aby redukowały
światło odbite żółtozielone, gdyż na nie oko jest najbardziej wrażliwe.
Światło czerwone i niebieskie odbija się od nich w większym stopniu i z
tego względu powłoki przeciwodblaskowe oglądane w świetle odbitym
wydają się fioletowe.
Aby ocenić jasność obrazu powstałego na siatkówce oka, należy
rozpatrzyć 3 wypadki:

• źrenica wyjściowa lunety jest równa źrenicy oka;

• źrenica wyjściowa lunety jest większa od źrenicy oka;

• źrenica wyjściowa lunety jest mniejsza od źrenicy oka

Jeżeli średnica źrenicy wyjściowej lunety d' jest równa średnicy źrenicy

oka (d' = d

0

), to na siatkówkę pada cały strumień świetlny, jaki wszedł do

obiektywu. Lecz energia świetlna wchodząca do lunety jest
proporcjonalna do powierzchni źrenicy wejściowej. Jest ona tyle razy
większa od energii świetlnej padającej na źrenicę oka nie uzbrojonego, ile
razy powierzchnia źreni cy wejściowej jest większa od powierzchni źrenicy
oka. Ponieważ zało żyliśmy, że d' = d

0

, więc zwiększenie energii świetlnej

wpadającej do oka wyniesie:

2

2

'

















d

d

W przypadku drugim, kiedy źrenica wyjściowa lunety jest większa od

źrenicy oka (d' > d

0

), ta właśnie źrenica oka staje się źrenicą wyjściową

lunety. Strumień świetlny wypełnia wtedy całą powierzchnię źrenicy oka,
a więc jasność obrazu utworzonego na siatkówce będzie w dalszym ciągu
taka sama, jak przedmiotu oglądanego okiem nie uzbrojonym, czyli równa
jedności.

Jeżeli średnica źrenicy wyjściowej lunety jest mniejsza niż średnica

źrenicy oka (d' > d

0

), to wówczas strumień świetlny nie wypełnia całej

źrenicy ocznej, a obraz na siatkówce będzie tyle razy mniej oświetlony, ile
razy powierzchnia źrenicy wyjściowej lunety jest mniejsza od powierzchni
źrenicy oka. A więc jasność lunety jest w tym wypadku jest
mniejsza od

jedności i wynosi
 

2

0

'













d

d