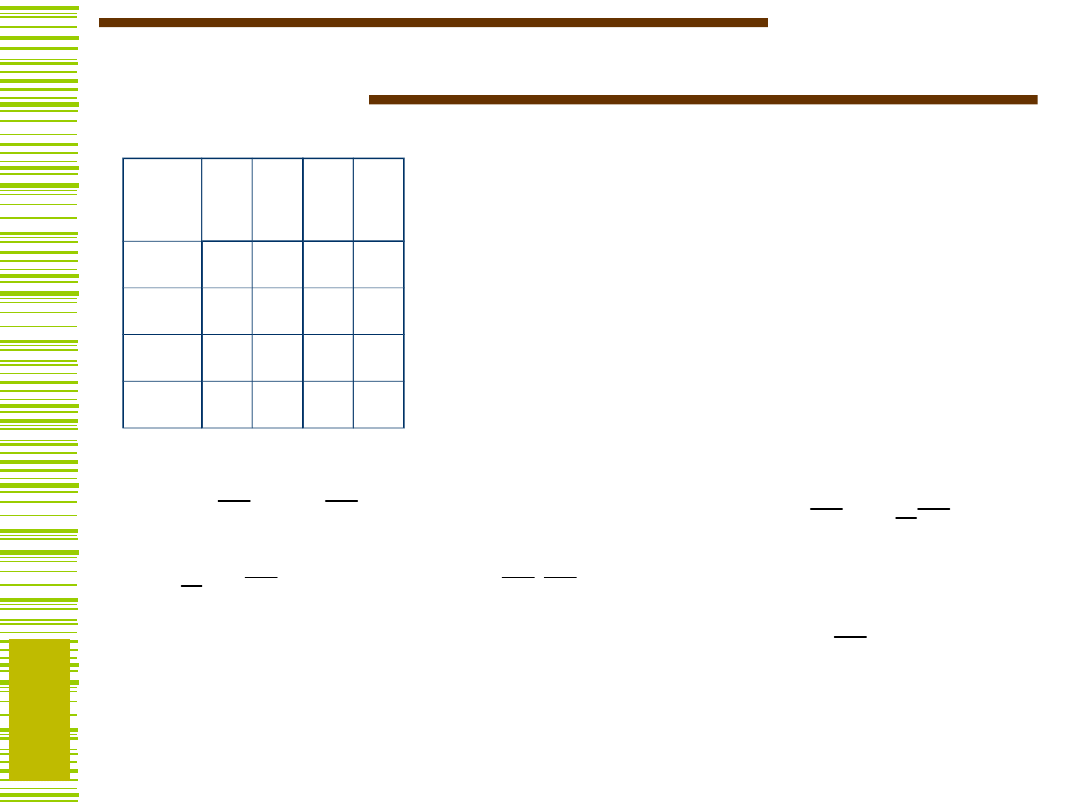
1

I

T
P

W

ZPT

Problem kodowania

x

s

0 1 0 1

A

A B 0 0

B

A C 0 0

C

D C 0 0

D

A B 0 1

Wariant I

A = 00
B = 01
C = 10

D = 11

Wariant I

A = 00
B = 01
C = 10

D = 11

Wariant II

A = 00
B = 11
C = 01

D = 10

Wariant II

A = 00
B = 11
C = 01

D = 10

2

1

2

1

1

Q

Q

x

Q

Q

D





2

1

2

1

2

1

2

Q

Q

x

Q

xQ

Q

Q

x

D







2

1

Q

xQ

y 

2

1

2

1

Q

Q

x

Q

x

D





x

D

2



2

1

Q

xQ

y 

Wariant II

Wariant II

Wariant I

Wariant I

2

I

T
P

W

ZPT

Kodowanie

3 stany - 3 różne kodowania

3 stany - 3 różne kodowania

4 stany - 3 różne kodowania

4 stany - 3 różne kodowania

5 stanów
-

5 stanów
-

140
kodowań

140
kodowań

7 stanów
-

7 stanów
-

840
kodowań

840
kodowań

9 stanów
-

9 stanów
-

ponad 10 milionów kodowań

ponad 10 milionów kodowań

Jak przewidzieć (obliczyć)
najlepsze kodowanie stanów?

Jak przewidzieć (obliczyć)
najlepsze kodowanie stanów?

Czy realne jest sprawdzenie wszystkich
możliwości

Czy realne jest sprawdzenie wszystkich
możliwości

3

I

T
P

W

ZPT

KODOWANIE

Jedyną rozsądną z punktu widzenia dzisiejszych
technologii i realną do omówienia w
ograniczonym

1)

czasie wykładu jest metoda

wykorzystująca podział
z własnością podstawienia.

Jedyną rozsądną z punktu widzenia dzisiejszych
technologii i realną do omówienia w
ograniczonym

1)

czasie wykładu jest metoda

wykorzystująca podział
z własnością podstawienia.

1)

A wszystkich wytrwałych w tym procesie
specjalnie nagradzam na egzaminie.

1)

A wszystkich wytrwałych w tym procesie
specjalnie nagradzam na egzaminie.

4

I

T
P

W

ZPT

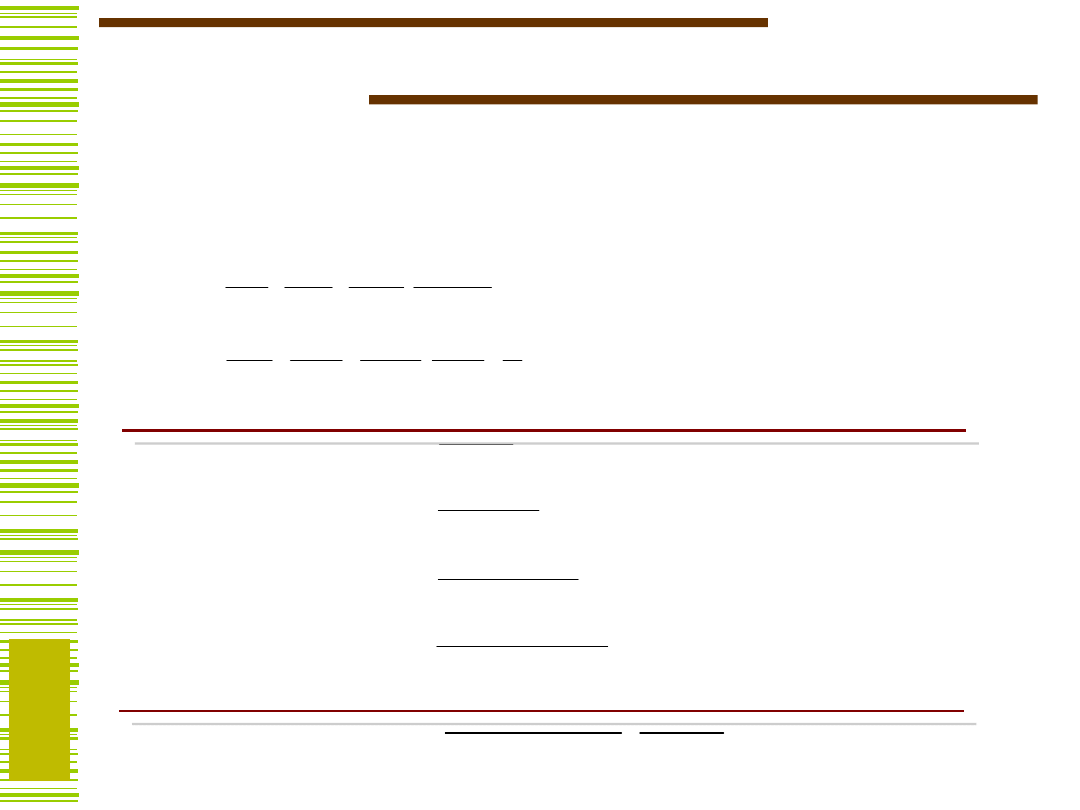
Elementy rachunku podziałów

Podziałem na zbiorze S jest system zbiorów P = {

B

i

},

którego bloki są rozłączne, czyli

B

i



B

j

=, jeśli tylko i  j.

Dla S = {1,2,3,4,5,6}, P = {{1,2}, {3,5}, {4,6} } jest

podziałem na S.

 =

)

4,6

5;

3,

;

1,2

(

Iloczyn podziałów, suma podziałów oraz relacja .

5

I

T
P

W

ZPT

Elementy rachunku podziałów…

Powiemy, że podział



a

jest nie większy od



b

(co oznaczamy:



a

 



b

), jeśli każdy blok z



a

jest zawarty w pewnym bloku z



b

.



b

=

)

3,5

;

2,6

;

1,4

(

)

3,5,6

;

1,2,4

(

)

3,5

;

6

;

4

;

1,2

(



a

=



c

=



c

≤



a

Tak



c



b

NIE!



(0) – podział najmniejszy

(1) – podział największy

6

I

T
P

W

ZPT

Elementy rachunku podziałów…



b

=

Iloczynem podziałów



a

•



b

nazywamy największy

(względem relacji ) podział, który jest nie większy od



a

oraz



b

.

)

3,5

;

2,6

;

1,4

(

)

3,5,6

;

1,2,4

(



a

=



a

•



b

=

)

3,5

;

6

;

2

;

1,4

(

7

I

T
P

W

ZPT

Elementy rachunku podziałów…

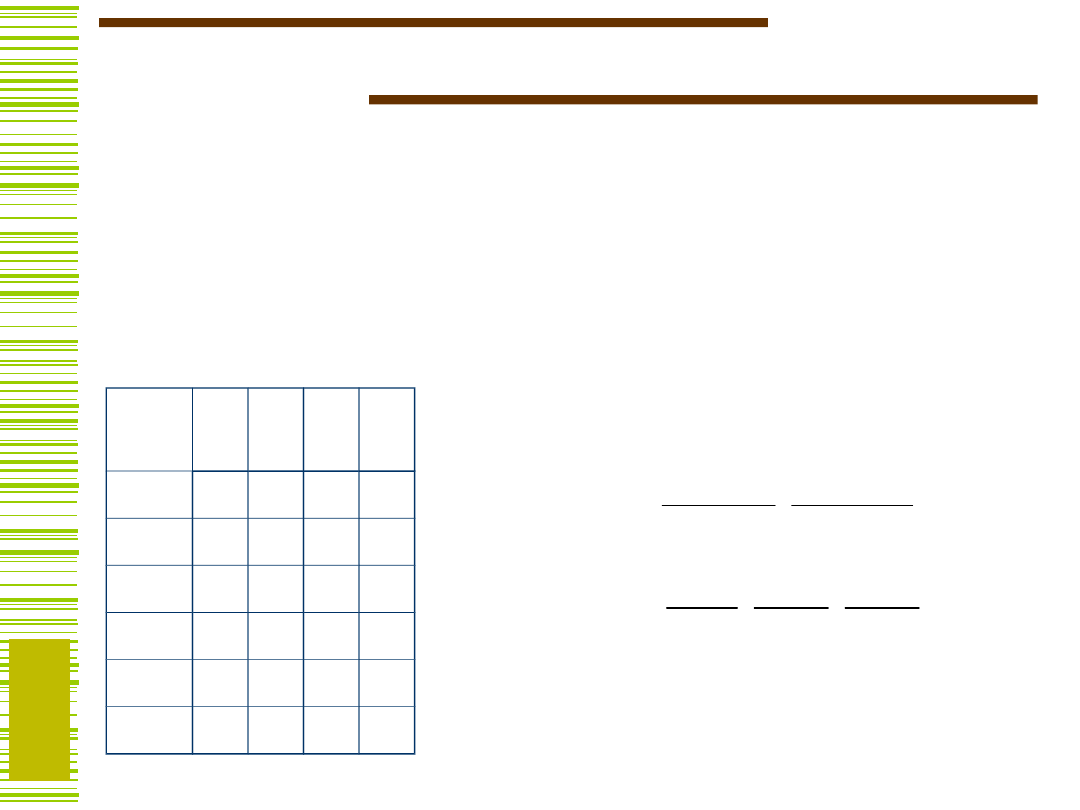
Sumą podziałów



a

+



b

nazywamy najmniejszy

(względem relacji ) podział, który jest nie mniejszy od



a

oraz



b

.





9

,

8

,

7

6

,

5

;

4

,

3

;

2

,

1

;







9

8

,

7

5

,

4

;

3

,

2

;

6

,

1

;

;





a



b





;...

6

,

2

,

1





a

+ 

b





;...

6

,

3

,

2

,

1





a

+ 

b





;...

6

,

4

,

3

,

2

,

1





a

+ 

b





9

,

8

,

7

;

6

,

5

,

4

,

3

,

2

,

1





a

+ 

b





;...

6

,

5

,

4

,

3

,

2

,

1





a

+ 

b

8

I

T
P

W

ZPT

Własność podstawienia

Podział  na zbiorze stanów automatu M=<S, I ,

δ> ma własność podstawienia (closed partition),
gdy dla każdej pary stanów S

i

, S

j

należącej do

tego samego bloku  i każdego wejścia I

k

stany

I

k

S

i

oraz I

k

S

j

należą do wspólnego bloku .

Podział  na zbiorze stanów automatu M=<S, I ,

δ> ma własność podstawienia (closed partition),
gdy dla każdej pary stanów S

i

, S

j

należącej do

tego samego bloku  i każdego wejścia I

k

stany

I

k

S

i

oraz I

k

S

j

należą do wspólnego bloku .

x

s

0

1

0

1

A

A

F

0

0

B

E

C

0

1

C

C

E

0

1

D

F

A

1

0

E

B

F

1

1

F

D E

0

0





F

D

C

E

B

A

,

,

;

,

,

1





Podziały z własnością podstawienia:

Podziały z własnością podstawienia:





F

E

D

B

C

A

,

;

,

;

,

2





9

I

T
P

W

ZPT

Twierdzenie

Dany jest automat M o zbiorze stanów S, |S| = n.

Do zakodowania stanów potrzeba Q

1

, ..., Q

k

elementów pamięci.



() – liczba bloków podziału 

Jeżeli istnieje podział  z własnością podstawienia i

jeżeli r spośród k zmiennych kodujących Q

1

, ..., Q

k

, gdzie

r = log

2



(), jest przyporządkowanych blokom podziału  tak,

że wszystkie stany zawarte w jednym bloku są oznaczone tymi
samymi kodami Q

1

, ..., Q

r

, to funkcje Q’

1

, ..., Q’

r

, są niezależne

od pozostałych (k – r) zmiennych.

Dany jest automat M o zbiorze stanów S, |S| = n.

Do zakodowania stanów potrzeba Q

1

, ..., Q

k

elementów pamięci.



() – liczba bloków podziału 

Jeżeli istnieje podział  z własnością podstawienia i

jeżeli r spośród k zmiennych kodujących Q

1

, ..., Q

k

, gdzie

r = log

2



(), jest przyporządkowanych blokom podziału  tak,

że wszystkie stany zawarte w jednym bloku są oznaczone tymi
samymi kodami Q

1

, ..., Q

r

, to funkcje Q’

1

, ..., Q’

r

, są niezależne

od pozostałych (k – r) zmiennych.

10

I

T
P

W

ZPT

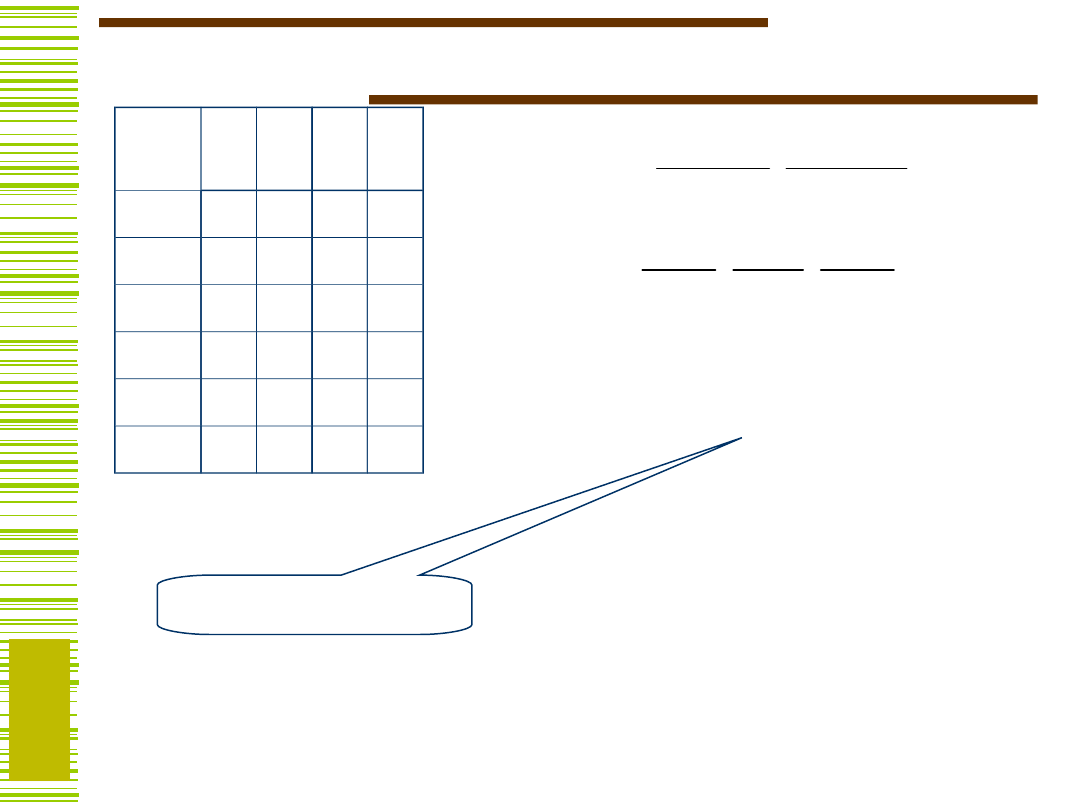
Przykład 1- interpretacja w.p.

x

s

0

1

0

1

A

A

F

0

0

B

E

C

0

1

C

C

E

0

1

D

F

A

1

0

E

B

F

1

1

F

D E

0

0





F

D

C

E

B

A

,

,

;

,

,

1





0 0

0 1
0 1
0 0
1 0
1 0

Kodowanie wg 

1

Kodowanie wg 

1





A
B
C

D

E

F

0
0
1
1
0
1





F

E

C

B

D

A

τ

,

;

,

;

,



Nie wystarcza to do

zakodowania



1

•



=

(0)

Warunek jednoznaczności kodowania!

Warunek jednoznaczności kodowania!

11

I

T
P

W

ZPT

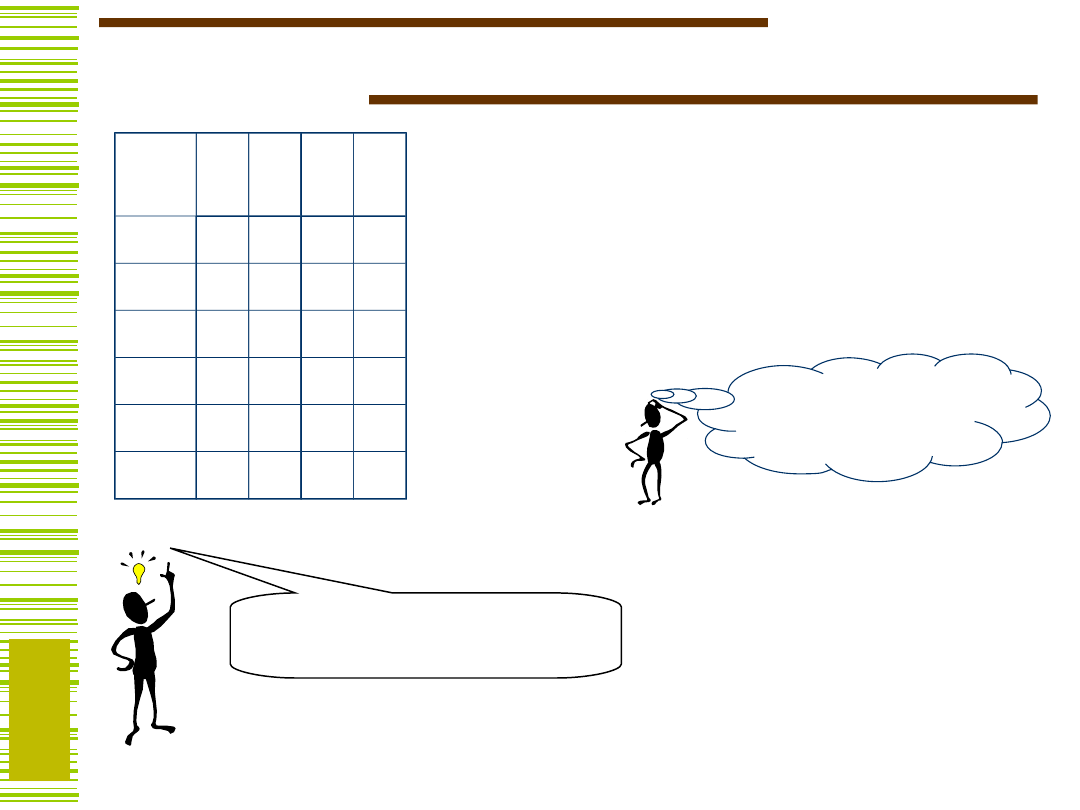
Przykład 1…

x

s

0 1 0 1

A

A F 0 0

B

E C 0 1

C

C E 0 1

D

F A 1 0

E

B F 1 1

F

D E 0 0

Q

1

Q

2

Q

3

A 0 0 0
B 0 0 1
C 1 0 1
D 1 0 0
E 0 1 0
F 1 1 0

Co to znaczy, że zastosujemy
kodowanie wg podziału
zamkniętego:

Co to znaczy, że zastosujemy
kodowanie wg podziału
zamkniętego:

Q

1

’ = D

1

= f(x,Q

1

)

Q

1

’ = D

1

= f(x,Q

1

)

Nie musimy obliczać funkcji

wzbudzeń, aby stwierdzić, że

pierwsza z nich, czyli D

1

będzie…

Niestety tylko jedną zmienną
zakodowaliśmy wg podziału zamkniętego,
zatem:

Niestety tylko jedną zmienną
zakodowaliśmy wg podziału zamkniętego,
zatem:

a co z
pozostałymi?

Q

2

’ = D

2

=

f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = D

3

=

f(x,Q

1

,Q

2

,Q

3

)

Q

2

’ = D

2

=

f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = D

3

=

f(x,Q

1

,Q

2

,Q

3

)

12

I

T
P

W

ZPT

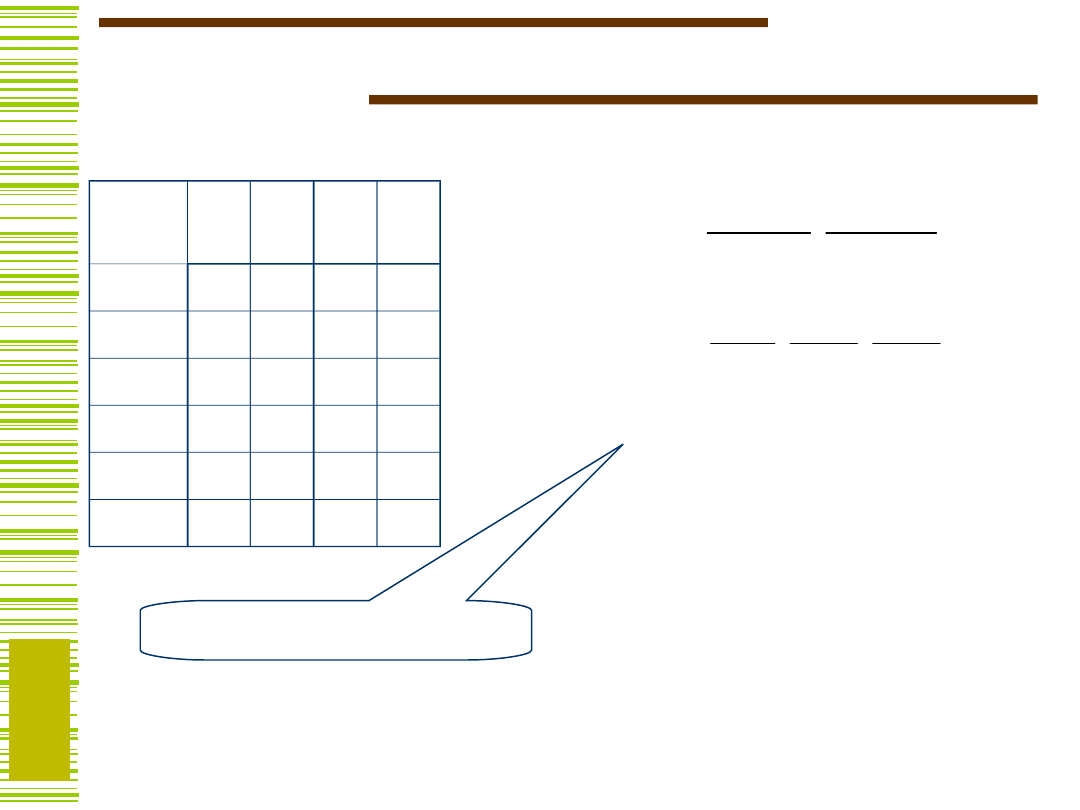
Przykład 1…

x

s

0

1

0

1

A

A

F

0

0

B

E

C

0

1

C

C

E

0

1

D

F

A

1

0

E

B

F

1

1

F

D

E

0

0





F

E

D

B

C

A

,

;

,

;

,

2



π





F

D

C

E

B

A

,

,

;

,

,

1



π

Kodowanie wg 

1

Kodowanie wg 

1

0 0

0 1
0 0
0 1
1 0
1 0

A
B
C

D

E

F

0
0
1
1
0
1



2



2

)

(0











2

1

Jest to kodowanie jednoznaczne

A może jest więcej podziałów zamkniętych:

A może jest więcej podziałów zamkniętych:

Później wykażemy, że oprócz 

1

Później wykażemy, że oprócz 

1

jest 

2

jest 

2

13

I

T
P

W

ZPT

PRZYKŁAD 1 c.d.

Przy tak dobranym kodowaniu pierwsza funkcja
wzbudzeń Q

1

’

tego automatu będzie zależna od

jednej zmiennej wewnętrznej, a druga i trzecia
łącznie (Q

2

’, Q

3

’) od dwóch zmiennych

wewnętrznych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

,Q

3

)

Q

3

’ = f(x,Q

2

,Q

3

)

Przy tak dobranym kodowaniu pierwsza funkcja
wzbudzeń Q

1

’

tego automatu będzie zależna od

jednej zmiennej wewnętrznej, a druga i trzecia
łącznie (Q

2

’, Q

3

’) od dwóch zmiennych

wewnętrznych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

,Q

3

)

Q

3

’ = f(x,Q

2

,Q

3

)

Kto nie wierzy, niech zakoduje, obliczy funkcje
Q

1

’, Q

2

’, Q

3

’ i sprawdzi.

Kto nie wierzy, niech zakoduje, obliczy funkcje
Q

1

’, Q

2

’, Q

3

’ i sprawdzi.

Dla całego roku!

Dla całego roku!

14

I

T
P

W

ZPT

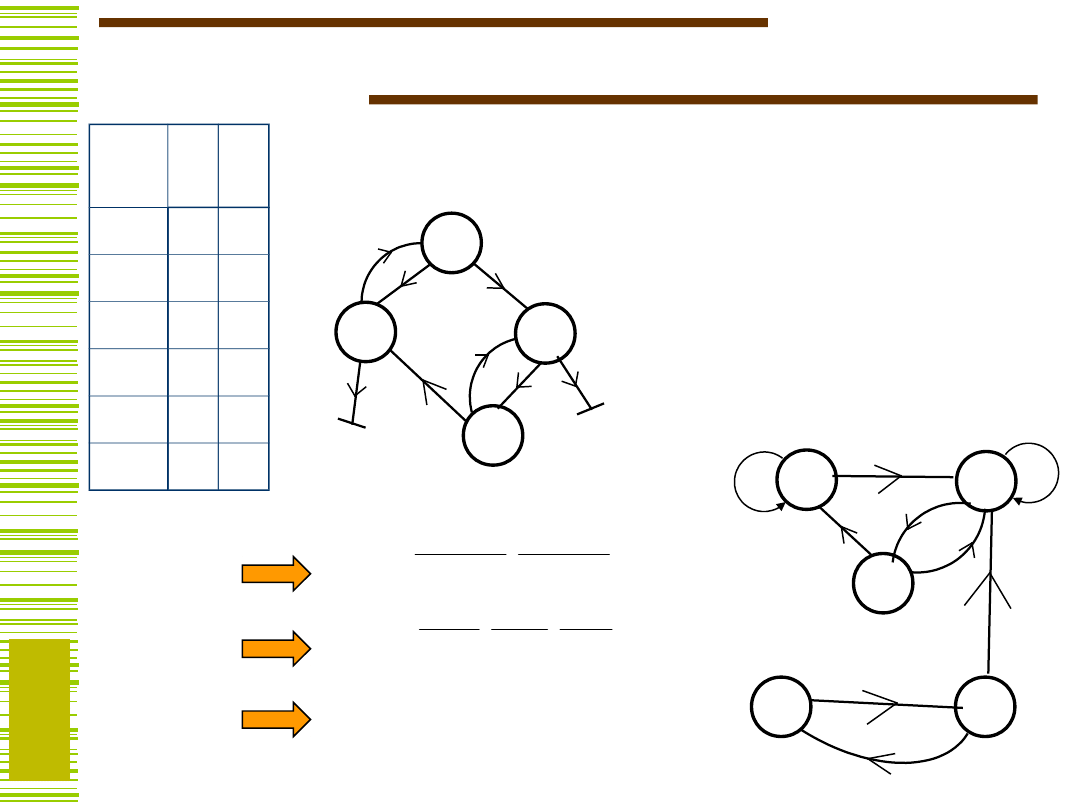
Obliczanie podziału zamkniętego

x

s

0 1

A

A F

B

E C

C

C E

D

F A

E

B F

F

D E

A,B

A,B

A,E

A,E

C,F

C,F

C,D

C,D

F

F

E

E

B,D

B,D

A,C

A,C

E,F

E,F

A,D

A,D

A,F

A,F

A,B

A,B

A,C

A,C

A,D

A,D





F

D,

C,

;

E

B,

A,

1









F

E,

;

D

B,

;

C

A,

2





 

1



Tworzymy graf par następników

dla różnych wierzchołków

początkowych

15

I

T
P

W

ZPT

PRZYKŁAD 2

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0

Generujemy podziały zamknięte

Generujemy podziały zamknięte

Do zakodowania stanów
automatu M potrzebne są 3
podziały 2-blokowe, takie że:

Do zakodowania stanów
automatu M potrzebne są 3
podziały 2-blokowe, takie że:

(0)















c

b

a

16

I

T
P

W

ZPT

PRZYKŁAD 2 c.d.

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0

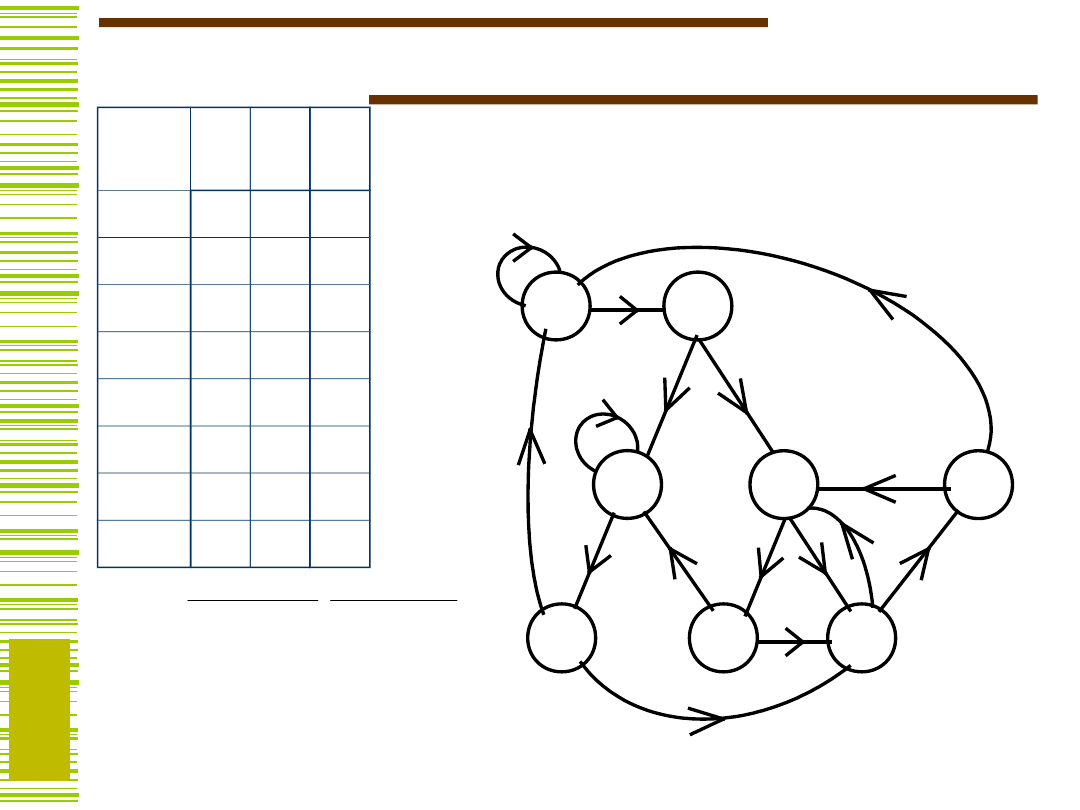
Graf par następników :

Graf par następników :





H

G,

F,

E,

;

D

C,

B,

A,

1





A,B

A,B

F,H

F,H

C,D

C,D

E,F

E,F

A,C

A,C

G,E

G,E

G,H

G,H

B,D

17

I

T
P

W

ZPT

PRZYKŁAD 2 c.d.

x

s

0

1

Z

A

H

B

0

B

F

A

0

C

G

D

0

D

E

C

1

E

A

C

0

F

C

D

0

G

B

A

0

H

D

B

0





G

F,

C,

B,

;

H

E,

D,

A,



G

F,

;

H

E,

C

B,

;

D

A,

;

G

F,

C

B,

;

H

E,

D,

A,

;

H

E,

D

A,

;

G

F,

C,

B,

;

A,D

A,D

D,H

D,H

B,F

B,F

+

=



2

+

=



2

18

I

T
P

W

ZPT

PRZYKŁAD 2 c.d.





H

G,

F,

E,

;

D

C,

B,

A,

1









G

F,

C,

B,

;

H

E,

D,

A,

2





Niestety:

Niestety:

Potrzebny jest więc jeszcze jeden podział :

Potrzebny jest więc jeszcze jeden podział :





)

0

(













G

F,

;

H

E,

;

C

B,

;

D

A,

2

1

)

(0

τ 











2

1





F

E,

D,

C,

;

H

G,

B,

A,



τ

19

I

T
P

W

ZPT

PRZYKŁAD 2 c.d.





H

G,

F,

E,

;

D

C,

B,

A,

1









G

F,

C,

B,

;

H

E,

D,

A,

2





0
0
0
0
1
1
1
1

0
1
1
0
0
1
1
0

Kodowanie wg 

1

Kodowanie wg 

1



2



2

A
B
C

D

E

F

G
H





F

E,

D,

C,

;

H

G,

B,

A,



τ





0
0
1
1
1
1
0
0

20

I

T
P

W

ZPT

PRZYKŁAD 2 c.d.

Przy tak dobranym kodowaniu dwie funkcje
wzbudzeń Q

1

’

i Q

2

’ tego automatu będą zależne od

jednej zmiennej wewnętrznej, a trzecia Q

3

’ (w

najgorszym przypadku) od trzech zmiennych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Przy tak dobranym kodowaniu dwie funkcje
wzbudzeń Q

1

’

i Q

2

’ tego automatu będą zależne od

jednej zmiennej wewnętrznej, a trzecia Q

3

’ (w

najgorszym przypadku) od trzech zmiennych, czyli

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

2

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Warto zakodować, obliczyć funkcje wzbudzeń
Q

1

’, Q

2

’, Q

3

’ i sprawdzić, czy rzeczywiście tak

jest.

Warto zakodować, obliczyć funkcje wzbudzeń
Q

1

’, Q

2

’, Q

3

’ i sprawdzić, czy rzeczywiście tak

jest.

21

I

T
P

W

ZPT

Komentarz

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

1

’ = f(x,Q

1

)

Q

2

’ = f(x,Q

1

,Q

2

,Q

3

)

Q

3

’ = f(x,Q

1

,Q

2

,Q

3

)

0 0

0

0 0

1

0 1

0

0 1

1

1 0

0

1 0

1

1 1

0

1 1

1

A
B
C
D
E
F
G
H

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

Każde inne kodowanie doprowadzi do bardziej
skomplikowanych funkcji wzbudzeń.

W szczególności dla kodowania wg naturalnego
kodu binarnego

1)

:

W szczególności dla kodowania wg naturalnego
kodu binarnego

1)

:

1)

Naturalny kod binarny jest przyjmowany domyślnie do kodowania

automatów w komercyjnych systemach projektowania układów
cyfrowych

1)

Naturalny kod binarny jest przyjmowany domyślnie do kodowania

automatów w komercyjnych systemach projektowania układów
cyfrowych

22

I

T
P

W

ZPT

Nie martwmy się…

W najnowszych

systemach istnieje

opcjonalna

możliwość

wprowadzenia

kodowania

obliczonego

zewnętrznie przez

użytkownika

23

I

T
P

W

ZPT

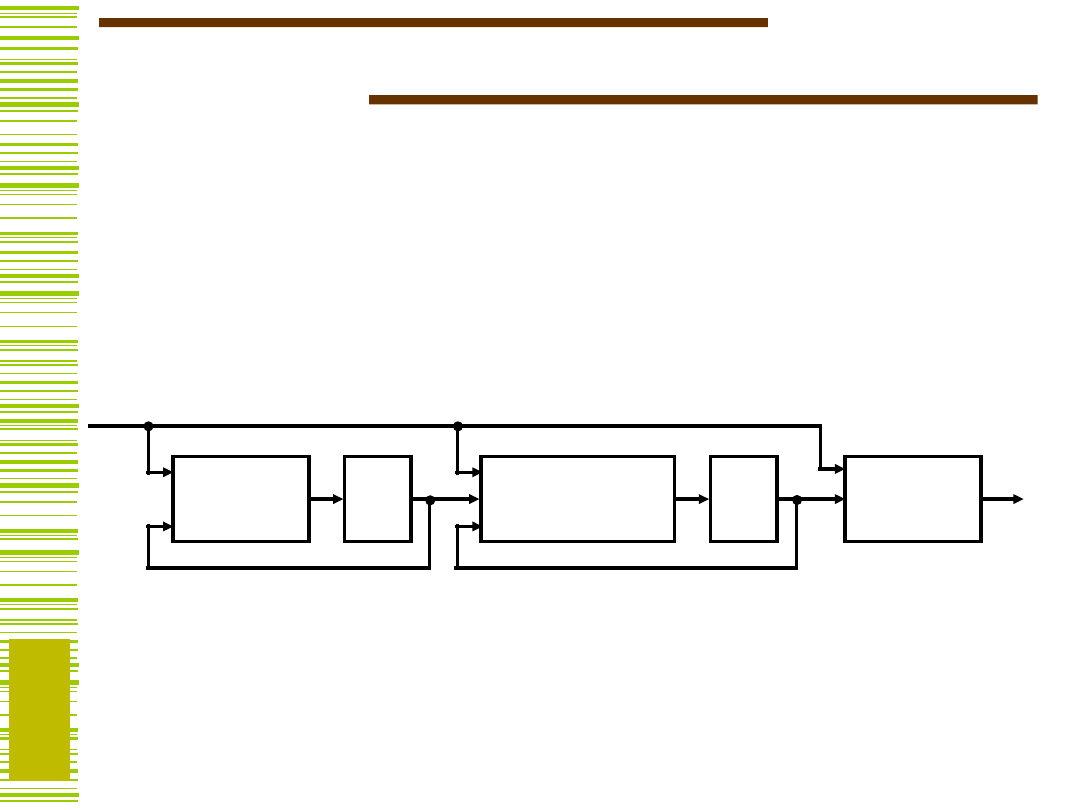
Dekompozycja szeregowa

Dany jest automat M o zbiorze stanów S. Warunkiem
koniecznym i wystarczającym dekompozycji szeregowej
automatu M na dwa szeregowo połączone automaty M

1

,

M

2

jest istnienie podziału  z własnością podstawienia i

podziału  takich, że 



 = 0.

Dany jest automat M o zbiorze stanów S. Warunkiem
koniecznym i wystarczającym dekompozycji szeregowej
automatu M na dwa szeregowo połączone automaty M

1

,

M

2

jest istnienie podziału  z własnością podstawienia i

podziału  takich, że 



 = 0.

f

1

(x,Q

1

)

D

1

f

2

(x,Q

1

,Q

2

)

D

2

f

0

(x,Q

2

)

x

x

q

1

q

1

Q

1

Q

1

Q

2

Q

2

q

2

q

2

z

z

24

I

T
P

W

ZPT

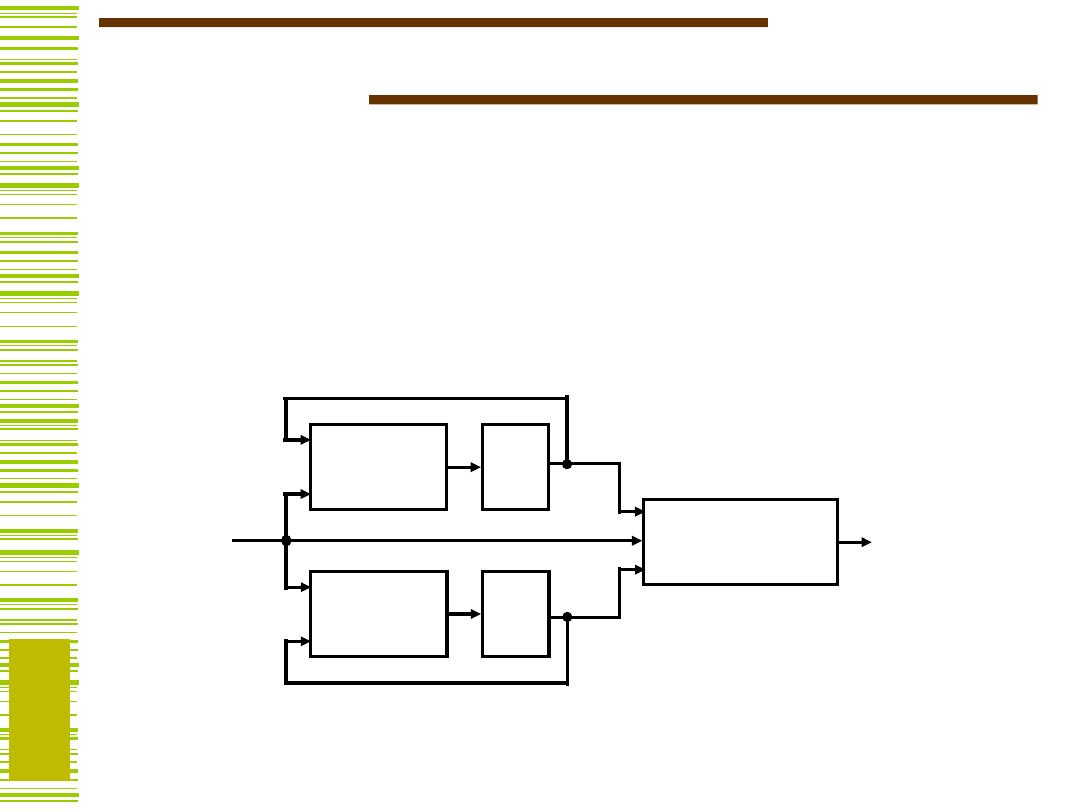
Dekompozycja równoległa

Automat M jest dekomponowalny na dwa podautomaty
M

1

, M

2

działające równolegle wtedy i tylko wtedy, gdy na

zbiorze S tego automatu istnieją dwa nietrywialne
podziały



1

, 

2

z własnością podstawienia takie, że



1





2

= (0)

Automat M jest dekomponowalny na dwa podautomaty
M

1

, M

2

działające równolegle wtedy i tylko wtedy, gdy na

zbiorze S tego automatu istnieją dwa nietrywialne
podziały



1

, 

2

z własnością podstawienia takie, że



1





2

= (0)

f

0

(x,Q

1

,Q

2

)

x

x

f

2

(x,Q

2

)

D

2

q

2

q

2

z

z

f

1

(x,Q

1

)

D

1

q

1

q

1

Q

1

Q

1

Q

2

Q

2

25

I

T
P

W

ZPT

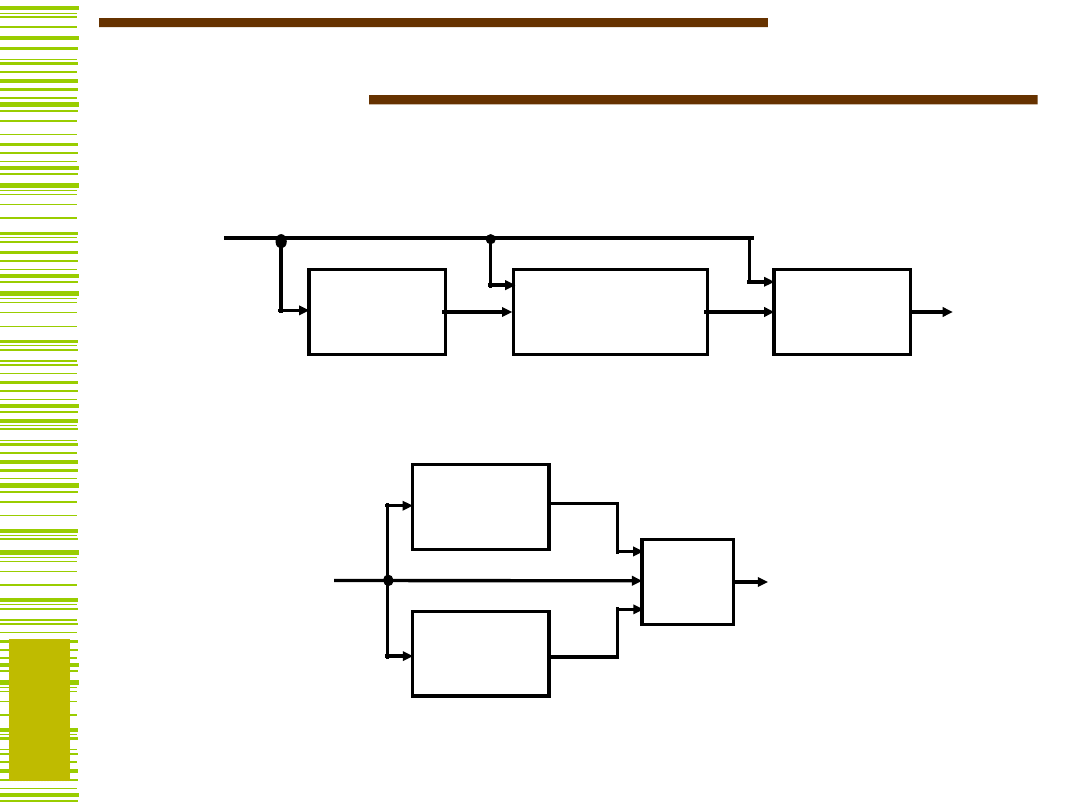
Schematy dekompozycji

M

1

()

M

2

()

WY

x

x

2

2

y

y

WY

x

x

M

2

(

2

)

y

y

M

1

(

1

)

Dekompozycja szeregowa

Dekompozycja szeregowa

Dekompozycja równoległa

Dekompozycja równoległa

26

I

T
P

W

ZPT

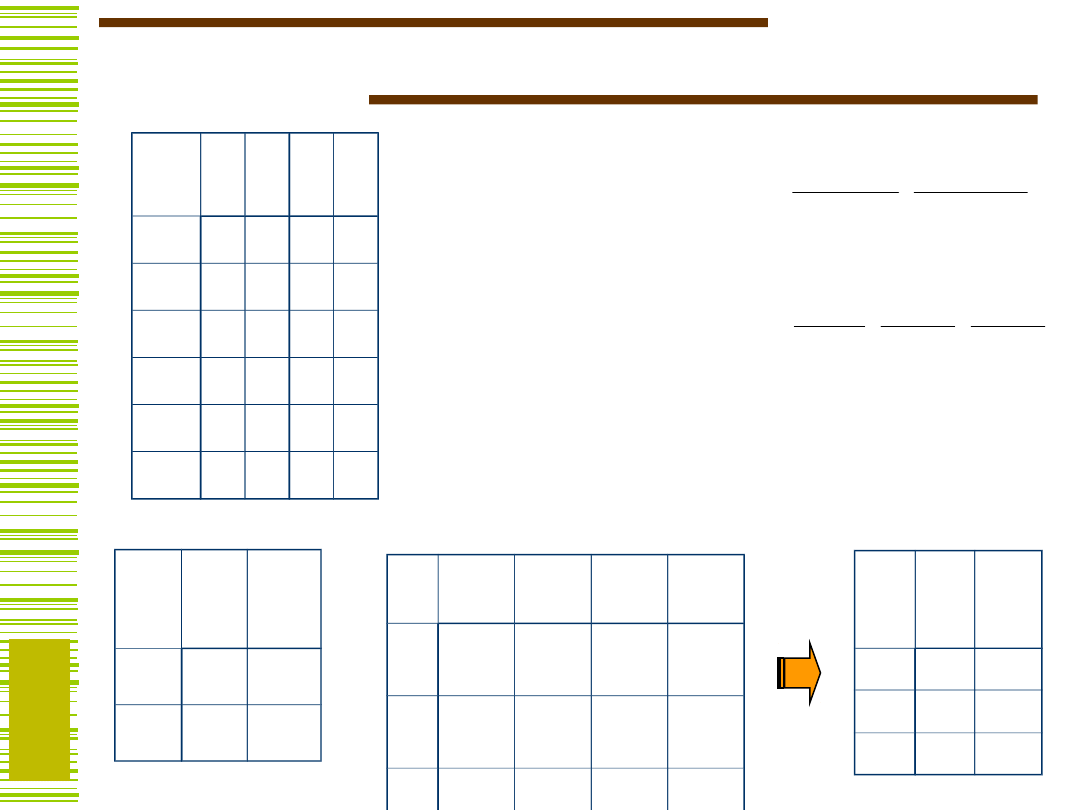
Dekompozycja szeregowa -

przykład

x

s

0 1 0 1

A

A F 0 0

B

E C 0 1

C

C E 0 1

D

F A 1 0

E

B F 1 1

F

D E 0 0

x

s

0

1

s

11

s

11

s

12

s

12

s

12

s

11

x

s

S

11

,

0

S

11

,

1

S

12

,

0

S

12

,

1

S

11

,0

S

11

,

1

S

12

,

0

S

12

,

1

s

2

1

s

21

s

23

s

23

s

21

0

0

1

0

s

2

2

s

23

s

22

s

22

s

23

0

1

0

1

s

2

3

s

22

s

23

s

21

s

23

1

1

0

0





F

D

C

E

B

A

,

,

;

,

,

1









 = (0)





 = (0)





F

E

C

B

D

A

τ

,

;

,

;

,



s

11

s

11

s

12

s

12

s

21

s

21

s

22

s

22

s

23

s

23

27

I

T
P

W

ZPT

Dekompozycja równoległa -

przykład

x

s

0

1

s

11

s

11

s

12

s

12

s

12

s

11

x

s

0

1

s

21

s

21

s

23

s

22

s

23

s

21

s

23

s

22

s

23

x

s

S

11

,

0

S

12

,

0

S

11

,

1

S

12

,

1

s

2

1

s

21

s

21

s

23

s

23

s

2

2

s

23

s

23

s

21

s

21

s

2

3

s

22

s

22

s

23

s

23



1





2

= (0)



1





2

= (0)





F

D

C

E

B

A

,

,

;

,

,

1





s

11

s

11

s

12

s

12





F

E

D

B

C

A

,

;

,

;

,

2





s

21

s

21

s

22

s

22

s

23

s

23

x

s

0 1 0 1

A

A F 0 0

B

E C 0 1

C

C E 0 1

D

F A 1 0

E

B F 1 1

F

D E 0 0

28

I

T
P

W

ZPT

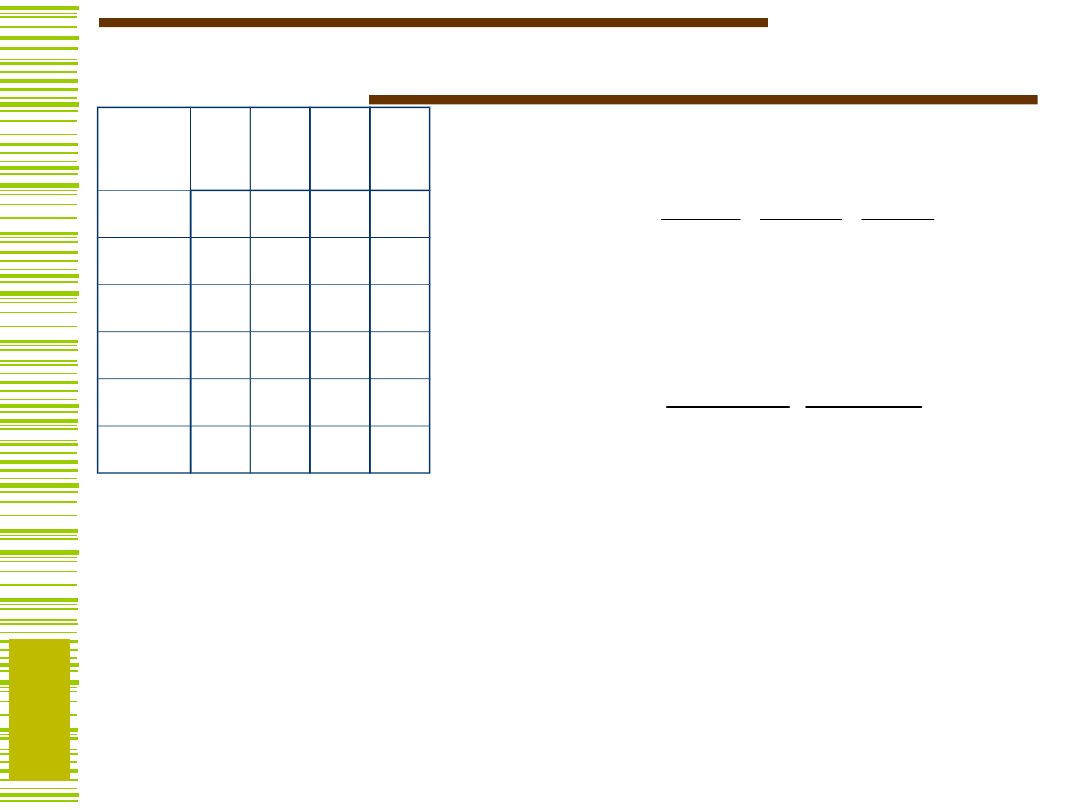
Dekompozycja z autonomicznym

zegarem

Niektóre automaty mają dekompozycję, w której

występuje autonomiczny zegar – podautomat niezależny
od wejść.

Podział 

i

zbioru stanów S automatu M jest zgodny z

wejściem, jeśli dla każdego stanu S

j

 S i dla wszystkich v

l

 V



(S

j

,v

1

),



(S

j

,v

2

), ...,



(S

j

,v

l

), ...,



(S

j

,v

p

),

są w jednym bloku podziału



i

.

Warunkiem koniecznym i dostatecznym istnienia

dekompozycji automatu M, w której występuje
autonomiczny zegar o log

2

(

)

 stanach jest, aby istniał

podział zamknięty

 i nietrywialny zgodny z wejściem

podział



i

zbioru stanów S tego automatu, taki że

 



i

Niektóre automaty mają dekompozycję, w której

występuje autonomiczny zegar – podautomat niezależny
od wejść.

Podział 

i

zbioru stanów S automatu M jest zgodny z

wejściem, jeśli dla każdego stanu S

j

 S i dla wszystkich v

l

 V



(S

j

,v

1

),



(S

j

,v

2

), ...,



(S

j

,v

l

), ...,



(S

j

,v

p

),

są w jednym bloku podziału



i

.

Warunkiem koniecznym i dostatecznym istnienia

dekompozycji automatu M, w której występuje
autonomiczny zegar o log

2

(

)

 stanach jest, aby istniał

podział zamknięty

 i nietrywialny zgodny z wejściem

podział



i

zbioru stanów S tego automatu, taki że

 



i

29

I

T
P

W

ZPT

PRZYKŁAD 3

x

s

0

1

0

1

A

D

C

0

1

B

C

D

0

0

C

E

F

0

1

D

F

E

0

0

E

B

A

0

1

F

A

B

0

0





F

D,

B,

;

E

C,

A,

O









F

E,

;

D

C,

;

B

A,





I

Podział zgodny z wejściem:

Podział zgodny z wejściem:

Π(0)

Π

Π

O

I







I

jest zamknięty



I

jest zamknięty

30

I

T
P

W

ZPT

PRZYKŁAD 3





F

E,

;

D

C,

;

B

A,

Π 

I





F

D,

B,

;

E

C,

A,

Π

O



0

0

0

0

0

1

0

1

1

0

1

0

0
1
0
1
0
1

Kodowanie wg 

I

Kodowanie wg 

I

wg 

O

wg 

O

A
B
C

D

E

F

Q

1

’ = f(Q

1

,Q

2

)

Q

1

’ = f(Q

1

,Q

2

)

Q

2

’ = f(Q

1

,Q

2

)

Q

2

’ = f(Q

1

,Q

2

)

Q

3

’ = ???

Q

3

’ = ???

y = f(x,Q

3

)

y = f(x,Q

3

)