Iloraz inteligencji ma w populacji rozkład 
normalny =100; =15. Znaleźć 

prawdopodobieństwo, że z populacji 
wylosujemy osobę z IQ:

a) nie większym niż 70

b) nie większym niż 120

c) większym niż 140

d) pomiędzy 70 i 130

Wejściówka

Wejściówka









x

z

Normalizacja

 

 

Iloraz inteligencji ma w populacji rozkład 
normalny =100; =15. Znaleźć 

prawdopodobieństwo, że z populacji 
wylosujemy osobę z IQ:

a) nie większym niż 60

b) nie większym niż 110

c) większym niż 130

d) pomiędzy 70 i 120

Wejściówka

Wejściówka









x

z

Normalizacja

 

 

Iloraz inteligencji ma w populacji rozkład 
normalny =110; =10. Znaleźć 

prawdopodobieństwo, że z populacji 
wylosujemy osobę z IQ:

a) nie większym niż 50

b) nie większym niż 120

c) większym niż 125

d) pomiędzy 60 i 110

Wejściówka

Wejściówka









x

z

Normalizacja

 

 

Populacja i próba

Populacja i próba

 

 

Próba

Próba

• Po co dobieramy próbę?

• Czym się różni próba od populacji

• Na czym polega reprezenatywność statystyczna?

 

 

Próba

Próba

 Czy wiarygodne są wyniki badań w których o odpowiedź poproszono
• Czytelników czasopisma X, którzy wypowiadali się odsyłając kartki 
z informacjami do czasopisma?

• Losowo wybranych z książki abonentów?

• Użytkowników portalu internetowego X

• Ankieta typu pop-up na kilkudziesięciu stronach internetowych?

 

 

Próba – po co dobieramy?

Próba – po co dobieramy?

 DOBÓR PRÓBY służy między innymi:
• Uzyskani reprezentatywności statystycznej bądź innego typu
• Kontroli obciążeń próby

Czyli innymi słowy: uzyskaniu wyników, które mają jakikolwiek 
sens

 

 

Definicje

Definicje

 POPULACJA
Określony teoretycznie zbiór elementów badania

POPULACJA BADANA
Zbiór elementów, z którego próba jest faktycznie pobierana

PRÓBA
Zbiór elementów, które zostają faktycznie poddane badaniu

OBCIĄŻENIE PRÓBY
Wybrane elementy nie są typowe dla szerszej populacji, z której 
zostały dobrane

 

 

Próba

Próba

REPREZENTATYWNA:
• Daje podstawy do 
uogólniania na  całą badaną 
populację
• Pozwala określić możliwy 
błąd 

przy uogólnianiu na  

populację

• Dobierana wg ściśle 
określonych 

zasad

• Zazwyczaj dość liczna

NIEREPREZENTATYWNA:
• Nie daje podstaw do 
statystycznych wnioskowań o
populacji
• Pozwala sformułować
przypuszczenia nt tendencji
• Zasady doboru nie są bardzo 
rygorystyczne
• Próba nie musi być bardzo 
liczna

 

 

Próba – sposoby doboru

Próba – sposoby doboru

REPREZENTATYWNA:

1. PROSTY DOBÓR LOSOWY

2. DOBÓR SYSTEMATYCZNY

3. DOBÓR WARSTWOWY

4. DOBÓR KWOTOWY

NIEREPREZENTATYWNA:

1. Próba okolicznościowa

2. Dobór celowy Metoda kuli 

śnieżnej

3. Dobór kwotowy 

4. Dobór informatorów

 

 

1. do każdego doboru losowego musimy mieć: OPERAT 
LOSOWANIA
Lista lub quasi-lista elementów, z których losuje się próbę

2. do doboru warstwowego i kwotowego: widza na temat rozkładu 
zmiennych, które mają stanowić podstawę warstw

Próba – co musimy wiedzieć

Próba – co musimy wiedzieć

 

 

• Posiadamy operat losowania z ponumerowanymi elementami

• Na podstawie tabel liczb losowych wybieramy kolejne elementy

• Tak długo, aż uzyskamy pożądaną liczebność

Dobór losowy

Dobór losowy

 

 

• Uproszczona forma doboru losowego

• Wybieramy co któryś element

• Interwał losowania uzyskujemy dzieląc wielkość populacji przez 

wielkość 

próby

• Element początkowy możemy wybrać na podstawie tabel liczb 

losowych

Dobór systematyczny

Dobór systematyczny

Np. Exit Poll

 

 

•Stanowi uzupełnienie a nie alternatywę dla poprzednich

•Próba dzielona jest na podstawie wybranych zmiennych na warstwy

•Proporcje poszczególnych warstw są takie jak w populacji.

•Zmienne warstwujące – takie, o których przypuszczamy, że mają 

wpływ na badaną zmienną

•Następnie w warstwach dobór ma charakter losowy

Dobór warstwowy

Dobór warstwowy

Np. badania preferencji

 

 

• Odmiana doboru warstwowego
• Różnica:
• po wyznaczeniu warstw nie prowadzimy losowania, tylko kierujemy 
się zasadą dostępności
•Mniej reprezentatywna niż poprzednia

Dobór kwotowy

Dobór kwotowy

Np. badania preferencji

 

 

•  Głównym celem doboru próby jest otrzymanie reprezenatywnej, 

ale

1. Nie można o próbie orzec, że jest albo nie jest reprezentatywna, 

bez wskazania wymagań, jakie powinna spełniać i bez 
uzasadnienia, że są one spełnione

UNO: próba może być reprezentatywna dla populacji ze względu na 

jedną lub kilka zmiennych, a nie być reprezentatywna ze względu 
na inne zmienne.

DUO: reprezentatywność jest też kwestią stopnia – wyniki w 

mniejszym bądź większym stopniu mogą odpowiadać wartościom 
parametrów w populacji. Jest to więc problem estymacji.

Na czym polega 

Na czym polega 

reprezentatywność

reprezentatywność

W próbach losowych nie da się prawie nigdy 

określić bezwzględnej dokładności 

oszacowania. Możemy jedynie – w przypadku 

losowego doboru próby- obliczyć 

prawdopodobieństwo dokonania oszacowania 

o określonej dokładności

 

 

Wielkość próby i 

Wielkość próby i 

reprezentatywność

reprezentatywność

Wielkość 

populacji

Wielkość próby

% populacji

10

10

100%

30

28

93%

60

52

87%

80

66

83%

110

86

78%

170

118

69%

210

136

65%

320

175

55%

550

228

41%

1100

285

26%

1700

313

18%

2400

331

14%

4000

351

9%

8000

367

5%

20 000

377

2%

100 000

384

0,4%

Tabela określająca liczebność próby potrzebną do uzyskania reprezentatywnych
wyników przy założeniu 5-procentowego błędu próby i 95- procentowego poziomu
ufności.

 

 

{POPULACJA

}

Próba losowa

(wybór jednostki losowy)

Próba celowa (nielosowa)

Metody (procedury)

Uzasadnienie 

teoretyczne w 

rachunku 

prawdopodobieńst

wa pozwalającego 

określić ryzyko 

popełnienia 

BŁĘDU

Uzasadnienie w 

wiedzy o 

rzeczywistości, 

celach badania – 

ryzyko błędu jest 

niemierzalne!!!

 

 





3

2

1







,

,





X:        1      2      3

k

x

2

k

s

2

k

sˆ

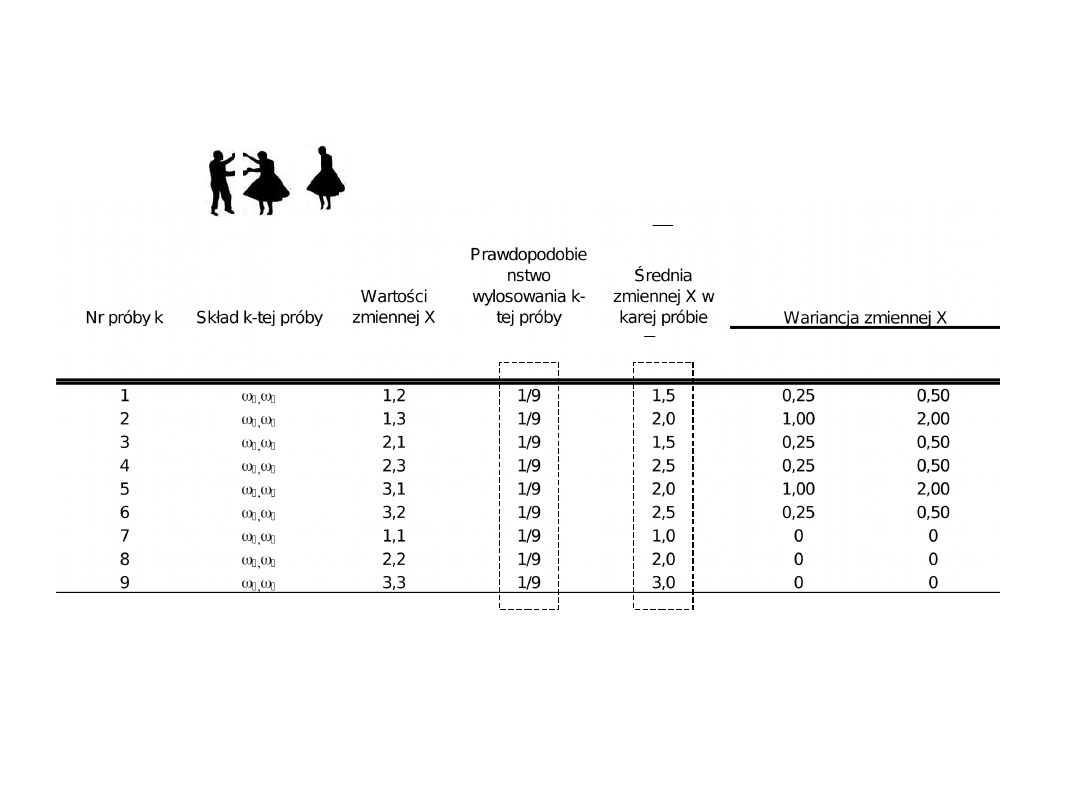
Losujemy z populacji  wszystkie 2-elementowe próby

3200000

20

5









N

k

X

Rozkład statystyki z 

próby (np.. średniej)

 

 

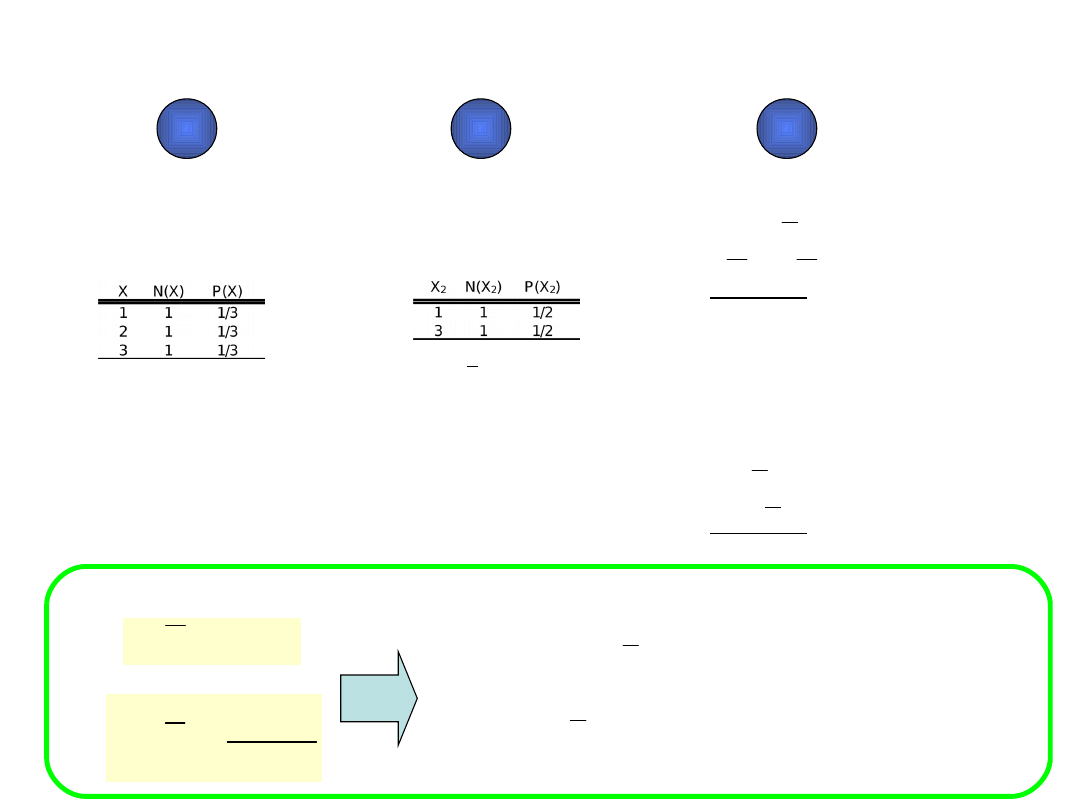
Trzy rozkłady i związki między 

Trzy rozkłady i związki między 

nimi

nimi

Rozkład statystyczny
zmiennej X w populacji

 

2



X

E

 

666

0

2

,

X

D



Rozkład zmiennej X w 
konkretnej próbie np. Nr 2

2

2



x

1

2

2



s

 

 

1,0

0,1

1

1,5

0,2

2

2,0

0,3

3

2,5

0,2

2

3,0

0,1

1

X

 

X

P

Rozkład 
prawdopodobieństwa
określonej statystyki z próby 
np. średniej       z próby

X

 

2



X

E

 

333

0

2

,

X

D



1

2

3

Między 1 a 3 zachodzą pewne związki

 

 

X

E

X

E



 

 

n

X

D

X

D

2

2



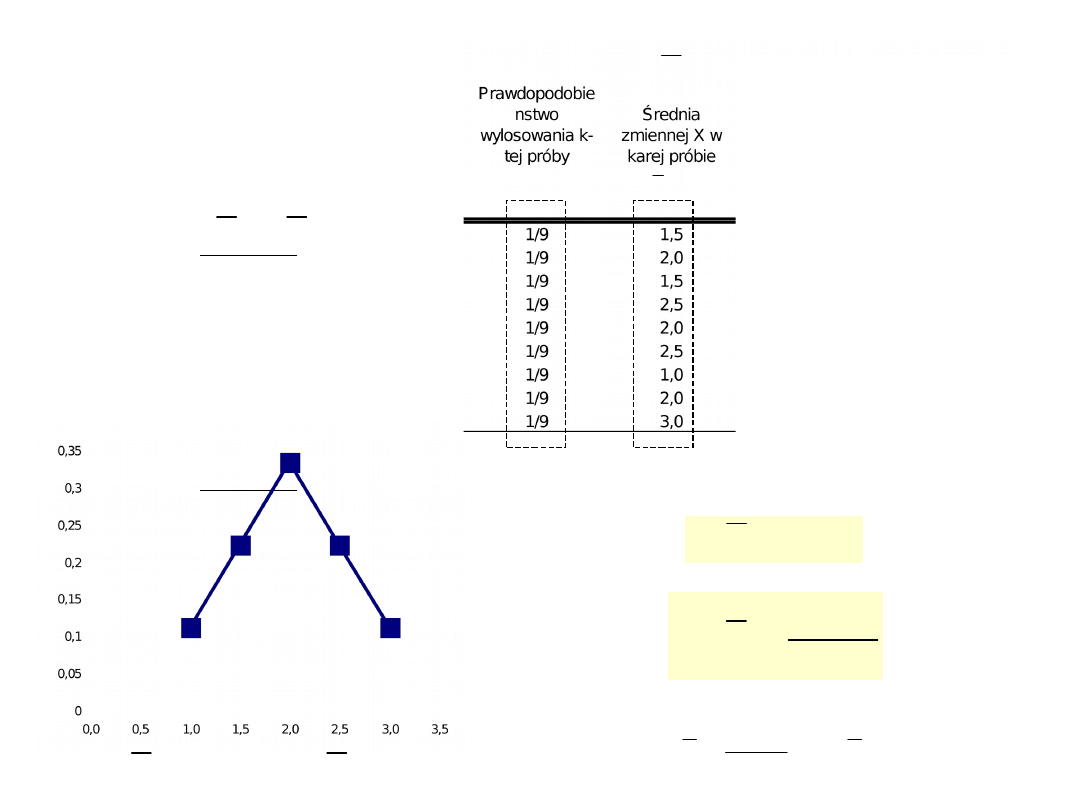
Zgodnie z tym, parametry rozkładu 
prawdopodobieństwa średniej z próby      : wartość 
oczekiwana i wariancja, zależą jedynie od parametrów 
rozkładu częstości zmiennej X w populacji, tj. od 
wartości średniej i wariancji tej zmiennej, a wariancja    
  zależy dodatkowo od liczebności prostej próby 
niezależnej

X

X

 

 

k

x

2

k

s

2

k

sˆ

 

2



X

E

X

Rozkład statystyki z 

próby (np.. średniej)

 

 

1,0

0,1

1

1,5

0,2

2

2,0

0,3

3

2,5

0,2

2

3,0

0,1

1

X

 

X

P

 

 

X

E

X

E



 

333

0

2

,

X

D



 

 

n

X

D

X

D

2

2



 

 

 

0

2

2

2











X

D

n

X

D

X

D

 

 

k

x

2

k

s

2

k

sˆ

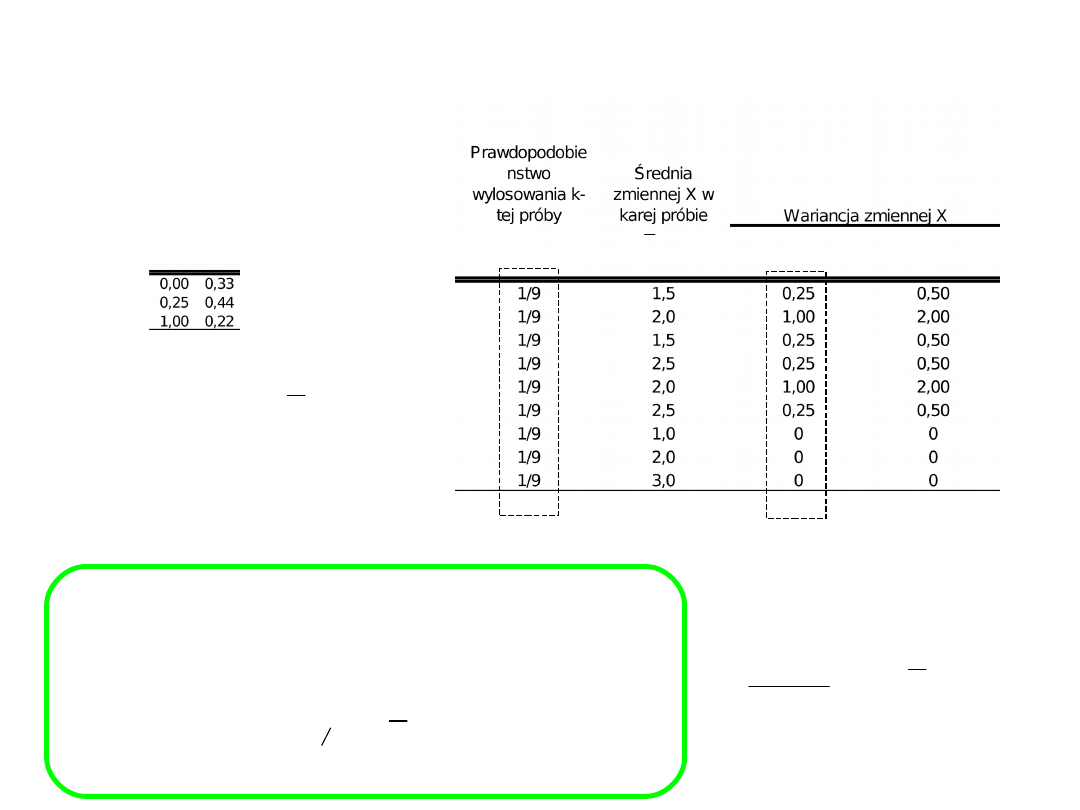
Rozkład statystyki z 

próby (np.. wariancji)

2

k

S

 

2

k

S

P

 

 

X

D

S

E

k

2

2



 

 

 

X

D

S

ˆ

E

S

nE

k

k

2

2

2





 

 

X

D

n

X

D

2

2



Jeśli próba jest dobrana za pomocą procedury doboru 
prostego losowego niezależnego, to wariancja 
zmiennej X z próby jest obciążonym estymatorem 
wariancji tej zmiennej w populacji.

 

 

X

D

S

E

k

2

2



 

 

 

 

X

E

X

E



 

 

X

nD

X

D

2

2



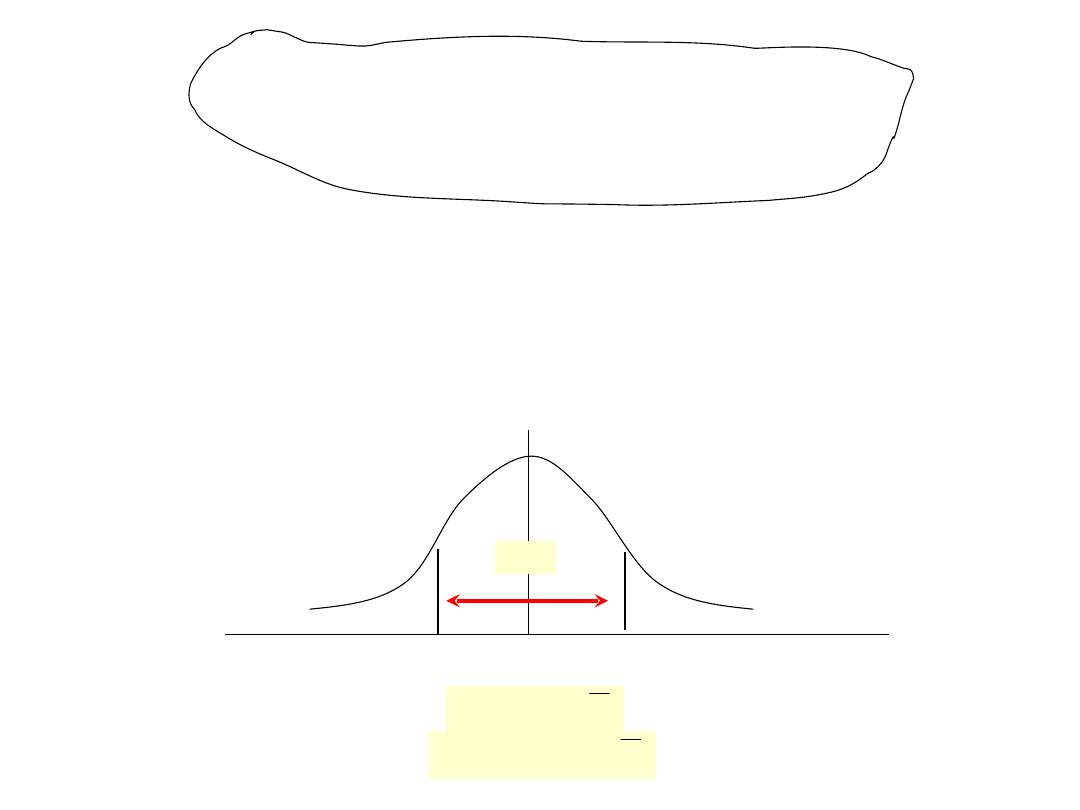
Średnia i wariancja w populacji są 

nieznane

! 

Nie są one zmiennymi, są to kontertne wartości

Losujemy próbę. W próbie otrzymujemy średną i wariancję. 

Ale jest to reliazacja zmiennej losowej.

Jak duży musi być przedział (a,b), aby z prawdopodobieństwem 

0,95 zawierał (pokrył) nieznaną średnią w populacji.

a

b

Błąd za duży

Błąd za duży

0,025

0,025

0,95

 

 

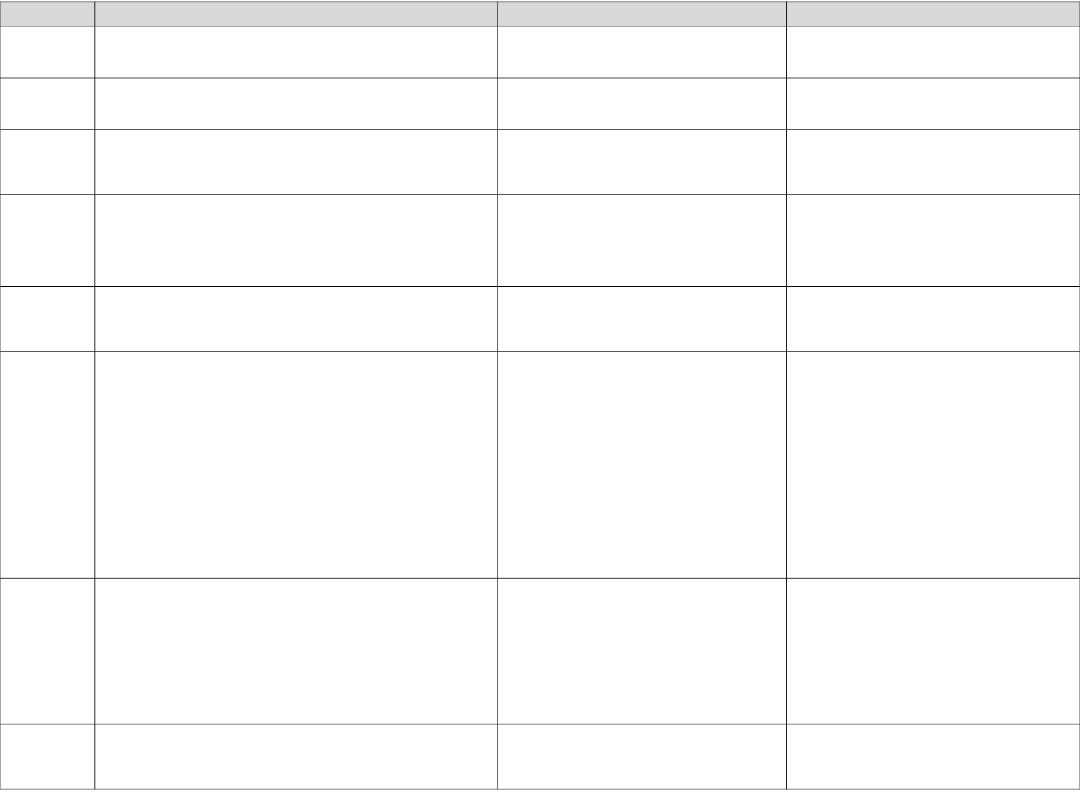
Próba 

Opis 

Plusy 

Minusy 

Próba 

prosta 

Każda jednostka populacja ma takie samo 

prawdopodobieństwo znalezienie się w próbie. 

Niskie koszty losowania, 

odpowiednia dla większości testów 

statystycznych. 

Inne schematy losowania próby 

mogą dawać lepsze rezultaty. 

Próba 

systema

tyczna 

Dobór z listy obejmującej wszystkie elementy 

danej zbiorowości co n-tej (np. co piędziesiątej) 

jednostki losowania. 

Tego typu próba jest lepsza od 

prostej próby losowej. 

Możliwość pokrycia się interwałów 

losowania z ukrytym 

uporządkowaniem danego operatu. 

Próba 

warstwo

wa 

Losowanie warstwowe polega na tym, że najpierw 

dzielimy zbiorowość statystyczną na jakościowo 

różniące się części, a następnie losujemy z każdej 

warstwy jednostki zbiorowości do próby. 

Próba jest bardziej 

reprezentatywna od prostej próby 

losowej pod względem większej 

liczby zmiennych. 

Wymaga więcej informacji o 

populacji. 

Próba 

zespoło

wa 

(grupow

a) 

Cechą charakterystyczną tego schematu jest to, 

że elementami losowania nie są poszczególne 

jednostki populacji, ale grupy. Podział danej 

zbiorowości na szereg grup i następnie 

wylosowanie pewnej ich liczby do badania, 

obejmuje na ogół wszystkie elementy danej grupy. 

Łatwość w losowaniu. 

Istnieje możliwość popełnienia 

sporych błędów przy szacowaniu 

parametrów populacji w przypadku 

niewłaściwego podziału na grupy. 

Próba 

random-

route 

Na podstawie podanego adresu ankieter znajduje 

inny, pod którym dobiera respondenta. Przy 

doborze adresów wykorzystuje się schemat 

losowania dwustopniowego. 

Próba jest tania. 

Możliwy negatywny wpływ 

ankietera na dobór kolejnego 

adresu według ustalonej ścieżki. 

Dwusto

pniowe 

losowan

ie próby 

Procedura postępowania jest następująca: Przy 

podejściu rygorystycznym stosowanie pewnych 

testów statystycznych wymaga wprowadzenia do 

nich korekt. 1.losujemy do próby pewną liczbę 

zespołowych jednostek losowania: nazwiemy to 

postępowanie losowaniem pierwszego stopnia, a 

losowanie JL jednostkami losowania pierwszego 

stopnia (JLPS). "2.wylosowane do próby JLPS 

dzielimy na mniejsze jednostki losowania zwane 

jednostkami losowania drugiego stopnia (JLDS); 

JLDS mogą być jednostkami zespołowymi bądź 

jednostkami badania". 3.przeprowadzamy 

losowanie drugiego stopnia. Wylosowane do próby 

JLDS tworzą ostateczną próbę: wchodzą do niej te 

jednostki badania, które należą do wylosowanych 

na drugim stopniu JLDS. 

Najbardziej precyzyjny schemat 

losowania. 

 

Próba 

kwotow

a 

Opiera się ona na znajomości struktury populacji 

generalnej wg przyjętych cech (tzw. zmiennych 

kontrolnych) i narzuceniu tej struktury na skład 

próby. Stosowane cechy - kryteria to: wiek, płeć, 

wielkość rodziny, dochód, rodzaj grupy społecznej 

lub działalności. Liczebność grup (segmentów) w 

próbie ustala się na podstawie przemnożenia 

rozkładu procentowego wybranych cech w 

populacji generalnej, przez ogólną liczebność 

próby. 

Daje możliwości kontrolowania 

większej liczby cech. Nie wymaga 

istnienia operatu. 

Wpływ ankietera na dobór 

respondenta. 

Próba 

losowo-

kwotow

a 

Na pierwszym stopniu doboru losuje się 

miejscowości miejskie i wiejskie (losowanie 

dwustopniowe). Drugi stopień doboru - jak w 

klasycznej próbie kwotowej. 

Daje możliwości kontrolowania 

większej liczby cech. 

Wpływ ankietera na dobór 

respondenta.