Przekazywanie ciepła

i elektrodynamika w

aparatach elektrycznych

dr inż. Mirosław Pawłot

Rok akademicki –

2014/2015

U-
6

Urządzenia elektryczne

Źródła ciepła w aparatach

elektrycznych

Źródłami ciepła w aparatach elektrycznych są przede wszystkim źródła

„prądowe”, tj.:

• Tory prądowe główne wiodące prądy robocze i w przypadku zakłóceń

prądy przeciążeniowe i zwarciowe

• Zestyki (połączeni) występujące w różnorodnych odmianach w torach

prądowych

• Osłony (okapturzenia) elektrycznie przewodzące – jedno- i

wielobiegunowe

• Elementy ferromagnetyczne (np. magnetowody elektromagnesów)

znajdujące się w zmiennym polu magnetycznym

Źródłami zewnętrznymi mogącymi mieć istotny wpływ na stopień

nagrzania aparatu elektrycznego lub urządzenia rozdzielczego mogą
być promieniowanie słoneczne lub sąsiadujące techniczne źródła ciepła
(np. piece, grzejniki itp..)

U-
6

Straty cieplne w

jednorodnych torach

prądowych

Straty cieplne w jednorodnych torach prądowych wyznacza się ze wzoru:

gdzie:
k- współczynnik naskórkowości informujący o podwyższeniu rezystancji

toru
prądowego w zależności od kształtu jego przekroju i częstotliwości
zmian prądu

ρ

20

- rezystywność materiału przewodu w temperaturze 20

o

C

l- długość przewodu
S- powierzchnia przekroju przewodu
α- temperaturowy współczynnik wzrostu rezystywności materiału

przewodu

U-
6









20

1

20

2













S

l

kI

P

Straty cieplne w

jednorodnych torach

prądowych

Wartości współczynnika naskórkowości k = R

~

/R

-

(f=50 Hz) dla

przewodów szynowych z Cu i Al., o przekroju prostokątnym b x h

U-
6

Wymia

ry b x h

b : h

Przewód

pojedynczy

Przewód

podwójny

Przewód

potrójny

mm

2

-----

Cu

Al

Cu

Al

Cu

Al

10 x 50

10 x 60

10 x 80

10 x

100

10 x

120

10 x

160

1:5

1:6

1:8

1:10

1:12

1:16

1,04

1,07

1,11

1,17

1,20

1,25

1,03

1,05

1,08

1,12

1,14

1,17

1,10

1,17

1,27

1,33

1,38

1,46

1,08

1,12

1,19

1,23

1,26

1,32

1,25

1,34

1,50

1,62

1,70

1,85

1,17

1,25

1,35

1,43

1,49

1,59

Uwaga: w przypadku przewodów wielokrotnych (wielopaskowych) odstęp

między nimi

w świetle jest równy grubości b pojedynczego przewodu

Straty cieplne w

jednorodnych torach

prądowych

Zestawienie wartości rezystywności ρ

20

i temperaturowego

współczynnika α wzrostu rezystywności dla wybranych przewodników

U-
6

Materiał

ρ

20

α

------

μΩ∙m

1/K

Cu

Al – miękkie

Al – twarde

Fe

0,0182

0,0278

0,0303

0,13

0,0038

0,0040

0,0040

0,0064

Straty cieplne w zestykach

Straty w zestykach zależą od wielu czynników:

• Materiału zestyków,
• Siły docisku,
• Grubości i struktury warstw nalotowych,
• Środowiska otaczającego,
• Obciążenia prądowego, itp..

U-
6

Straty cieplne w zestykach

Przykład:
Połączenia śrubowe szyn płaskich są tak skonstruowane i

wykonane, aby w stanie fabrycznie nowym rezystancja
połączenia była równa rezystancji odcinka szyny o długości
połączenia (zestyku). W trakcie eksploatacji rezystancja ta
z reguły rośnie – za dopuszczalną wartość graniczną dla
szyn aluminiowych przyjmuje się krotność równą 3,5, co
może stanowić podstawę do szacowania strat cieplnych dla
zestyków tego rodzaju.

U-
6

Straty wydzielane w

ekranach (osłonach) torów

prądowych

Straty cieplne w osłonach torów prądowych są kłopotliwe do wyznaczenia

ze względu na złożoność procesów elektrodynamicznych.

Najbardziej popularnym okapturzeniem jest okapturzenie cylindryczne

przewodów rurowych w układzie jednobiegunowym płaskim .

U-
6

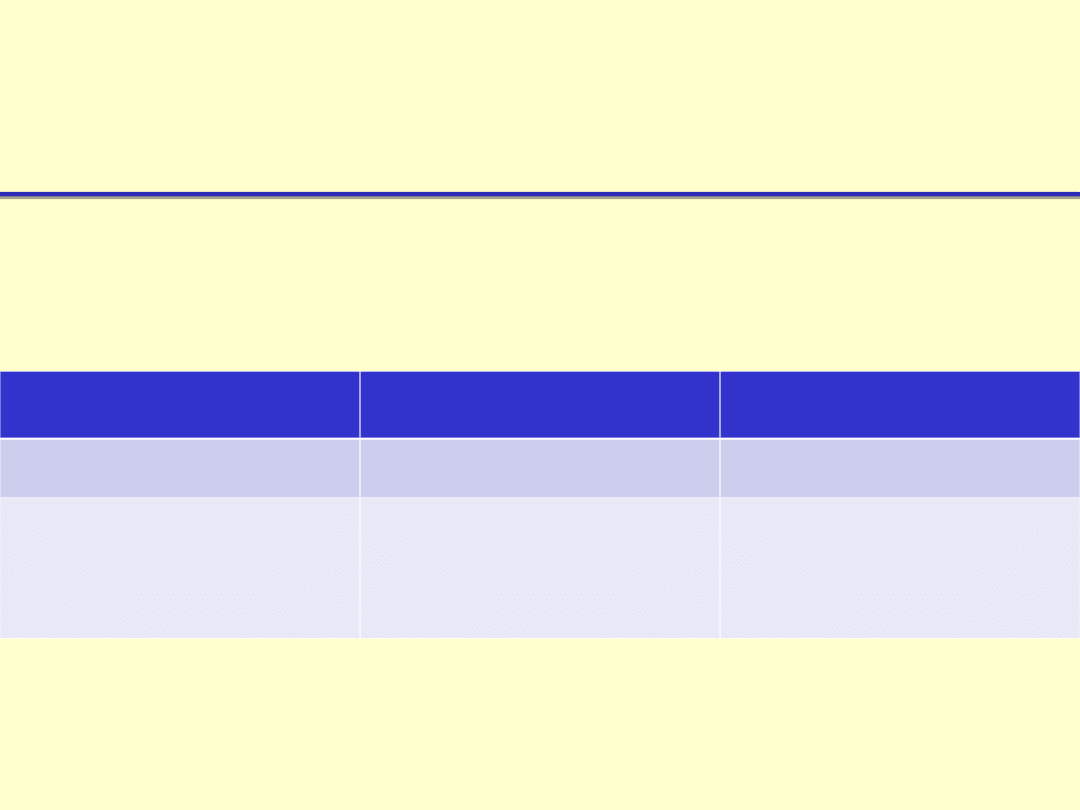
Szkic przewodu rurowego w
ekranie

Straty wydzielane w

ekranach (osłonach) torów

prądowych

Straty wydzielane w ekranie cylindrycznym wynoszą:

Gdzie:

- współczynnik korygujący wartości współczynnika

mocowego

okapturzenia K

a- odstęp między osiami przewodów fazowych w cm
K- współczynnik mocowy okapturzenia, stanowiący stosunek mocy

cieplnej rzeczywiście wydzielanej w okapturzeniu do wartości
występującej w przypadku, gdy prąd I

e

w okapturzeniu jest

równy prądowi I w osłanianym przewodzie

U-
6

 









20

1

'

20

2







e

e

e

e

e

e

e

S

l

I

k

mK

P





















'

,k

a

d

f

m

e

2















I

I

K

e

Straty wydzielane w

ekranach (osłonach) torów

prądowych

U-
6

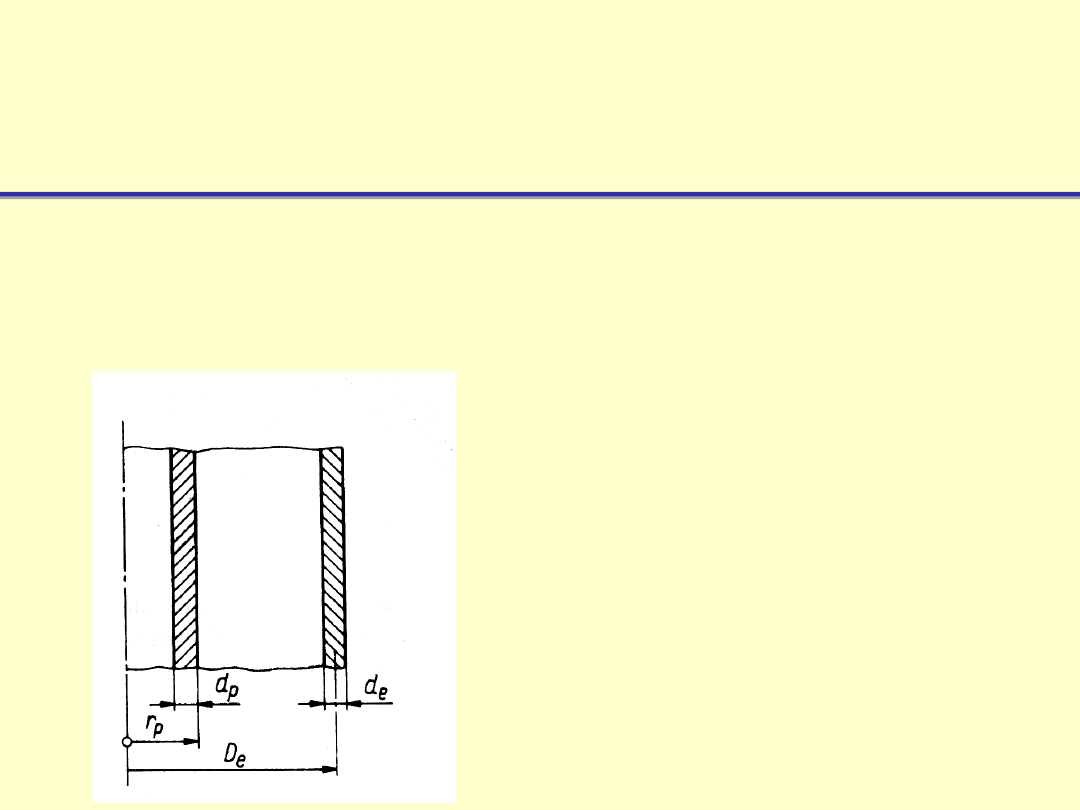
Współczynnik korekcyjny m dla
współczynnika mocy strat w
ekranie

Straty wydzielane w

ekranach (osłonach) torów

prądowych

k

e

- współczynnik naskórkowości dla ekranu (okapturzenia)

I

e

- prąd w ekranie w A

ρ’

20

- rezystywność materiału ekranu w temperaturze 20

o

C

l

e

= 1m- długość obliczeniowa ekranu

S

e

- powierzchnia przekroju ekranu w mm

2

- temperatura ekranu w

o

C

α

e

- temperaturowy współczynnik wzrostu rezystywności materiału

ekranu w 1/K

U-
6

e



Straty wydzielane w

ekranach (osłonach) torów

prądowych

Wielkość pomocniczą (tzw. współczynnik okapturzenia) k’

wyznacza się ze wzoru:

Gdzie:
D

e

- średnica ekranu w cm

d

e

- grubość ścianki ekranu w cm

f- częstotliwość prądu w 1/s
- rezystywność materiału ekranu w temperaturze w

U-
6

 

5

2

10

2

'







e

e

e

d

D

f

k







 

e





e



m

mm

2





Przekazywanie ciepła na

drodze przewodzenia

Wartość mocy cieplnej (strumienia cieplnego) przekazywanej

drogą przewodzenia P

p

w watach wyznaczona jest prawem

Fouriera:

Gdzie:
λ- przewodność cieplna ciała (środowiska) przewodzącego ciepło

w W/(mK)

S- powierzchnia dla przewodzenia ciepła w m

2

- gradient temperatury w K/m

U-
6

l

S

P

p

d

d









l

d

d



Przekazywanie ciepła na

drodze przewodzenia

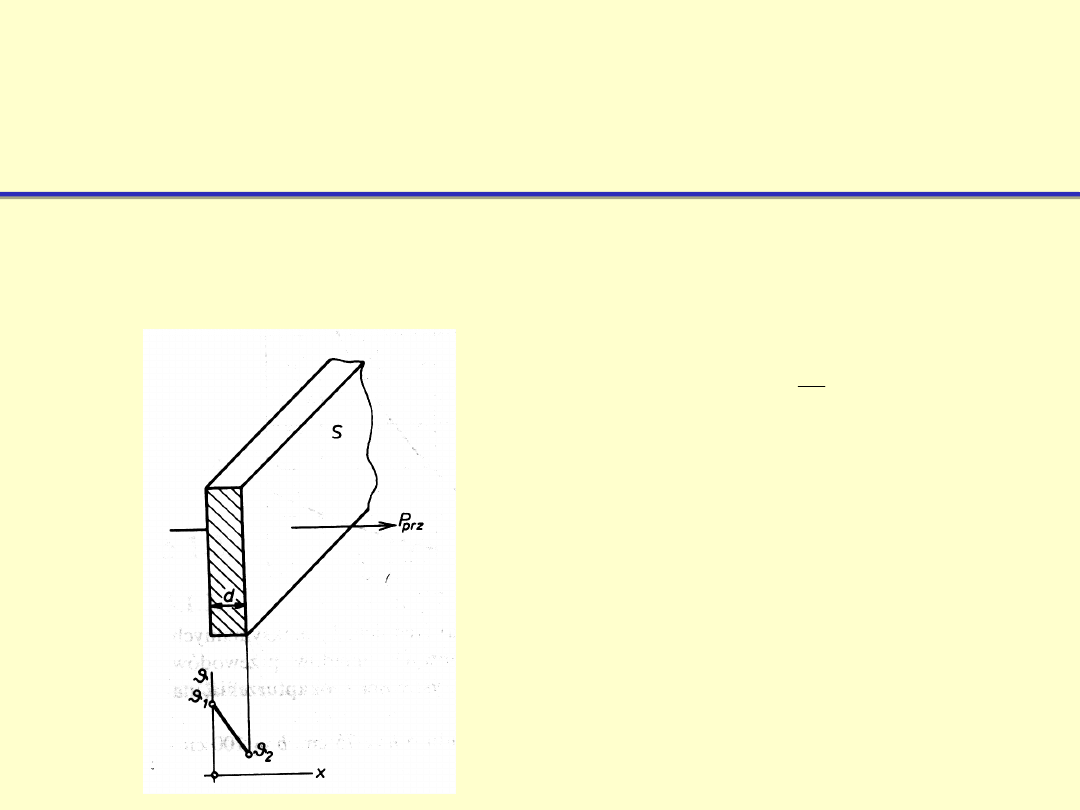
W warunkach ustalonych przewodzenia ciepła, np. przez ściankę płaską o

grubości d przy różnicy temperatur powierzchni ścianki

wzór określający

wartość mocy przekazywanej drogą przewodzenia przyjmuje postać:

U-
6





2

1











d

S

P

p

2

1







Przewodzenie ciepła
przez ściankę płaską w
stanie cieplnie ustalonym

Przekazywanie ciepła na

drodze przewodzenia

Wprowadzając pojęcie oporu cieplnego dla przewodzenia ciepła

(do wcześniejszej zależności):

można zapisać (w analogii do prawa Ohma):

odpowiednio z analogiami: napięcie – różnica temperatur, prąd –

strumień cieplny, rezystancja – opór cieplny

U-
6

p

p

R

P















2

1

S

d

R

p





Przekazywanie ciepła na

drodze przewodzenia

Zestawienie wartości współczynnika przewodności cieplnej λ (dla

wybranych materiałów stałych)

MATERIAŁ

λ [W/mK]

Miedź

Aluminium

Srebro

Mosiądz

Stal

Żeliwo

Cynk

Cyna

Płyta

azbestowa

Szkło okienne

Guma

PCW

Powietrze

395

229

165

81-116

59

58

113

64

0,7

1,16

0,04-1,67

0,17-0,19

0,023

U-
6

Przekazywanie ciepła na

drodze promieniowania

Moc cieplna (strumień ciepła) przekazywana drogą

promieniowania P

r

w watach jest wyznaczana z równania

Stefana-Boltzmana:

w którym ε jest wypadkowym współczynnikiem czerni (absorbcji)

ciała dla ciała doskonale czarnego ε=1, dla „białego” (lustro,
polerowany metal) ε≈0, dla ciał o powierzchniach szarych i
barwnych wartości pośrednie.

Gdy ciało (2) przejmujące promieniowanie cieplne otacza źródło

ciepła (1), wówczas:

U-
6



























 













 



4

2

4

1

0

100

100

p

r

S

c

P























1

1

1

1

2

2

1

1

12









p

p

S

S

Przekazywanie ciepła na

drodze promieniowania

c

0

=5,77 W/m

2

K

4

– emisyjność ciała doskonale czarnego

S

p

,S

p1

– powierzchnia ciała promieniującego ciepło

S

p2

– powierzchnia ciała odbierającego ciepło wypromieniowane z

powierzchni S

p1

ciała (1)

Θ

1

– temperatura bezwzględna powierzchni ciała

promieniującego ciepło

Θ

2

– temperatura bezwzględna powierzchni ciała przejmującego

ciepło
(np. obudowa rozdzielnicy)

U-
6

Przekazywanie ciepła na

drodze promieniowania

Zestawienie wartości współczynnika czerni

U-
6

Materiał powierzchni promieniującej ciepło

ε

Aluminium bez warstwy tlenkowej

Aluminium, przewody szynowe utlenione, we wnętrzu

Miedź, polerowana

Miedź

Miedź, przewody szynowe utlenione, we wnętrzu

Miedź utleniona na czarno

Mosiądz, polerowany

Mosiądz, walcowany

Stal, piaskowana

Żelazo, cynkowane

Szkło, gładkie

Materiały elektroizolacyjne (PCW, żywica itp..)

Farby, lakiery

0,07

0,25

0,04

0,09

0,25

0,78

0,05

0,07

0,67

0,25

0,93

0.95

0,9

Przekazywanie ciepła na

drodze promieniowania

Poprzez wprowadzenie współczynnika oddawania ciepła drogą

promieniowania α

r

:

można równanie Stefana-Boltzmana zapisać w postaci:

gdzie:

U-
6

2

1

4

2

4

1

0

100

100





































 













 



c

r





2

1











r

r

r

S

P

273

1

1









273

2

2









Przekazywanie ciepła na

drodze promieniowania

Analogicznie jak w przypadku przewodzenia ciepła, opór cieplny

promieniowania:

wprowadzony do równania Stefana-Boltzmana przedstawia je w

postaci analogicznej do prawa Ohma dla elementu obwodu
elektrycznego:

U-
6

r

r

r

S

R



1



r

r

R

P





2

1





Przekazywanie ciepła na

drodze konwekcji

Przekazywanie ciepła drogą unoszenia (w gazach i cieczach)

ujmowane jest liczbowo prawem Newtona dla przekazywanej w
ten sposób mocy cieplnej

(strumienia cieplnego) P

k

w watach:

gdzie:
α

k

- współczynnik oddawania ciepła w drodze konwekcji w W/(m

2

K)

S

k

- powierzchnia ciała oddającego ciepło w drodze konwekcji w m

2

- temperatura ciała
- temperatura otoczenia , w strefie poza warstwą graniczną

U-
6





2

1













k

k

k

S

P

1



2





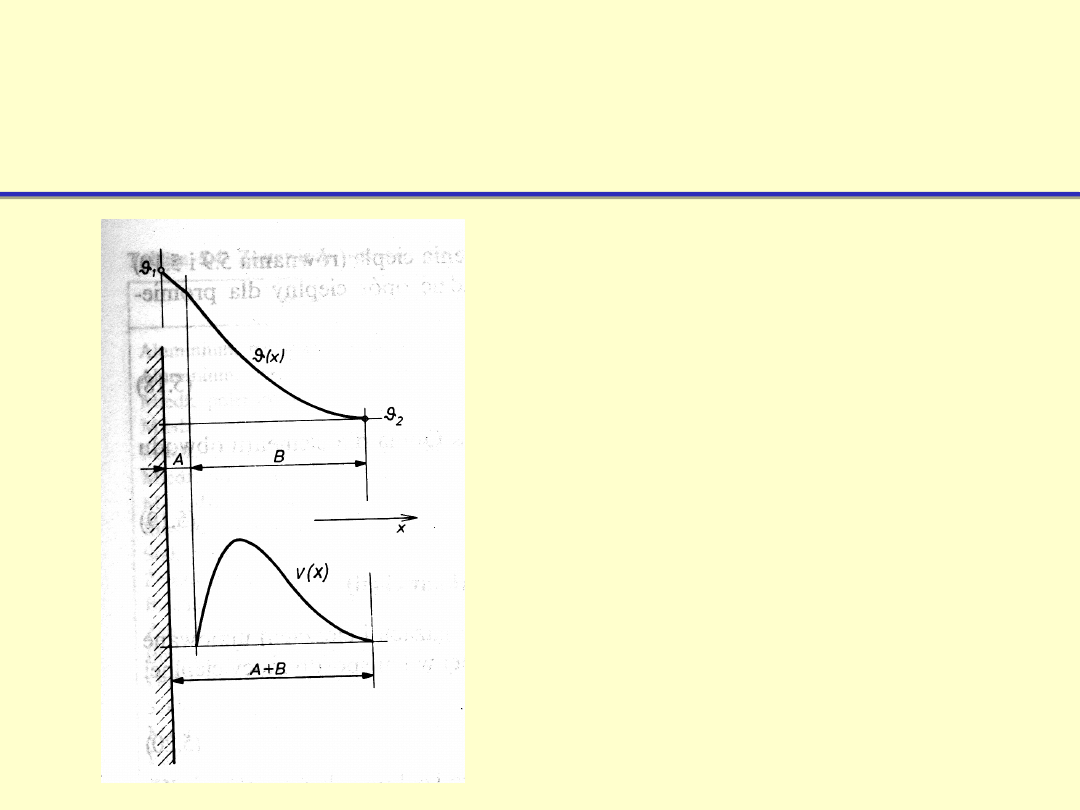
Przekazywanie ciepła na

drodze konwekcji

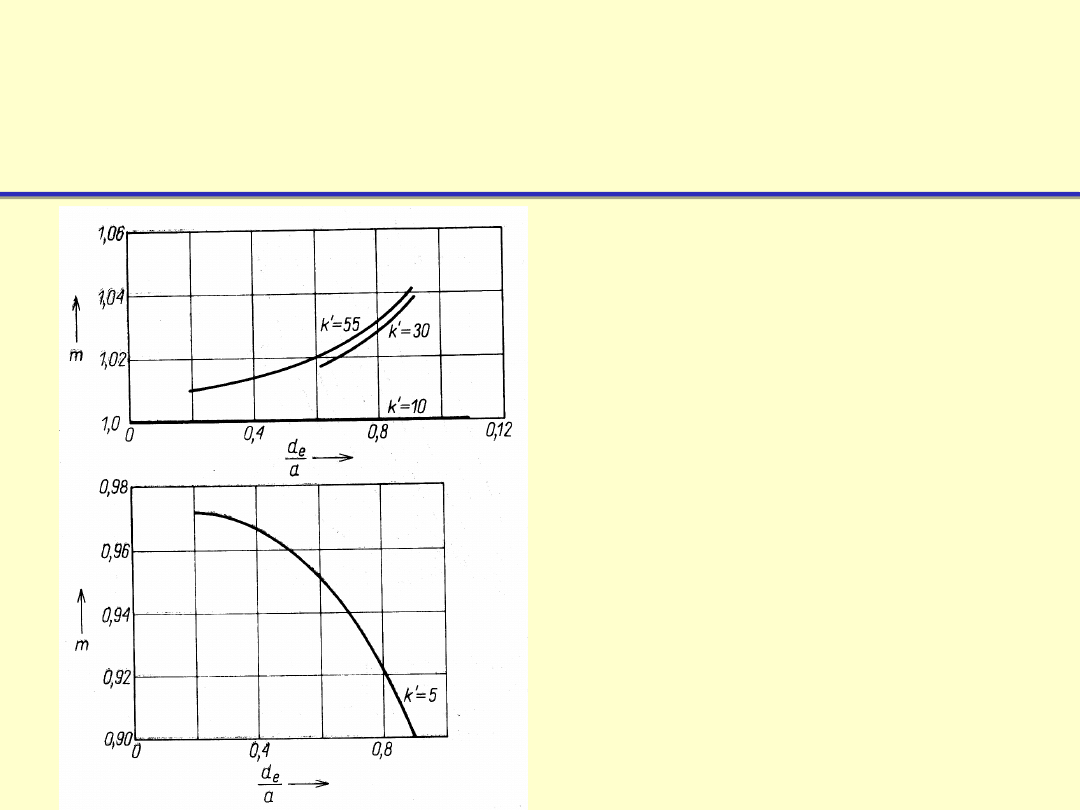
Rozkład temperatury i

prędkości υ płynu w pobliżu
pionowej ścianki nagrzanej: A –
obszar przewodzenia ciepła (na
rys. znacznie powiększony) ,
B – obszar konwekcji, A+B –
warstwa graniczna

U-
6



Przekazywanie ciepła na

drodze konwekcji

Analogicznie jak w przypadkach przewodzenia i promieniowania

ciepła można do równania wynikającego z prawa Newtona
wprowadzić opór cieplny:

i przedstawić je w postaci analogicznej do prawa Ohma dla

obwodów elektrycznych

U-
6

k

k

k

S

R



1



k

k

R

P







2

1





Przekazywanie ciepła na

drodze konwekcji

W zagadnieniach termokinetyki aparatów elektrycznych i

urządzeń rozdzielczych największe trudności sprawia poprawne
wyznaczenie wartości współczynnika konwekcji α

k

.

Współczynnik ten jest w sposób złożony uzależniony od:
• Temperatury i wymiarów powierzchni ciała oddającego ciepło
• Własności fizycznych płynu (cieczy, gazu) unoszącego ciepło

(przewodności cieplnej, gęstości, ciepła właściwego, lepkości
kinematycznej)

• Charakteru przepływu płynu unoszącego ciepło – uspokojonego

(laminarnego) lub zaburzonego (turbulentnego)

U-
6