WYTRZYMAŁOŚĆ

MATERIAŁÓW

Prowadzący

prof. dr hab. inż. Kazimierz WÓJS

Wykład 11

Opracował

dr inż. Andrzej

Sitka

ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

PRAWO HOOKE’A - WYKRESY

PRAWO HOOKE’A - WYKRESY

ROZCIĄGANIA

ROZCIĄGANIA

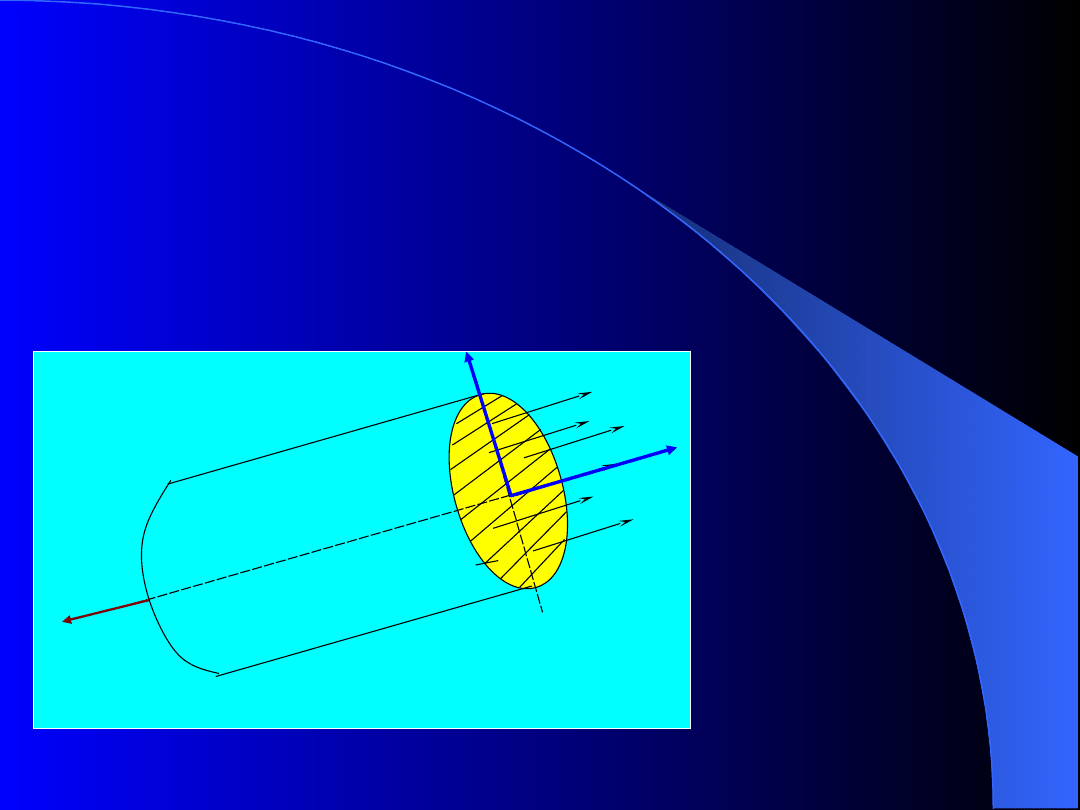
ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

Rozciąganie proste wystąpi wtedy, gdy w wyniku

redukcji sił wewnętrznych względem środka przekroju
poprzecznego ciała otrzymamy wyłącznie wektor główny,
normalny do tego przekroju (o zwrocie skierowanym od
przekroju), który jest statycznie równoważny naprężeniu
 równomiernie rozmieszczonemu na powierzchni

przekroju poprzecznego.

Równowaga pręta

rozciąganego

A



N

N – siła osiowa,

A –pole przekroju
pręta



–

naprężenie

normalne

x

y

ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

Warunek równowagi

- suma rzutów wszystkich sił na

kierunek osi pręta

0

)

(











A

ix

N

dA

P



(1)





)

(A

dA

N



(2)

Oznacza to, że wektor główny jest równy sile
obciążającej oraz brak innych niż  naprężeń na

powierzchni przekroju A.

Gdy naprężenie
jednakowe w całym
przekroju, to :

A

N





ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

Równowaga pręta ściskanego

Równowaga pręta

ściskanego

N – siła osiowa,

A –pole przekroju
pręta,



–

naprężenie

ściskające

A



N

ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

const

A

N

dA

dN









Warunki występowania

rozciągania prostego:

1.

Zachowanie zasady de Sainta Venanta

2.

Pręt musi być pryzmatyczny (wykonany z
materiału jednorodnego)

 

Wówczas naprężenie jest jednakowe w całym

przekroju pręta

(3)

ROZCIĄGANIE PROSTE

ROZCIĄGANIE PROSTE

(5)

Wytężenie materiału

– stopień zbliżenia

obciążenia materiału do stanu krytycznego.

Warunek

wytrzymałości

pręta:

dop

A

N









(4)

Naprężenie dopuszczalne 

dop

wynosi:

n

nieb

dop







n – współczynnik bezpieczeństwa (n  1),


nieb

– naprężenie niebezpieczne

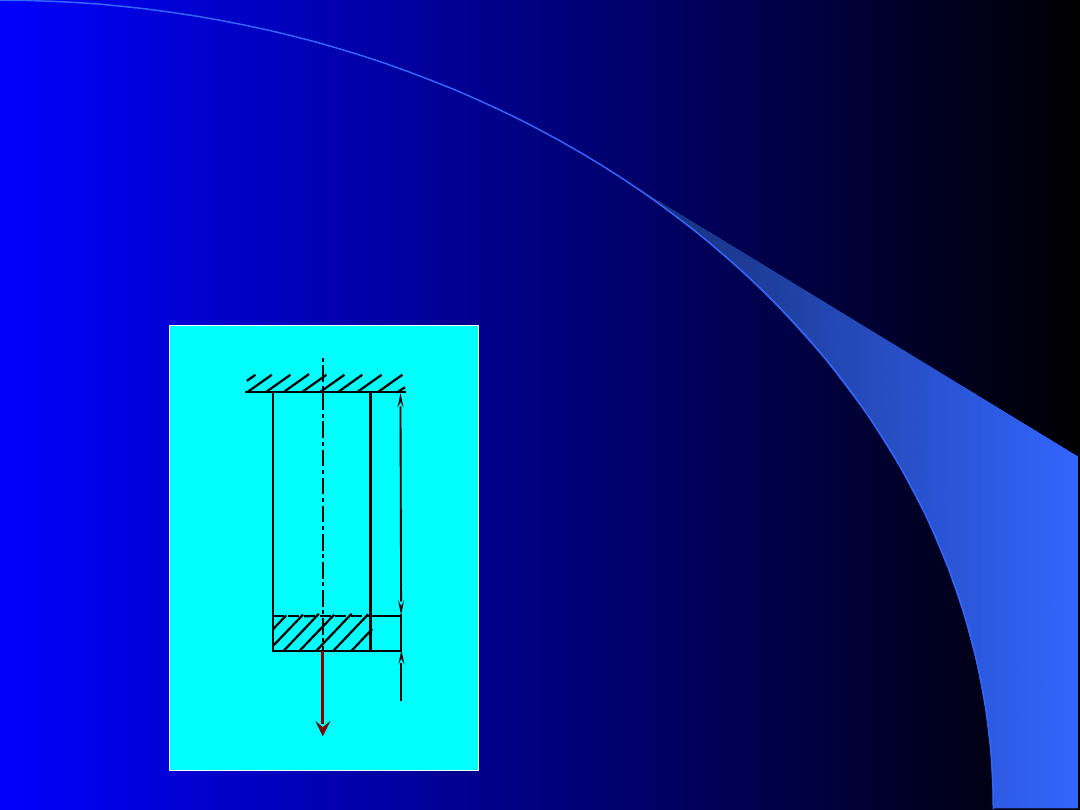
PRAWO HOOCKE’A

PRAWO HOOCKE’A

Robert Hooke (1676) obserwując rozciąganie prętów
pryzmatycznych wykonanych z różnych materiałów
stwierdził, że wydłużenie l pręta pryzmatycznego jest

wprost proporcjonalne do siły rozciągającej P i do
długości

początkowej

l

pręta

a

odwrotnie

proporcjonalne do pola przekroju poprzecznego pręta
A.

l



l

P

Wydłużenie pręta

rozciąganego

A

E

l

P

l 



l – wydłużenie pręta,
P –

siła rozciągająca,

l – długość pręta przed rozciąganiem,

A – pole przekroju pręta,

E – współczynnik proporcjonalności -

Moduł sprężystości (Younga), N/m

2

PRAWO HOOKE’A

(6)

PRAWO HOOKE’A

PRAWO HOOKE’A

W wielu przypadkach łatwiej operuje się
pojęciem

wydłużenia

, jakie doznaje jednostka

długości pręta, nazywanym wydłużeniem
względnym lub jednostkowym:

l

l







(7)

Niekiedy wydłużenie podaje się w
procentach:

%

100







l

l



(8)

przedstawimy prawo Hooke’a w
postaci:

PRAWO HOOKE’A

PRAWO HOOKE’A

Po podstawieniu do wzoru (6) :

i

A

P





E







(10)

Dla stali moduł Younga w temperaturze 20C wynosi

E=2,1 10

5

MPa.

l

l







W budowie maszyn prawo Hooke’a można
stosować zarówno w przypadku rozciągania jak i
ściskania.

Naprężenia rozciągające

oznaczamy znakiem

plus (+),

Naprężenia ściskające

natomiast znakiem

minus (-).

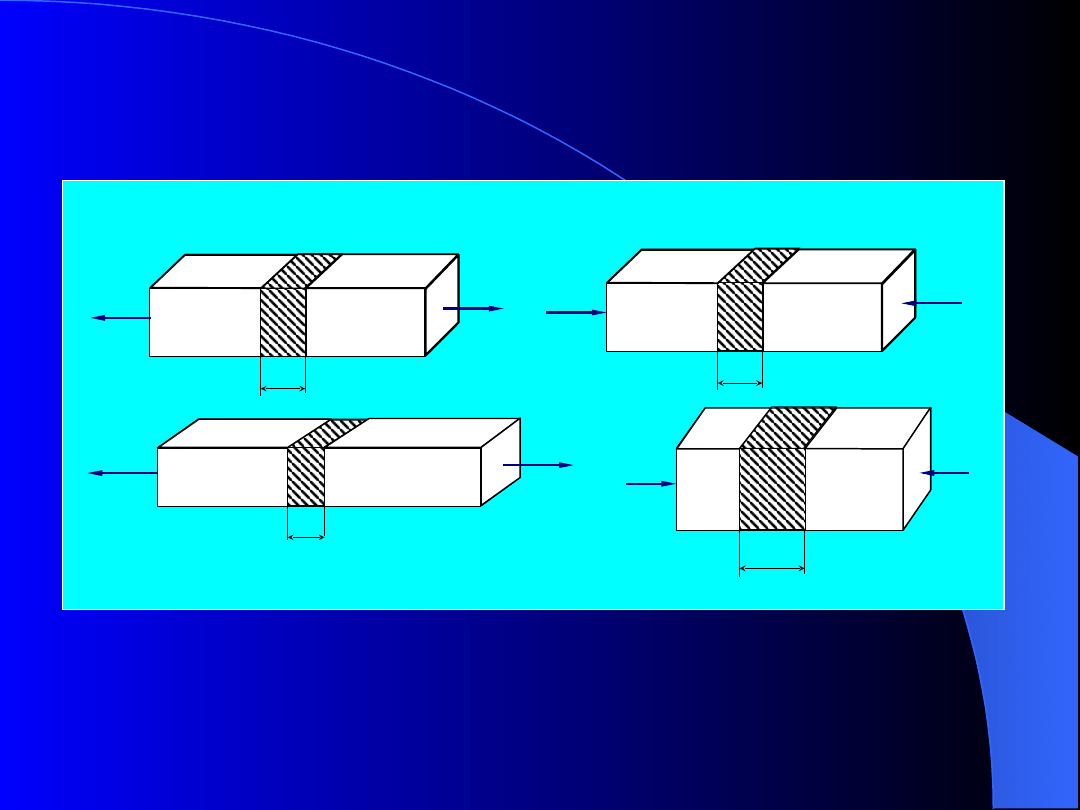
Oprócz odkształceń wzdłużnych (wydłużenie i
skrócenie) przy rozciąganiu występują jeszcze

odkształcenia poprzeczne

.

P

P

a

h

P

P

b

h

h

1

P

P

h

1

P

P

Rys.4. Zmiany wymiarów pręta przy: a) rozciąganiu,

b) ściskaniu

Przy rozciąganiu grubość pręta ulega zmniejszeniu z

wartości h do h

1

. Przy ściskaniu pręt „pęcznieje” i jego

grubość wzrasta z wartości h do h

1

(rys.4). Różnica

grubości końcowej i początkowej nazywa się

zwężeniem całkowitym

h = h

1

– h.

Stosunek

zwężenia

całkowitego

do

grubości

początkowej

nazywamy

zwężeniem jednostkowym 

1

h

h





1



(11)

ODKSZTAŁCENIE
POPRZECZNE

Przy rozciąganiu zwężenie ma wartość ujemną,

gdyż h > h

1

. Przy ściskaniu - wartość dodatnią (h

< h

1

) zwaną spęcznieniem.

Z tego wynika, że:

•

przy rozciąganiu  > 0,



1

< 0,

•

przy ściskaniu

 < 0,



1

> 0.

Bezwzględna wartość stosunku zwężenia

(spęcznienia)

jednostkowego



1

do

jednostkowego wydłużenia (skrócenia) 
nazywamy

współczynnikiem odkształcenia

poprzecznego

lub

liczbą Poissona 







1



(12)

Liczba Poissona przyjmuje wartości w granicach
0  0,5.

 

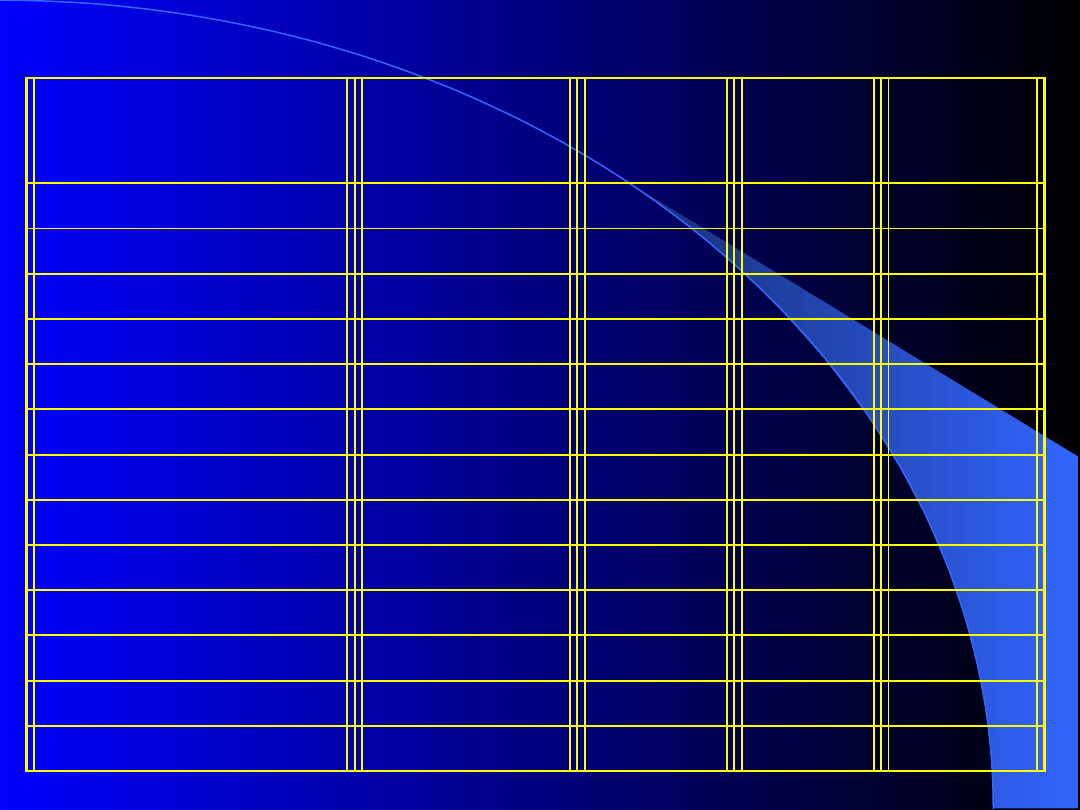
Rodzaj materiału

Moduł Younga

E

MPa

Liczba

Poissona



Wytrzyma

ł.

na

rozciągan

ie

R

m

MPa

Granica

plastycznoś

ci R

e

MPa

Stal (St3S)

2,1  10

5

0,3

380

220

Żeliwo (Zl300)

1,2  10

5

0,23-0,24

300

 

Miedź

1,0  10

5

0,32

210

70

Mosiądz

0,9  10

5

0,36

340

 

Brąz

1,1  10

5

0,33

300

 

Aluminium

0,72  10

5

0,34

100

 

Dural

0,72  10

5

0,33

130

50

Beton

1,4  10

5

0,17

 

 

Szkło

0,7  10

5

0,25

40

 

Drewno dębowe

0,1-0,2  10

5

 

110

 

Guma twarda

10

 

12

 

Polistyren

0,28  10

5

 

40

 

Polietylen

0,014  10

5

 

 

 

Tab.1. Wartości fizyczne i wytrzymałościowe dla wybranych
materiałów

WŁASNOŚCI MECHANICZNE CIAŁ

WŁASNOŚCI MECHANICZNE CIAŁ

STAŁYCH

STAŁYCH

Własności mechaniczne ciał stałych

–

zachowanie się tych ciał pod wpływem działania
obciążenia mechanicznego (pola sił). W zależności od
rodzaju materiału , ciała odznaczają się różnymi
cechami, takimi jak:

plastyczność

– całkowite nieodwracalne

odkształcenie wywołane obciążeniem,

wytrzymałość

– zdolność do przenoszenia

obciążeń aż do momentu uzyskania obciążenia
granicznego przy, którym następuje utrata sił
spójności (rozerwanie materiału).

sprężystość

– zdolność ciała do powrotu do

pierwotnych wymiarów i kształtu po usunięciu
obciążeń zewnętrznych,

Materiały konstrukcyjne

Materiały konstrukcyjne

W budowie maszyn i konstrukcjach największe
zastosowanie znajdują stale niskowęglowe (stopy
żelaza z węglem gdzie C < 0.3%). Stale takie są
trudno hartowalne i z tego powodu nazywane są
stalami miękkimi.

Wykres

rozciągania

uzyskuje

się

podczas

wykonywania

próby

wytrzymałościowej

(próba

rozciągania)

wykonywanej

na

specjalnie

przygotowanej próbce lub bezpośrednio na odcinku
pręta.

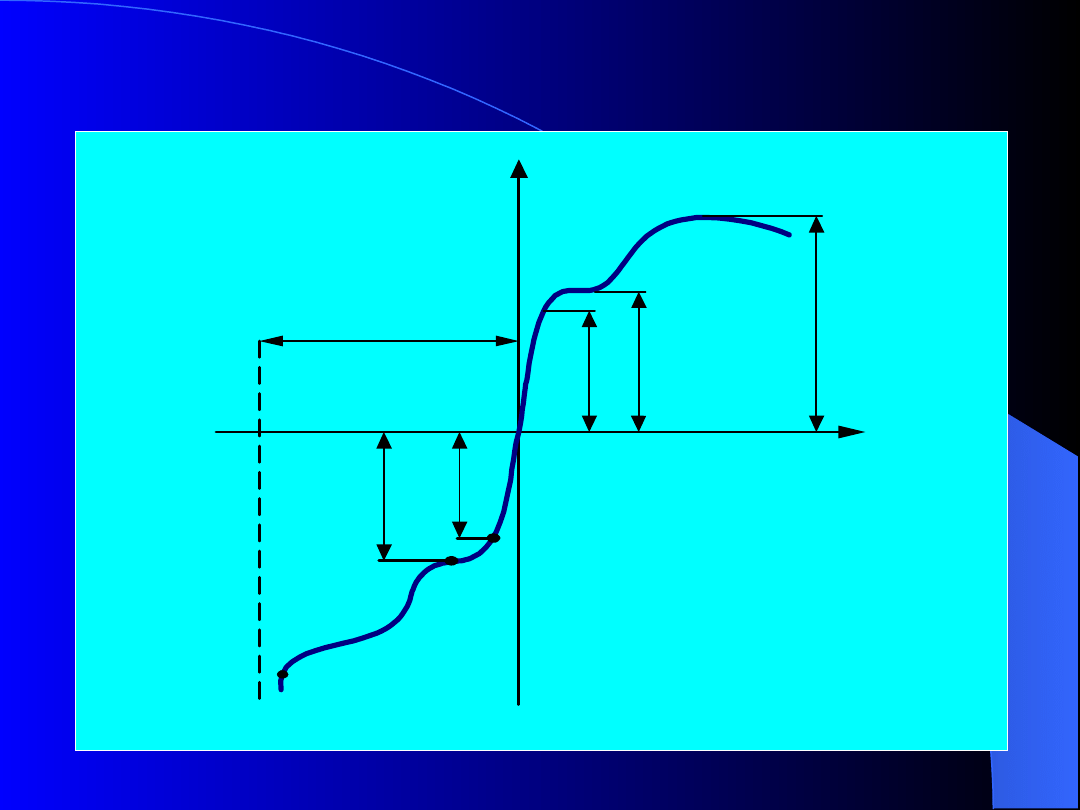
Wykres rozciągania materiału

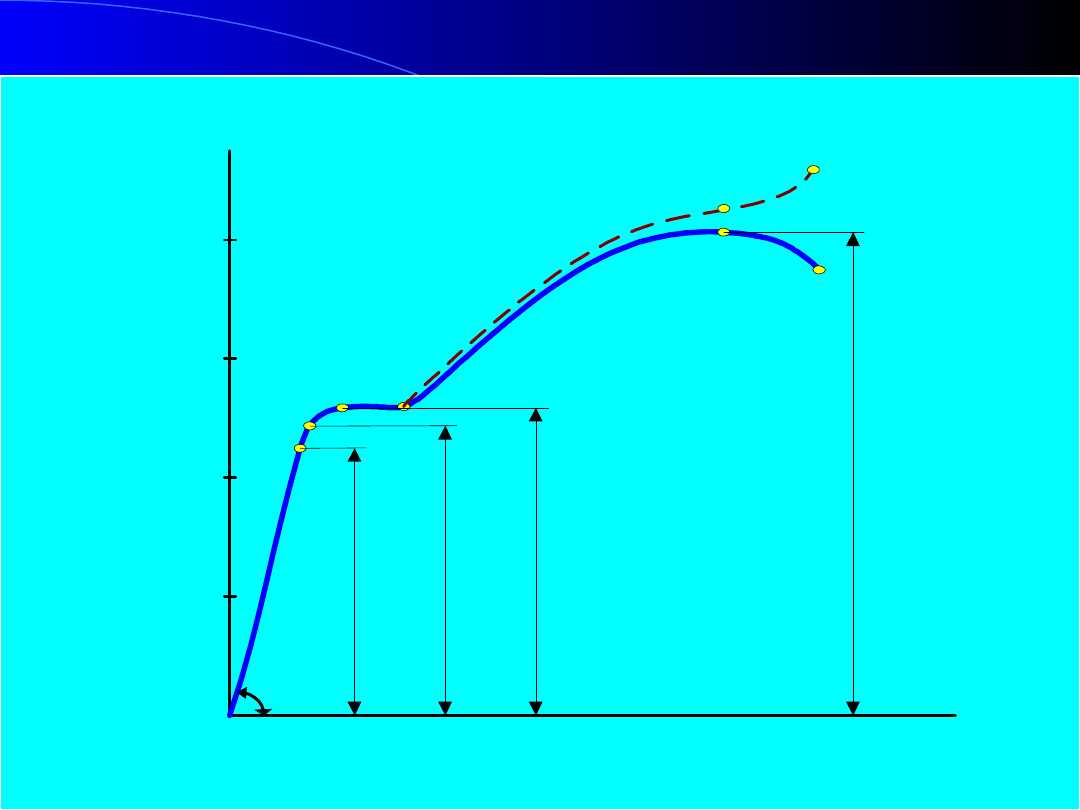
Wykres rozciągania stali

Wykres rozciągania stali

niskowęglowych

niskowęglowych

A

B

C

D



pr

op



sp

rę

ż



pl

as

t

(

R

e

)

R

m

L

K

L'

K'



MPa

100

200

300

400

0





tg = E

Poszczególne

punkty

na

wykresie

oznaczają:

A

–

granicę

proporcjonalności

(granica

stosowalności prawa Hooke’a),

B – granicę sprężystości

– w

praktyce przyjmuje się,

że leżące w pobliżu siebie punkty A i B mają jednakową

wartość:

sprę

prop







(13)

C,D – granicę plastyczności R

e

,

- wyraźnie

widoczna na wykresie rozciągania i łatwa do

wyznaczenia tylko dla niektórych materiałów , np.

stali niskowęglowych.

0

A

P

R

e

e



(14)

K – granica wytrzymałości na rozciąganie

R

m

(doraźna wytrzymałość materiału).

Wytrzymałością na rozciąganie R

m

jest to

iloraz maksymalnej siły rozciągającej P

max

uzyskanej w

procesie rozciągania próbki przez pole A

0

przekroju

początkowego próbki:

(15)

0

max

A

P

R

m



Po osiągnięciu naprężeń R

m

na próbce powstaje

lokalne przewężenie (tzw. szyjka) pokazane na rys.6.
W miejscu tym próbka ulega rozerwaniu – odcinek KL
z wykresu rozciągania .

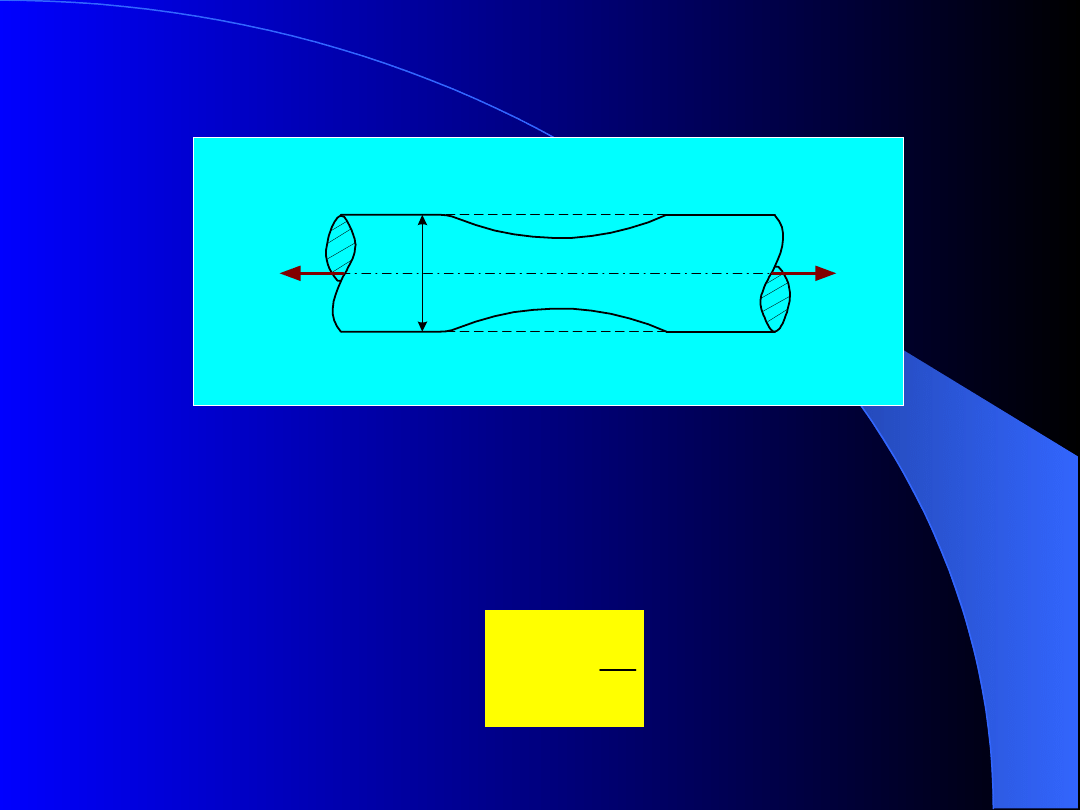
Na rzeczywistym wykresie rozciągania próbki linia

kreskowana powstaje przy naprężeniu wyznaczanym

z zależności:

(16)

d

0

P

P

A

P

rz





Tworzenie się szyjki wskutek

rozciągania próbki

Rys.
6

gdzie:


rz

– rzeczywiste naprężenie w próbce,

A – rzeczywista powierzchnia przekroju poprzecznego

części pomiarowej próbki. Określa się ją przyjmując

stałą objętość materiału:

Wykresy rozciągania stali

Wykresy rozciągania stali

niskowęglowych

niskowęglowych







1

0

A

A

(17)

Związek naprężenia rzeczywistego z umownym ma

postać:













 1

rz

(18)

Umowna granica plastyczności R

0,2

–

naprężenie

odpowiadające

działaniu

siły

rozciągającej, wywołującej w próbce wydłużenie
trwałe wynoszące 0,2% długości.

(19)

Siłę P

0,2

odpowiadającą wydłużeniu części

pomiarowej L

0

o 0,2% wyznacza się jak

pokazano na rys.7.

0

2

,

0

2

,

0

A

P

R 

L

0,2

0

L

P

0,

2

P

Wykres rozciągania stali

Wykres rozciągania stali

niskowęglow

niskowęglow

ej

ej

Wyznaczenie siły P

0,2

odpowiadającej wydłużeniu

próbki 0,2%

n - współczynnik bezpieczeństwa (liczba większa

od jedności).

(21)

n

R

e

dop





n

R

m

dop





(20)

lub

Za

naprężenia niszczące

przyjmuje się

wytrzymałość na rozciąganie R

m

albo granicę

plastyczności R

e

,

Naprężenia dopuszczalne określamy więc w
postaci:

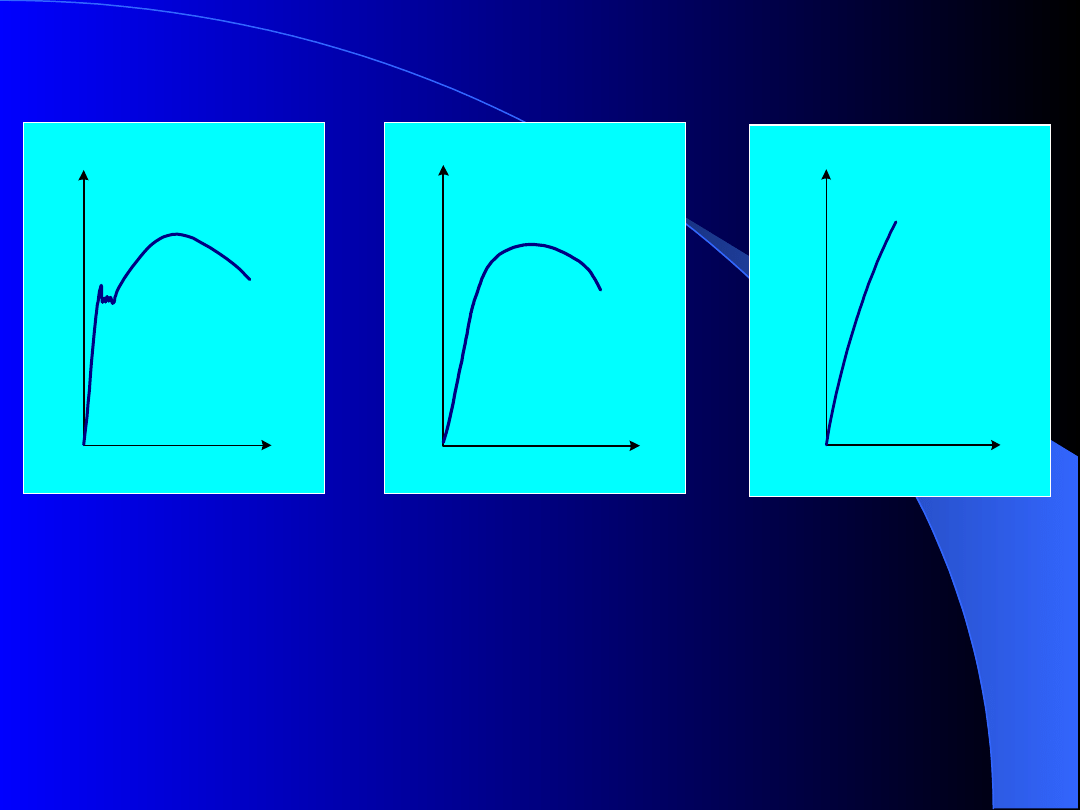
Wykresy rozciągania

Wykresy rozciągania

różnych

różnych

materiałów

materiałów

L

P

L

P

P

L

Rys. 8. Wykres rozciągania próbki:

a) z lokalnym maksimum siły (z wyraźną granicą

plastyczności) – niskowęglowe stale, stopy
aluminium

b) bez wyraźnej granicy plastyczności (miedź)
c) wykres rozciągania materiałów kruchych (żeliwo)

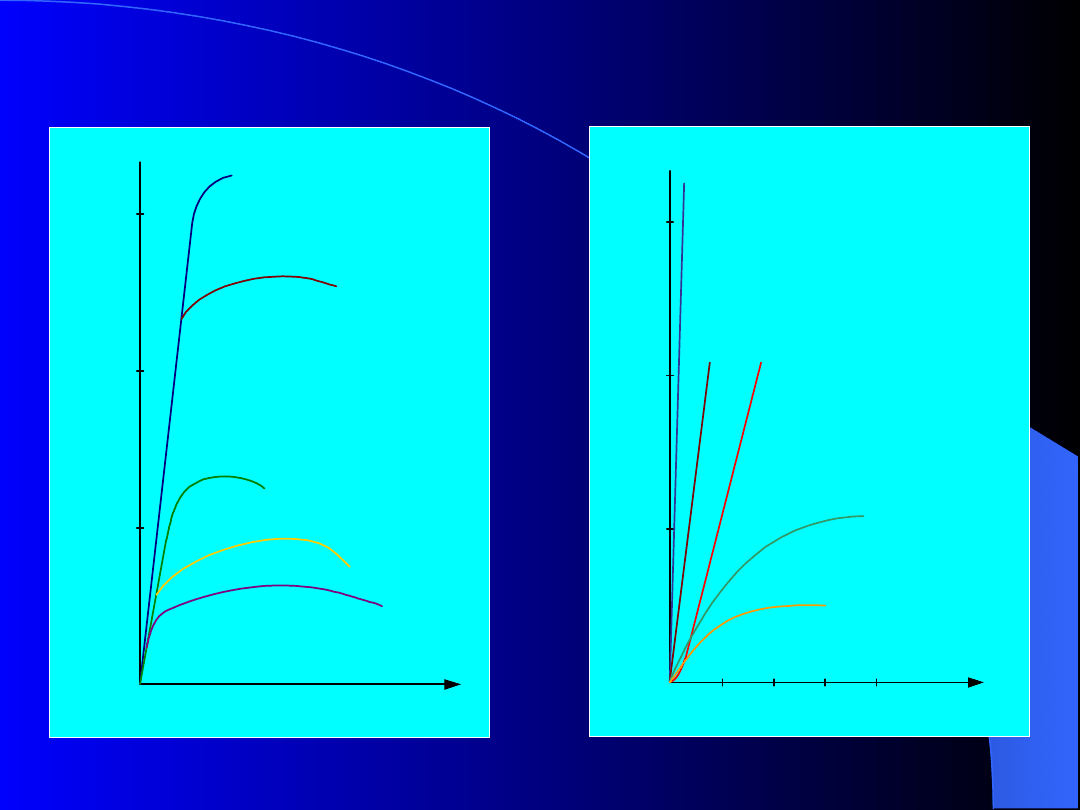
Wykresy rozciągania

Wykresy rozciągania

różnych

różnych

materiałów

materiałów

miedź



MPa

400

800

1200

0



mosiądz

dural

stal nierdzewna

stal sprężynowa

guma twarda



MPa

10

20

30

0



polichlorek winylu (PCW)

rzemień

skóra twarda

sklejka

80

60

40

20

%

Wykresy ściskania

Wykresy ściskania

i rozciągania stali

i rozciągania stali

niskowęglowej

niskowęglowej



l

0



pl

as

t



pr

op



pr

op

as

ym

pt

ot

a

D

C

0

R

m

R

e

(

pl

as

t

)



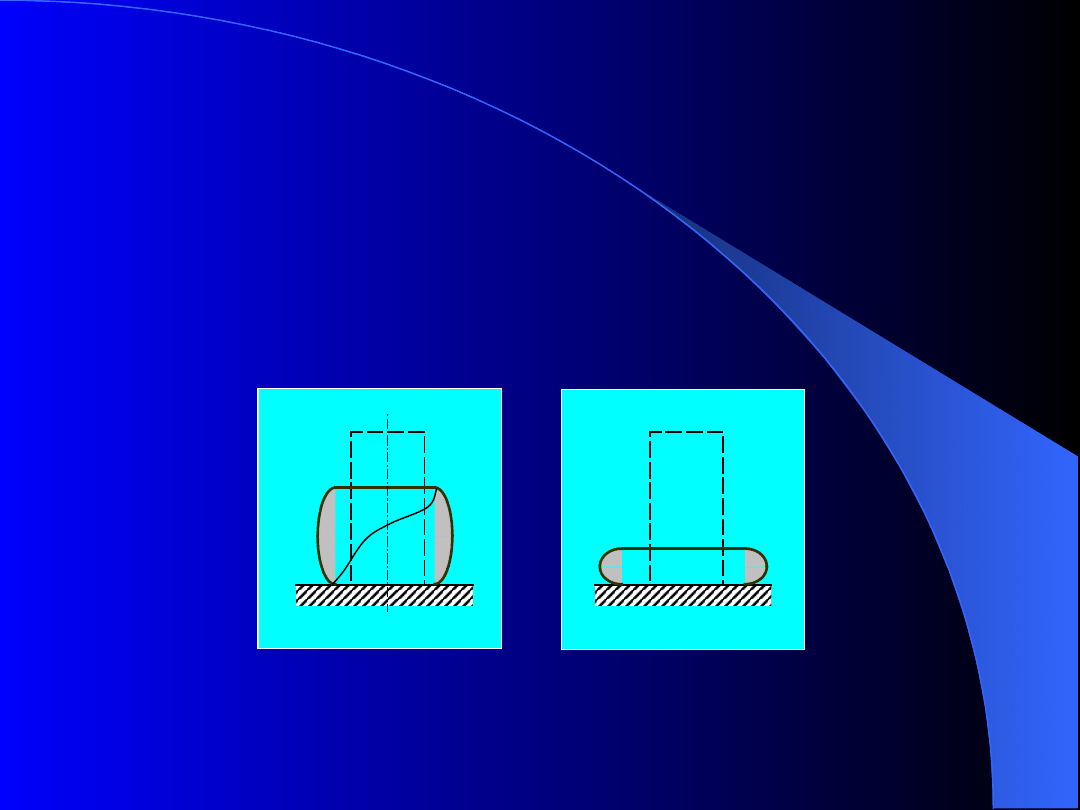
Wykresy ściskania metali

Wykresy ściskania metali

plastycznych

plastycznych

Po osiągnięciu granicy plastyczności wysokość

próbki

ściskanej

wyraźnie

się

zmniejsza

a

powiększają się jej wymiary poprzeczne (kształt
baryłki).

Próbki wykonane z materiałów mniej plastycznych w
tym stanie ulegają ukośnemu pęknięciu (rys.11a).

a

b

Rys.11. Deformacja walcowych próbek

ściskanych: a) do kształtu baryłki,

b) do kształtu krążka

Wytrzymałość na ściskanie

– iloraz siły

maksymalnej P

max

, przy której nastąpiło

pęknięcie próbki przez pole A

0

przekroju

początkowego:

0

max

A

P

R

c



(22)

Próbki wykonane z materiałów o dużej plastyczności
(stal niskowęglowa, miedź) bez widocznych pęknięć
lub uszkodzeń dają się spłaszczać przyjmując kształt
krążka (rys.11b).

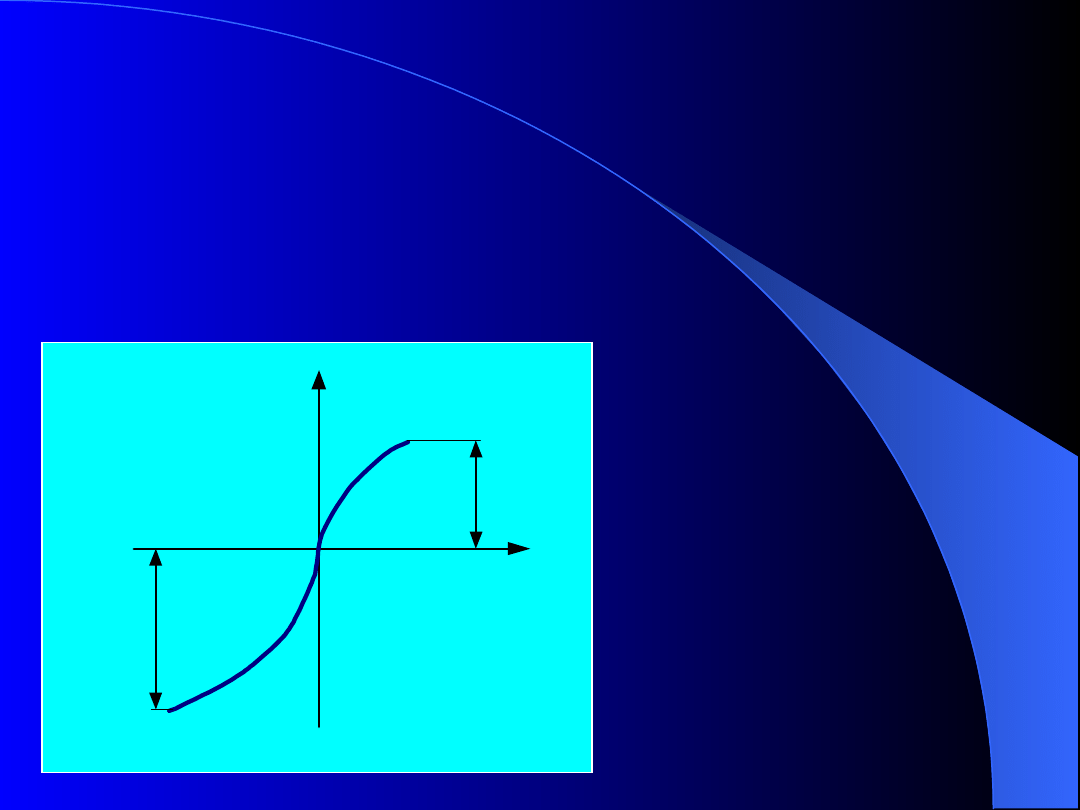
Wykres r

Wykres r

ozciąganie i ściskanie żeliwa

ozciąganie i ściskanie żeliwa

 Żeliwo wyróżnia się tym, że w żadnym zakresie

obciążeń odkształcenia nie są proporcjonalne do
naprężeń. W czasie próby rozciągania nie daje się
zauważyć jakiejkolwiek granicy proporcjonalności lub
plastyczności. W pewnej chwili próbka pęka bez
wyraźnych odkształceń.



0

R

m



R

c

Rys.12. Wykres rozciągania i

ściskania żeliwa

Wytrzymałość na r

Wytrzymałość na r

ozciąganie i

ozciąganie i

ściskanie

ściskanie

Materiały

kruche

mają

znacznie

większą

wytrzymałość na ściskanie R

c

w porównaniu z

wytrzymałością na rozciąganie R

m

:

żeliwo R

c

= (4  5)R

m

,

beton R

c

= (5  20)R

m

,

granit R

c

= (40  70)R

m

.

Zadania statycznie niewyznaczalne

Zadania statycznie niewyznaczalne

 

Przykład 1

Sztywna belka o ciężarze G przyłożonym w środku

(punkt 0) obciążona siłą P w punkcie D jest zamocowana na
sztywnej ścianie w przegubie R i zawieszona na
odkształcalnych cięgnach 1 i 2 (przeguby w punktach
B,C,K,L). Wyznaczyć wartości naprężeń w obu cięgnach,
jeżeli moduły Younga i przekroje poprzeczne cięgien są
takie same (E=E

1

=E

2

, A=A

1

=A

2

). Początek układu

współrzędnych umieszczono w punkcie R.

Dane: G, P, b, l, E, A.

Wyznaczyć: 

1

i 

2

Niewiadome: R

x

, R

y

, S

1

,S

2

- układ jest statycznie

niewyznaczalny

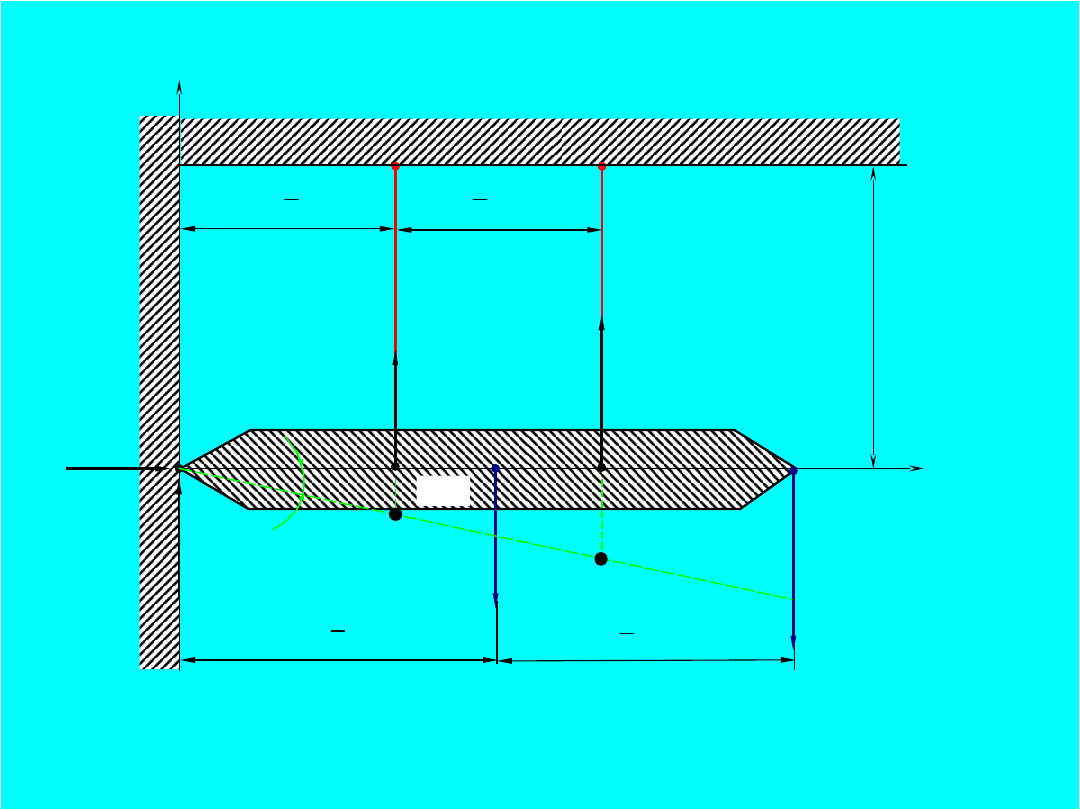
G

K

L

R

R

x

R

y

S

1

S

2

1

2

l

D

C

B

0

B’

C’

P





l

2



l

1

x

y

2

b

2

b

3

b

3

b

Dodatkowe równania ułożymy z warunków
geometrycznych i związków fizycznych (prawo
Hoocka)

Warunki równowagi:







0

x

ix

R

P















0

2

1

P

G

S

S

R

P

y

iy













0

2

3

2

3

2

1

b

P

b

G

b

S

b

S

M

R

Związki fizyczne (prawo
Hooke’a):

Warunki geometryczne:

Na skutek działania obciążenia cięgna ulegną
wydłużeniu, a belka obróci się o kąt . Wydłużenia
muszą się mieścić w zakresie proporcjonalności
materiału – muszą być małe. Pozwala to na pominięcie
poziomych przemieszczeń punktów B,C.

3

2

3

2

1

b

l

b

l







A

E

l

S

l

i

i





gdzie i zależna jest od ilości cięgien, i = 1,2.

zatem:

Podstawiając

związek

fizyczny

do

warunku

geometrycznego otrzymujemy:

b

A

E

l

S

b

A

E

l

S

2

3

3

2

1



2

2

1

S

S 

Po podstawieniu powyższej zależności do warunków
równowagi wyznaczymy reakcje:

0



x

R

P

G

S

2

,

1

6

,

0

2





P

G

S

6

,

0

3

,

0

1





P

G

R

y

8

,

0

1

,

0





Naprężenia wyznaczamy z zależności:

A

P

G

A

S

6

,

0

3

,

0

1

1









A

P

G

A

S

2

,

1

6

,

0

2

2







