Pole elektryczne

Wykład 10

1

Zasady zaliczania w semestrze I

• Przedmiot w tym semestrze jest zaliczany na ostatnich zajęciach
• Zaliczanie w formie pracy pisemnej polega na odpowiedzi na 6

pytań definicyjnych i jedno opisowe.(

Obowiązuje materiał z

kursu i wykładów)

• Podstawą do wpisania do indeksu zaliczenia przedmiotu

jest wcześniejsze zaliczenie ćwiczeń rachunkowych i
kursu.

• Osoby które nie zaliczą przedmiotu na ostatnich zajęciach przed

kolejnym zaliczeniem muszą uzyskać pozytywny wpis z ćwiczeń
i zaliczyć kurs

Terminy zaliczeń

Zaliczenia na ostatnich zajęciach:

Zaliczenia w sesji:

Kolejne terminy poprawkowe:

POLE ELEKTRYCZNE
Ładunek elektryczny
Prawo Coulomba
Natężenie pola elektrycznego
Linie sił pola elektrycznego
Strumień pola elektrycznego
Prawo Gaussa
Napięcie i potencjał
Pojemność elektryczna i kondensatory
Gęstość energii pola elektrycznego
Dielektryki
Twierdzenie

Gaussa

w

przypadku

obecności

dielektryków. Wektor indukcji elektrycznej

4

POLE ELEKTRYCZNE

Zjawiska elektryczne towarzyszyły człowiekowi od

samego początku jego pojawienia się. Wyładowania
atmosferyczne

napawały

grozą,

zaś

zjawiska

bioelektryczne i elektryzacja pewnych materiałów
nasuwały przypuszczenia o niewidzialnej sile, która
potrafi ożywić to co martwe.

Pierwsze doświadczenia

(w dzisiejszym słowa tego

znaczeniu) z elektryczności przeprowadzane były już w

starożytności, już Tales z Miletu (600 lat p.n.e.)

wspomina o tym, że potarty bursztyn wykazuje

właściwości przyciągania drobnych przedmiotów.

Ogólnie też znane były objawy elektryczności
atmosferycznej, takie jak pioruny, ale natura ich była nie
wyjaśniona aż do drugiej połowy XVII wieku. Wiedziano
jednak, że można się ustrzec przed uderzeniem
pioruna stosując wysokie, zaostrzone maszty.
Podczas prac archeologicznych w Egipcie na
ścianach starożytnych świątyń znaleziono napisy
wyjaśniające

stosowanie

masztów

jako

środka

zabezpieczającego przed „niebieskim ogniem”.

5

Dopiero wiek XIX i XX wprzągł szeroko

elektryczność w służbę człowieka. Ze zjawiskami
elektrycznymi mamy do czynienia nie tylko w przypadku
przepływu prądu elektrycznego.

Pola

elektrostatyczne

często

występują

w

nowoczesnych

mieszkaniach

stając

się

źródłem

iskrzenia

. Naelektryzowany sweter przyciąga skrawki

papieru, a ekran telewizora cząstki kurzu.

Łatwo zauważyć, że do tego oddziaływania nie

jest konieczny bezpośredni kontakt.

Jedno ciało naelektryzowane działa na drugie ciało

naelektryzowane nawet z pewnej odległości

.

Doświadczeń takich można zaplanować i wykonać
bardzo dużo. Można naelektryzować wiele materiałów,
np. przez tarcie, lub też wytwarzać elektryczność
statyczną za pomocą odpowiednich maszyn.

6

Wyniki tych doświadczeń są następujące –

naelektryzowane ciała działają na siebie z
odpowiednimi siłami, zależnymi, ogólnie rzecz
biorąc, od odległości, przyciągają się wzajemnie
lub odpychają.

Sama przyczyna oddziaływania jest

jednak dla obserwatora nieuchwytna. Dla jej
objaśnienia wprowadzono wielkość (abstrakcyjną),
zwaną ładunkiem elektrycznym.

Ładunku elektrycznego nie można zobaczyć –
można o jego istnieniu wnioskować jedynie
poprzez występowanie zjawisk elektrycznych

.

7

11.1. Ładunek elektryczny

 

Podstawową

własnością

ładunku

elektrycznego jest to, że mamy do czynienia z
dwoma

jego

rodzajami.

Ładunek

doznaje

odpychania od dowolnego innego z tej samej
grupy, natomiast jest przyciągany przez dowolny
ładunek z innej grupy.

Powiemy, że jeśli dwa małe elektrycznie

naładowane ciała A i B umieszczone w pewnej
odległości od siebie odpychają się oraz jeśli A przyciąga
trzecie naelektryzowane ciało C, to z pewnością można
stwierdzić, że ciała B i C również się przyciągają.

Fizycy współcześni traktują istnienie dwu rodzajów

ładunków jako przejaw istnienia przeciwstawnych stanów tej
samej wielkości fizycznej.

Które z ładunków są ujemne, a które

dodatnie?

Jest rzeczą czysto umowną, które z

ładunków nazwiemy dodatnimi, a które ujemnymi.

Zgodnie z umową elektrony mają ujemny ładunek.

8

Ładunki

elektryczne

podlegają

dwóm

fundamentalnym prawom:

> Ładunek podlega prawu zachowania.

> Ładunek może przybierać jedynie

wartości będące (co do modułu) wielokrotnością
ładunku elektronu.

9

11.2. Prawo zachowania ładunku

Wprowadzimy

jako

postulat

teorii

prawo

zachowania ładunku w następującej postaci:

Całkowity

ładunek

elektryczny

układu

odosobnionego w dowolnej chwili nie może ulegać
zmianie.

Eksperymenty potwierdzają to prawo, np.

zjawisko tworzenia pary elektron-pozyton.

e

_

e

+

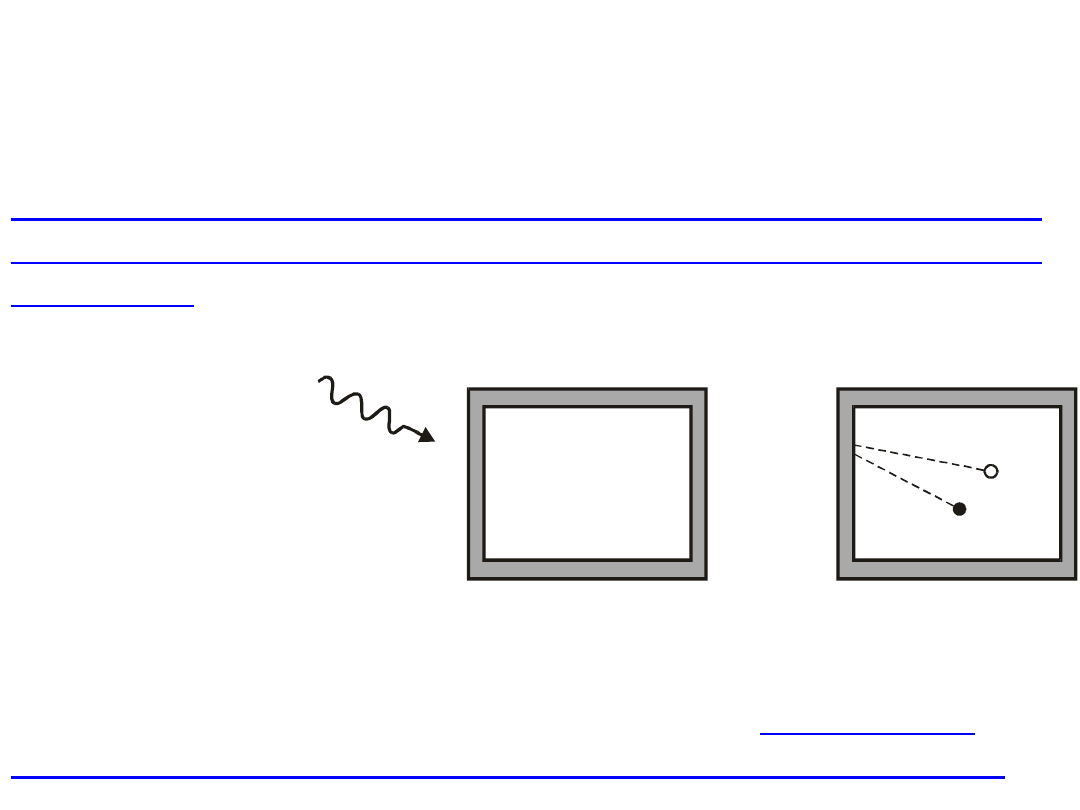
Jeżeli
bombardujemy
promieniami 

umieszczone w
próżni pudło o

cienkich ściankach (rys.7.1), to przy odpowiednich
warunkach możemy zaobserwować zjawisko tworzenia
pary elektron-pozyton wewnątrz układu.

Utworzone

zostały dwie elektrycznie naładowane cząstki, ale
całkowity ładunek układu nie uległ zmianie.

10

Współczesne eksperymenty z bardzo dużą dokładnością
pokazują, że wartość bezwzględna ładunku elektronu i
pozytonu jest jednakowa.

Brak zachowania ładunku byłby niezgodny ze

współczesną teorią elektromagnetyzmu.

Prawo

zachowania ładunku jest słuszne w dowolnym
układzie inercjalnym, a ładunek elektryczny jest
wielkością relatywistycznie niezmienniczą.

11

11.3. Ładunek elektryczny elektronu

 

Występujące

w

przyrodzie

ładunki

są

wielokrotnością

ładunku

elektronu,

który

oznaczać będziemy przez e.

Kwantyzacja ładunku

jest powszechnym prawem przyrody.

Dotychczasowe pomiary wykazują, że wszystkie
naładowane cząstki elementarne mają identyczne co do
wartości bezwzględnej ładunki.

W rozważaniach naszych będziemy przyjmowali,

że punktowe ładunki mogą przybierać dowolną wartość
q.

Ładunek

punktowy

jest

idealizacją

bliższą

rzeczywistości niż wyobrażenia o ciągłym jego
rozkładzie.

W pewnych przypadkach będziemy posługiwać

się ciągłym rozkładem ładunku, będzie to wówczas
jednak wynik uśredniania po wielkiej liczbie ładunków
elementarnych.

12

Jednostką

ładunku

elektrycznego

jest

kulomb [C], przy czym 1 kulomb jest to ładunek
przenoszony przez prąd elektryczny o natężeniu 1
ampera [A] w czasie 1 sekundy [s].

 

Ładunek elementarny (ładunek elektryczny

elektronu) e wynosi:

]

s

[

]

A

[

]

C

[





C

10

6

.

1

e

19







13

11.4 Prawo Coulomba

 

W roku 1785 Coulomb na podstawie doświadczeń

z

wagą

skręceń

wypowiada

prawo

dotyczące

oddziaływania

dwu

nieruchomych,

punktowych

ładunków elektrycznych. Zgodnie z tym prawem:

Dwa

nieruchome

punktowe

ładunki

elektryczne odpychają się lub przyciągają z siłą
proporcjonalną do iloczynu tych ładunków, a
odwrotnie proporcjonalną do ich odległości.

Wyrazimy to przy pomocy równania:

12

12

2

12

2

1

12

r

r

r

q

q

k

F







gdzie q

1

i q

2

są wielkościami skalarnymi określającymi

wielkość i znak ładunków. Wielkość jest siłą
działającą na ładunek, zaś wektor

jest skierowany od ładunku q

2

do q

1

12

F



12

r

14

+

_

+

q q

1

2

q q

1

2

F r

1 2

1 2

F r

1 2

1 2

+

__

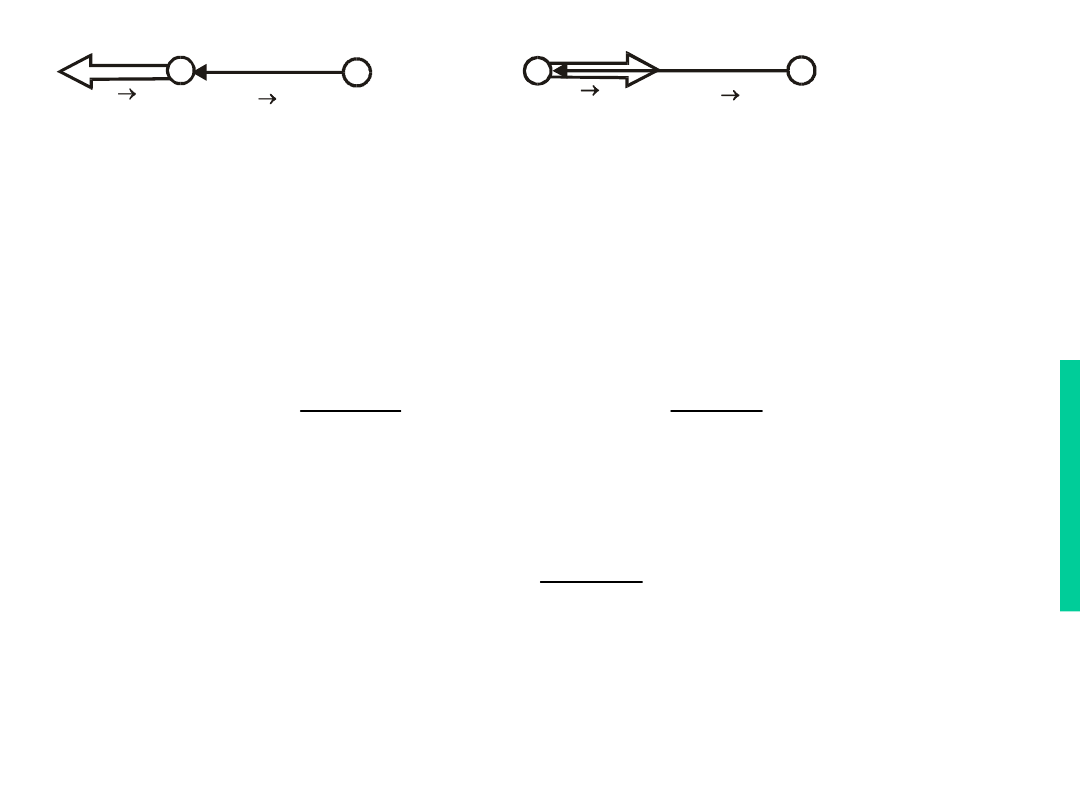
Rys.7.2. Jeżeli wektor jest siłą jaką działa

ładunek q

2

na ładunek q

1

, to wektor

prowadziliśmy od ładunku q

2

do q

1

.

12

F



12

r

W układzie jednostek SI stałą k można zapisać w
postaci:

(7.2)

 

gdzie

jest przenikalnością elektryczną

próżni.















 













2

2

r

9

r

o

C

m

N

/

10

9875

.

8

4

1

k



























N

m

C

10

8859

.

0

2

2

11

o

15

Porównajmy siłę grawitacyjną pomiędzy

elektronem i protonem w atomie wodoru

F = 3.61·10

-

47

N

z siła elektryczną pomiędzy nimi w tym

samym atomie

F = 2.27·10

-8

N

.

Widać

wyraźnie jak wielka jest różnica pomiędzy nimi – 39
rzędów

To, że siły grawitacyjne dla "dużych" ciał

dominują wynika stąd, że liczby protonów i elektronów
są równe.

W tym miejscu wypada podkreślić, że nie

istnieje, żaden związek między masą i
ładunkiem.

16

Stała 

r

występująca we wzorze (7.2) nosi nazwę

względnej przenikalności elektrycznej ośrodka i wyraża
się liczbą niemianowaną. W tabeli 7.1 podano względne
przenikalności elektryczne 

r

kilku substancji.

Tabela 7.1. Względne

przenikalności

elektryczne różnych

ośrodków

.

Ośrodek

Względna

przenikalność

elektryczna 

r

Próżnia
Powietrze
Parafina
Nafta
Olej
transformatorowy
Benzen
Chloroform
Szkło
Alkohol
Woda

1

1.0006

2.0
2.0
2.2
2.3
4.8

510

27
81

17

Znając 

r

i 

o

możemy określić przenikalność

elektryczną  każdego ośrodka materialnego:

(7.3)

Fakt, że oddziaływanie ładunków zależy od

ośrodka, tłumaczy się zjawiskiem polaryzacji
elektrycznej ośrodka.

Mianowicie, ładunek q

1

wprowadzony do ośrodka

zostaje otoczony płaszczem ładunków przeciwnego
znaku, które neutralizują częściowo ładunek q

1

. To

samo zachodzi dla drugiego ładunku q

2

, w rezultacie

czego siła ich oddziaływania ulega zmniejszeniu. W
związku z tym

względne przenikalności

elektryczne ośrodków są zawsze większe od
jedności

r

o









18

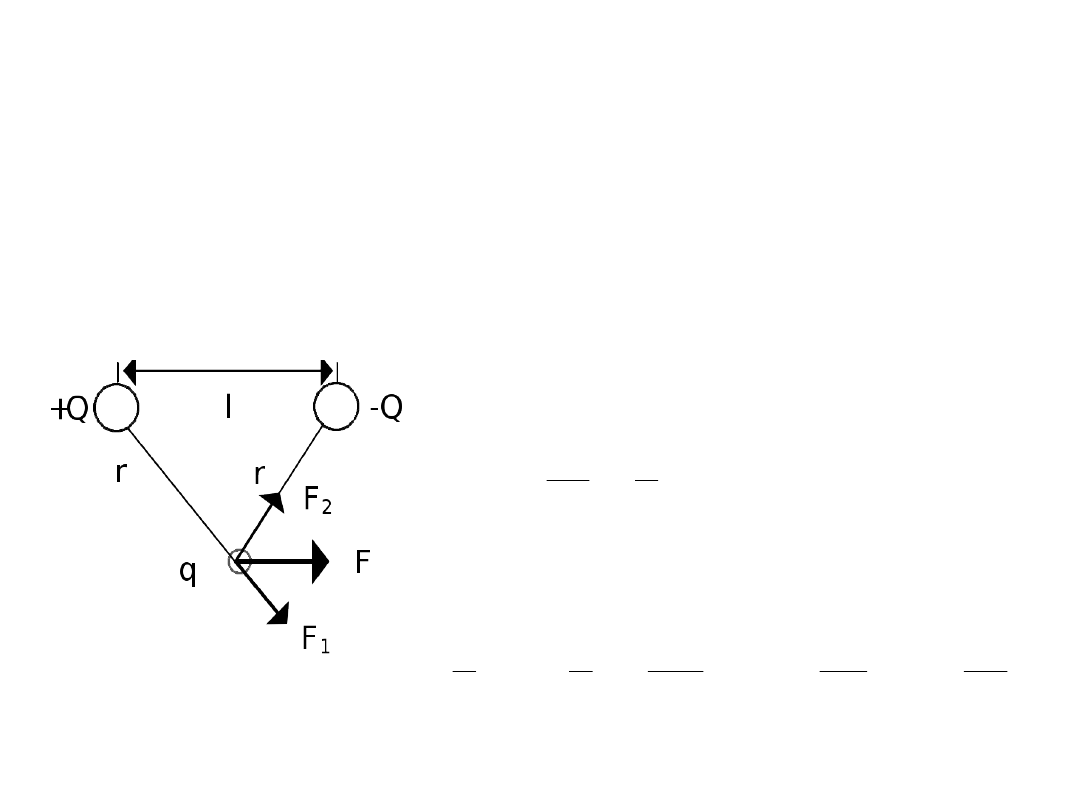
Zasada superpozycji

Siłę wypadkową

(tak jak w grawitacji)

obliczamy dodając

wektorowo siły dwu ciałowe

.

Przykład 1

Dipol elektryczny składa się z dwóch ładunków
oddalonych od siebie l. Jaka siła jest wywierana na
ładunek q umieszczony tak jak na rysunku?

Z podobieństwa trójkątów

stąd

r

l

F

F



1

3

3

2

1

r

p

qk

r

Ql

qk

r

Qq

k

r

l

F

r

l

F





















gdzie p = Ql jest

momentem

dipolowym

.

19

11.5 Natężenie pola elektrycznego

 

Przestrzeń otaczająca ładunki elektryczne

posiada taką właściwość, że na umieszczone w
dowolnym jej punkcie inne ładunki działa siła.
Mówimy, że wokół ładunków elektrycznych istnieje pole
elektryczne.

Istnienie pola elektrycznego można wykryć

wprowadzając do przestrzeni w której ono działa
ładunek próbny q

0

. W polu elektrycznym na ładunek

próbny działa siła .

Umożliwia to wprowadzenie

pojęcia: natężenia pola elektrycznego.

Natężenie pola elektrycznego definiuje się jako
stosunek siły , działającej na dodatni ładunek próbny
q

0

, do wartości tego ładunku.

F



E



F



0

q

F

E







Natężenie pola elektrycznego jest
wektorem.

W

każdym

punkcie

przestrzeni wektor może mieć inną
wartość i inny kierunek.

(7.4)

20

Jednostką natężenia pola w układzie SI,

wynikającą ze wzoru (7.4) jest [N/C], jednakże w
praktyce przyjęło się używać jednostki równoważnej
[V/m].

 

Obliczenie natężenia pola elektrycznego w

dowolnym punkcie przestrzeni jest w zasadzie
możliwe zawsze, jeżeli znamy rozkład ładunków
wytwarzających to pole

. Z prawa Coulomba (7.1) i

definicji pola elektrycznego (7.4) możemy wyznaczyć
natężenie pola elektrycznego wytworzonego przez
ładunek punktowy q.

m

V

s

A

m

s

A

V

s

A

m

/

J

C

N

















r

r

r

q

4

1

r

r

q

r

q

q

4

1

q

F

E

2

o

2

o

o























(7.5)

21

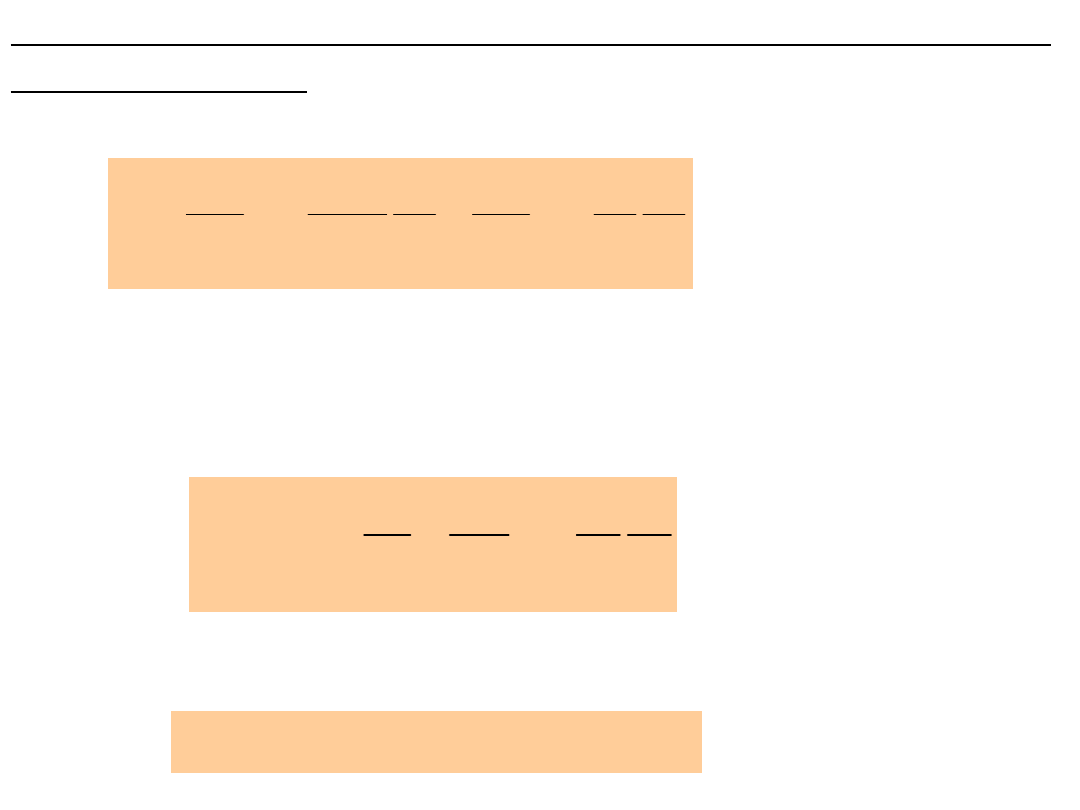
Jeżeli pole elektryczne jest wytwarzane przez pewną
liczbę ładunków punktowych

to

wówczas siła działająca na ładunek próbny q

o

wynosi:

(7.6)

Widać, że siła jest proporcjonalna do q

o

.

Zatem natężenie pola elektrycznego
wytworzonego przez układ

ładunków

o postaci:

(7.7)

jest wektorową sumą natężeń pól pochodzących od
każdego z ładunków układu

(7.8)





N

j

2

1

q

,

...

q

,

,...

q

,

q

o

F



oj

oj

2

oj

j

N

1

j

o

oj

oj

2

oj

j

o

N

1

j

o

r

r

r

q

4

q

r

r

r

q

q

4

1

F























o

F







z

,

y

,

x

E







N

j

2

1

q

,

,...

q

,

,...

q

,

q





oj

oj

2

oj

j

N

1

j

o

o

r

r

r

q

4

1

q

F

z

,

y

,

x

E





















N

j

2

1

E

,...

E

...

E

E

z

,

y

,

x

E





















22





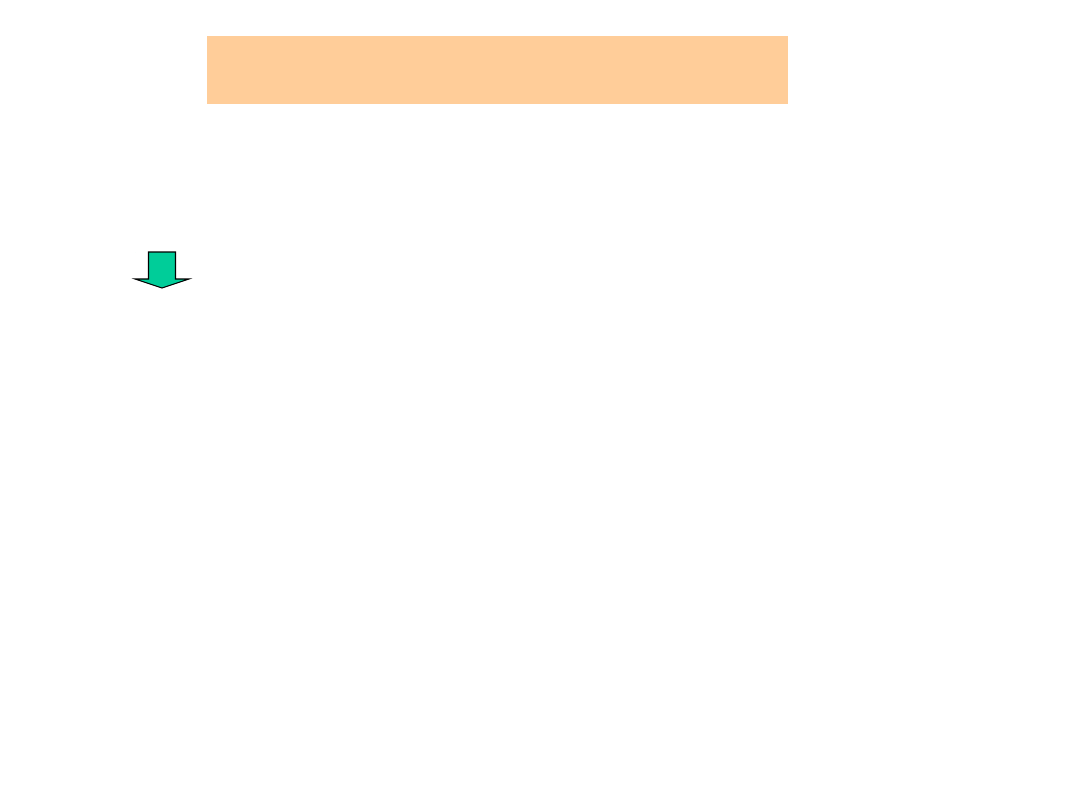
N

j

2

1

E

,...

E

...

E

E

z

,

y

,

x

E





















Widzimy, że natężenie pola elektrycznego E(x,y,z)
w danym punkcie ośrodka zależy jedynie od
rozkładu przestrzennego ładunków i właściwości
elektrycznych ośrodka ().





N

j

2

1

q

,

,...

q

,

,...

q

,

q

23

Pojęcie ładunków punktowych uogólnimy teraz na
ciągły rozkład ładunku.

Objętościowy rozkład ładunku opisujemy za

pomocą skalarnej funkcji , którą nazywamy gęstością

ładunku

(7.9)

 

Gęstość (x,y,z) w ogólnym przypadku jest funkcją

położenia. W układzie SI objętościową gęstość ładunku
 wyrażamy w [C/m

3

]. Ładunek dQ zawarty w małym

prostopadłościanie o objętości dV= dx dy dz
umieszczony w punkcie (x,y,z) jest dany przez:

(7.10)

W skali atomowej gęstość ładunku zmienia się silnie

od punktu do punktu. Pojęciem gęstości będziemy się
posługiwać w odniesieniu do układów makroskopowych.





z

,

y

,

x

f

dV

dQ











dz

dy

dx

z

,

y

,

x

dQ 



24

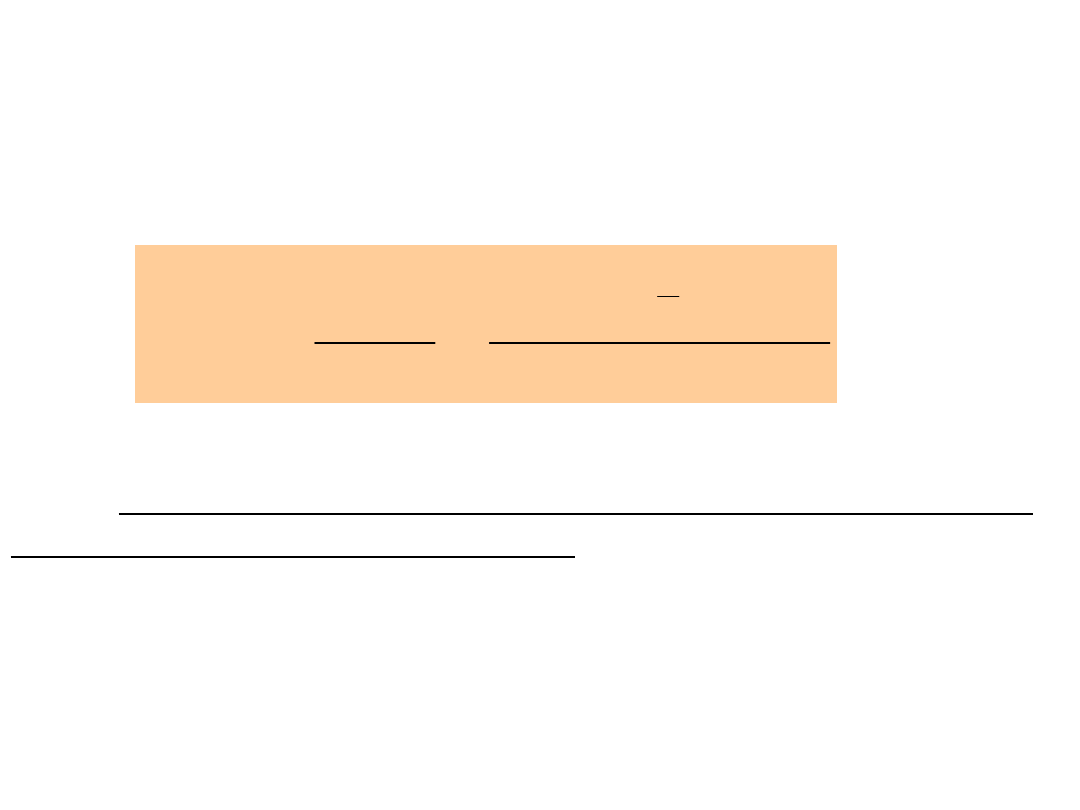
Dla ciągłego rozkładu ładunków natężenie pola
elektrycznego

, pochodzące od ładunków w innych

punktach jest dane przez całkę:

(7.11)

Jest to całka objętościowa po objętości V w

której występuje ładunek. Przy ustalonym punkcie
(x,y,z), w którym wyznaczamy natężenie pola,
całkowanie przebiega po wszystkich punktach (x’,y’,z’)
obszaru V w których występują ładunki.

 





z

,

y

,

x

E











2

V

r

o

r

'

dz

'

dy

'

dx

r

r

'

z

,

'

y

,

'

x

4

1

z

,

y

,

x

E















25

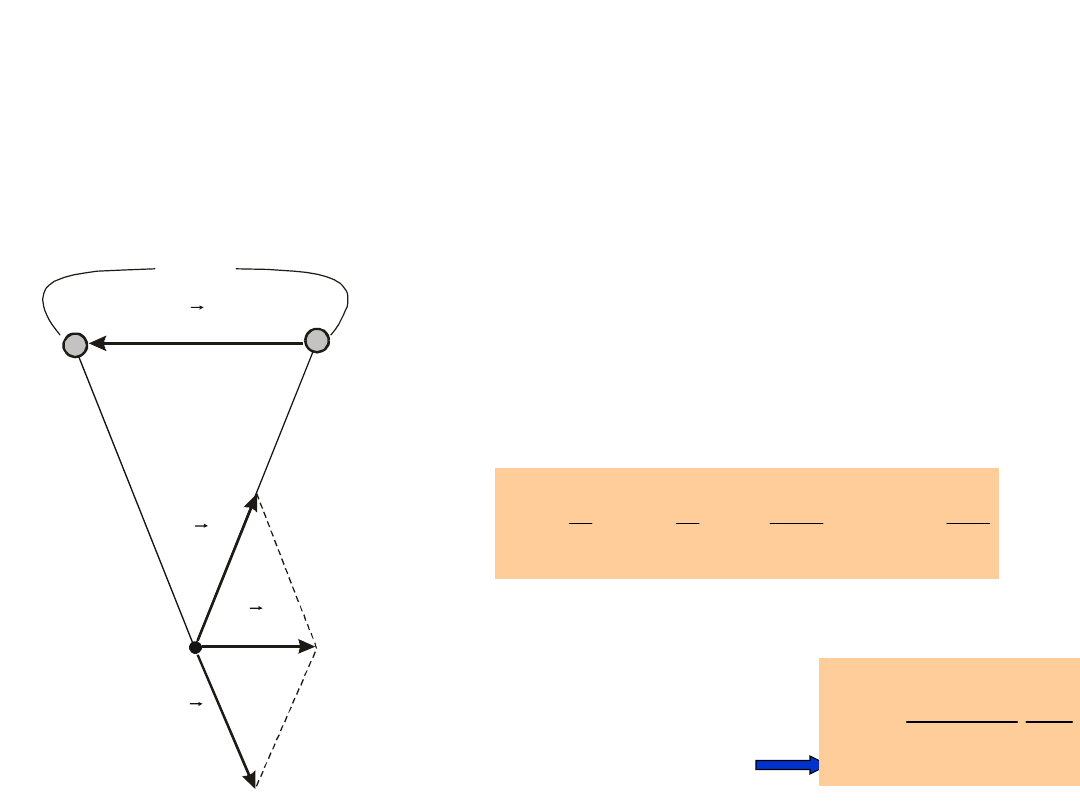
Rozpatrzymy teraz pole elektryczne w punkcie P

dla przypadku przedstawionego na rysunku poniżej.
Punkt P leży w jednakowej odległości od ładunków +Q i
–Q. Układ ładunków +Q i –Q położonych w odległości l
od

siebie

nazywamy

dipolem

elektrycznym

scharakteryzowanym momentem dipolowym

l

Q

p







r

r

+

-

+ Q

- Q

D ip o l

q

1

F

2

F

F

l

Zwrot wektora skierowany

jest od ładunku ujemnego do
dodatniego.Ze

względu

na

podobieństwo trójkątów mamy

, czyli

l



r

/

l

F

/

F



1

3

2

1

r

p

qk

r

Qq

k

r

l

F

r

l

F

o

o



















Siła

działająca

ze

strony

dipola

na

ładunek

q

jest

odwrotnie
proporcjonalna

do

sześcianu

odległości

między nimi. Czyli
pole dipola

3

4

1

r

p

E

o







26

11.6. Linie sił pola elektrycznego

 

Michael Faraday, nie doceniając przedstawienia

pola elektry-cznego jako wektora, operował zawsze
pojęciem linii sił.

Zresztą ciągle jeszcze

linie sił są wygodną formą

modelowego opisu pola elektrycznego

. Będziemy je

używać do tego celu, ale nie będziemy ich
wykorzystywać do rozważań ilościowych.

 

Zależność pomiędzy liniami sił a wektorem

natężenia pola elektrycznego jest następująca:

1.     Styczna do linii sił w dowolnym punkcie pola
wyznacza kierunek natężenia pola w tym punkcie.

2.     Linie sił wykreśla się tak, aby liczba linii na
jednostkę powierzchni przekroju była proporcjonalna do
wielkości . Gdy linie leżą blisko siebie, jest duże,
a gdy są odległe, jest małe.

E



E



E



E



27

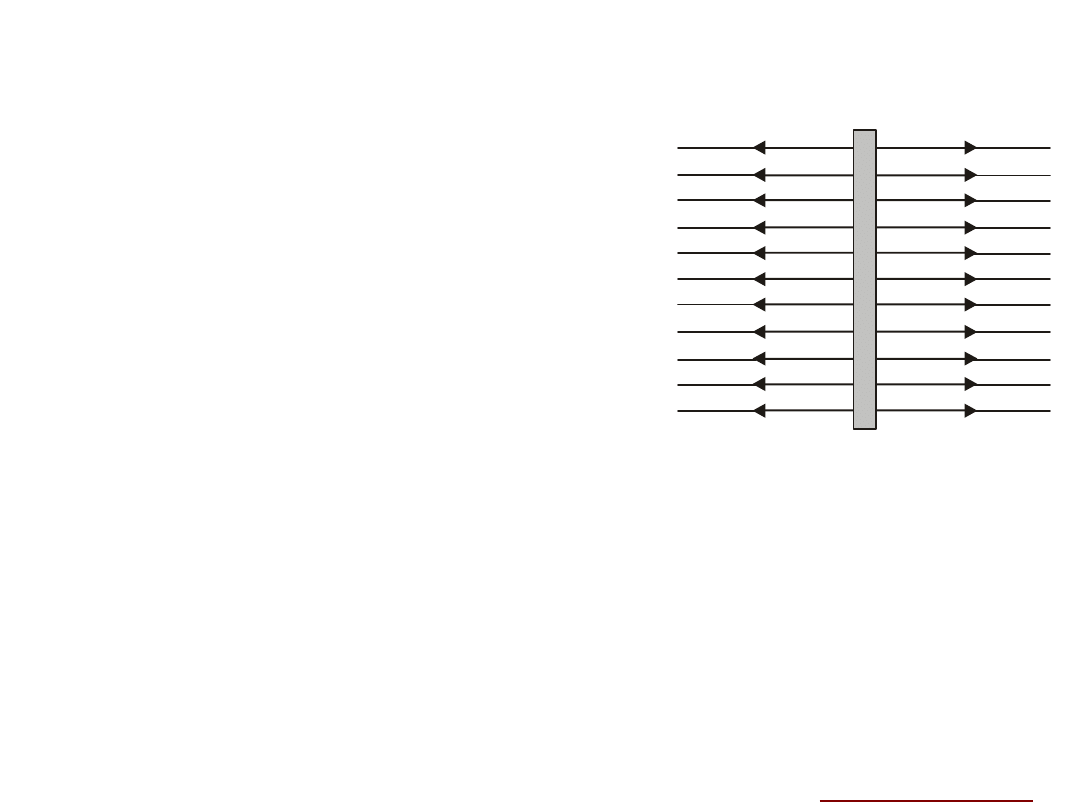
Rysunek obok przedstawia linie sił
dla

jednorodnej

płaszczyzny

naładowanej dodatnio.

Założenie,

że

rozpatrujemy

płaszczyznę

nieskończoną,

oznacza, że w przypadku płytki o
wymiarach

skończonych

rozważamy

tylko

te

punkty,

których odległość od płytki jest
mała w porównaniu z odległością
od

najbliższego

jej

brzegu.

Dodatni

ładunek

próbny,

umieszczony przed taką płytką,
oddalałby się od niej wzdłuż linii
prostopadłej

do

płaszczyzny

płytki.

+

+

+

+

+

+

+

+

A więc

wektor natężenia pola elektrycznego w

każdym punkcie blisko płytki musi być do niej
prostopadły.

Linie

sił

są

rozmieszczone

równomiernie, co oznacza, że ma tę samą
wartość dla wszystkich punktów przestrzeni
leżących blisko powierzchni płytki. Pole takie
nazywamy polem jednorodnym

.

E



28

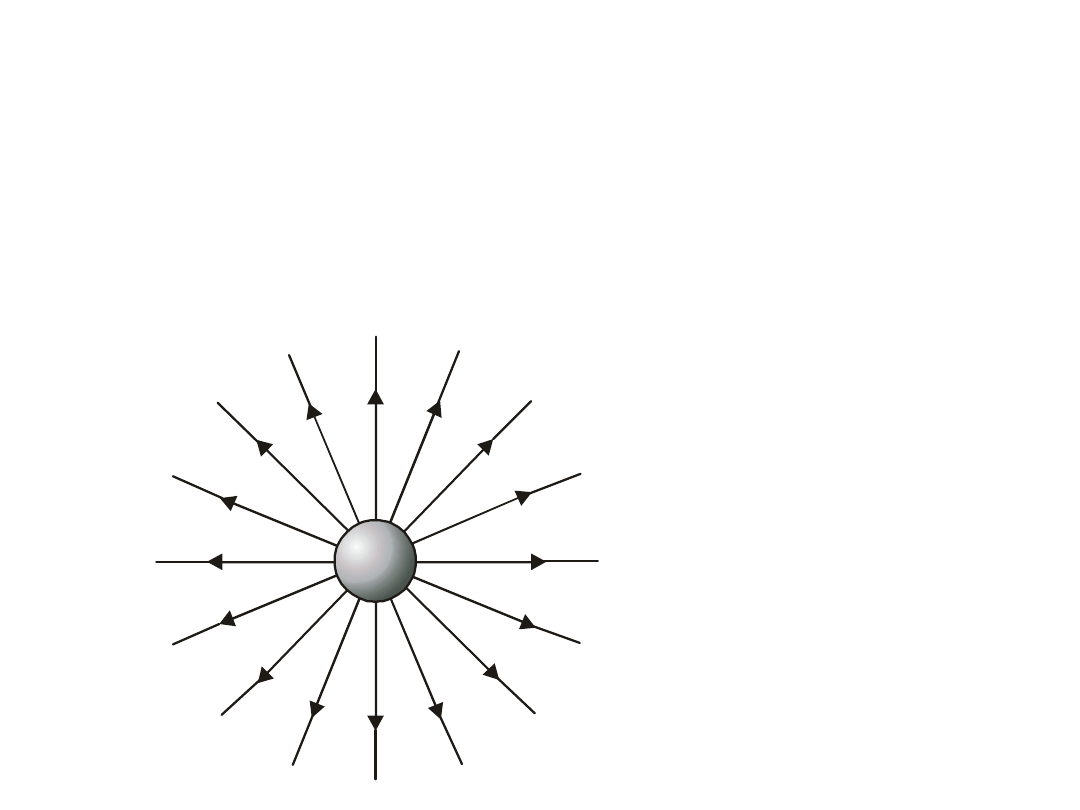
Na rysunku poniżej widzimy linie sił dla

dodatnio naładowanej kuli. Z symetrii zagadnienia
wynika, że linie te muszą leżeć wzdłuż promieni. Są one
skierowane na zewnątrz kuli, ponieważ próbny ładunek
dodatni byłby przyspieszany w tym kierunku. Natężenie
pola elektrycznego nie jest stałe, lecz maleje ze
wzrostem odległości od kuli. Wynika to w sposób
oczywisty z rozmieszczenia linii sił, które na większych
odległościach oddalają się od siebie.

 

 

 

Rys.7.5. Linie
sił

pola

elektrycznego
wytworzonego
przez dodatnio
naładowaną
kulę.

+ + +

++

+

+

++

++

+

++

++

29

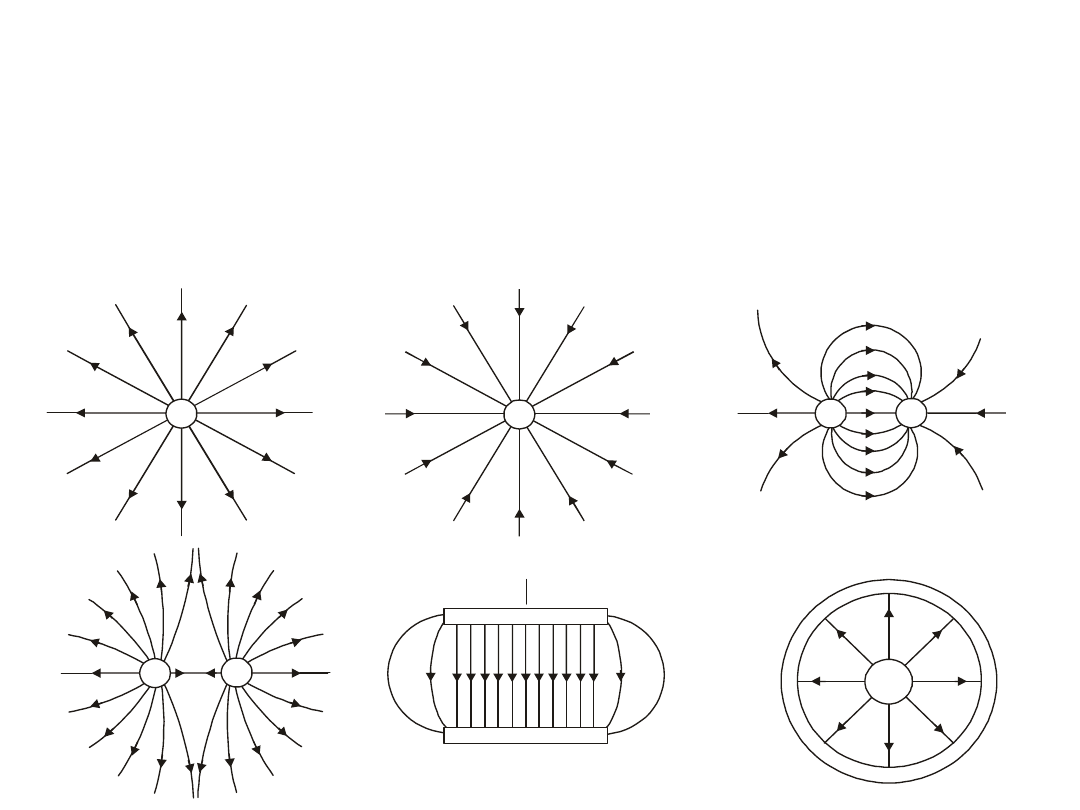
Na rysunku 7.6 pokazano przebieg linii sił różnych pól
elektrycznych. Linie pola zaczynają się zawsze na
ładunkach dodatnich, a kończą na ładunkach ujemnych.

W niektórych przypadkach linie pola biegną do
nieskończoności; uważamy wtedy, że odpowiednie
ładunki, na których te linie się kończą, znajdują się
nieskończenie daleko.

+

+

_

_

a ) b ) c )

+

+

+ + +

_ _ _

+

_

_

_

_

_

_

d ) e ) f )

30

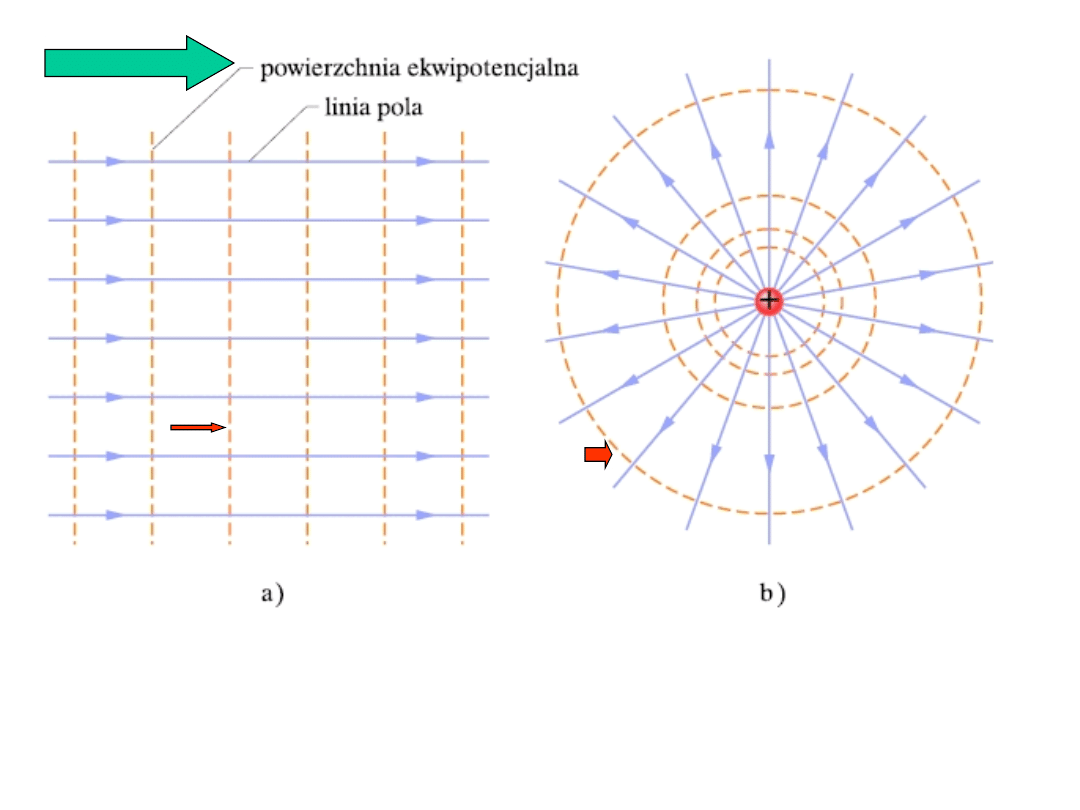
Linie pola elektrycznego i przekroje powierzchni

ekwipotencjalnych dla pola jednorodnego i ładunku punktowego

31

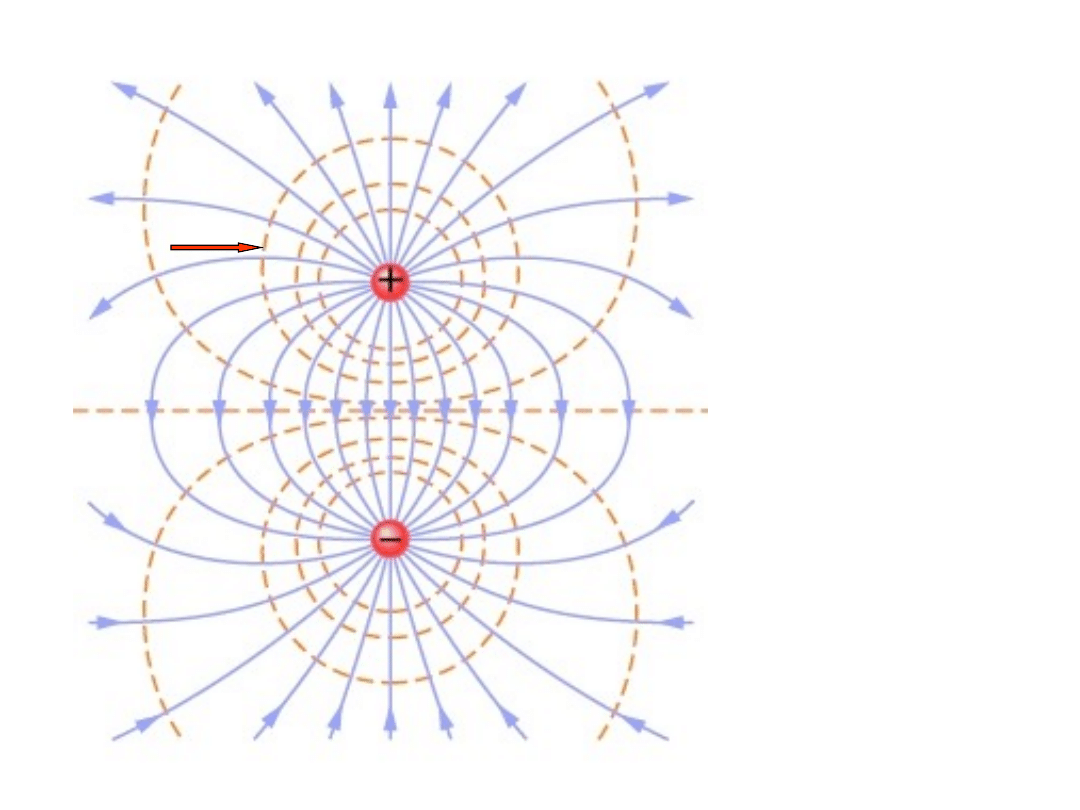
Pola dipola

elektrycznego

32

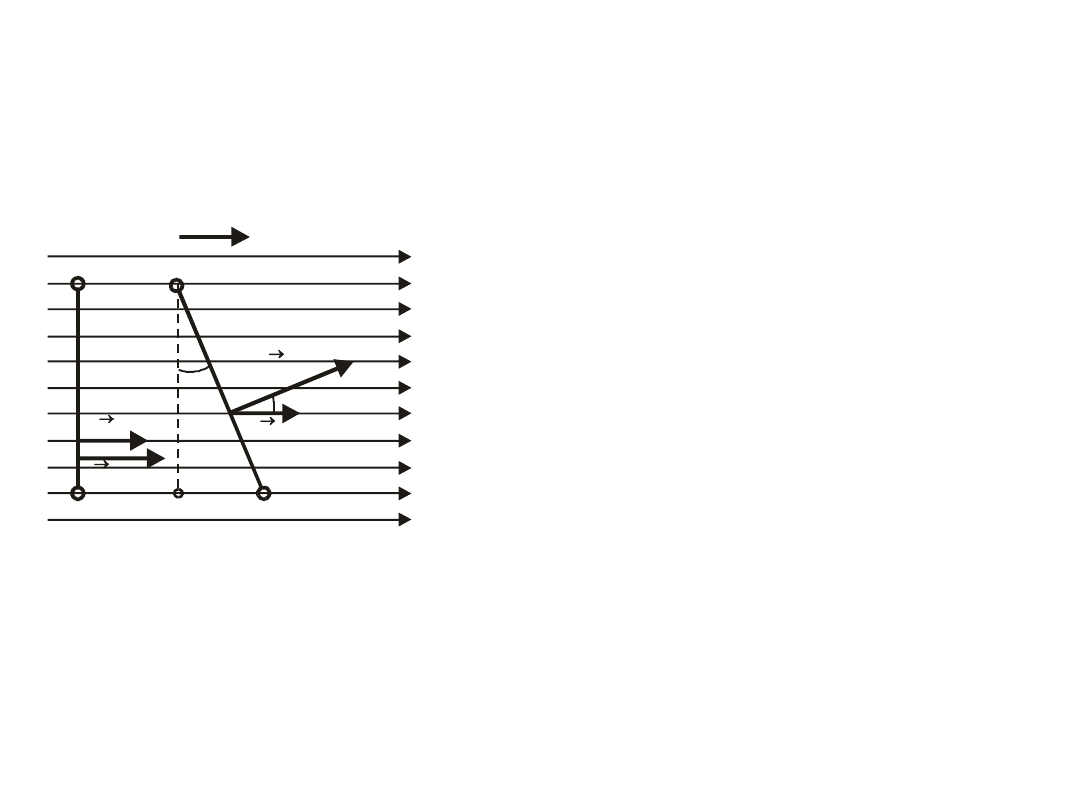
11.7 Strumień pola elektrycznego

 

Płynąca ciecz (np. woda) w istocie swojej ma mało

wspólnego z polem elektrycznym, ale świetnie się
nadaje do konstrukcji modeli pola elektrycznego.

 











A

a

A

b

a ) b )

Rysunek

7.7.

przedstawia

jednorodne pole przepływu wody
(np. w rzece) charakteryzujące
się stałym wektorem przepływu
, czyli stałą prędkością cieczy w
dowolnym punkcie.

 Rysunek

7.7a

przedstawia

płaską

płaszczyznę

o

powierzchni A

a

zanurzoną w

„polu przepływowym wody” pod
kątem prostym do wektora
.









33

Strumień masy wody

( w [kg/s] ) przez tę

powierzchnię (czyli masa wody przepływająca w
jednostce czasu przez powierzchnię A

a

) wynosi:

(7.12)

gdzie  jest gęstością cieczy.
Jeżeli powierzchni A

a

przyporządkujemy wektor

prostopadły do powierzchni i o module równym A

a

to

(7.12) możemy zapisać:

(7.13)

Z (7.13) widać, że strumień pola przez powierzchnię
jest wielkością skalarną

.

a

,





a

a

,

A















a

A



a

a

,

A



















34

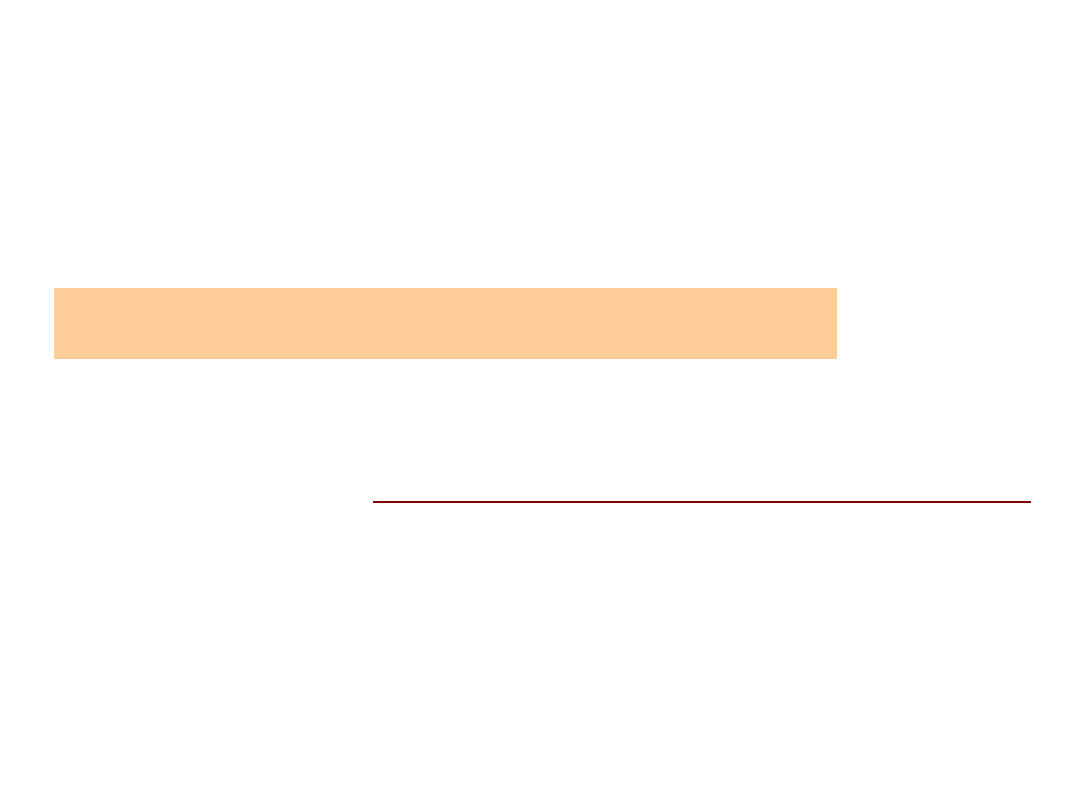
Rysunek 7.7b przedstawia płaską powierzchnię

A

b

, której rzut

jest równy A

a

.

Wydaje się rzeczą jasną, że strumień masy
przez powierzchnię A

b

musi być taki sam, jak przez

powierzchnię A

a

. Aby to sobie unaocznić, możemy

zapisać:

(7.14)







cos

A

b

b

,









b

b

a

a

,

b

,

A

cos

A

A



































Po tych wstępnych rozważaniach nad zajmiemy
się teraz , tzn.

strumieniem pola elektrycznego

.

Może się wydawać, że w tym przypadku nic nie płynie.
Jednakże

z formalnego punktu widzenia równania

(7.13) i (7.14) nie odnoszą się tylko do cieczy, lecz
także do dowolnego pola wektorowego

(stałego w tym przypadku).





E







35

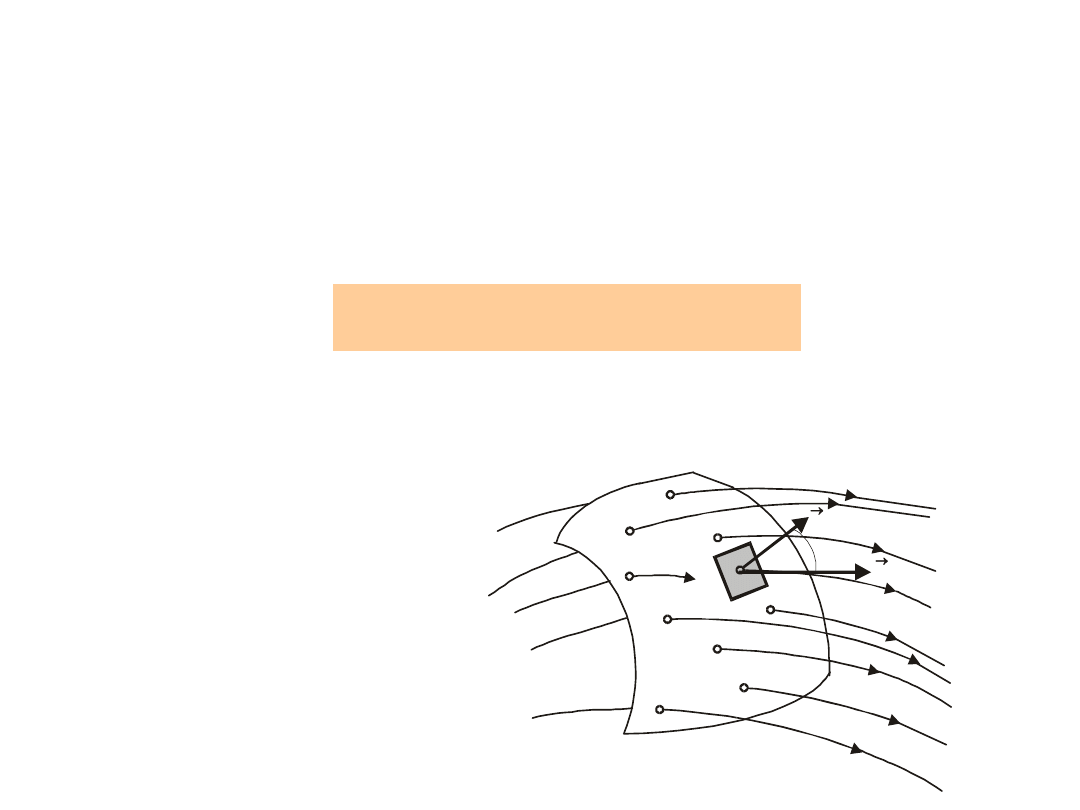
Jeżeli na rys.7.7. zamienimy na , a linie
przepływu wody na linie sił pola elektrycznego –
cała dotychczasowa dyskusja tego paragrafu
pozostaje w mocy.

Zatem strumieniem elementarnym

natężenia pola elektrycznego przez element
powierzchni nazywamy iloczyn skalarny

(7.15)

gdzie jest to wektor prostopadły do
elementu powierzchni ds, o długości równej polu
tego elementu. W układzie SI strumień wyrażamy
w [Vm].





E



E

d

E



s

d

















cos

ds

E

s

d

E

d

E





s

d





d s

E

S

Definicja strumienia

pola elektrycznego

36

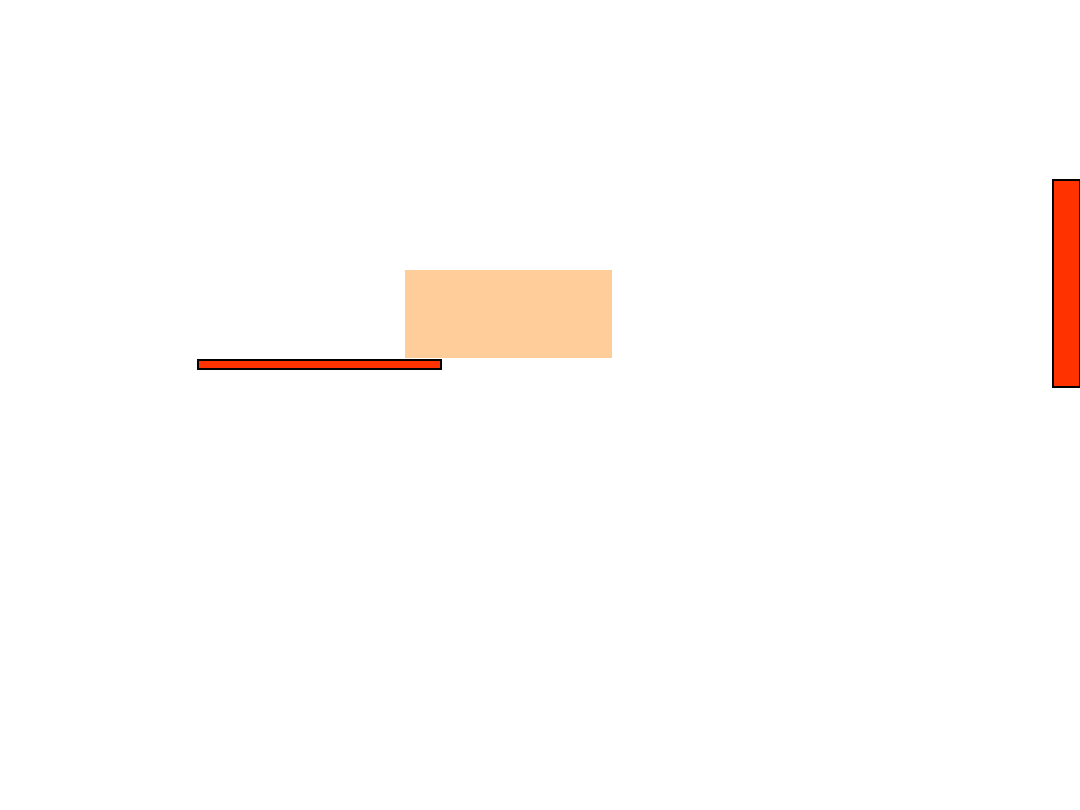
Aby obliczyć strumień pola elektrycznego

przez dowolną powierzchnię S należy zsumować
wszystkie strumienie elementarne

przenikające

powierzchnię S.

Wobec powyższego, strumień przez daną

powierzchnię S nazywamy całką powierzchniową o
postaci:

(7.16)

E



E

d

S

,

E



 





S

S

,

E

s

d

E





37

11.8 Prawo Gaussa

 

Wyprowadzimy prawo Gaussa w najprostszym

przypadku, dla ładunku punktowego q otoczonego kulą
o promieniu r i środku pokrywającym się z położeniem
ładunku. Strumień



E

dla tego układu jest

(11)

Jak widzimy strumień pola nie zależy od wielkości
powierzchni.

Pokażemy teraz, że zawsze całkowity strumień
natężenia pola elektrycznego ładunku punktowego
przez powierzchnię dowolnego kształtu będzie równy

r

o

r

o

q

r

r

q

r

E

S

d

E

E





























2

2

2

4

4

1

4





r

o

/

q





38

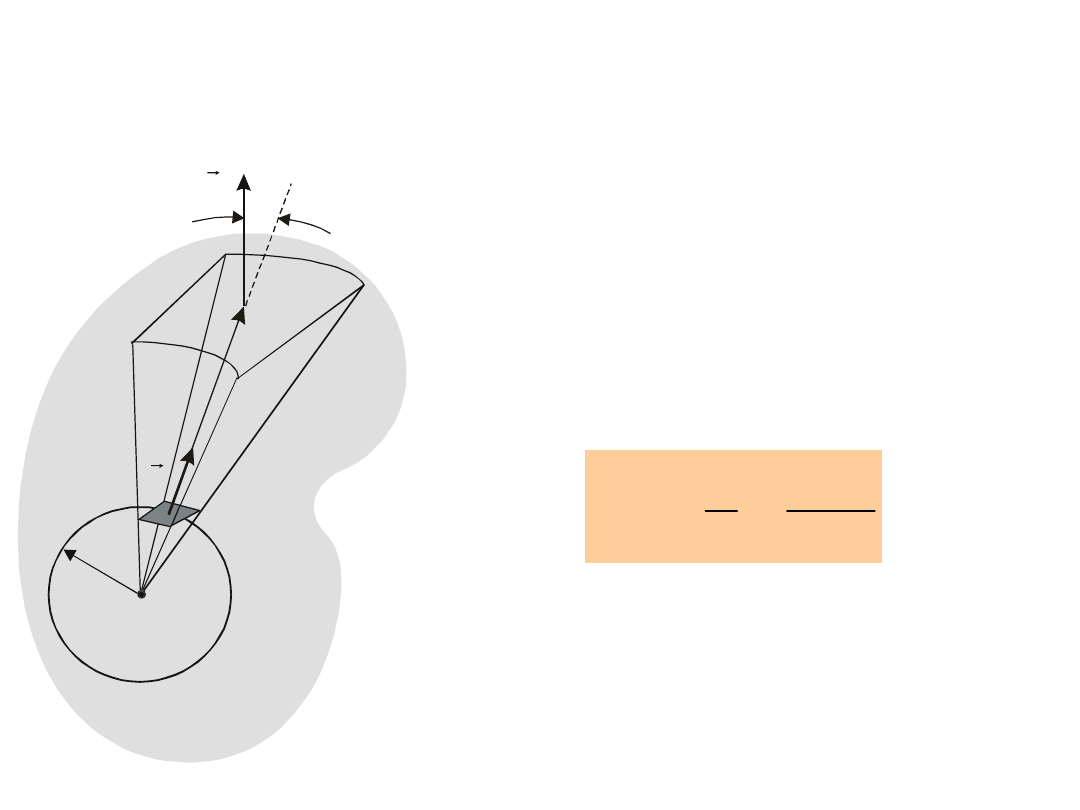
Rozpatrzymy dowolną powierzchnię, która

zawiera kulę wraz z ładunkiem (rys. 4.4) i udowodnimy,
że całkowity strumień przez tę powierzchnię jest
identyczny jak strumień przez powierzchnię kulistą.

r

R

A

a



Strumień przez dowolną
zamkniętą powierzchnię
zawierającą ładunek q.

Stożek o wierzchołku w

punkcie położenia ładunku q
wycina

mały

element

powierzchni z powierzchni
kulistej i element powierzchni
z powierzchni dowolnej.
Powierzchnia elementu jest
większa

od

powierzchni

elementu



cos

r

R

a

A

1

2















a

a

A



A



39

ze względu na ten sam kąt bryłowy oraz ze

względu na nachylenie elementu do kierunku
radialnego.

Kąt



jest kątem zawartym pomiędzy zewnętrzną

normalną a kierunkiem radialnym. Strumień natężenia
pola przez oba elementy jest równy





cos

R

A

r

a

d

2

2





A



a

E

a

E

d

r

r

a

,

E













oraz





cos

A

E

A

E

d

R

R

A

E,











Wstawiając do równania na strumień
wartości

A

E,

d



R

q

E

r

o

R

2

4

1









cos

r

R

a

=

A

1

2













i

dostajemy

40

a

E

a

q

d

r

r

o

A

E,











4

Wynik ten oznacza, że strumienie przez oba
elementy są równe. Również całkowity strumień
przez obie powierzchnie będzie jednakowy, a
więc strumień natężenia pola przez dowolną
zamkniętą powierzchnię otaczającą ładunek q
będzie równy q/



o



r

.

Jeżeli ładunek leży na zewnątrz zamkniętej dowolnej
powierzchni, to strumień przez tę powierzchnię znika.
Jeżeli mamy n ładunków punktowych objętych
powierzchnią, to strumień przez tę powierzchnię
wynosi:





n

1

=

i

r

o

E

i

q







Skorzystaliśmy

z

zasady

superpozycji pól elektrycznych
pochodzących od poszczególnych
ładunków

n

,....., q

, q

q

2

1

41

W przypadku ładunku o gęstości objętościowej (x,y,z)

(14)

Prawo Gaussa brzmi: strumień natężenia
pola

elektrycznego

przez

dowolną

powierzchnię

zamkniętą

równa

się

iloczynowi

całkowitego

ładunku

zamkniętego w tej powierzchni przez



o



r

.

.









V

r

o

S

dV

S

d

E







1





q/



o



r

42

11.11

Napięcie i potencjał

 

Ze wzoru (7.5)

wynika, że na ładunek q

0

znajdujący się w polu

elektrycznym działa siła

. Siła ta może

wykonać pracę przesuwając ładunek.

Elementarna

praca

wykonywana

przez

siłę

elektryczną przy przesunięciu ładunku na elemencie
drogi wynosi

(7.24)

Praca sił pola elektrycznego na drodze między
punktami A i B wyrazi się zatem wzorem

(7.25)

E

q

F

0







l

d



l

d

E

q

l

d

F

dW

0

















l

d

E

q

l

d

F

W

B

A

0

B

A

AB





















r

r

r

q

4

1

r

r

q

r

q

q

4

1

q

F

E

2

o

2

o

o























43

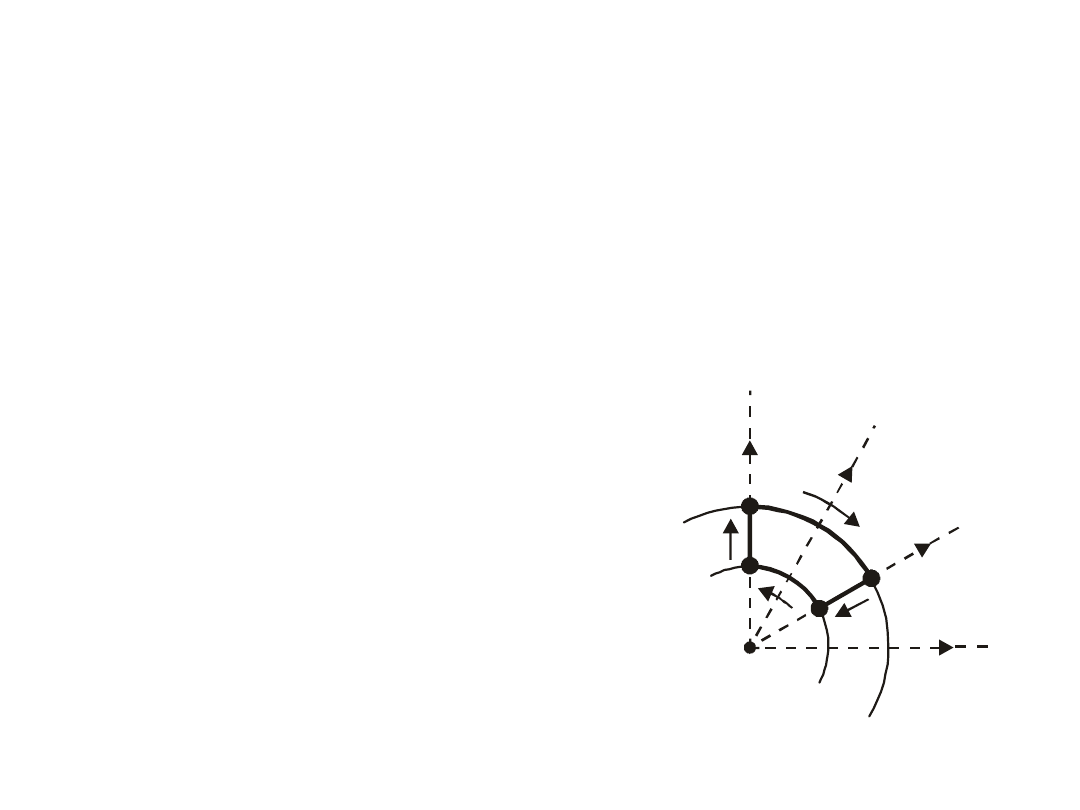
Można wykazać, że pole elektrostatyczne,

tzn. takie które nie zmienia się w czasie, jest
polem potencjalnym, czyli że siły elektryczne są
siłami zachowawczymi. Oznacza to, że wartość pracy
W

AB

nie zależy od wyboru drogi między punktami A i B.

Z własności sił potencjalnych wiadomo też, że praca
takich sił na drodze zamkniętej jest równa zeru

.

Powyższe sprawdzimy dla najprostszego przypadku
przesuwania ładunku próbnego q

0

w polu ładunku

punktowego Q po drodze ABCDA, zaznaczonej na
rysunku 7.10.

Q

A

B

C

D

Rys.7.10. Całkowita praca na drodze

zamkniętej ABCDA potrzebna na
przesunięcie ładunku q

0

w polu

elektrycznym ładunku Q jest równa
zeru – co oznacza, że pole elektryczne
jest polem potencjalnym

.

44

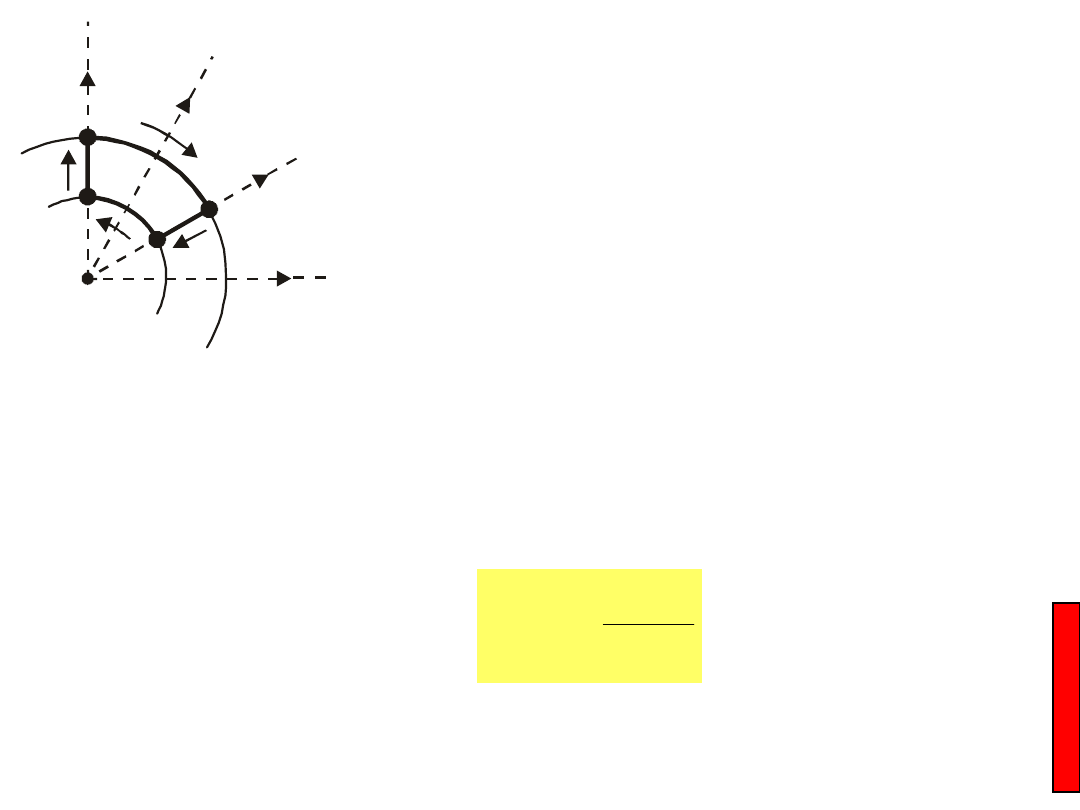
Q

A

B

C

D

Odcinki AB i CD tej drogi leżą

na liniach sił pola, odcinki BC i DA –
na łukach kół, które w każdym swym
punkcie są prostopadłe do linii sił.
Praca sił pola na odcinku AB jest
równa

co

do

wartości,

lecz

przeciwna co do znaku względem
pracy wykonanej na odcinku CD.

Prace na odcinkach BC i AD są równe zeru ze

względu na prostopadłość kierunków siły i przesunięcie.
A zatem całkowita praca na drodze zamkniętej ABCDA
jest równa zeru.

Zdefiniujemy obecnie napięcie elektryczne U

AB

między punktami A i B, mianowicie

(7.26)

Napięciem elektrycznym między punktami A i

B nazywamy stosunek pracy W

AB

wykonanej przy

przesunięciu ładunku q

0

z punktu A do B do

wielkości tego ładunku.

0

AB

AB

q

W

U



45

Napięciem elektrycznym między punktami A i B

nazywamy stosunek pracy W

AB

wykonanej przy

przesunięciu ładunku q

0

z punktu A do B do wielkości

tego ładunku

.

Należy podkreślić, że niezależność pracy od

kształtu drogi umożliwia jednoznaczne określenie
napięcia między danymi punktami A i B.

Przejdziemy teraz do określenia potencjału:

Potencjałem danego punktu A nazywamy napięcie

między punktem A i punktem nieskończenie odległym.

Zatem

potencjał V

A

jest związany z pracą

przesunięcia ładunku q

0

od punktu A do

nieskończoności

0

A

A

q

W

V





46

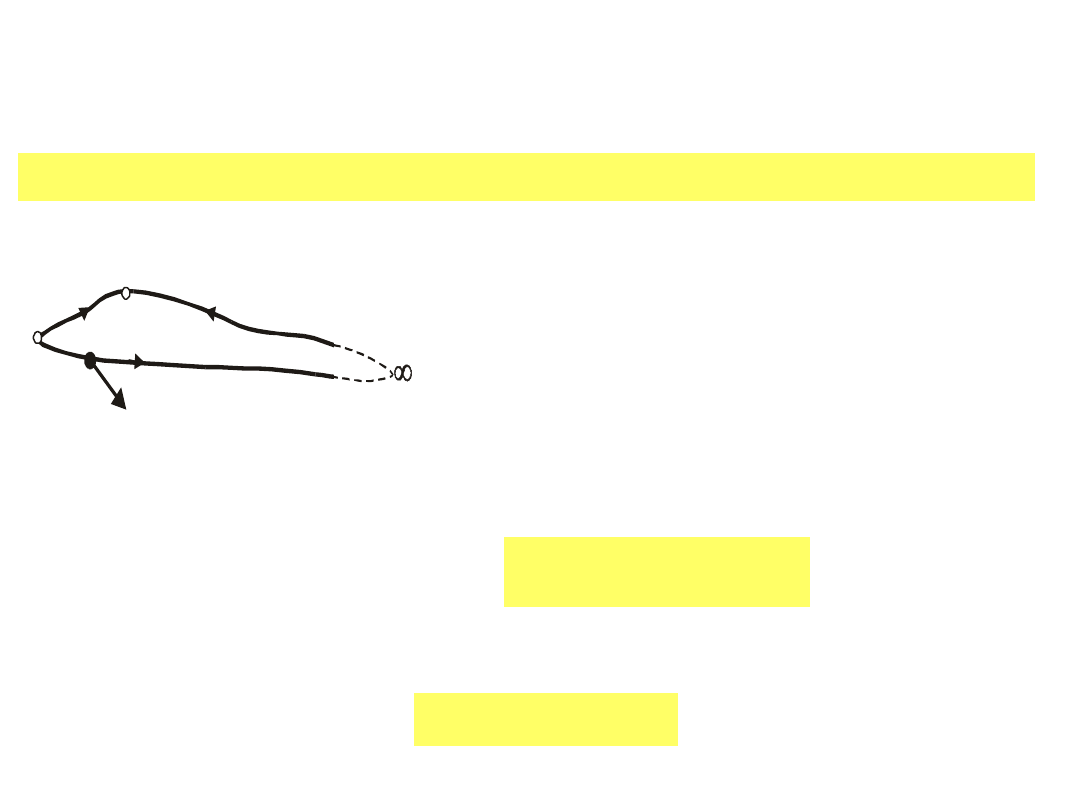
Aby uzyskać zależność między napięciem a

potencjałem rozważmy pracę wykonaną na drodze od
punktu A do nieskończoności, a następnie od
nieskończoności do B (rys.7.11). Praca ta wynosi





B

A

0

B

0

A

0

B

0

A

0

B

A

B

A

V

V

q

V

q

V

q

U

q

U

q

W

W

W



























A

B

q

0

F

Rys.7.11.

Praca

przesunięcia

ładunku q

0

od punktu A do punktu

, a następnie do punktu B jest

równa pracy na drodze AB

Z drugiej strony, ponieważ praca nie zależy od wyboru
drogi, musi być ona równa pracy na odcinku AB, czyli:

Z porównania ostatnich dwóch związków wynika, że

AB

0

AB

U

q

W



B

A

AB

V

V

U





47

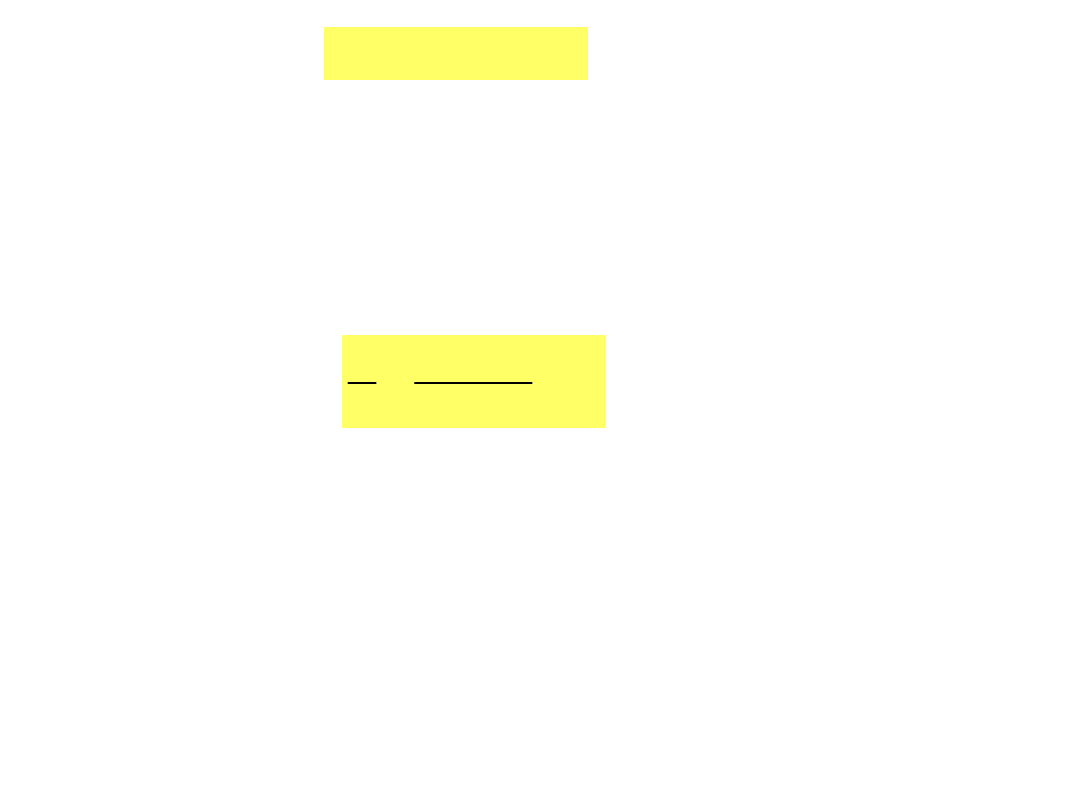
B

A

AB

V

V

U





Napięcie

między

dwoma

punktami

pola

elektrycznego równa się różnicy potencjału tych
punktów.

Z wzorów definicyjnych napięcia elektrycznego (7.26) i
potencjału (7.27) wynika, że napięcie i potencjał mają
wspólną jednostkę.

Jednostka ta:

nazywa się

woltem [V].

V

s

A

s

V

A

C

J











48

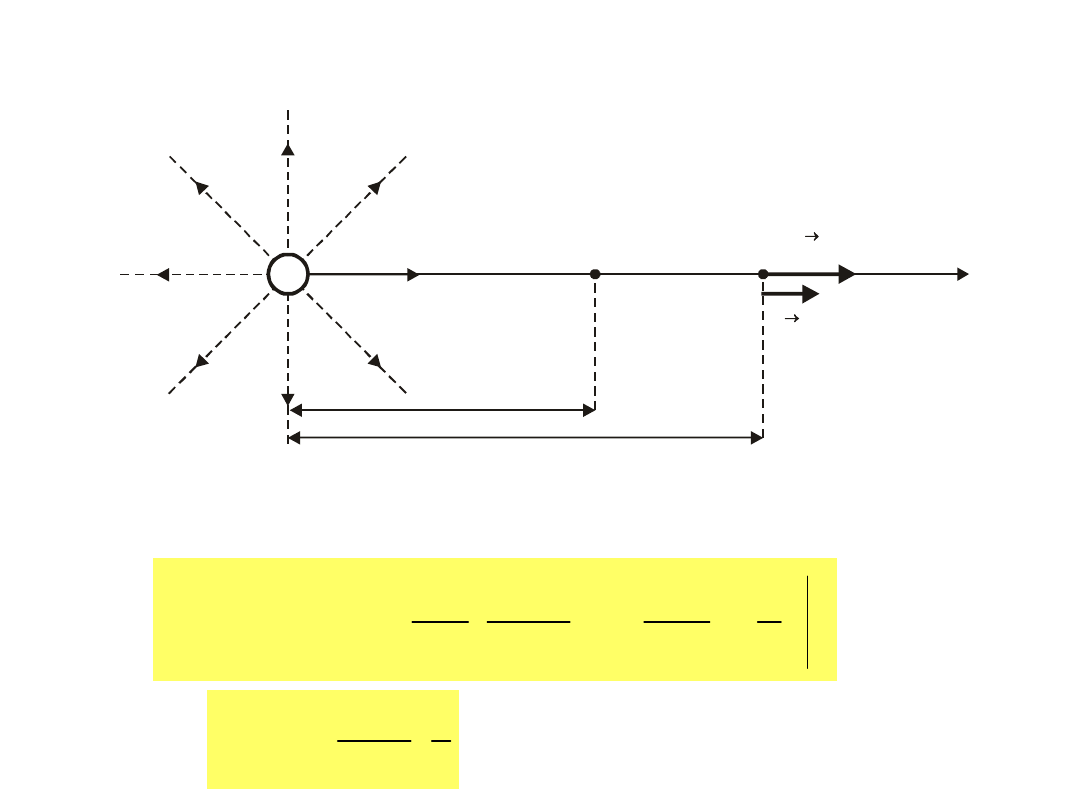
Obliczmy teraz potencjał pola elektrycznego od

odosobnionego ładunku punktowego Q w punkcie A
odległym od Q o r.

+ Q

+

r

x

d x

E

+ q

0

x

Praca jaką wykonuje pole elektryczne przesuwając
ładunek q

0

od A do nieskończoności wynosi



















 





















r

0

r

2

0

r

A

x

1

4

Qq

dx

x

q

Q

4

1

x

d

F

W





r

1

4

Qq

W

0

A









(7.28
)

49

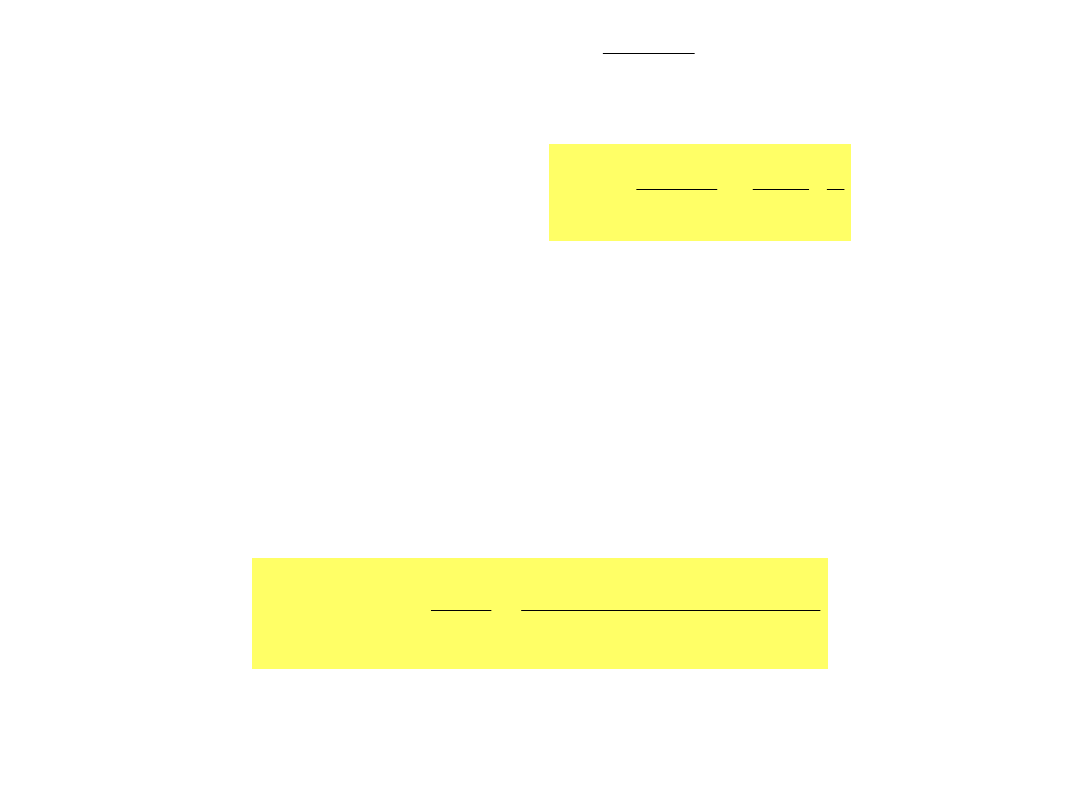
Korzystając z wzoru (7.27)

obliczamy potencjał pola

(7.29)

Ponieważ potencjał pola elektrycznego jest skalarem,
potencjał dla układu ładunków jest sumą potencjałów,
pochodzących od każdego ładunku z osobna. Wynika to
z zasady superpozycji, którą stosuje się również do
potencjałów.

Potencjał dowolnego rozkładu ładunków

możemy przedstawić jako całkę

(7.30)

r

1

4

Q

q

W

V

0

A

A











0

A

A

q

W

V





















V

r

'

dz

'

dy

'

dx

'

z

,

'

y

,

'

x

4

1

z

,

y

,

x

V

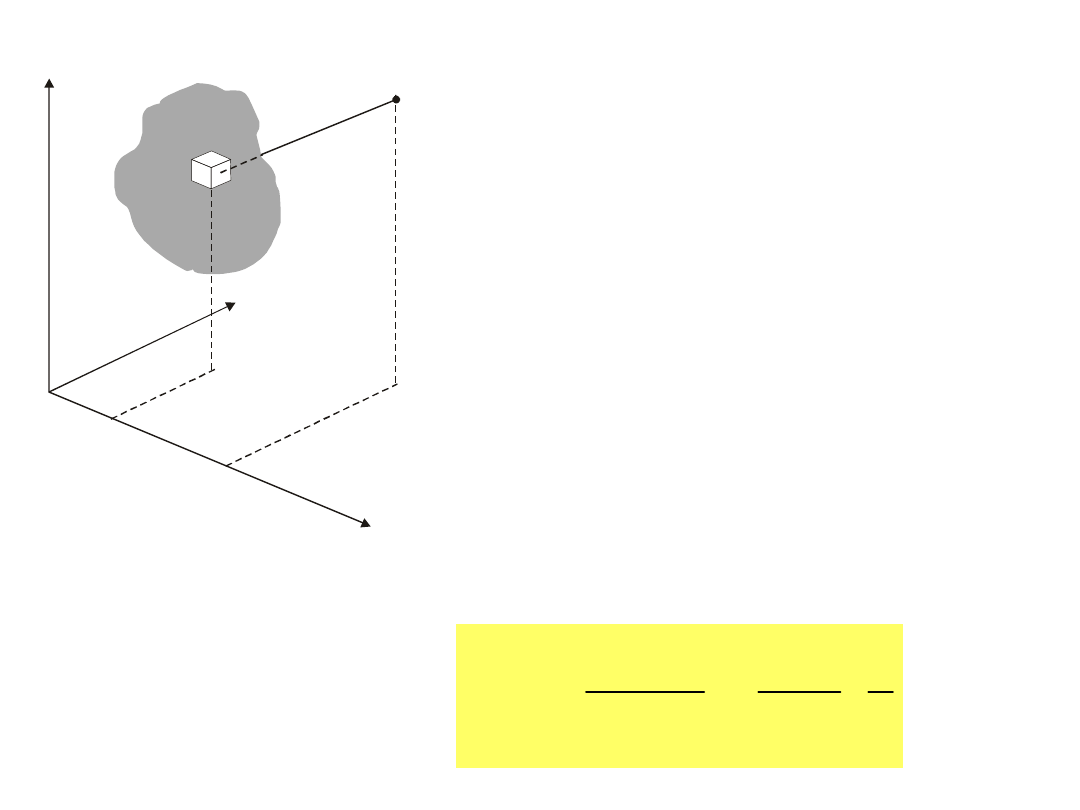
gdzie  to gęstość objętościowa ładunku zgromadzonego

w obszarze V, r oznacza odległość między elementami

objętości dV=dx’dy’dz’, a punktem (x,y,z), w którym

pytamy o potencjał (rys.7.13).

50

z

x ’

x

x

( x ’ ,y ’ ,z ’ )

d V = d x ’ d y ’ d z ’

r

P u n k t, w k t ó r y m

o b l i c z a m y

p o te n c j a ł p o l a

( x ,y , z )

Rys.7.13. Potencjał V(x,y,z)
pochodzący od dowolnego rozkładu
ładunków

Potencjał charakteryzuje pole
elektryczne w tym samym
stopniu co natężenie pola.
Graficznie

pole

można

przedstawić

za

pomocą

powierzchni
ekwipotencjalnych,

które

charaktery-zują się tym, że w
każdym ich punkcie potencjał
ma stałą wartość. Można
udowodnić, że linie pola
muszą być prostopadłe do
powierzchni

ekwipo-

tencjalnych.

Na

przykład

powierzchnie

ekwipotencjalne pola ładunku punktowego są, jak widać
ze wzoru (7.29), sferami o promieniu r.

r

1

4

Q

q

W

V

0

A

A











51

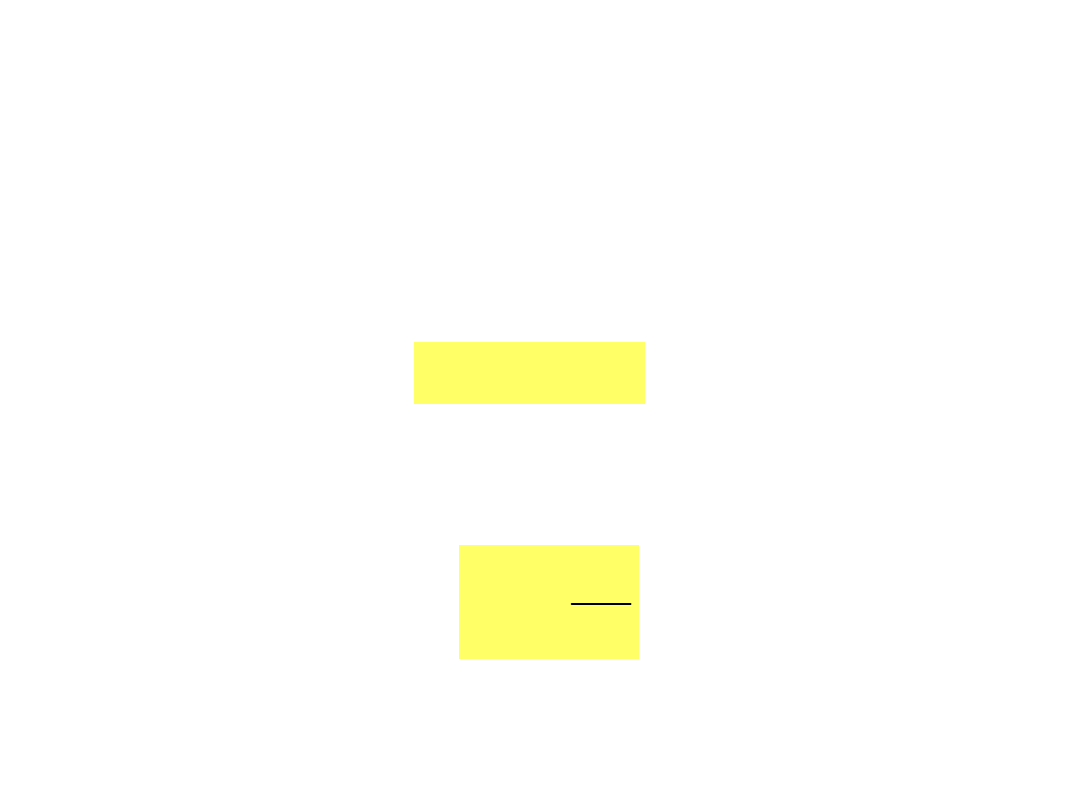
Powierzchnia przewodnika, na którym ładunki

znajdują się w równowadze, jest zawsze powierzchnią
ekwipotencjalną, w przeciwnym bowiem razie siły
elektryczne nie byłyby prostopadłe do powierzchni i
spowodowałyby ruch ładunków.

Znajomość potencjału w dowolnym punkcie

umożliwia obliczenie natężenia tego pola. Ze wzoru
(7.24) wynika, że

(7.31)

(znak minus jest związany z tym, że potencjał maleje w
kierunku wektora ). Stąd otrzymujemy:

(7.32)

Z wzoru (7.32) widać, że natężenie pola elektrycznego
wyrażamy w [V/m].

l

d

E

dV











dl

dV

E 



52

11.12

Pojemność elektryczna i kondensatory

53

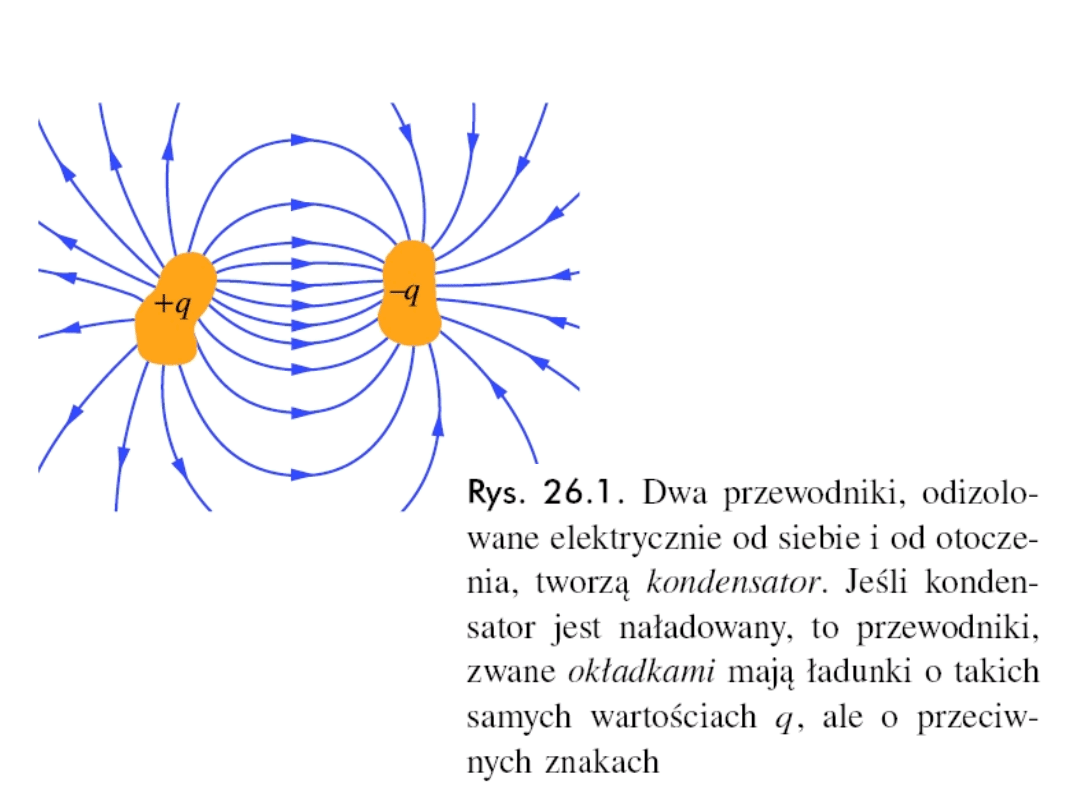
11.12

Pojemność elektryczna i kondensatory

Kondensatorem nazywamy dwa blisko siebie

położone przewodniki o różnych potencjałach i
przeciwnych ładunkach.

Interesuje nas związek

między ładunkiem Q na jednej z płytek a różnicą
potencjału między nimi. Okazuje się, że

dla ustalonej

pary przewodników stosunek ładunku do różnicy
potencjałów jest stały. Stałą tę nazywamy
pojemnością kondensatora i oznaczamy przez C.

2

1

V

V

Q

C





Rozpatrzymy

dwie

przewodzące

płytki

o

jednakowych rozmiarach ustawione równoległe w
odległości d od siebie (rys.7.14). Niech powierzchnia
każdej z płytek wynosi S. Niech na jednej płytce
znajduje się ładunek Q, a na drugiej –Q. Potencjały obu
płytek wynoszą odpowiednio V

1

i V

2

.

54

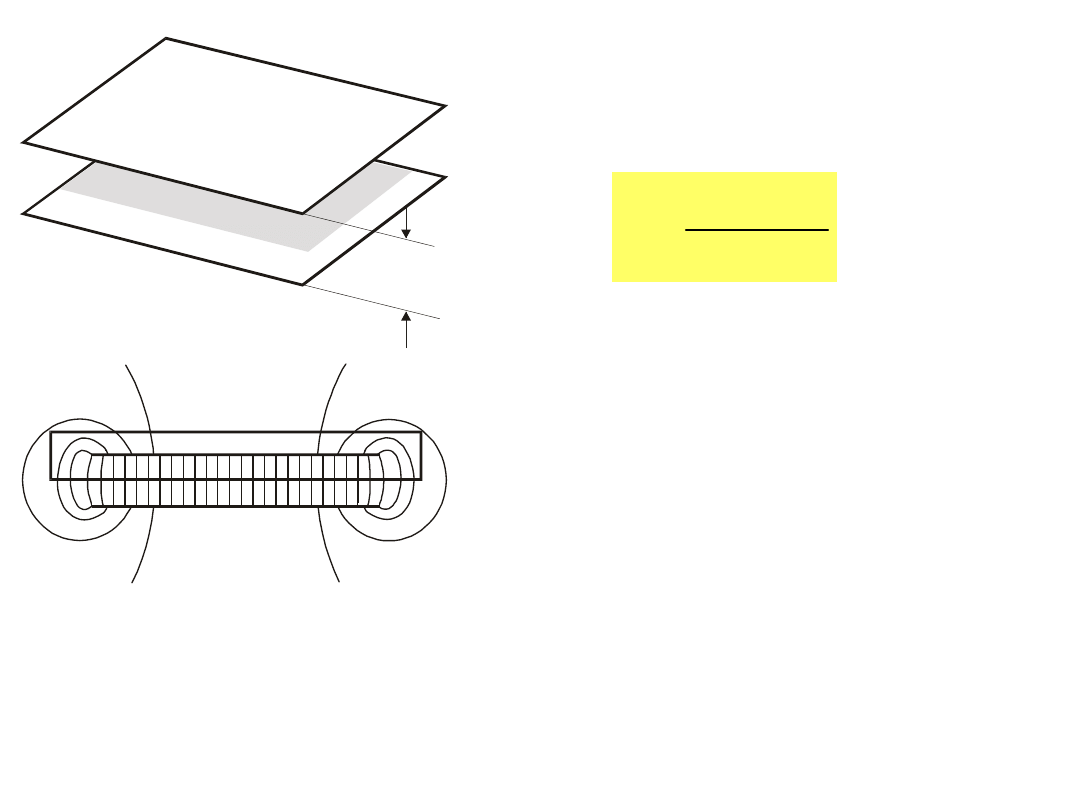
P o w ie rz c h

n i a S

Ł a d u n e k + Q

Ł a d u n e k -Q

V

1

V

2

d

a )

b )

A

D

V

1

V

2

C

B

Rys.7.14. Kondensator płaski

W obszarze między płytkami
wartość

natężenia

pola

elektrycznego jest równa

(7.34)

Przebieg linii pola (rys.7.14b)
wskazuje, że pole to jest
jednorodne z wyjątkiem
obszarów brzegowych.
Obliczymy strumień indukcji
przez powierzchnię
prostopadłościenną (ABCD)
(rys.7.14b) zamykającą jedną
okładkę. Strumień przez
powierzchnię górną CD i
boczne AD i BC możemy
zaniedbać ponieważ przechodzi
tam niewielka liczba linii sił
pola.

d

V

V

E

2

1





55

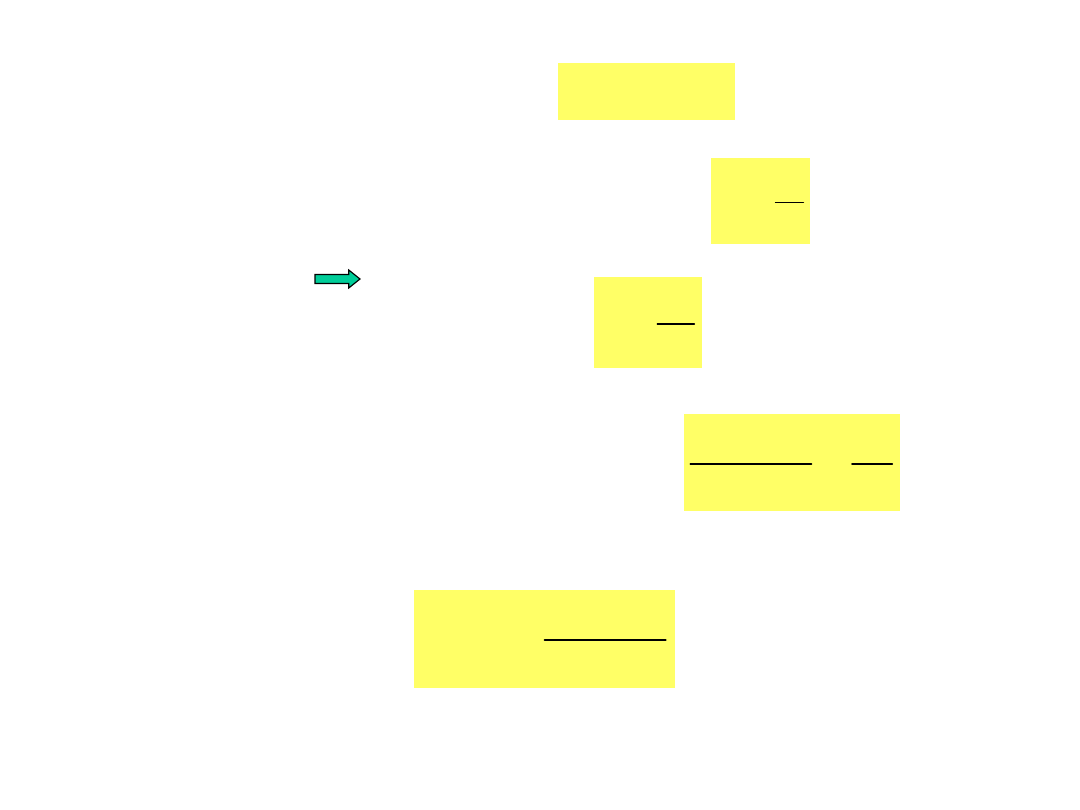
Pozostaje powierzchnia AB, dla której

(7.35)

Według prawa Gaussa

, zatem

(7.36)

stąd na mocy (7.22)

(7.37)

Porównując (7.34) z (7.37) otrzymujemy

Całkowity ładunek Q znajdujący się na jednej z elektrod
kondensatora jest równy

(7.38)

Równanie to tym lepiej opisuje realną sytuację, im
mniejszy jest stosunek odległości d między płytkami do
długości ich boków.

E

D

r

o











DS

S

,

D





Q

S

,

D





S

Q

D 

S

Q

E





S

Q

d

V

V

2

1







d

V

V

S

Q

2

1









56

Po podstawieniu (7.38) do (7.33) otrzymujemy wzór na
pojemność kondensatora płaskiego

(7.39)

W jednostkach układu SI ładunek Q we wzorze (7.33)
wyraża się w kulombach [C], potencjał zaś w woltach
[V]. W układzie tym jednostką pojemności jest farad
[F]. Farad jest jednostką bardzo, bardzo dużą.
Kondensator jedno faradowy miałby gigantyczne
rozmiary. Dlatego też zazwyczaj w praktyce stosuje się
jednostki mniejsze: mikrofarady i pikofarady .

 

d

S

C

r

o







57

11.13

Gęstość energii pola elektrycznego

 Załóżmy, że początkowo nie naładowany kondensator
stopniowo ładowano, przy czym różnica potencjałów
wzrastała od 0 do . Ładunek na okładkach
kondensatora będzie wzrastał od 0 do , gdzie
= C. Praca wykonana przy przemieszczaniu
ładunku dq od ujemnie naładowanej płytki do
naładowanej dodatnio wynosi

Całkowita praca, czyli energia zmagazynowana w
kondensatorze

(4.35)

o

V

o

Q

o

Q

o

V

Vdq

dW

C

Q

dq

C

q

dq

V

W

o

V

0

Q

o

o

2

0

2

1







 

Interesujące jest aby przekształcić wzór (4.35) i
zapisać energię zgromadzoną w kondensatorze nie
w zależności od ładunku, ale w zależności od
natężenia pola elektrycznego.

58

Dla kondensatora płaskiego, uwzględniając (4.31),

mamy

czyli

Podstawiając to wyrażenie do (4.35) otrzymamy

Uwzględniając z kolei (4.34) mamy

Teraz dzieląc obie części przez objętość kondensatora
Sd

o

, otrzymujemy gęstość energii pola elektrycznego

S

Q

d

o

o

r

r

o

o

d

V

















S

Q

d

E

r

o

o

o









 V

SE

Q

r

o

o











C

SE

ε

ε

W

r

o

2

2

1



o

2

Sd

2

E

W

r

o







2

2

1

E

w

r

o







(4.36)

59

Energia zużyta na przemieszczenie ładunku

gromadzona jest w polu elektrycznym kondensatora, a
gęstość energii pola elektrycznego wynosi



o



r

E

2

/2

(J/m3).

Z bardziej ogólnych ale zarazem bardziej

złożonych rozważań wynika, że całkowita energia
konieczna do uformowania dowolnego rozkładu
ładunków, jest równa dokładnie całce po



o



r

E

2

/2

liczonej po całej przestrzeni V, gdzie E jest polem
utworzonym przez taki rozkład ładunku

(4.37)

Wobec tego wyrażenie (4.36) ma bardziej ogólne
znaczenie i pozwala przyjąć fizyczną interpretację
energii zgromadzonej w jednostce objętości pola
elektrycznego.

dV

E

W

r

o





2

2





2

2

1

E

w

r

o







(4.36
)

60

11.14 Dielektryki

 W poprzednich punktach generalnie rozważaliśmy
pola utworzone przez ładunki w przewodnikach
znajdujących się w próżni. Wiadomo, że jeżeli między
okładkami kondensatora umieścimy substancję, to
pojemność kondensatora wzrasta do C’. Wówczas
biorąc stosunek C’ do C możemy określić względną
przenikalność dielektryczną substancji

(4.38)

We wzorze tym C jest pojemnością kondensatora
próżniowego.

C

'

C

r





61

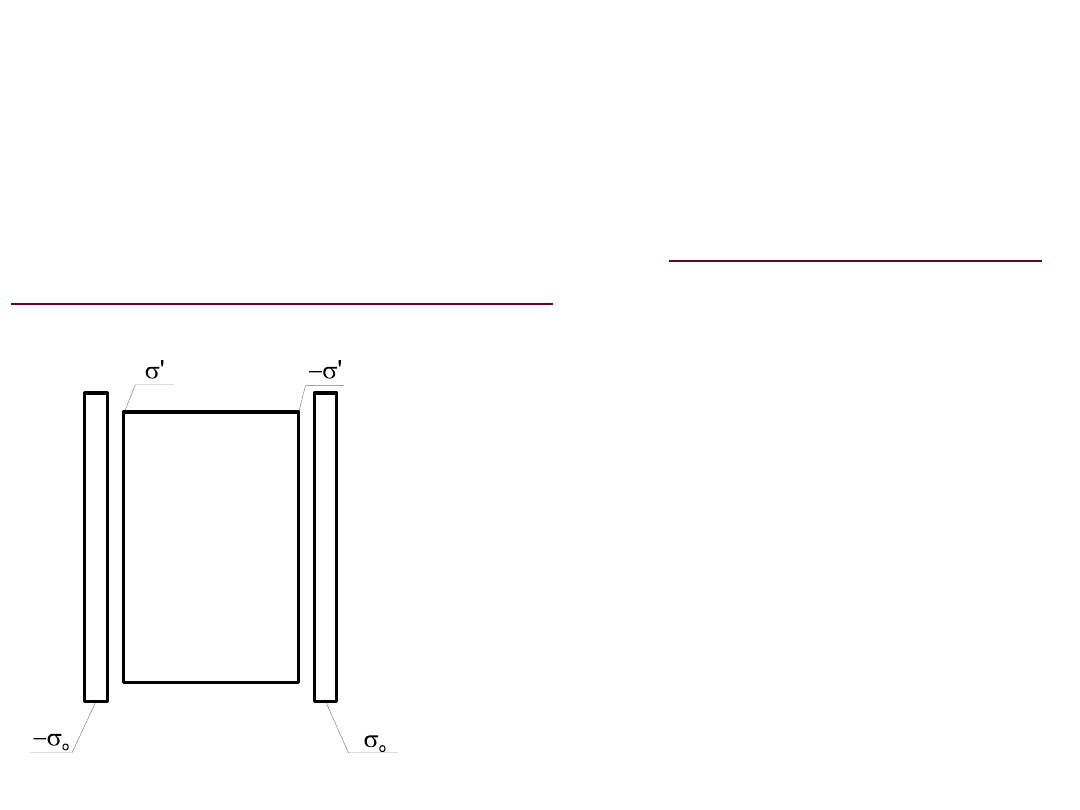
Dielektryki są to ciała, w których ładunki nie mają
możliwości

swobodnego

przemieszczania.

Jeżeli

dielektryk

umieścimy

w

zewnętrznym

polu

elektrycznym, to na jego granicach indukują się ładunki
(rys. 4.12) na skutek ograniczonego przesunięcia
ładunków w skali mikroskopowej.

Zjawisko to nazywa

się polaryzacją dielektryka

. Efekt polaryzacji jest

jakościowo podobny do powstania łańcucha dipoli. Na
jednym końcu łańcucha dipole mają ładunki dodatnie, a
na drugim ujemne, a więc dielektryk jako całość
wykazuje istnienie

ładunków

na

swoich

powierzchniach prostopadłych do
kierunku linii sił pola. Ładunki te
nazywa

się

ładunkami

nie

związanymi.

Po

usunięciu

zewnętrznego pola elektrycznego
ładunek

na

powierzchniach

dielektryka znika.

+
+

+

+

+

+

+

+

+

+

+

+

+

+

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

+

Rys. 4.12. Powstanie ładunku

indukowanego' na powierzchni

dielektryka umieszczonego między

okładkami kondensatora.

62

Wskutek zjawiska polaryzacji zmienia się wartość

natężenia pola w ośrodku dielektrycznym w stosunku do
tego natężenia pola, jakie istnieje w danym obszarze
”wypełnionym” próżnią. Jest to wynik nałożenia się na
pole zewnętrzne dodatkowego pola wytworzonego przez
ładunki związane.

Przed opisem ilościowym tego zjawiska, omówimy

rodzaje polaryzowalności dielektryka.

W cząsteczkach niektórych dielektryków (np. H

2

,

Cl

2

, CCl

4

, węglowodory) elektrony są rozmieszczone

niejednorodnie dookoła jąder. W cząsteczkach tych
środki ciężkości ładunków dodatnich i ujemnych, przy
braku zewnętrznego pola elektrycznego, pokrywają się i
moment dipolowy równa się zeru. Z tego powodu
cząsteczki

takich

dielektryków

nazywamy

niespolaryzowanymi.

Jeśli

niespolaryzowaną

cząstkę

dielektryka

umieścimy w zewnętrznym polu elektrycznym, to
następuje rozsunięcie środków ciężkości ładunku
dodatniego i ujemnego cząsteczki i wzbudzi się w niej
moment dipolowy

63

Moment elektryczny dipola takiego dielektryka równa
się

(4.39)

gdzie  jest współczynnikiem polaryzowalności atomu.
Kierunek wektora pokrywa się z kierunkiem
wektora natężenia zewnętrznego pola
elektrycznego.

E

p

o

e











e

p



E



64

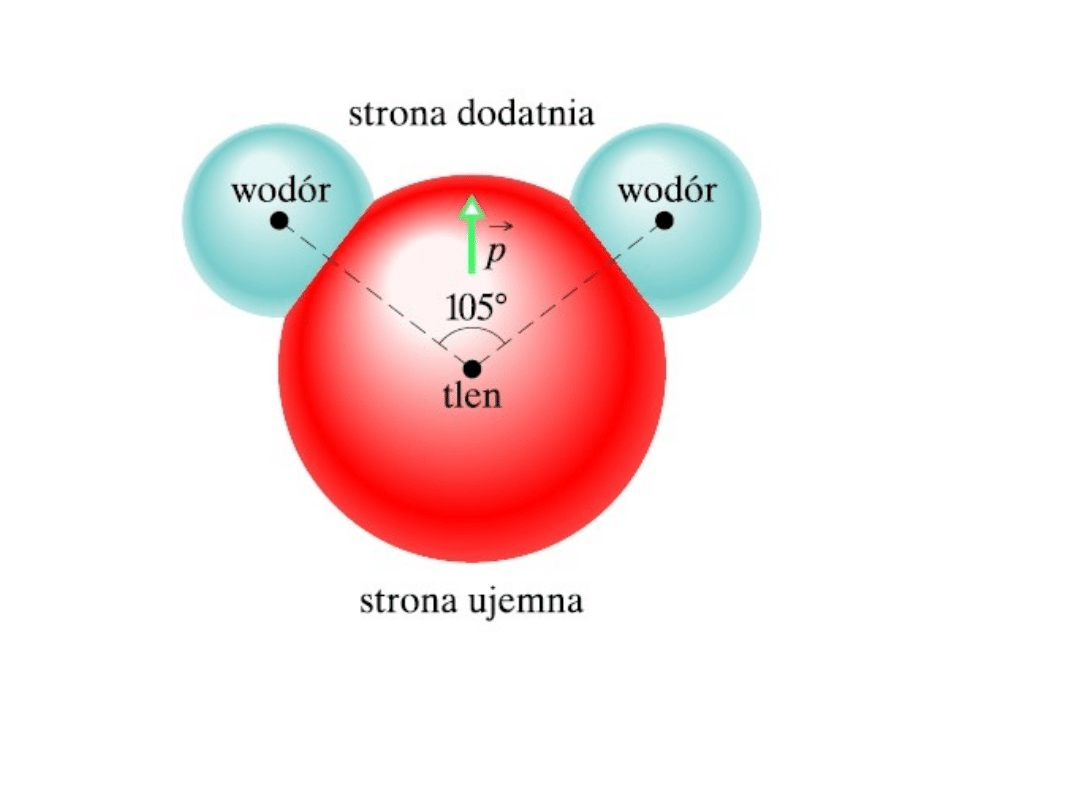
Liczną grupę stanowią

cząsteczki o samoistnym

momencie dipolowym

, w których środek ciężkości

średniego ładunku dodatniego nie pokrywa się z
środkiem ciężkości średniego ładunku ujemnego

.

Przykładem mogą być cząsteczka H

2

O (również NH

3

, HCl,

CH

3

Cl) w której atomy wodoru i tlenu rozłożone są

niesymetrycznie.

Takie

cząsteczki

nazywamy

spolaryzowanymi. W wyniku nieuporządkowanego ruchu
cieplnego cząsteczek, wektory ich momentów dipolowych
wykazują chaotyczną orientację i wypadkowy moment
dipolowy w dowolnej objętości dielektryka równa się
zeru.

Jednak

pod

wpływem

zewnętrznego

pola

elektrycznego, cząsteczki dielektryka dążą do zajęcia
takiego położenia, aby kierunek wektorów ich momentów
dipolowych był zgodny z kierunkiem wektora .

Pojawia się więc orientacja momentów dipolowych
cząsteczek przeważnie wzdłuż linii sił pola. Orientacja ta
jest tym większa, im silniejsze jest pole elektryczne w
dielektryku oraz im słabszy jest ruch cieplny cząsteczek,
tj. im niższa jest temperatura.

Powyższe zjawisko nosi

nazwę

polaryzacji

skierowanej

dielektryka

o

cząsteczkach spolaryzowanych.

e

p



e

p



E



65

66

Cząsteczki niespolaryzowane uzyskują w polu

elektrycznym momenty dipolowe indukowane w wyniku
odkształcenia orbit elektronowych. Zachodzi wówczas
tzw.

polaryzacja elektronowa dielektryka.

W dielektrykach jonowych (krystalicznych) typu

NaCl, CsCl; wszystkie jony dodatnie przesuwają się pod
wpływem

pola

elektrycznego

w

kierunku

odpowiadającym kierunkowi natężenia , natomiast
wszystkie jony ujemne w kierunku przeciwnym. Ten
rodzaj polaryzacji nosi

nazwę polaryzacji jonowej

.

E



67

Jako wskaźnik ilościowy polaryzacji dielektryka

służy wektor polaryzacji

.

Wektorem polaryzacji nazywamy granicę stosunku
momentu

elektrycznego

określonej

objętości

dielektryka do tej objętości, gdy ta ostatnia dąży
do zera

(4.40)

gdzie N oznacza liczbę dipoli zawartych w objętości V
dielektryka, a moment elektryczny i-tego dipola.

W przypadku dielektryka jednorodnego o cząsteczkach
niespolaryzowanych, umieszczonego w jednorodnym
polu elektrycznym,

(4.41)

gdzie oznacza liczbę cząsteczek w jednostce
objętości.







N

1

=

i

ei

V

e

p

V

lim

P





1

0

e

P



ei

p



e

o

e

p

N

P







o

N

68

Wynika stąd, że wektory wszystkich

cząsteczek

wykazują

jednakowy

kierunek,

odpowiadający kierunkowi wektora natężenia
pola w dielektryku. Stosując wzór (4.39) otrzymujemy

(4.42)

Współczynnik

nazywamy podatnością

dielektryczną substancji.

ei

p



E



E

E

N

P

o

o

o

e























o

e

N



69

11.15 Twierdzenie Gaussa w przypadku obecności
dielektryków. Wektor indukcji elektrycznej

 

Stwierdziliśmy, że w dielektryku na pole

elektryczne

ładunków

swobodnych

nakłada

się

dodatkowe pole elektryczne. Z tego względu wektor
natężenia pola elektrycznego powinien zależeć od
właściwości elektrycznych dielektryka. Okazuje się, że
wartość liczbowa jest zawsze odwrotnie
proporcjonalna do stałej dielektrycznej  ośrodka. Z
tego

względu

w

celu

jednoznacznego

scharakteryzowania pola elektrycznego celowe jest
wprowadzenie takiej wielkości , która by nie
zależała od stałej dielektrycznej danej substancji.
Można z łatwością wykazać, że warunek ten spełnia
wielkość wektorowa zdefiniowana następująco:

(4.43)

E

D

o









Wielkość nazywamy wektorem indukcji
elektrycznej

E



E



D



D



70

Wektor charakteryzuje zatem to pole

elektryczne, które wytwarzają w danej substancji
same tylko ładunki swobodne

. Ładunki związane,

powstające w dielektryku, mogą jednak wywołać
zmianę rozkładu w przestrzeni ładunków swobodnych
wytwarzających pole.

W układzie jednostek SI indukcję elektryczna mierzy się
w C/m

2

.

Strumień indukcji elektrycznej

w dowolnym

środowisku

przez element powierzchni jest określony

przez iloczyn skalarny

:

D



j

j

D

S

d

D

d











gdzie wektor określa pole i orientację j-tego
elementu powierzchni, a jest uśrednionym
wektorem indukcji elektrycznej dla j-tego elementu.

j

S

d



j

D



71

Całkowity strumień przez powierzchnię będzie równy:

(4.45)

gdzie zgodnie z definicją wektora indukcji elektrycznej
uwzględniono tylko ładunki swobodne.

W próżni

, a zatem równanie (4.45) przybiera

postać

(4.46)











swob

S

D

q

S

d

D







E

D

o













swob

S

o

q

S

d

E







Pole w dowolnym środowisku różni się od pola w

próżni tym, że wytwarzają je ładunki zarówno
swobodne,

jak

i

związane

.

Dlatego

też

w

najogólniejszym przypadku do prawej strony równania
(4.46) należy dodać sumę algebraiczną ładunków
związanych objętych przez powierzchnię zamkniętą S

72













zwią

swob

S

o

q

q

S

d

E







Ładunki swobodne wytwarzają zewnętrzne pole
elektryczne,

natomiast

ładunki

związane

wytwarzają pole wewnętrzne spolaryzowanego
dielektryka.

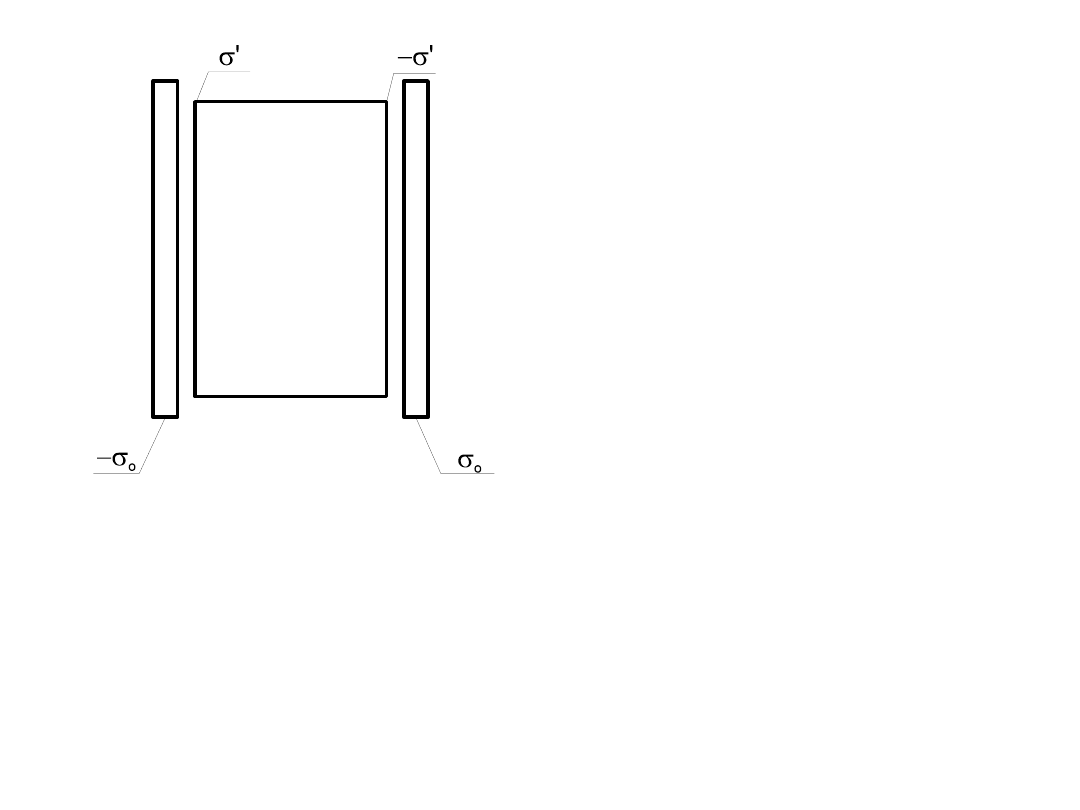
Rozpatrzymy warstwę jednorodnego dielektryka

zawartą między dwoma nieskończonymi równoległymi
płaszczyznami, naładowanymi do stałych gęstości
powierzchniowych ładunków swobodnych +



, –



(rys.

4.11). W wyniku polaryzacji dielektryka na jego
powierzchniach AA' i BB' powstają ładunki związane,
których gęstości powierzchniowe są równe odpowiednio
i . Na skutek tego pole elektryczne
ładunków związanych jest skierowane przeciwnie
względem pola zewnętrznego , wytworzonego przez
ładunki swobodne. Natężenie pola wypadkowego

p





p





p

E

o

E



p

o

E

E

E











73

+
+

+

+

+

+

+

+

+

+

+

+

+

+

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

+

74

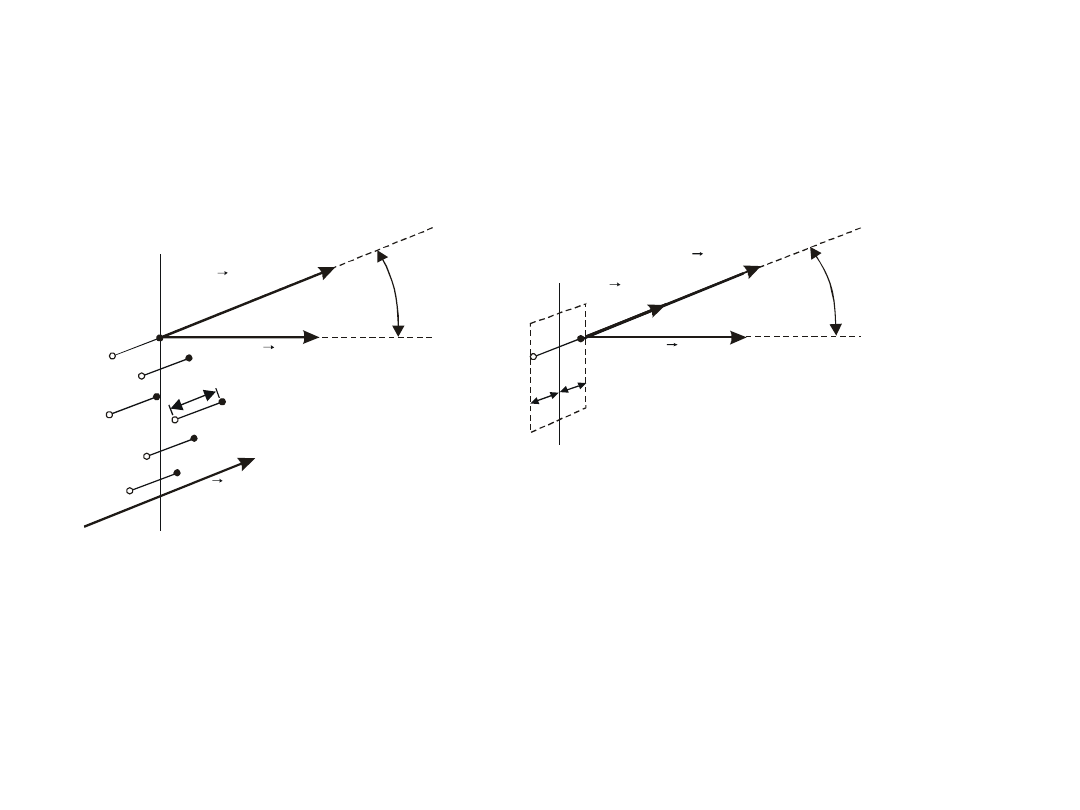
Znajdziemy teraz sumę ładunków związanych,

które powstały w wyniku polaryzacji dielektryka,
objętego zamkniętą powierzchnią S. Na rys. 4.13
przedstawiony jest tak mały element S tej powierzchni,

że można go uważać za płaski.

l





( a ) ( b )

 S

 S

l/ 2 l/ 2

E

E

e

P

e

P

n

n

+

+

+

+

+

+

-

-

-

-

-

-

-

Rys. 4.13. Powstawanie ładunku związanego

Ładunki dipoli znajdujących się na zewnątrz

powierzchni zamkniętej nie wywierają w ogóle żadnego
wpływu na strumień natężenia pola przez tę
powierzchnię. Suma algebraiczna wszystkich ładunków
dipoli całkowicie objętych powierzchnią, równa się zeru.

75

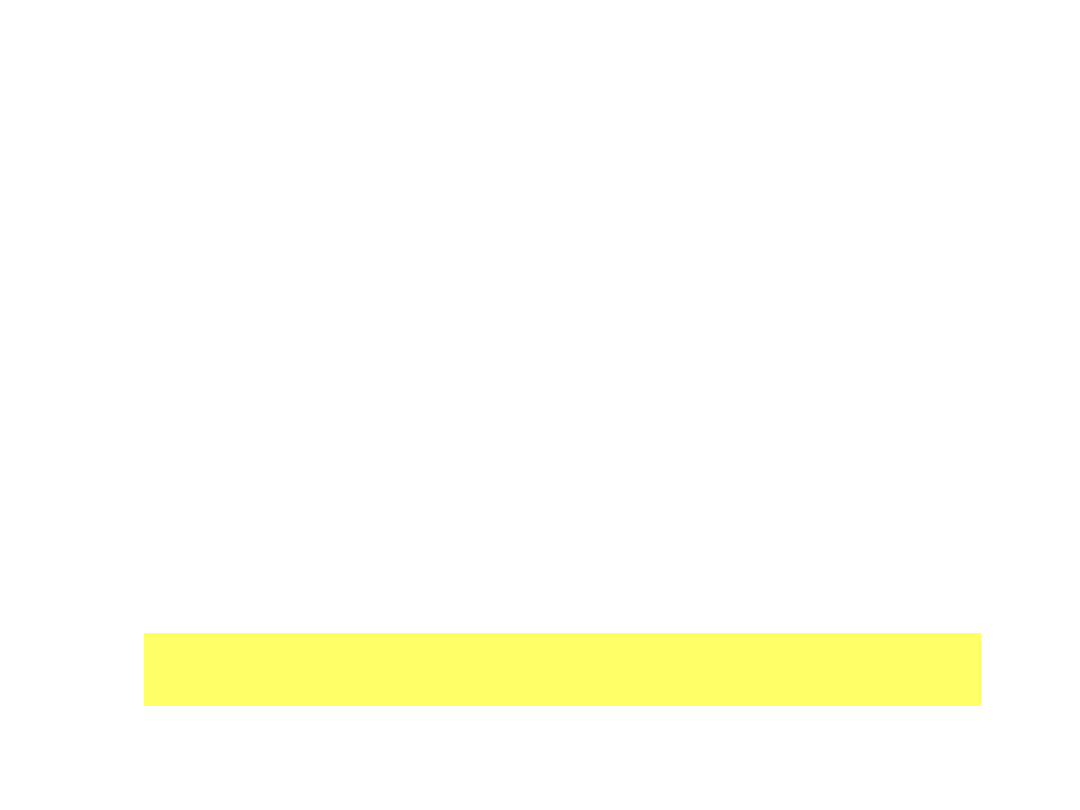
Przy obliczaniu q

zwią

uwzględnia się zatem tylko te

dipole, które przecinają powierzchnię S. Jest rzeczą
oczywistą, że przecinane są jedynie takie dipole,
których środki ciężkości leżą po lewej i po prawej
stronie powierzchni S w odległościach mniejszych niż
(l/2)cos



, gdzie l oznacza długość dipola, a



jest kątem

zawartym między zewnętrzną normalną do elementu
S powierzchni a momentem dipola.
Warunek ten spełniają wszystkie dipole, których środki
leżą wewnątrz objętości lScos



. Jeżeli liczba

cząsteczek dielektryka w jednostce objętości równa się
, to liczba dipoli przeciętych przez element S

powierzchni wynosi lScos



. Każdy przecięty dipol

ma wewnątrz zamkniętej powierzchni nie zobojętniony
ładunek –q.

Całkowity ładunek związany , odpowiadający
powierzchni S, równa się zatem

.

e

p



o

N

o

N

ą

zwi

q



S

cos

p

N

S

cos

ql

N

q

e

o

o

zwią



















76

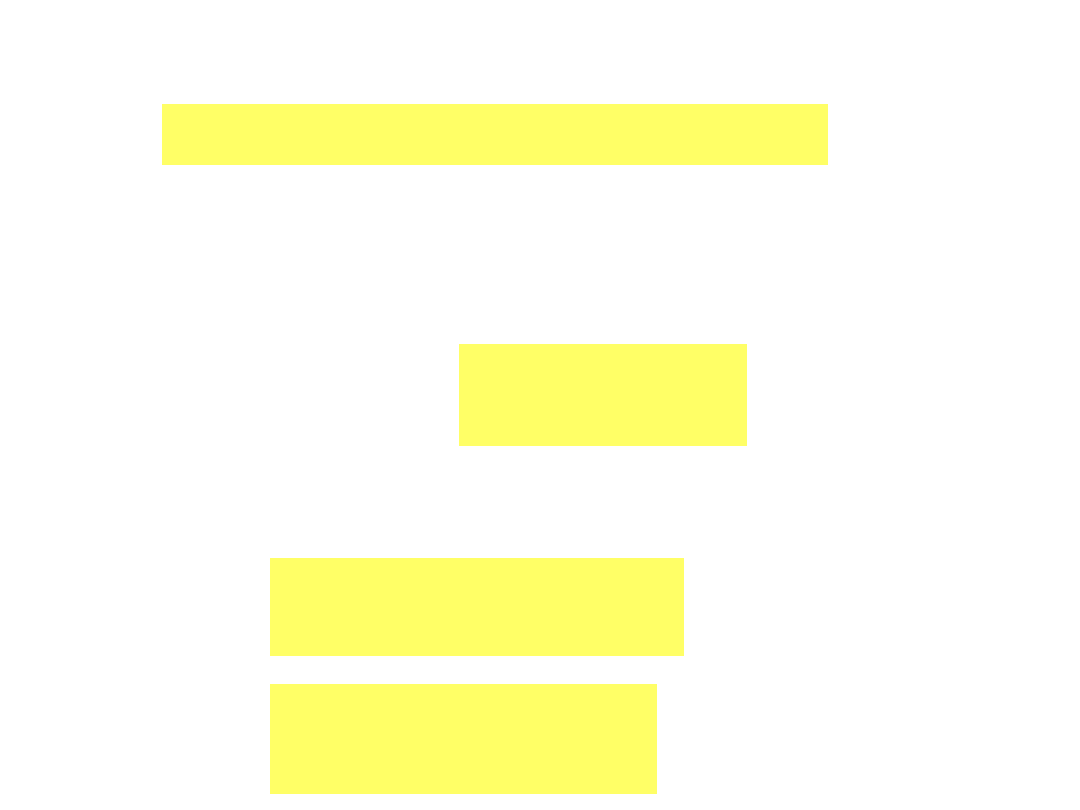
Dzięki założeniu równoległości wszystkich dipoli,
iloczyn

równy jest modułowi wektora

polaryzacji. W związku z tym

(4.48)

gdzie jest wektorem jednostkowym normalnym do
powierzchni S.
W celu uzyskania ogólnej sumy ładunków związanych,
znajdujących się wewnątrz zamkniętej powierzchni S,
należy wyrażenie (4.48) scałkować po powierzchni S

(4.49)

W związku z tym, twierdzenie Gaussa dla dowolnej
substancji spolaryzowanej, zgodnie ze wzorem (4.47),
zapisujemy w postaci

,

stąd

(4.50)

e

o

p

N

S

d

P

S

n

P

S

cos

P

q

e

e

e

zwią



































n

S

d

P

q

S

e

zwią















S

d

P

q

S

d

E

S

e

swob

S

o





































swob

S

e

o

q

S

d

P

E









77













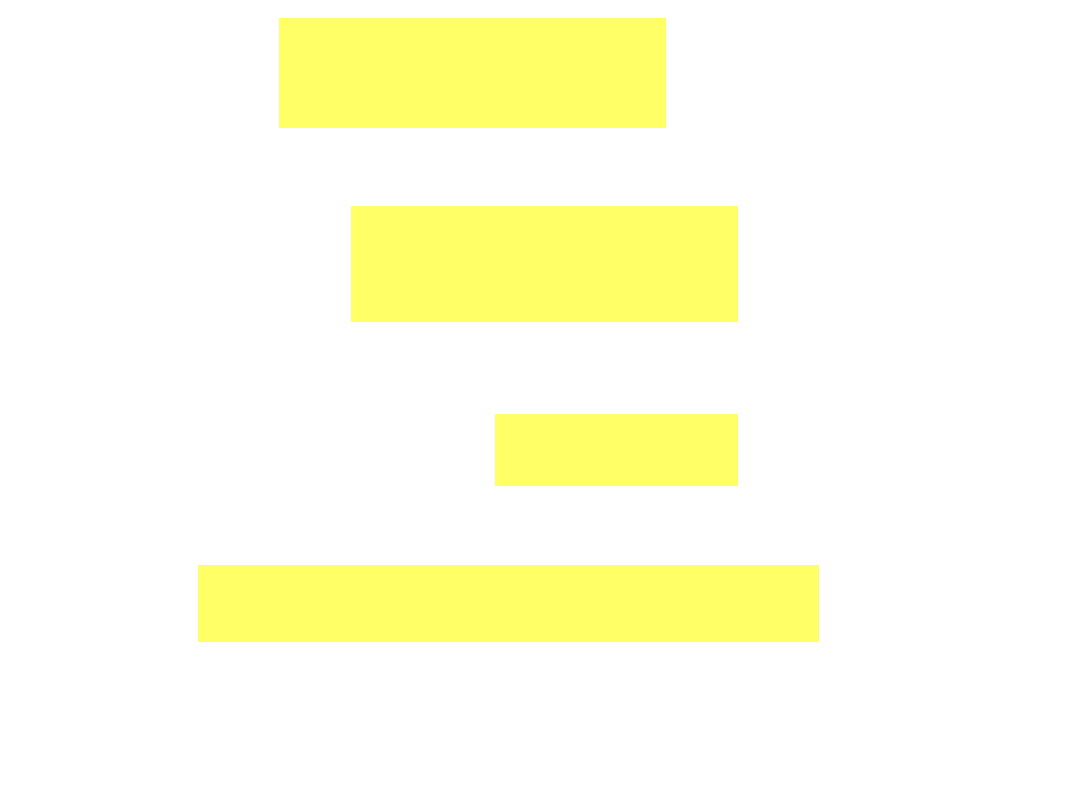
swob

S

e

o

q

S

d

P

E









Wstawiając tu

z równania (4.45) otrzymujemy

Ponieważ równanie to powinno być spełnione dla
dowolnej zamkniętej powierzchni S, przeto

(4.51)

Uwzględniając (4.42) mamy

(4.52)



swob

q















S

S

e

o

S

d

D

S

d

P

E













e

o

P

E

D

















E

E

E

D

e

o

e

o

o



























1

E

E

N

P

o

o

o

e



















78

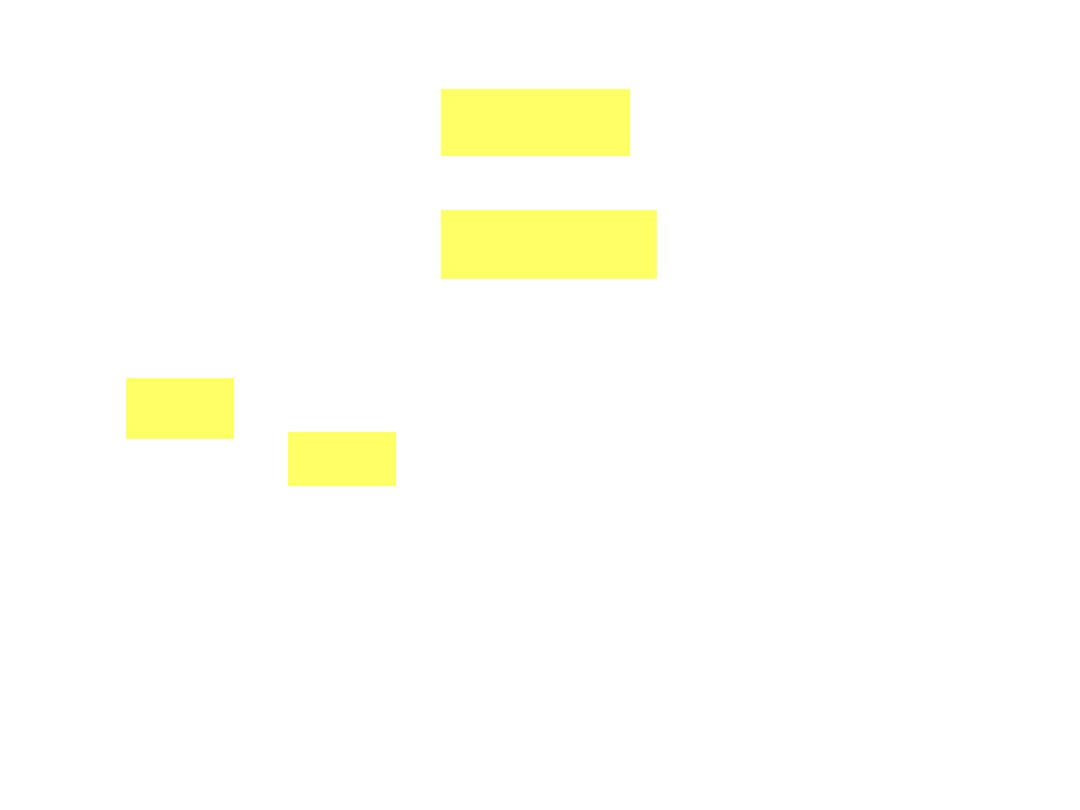
Z drugiej strony, w myśl definicji (4.43), wektor
równy jest

Zatem

(4.53)

Stała

dielektryczna

równa

się

podatności

dielektrycznej zwiększonej o 1

. Obydwie te

wielkości są bezwymiarowe. Dla próżni

, a

.

D



E

D

r

o











e

r







1

1



r



0



e



79

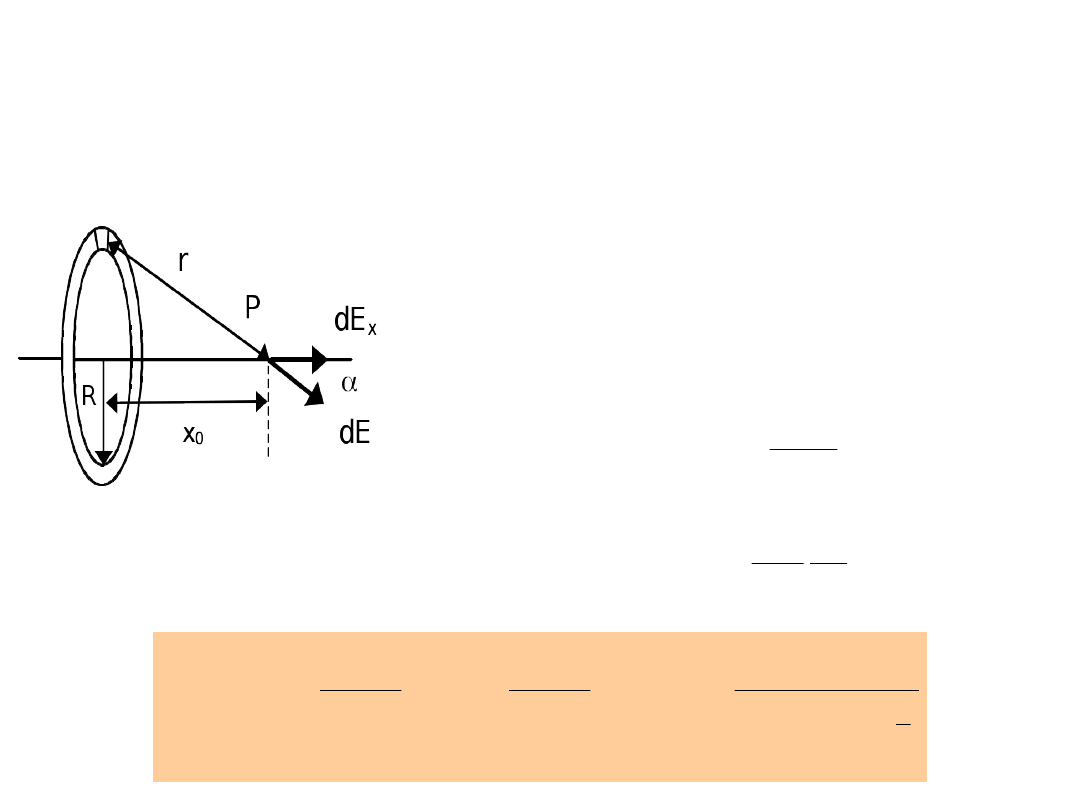
Przykład

Całkowity ładunek naładowanego pierścienia o

promieniu R wynosi Q. Jakie jest pole elektryczne na osi
pierścienia w odległości x

0

od środka ? Pole wytwarzane

przez element dl pierścienia jest równe

dE

x

= dE(cos



)

 

cos



= x

0

/r

 Jeżeli



= Q/2R jest liniową

gęstością ładunku to

2

d

d

r

l

k

E





oraz

r

x

r

l

k

E

x

0

2

d

d





stąd

2

3

2

2

0

0

3

0

3

0

)

(

)

2

(

d

R

x

Q

kx

R

r

x

k

l

r

x

k

E

E

x



















80

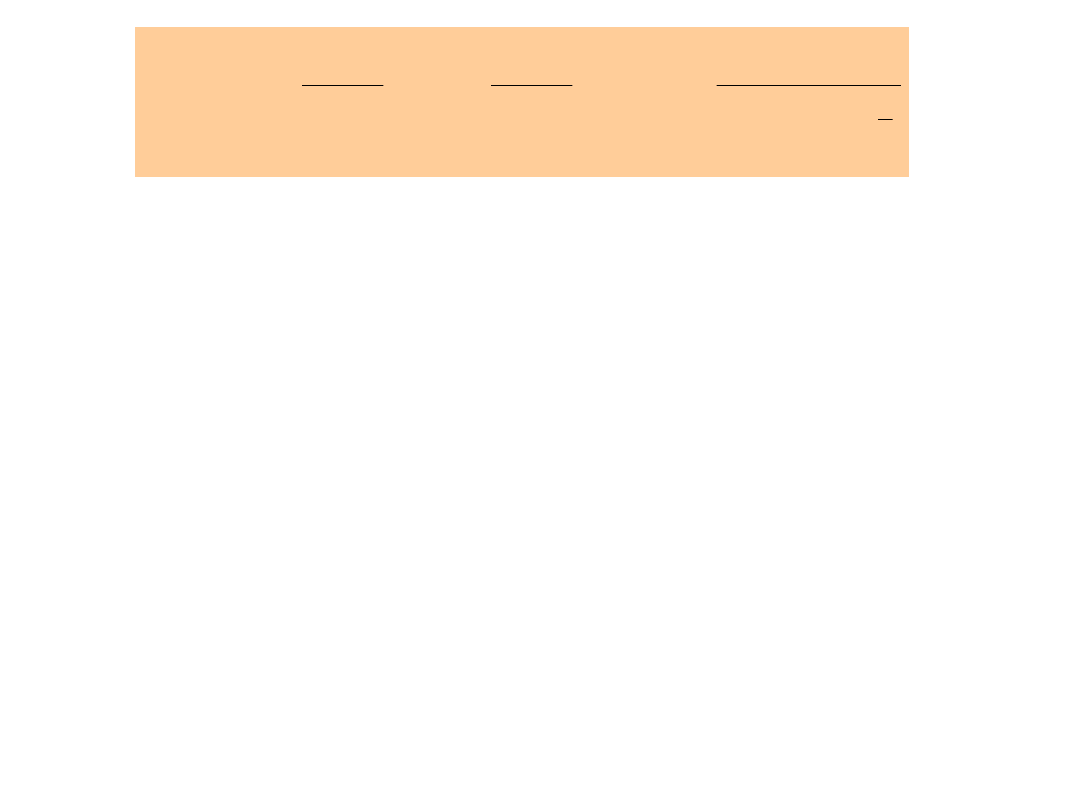
2

3

2

2

0

0

3

0

3

0

)

(

)

2

(

d

R

x

Q

kx

R

r

x

k

l

r

x

k

E

E

x



















Zwróćmy uwagę, że w środku pierścienia (x

0

= 0)

E = 0, a dla x

0

>> R pole E  kQ/x

0

2

i jest takie samo

jak pole ładunku punktowego w tej odległości.

Jedną z zalet posługiwania się pojęciem pola

elektrycznego jest to, że nie musimy zajmować się
szczegółami źródła pola. Np. pole E = kQ/r

2

może

pochodzić od wielu źródeł.

81

Niektóre zastosowania twierdzenia Gaussa

 11.8.1

Równomiernie naładowana kula

Ponieważ równomiernie naładowaną kulę można

traktować

jako

składającą

się

z

szeregu

koncentrycznych warstw, więc przy obliczaniu pola
wewnątrz kuli można stosować wzór

Zauważmy, że kładąc r = R w powyższe równanie
mamy natężenie pola na powierzchni kuli

,

(4.15)

'

r

r

Q

E

o





2

4

1







2

4

1

R

Q

E

o





gdzie

Q

jest

całkowitym

ładunkiem kuli.

82

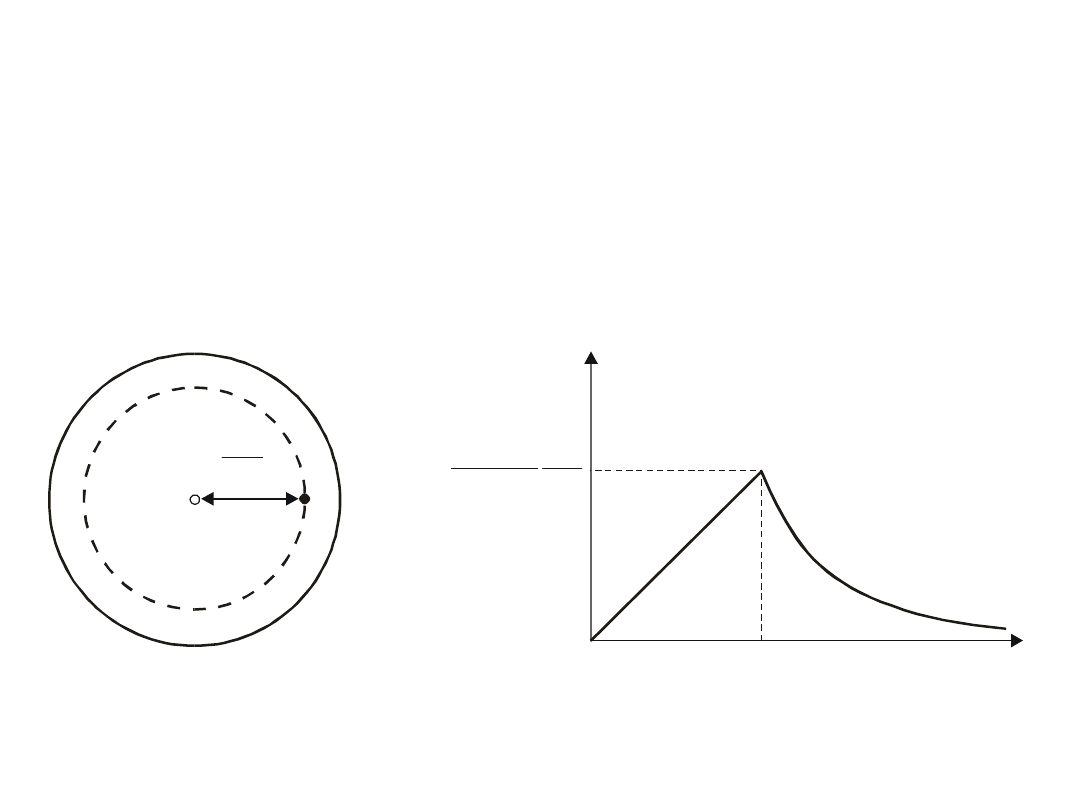
W celu obliczenia pola E w dowolnym punkcie P

znajdującym się wewnątrz kuli wybieramy powierzchnię
gaussowską przechodzącą przez ten punkt P, jak
pokazano na rys. 4.5. Sfera ta obejmuje objętość 4



r

3

/3,

która stanowi (r/R)

3

całej objętości kuli. Wobec tego

ładunek wnętrza tej sfery wynosi Q

w

= Q(r/R)

3

. Stosując

twierdzenie Gaussa

2

r

o

R

Q

4

1



 

( a ) ( b )

E

R

r

r

3

3

R

r

Q

Q

w



P

Rys 4.5

83

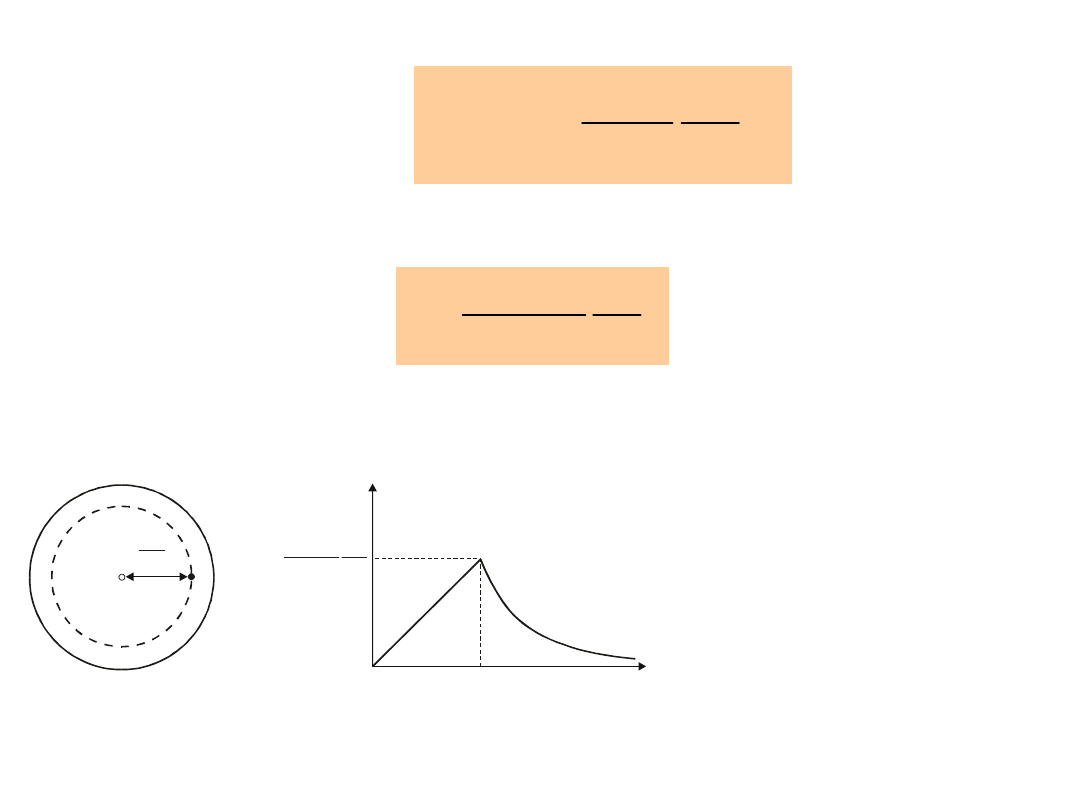
Stosując twierdzenie Gaussa

,

otrzymujemy pole wnętrza równomiernie naładowanej
kuli o promieniu R

.

(4.16)

Na rys. 4.5b pokazano zależność tego pola od r.

3

3

2

1

4

r

R

Q

r

E

r

o









r

R

Q

E

r

o

3

4

1









2

r

o

R

Q

4

1



 

( a ) ( b )

E

R

r

r

3

3

R

r

Q

Q

w



P

Rys. 4.5. (a) Powierzchnia gaussowska przechodząca przez P obejmująca

ładunek Qw.

(b) Zależność pola elektrycznego od odległości od środka równomiernie

naładowanej kuli.

84

11.8.2

Powierzchniowy rozkład ładunku

 

Rozważymy pole elektryczne wytworzone przez

równomiernie naładowaną nieskończoną płaszczyznę

o

gęstości powierzchniowej ładunku



(jednostką



jest

C/m

2

). Powierzchnię gaussowską wybieramy w postaci

prostopadłościanu lub cylindra o płaskich przekrojach
poprzecznych położonych w odległości a od
powierzchni, jak pokazano na rys. 4.6. Ładunek
znajdujący się wewnątrz powierzchni całkowania równy
jest . Strumień pola wychodzący w obydwie
strony naładowanej płaszczyzny jest jednakowy, więc
całkowity strumień natężenia pola elektrycznego wynosi

o

ES

S

d

E

2











o

S

o

w

S

Q





85

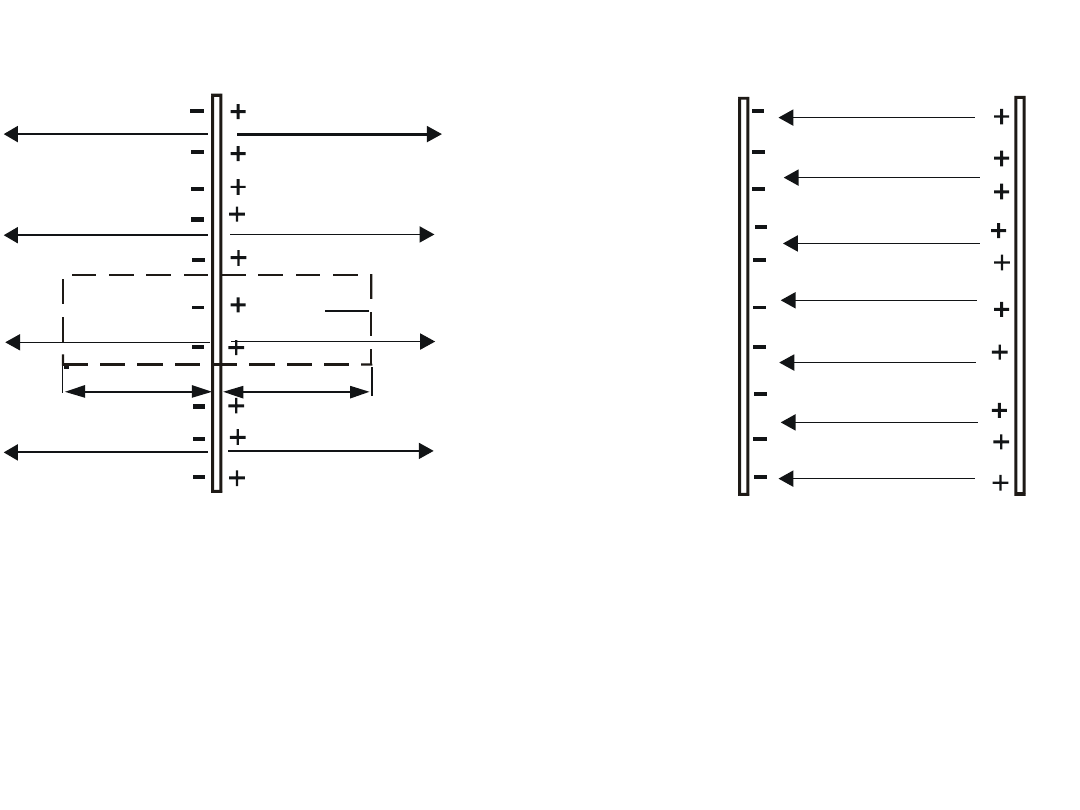
S

o

I I I I I I

a b

a

a

Fig. 4.6. Nieskończona
powierzchnia metalowa o
gęstości powierzchniowej
ładunku

.

Fig. 4.7. Pole elektryczne
między dwoma płaszczyznami
o równych gęstościach ładunku
powierzchniowego lecz
przeciwnych znakach

86

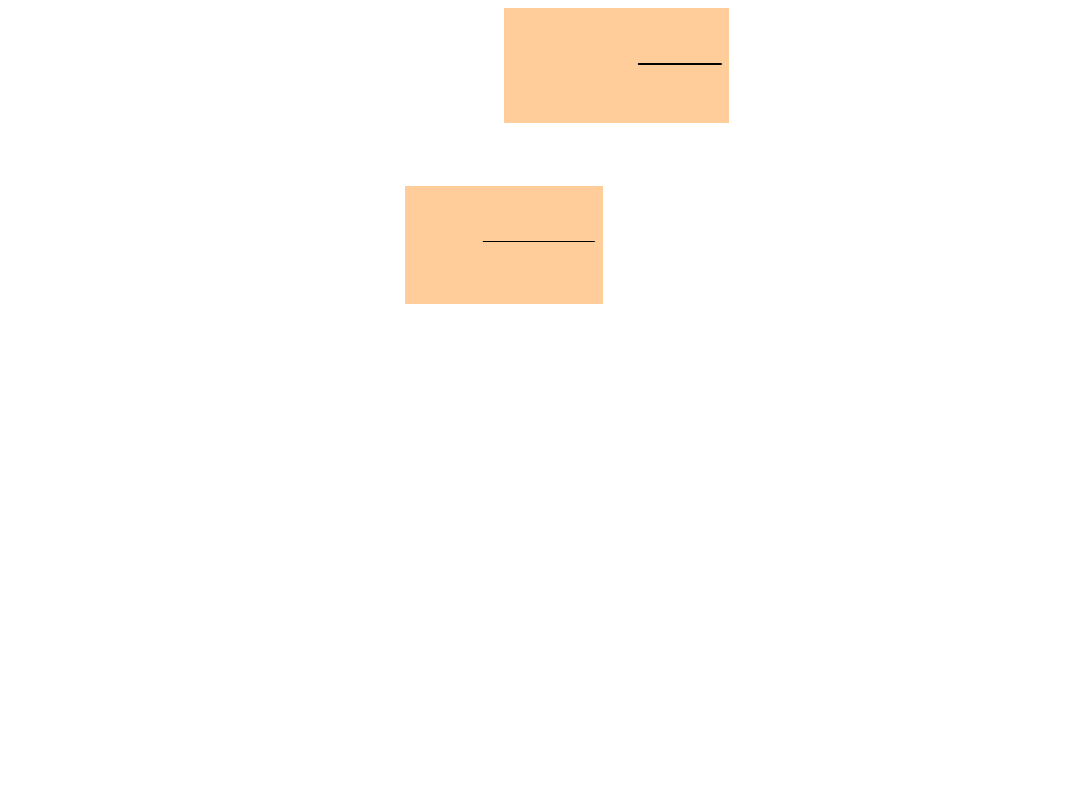
Zgodnie z twierdzeniem Gaussa

,

czyli pole elektryczne naładowanej płaszczyzny jest
równe

.

(4.17)

W praktyce często spotykamy się z przyrządami, w
których znajdują się dwie równoległe płaszczyzny
naładowane równymi lecz przeciwnymi ładunkami (rys.
4.7).

Natężenie

pola

spowodowane

ładunkiem

płaszczyzny a wynosi

i jest skierowane

do tej płaszczyzny. Pole wytworzone przez płaszczyznę
b wynosi

i jest skierowane od tej płaszczyzny.

r

o

b

/

E







2



r

o

a

/

E







2



r

o

E







2



r

o

o

o

S

ES









2

87

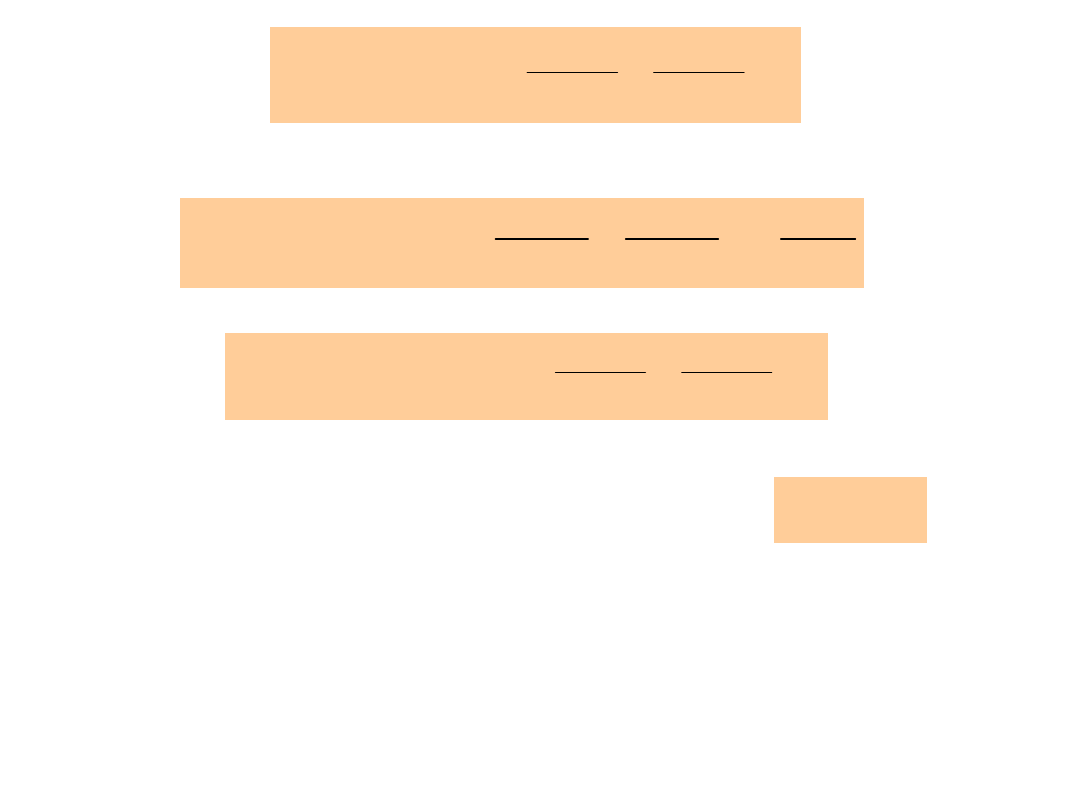
W obszarze I:

W obszarze II:

(4.18)

W obszarze III:

Widzimy więc, że na zewnątrz płaszczyzn pole

elektryczne

znika,

natomiast

między

płaszczyznami wynosi

.

r

o

/







0

2

2











r

o

r

o

bI

aI

I

E

E

E













r

o

r

o

r

o

II

b

II

a

II

E

E

E

































2

2

0

2

2













r

o

r

o

III

b

III

a

III

E

E

E













88

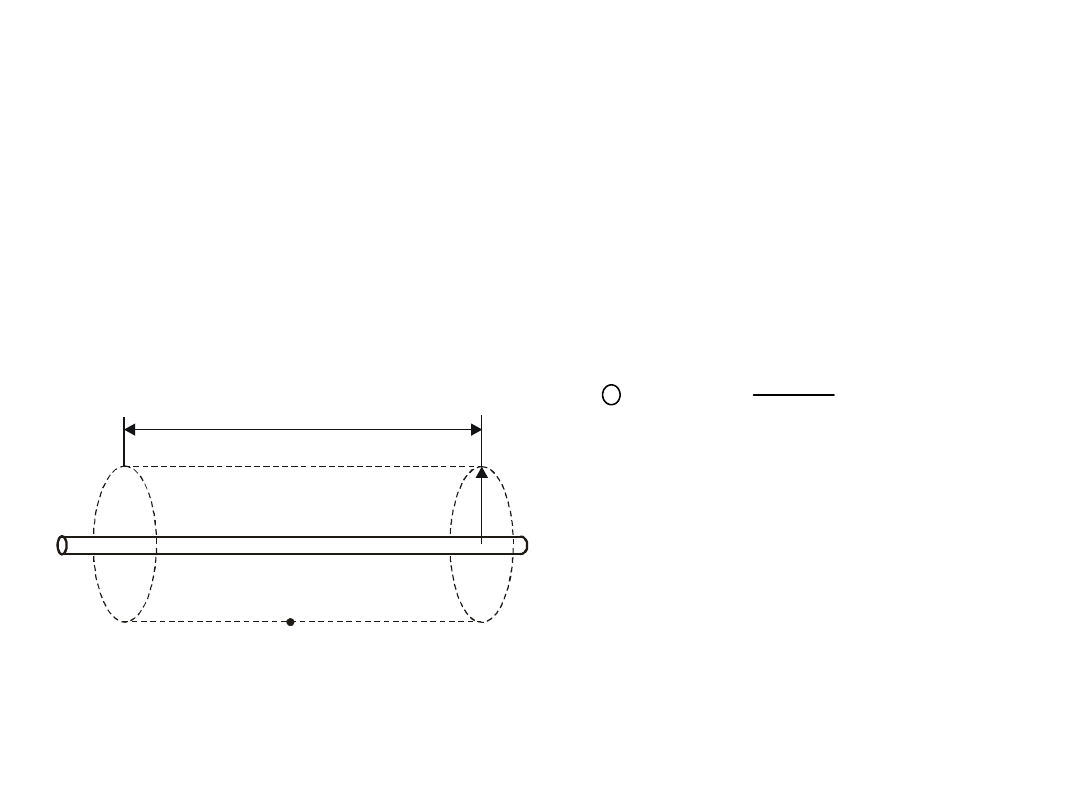
11.8.3

Liniowy rozkład ładunku

Rozpatrzymy teraz pole elektryczne wytworzone

w odległości r przez równomiernie naładowany
prostoliniowy przewodnik lub pręt, którego długość
wyraźnie przewyższa odległość r. Niech  oznacza

ładunek przypadający na jednostkę długości pręta. Jako
powierzchnię gaussowską wybieramy walec o długości
L (rys. 4.8). Wewnątrz powierzchni walcowej znajduje
się ładunek

. Zgodnie z prawem

Gaussa

L

Q

w











r

o

L

S

d

E











P

r

L

Rys. 4.8. Odcinek długiego
naładowanego pręta. Powierzchnię
gaussowską stanowi walec o
długości L i promieniu r.

Ze względu na symetrię,
linie sił pola mają kształt
prostych radialnych.
Dlatego wektory i są
wzajemnie prostopadłe na
bocznej powierzchni
zamykającej walec i
równoległe na
powierzchni walcowej. Z
tego powodu możemy
napisać

E



S

d



89

Porównując to wyrażenie do

, mamy

,

stąd natężenie pola elektrycznego liniowo rozłożonego
ładunku ma postać

(4.19)







rL

E

S

d

E



2





r

o

L







r

o

L

rLE











2

r

E

r

o









2



90

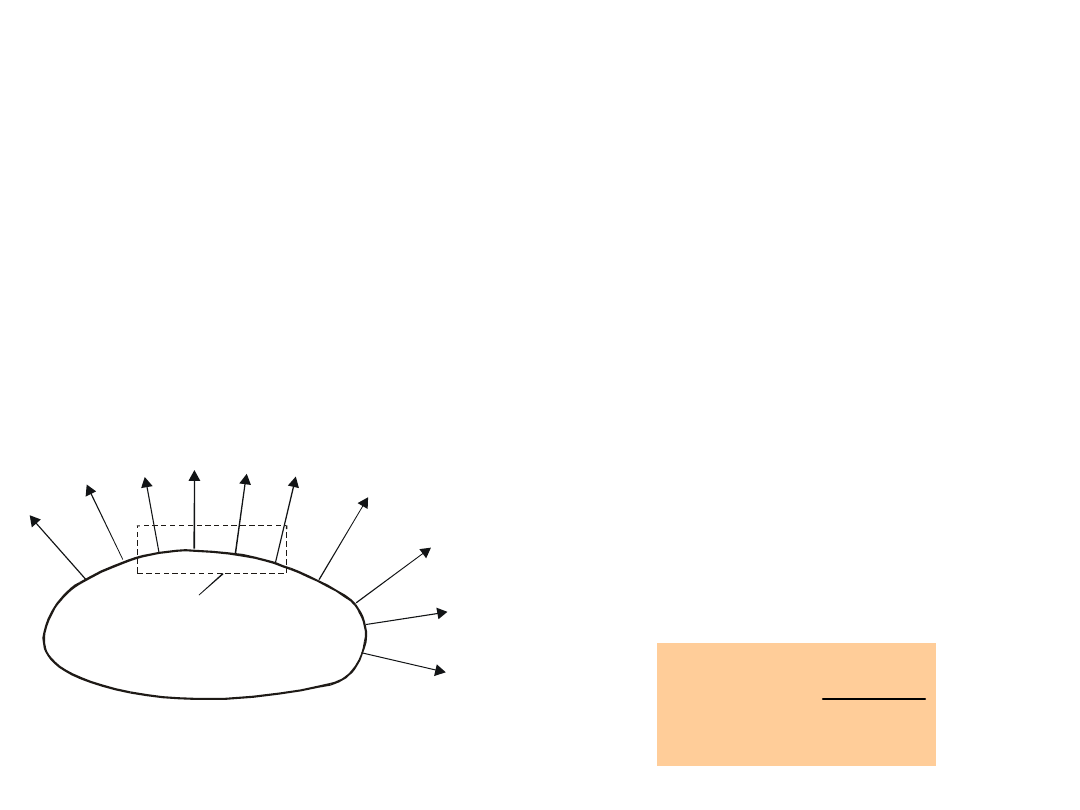
11.9 Powierzchnia przewodnika

 

Większość ciał stałych możemy podzielić na dwie

grupy: przewodniki i izolatory (dielektryki). Dodatkowy
ładunek umieszczony na powierzchni lub wewnątrz
dielektryka pozostaje nieruchomy. Inaczej jest w
przewodnikach,

które

zawierają

dużą

liczbę

swobodnych elektronów nie związanych z konkretnymi
atomami. Dlatego w przewodniku pole elektryczne
może istnieć jedynie w ciągu krótkiego okresu czasu
dopóki swobodne elektrony nie zgromadzą się na
powierzchni przewodnika pod wpływem działania
zewnętrznego

pola

i

nie

utworzą

przeciwnie

skierowanego pola.

P o w ie r z c h n ia S



P r z e w o d n ik

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+ + +

Wewnątrz prostopadłościanu o
podstawie

S znajduje się

ładunek S.

Wydzielmy na powierzchni
(rys.

4.9)

nieduży

prostopadłościan o podstawie
S. Zgodnie z twierdzeniem

Gaussa

r

o

S

S

E













91

r

o

S

S

E













czyli natężenie pola na powierzchni przewodnika
wynosi

(4.20)

r

o

E









92

11.10

Przewodniki i izolatory – rozkład

ładunków

Większość ciał stałych można podzielić na

przewodniki i izolatory

. W

izolatorze

nadmiarowy

ładunek może być rozmieszczony w całej objętości
natomiast

w przewodnikach

swobodne elektrony będą

się zbierały na powierzchni dopóty, dopóki nie
wytworzy się pole równoważące pole zewnętrzne.

Rozpatrzmy dowolny w kształcie przewodnik.
Wybierzmy powierzchnię zamkniętą tuż poniżej
powierzchni przewodnika. Zastosujmy prawo Gaussa
do tej powierzchni

0

.

d



wewn

Q





S

E

93

Wewnątrz przewodnika w dowolnym punkcie
powierzchni S pole musi być równe zeru, bo inaczej
elektrony poruszałyby się czyli

 

Zatem

0 = Q

wewn.

/



0

Stąd

Q

wewn.

= 0

 

Tak więc ładunek wewnątrz dowolnej

zamkniętej powierzchni (przewodnika) musi być
równy zeru; cały ładunek gromadzi się na
powierzchni.

0

d 



S

E

94