Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

Obiekt mostowy – budowla komunikacyjna, której

zadaniem jest przeprowadzenie trasy komunikacyjnej

nad przeszkodą (rzeką, drogą, linią kolejową) lub

zastąpienie nasypu.

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

Podstawowymi parametrami

charakteryzującymi obiekt mostowy są:



w kierunku poziomym,



w kierunku pionowym,



położenie w planie

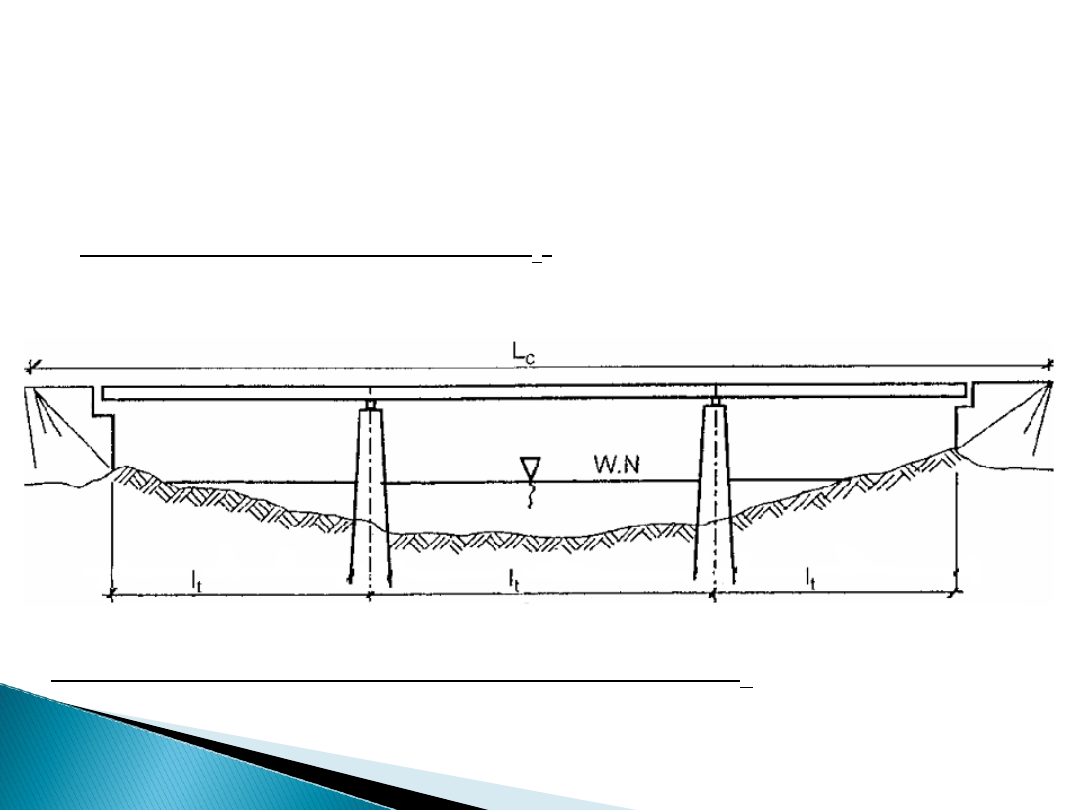
• w kierunku poziomym – przekrój podłużny

mostu:

- rozpiętość teoretyczna (podporowa) przęsła l

t

– pozioma

odległość mierzona wzdłuż przęsła, między punktami
podparcia na dwóch sąsiednich podporach. Punkty te
wyznaczają osie łożysk lub osie podpór;

- długość całkowita obiektu – L

c

– odległość mierzona po osi

podłużnej obiektu,

pomiędzy najdalej wysuniętymi punktami;

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

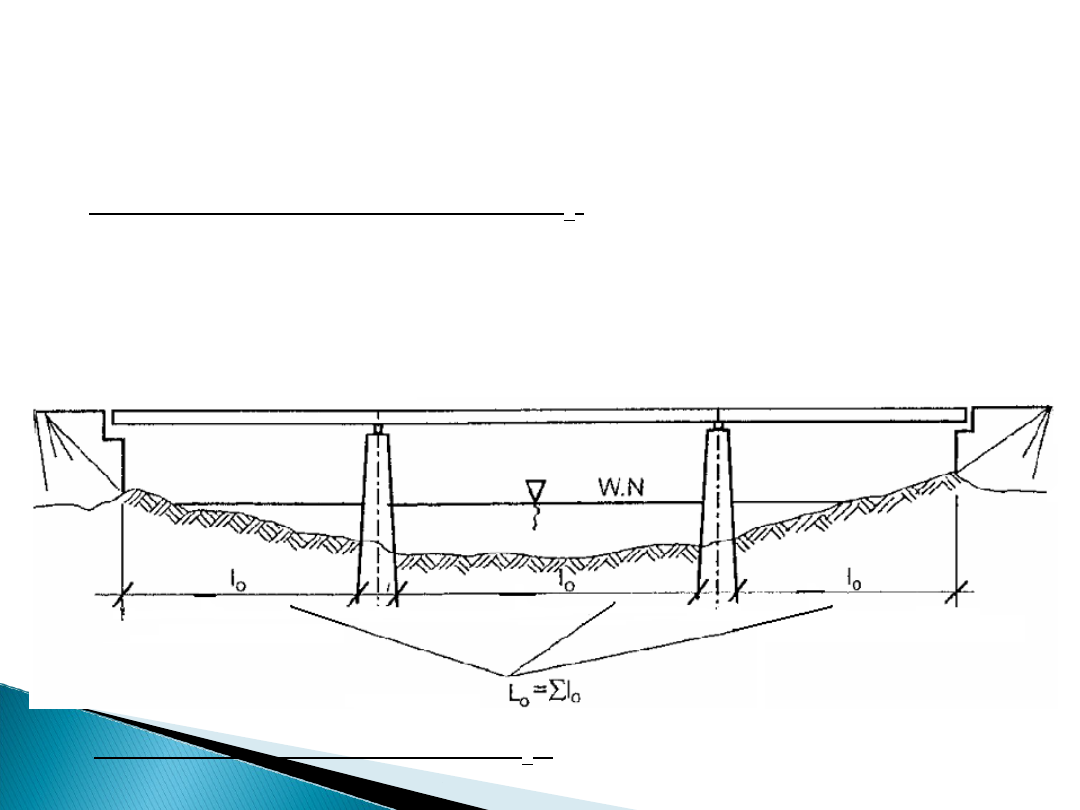
• w kierunku poziomym – przekrój podłużny mostu:

- rozpiętość przęsła w świetle – l

0

- mierzona wzdłuż osi

przęsła pomiędzy

dwoma miarodajnymi punktami podpór. Punkty te mogą

być wyznaczone przez wielką miarodajną wodę czy
pomiędzy najdalej wysuniętymi punktami podpór
(przestrzeń pod konstrukcjami, pod którymi odbywa się
ruch).

- długość mostu w świetle – L

0

- suma długości w świetle

wszystkich przęseł.

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

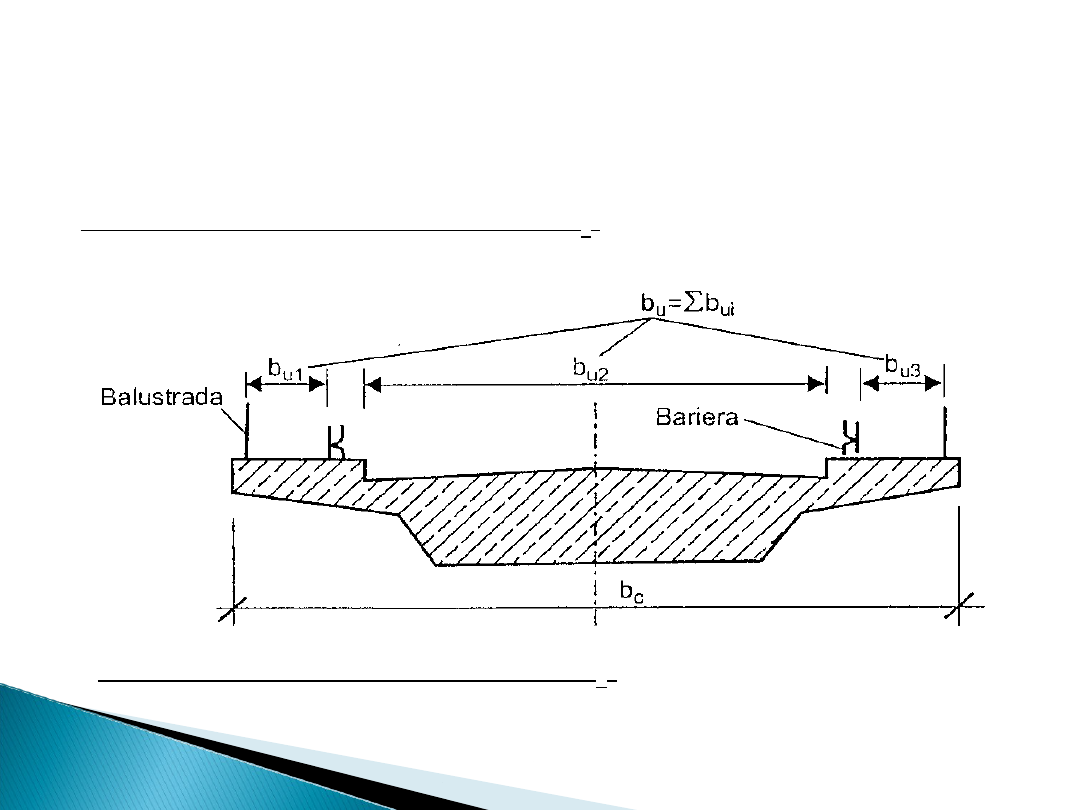
• w kierunku poziomym – przekrój poprzeczny

mostu:

- całkowita szerokość pomostu – b

c

– odległość pomiędzy

zewnętrznymi krawędziami przekroju poprzecznego przęsła;

- szerokość użytkowa pomostu – b

u

- suma szerokości

wszystkich pasów

ruchu wraz z pasami bezpieczeństwa, a więc z

wyłączeniem przestrzeni zajętej np. przez urządzenia
bezpieczeństwa ruchu (bariery).

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

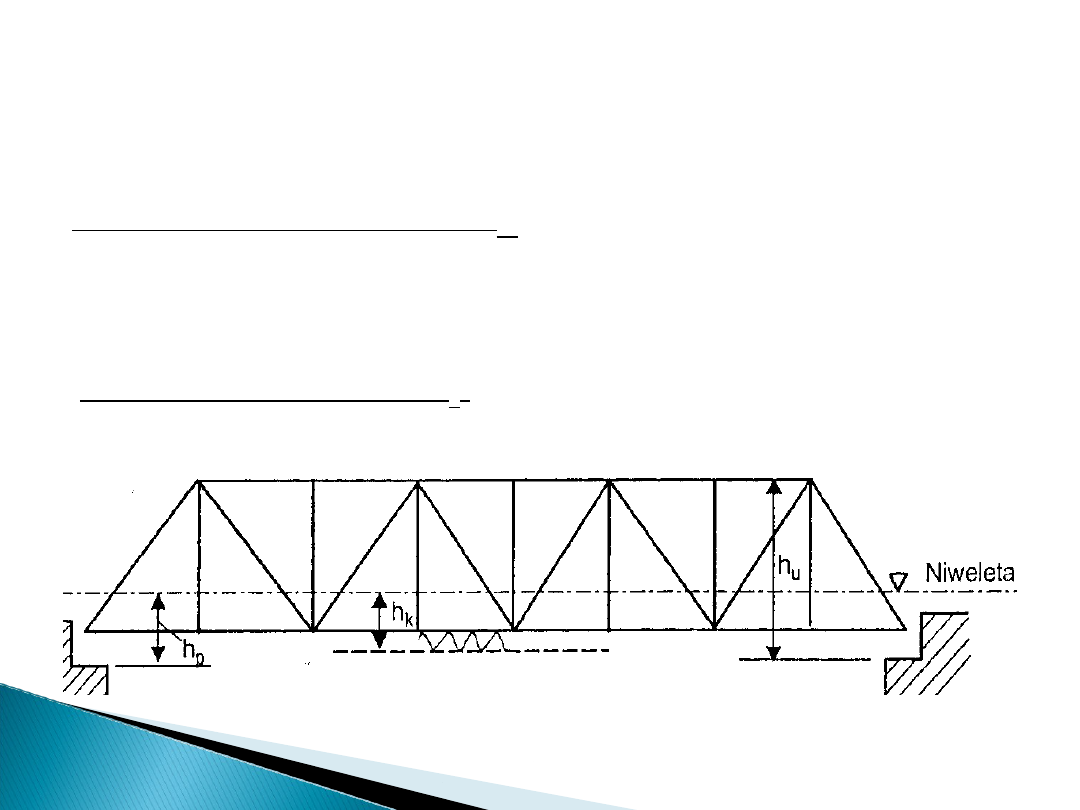
• w kierunku

pionowym:

- wysokość konstrukcyjna – h

k

- największa odległość między

dolną krawędzią

przęsła a niweletą drogi na moście lub rzędną główki szyny.

Przy czym dolną krawędź oznacza dowolny element
podwieszony do konstrukcji np. rurociąg lub urządzenie
odwadniające.

- wysokość podporowa– h

p

– odległość między niweletą drogi

na moście nad podporą i górną krawędzią ciosu lub ławy
podłożyskowej;

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

Rys. Przęsło mostu z jazdą

dołem

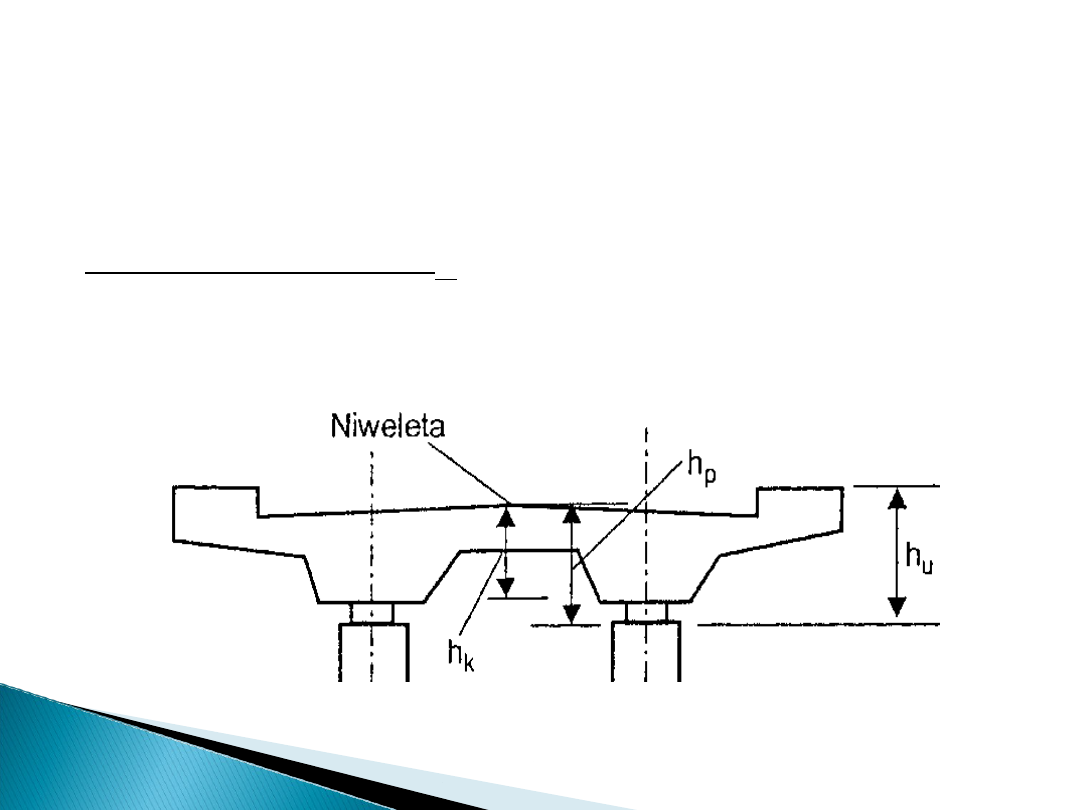
• w kierunku

pionowym:

-

wysokość ustrojowa– h

u

- odległość mierzona od punktu

podparcia przęsła (od

dolnej krawędzi łożysk) do górnej krawędzi konstrukcji. Z

reguły większa od

wysokości konstrukcyjnej.

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

Rys. Przęsło mostu płytowo-

belkowego

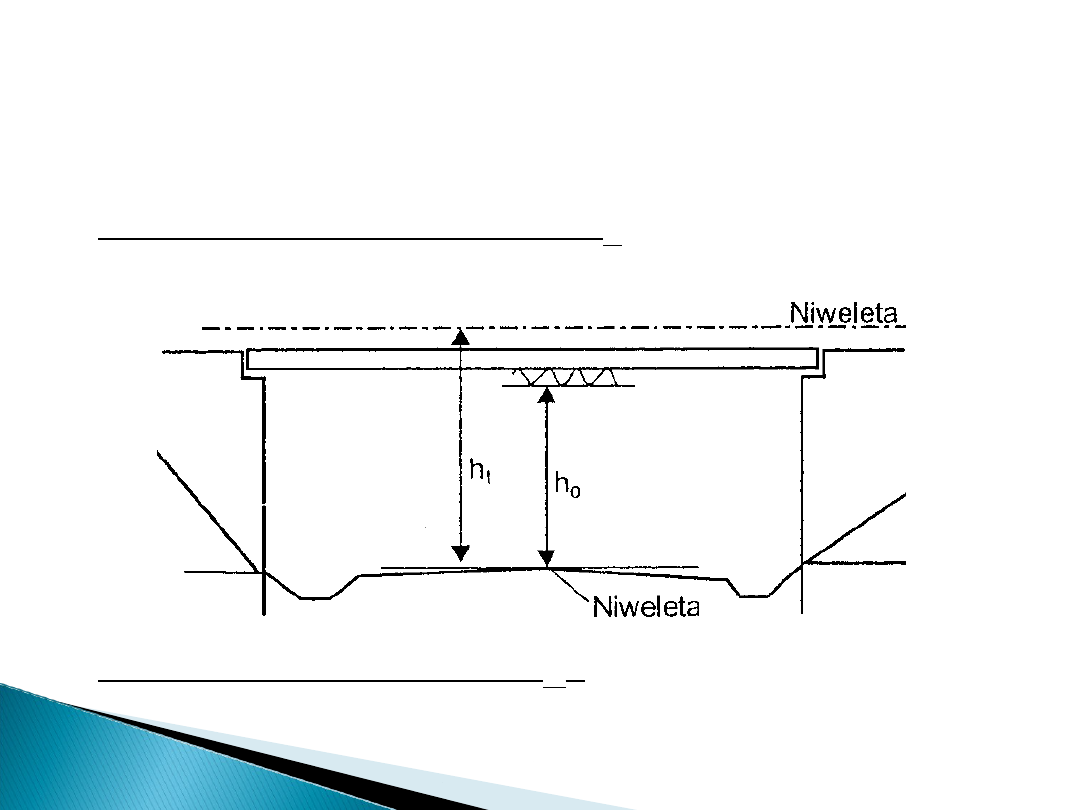
• w kierunku

pionowym:

- wysokość mostu nad terenem – h

t

- największa wysokość

między niweletą osi drogi na moście i terenem (dnem rzeki,
doliny itp.);

- wysokość mostu w świetle– h

0

- najmniejsza odległość

pionowa między dolną krawędzią przęsła a najwyższym
punktem przeszkody pod przęsłem. Punktem tym może być
niweleta drogi pod wiaduktem, rzędna główki szyny lub
poziom wielkiej wody.

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

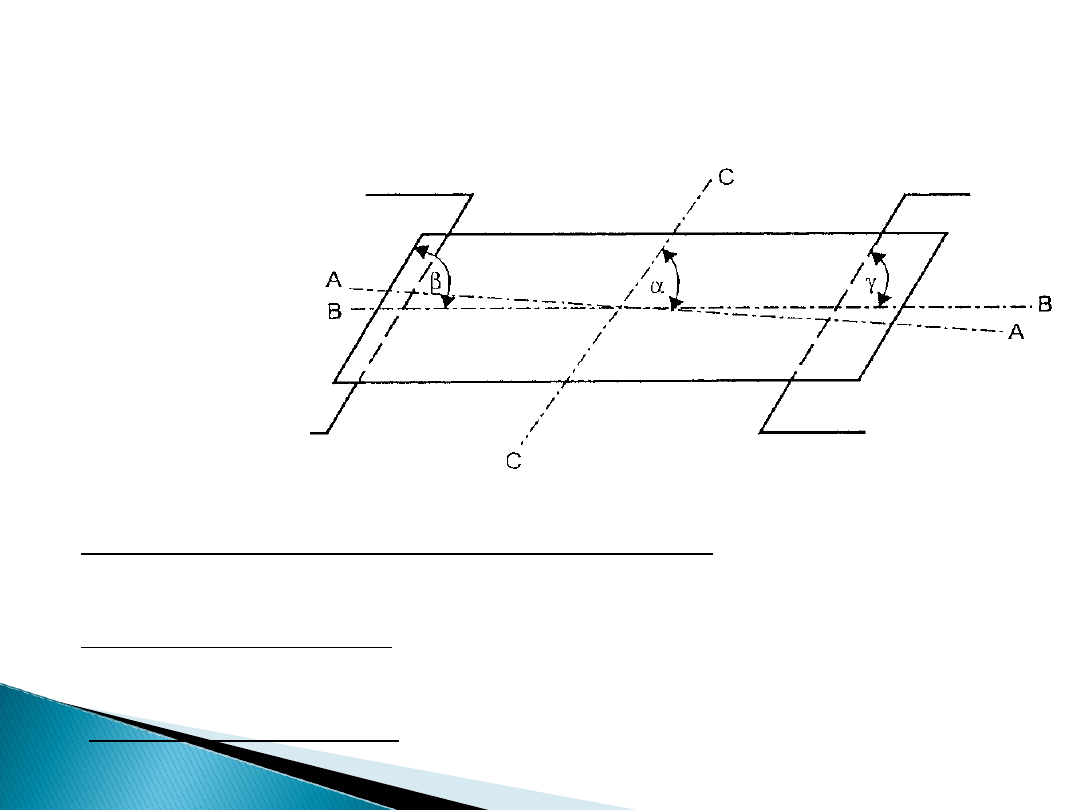
• położenie w planie:

- kąt skrzyżowania mostu z przeszkodą - α – mierzony w rzucie

poziomym kąt ostry między osią drogi na moście i osią
przeszkody;

- kąt skosu przęsła - β – mierzony w rzucie poziomym kąt ostry

między osią podłużną konstrukcji przęsła i prostą łączącą
punkty podparcia przęsła;

- kąt skosu podpór - γ – mierzony w rzucie poziomym kąt ostry

między licem podpory a osią podłużną konstrukcji przęsła.

A-A – oś drogi,
B-B – oś

konstrukcji,

C-C – oś

przeszkody.

Podstawowe parametry

Podstawowe parametry

geometryczne obiektów mostowych

geometryczne obiektów mostowych

Obciążenia mostów drogowych

Obciążenia mostów drogowych

i kolejowych

i kolejowych

PN-EN 1991-1-3. Eurokod 1: Oddziaływania na
konstrukcje. Część 1-4: Oddziaływania ogólne.
Obciążenie śniegiem.

PN-EN 1991-1-4. Eurokod 1: Oddziaływania na
konstrukcje. Część 1-4: Oddziaływania ogólne.
Oddziaływania wiatru.

PN-EN 1991-2. Eurokod 1: Oddziaływania na
konstrukcje. Część 2: Obciążenia ruchome mostów

PN-EN 1991-1-5. Eurokod 1: Oddziaływania na
konstrukcje. Część 1-5: Oddziaływania ogólne.
Oddziaływania termiczne

Obciążenie śniegiem może być istotne:

• dla obiektów mostowych zadaszonych;
• w określonych rejonach świata,
• w trakcie budowy obiektów
mostowych

Obciążenia mostów śniegiem

Obciążenia mostów śniegiem

Ogólne zasady oddziaływania quasi-

statycznego wiatru na elementy obiektów
mostowych:

• dotyczy obiektów mostowych o przęsłach:
- nie dłuższych niż 200m i zlokalizowanych nie
wyżej niż 200m
powyżej powierzchni gruntu,
- nie podlegających efektom aerodynamicznym;

• dla przęseł o długości do 40m nie ma
konieczności
uwzględniania wpływów aerodynamicznych;

• nie obejmuje oddziaływania aerodynamicznego
pojazdów.

Obciążenia mostów wiatrem

Obciążenia mostów wiatrem

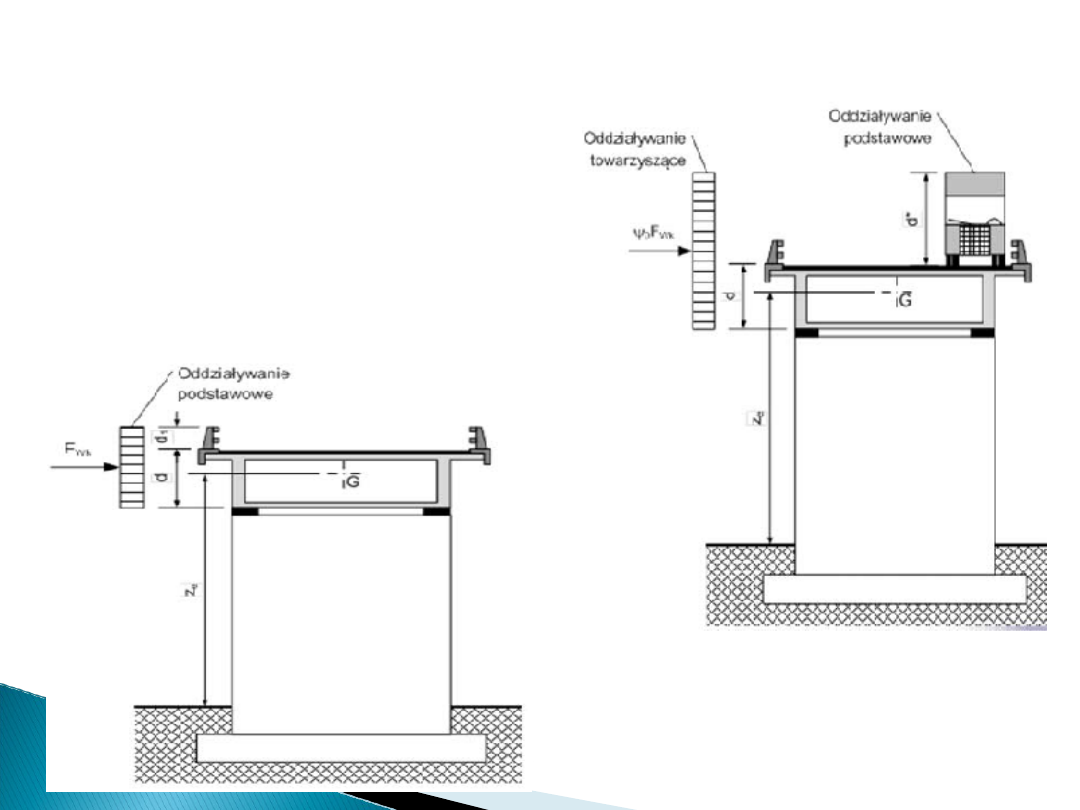
Obciążenia mostów wiatrem

Obciążenia mostów wiatrem

Powierzchnie oddziaływania
wiatru:

• pomost

• filary

• wyposażenie (bariery,
balustrady itp.)

• pojazdy i tłum

Obciążenia wywołane ruchem na mostach drogowych,

kładkach dla pieszych i mostach kolejowych składają się

z:



obciążeń zmiennych,



obciążeń w wyjątkowych sytuacjach obliczeniowych,

Obciążenia przedstawiane są z użyciem różnych modeli,

ale oddzielnie do obliczeń wytrzymałościowych i do

sprawdzenia na zmęczenie.

Obciążenia ruchome mostów

Obciążenia ruchome mostów

drogowych i kolejowych

drogowych i kolejowych

Zalecane jest, by w normalnych warunkach stosowania (tzn. z

wyłączeniem sytuacji wyjątkowej) obciążenie ruchem i pieszymi

traktowano jako oddziaływania zmienne.

Wartości reprezentatywne – określane w celu

kalibracji głównych

Modeli Obciążeń:

• wartości charakterystyczne - wartości statystyczne

tzn.

odpowiadającymi określonemu

prawdopodobieństwu

przekroczenia podczas trwałości obliczeniowej

mostu lub

wartości nominalne;

• wartości częste;

• wartości nieczęste;

• wartości prawie stałe.

Oddziaływania zmienne

Oddziaływania zmienne

Mosty drogowe

Mosty drogowe

PN-EN 1991-2. Eurokod 1: Oddziaływania na
konstrukcje. Część 2: Obciążenia ruchome mostów

Obszar stosowania:



Modele obciążeniowe podane w EC1 dotyczą tylko mostów drogowych,

których przęsła mają rozpiętość mniejszą od 200m oraz jezdnie nie szersze

niż 42,0m;



Modele i związane z nimi reguły powinny uwzględniać wszystkie normalnie

przewidywalne sytuacje ruchowe, które należy uwzględniać w

projektowaniu;

Oddziaływania zmienne mostów

Oddziaływania zmienne mostów

drogowych

drogowych

Przedstawienie oddziaływań:

• podziały jezdni na pasy umowne,
• położenie i numeracja pasów w

projektowaniu,

• modele obciążeń ruchu drogowego.

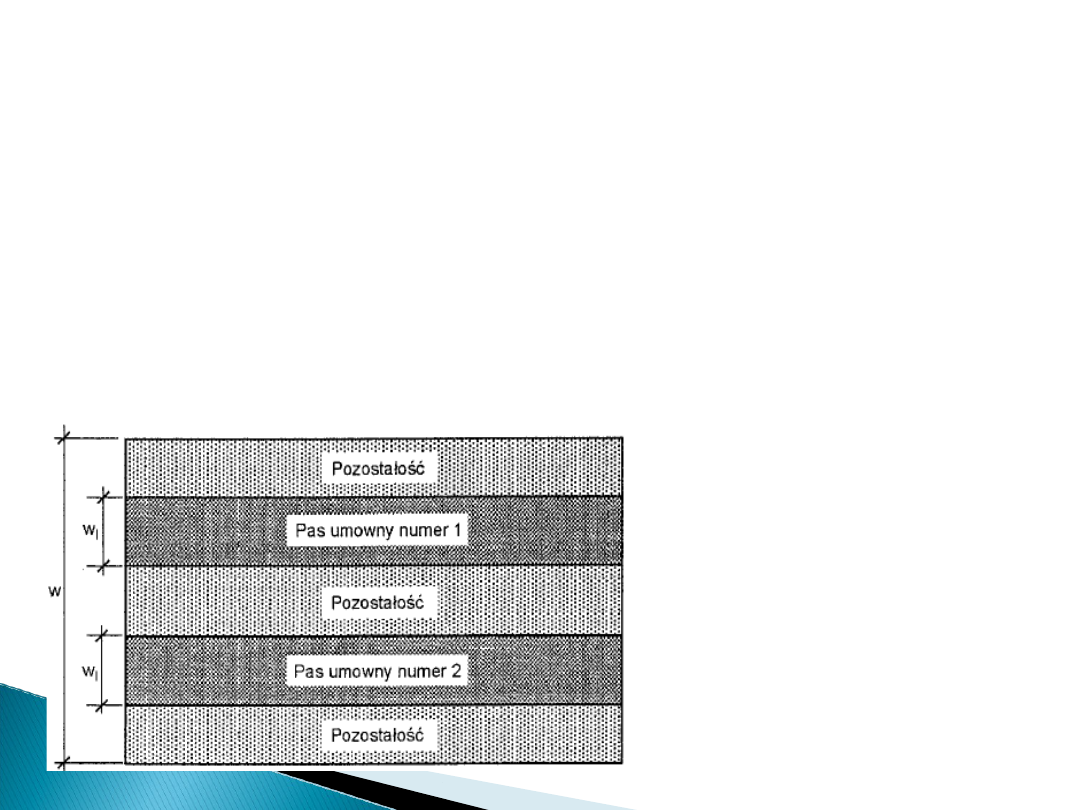
Szerokość pasów umownych – w

i

, oraz ich liczbę w

zależności od szerokości jezdni - (Tab.4.1EC):

Wartość „Int” – część całkowita

Szerokość jezdni – „w” - mierzy się między
krawężnikami lub między wewnętrznymi krawędziami
barier ochronnych. Nie uwzględnia się odległości ani
między stałymi barierami ochronnymi lub krawężnikami
pasa dzielącego, ani szerokości tych barier ochronnych.

Oddziaływania zmienne mostów

Oddziaływania zmienne mostów

drogowych

drogowych

Podział jezdni na pasy umowne

Przykład

Dla szerokość jezdni: w = 11m

a szerokość obszaru pozostałego

wynosi:

Oddziaływania zmienne mostów

Oddziaływania zmienne mostów

drogowych

drogowych



gdy jezdnia na moście jest fizycznie podzielona na dwie części w sposób

trwały, to liczbę pasów ruchu ustala się oddzielnie dla każdej części;



w przypadku bariery rozbieralnej jezdnię traktuje się jako całość, łącznie

z pasami awaryjnymi oraz utwardzonym poboczem;



ponumerowanym pasom ruchu przyporządkowuje się schemat i wartość

obciążenia,



jeśli dwie niezależne jezdnie znajdują się na jednym pomoście, nawet gdy

są oddzielone fizycznie, pas o danym numerze może wystąpić tylko raz.



liczbę pasów, ich

położenie na

jezdni i numerację dobiera

się tak,

by efekty wywołane

modelami

obciążeń były najbardziej
niekorzystne ( pas dający
najniekorzystniejszy

skutek

numeruje się jako Pas

Numer 1 itd.);

Zasady położenia i numeracji

Zasady położenia i numeracji

pasów

pasów



obciążenia pionowe (wartości charakterystyczne):

- model obciążenia 1 – LM1,

- model obciążenia 2 – LM2,

- model obciążenia 3 – LM3,

- model obciążenia 4 – LM4;



obciążenia poziome (wartości charakterystyczne):

- siły hamowania i przyśpieszenia,

- siły odśrodkowe;



siły statyczne;



siły dynamiczne.

Modele obciążeń, nie opisują obciążeń

rzeczywistych. Zostały one dobrane i
skalibrowane tak, aby ich skutki przedstawiały
skutki ruchu rzeczywistego.

Modele obciążeń mostów

Modele obciążeń mostów

drogowych

drogowych

Obciążenia skupione i równomiernie rozłożone, które obejmują większość
skutków ruchu samochodów ciężarowych i osobowych, służące do
sprawdzeń ogólnych. Składa się z dwóch układów częściowych:

• Dwuosiowe Obciążenia Skupione (tandem TS):
Ciężar na oś (na koło przypada połowa obciążenia nacisku

osi):

α

Qi

*Q

ik

np. w mostach bez znaków
drogowych

Model obciążenia pionowego 1

Model obciążenia pionowego 1

(LM1)

(LM1)

• Równomiernie Rozłożone Obciążenia (układ UDL):
Ciężar -

α

iq

*q

ik

„Qik” - wartość obciążenia zależnego od numeru pasma „i”;

„qik” - wartość obciążenia.

Współczynniki korekcyjne zależne są od klasy drogi lub
spodziewanego ruchu (ustalane z administracją drogową).
Przyjmuje się:

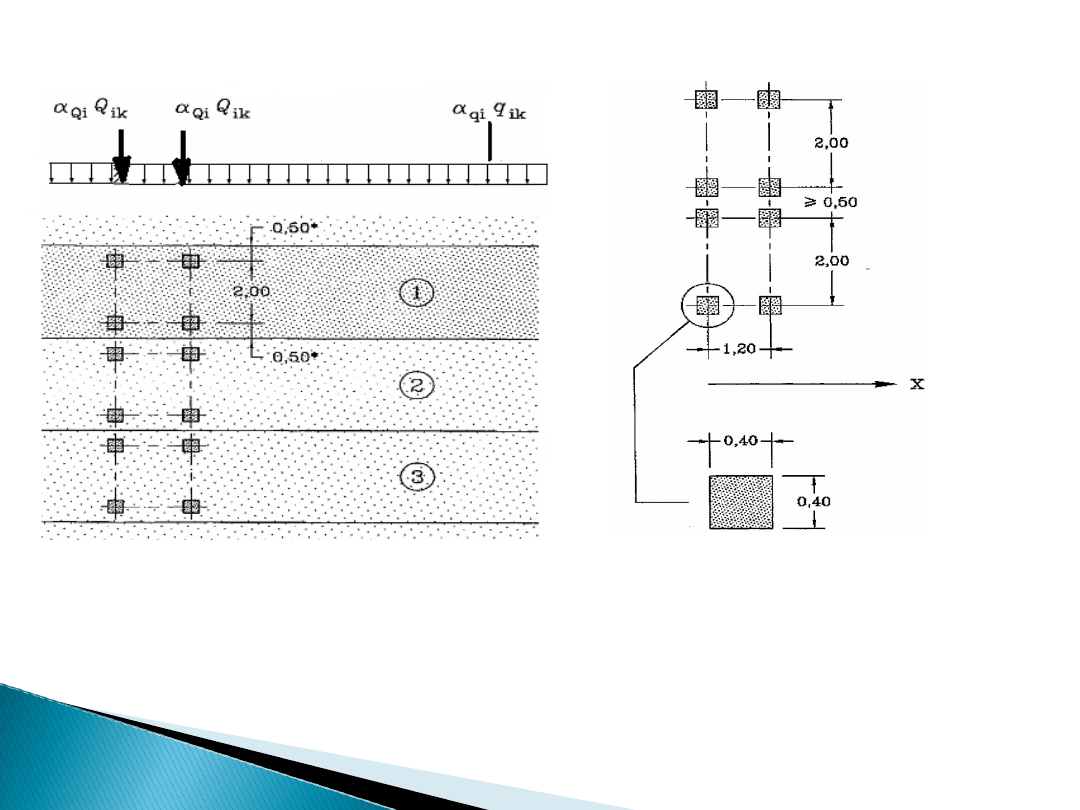
W modelu tym wybiera się położenia pasów numerowanych i umiejscowieniu
układów tandemowych. Stosowany w każdej sytuacji obliczeniowej.
W przypadku sprawdzeń lokalnych układ tandemowy należy ustawiać w
najbardziej niekorzystnym położeniu.

-

powierzchni
a kontaktu
koła

Rys 4.2a) Zastosowanie

Modelu Obc. 1

Rys 4.2b) Zastosowanie układów

tandemowych

do sprawdzeń lokalnych

Model obciążenia pionowego 1

Model obciążenia pionowego 1

(LM1)

(LM1)

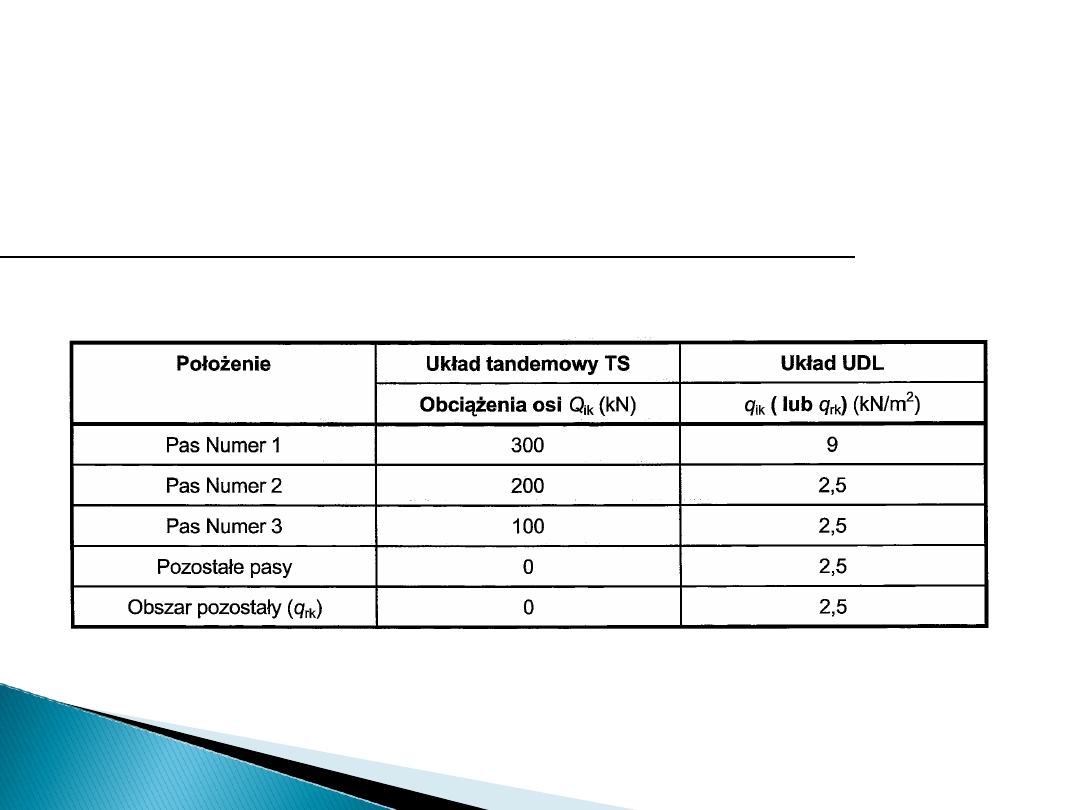
Model obciążenia pionowego 1

Model obciążenia pionowego 1

(LM1)

(LM1)

Podstawowe wartości obciążeń – Tab. 4.2 EC:

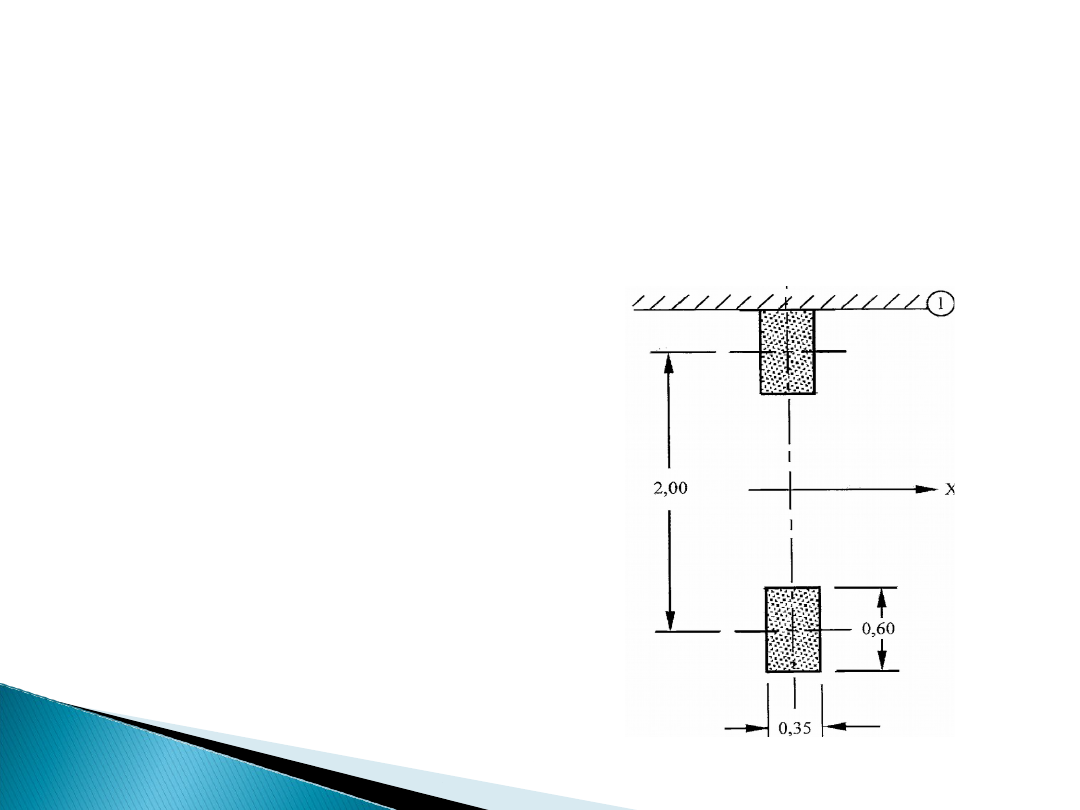
Wykorzystywany jest niezależnie od modelu 1 i powinien być
używany do sprawdzeń lokalnych. Pojedyncza oś przyłożona na
powierzchniach kontaktowych specjalnych opon, stosowana
przy obliczaniu bardzo krótkich elementów konstrukcyjnych.

Składa się z pojedynczej osi -

β

Q

*Q

ak

,

gdzie:
„Q

ak

” - wartość obciążenia równa

400kN.

„β

Q

”- odpowiada wartości α

Qi

z

LM1

Rys 4.3 Zastosowanie Modelu

Obc. 2

1-

krawęż
nik

kierunek osi
podłużnej

mostu

Ustawia się je w dowolnym

miejscu

jezdni, tak aby uzyskać

ekstremalną

wartość sił wewnętrznych.

Stosowany w każdej sytuacji

obliczeniowej.

Model obciążenia pionowego 2

Model obciążenia pionowego 2

(LM2)

(LM2)

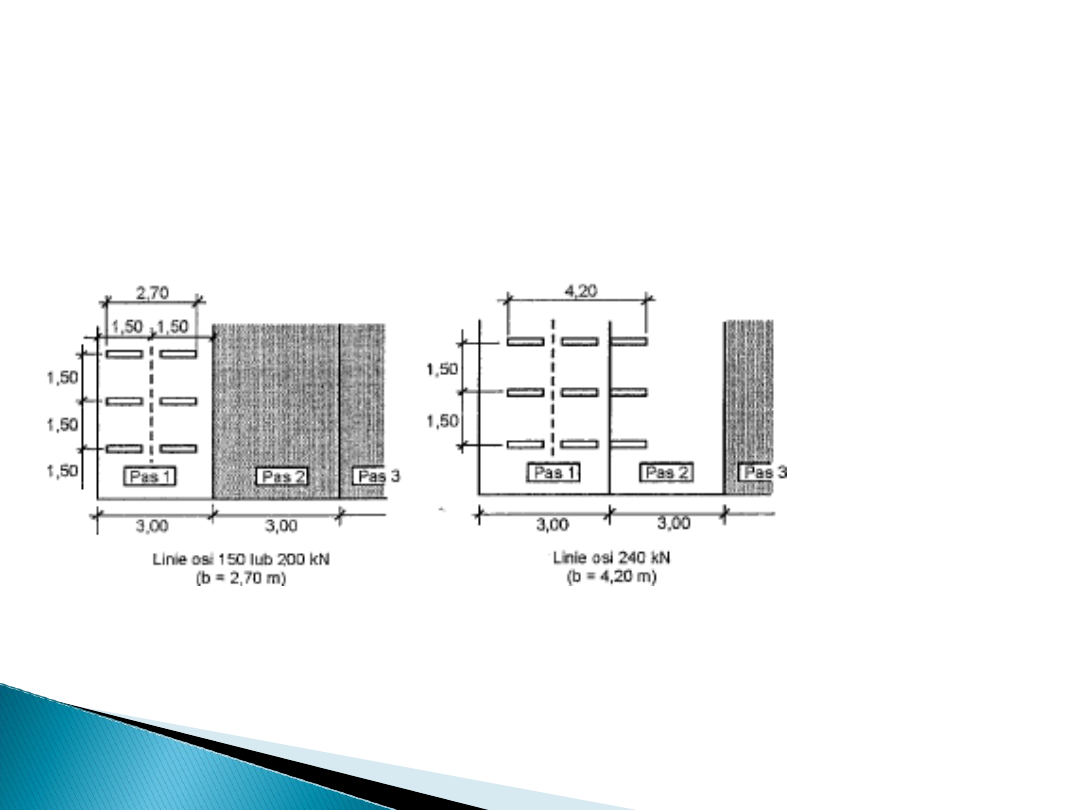
Zbiór zestawów nacisków osi przedstawiający

pojazdy specjalne (np. dla transportu przemysłowego),
które mogą być włączone do ruchu na drogach na
podstawie zezwolenia. Stosowany jest tylko na specjalne
życzenie, w niektórych sytuacjach obliczeniowych.

Rys 4.4

Zastosowanie

Modelu

Obc. 3

Wprowadzono 8 klas pojazdów specjalnych.

Liczba rozpatrywanych modeli może być różna. Pojazdy te
ustawia się na jednym (nr 1) pasie obciążenia lub na
dwóch sąsiednich (nr 1 i 2). Obciążenie ustawiane jest w
możliwie najniekorzystniejszych położeniach jezdni.

Model obciążenia pionowego 3

Model obciążenia pionowego 3

(LM3)

(LM3)

Obciążenie tłumem pieszych przedstawiane w postaci

obciążenia równomiernie rozłożonego o intensywności

5,0kN/m².

Nie mnoży się go dodatkowo przez współczynnik

dynamiczny.

Stosowany jest na specjalne życzenie.

Powinno być ustawione na odpowiednich odcinkach

długości i szerokości pomostu, z wyłączeniem pasa

dzielącego.

Uwzględnia się go wyłącznie z sytuacją przejściową.

Model obciążenia pionowego 4

Model obciążenia pionowego 4

(LM4)

(LM4)



Siły hamowania i przyśpieszenia

Q

lk

- przyjmowane jako siły podłużne zaczepione na poziomie jezdni o

wartości:

gdzie:

L- długość pomostu lub rozpatrywanej jego części

r - promień krzywizny osi środkowej jezdni [m],
Q

v

- całkowity maksymalny ciężar pionowy obciążeń skupionych

tandemowych głównego układu obciążenia.



Siła odśrodkowa Q

tk

- przyjmowane jako siły działające po promieniu łuku i

zaczepiona na

poziomie nawierzchni, o wartościach podanych w Tab.

7.16.

Obciążenia poziome – wartości

Obciążenia poziome – wartości

charakterystyczne

charakterystyczne

Jednoczesność występowania podanych układów
obciążeń jest uwzględniona przez rozpatrywanie grup
obciążenia.

Przewiduje się 5 grup obciążenia, które są kombinacją
różnych modeli obciążeń oraz dodatkowych sił od
hamowania i sił odśrodkowych.

Grupy obciążeń ruchomych mostów

Grupy obciążeń ruchomych mostów

drogowych

drogowych

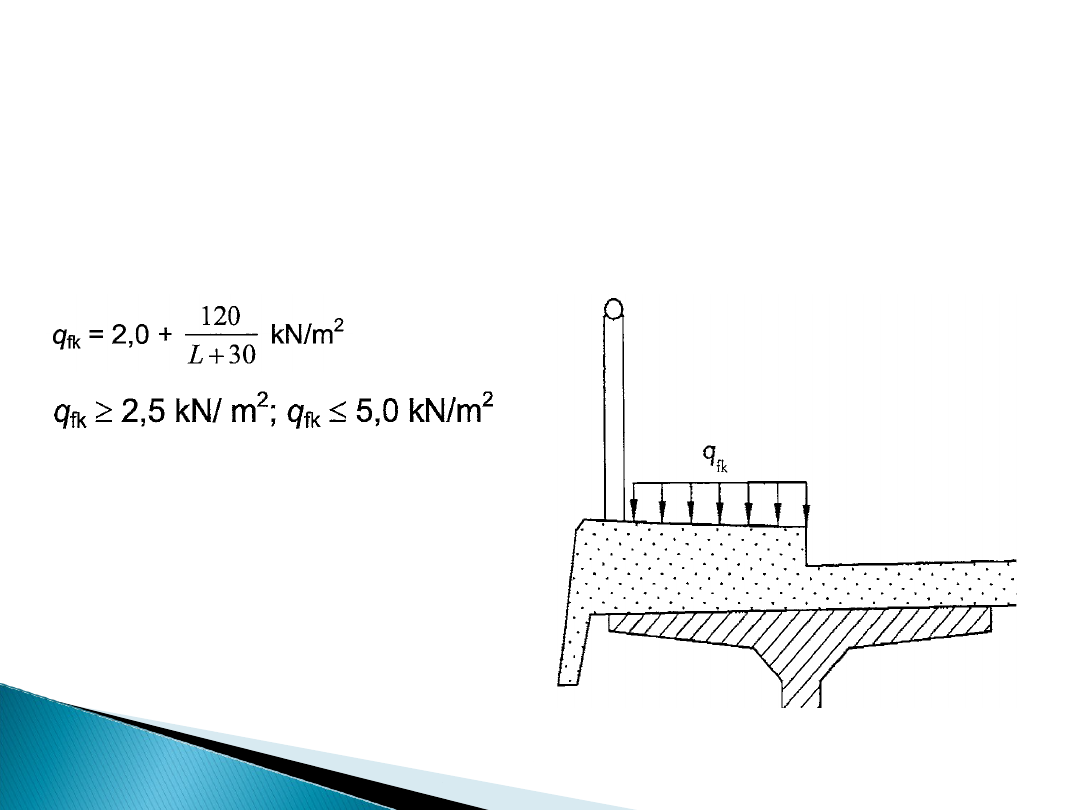
Obciążenie chodników i kładek dla

Obciążenie chodników i kładek dla

pieszych

pieszych

Jako obciążenie normatywne przyjmuje się obciążenie

równomiernie rozłożone o wartości q

k

= 5kN/m², jednakże

w przypadku kładek dla pieszych, o rozpiętości
poszczególnych przęseł przekraczającej 10m, powinny być
uwzględniane następujące wartości:

gdzie: L- rozpiętość przęsła

[m]

W przypadku mostów
drogowych z chodnikami
lub ścieżkami
rowerowymi powinna być
uwzględniana tylko
wartość 5kN/m² .

Obciążenie tłumem pieszych przyjmuje się o wartości 2,5kN/m².

Ruch odbywający się na mostach wywołuje widmo naprężeń, które

może powodować zmęczenie. Zależy od geometrii pojazdów, obciążeń

osi,

rozstawu pojazdów, składu ruchu i jego skutków dynamicznych.

Określono 5 modeli obciążeń zmęczeniowych składających się z sił

pionowych:



Model Obciążenia Zmęczeniowego 1 (podobny do LM1);



Model Obciążenia Zmęczeniowego 2 (zestaw „częstych”
samochodów ciężarowych);



Model Obciążenia Zmęczeniowego 3 (model pojedynczego
pojazdu);



Model Obciążenia Zmęczeniowego 4 (zestaw „standardowych”
samochodów ciężarowych);



Model Obciążenia Zmęczeniowego 5 (oparty na danych z z
pomiarów ruchu drogowego).

Modele obciążeń zmęczeniowych

Modele obciążeń zmęczeniowych

Oddziaływania w sytuacjach

Oddziaływania w sytuacjach

obliczeniowych wyjątkowych

obliczeniowych wyjątkowych

Uwzględnia się je jeśli nie przewidziano zabezpieczeń

ochronnych

przed:

• wjechaniem pojazdu na chodnik,

• uderzeniem pojazdu w podporę,

• uderzeń łodzi, statków lub samolotów ( nad kanałami i

wodą żeglowną).

Obciążenia wyjątkowe są przyjmowane zawsze ze

współczynnikiem obciążeniowym γA=1

Siły uderzenia od pojazdów pod mostem:



siły uderzenia filary oraz inne elementy

podporowe;



siły uderzenia w pomosty;
Oddziaływania pojazdów na moście:



pojazdy na chodnikach i ścieżkach rowerowych;



siły uderzenia w krawężniki;



siły uderzenia w elementy konstrukcyjne.

Oddziaływania w sytuacjach

Oddziaływania w sytuacjach

obliczeniowych wyjątkowych

obliczeniowych wyjątkowych

Mosty kolejowe

Mosty kolejowe

PN-EN 1991-2. Eurokod 1: Oddziaływania na
konstrukcje. Część 2: Obciążenia ruchome mostów

• ruchome obciążenia pionowe:

- model obciążenia „71”,
- model obciążenia „SW”,
- model obciążenia „pociąg bez ładunku”,
- model obciążenia „HSLM”;

• obciążenia pionowe nasypów;
• efekty dynamiczne;
• ruchome obciążenia poziome:

- siły odśrodkowe,
- siły uderzenia bocznego,
- siły przyśpieszania i hamowania;

• oddziaływań aerodynamicznych od przejeżdżających

pociągów.

Obciążenia mostów kolejowych

Obciążenia mostów kolejowych

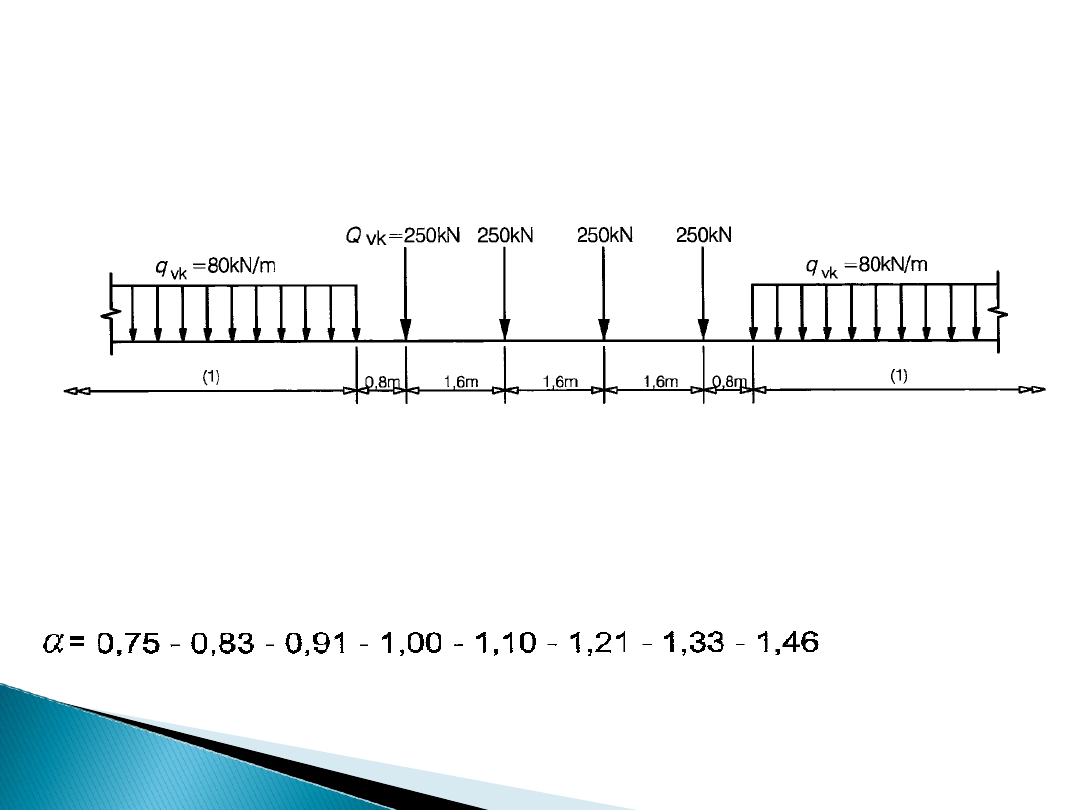
Przedstawia statyczny efekt obciążenia pionowego

wywołany normalnym ruchem kolejowym.

Rys.6.1 Wartości charakterystyczne obciążeń pionowych modelu 71

Do określenia wartości obliczeniowych mnoży się

wartości

charakterystyczne przez współczynnik α równy jednej z

wartości:

w zależności od kategorii linii
kolejowej.

Model obciążenia pionowego 71

Model obciążenia pionowego 71

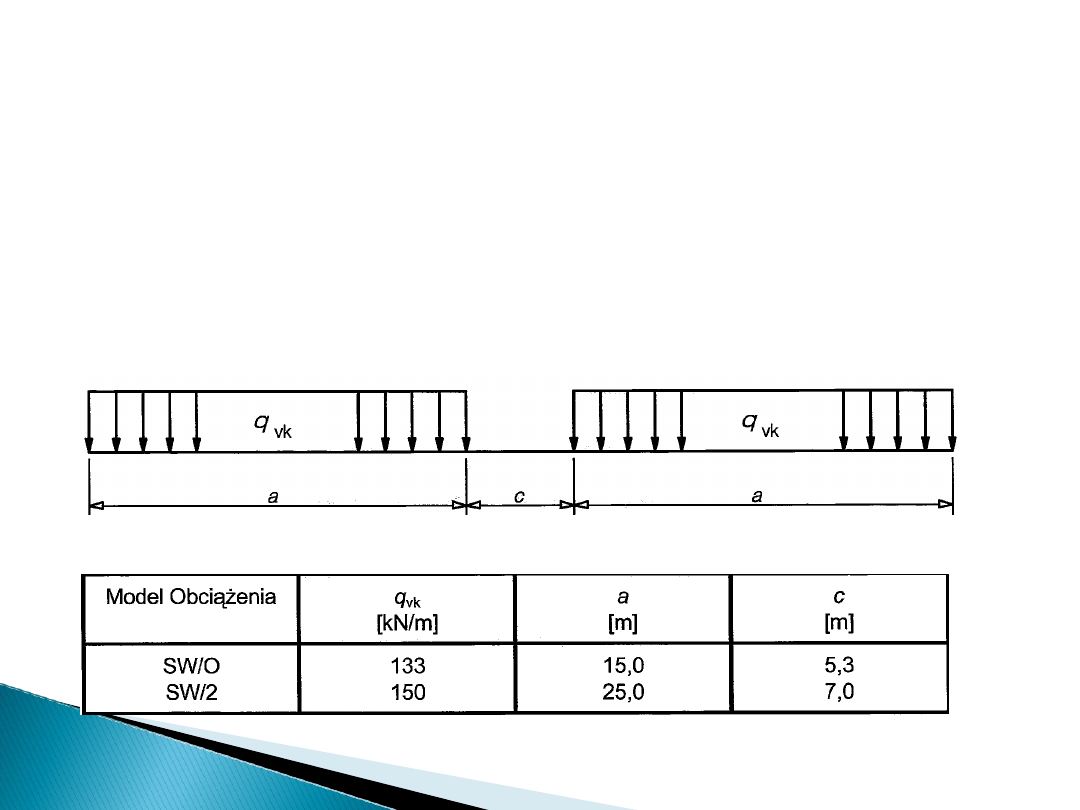
• Model SW/0

- przedstawia statyczny efekt obciążenia pionowego
wywołany

normalnym ruchem kolejowym na belkach ciągłych.
• Model SW/2

- przedstawia statyczny efekt obciążenia pionowego
wywołany

ciężkim ruchem kolejowym.

Rys.6.2 Model obciążenia SW/0 i SW/2

Tab.6.1 Wartości charakterystyczne obciążeń
pionowych w modelach SW/0 i SW/2

Model obciążenia pionowego SW

Model obciążenia pionowego SW

• Model obciążenia pionowego „pociąg bez

ładunku”:
- składa się z obciążenia pionowego równomiernie
rozłożonego o

wartości charakterystycznej 10,0kN/m.
• Model obciążenia pionowego „HSLM”:

- przedstawia obciążenia od pociągów pasażerskich
przy

prędkościach powyżej 200km/h.

Pozostałe modele obciążenia

Pozostałe modele obciążenia

pionowego

pionowego

Współczynnik dynamiczny

Współczynnik dynamiczny

W projektowaniu kolejowych obiektów mostowych

należy uwzględnić współczynnik dynamiczny, którego
wartość zależna jest od jakości utrzymania toru:

• w przypadku starannego utrzymania

toru:

• w przypadku typowego utrzymania

toru:

L – długość miarodajna, przyjmowana zgodnie z

Tab. 6.2 EC

przy

:

przy

:

Współczynnik uwzględnia zwiększenie naprężeń w

konstrukcji, jednak nie uwzględnia skutków rezonansu
i nadmiernych drgań pomostu. Stosowany jest tylko do
prędkości do 200km/h.



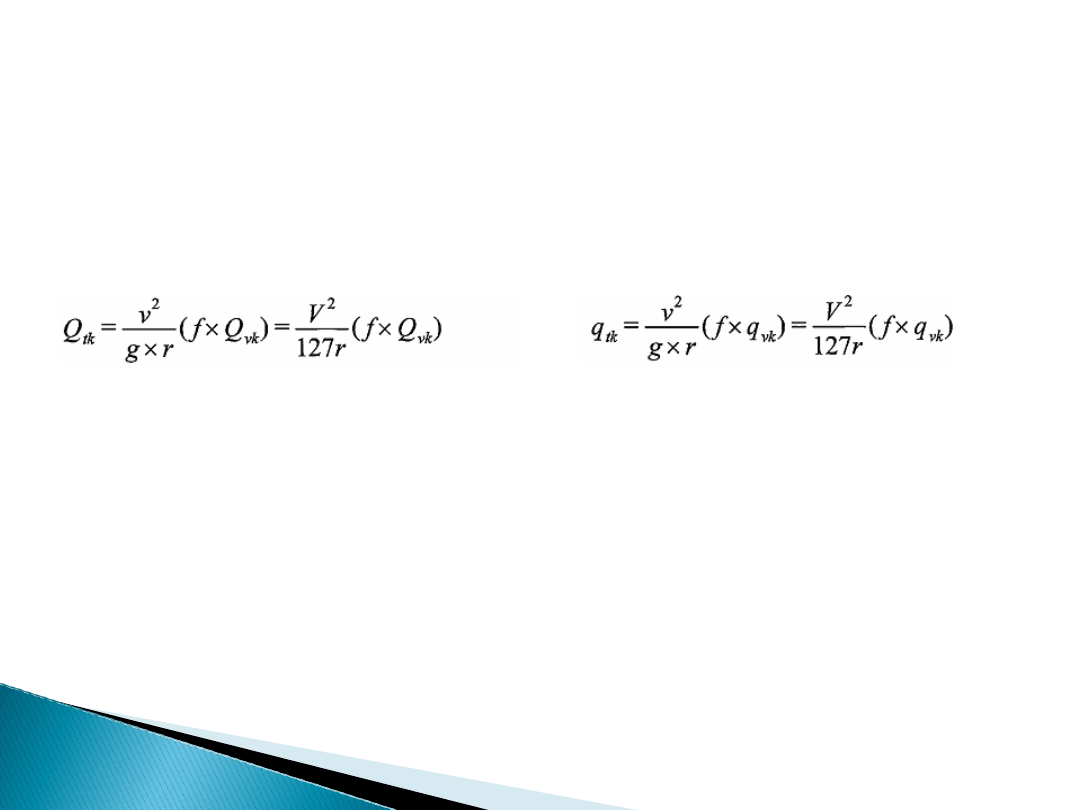
Siła odśrodkowa

– obliczana w wypadku występowania zakrzywienia toru na

moście, na całej długości lub na jego części:

gdzie:
Q

tk

,q

tk

- wartości charakterystyczne sił

ośrodkowych [kN, kNm],

Q

vk

,q

vk

- wartości charakterystyczne obciążeń

pionowych,

f- współczynnik redukcyjny,
v- prędkość max [m/s],
g- przyśpieszenie ziemskie,
r- promień krzywizny [m].

Przyjmuje się, że działa na zewnątrz w kierunku poziomym
na wysokości 1,8m nad płaszczyzną jazdy.

Obciążenia poziome – wartości

Obciążenia poziome – wartości

charakterystyczne

charakterystyczne



Siły uderzeń bocznych:

– siła skupiona działająca poziomo na poziomie główki

szyny, prostopadle do osi toru.
Wartość charakterystyczna wynosi: Q

sk

= 100kN.

Wartość obliczeniowa - Q

sk

*α , gdzie α≥1



Siły przyśpieszenia i hamowania:
- przyjmowane w postaci sił równomiernie rozłożonych na

długości linii wpływu L

a,b

działających na poziomie główki

szyny w kierunku podłużnym toru.
Wartości charakterystyczne:
siła przyśpieszenia: Q

lak

= 33[kN/m] , L

a,b

[m]<1000[kN]

dla modeli: 71, SW/0, SW/2 i

HSLM
siła hamowania: Q

Ibk

= 20[kN/m] , L

a,b

[m]<6000[kN]

dla modeli: 71, SW/0 i HSLM
Q

Ibk

= 35[kN/m] , L

a,b

[m]

dla modelu: SW/2

Obciążenia poziome – wartości

Obciążenia poziome – wartości

charakterystyczne

charakterystyczne

Sytuacja wyjątkowa

Sytuacja wyjątkowa

Projektując nowe bądź sprawdzając istniejące obiekty

mostowe, należy uwzględnić możliwość wykolejenia
taboru, które należy traktować jako wyjątkową sytuację
obliczeniową. W obliczeniach uwzględnia się dwa
przypadki:

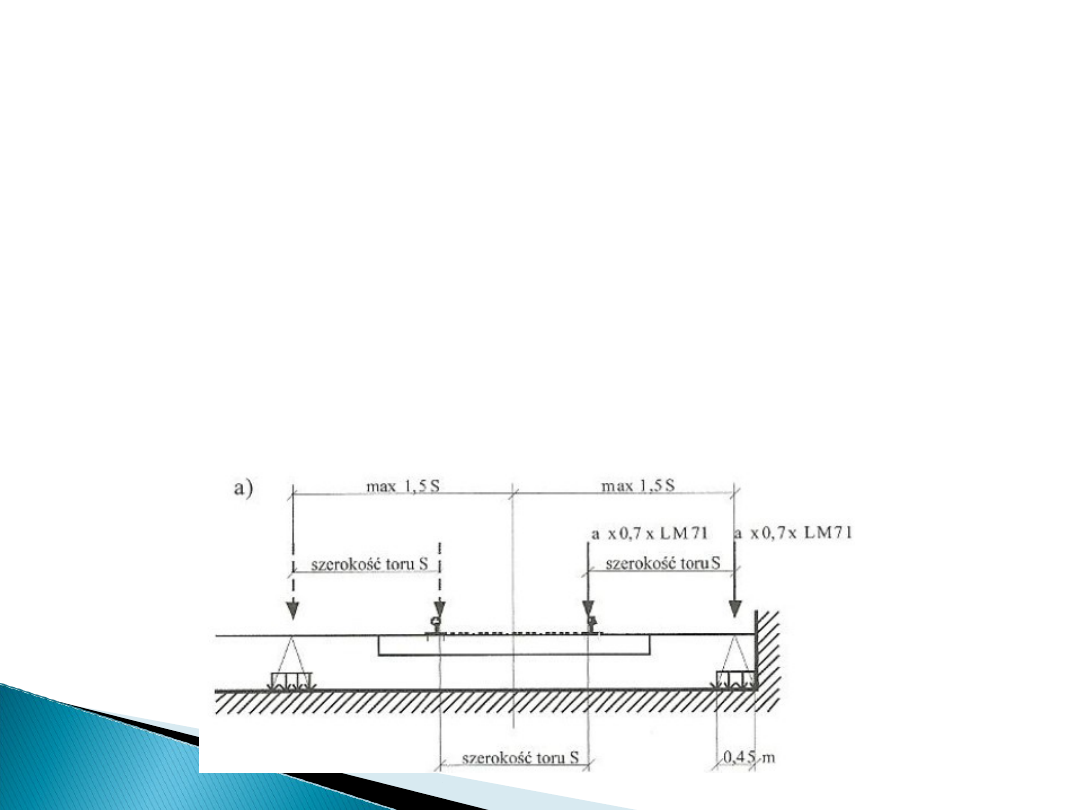
• Sytuacja obliczeniowa I: wykolejenie taboru kolejowego z

wykolejonymi pojazdami pozostają na obszarze toru na
przęśle po ich zatrzymaniu za pomocą sąsiedniej szyny
lub wystającej ściany:

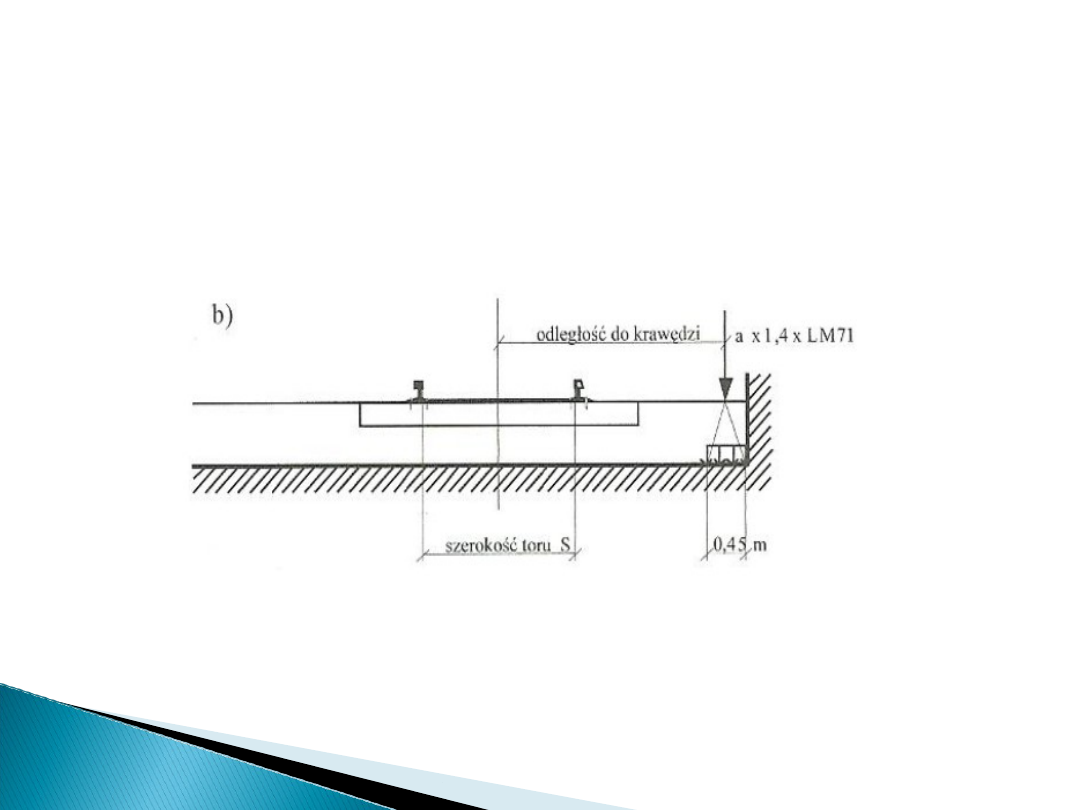
• Sytuacja obliczeniowa II: wykolejenie taboru kolejowego

z wykolejonymi pojazdami zawieszonymi na krawędzi
mostu i obciążającymi krawędź przęsła:

Sytuacja wyjątkowa

Sytuacja wyjątkowa