PODSTAWY PRZETWARZANIA

CYFROWEGO – projekt

Filtr IIR

Michał Turski

17.03.2009

Temat:

Napisz program do projektowania cyfrowych filtrów
BS (pasmowozaporowych) metodą transformacji
biliniowej.
Użytkownik powinien mieć możliwość
wprowadzania danych.*

Założenia projektowe

(+przykładowe parametry)

• Minimalne tłumienie w paśmie

zaporowym: 60 [dB];

• Maksymalne pofalowanie w paśmie

przepustowym : 3 [dB];

• Metoda transformacji biliniowej.

Założenia projektowe

(przykładowe parametry)

• Częstotliwość próbkowania: 2000 Hz
• Dolna częstotliwość pass1: 100 Hz
• Dolna częstotliwość stop1: 300 Hz
• Górna częstotliwość stop2: 700 Hz
• Górna częstotliwość pass2: 900 Hz

Na wykresach częstotliwość jest znormalizowana

względem fp/2.

Transformacja biliniowa

- Wadą przekształcenia biliniowego jest nieliniowe przekształcanie osi częstotliwości

przestrzeni s w oś częstotliwości przestrzeni z:

- Powoduje to, ze otrzymana charakterystyka jest zniekształcona, co objawia się poprzez

zagęszczenie osi częstotliwości dla dużych częstotliwości. Aby tego uniknąć należy

zadaną częstotliwość graniczną filtru cyfrowego



wstawić do wzoru, a następnie

otrzymaną wartość użyć w procedurze projektującej prototyp analogowy filtru cyfrowego.

















2

tan

2



T

Transformacja biliniowa

s

T

z
z





















2 1

1

1

1

- Transformacja biliniowa, jest bardzo popularną metodą

projektowania filtrów cyfrowych. Przekształca oś urojoną

przestrzeni s w koło jednostkowe w przestrzeni z jednoznacznie,

unikając nakładania się charakterystyk. Co więcej, lewa

półpłaszczyzna przestrzeni s jest przekształcana do wewnątrz

koła jednostkowego, zaś prawa półpłaszczyzna jest

odwzorowywana na zewnątrz koła. Transformata biliniowa jest

powiązana z numeryczną aproksymacją całkowania przy pomocy

metody trapezów.

- Zależność pomiędzy zmienną s, a zmienną z:

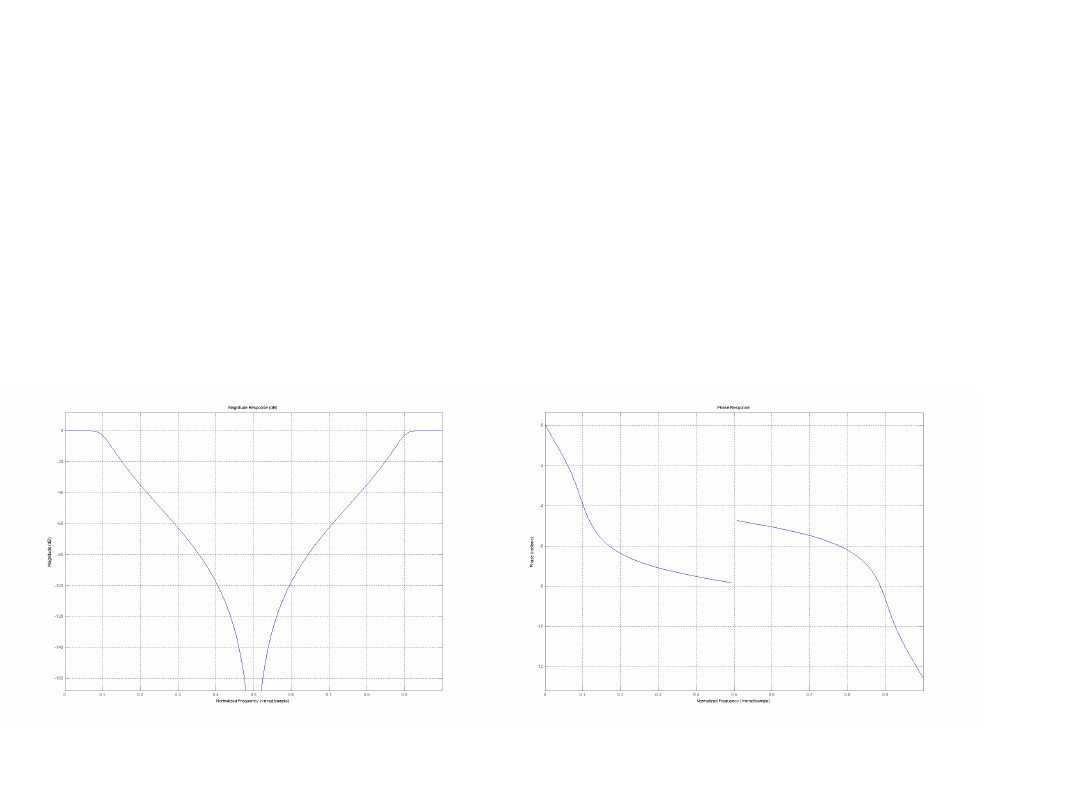
Filtr Butterwortha

Filtr

Butterwortha,

nie

posiada

zafalowań

w

paśmie

przepustowym i zaporowym oraz ma charakterystykę fazową

najbardziej zbliżoną do liniowej, ale za to odznacza się najmniej

stromym zboczem pasm przejściowych (przy takim samym

rzędzie filtru)

Charakterystyka amplitudowa Charakterystyka fazowa

Rząd filtru: 5

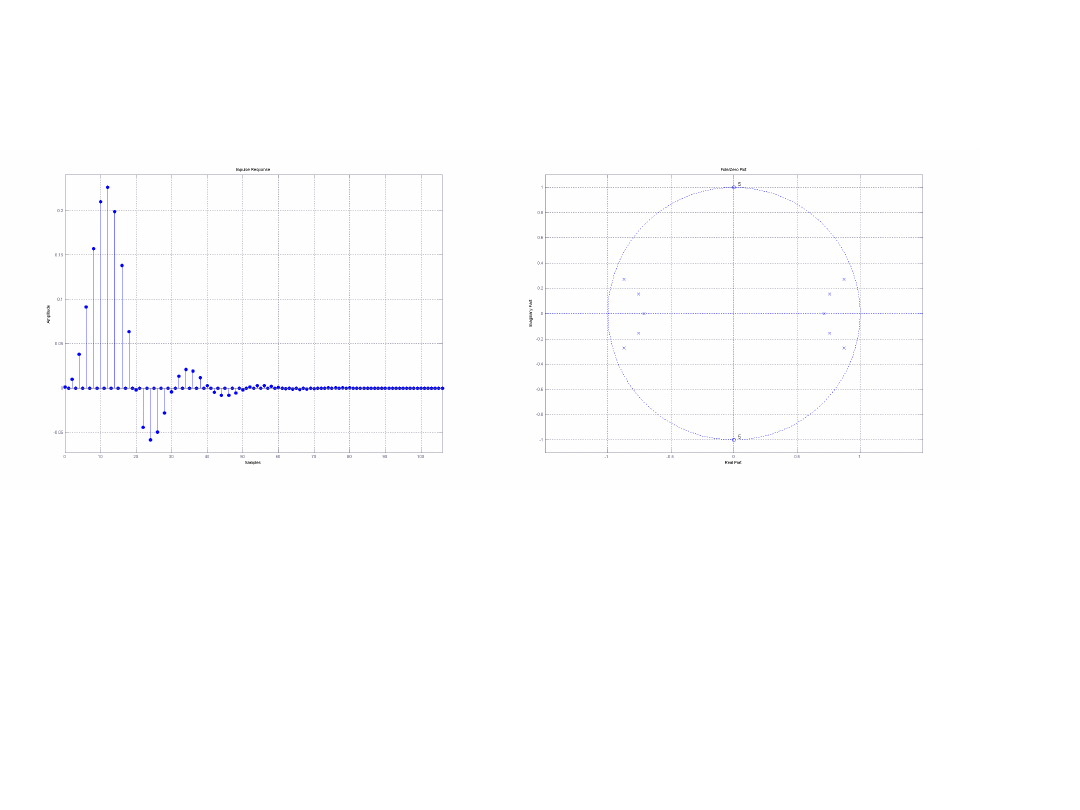
Odpowiedź impulsowa Rozkład zer i biegunów

Widać że filtr jest stabilny. Odpowiedź impulsowa maleje do zera
oraz wszystkie bieguny transmitancji wewnątrz okręgu
jednostkowego.

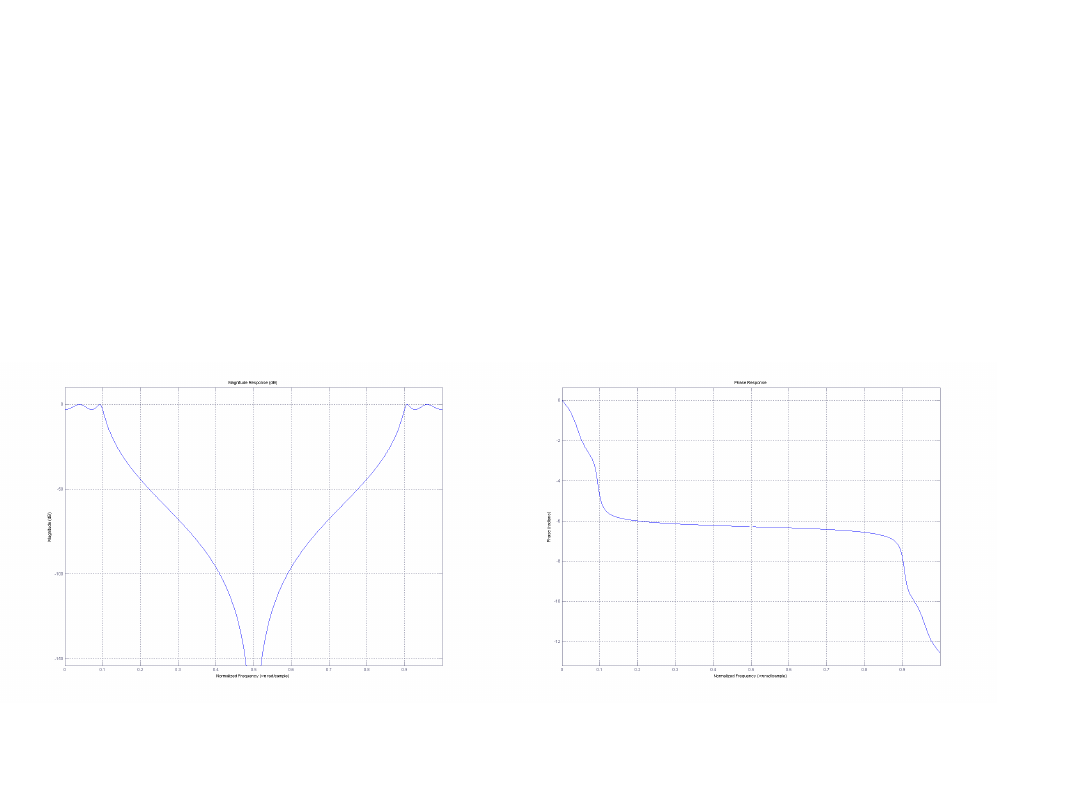
Filtr Czebyszewa typu I

Filtr Czebyszewa typu I, posiada zafalowania w paśmie

przepustowym, nie posiada zafalowań w paśmie zaporowym, ma

węższe pasmo przejściowe niż filtr Butterwortha, lecz okupione

bardziej nieliniową charakterystyką fazową

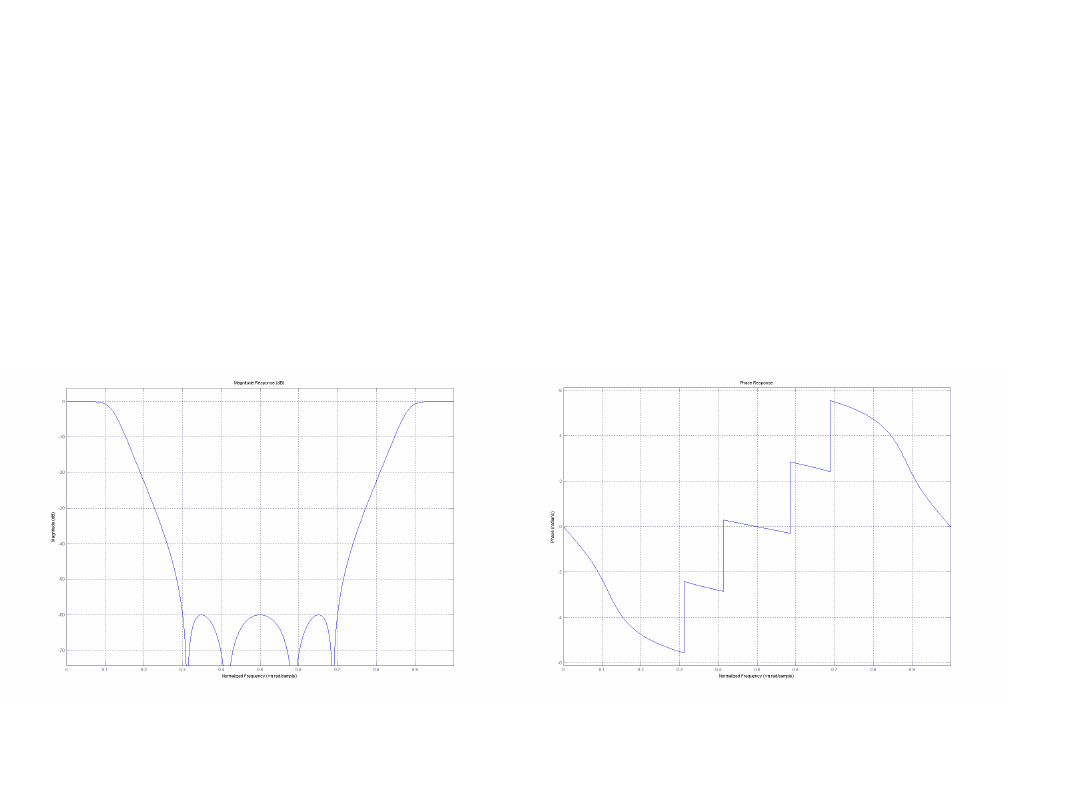
Charakterystyka amplitudowa Charakterystyka fazowa

Rząd filtru: 4

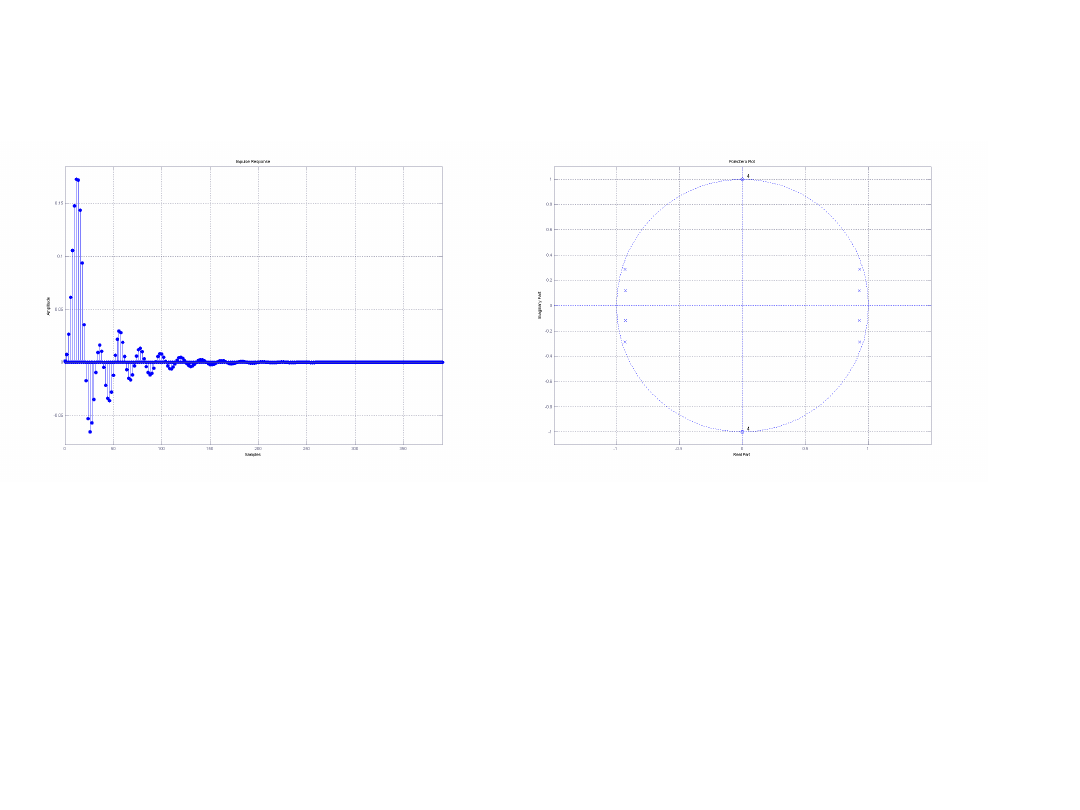
Odpowiedź impulsowa Rozkład zer i biegunów

Widać że filtr jest stabilny. Odpowiedź impulsowa maleje do zera oraz
wszystkie bieguny transmitancji wewnątrz okręgu jednostkowego.

Filtr Czebyszewa typu II

Filtr Czebyszewa typu II, charakteryzuje się zafalowaniami w

paśmie zaporowym a nie przepustowym

Charakterystyka amplitudowa Charakterystyka fazowa

Rząd filtru: 4

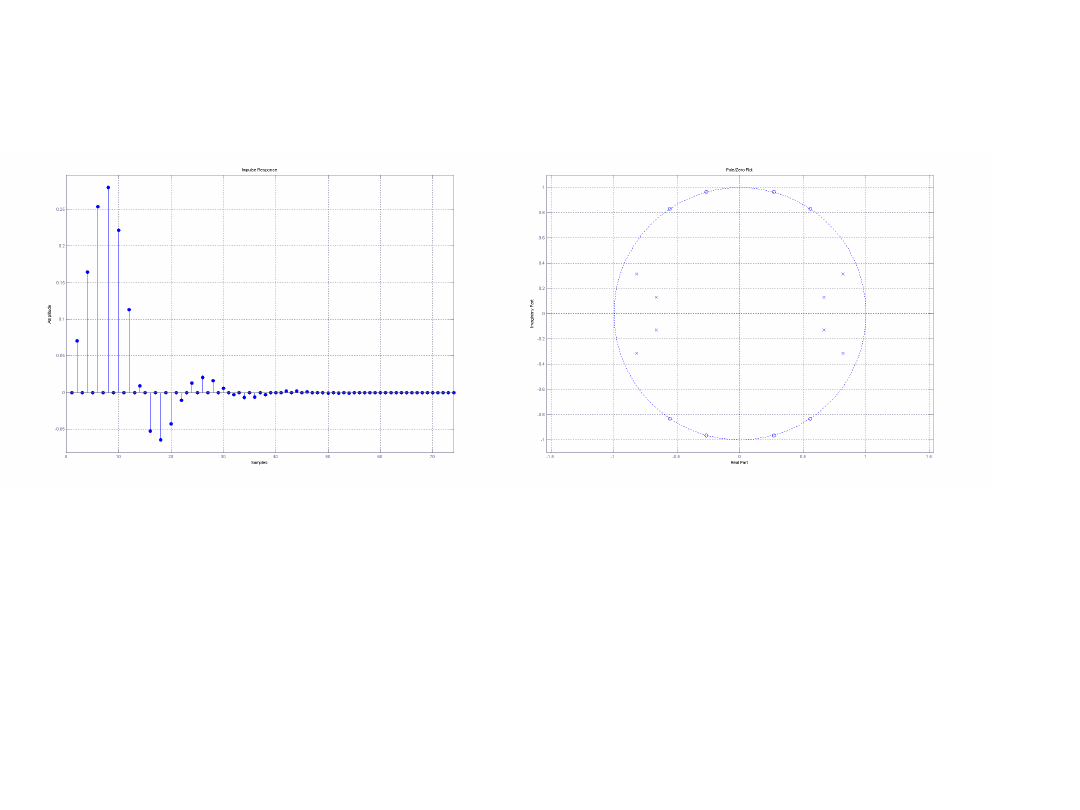
Odpowiedź impulsowa Rozkład zer i biegunów

Widać że filtr jest stabilny. Odpowiedź impulsowa maleje do zera oraz
wszystkie bieguny transmitancji wewnątrz okręgu jednostkowego.

Filtr Eliptyczny

Filtr eliptyczny, posiada zafalowania w obu pasmach, ale przy

takim samym rzędzie filtra odznacza się najmniejszą stromością

zboczy

pasm

przejściowych

i

najbardziej

nieliniową

charakterystyką fazową

Charakterystyka amplitudowa Charakterystyka fazowa

Rząd filtru: 3

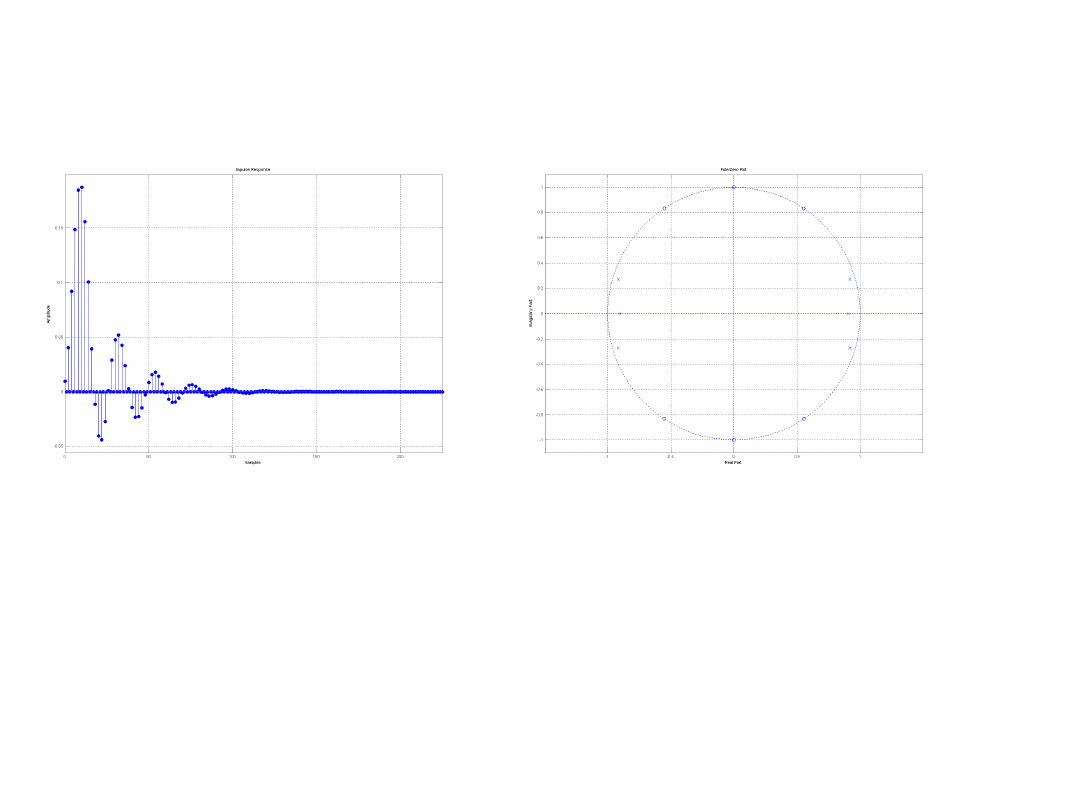
Odpowiedź impulsowa Rozkład zer i biegunów

Widać że filtr jest stabilny. Odpowiedź impulsowa maleje do zera oraz
wszystkie bieguny transmitancji wewnątrz okręgu jednostkowego.

Literatura

- Wykład z Podstaw Cyfrowego Przetwarzania Sygnałów ;-)

(wiadomo najważniejszy)

- Zieliński P.T.: Od teorii do cyfrowego przetwarzania sygnałów,
AGH, Kraków 2002

- http://castor.am.gdynia.pl/~luksza/doc/matlab/