Macierz Jacobianowa – Jacobiany manipulatora

Macierz Jacobianowa – Jacobiany manipulatora

Sterowanie i

Sterowanie i

Programowanie

Programowanie

Robotów

Robotów

Wykład nr 05 / 06

Wykład nr 05 / 06

dr inż. Tomasz Trawiński

Politechnika Śląska, Wydział

Politechnika Śląska, Wydział

Elektryczny

Elektryczny

KATEDRA MECHATRONIKI

KATEDRA MECHATRONIKI

















































)

(

)

(

)

(

)

(

6

6

1

1

1

1

)

6

(

q

f

q

q

f

q

q

f

q

q

f

q

n

n

n











J

Macierz Jacobianowa

Macierz Jacobianowa

• Z matematycznego punktu widzenia równania

kinematyki prostej określają funkcję między przestrzenią
pozycji i orientacji kartezjańskich a przestrzenią pozycji
przegubów.

• Natomiast związki prędkościowe pomiędzy

przestrzeniami pozycji/orientacji oraz przegubów
określone są przez Jacobiany tej funkcji.

Macierz Jacobianowa

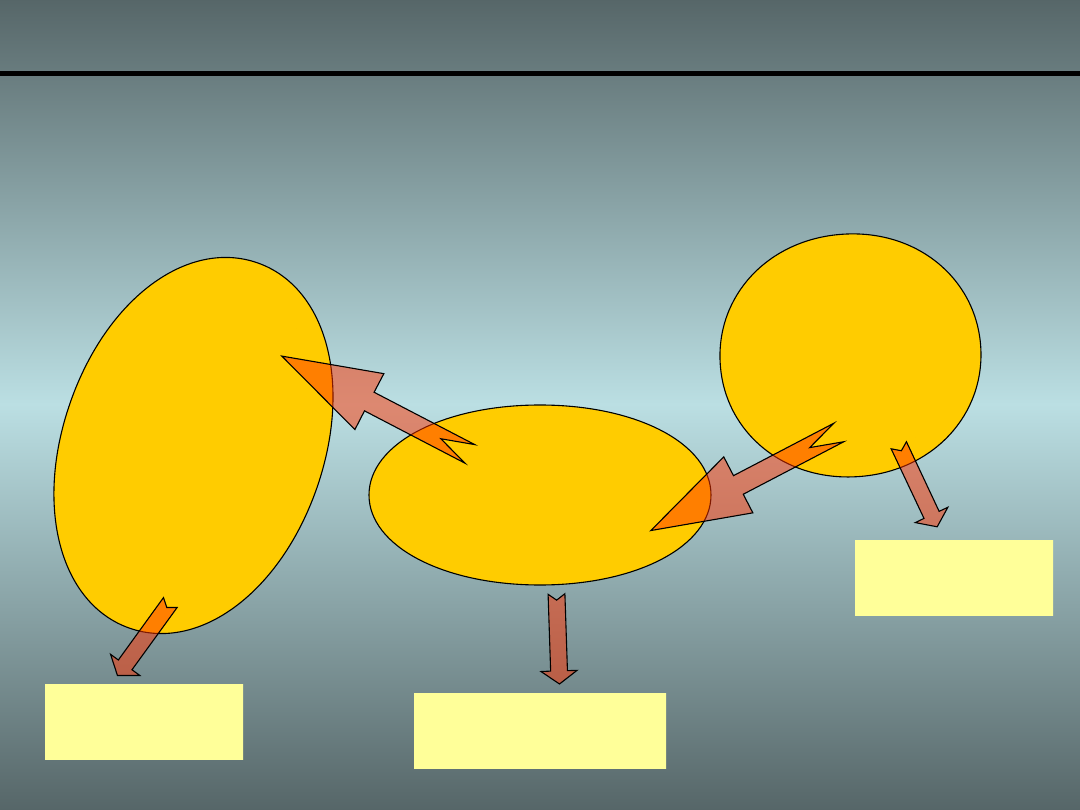
Macierz Jacobianowa

• Załóżmy że mamy manipulator o n-członach

Wektor

Prędkości

Przegubowych

Macierz

Jacobianowa

Wekto

r

Prędko

ści

Liniow

ej i

Kątow

ej

Końcó

wki

Manip

ulatora

n -
wymiarowy

6 -
wymiarowy

6  n -

wymiarowa

Macierz Jacobianowa

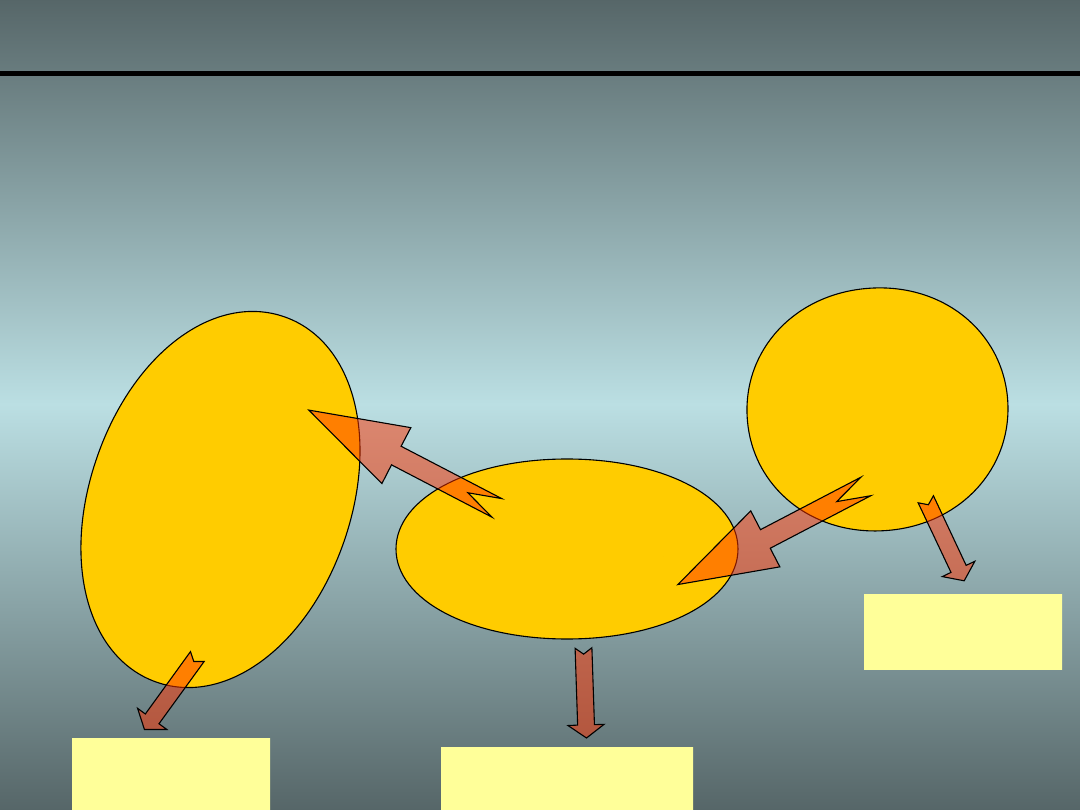
Macierz Jacobianowa

• Jako przekształcenie pomiędzy prędkościami

przegubowymi a prędkością liniową i kątową
dowolnego punktu na manipulatorze

Wektor

Prędkości

Przegubowych

Macierz

Jacobianowa

Wekto

r

Prędko

ści

Liniow

ej i

Kątow

ej

Pkt. na

Manip

ulatorz

e

n -
wymiarowy

6 -
wymiarowy

6  n -

wymiarowa

Dla n-członowego manipulatora

Dla n-członowego manipulatora

oraz















1

0

0

0

0

n

n

n

d

R

T





T

n

n

q

q

q

q

1

2

1







q

Ruch

manipulatora

 

t

d

n

0

 

t

R

n

0





T

n

n

t

q

t

q

t

q

t

q

t

)

(

),

(

,

),

(

),

(

)

(

1

2

1







q

Poszukujemy relacji określających związek pomiędzy

prędkością liniową i kątową końcówki roboczej (ale

nie tylko końcówki) z prędkościami przegubowymi

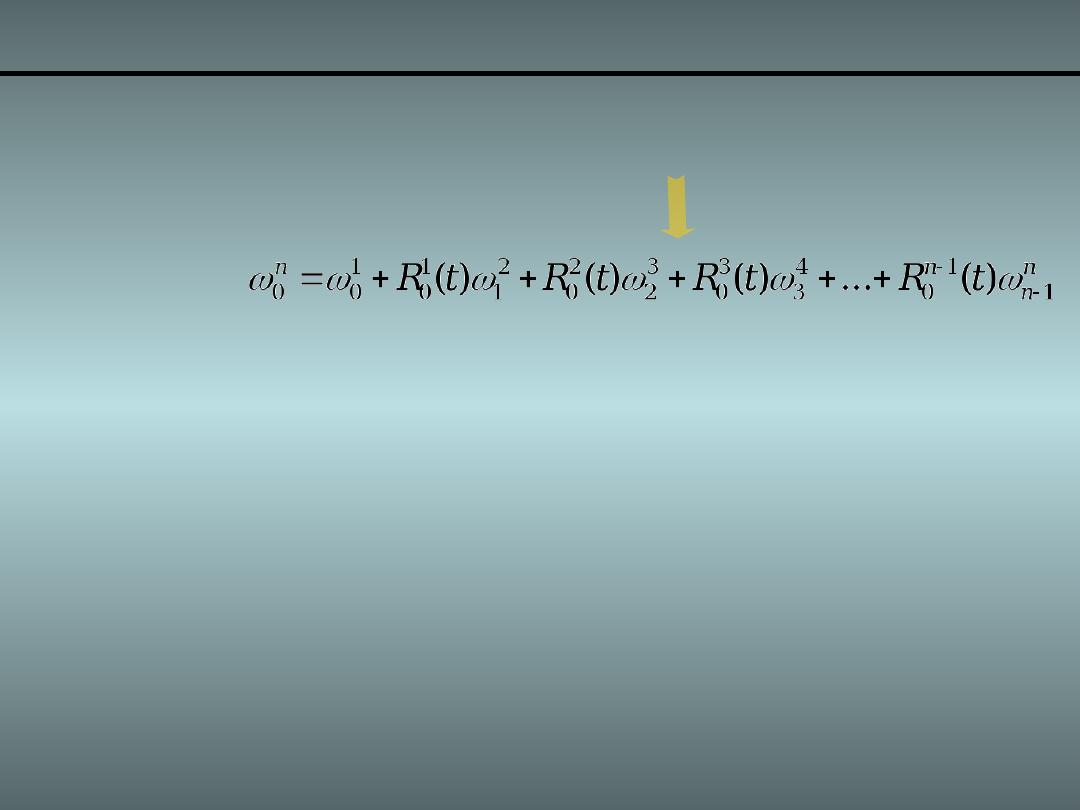
prędkość kątową końcówki określa:

Niech:

Niech:

prędkość liniową końcówki określa:

n

n

d

v

0

0





T

n

t

R

t

R

S

)

(

)

(

)

(

0







poszukujemy pewnych wyrażeń postaci:

q

J

v



v

n



0

q

J

ω







n

0

A w zapisie macierzowym:

A w zapisie macierzowym:

 





























q

ω

v



J

J

v

n

n

0

0







n

3

3















J

J

v







1

3

3

0

0













n

n

ω

v



 





1

n q

Wyprowadzenie macierzy J

Wyprowadzenie macierzy J





• Jeśli przegub „i” jest obrotowy to

zmienna przegubowa „q

i

” jest

równa „

i

”, a osią obrotu jest „z

i-1

”

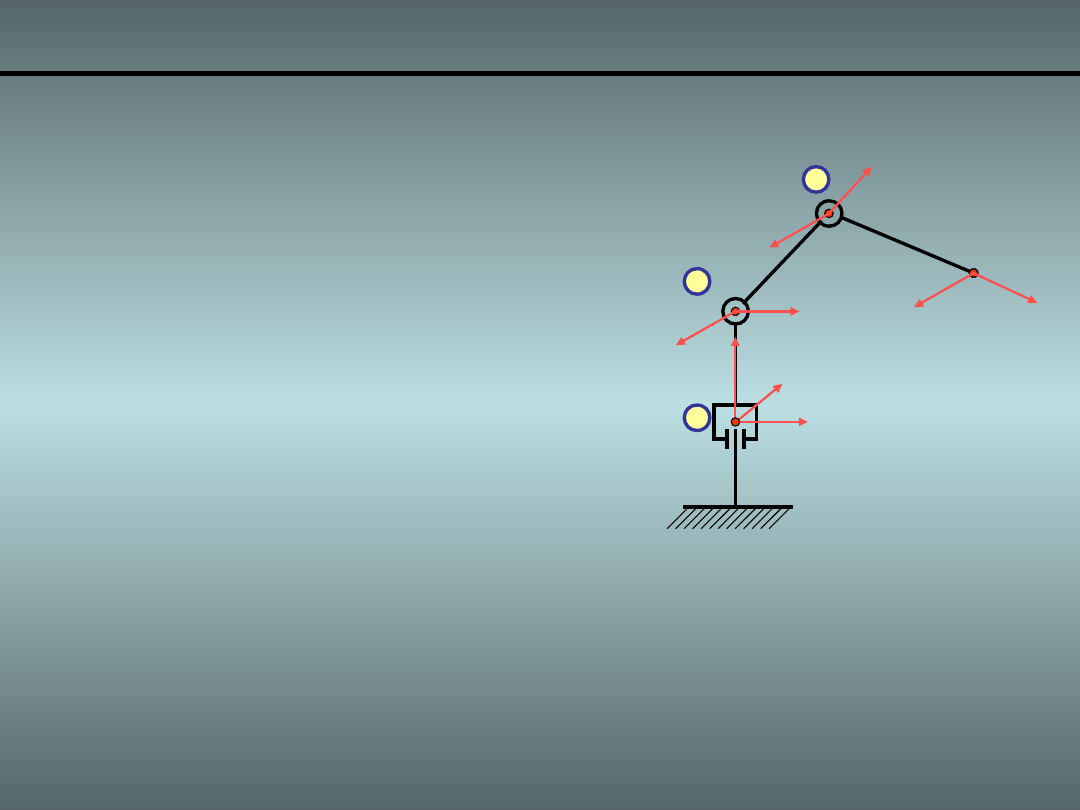
• Prędkość

kątowa członu

„i” wyrażona w

układzie „i-1”

wynosi:

k

i

i

i

q





 1



z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3

0

0

2

1

3

1

1

2

2

3

3

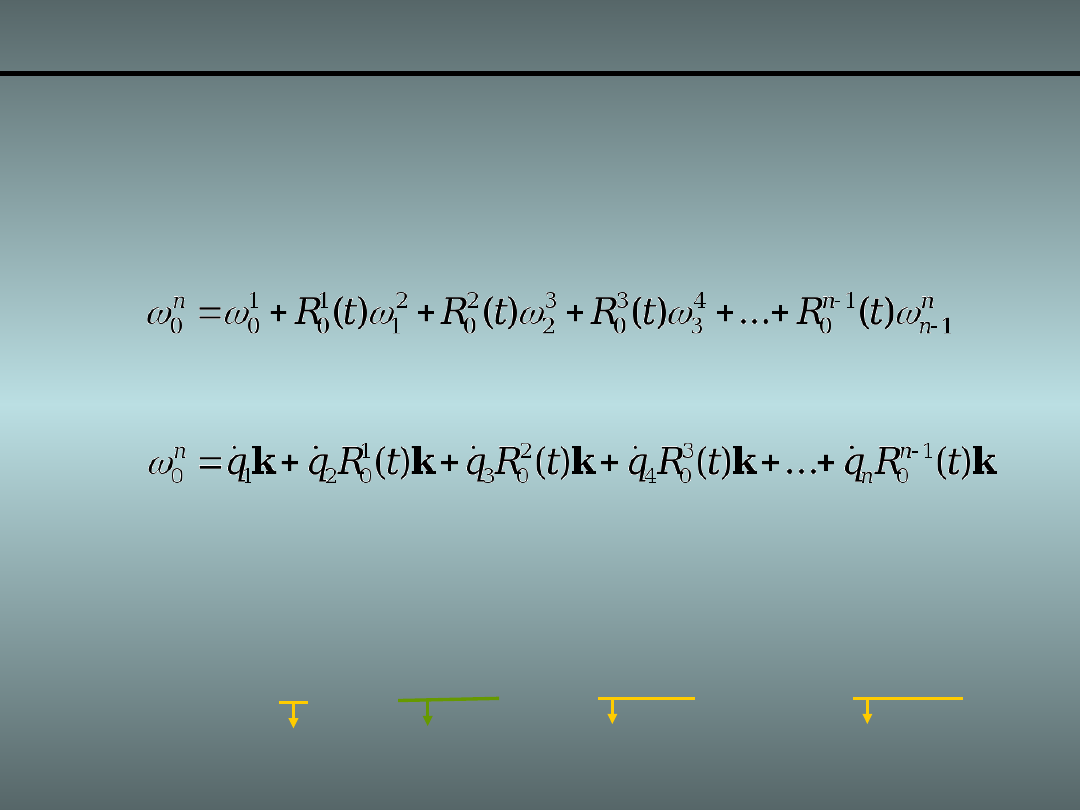
Wyprowadzenie macierzy J

Wyprowadzenie macierzy J





• Podstawiając wyrażenie:

k







i

i

i

q

1



do

Wprowadzając zmienną pomocniczą 

i

(1-dla przegubu

obrotowego, 0 – dla pryzmatycznego):

otrzymamy:

k

k

k

k

)

(

...

)

(

)

(

1

0

2

0

3

3

1

0

2

2

1

1

0

t

R

q

t

R

q

t

R

q

q

n

n

n

n































z

0

z

1

z

2

Z

n-1

Wyprowadzenie macierzy J

Wyprowadzenie macierzy J





• Prędkość kątowa w bazowym układzie współrzędnych, w

zwięzłej formie, dana jest wyrażeniem

1

1

0









i

i

n

i

i

n

z

q











T

i

i

R

z

1

0

0

,

1

0

1











k

k

0

z

gdzie:

• Macierz J



ma postać:





1

0

1

,

,





n

n

z

z









J

Wyprowadzenie macierzy J

Wyprowadzenie macierzy J

v

v

• Prędkość liniowa końcówki manipulatora:











n

i

i

i

n

n

q

q

d

d

1

0

0





• Tak więc „i” kolumna macierzy J

v

równa się:

i

n

q

d





0























i

n

v

q

d

0

J

•

Rozróżnia się dwa przypadki:

1. Dla przegubu pryzmatycznego
2. Dla przegubu obrotowego

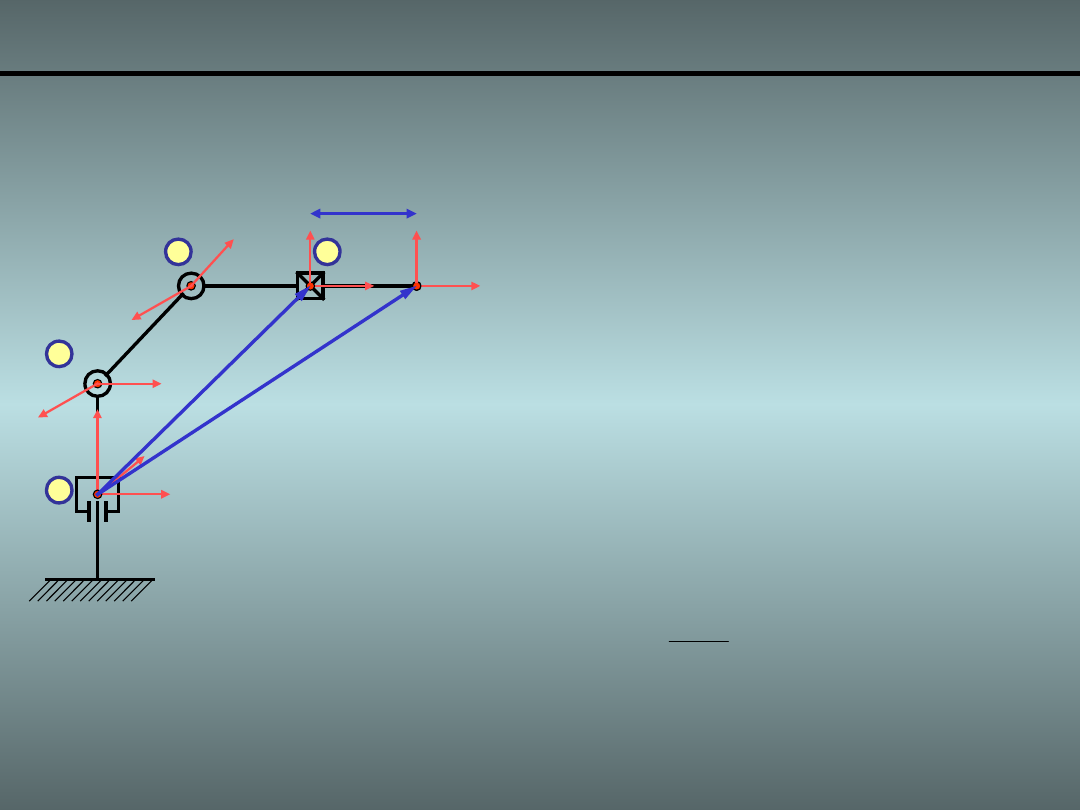
Wyprowadzenie macierzy J

Wyprowadzenie macierzy J

v

v

– przegub pryzmatyczny

– przegub pryzmatyczny

• Różniczkując powyższe wyrażenie

względem zmiennej przegubowej

i

k

i

i

i

i

i

i

a

R

d

d

1

1









1

1

0

1

1

0

0















i

i

i

i

i

i

i

n

z

d

R

d

d

R

d









k

1

0









i

i

n

z

q

d

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3

0

0

2

1

3

1

1

2

2

3

3

z

z

4

4

x

x

4

4

4

4

4

4

d

4

0

d

3

0

d

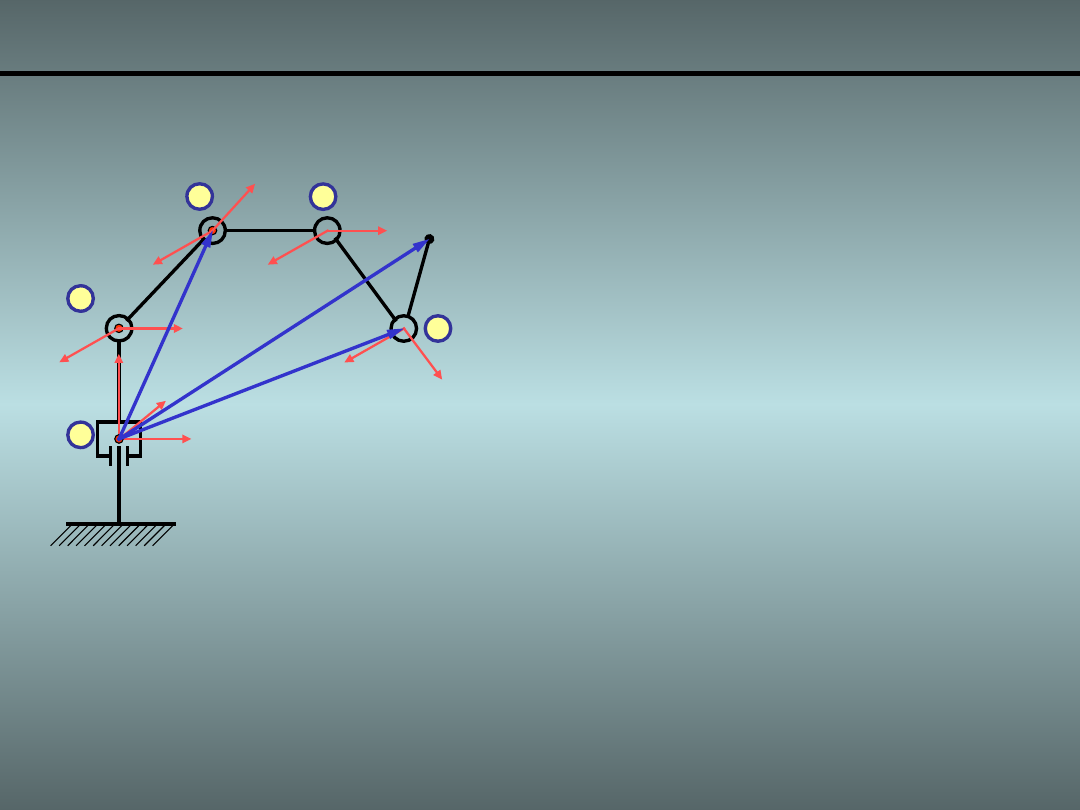
Wyprowadzenie macierzy Jv – przegub obrotowy

Wyprowadzenie macierzy Jv – przegub obrotowy

n

i

i

i

n

d

R

d

d

1

1

0

1

0

0











n

i

i

i

n

d

R

o

o

1

1

0

1











• Jeśli tylko przegub „i”

jest napędzany to
są stałe.

1

0

1

0





i

i

R

d

i

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

0

0

2

1

3

1

1

2

2

3

3

4

z

z

3

3

z

z

4

4

x

x

4

4

5

4

4

5

5

Wyprowadzenie macierzy J

Wyprowadzenie macierzy J

v

v

– przegub obrotowy

– przegub obrotowy

• Różniczkując:

• Ponieważ ruch członu „i”

jest obrotem wokół osi
„z

i-1

” to:

• Stąd:

n

i

i

i

i

d

R

q

R

1

1

0

1

0











k



)

(

1

1











i

n

i

i

o

o

z

q



1



i

z





















n

i

i

i

n

d

q

R

d

1

1

0

0

k





1





i

n

o

o

)

(

1

1

0















i

n

i

i

n

o

o

z

q

d

n

i

i

n

i

d

q

d

1

1







 k





n

i

i

n

d

R

d

1

1

0

0











Wyprowadzenie macierzy J

Wyprowadzenie macierzy J

v

v

– przegub obrotowy

– przegub obrotowy

• Jacobian J

v

ma postać:





vn

vi

v

v

J

J

J

,

,

,

,

1







J

)

(

1

1











i

n

i

vi

o

o

z

J

1





i

vi

z

J

– dla przegubu obrotowego

– dla przegubu pryzmatycznego

Całkowita postać Jacobianu manipulatora n-

Całkowita postać Jacobianu manipulatora n-

członowego

członowego





























1

1

1

i

i

n

i

i

z

o

o

z

J





n

i

J

J

J

,

,

,

,

1







J

















0

1

i

i

z

J

– dla przegubu

obrotowego

– dla przegubu

pryzmatycznego

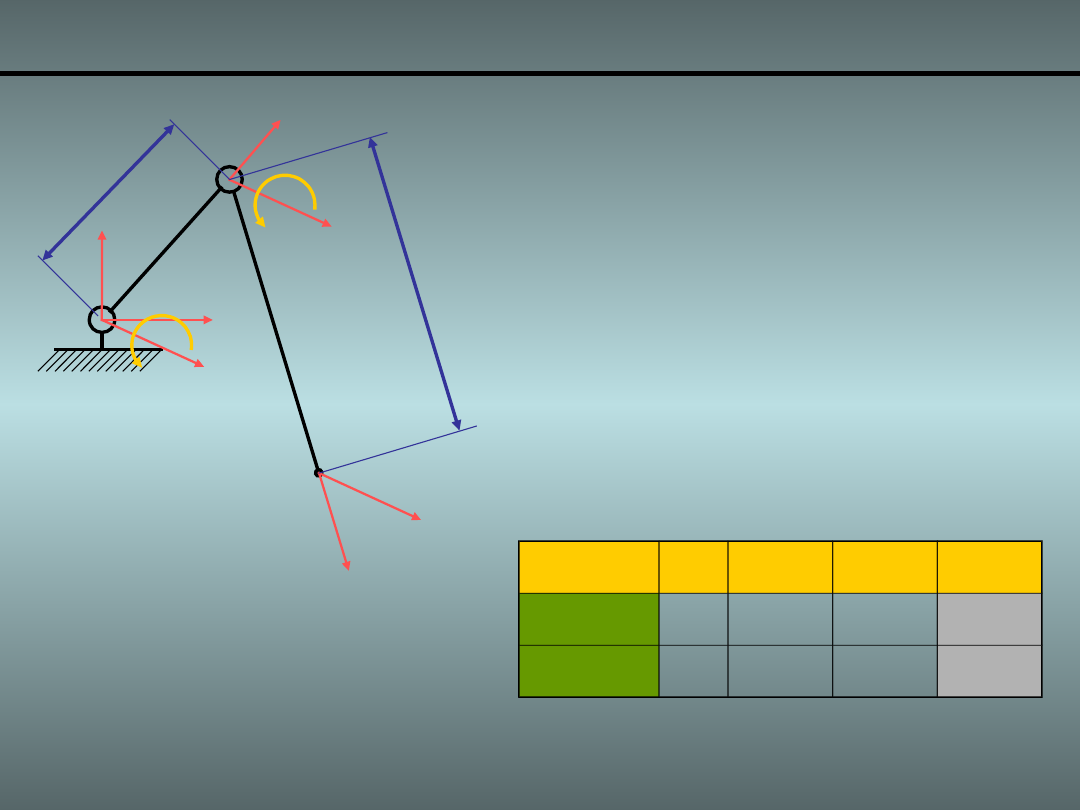
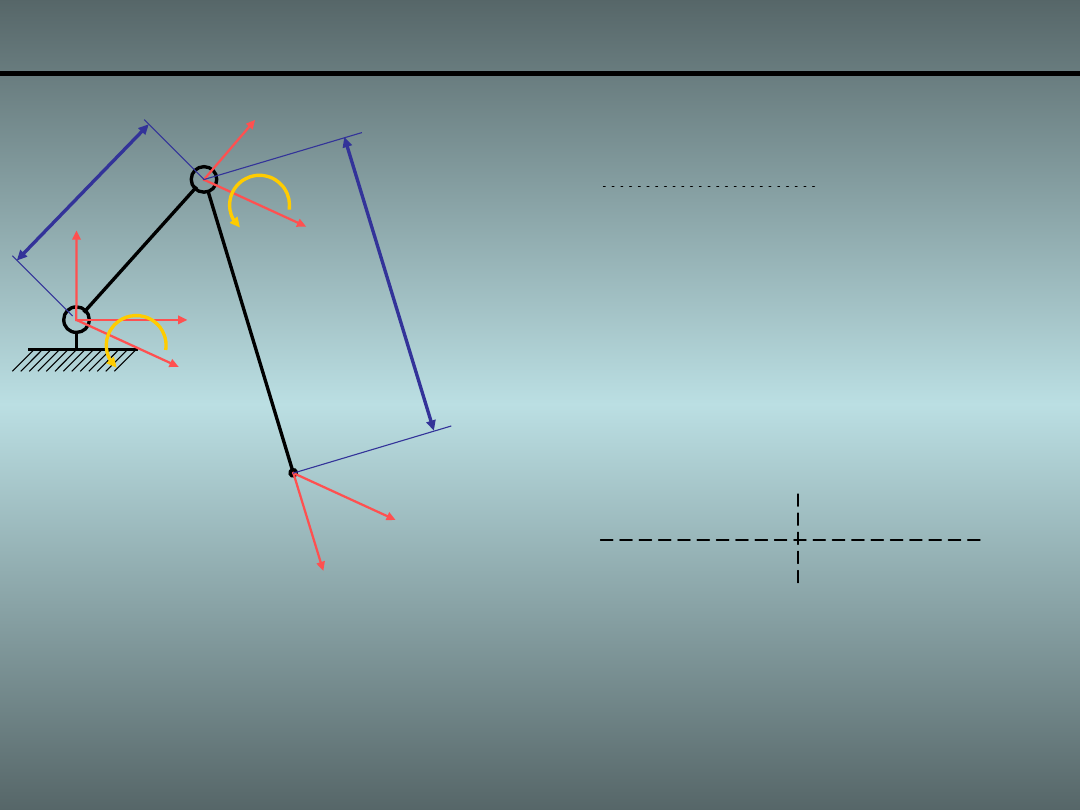
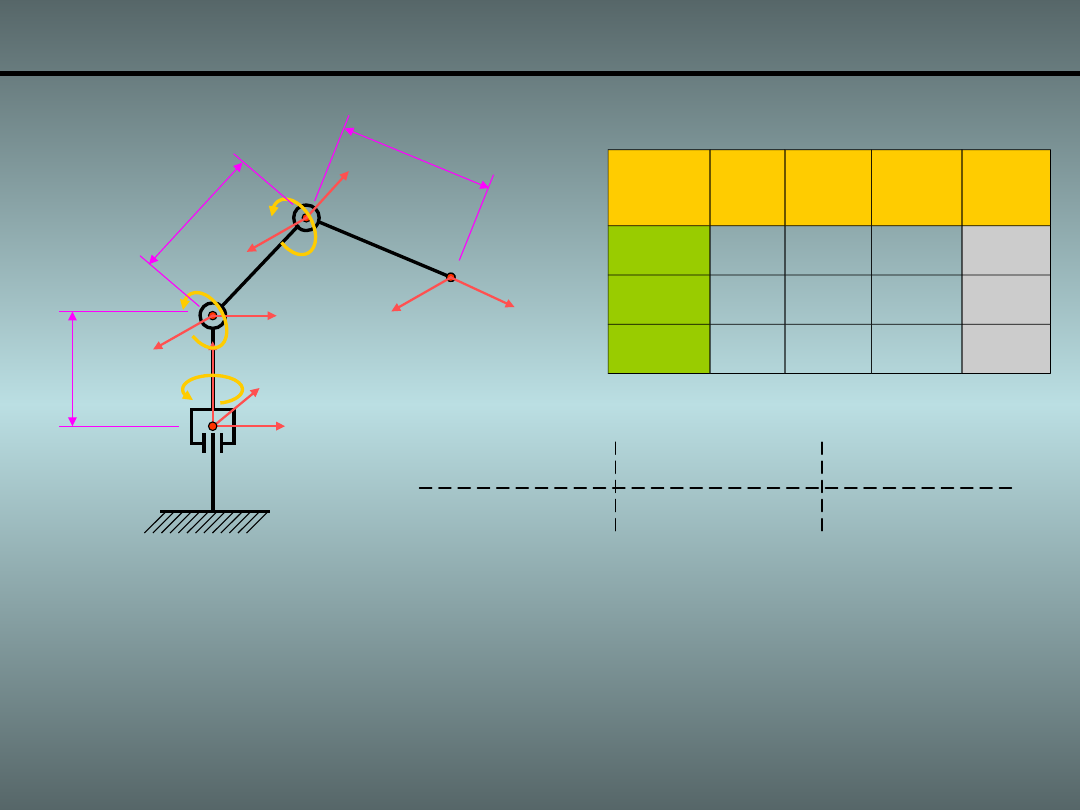
Przykład 1. Manipulator płaski z łokciem 1/7

Przykład 1. Manipulator płaski z łokciem 1/7

z

z

0

0

x

x

0

0

y

y

0

0

x

x

1

1

z

z

1

1

z

z

2

2

x

x

2

2

a

a

1

1

a

a

2

2





1

1





2

2

Człon

Człon

a

a

i

i





i

i

d

d

i

i





i

i

1

1

a

1

0

0



1

2

2

a

2

0

0



2

Przykład 1. Manipulator płaski z łokciem 2/7

Przykład 1. Manipulator płaski z łokciem 2/7

Postać macierzy
Jacobianowej dla
manipulatora płaskiego:























1

0

1

2

1

0

2

0

)

(

)

(

z

z

o

o

z

o

o

z

J

























1

1

1

)

(

i

i

n

i

i

z

o

o

z

J

z

z

0

0

x

x

0

0

y

y

0

0

x

x

1

1

z

z

1

1

z

z

2

2

x

x

2

2

a

a

1

1

a

a

2

2





1

1





2

2

Przykład 1. Manipulator płaski z łokciem

Przykład 1. Manipulator płaski z łokciem

3/7

3/7

Macierze przekształceń T:





































































1

0

0

0

0

1

0

0

sin

sin

0

cos

sin

cos

cos

0

sin

cos

2

1

2

1

1

2

1

2

1

2

1

2

1

1

2

1

2

1

2

0





























a

a

a

a

T























0

sin

cos

1

1

1

1

1





a

a

o





























1

0

0

0

0

1

0

0

sin

0

cos

sin

cos

0

sin

cos

1

1

1

1

1

1

1

1

1

0













a

a

T























0

0

0

0

o







































0

sin

sin

cos

cos

2

1

2

1

1

2

1

2

1

1

2













a

a

a

a

o

Współrzędne środków układów współrzędnych w bazowym ukł.
współrzędnych:































1

0

1

2

1

0

2

0

z

z

o

o

z

o

o

z

J

Przykład 1. Manipulator płaski z łokciem

Przykład 1. Manipulator płaski z łokciem

4/7

4/7

Osie z

i

układów współrzędnych wyrażone w bazowym układzie

współrzędnych





































































1

0

0

0

0

1

0

0

sin

sin

0

cos

sin

cos

cos

0

sin

cos

2

1

2

1

1

2

1

2

1

2

1

2

1

1

2

1

2

1

2

0





























a

a

a

a

T























1

0

0

1

z





























1

0

0

0

0

1

0

0

sin

0

cos

sin

cos

0

sin

cos

1

1

1

1

1

1

1

1

1

0













a

a

T























1

0

0

0

z

Współrzędne środków układów współrzędnych w bazowym ukł.
współrzędnych

Przykład 1. Manipulator płaski z łokciem

Przykład 1. Manipulator płaski z łokciem

5/7

5/7

Iloczyny wektorowe:





























0

cos

cos

sin

sin

0

sin

sin

cos

cos

1

0

0

det

2

1

2

1

1

2

1

2

1

1

2

1

2

1

1

2

1

2

1

1

0

2

0

k

j

i

k

j

i













































































a

a

a

a

a

a

a

a

o

o

z

















































0

cos

cos

sin

sin

2

1

2

1

1

2

1

2

1

1

0

2

0













a

a

a

a

o

o

z

Przykład 1. Manipulator płaski z łokciem

Przykład 1. Manipulator płaski z łokciem

6/7

6/7

Iloczyny wektorowe:





























0

cos

sin

0

sin

cos

1

0

0

det

2

1

2

2

1

2

2

1

2

2

1

2

1

2

1

k

j

i

k

j

i





























































a

a

a

a

o

o

z













































0

cos

sin

2

1

2

2

1

2

1

2

1









a

a

o

o

z

Przykład 1. Manipulator płaski z łokciem

Przykład 1. Manipulator płaski z łokciem

7/7

7/7

Macierz Jacobianowa manipulatora płaskiego z łokciem:







































































1

0

0

1

0

0

0

cos

sin

0

cos

cos

sin

sin

)

(

2

1

2

2

1

2

2

1

2

1

1

2

1

2

1

1





















a

a

a

a

a

a

q

J

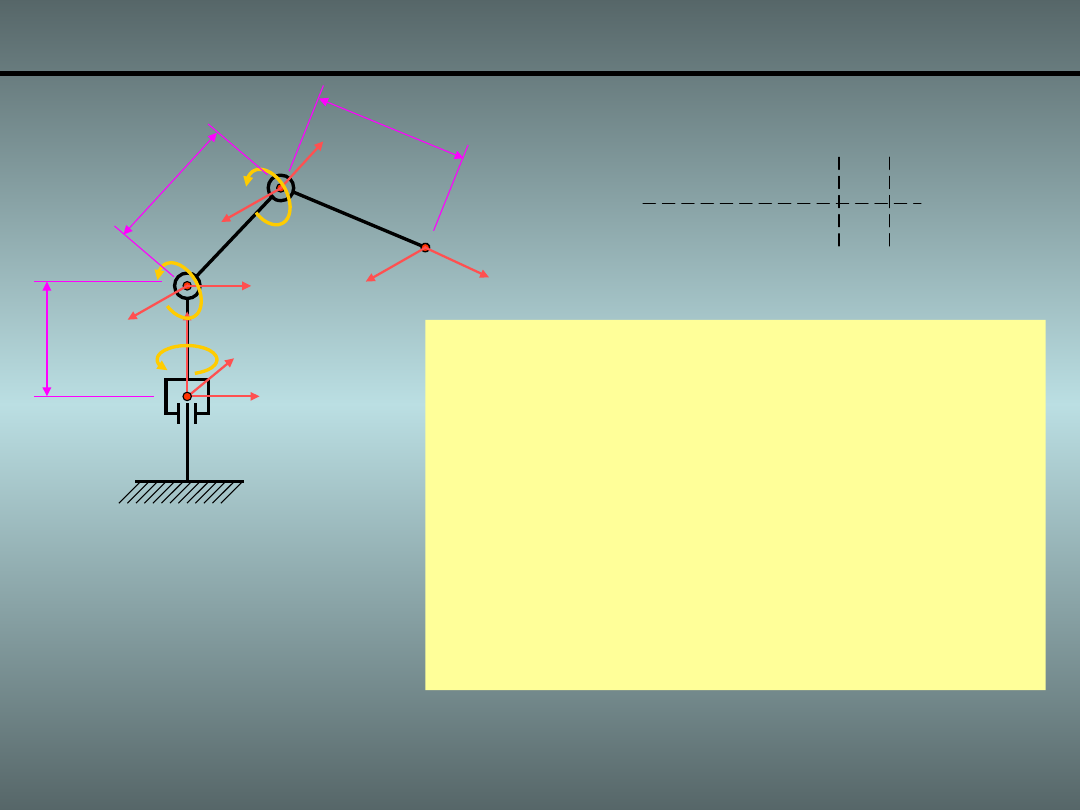
Przykład 2.

Przykład 2.

Manipulator RRR

Manipulator RRR

1/x

1/x

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3





1

1





2

2





3

3

d

d

1

1

a

a

2

2

a

a

3

3

Czło

Czło

n

n

a

a

i

i





i

i

d

d

i

i





i

i

1

1

0

/2

d

1



1

2

2

a

2

0

0



2

3

3

a

3

0

0



3



























2

1

0

2

3

2

1

3

1

0

3

0

)

(

)

(

)

(

z

z

z

o

o

z

o

o

z

o

o

z

J

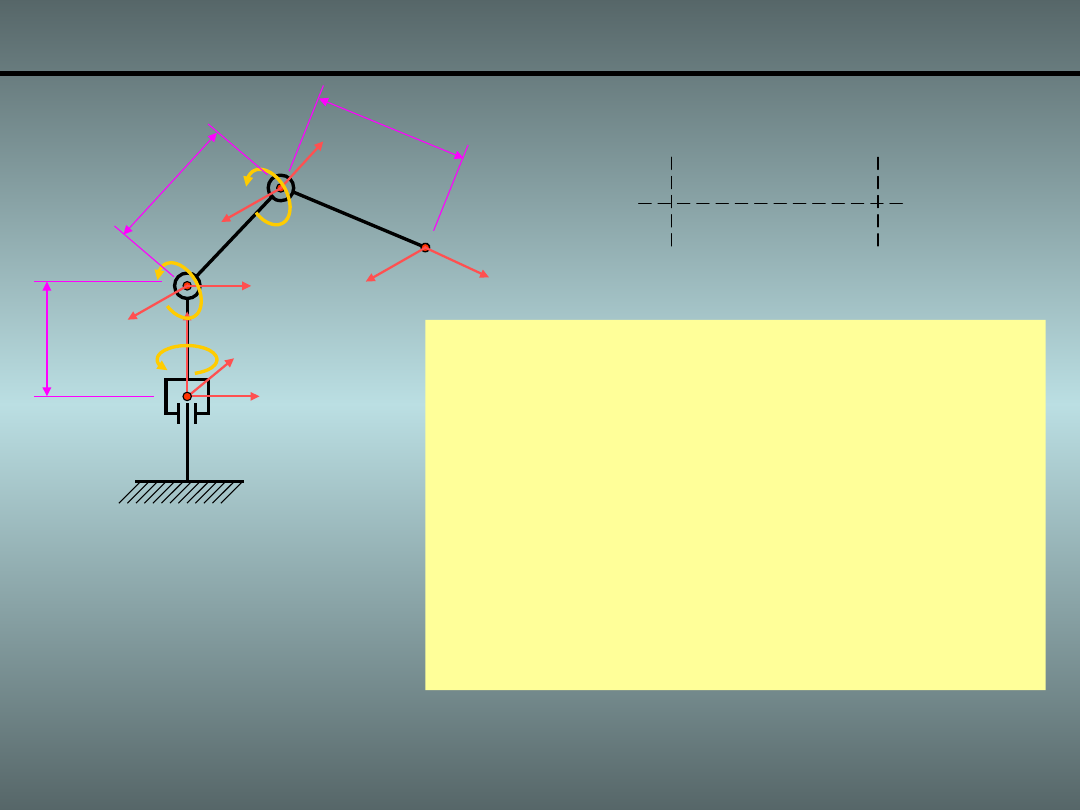
Przykład 2.

Przykład 2.

Manipulator RRR

Manipulator RRR

2/x

2/x

%% Jacobian przegubu pierwszego

% Pierwszy - czlon 1

% wspolrzedne srodka ukladu O0

O0=[0;0;0];

% wspolrzedne osi z0

z0=[0;0;1];

% wpolrzedne trzeciego srodka (!!)

O3=T30(1:3,4);

% Jacobian predkosci liniowej pierwszego przegubu

Jv1=simple([0 -1 0;1 0 0; 0 0 0]*[O3-O0]);

% Jacobian predkosci katowej pierwszego przegubu

Jw1=[z0];

% JACOBIAN PREDKOSCI Pierwszego Przegubu

J1=simple([[[Jv1];[Jw1]]]);

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3





1

1





2

2





3

3

d

d

1

1

a

a

2

2

a

a

3

3



















0

0

3

0

)

(

z

o

o

z

J

Przykład 2.

Przykład 2.

Manipulator RRR

Manipulator RRR

3/x

3/x

%% Jacobian przegubu drugiego

% Przegub obrotowy

% wspolrzedne srodka ukladu O1

O1=T10(1:3,4);

% wspolrzedne osi z1

z1=T10(1:3,3);

% wpolrzedne 3 srodka (!!)

O3=T30(1:3,4);

% Jacobian predkosci liniowej drugiego przegubu

Jv2=simple([0 -z1(3) z1(2);z1(3) 0 -z1(1);

-z1(2) z1(1) 0]*[O3-O1]);

% Jacobian predkosci katowej drugiego przegubu

Jw2=[z1];

% JACOBIAN PREDKOSCI Drugiego Przegubu

J2=simple([[[Jv2];[Jw2]]]);

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3





1

1





2

2





3

3

d

d

1

1

a

a

2

2

a

a

3

3



















1

1

3

1

)

(

z

o

o

z

J

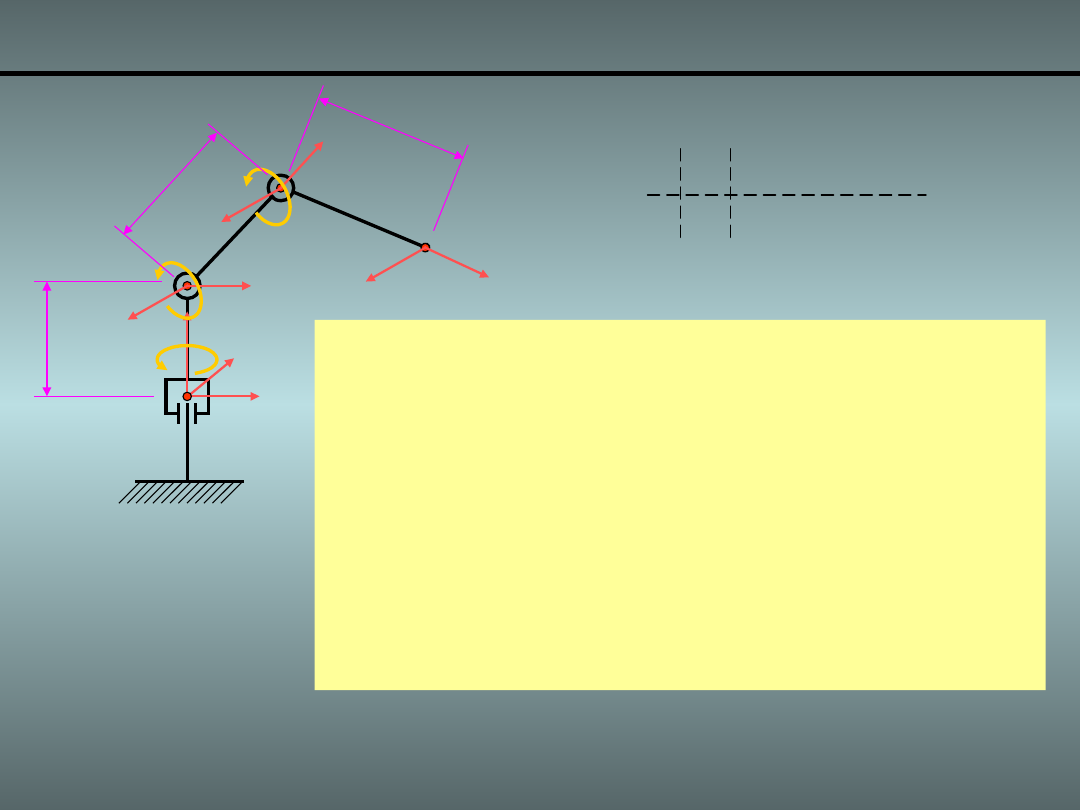
Przykład 2.

Przykład 2.

Manipulator RRR

Manipulator RRR

4/x

4/x

%% Jacobian przegubu trzeciego

% Przegub obrotowy

% wspolrzedne srodka ukladu O2 - znajduja sie w macierzy przeksztalcen

jednorodnych

% T20 - sa to trzy wiersze ostatniej kolumny

O2=T20(1:3,4);

% wspolrzedne osi z2 - sa to trzy wiersze trzeciej kolumny macierzy T20

z2=T20(1:3,3);

% wpolrzedne trzeciego srodka - znajdujemy w macierzy T30

O3=T30(1:3,4);

% Jacobian predkosci liniowej drugiego srodka ciezkosci

Jv3=simple([0 -z2(3) z2(2);z2(3) 0 -z2(1); -z2(2) z2(1) 0]*[O3-O2]);

% Jacobian predkosci katowej pierwszego srodka ciezkosci

Jw3=[z2];

% JACOBIAN PREDKOSCI Trzeciego przegubu

J3=simple([[[Jv3];[Jw3]]])

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3





1

1





2

2





3

3

d

d

1

1

a

a

2

2

a

a

3

3



















2

2

3

2

)

(

z

o

o

z

J

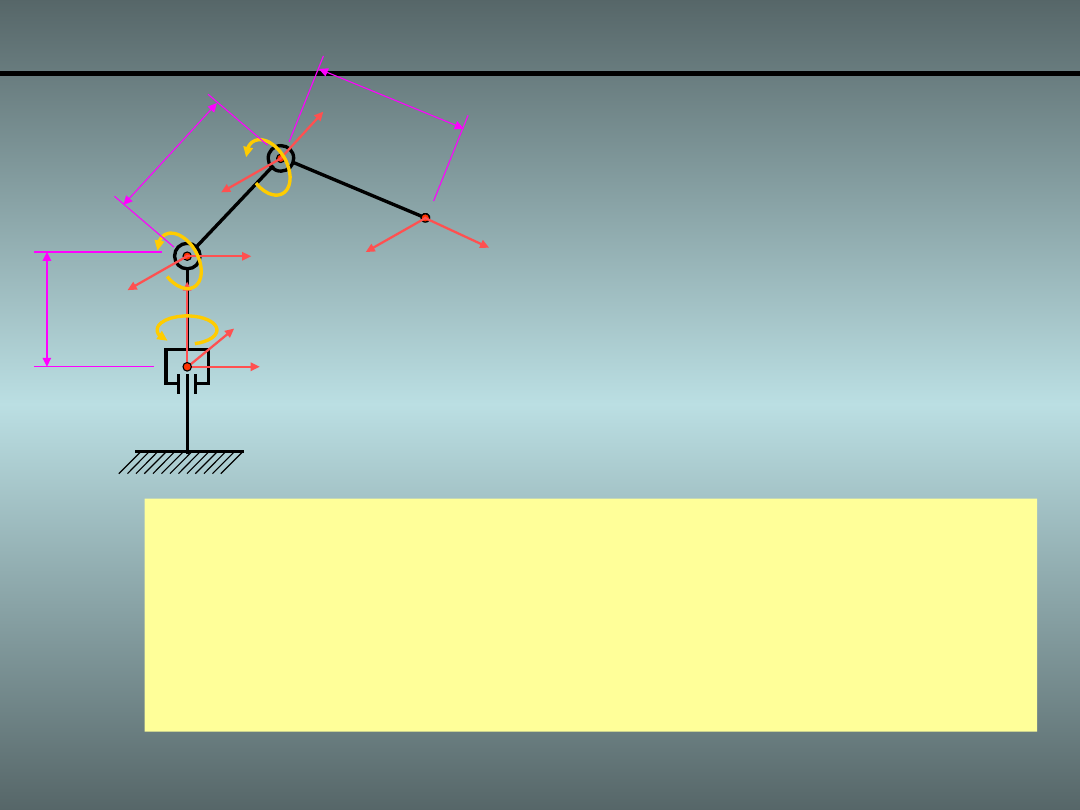
Przykład 2.

Przykład 2.

Manipulator RRR

Manipulator RRR

4/x

4/x

J =

[ -sin(Q1)*(a3*cos(Q2 + Q3) + a2*cos(Q2)),

-cos(Q1)*(a3*sin(Q2 + Q3) + a2*sin(Q2)), -a3*sin(Q2 +

Q3)*cos(Q1)]

[ cos(Q1)*(a3*cos(Q2 + Q3) + a2*cos(Q2)),

-sin(Q1)*(a3*sin(Q2 + Q3) + a2*sin(Q2)), -a3*sin(Q2 +

Q3)*sin(Q1)]

[ 0,

a3*cos(Q2 + Q3) + a2*cos(Q2), a3*cos(Q2 + Q3)]

[ 0,

sin(Q1), sin(Q1)]

[ 0,

-cos(Q1), -cos(Q1)]

[ 1,

0,

0]

z

z

0

0

x

x

0

0

y

y

0

0

z

z

1

1

x

x

1

1

z

z

2

2

x

x

2

2

x

x

3

3

z

z

3

3





1

1





2

2





3

3

d

d

1

1

a

a

2

2

a

a

3

3