Wyrażenie regularne (regex,

regexp)

Alternatywna forma opisu językow regularnych
Poniższe zapisy reprezentują wyrażenie regularne:

1.

Ø – zbiór pusty , L(Ø)= Ø

2.

ε – łańcuch pusty , L(ε) = {ε}

3.

a – symbol , L(a) = {a}

Jeżeli E jest wyrażeniem regularnym to:

4.

L(E*)=( L(E) )*

5.

L( (E) ) = L(E)

Jeżeli E

1

i E

2

są wyrażeniami regularnymi to:

6.

L(E

1

+E

2

) = L(E

1

) υ L(E

2

)

7.

L(E

1

E

2

) = L(E

1

)L(E

2

)

podstawa

krok

indukcyjny

DAS a wyrażenia regularne

Przekształcenia DAS na wyrażenie regularne
Usuwanie stanu s:
jeżeli stan s ma k poprzedników q

1

,q

2

,…,q

k

oraz m następników p

1

,p

2

,…,p

m

(różnych od

s) to po usunięciu stanu s rekompensując
połączenie ij dokładamy etykiety Q

i

S*P

j

gdzie Q

i

wyrażenie regularne od q

i

do s, S

wyrażenie regularne dla pętli w s, P

j

wyrażenie regularne od s do p

j

DAS a wyrażenia regularne

1.Etykietujemy łuki przejść grafu DAS poprzez wyrażenie regularne
2. Dla każdego stanu niekceptacyjnego q : usuwamy stan q

zgodnie z powyższym postępowaniem.

3. Dla każdego stanu akceptacyjnego:
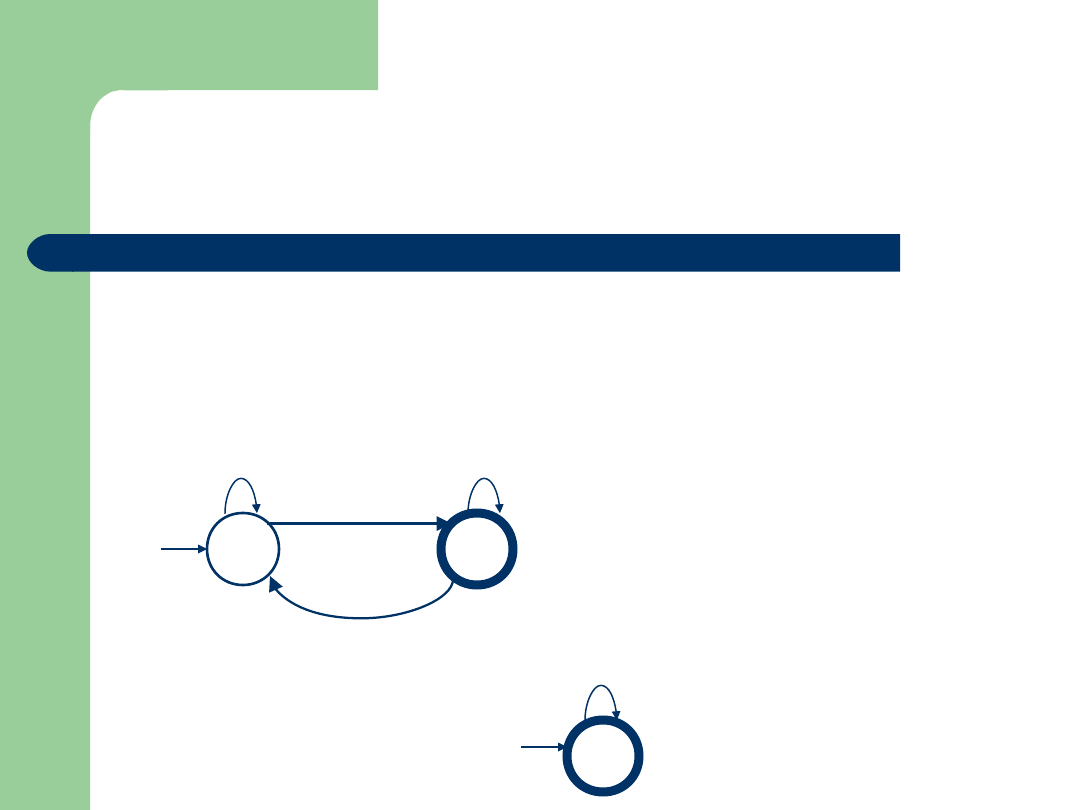
a) Jeżeli stan akcetpujący≠ stanu początkowego: redukujemy

automat do postaci dwustanowej:

R

S

T

U

Z reprezentcają:

(R+SU*T)*SU*

b) Jeżeli stan akceptujący = stan początkowy, redukujemy
automat do postaci jednostanowej:

R

Z reprezentacją:

R*

DAS a wyrażenia regularne

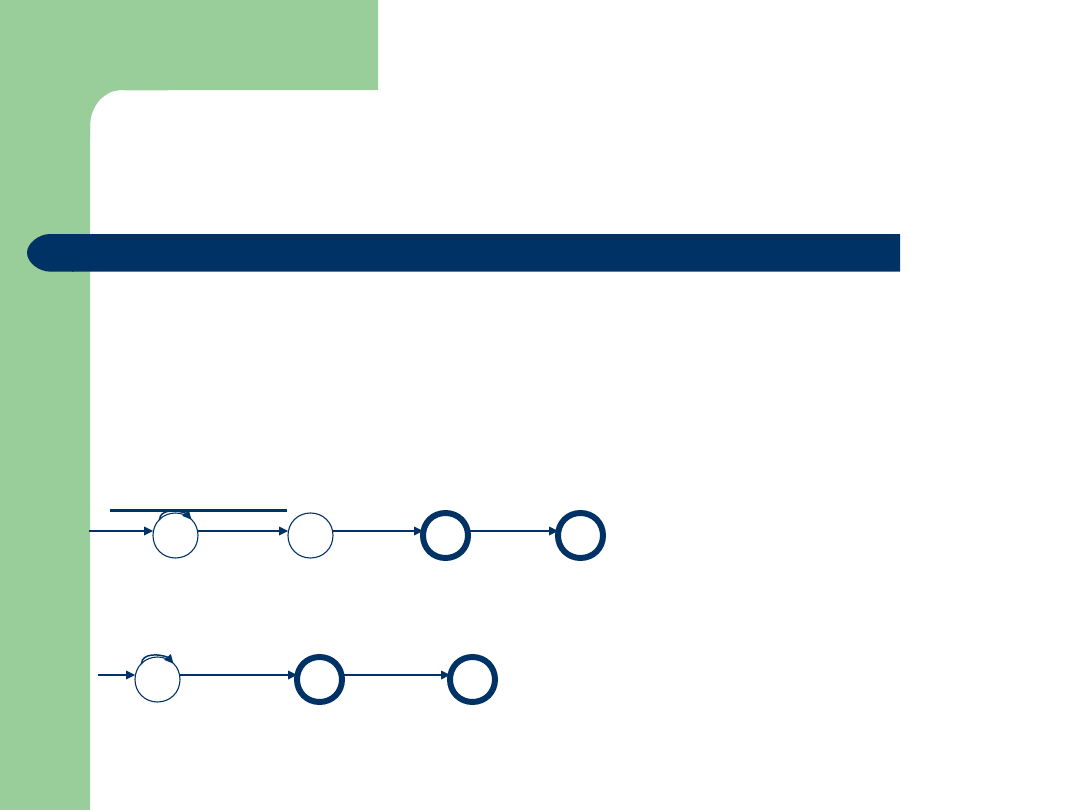
4. Wyrażenie regularne reprezentujące

cały automat jest sumą wyrażeń z pkt.
3.

Przykład

0+1

A

1(0+1)

0+1

C

D

Po wyeliminowaniu B:

0,1

1

0,
1

0,
1

A

B

C

D

Finalnie:

(0+1)*1(0+1)+(0+1)*1(0+1)(0+1)

Przekształcanie wyrażeń

regularnych na automaty



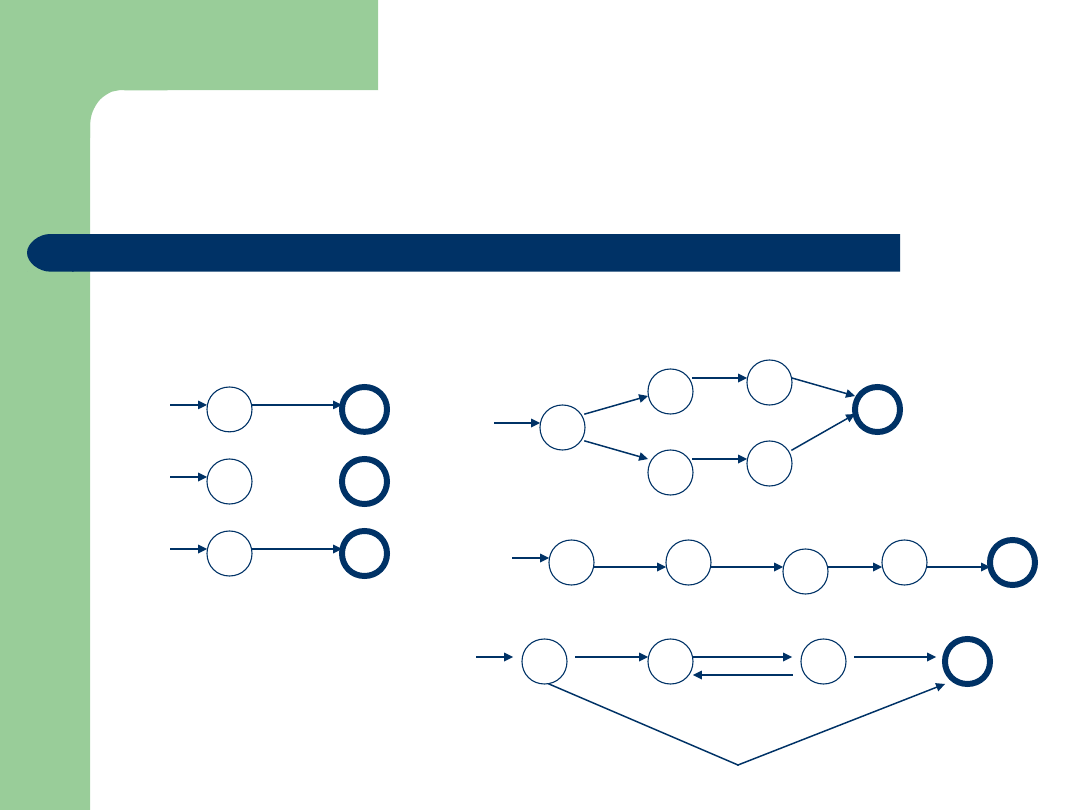
Przekształcamy do ε-NDAS o dokładnie jednym stanie

akceptującym, bez krawędzi wychodzących ze stanów:

akceptującego lub początkowego.

ε

a

ε

Ø

a

R

S

ε

ε

ε

ε

ε

R

S

R+S

RS

ε

ε

ε

R

ε

ε

R*

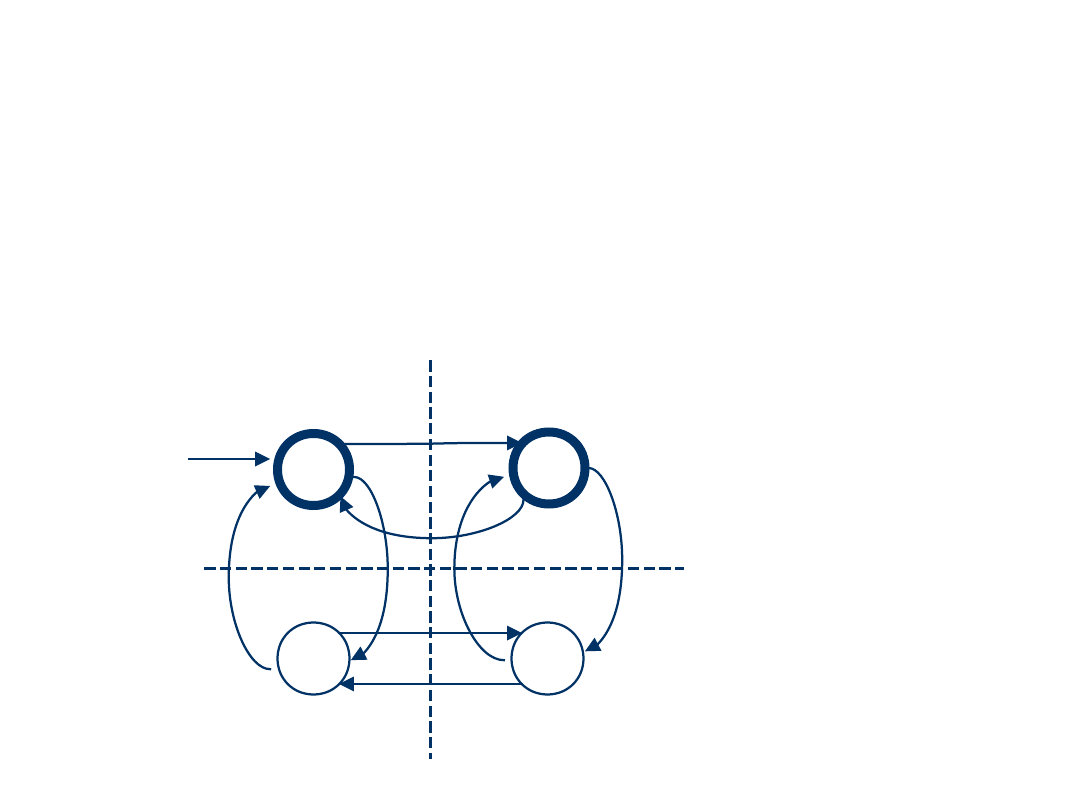
Konwersja DAS na wyrażenie regularne (jeżeli poleceniem byłoby

przekształcenie ENAS na wyrażenie regularne, to najpierw

przekształcamy ENAS na DAS i późnie dopiero DAS na wyrażenie

regularne.

Przykład: przekształćmy poniższy DAS na wyrażenie regularne.

q

0

q

1

q

2

q

3

1

1

0

0

0

0

1

1

pażysta liczba

1,

pażysta liczba

0

niepażysta liczba 1,

pażysta liczba 0

niepażysta liczba 1,

niepażysta liczba 0

pażysta liczba 1,

niepażysta liczba 0

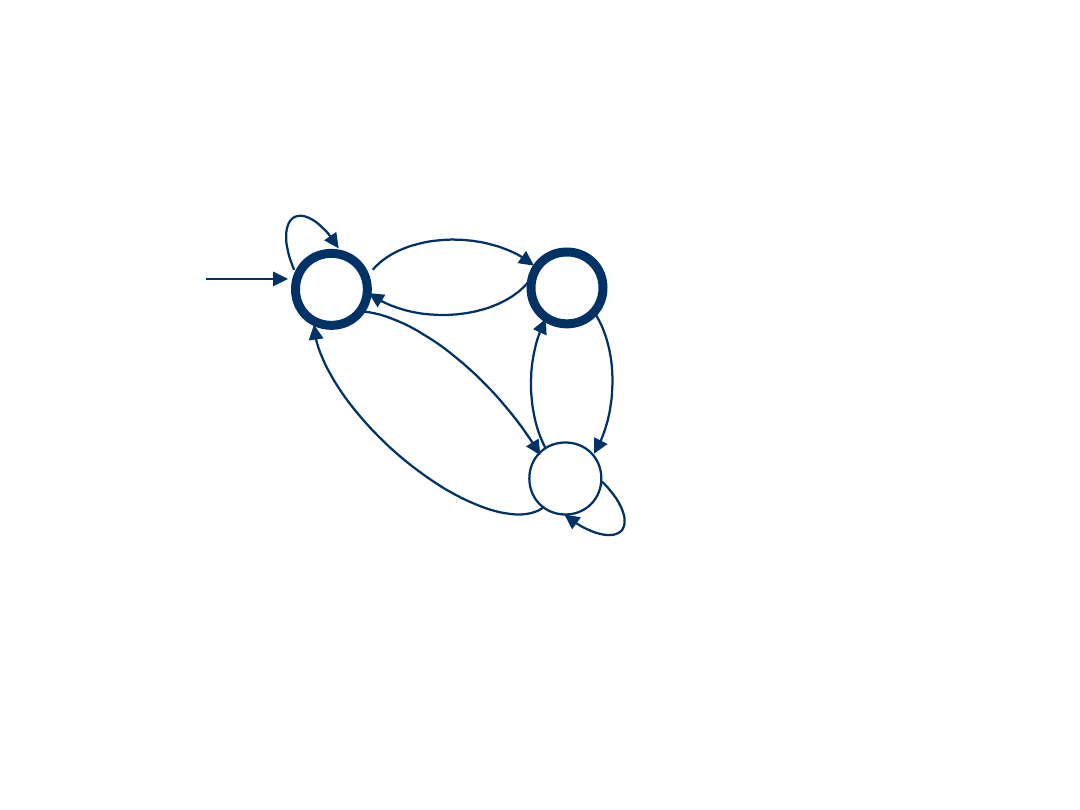
Eliminujemy stany niekońcowe, zacznijmy np. od q

2

q

0

q

1

q

3

1

1

0

0

01

10

11

00

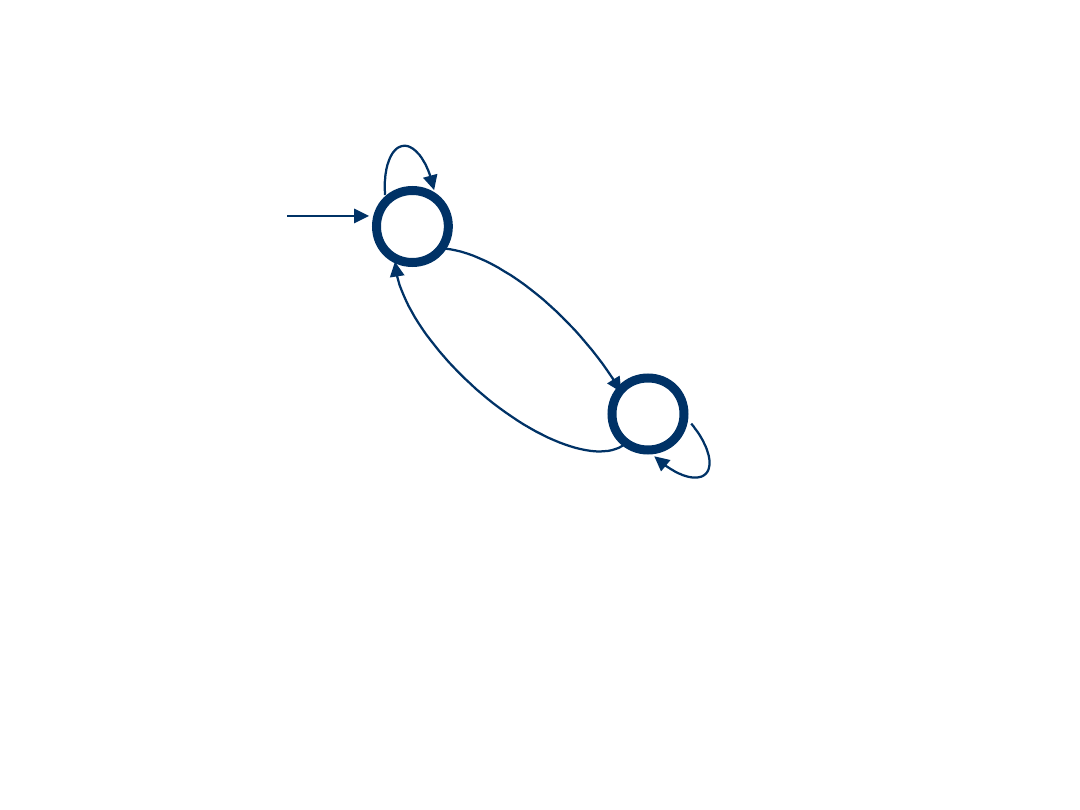
Eliminujemy stany niekońcowe, teraz q

3

q

0

q

1

1+

[01

+(1

1)*

+0

]

00+[01+(11)*+10]

1+

[0+

(11

)*+

10

]

[0+(11)*+0]

Szukane wyrażenie będzie zatem suma wyrażeń:

1)akceptowującego z pominięciem q

0

(nie możemy q

0

wyeliminować ponieważ jest to stan początkowy)

2) po eliminacji q

1

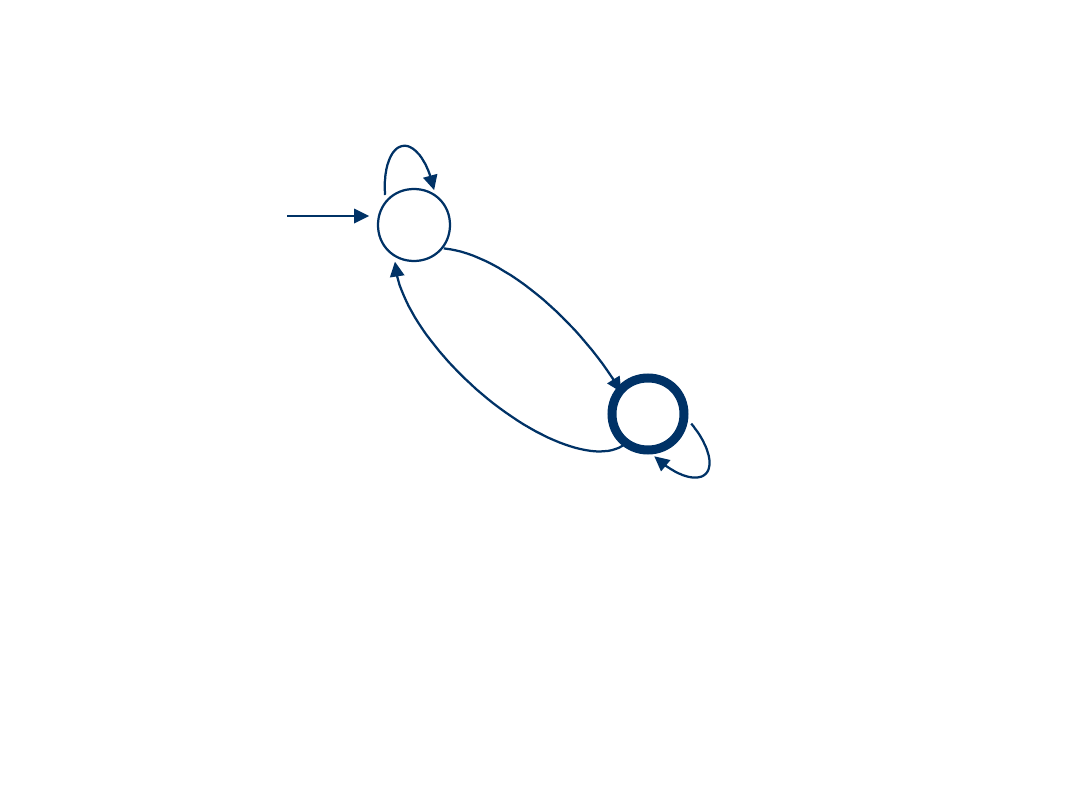
1) Pominięcie q

0

(ściślej stan q

0

pozostaje dalej, jednak interesuje

nas wyrażenie akceptowalne poprzez stan q

1

)

q

0

q

1

1+

[01

+(1

1)*

+0

]

00+[01+(11)*+10]

1+

[0+

(11

)*+

10

]

[0+(11)*+0]

Wyrażeniem jest:

//(pamiętamy wzór (R+SU*T)*SU*)

{ {00+[01+(11)*+10]} + {1+[01+(11)*+0]} {[0+(11)*+0]}* {1+[0+(11)*+10]} }

{1+[01+(11)*+0]} {[0+(11)*+0]}*

2) Eliminacja q

1

{00+[01+(11)*+10]}+{1+[01+(11)*+0]} {[0+(11)*+0]}*

{1+[0+(11)*+10]}

Wyrażeniem jest:

{00+[01+(11)*+10]}+{1+[01+(11)*+0]} {[0+(11)*+0]}* {1+[0+(11)*+10]}

Zatem finalnie, poszukiwanym wyrażeniem jest suma wyrażeń z
1) i 2) czyli:

{ {00+[01+(11)*+10]} + {1+[01+(11)*+0]} {[0+(11)*+0]}* {1+[0+(11)*+10]} }
{1+[01+(11)*+0]} {[0+(11)*+0]}* +

+ {00+[01+(11)*+10]}+{1+[01+(11)*+0]} {[0+(11)*+0]}* {1+[0+(11)*+10]}

Oczywiście powyższe wyrażenie można dalej jeszcze uprościć.

q

0