ZBIORY

-4          10
        4
11                 8

Często mówimy: zbiór książek, zbiór znaczków, zbiór liczb, 
zbiór roślin, uczniów,… 
Elementami wymienionych zbiorów są np.: książki, znaczki, 
liczby,…
Zbiory oznaczamy wielkimi literkami alfabetu: A, B, C, …, X, Y, 
Z,  
a ich elementy małymi literami: a, b, c, ….. x, y, z.

Zapis matematyczny: 

a є A 

czytamy: 

element a należy do 

zbioru A

zapis 

k є A 

czytamy:

 

element k nie należy do zbioru A

                             
    a
     k           c          
                             
d  
            e    

c  є  A
a  є  
A
d  є  
A
e  є  
A

A

Zbiór

 jest pojęciem pierwotnym w matematyce, to znaczy jest 

takim pojęciem, które przyjmujemy bez definicji.

Zbiór

 to inaczej ogół elementów, które łączy wspólna cecha, 

przynależność do grupy. 

przykłady zbiorów:

   

A – zbiór owoców                       B - zbiór liczb                             

  C – zbiór zwierząt     

   



     -3         0
           7
   ¼        1     
          
        ¾

A                  B             
    C

RODZAJE ZBIORÓW

•

skończony

 – mający skończoną liczbę elementów;

                np.: A - zbiór naturalnych dzielników liczby 6

                  A = {1,2,3,6}

 

                       B – zbiór liczb całkowitych ujemnych większych od -7
                       B = {-6,-5,-4,-3,-2,-1}

•

nieskończony

 – zbiór, do którego należy nieskończenie wiele 

elementów;

                

np.: N – zbiór liczb naturalnych

                        C – zbiór liczb całkowitych
                        R – zbiór liczb rzeczywistych

•

 pusty 

– zbiór do którego nie należy żaden element; 

              zbiór taki oznaczamy 

Ф

SPOSOBY PRZEDSTAWIENIA ZBIORÓW

a) opis słowny 

                np.:  zbiór K jest zbiorem naturalnych dzielników liczby 

20

b) wypisanie elementów należących do zbioru

                                K = {1,2,4,5,10,20}

c) podanie warunku, który muszą spełniać elementy 

zbioru

 

                               K

 

= { x:  x є N  

٨

   x│20 }

Zapamiętaj!

  

٨

  to matematyczny znak „i” który łączy dwa warunki

 

x│20 

czytamy: x dzieli 20 albo x jest dzielnikiem liczby 20

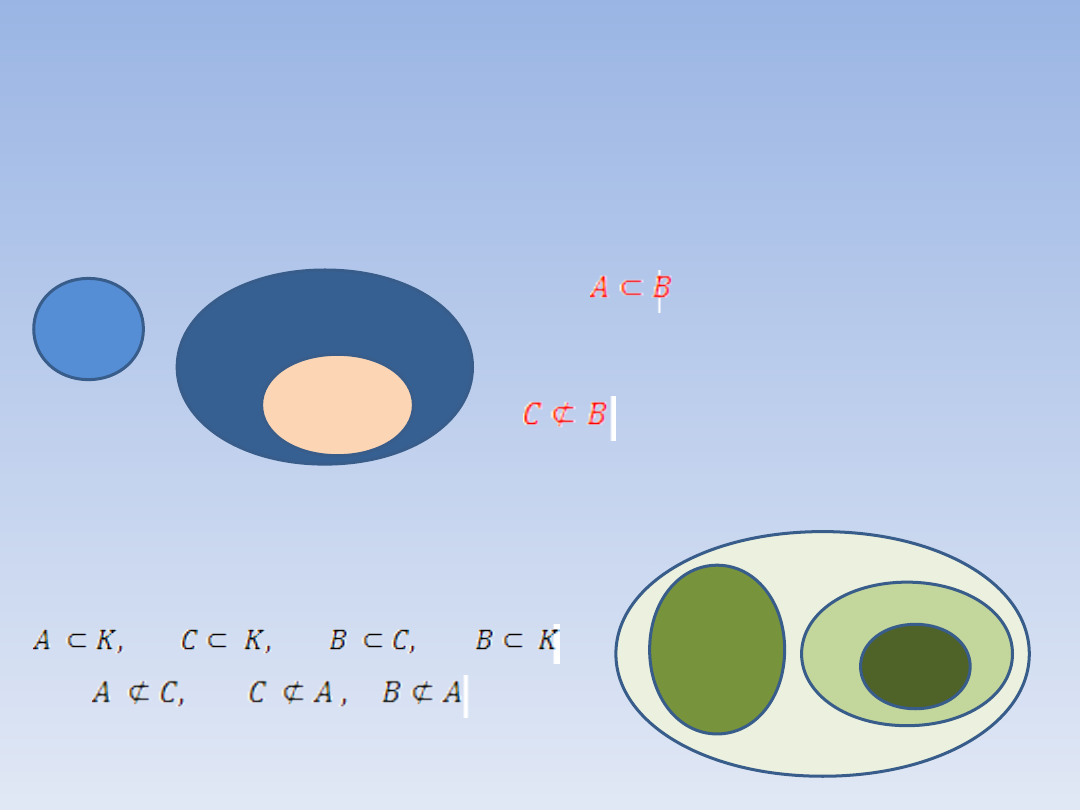
ZAWIERANIE SIĘ ZBIORÓW

Zbiór A jest 

podzbiorem

 zbioru B, gdy każdy element zbioru A 

jest elementem zbioru B.

 

B

A

-  zbiór A jest 

zawarty

  w 

zbiorze B 
         ( A jest podzbiorem B)

-  zbiór C nie jest  podzbiorem 
zbioru B

przykład:

C

C

B

A

K

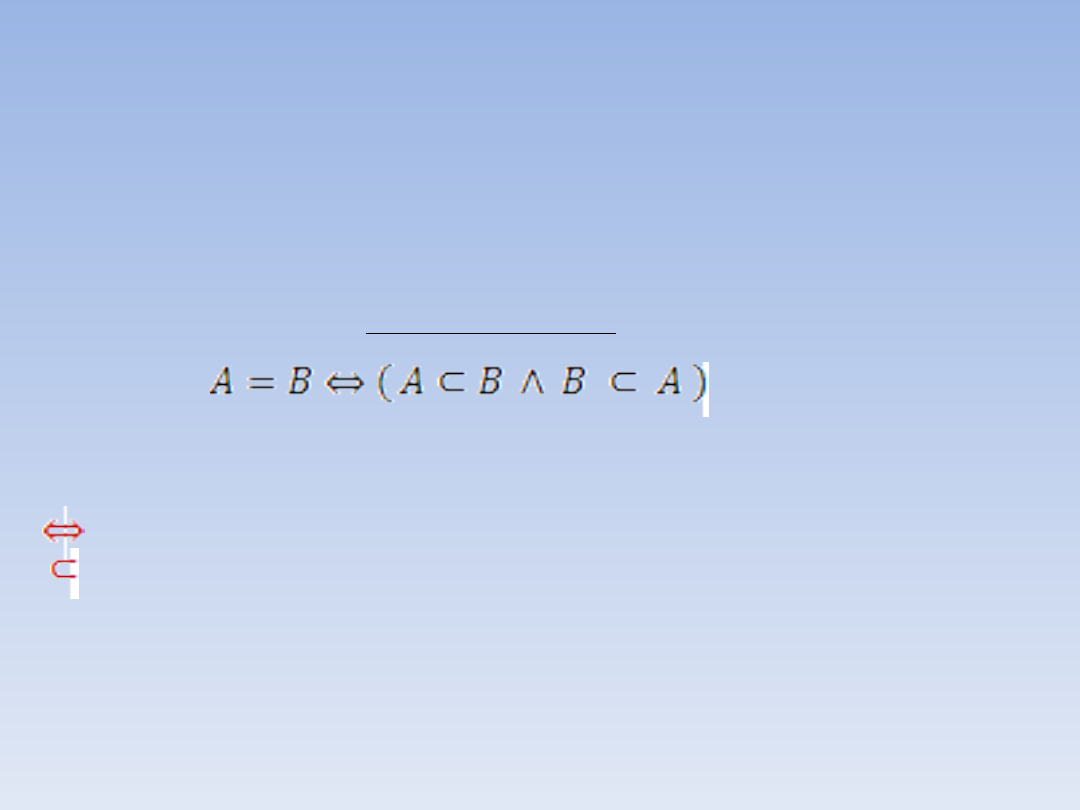
RÓWNOŚĆ ZBIORÓW

     Dwa zbiory A i B są 

równe

 gdy mają te same elementy (gdy 

zbiór A jest podzbiorem zbioru B i jednocześnie zbiór B jest 
podzbiorem zbioru A).

Matematycznie równość zbiorów przedstawia zapis: 

Zapamiętaj!

  

    czytamy: wtedy i tylko wtedy

    

  czytamy: zawiera się

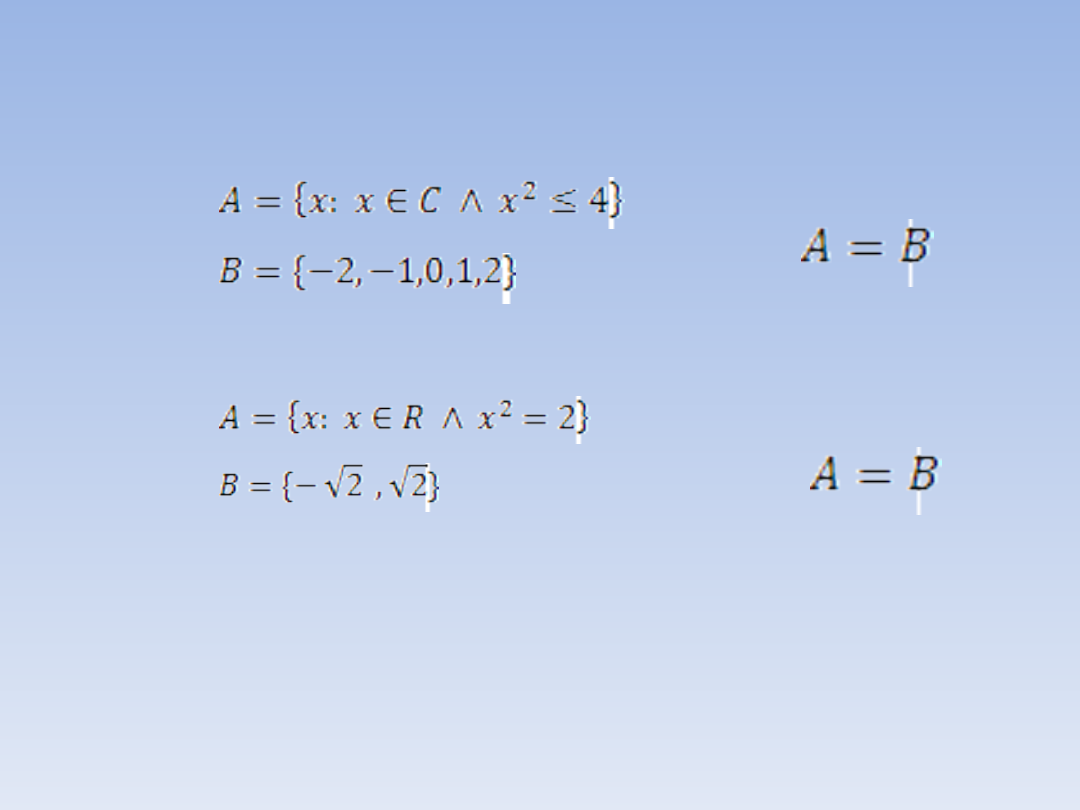
Przykłady zbiorów równych:

a)    

b)  

Wypisując elementy zbioru A otrzymasz elementy zbioru B.

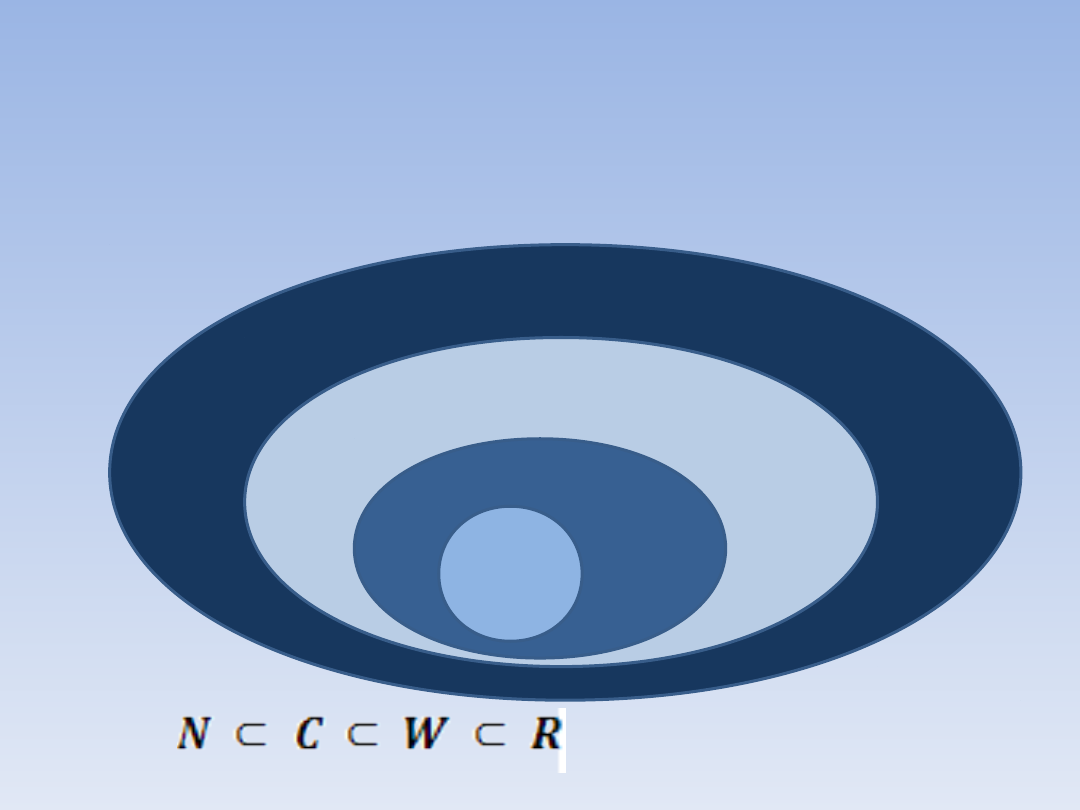
W gimnazjum była mowa o liczbach. Najmniejszym zbiorem 
liczbowym jest zbiór liczb naturalnych N. Zbiór liczb 
naturalnych jest podzbiorem zbioru liczb całkowitych C. Zbiór 
C jest podzbiorem zbioru liczb wymiernych W. Zbiór liczb 
wymiernych podzbiorem zbioru liczb rzeczywistych R.

N

C

W

R