Aproksymacyjne wyszukiwanie

informacji w bazach danych

Wykład - Bazy danych 3 – kierunek

Informatyka sem. VII

Politechnika Śląska Instytut Informatyki

Rodzaje zapytań



precyzyjne



zakresowe



aproksymacyjne

Politechnika Śląska Instytut Informatyki

Rodzaje zapytań
aproksymacyjnych



Wektorowe – wyszukiwanie na podstawie podobieństwa dwóch

wektorów, z których jeden reprezentuje wyszukiwany obiekt, a

drugi kryteria pytania



Oparte na prawdopodobieństwie – wyszukiwanie na

podstawie prawdopodobieństwa spełnienia przez obiekt

warunków pytania,



Rozmyte – wyszukiwanie na podstawie stopnia zgodności

obiektu z kryteriami pytania



W języku naturalnym – semantyka języka określa sposób

interpretacji pytania

Politechnika Śląska Instytut Informatyki

Rys historyczny

Twórca teorii zbiorów rozmytych:

Lotfi

Zadeh

(1965r.)

Praca inicjująca stosowanie zbiorów
rozmytych
w bazach danych:
opracowanie

V. Tahaniego

o wyszukiwaniu

informacji rozmytej

(1976r.)

Politechnika Śląska Instytut Informatyki

Badania nad zastosowaniem teorii
zbiorów rozmytych w bazach danych
(1)



Zadawanie rozmytych pytań do bazy danych:



Translator języka naturalnego wykorzystujący teorię
zbiorów rozmytych PRUF - (Zadeh - 1978)



Pierwszy rozmyty języka zapytań (Takahashi - 1991)
(X jest

bardzo

niski)



Fuzzy Query – tworzony od połowy 1997r. Przez
Sonalysts



Fquery – IBS PAN Warszawa (J. Kacprzyk, S.
Zadrożny) dla MS Access



SQLf – P. Bosc, O. Pivert itd.

Politechnika Śląska Instytut Informatyki

Badania nad zastosowaniem teorii
zbiorów rozmytych w bazach
danych (2)



Zapamiętywanie rozmytych informacji

w bazie danych:



rozmyte modele danych (B. P. Buckles, F. E. Petry)



Rozmyty relacyjny model GEFRED – Uniwersytet w

Granadzie (J. Cubero, M. Vila, K. Pons, J. Medina)



Rozmyte modele obiektowych baz danych – Belgia

(R. De Caluwe itd.)



Zbiory rozmyte w bazach danych systemów

geograficznych (M. Cobb, A. Yazici, K. Akkaya, V.

Robinson)

Politechnika Śląska Instytut Informatyki



Precyzyjne pytania - dokładne dane w BD



Rozmyte pytania - dokładne dane w BD



Precyzyjne pytania - rozmyte dane w BD



Rozmyte pytania - rozmyte dane w BD

Rodzaje pytań oraz przechowywanych
danych

Politechnika Śląska Instytut Informatyki

Problemy



Jak przedstawić w składni języka SQL

rozmyte sformułowania i jak ma

przebiegać proces interpretacji takich

zapytań?



W jaki sposób przechowywać w bazie

rozmyte dane?

Politechnika Śląska Instytut Informatyki

Teoria zbiorów rozmytych
-podstawowe pojęcia

Zbiór rozmyty

– zbiór par, w pewnej

numerycznej przestrzeni rozważań X

A = {(µ

A

(x), x)},

dla każdego x  X,

gdzie:

µ

A

– funkcja przynależności zbioru

rozmytego A – każdemu elementowi

zbioru x  X przypisuje stopień

przynależności µ

A

(x) do zbioru A, przy

czym

µ

A

(x)  [0, 1]

Politechnika Śląska Instytut Informatyki

Przykładowa funkcja
przynależności



D

0 l m n
o

a dm b

•Liczba rozmyta
•Przedział
rozmyty

•Przedział
dokładny

•Wartość
dokładna

Politechnika Śląska Instytut Informatyki

Reprezentacja liczb rozmytych



Liczba rozmyta typu LR:

A1 = (m, a, b)



Przedział rozmyty typu LR:

A2 = (m, n, a, b)

Politechnika Śląska Instytut Informatyki

Postać zapytania w języku SQL

Select <lista atrybutów>
From <lista tabel>
Where <warunki>
Group by <lista atrybutów>
Having <warunki filtrujące>
Order by <lista atrybutów>

Politechnika Śląska Instytut Informatyki

Miejsca występowania wartości
rozmytych w pytaniach
niezagnieżdżonych



Warunki filtrujące we frazie

WHERE



Warunki filtrujące we frazie

HAVING



Grupowanie wg wyrażeń zawierających

wartości rozmyte –

GROUP BY



Porządkowanie wg kolumn zawierających

wartości rozmyte –

ORDER BY



Wartości rozmyte we frazie

SELECT

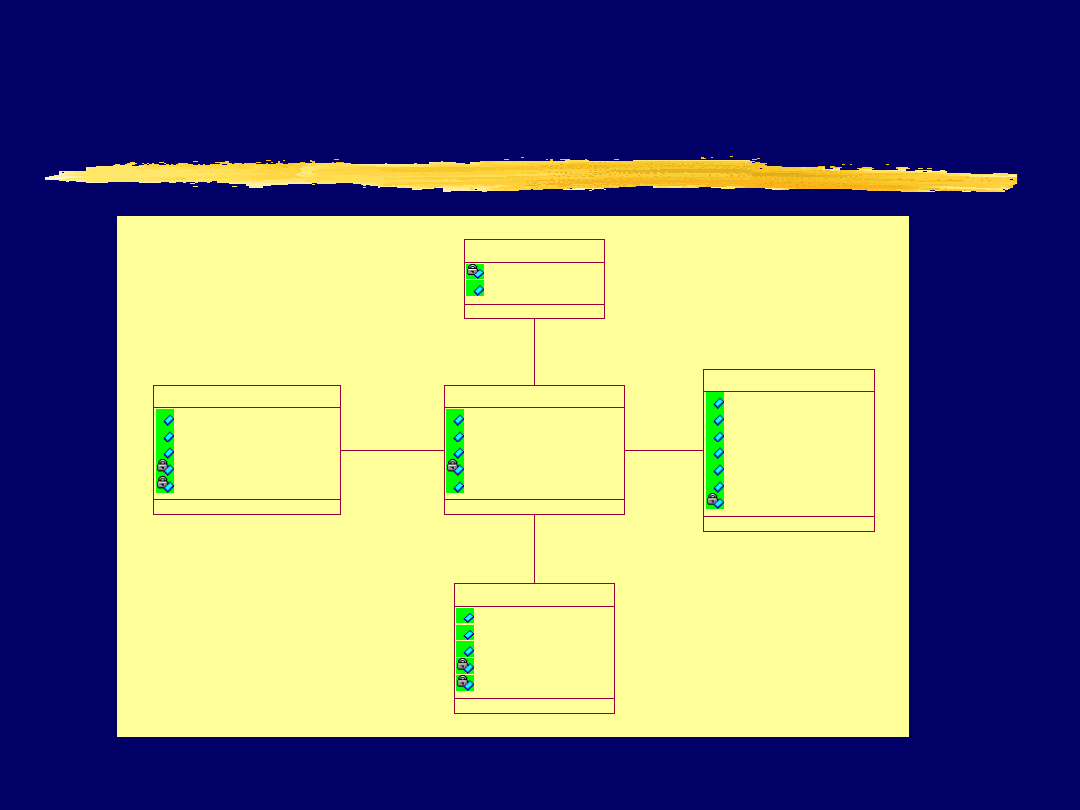
Politechnika Śląska Instytut Informatyki

Diagram bazy danych

pracownicy

imie : String
nazwisko : String
plec : String
wiek : Integer
nr_zakl : Integer
staz_pracy : Integer
nr_prac : Integer

zuzycie

papier : Integer
toner : Integer
plytki_CD : Integer
nr_zakl : Integer
rok : Date

instytuty

nr_inst : Integer
nazwa : String

zaklady

nazwa : String
liczba_prac : Integer
liczba_pokoi : Integer
nr_zakl : Integer
nr_inst : Integer

1

0..*

1

+zatrudnia

0..*

0..*

1

0..*

+zużywa

1

0..*

1

0..*

+należy

1

zapotrzebowanie

papier : ftrapezium
toner : ftrapezium
plytki_CD : ftrapezium
nr_zakl : Integer
rok : Date

1

0..*

1

+zamawia

0..*

Politechnika Śląska Instytut Informatyki

Interpretacja rozmytych warunków
filtrujących w pytaniach SQL

Przykład

Wyszukaj pracowników w wieku

około 50

lat.

Politechnika Śląska Instytut Informatyki

Wartość rozmyta około 50



X

0 40 45 55
60

1

...

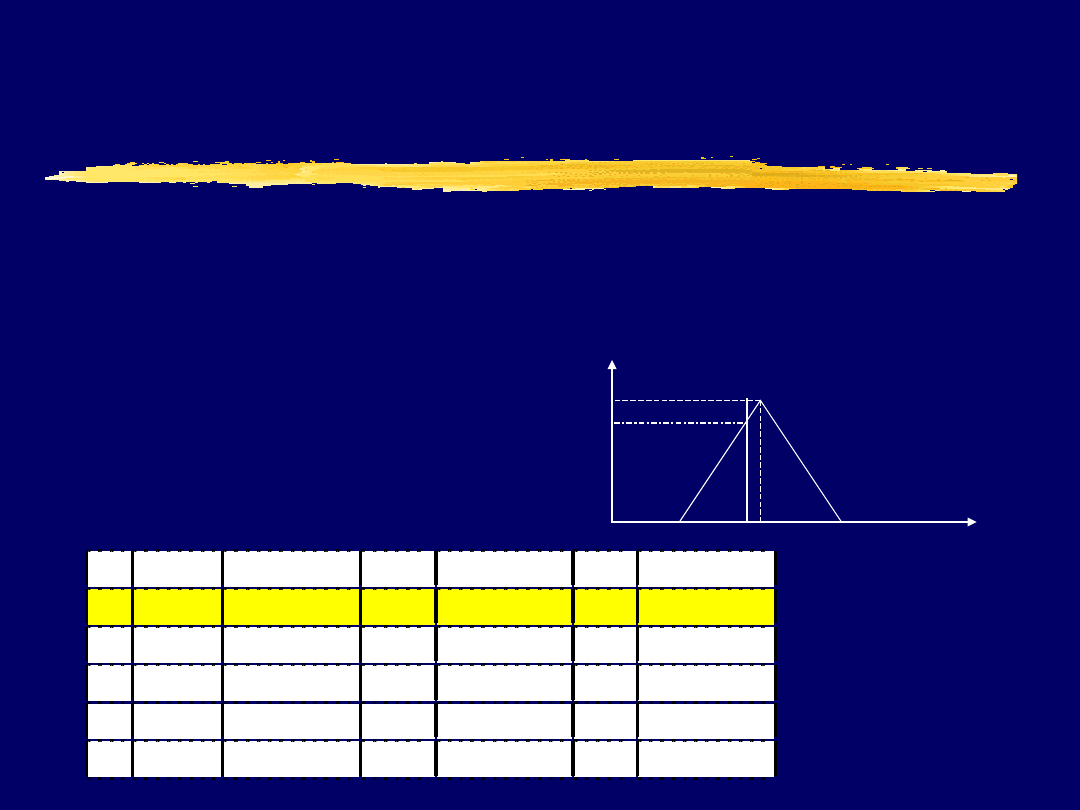
Politechnika Śląska Instytut Informatyki

1



T

(x)

wiek

0 40 48 50
60

(48) =

0.8

SELECT imie, nazwisko

FROM pracownicy

WHERE wiek JEST okolo 50

Nr Imie

Nazwisko Wiek Staz_pracy Plec Adres

1 J an

Kowalski

48

19

M

Zabrze

2 Kasia Nowak

38

10

K

Chorzów

3 Marcin Sowa

21

1

M

Gliwice

4 J akub Sroka

53

22

M

Kraków

5 Anna Maj

47

8

K

Katowice

Zapis w notacji języka SQL

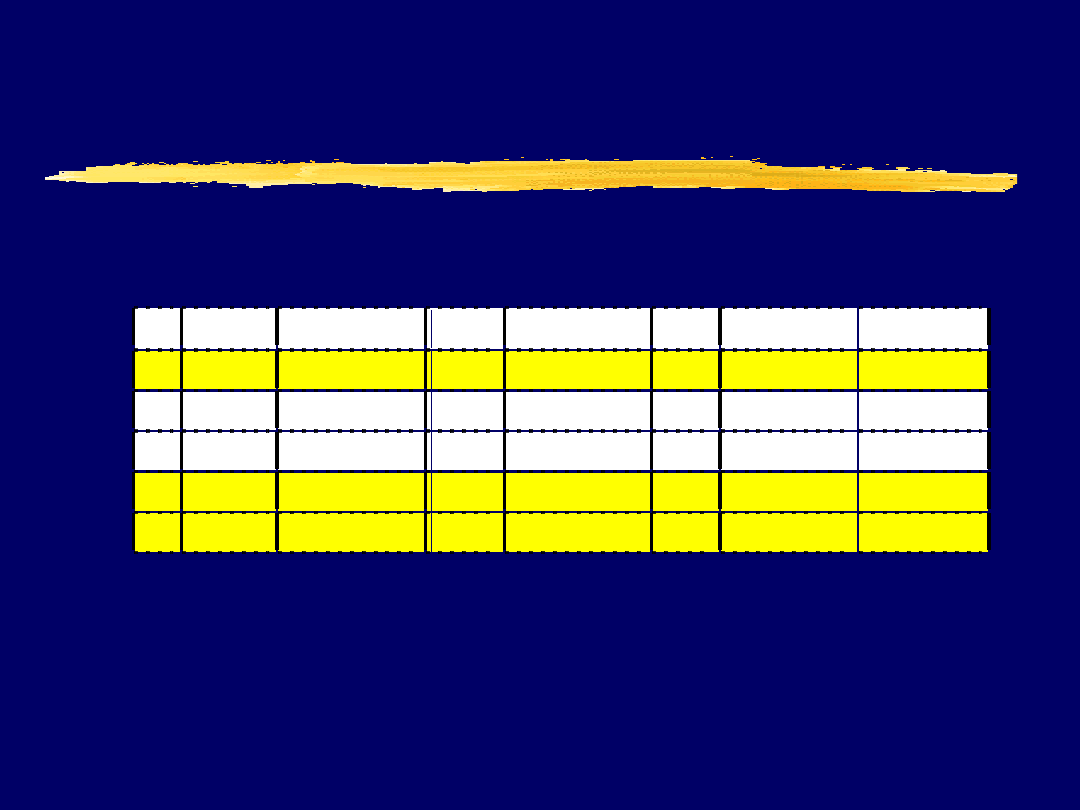
Politechnika Śląska Instytut Informatyki

Nr Imie

Nazwisko Wiek Staz_pracy Plec Adres



50

(wiek)

1 J an

Kowalski

48

19

M

Zabrze

0,8

2 Kasia Nowak

38

10

K

Chorzów 0,0

3 Marcin Sowa

21

1

M

Gliwice

0,0

4 J akub Sroka

53

22

M

Kraków

0,7

5 Anna Maj

47

8

K

Katowice 0,7

Uzupełnienie tabeli o tymczasową
kolumnę zawierającą stopień zgodności

Politechnika Śląska Instytut Informatyki

Warunki złożone

Where W

Where W

1

AND W

2

... OR W

k

W

i

AND W

j



min (



(w

i

),



(w

j

))

t-norma

W

i

OR W

j



max(



(w

i

),



(w

j

))

s-norma

Politechnika Śląska Instytut Informatyki

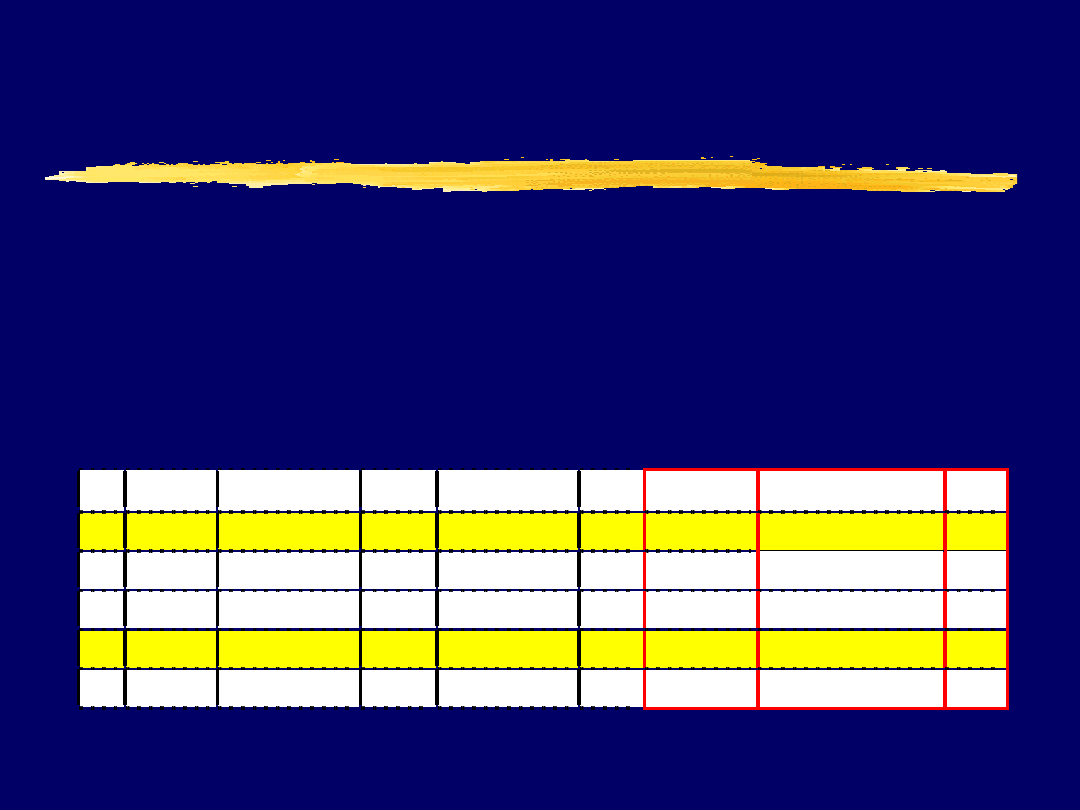
Wyszukaj pracowników w wieku około 50 lat,
mających staż pracy około 20 lat.

SELECT imie, nazwisko
FROM pracownicy
WHERE wiek JEST okolo 50 AND staz_pracy JEST okolo 20

Uzupełniona tabela o tymczasowe kolumny
zawierające wartości stopni zgodności

Nr Imie

Nazwisko Wiek Staz_pracy Plec 

50

(wiek) 

20

(staz_pracy) 

1 J an

Kowalski

48

19

M

0,8

0,9

0,8

2 Kasia Nowak

38

10

K

0,0

0,0

0,0

3 Marcin Sowa

21

1

M

0,0

0,0

0,0

4 J akub Sroka

53

22

M

0,7

0,8

0,7

5 Anna Maj

47

8

K

0,7

0,0

0,0

Politechnika Śląska Instytut Informatyki

Podstawa wyboru wierszy



Maksymalny stopień zgodności z
warunkami pytania



Przekroczenie średniego stopnia
zgodności



Przekroczenie pewnej zadanej wartości
progowej

Politechnika Śląska Instytut Informatyki

Wprowadzenie do zapisu pytań SQL
warunku na stopień zgodności

Przykład

Wyszukaj pracowników, którzy mają około 50 lat, w

odpowiedzi należy uwzględnić wiersze ze stopniem zgodności

z kryterium pytania większym niż 0.7.

Dotychczasowy zapis pytania:

SELECT imie, nazwisko
FROM pracownicy
WHERE wiek JEST okolo 50

Politechnika Śląska Instytut Informatyki

Trzy formy zapisu warunku na stopień
zgodności



forma dołączana do warunku rozmytego

WHERE wiek jest okolo 50 AND DG > 0.7;



forma funkcyjna

WHERE DG(p.wiek, okolo 50) > 0.7;



forma operatorowa

WHERE (wiek jest okolo 50) > 0.7;

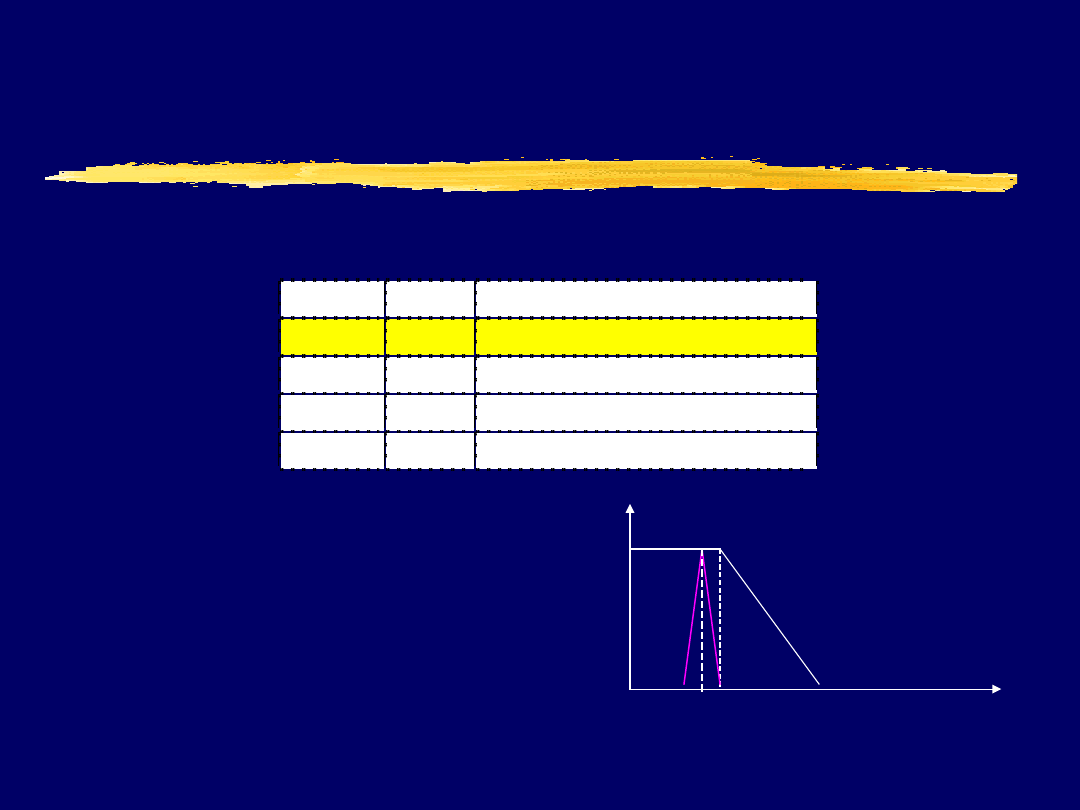
Politechnika Śląska Instytut Informatyki

Wartości rozmyte w kolumnach tabeli

tabela: zapotrzebowanie (nr_zakl, rok, zapotrzebowanie_na _papier)

Przykład
Wyszukać zakłady, które złożyły zapotrzebowanie na niewielką ilość

papieru.

SELECT nr_zakl
FROM zapotrzebowanie
WHERE zapotrzebowanie_na_papier jest niewielkie;



T

(x)

x

1

0 8 10 20

Nr_zakl rok

zapotrzebowanie_na_papier

1

2003

okolo 8

2

2003

okolo 25

3

2003

okolo 30

4

2003

okolo 15

Politechnika Śląska Instytut Informatyki

Agregacja w pytaniach
rozmytych (1)

Funkcje agregujące na danych rozmytych
(we frazie SELECT)

„Wyznacz wartość średniego zapotrzebowania na tonery.”

SELECT AVG(

toner

)

FROM zapotrzebowanie

WHERE rok = ‘2003’;

Politechnika Śląska Instytut Informatyki

Agregacja w pytaniach
rozmytych (2)

Nakładanie warunków na funkcje agregujące
w pytaniach rozmytych (fraza HAVING):



Agregacja wartości ostrych – nakładany warunek rozmyty



Agregacja wartości rozmytych – nakładany warunek ostry



Agregacja wartości rozmytych – nakładany warunek
rozmyty



Rozmyte kwantyfikatory operujące na grupie wierszy

Politechnika Śląska Instytut Informatyki

Agregacja w pytaniach
rozmytych (3)

Agregacja wartości ostrych – nakładany

warunek rozmyty

Wyszukać te zakłady, w których jest zatrudnionych około

10 kobiet, przy czym stopień zgodności z tym warunkiem

powinien być większy od 0.65.

SELECT nr_zakl
FROM pracownicy
WHERE plec = ‘K’
GROUP BY nr_zakl
HAVING (count(nr_prac) jest

okolo 10

) >

0.65

Politechnika Śląska Instytut Informatyki

Agregacja w pytaniach rozmytych (4)

Przykład

Wyznacz dla każdego zakładu wartość średniego
zapotrzebowania na papier. Wyszukaj te zakłady,
w których wartość ta przekracza 30 ryz.

SELECT nr_zakl, AVG(zapotrzebowanie_na_papier)
FROM zapotrzebowanie
GROUP BY nr_zakl
HAVING AVG(zapotrzebowanie_na_papier) > 30;

Politechnika Śląska Instytut Informatyki

Agregacja w pytaniach
rozmytych (5)

Agregacja wartości rozmytych

Wyszukać te instytuty, których sumaryczne

zapotrzebowanie na papier w danym roku wynosiło około

1000 ryz. W odpowiedzi powinny znaleźć się wiersze o

stopniu zgodności co najmniej 0.7.

SELECT nr_inst, rok
FROM zapotrzebowanie z JOIN instytuty i

ON z.nr_inst = i.nr_inst

GROUP BY i.nr_inst, rok
HAVING (sum(

papier

) jest

okolo 1000

) >=

0.7

;

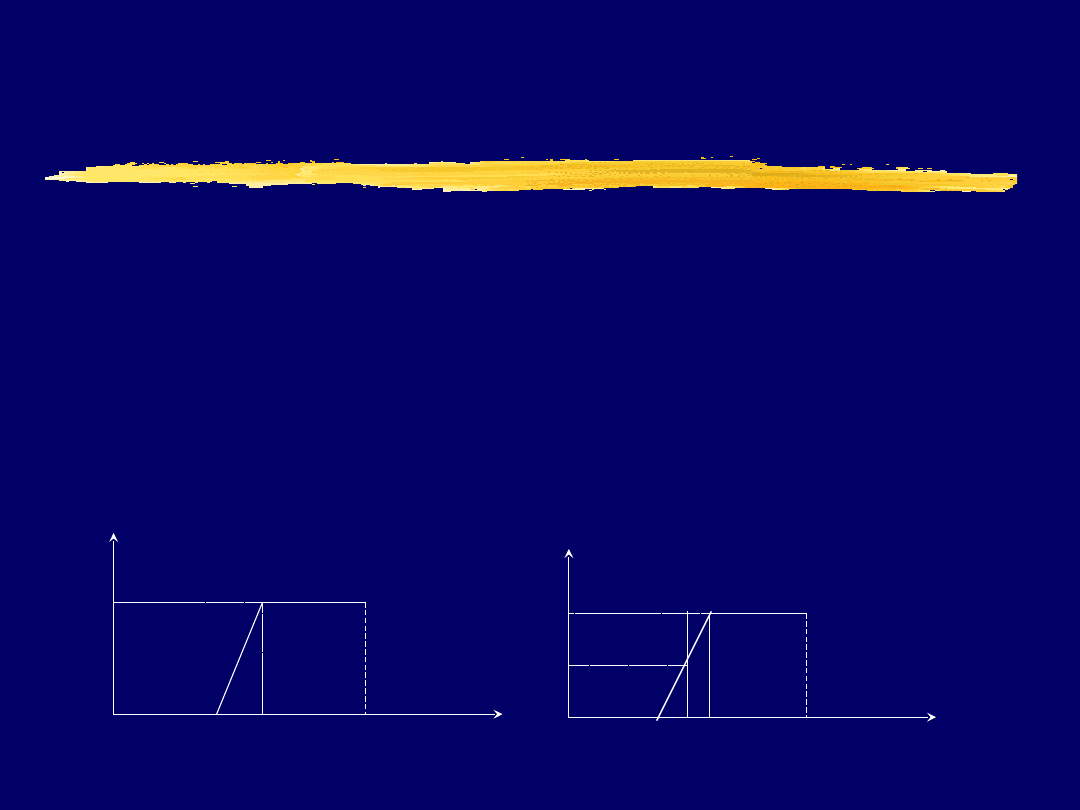
Politechnika Śląska Instytut Informatyki

Rozmyte kwantyfikatory (prawie
wszystkie, prawie żaden, około połowa...)

Wyszukaj te zakłady, w których prawie wszyscy pracownicy to
mężczyźni. W odpowiedzi powinny znaleźć się wiersze o
stopniu zgodności co najmniej 0.7.

SELECT nr_zakl, prawie_wszystkie(plec = ‘M’)
FROM pracownicy
GROUP BY nr_zakl
HAVING prawie_wszystkie(plec = ‘M’) >= 0.7;

0 0.9 0.95 1
X



1

Funkcja przynależności dla
wartości lingwistycznej
prawie_wszystkie

0 0.9 0.925 1
X



1

0.5

Stopień zgodności obliczonego odsetka
(0.925) z wartością lingwistyczną
prawie_wszystkie

...

...

Politechnika Śląska Instytut Informatyki

Grupowanie danych



grupowanie rozmyte dokładnych danych



grupowanie rozmytych danych

Politechnika Śląska Instytut Informatyki

Grupowanie rozmyte dokładnych
danych

grupowanie względem wartości lingwistycznych

Dane: pomiary temperatury w kolejnych dniach
Wartości lingwistyczne: bardzo zimno, zimno, ciepło, bardzo ciepło itd.

grupowanie według arbitralnego podziału dziedziny atrybutu

Dane: staż pracy poszczególnych pracowników
Podział dziedziny: około 5 lat, około 10 lat, około 15 lat itd.

grupowanie rozmyte z zastosowaniem metody hierarchicznej

Początkowo każda dana tworzy grupę
Iteracyjne łączenie dwóch najbliższych grup

grupowanie rozmyte według autorskiego algorytmu

Połączenie idei metody hierarchicznej z klasycznym grupowaniem

bazującym na uporządkowaniu danych

Politechnika Śląska Instytut Informatyki

Metody wyznaczania odległości
między grupami



najmniejsza odległość pomiędzy dowolną daną grupy A i daną grupy B:



największa odległość pomiędzy dowolną daną grupy A i daną grupy B:



średnia arytmetyczna wszystkich odległości pomiędzy wszystkimi danymi

grup A i B:



odległość pomiędzy punktem centralnym (wartością średnią) grupy A

i punktem centralnym (wartością średnią) grupy B:

gdzie m

A

, m

B

są wektorami: m

A

, m

B

.

     

|

|

min

)

,

(

,

min

B

A

B

x

A

x

x

x

B

A

d

B

A









|

|

max

)

,

(

,

max

B

A

B

x

A

x

x

x

B

A

d

B

A









 









A

x

B

x

B

A

śr

A

B

x

x

B

card

A

card

B

A

d

|

|

)

(

)

(

1

)

,

(

|

|

)

,

(

B

A

mean

m

m

B

A

d





Politechnika Śląska Instytut Informatyki

Grupowanie rozmytych danych



Uwzględnienie w grupowaniu wszystkich parametrów opisujących wartości

rozmyte



Grupowanie według wartości modalnych



Uwzględnienie wymienionych algorytmów grupowania rozmytego

Politechnika Śląska Instytut Informatyki

Pytania zagnieżdżone

Przykład pytania zagnieżdżonego

:

Wyszukaj zakłady, które w roku 2002 złożyły zapotrzebowanie na liczbę

ryz papieru mniej więcej równą średniemu zużyciu we wszystkich

zakładach.

Dostępne tabele:

Zapotrzebowanie (nr_zakl, rok, zapotrzebowanie_na_papier)
Zuzycie (nr_zakl, rok, zuzycie_papieru)

SELECT nr_zakl
FROM zapotrzebowanie

WHERE rok = ‘2002’ AND zapotrzebowanie_na_papier mniej wiecej

(SELECT AVG(zuzycie_papieru)

FROM zuzycie

WHERE rok = ‘2002’);

Politechnika Śląska Instytut Informatyki

Problem zapisu warunku na wartość stopnia
zgodności


forma dołączana do warunku rozmytego



forma funkcyjna



forma operatorowa

Wartości rozmyte w pytaniach
zagnieżdżonych



w podzapytaniu wewnętrznym



w podzapytaniu zewnętrznym



w warunku wiążącym oba podzapytania

Politechnika Śląska Instytut Informatyki

Pytanie zagnieżdżone w formie
operatorowej

W odpowiedzi powinny znaleźć się wiersze ze
stopniem zgodności co najmniej 0.7.

SELECT nr_zakl
FROM zapotrzebowanie
WHERE rok = ‘2002’

AND (zapotrzebowanie_na_papier mniej wiecej

(SELECT AVG(zuzycie_papieru)

FROM zuzycie

WHERE rok = ‘2002’))>= 0.7;

Politechnika Śląska Instytut Informatyki

Warunki wiążące w pytaniach
zagnieżdżonych

Porównanie wartości podzapytania zewnętrznego
z wartością wyznaczaną w pytaniu wewnętrznym:



Dokładna - rozmyta



Rozmyta - dokładna



Rozmyta -rozmyta



Wartości rozmyte w warunku korelacji
wiążącym pytania zagnieżdżone

Politechnika Śląska Instytut Informatyki

Zależne kontekstowo interpretacje wartości
rozmytych

Przykład:

Wyszukać w bazie danych uczelni wysokich

studentów. Uwzględnić wiersze ze stopniem

zgodności przekraczającym 0.8.

Dana tabela:

Studenci (nr_stud, nr_kier, nazwisko, plec, wzrost)

Tradycyjne podejście

SELECT nazwisko
FROM studenci
WHERE (s.wzrost jest wysoki_wzrost) > 0.8

Politechnika Śląska Instytut Informatyki

Dane są następujące tabele:

Studenci (nr_stud, nr_kier, nazwisko, plec, wzrost),

Wzrost (plec, wysoki_wzrost),

SELECT nazwisko
FROM Studenci s JOIN

Wzrost

w

ON

s.plec = w.plec

WHERE (s.wzrost jest w.wysoki_wzrost) > 0.8

Podejście kontekstowe

Politechnika Śląska Instytut Informatyki

Implementacja w SZBD PostgreSQL

Dlaczego SZBD PostgreSQL?



dostępny kod



możliwość tworzenia własnych typów,

funkcji i operatorów

Politechnika Śląska Instytut Informatyki

Implementacja typu rozmytego



X

0 l m n
o

a dm b

Reprezentacja wewnętrzna: a, m, dm, b

Reprezentacja zewnętrzna: ‘l/m~n\o’

Przy wprowadzaniu danych: okolo(l, m, n, o)

Funkcje konwersji wartości rozmytych do wartości lingwistycznych

1

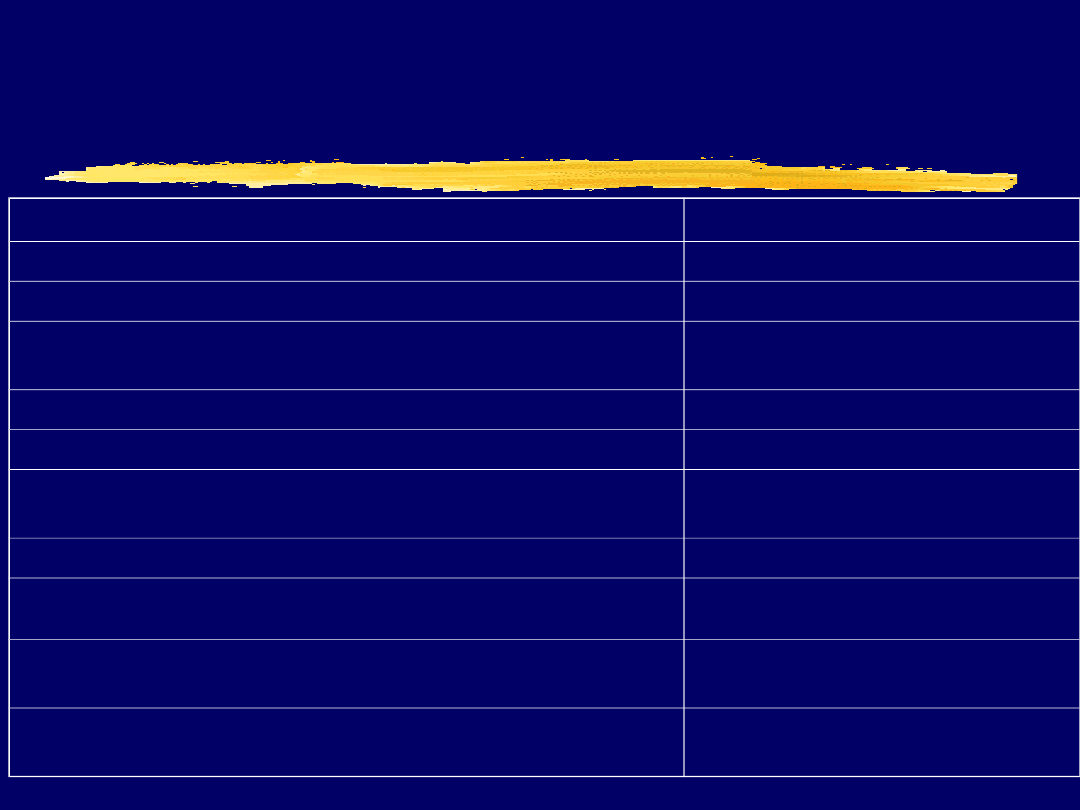
Politechnika Śląska Instytut Informatyki

Zaimplementowane funkcje i
operatory

Rodzaj

nazwa

Funkcje i operatory arytmetyczne

+, -, *, /

Funkcje i operatory porównania

>=, >, <=, <, <>, =

Funkcje i operatory wyznaczające wartość stopnia

zgodności

~=

Funktory iloczynu, sumy i negacji rozmytych

&&&, |||, ~

Wartości predefiniowane dla typu rozmytego

okolo_kilka, okolo_godzina itp.

Funkcje konwersji typu rozmytego do postaci

alfanumerycznej

sekundy_to_lingw, dni_to_lingw

Funkcje agregujące na wartościach typu rozmytego

avg, sum, min, max

Funkcje realizujące rozmyte kwantyfikatory

prawie_zaden, prawie_wszystkie,
okolo_polowa itd.

Funkcje i operatory realizujące rozmyte grupowanie

danych

<, =, <<<

Funkcje i operatory realizujące rozmyty warunek

wiążący podzapytania

*=, *>=, *>, *<=, *<, *<>

Politechnika Śląska Instytut Informatyki

Testowa baza Zawodnicy



6 tabel



10 000 rekordów



12 złożonych testowych zapytań

Politechnika Śląska Instytut Informatyki

Baza danych zawodnicy

Struktura bazy danych zawodnicy

Osoby (id_oso, imie, nazwisko, plec, data_ur,
wzrost, waga, data_przyjecia, funkcja),
Obecności (id_obe, id_tre, id_oso, sennosc, zmeczenie, stres, zlosc);
Serie (id_ser, id_obe, nr, suma),
Strzaly (id_strz, id_ser, nr, wynik),
Treningi (id_tre, data, godz_od, godz_do, id_oso, id_war)
Warunki (id_war, data, temperatura, wiatr, widocznosc)

 

Id_oso – w tabeli treningi oznacza id. trenera

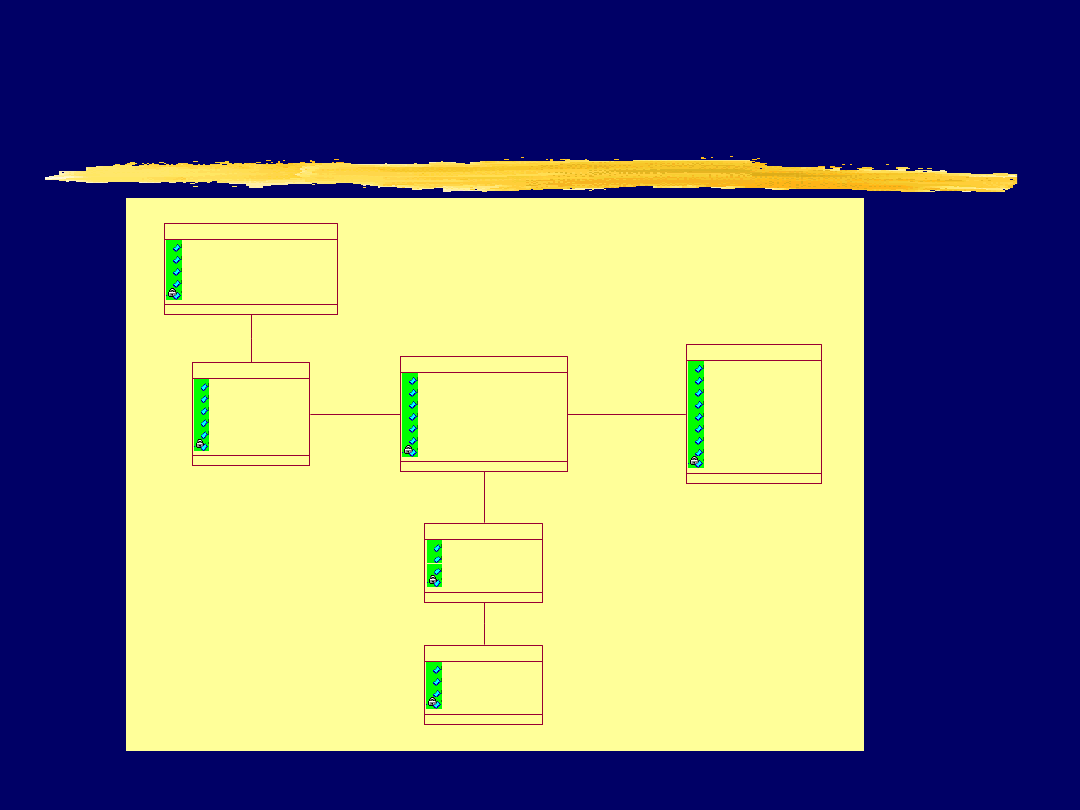
Politechnika Śląska Instytut Informatyki

Diagram bazy danych Zawodnicy

strzaly

nr : Integer
wynik : Integer
id_ser : Integer
id_strz : Integer

serie

nr : Integer
suma : Integer
id_obe : Integer
id_ser : Integer

1

0..n

1

0..n

warunki

data : date
wiatr : ftrapezium
temperatura : ftrapezium
widocznosc : ftrapezium
id_war : Integer

treningi

data : date
godz_od : time
godz_do : time
id_war : Integer
id_oso : Integer
id_tre : Integer

1

0..n

1

0..n

osoby

imie : String
nazwisko : String
plec : String
data_ur : date
wzrost : Integer
waga : Integer
data_przyst : date
funkcja : String
id_oso : Integer

obecnosci

id_oso : Integer
id_tre : Integer
sennosc : ftrapezium
zmeczenie : ftrapezium
stres : ftrapezium
zlosc : ftrapezium
id_obe : Integer

0..n

1

0..n

1

1

0..n

1

0..n

0..n

1

1

0..n

Politechnika Śląska Instytut Informatyki

Przykłady definicji zmiennych
lingwistycznych (1)

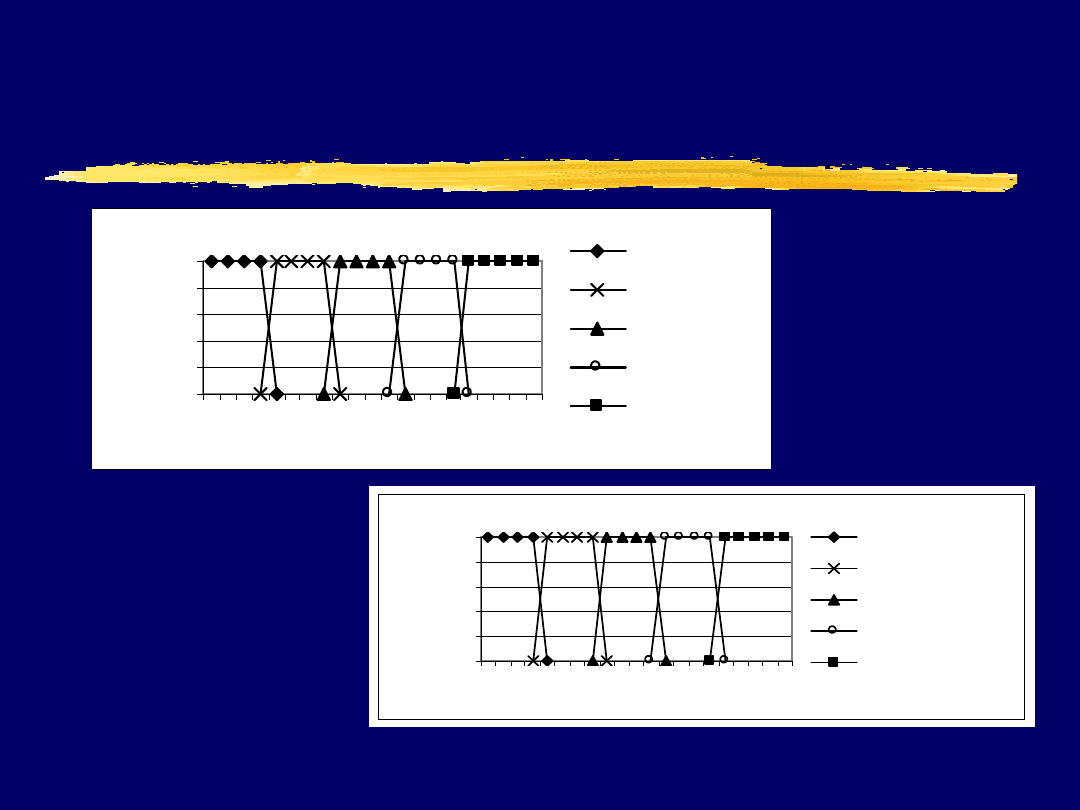
wiatr

0

0,2

0,4

0,6

0,8

1

0

20

40

60

80

100

procenty

st

o

p

ie

ń

p

rz

yn

al

eż

n

o

śc

i

bezw ietrzny
slaby_w iatr
sredni_w iatr
silny_wiatr
wichura

widoczność

0

0,2

0,4

0,6

0,8

1

0

20

40

60

80

100

procenty

st

o

p

ie

ń

p

rz

y

n

al

eż

n

o

śc

i

zla_widocznosc

slaba_widocznosc

srednia_widocznosc

dobra_widocznosc

doskonala_widocznosc

Politechnika Śląska Instytut Informatyki

Przykłady definicji zmiennych
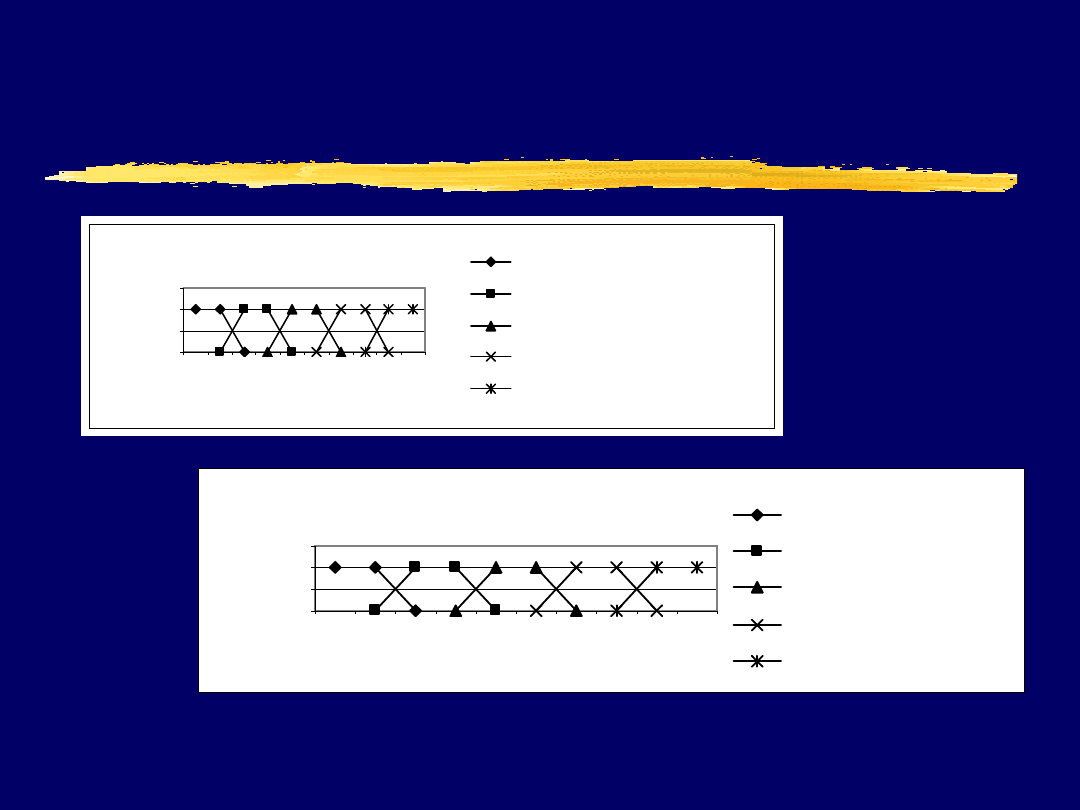
lingwistycznych (2)

wzrost mężczyzny

0

0,5

1

1,5

1 160 162 168 172 178 180 190 195 240

wzrost [cm]

st

o

p

ie

ń

p

rz

yn

al

eż

n

o

śc

i

bardzo_niski_wzrost_mezczyzny

niski_wzrost_mezczyzny

sredni_wzrost_mezczyzny

wysoki_wzrost_mezczyzny

bardzo_wysoki_wzrost_mezczyzny

waga mężczyzny

0

0,5

1

1,5

1

55

60

65

70

80

90

100

120

200

waga [kg]

st

op

ie

ń

pr

zy

na

le

żn

oś

ci

bardzo_mala_waga_mezczyzny

mala_waga_mezczyzny

srednia_waga_mezczyzny

duza_waga_mezczyzny

bardzo_duza_waga_mezczyzny

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte (1)

wartości rozmyte we frazie where

„

Wyszukaj nazwiska wysokich zawodników średniej wagi, którzy

przy słabej widoczności choć raz trafili w dziesiątkę. W
odpowiedzi powinny znaleźć się wszystkie wiersze spełniające ze
stopniem zgodności większym niż 0 kryteria pytania.”

SELECT DISTINCT os.id_oso, os.imie, os.nazwisko
FROM osoby os
JOIN obecnosci ob ON os.id_oso = ob.id_oso
JOIN treningi t ON ob.id_tre = t.id_tre
JOIN warunki w ON t.id_war = w.id_war
JOIN serie s ON s.id_obe = ob.id_obe
JOIN strzaly st ON s.id_ser = st.id_ser
WHERE ((os.wzrost ~= wysoki_wzrost_mezczyzny()) &&&
(os.waga ~= srednia_waga_mezczyzny()) &&&
(w.widocznosc ~= slaba_widocznosc())) > 0.0
AND st.wynik = 10;

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte (2)

wartości rozmyte we frazie where

„Wyszukaj daty treningów wraz z liczbą zawodników,
którzy przystępując do treningu byli wyspani lub
wypoczęci, zaś w czasie treningów nie denerwowali
się (nie odczuwali stresu). W odpowiedzi powinny
znaleźć się wszystkie wiersze spełniające ze stopniem
zgodności większym niż 0,5 kryteria pytania.”

0

0,5

1

1,5

2

w&w

w&w

klasy zapytań

c

z

a

s

[

s

]

rozmyte
dokładne

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte (3a)

wartości rozmyte we frazie WHERE i HAVING

„Wyszukaj zawodników, którzy odbywali dwa
pierwsze treningi z małym stresem i mieli na nich
chociaż jedną bardzo dobrą serię. W odpowiedzi
powinny się znaleźć wiersze spełniające kryteria
pytania ze stopniem większym niż 0.”

„Wyszukaj warunki pogodowe panujące w czasie
tych treningów, w trakcie których prawie wszyscy
zawodnicy byli wyspani (stopień zgodności z
warunkiem rozmytym wyspany powinien być nie
mniejszy niż 0,8, a własność prawie wszystkie
winna być spełniona ze stopniem zgodności nie
mniejszym niż 0,7)”.

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte
(4)

grupowanie względem wartości rozmytych

„Wyszukaj średnią liczbę punktów uzyskanych we
wszystkich seriach dla poszczególnych
zdefiniowanych przedziałów wartości siły wiatru.”
„Określ wpływ zmęczenia zawodników na celność ich
strzałów. (Wyznacz średnią liczbę punktów uzyskaną
dla poszczególnych stanów zmęczenia).”

0

1

2

3

4

g

g

klasy zapytań

c

z

a

s

[

s

]

rozmyte
dokładne

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte (5)

wartości rozmyte w pytaniach
zagnieżdżonych
w podzapytaniach wewnętrznym i
zewnętrznym

„Wyszukaj

nazwiska

zawodników,

którzy

w

poszczególnych treningach mieli najwięcej dobrych
serii. W odpowiedzi powinny znaleźć się wiersze ze
stopniem zgodności przekraczającym 0.”

„Wyszukaj treningi, w których liczba bardzo_dobrych
serii była większa niż dobrych. W rozwiązaniu
należy uwzględnić wiersze ze stopniem zgodności
przekraczającym 0.8.”

Politechnika Śląska Instytut Informatyki

Przykładowe pytania rozmyte (6)

wartości rozmyte w pytaniach
zagnieżdżonych
wartości rozmyte w warunku łączącym

„Wyszukaj treningi przeprowadzone w najsłabszej
widoczności, na których choć jeden zawodnik trafił
dziesiątkę.”

„Wyszukaj wyniki i cechy psychomotoryczne
(senność,

zmęczenie,

stres)

uczestników

treningów, w czasie których wiatr był taki jak wiatr
na najmniej udanym treningu. W odpowiedzi
powinny się znaleźć wiersze spełniające kryteria
pytania ze stopniem zgodności przekraczającym
0.5. ”

„Wyszukaj daty tych treningów, na których
odsetek wyspanych zawodników jest największy.”

Politechnika Śląska Instytut Informatyki

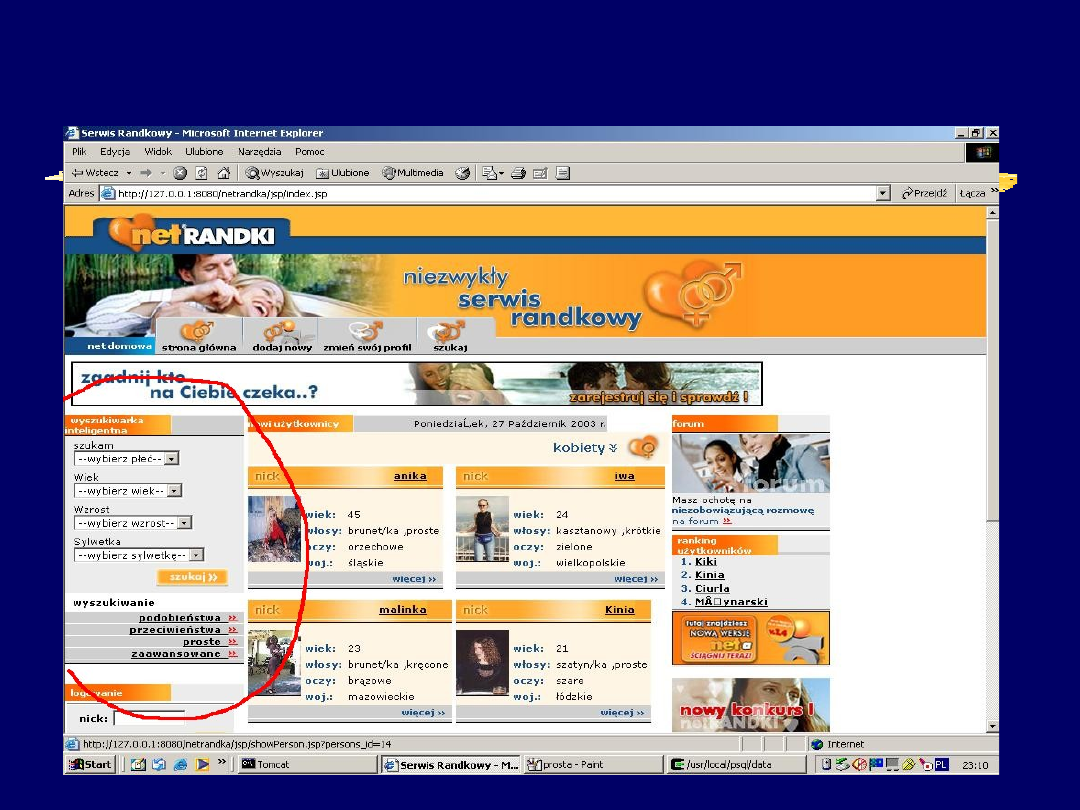
Serwisy wspomagające
nawiązywanie kontaktów
międzyludzkich

Poznawanie ciekawych

osób
o podobnych

zainteresowaniach

cechach charakteru czy
odpowiadającym wyglądzie

Politechnika Śląska Instytut Informatyki

Problemy:



Sprecyzowanie wymagań, jakie
powinna spełniać najbardziej
odpowiadająca osoba



Otrzymanie w odpowiedzi danych co
najmniej kilku osób, spełniających

w określonym stopniu podane kryteria

Politechnika Śląska Instytut Informatyki

Wprowadzenie do języka zapytań
elementów teorii zbiorów rozmytych
pozwala na:



Formułowanie rozmytych,
nieprecyzyjnych warunków
wyszukiwania (np. średni wzrost,
szczupła sylwetka itd.)



Określenie w odpowiedzi częściowej
przynależności elementu do
zdefiniowanego zbioru

Politechnika Śląska Instytut Informatyki

Warstwy logiki rozmytej
w prezentowanym serwisie

warstwa uproszczonych operatorów

warstwa zapytań SQL

warstwa definicji cech

funkcje podstawowe + operatory

Politechnika Śląska Instytut Informatyki

Warstwa najniższa:
funkcje podstawowe + operatory

Zaimplementowano:



Funkcje charakterystyczne: liniową, trójkątną, trapezową,

wykładniczą oraz połączenie trapezowej i wykładniczej



Operatory rozmyte:



operator sumy OR (max spośród dwóch parametrów –



s-norma Zadeh’a)



operator iloczynu AND (min spośród dwóch parametrów - t-

norma Zadeh’a)



operator negacji NOT – różnica wartości 1 i parametru



operator koncentracji CON – druga potęga wartości parametru



operator rozproszenia DIL – pierwiastek z wartości parametru

Politechnika Śląska Instytut Informatyki

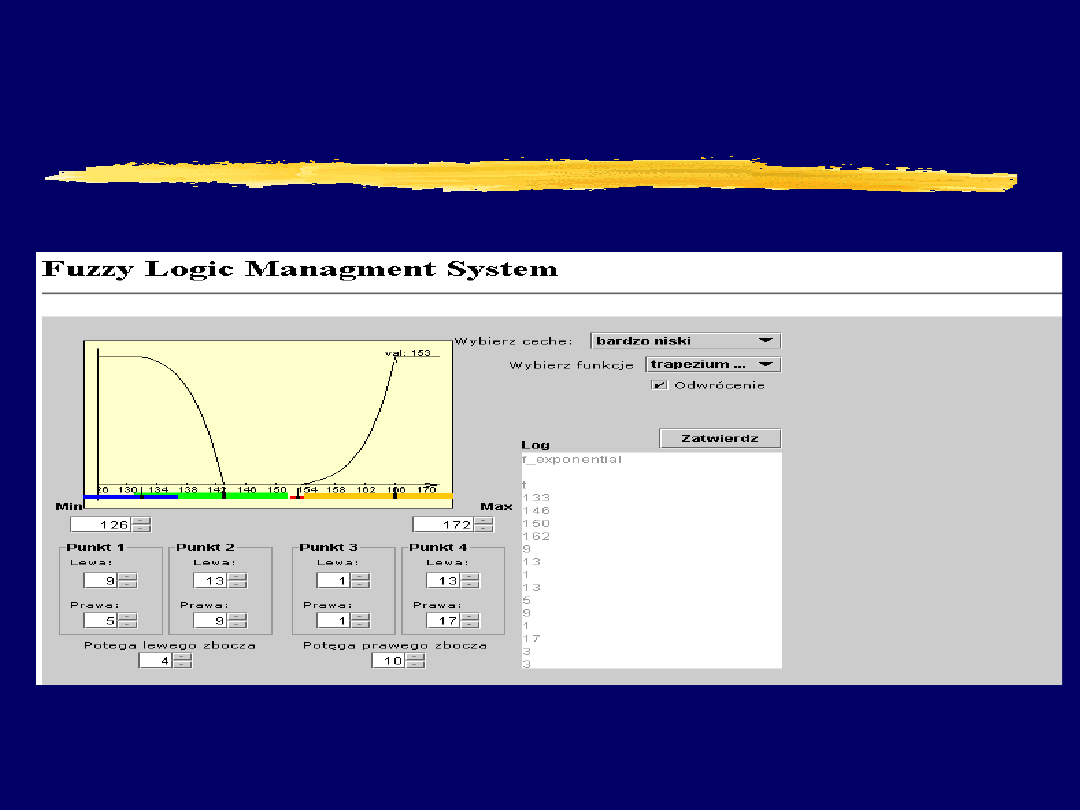
Warstwa definicji cech,
należących do kryterium
wyszukiwarki



Przykładowe cechy, jakie zdefiniowano w systemie:



dotyczące wzrostu: is_very_short, is_short, is_medium,
is_high, is_very_high



dotyczące wieku: is_teenage, is_young, is_mature,
is_senior



dotyczące sylwetki: is_thin, is_normal, is_fluffy



Do każdej cechy przyporządkowana jest dowolna
funkcja charakterystyczna, którą można odpowiednio
kształtować z poziomu interfejsu użytkownika



Personalizacja zapytań (w zależności od cech osoby
korzystającej z przeglądarki)

Politechnika Śląska Instytut Informatyki

Aplikacja do zarządzania
zapytaniami rozmytymi

Politechnika Śląska Instytut Informatyki

Zapytanie SQL

Przykład:
zapytanie wybiera osoby wysokie, młode

lub średnie wiekiem, o szczupłej

sylwetce, przy następujących danych osoby

pytającej: wzrost 176cm, waga 65 kg:

SELECT * FROM persons
WHERE activity = true AND sex = ‘F’ AND
(is_high(176,height) OP_AND

is_thin(65,weight) op_and

is_young(20,age) OP_OR

is_medium(20,age))>0;

Politechnika Śląska Instytut Informatyki

Wyszukiwarka rozmyta