Zbiory

1

Zbiór

•

podstawowe pojęcie matematyczne

2

Zbiór

•

podstawowe pojęcie matematyczne

•

potoczne rozumienie: pojemnik, pudełko, worek

3

Zbiór

•

podstawowe pojęcie matematyczne

•

potoczne rozumienie: pojemnik, pudełko, worek

•

to czym jest zbiór, zależy tylko i wyłącznie od tego
co do tego zbioru należy

4

Przykład.

Rektor UJ jest pracownikiem administracyjnym.

5

Przykład.

Rektor UJ jest pracownikiem administracyjnym.

Rektor UJ należy do zbioru pracowników administracyj-
nych UJ

6

Przykład.

Rektor UJ jest pracownikiem administracyjnym.

Rektor UJ należy do zbioru pracowników administracyj-
nych UJ

Rektor UJ ∈ zbiór pracowników administracyjnych UJ

7

Przykład.

Rektor UJ jest pracownikiem administracyjnym.

Rektor UJ należy do zbioru pracowników administracyj-
nych UJ

Rektor UJ

|

{z

}

r

∈ zbiór pracowników administracyjnych UJ

|

{z

}

P

8

Przykład.

Rektor UJ jest pracownikiem administracyjnym.

Rektor UJ należy do zbioru pracowników administracyj-
nych UJ

Rektor UJ

|

{z

}

r

∈ zbiór pracowników administracyjnych UJ

|

{z

}

P

r ∈ P

9

a ∈ X —

10

a ∈ X — „obiekt a należy do zbioru X”

11

a ∈ X — „obiekt a należy do zbioru X”

albo:

12

a ∈ X — „obiekt a należy do zbioru X”

albo: „obiekt a jest elementem zbioru X

13

należy vs zawiera

14

należy vs zawiera

•

8 należy do zbioru liczb parzystych

15

należy vs zawiera

•

8 należy do zbioru liczb parzystych

•

zbiór liczb podzielnych przez 4 zawiera się w zbiorze
liczb parzystych

16

należy vs zawiera

•

8 należy do zbioru liczb parzystych

•

zbiór liczb podzielnych przez 4 zawiera się w zbiorze
liczb parzystych

•

Jan jest Polakiem

17

należy vs zawiera

•

8 należy do zbioru liczb parzystych

•

zbiór liczb podzielnych przez 4 zawiera się w zbiorze
liczb parzystych

•

Jan jest Polakiem

•

zbiór Polaków zawiera się w zbiorze Europejczyków

18

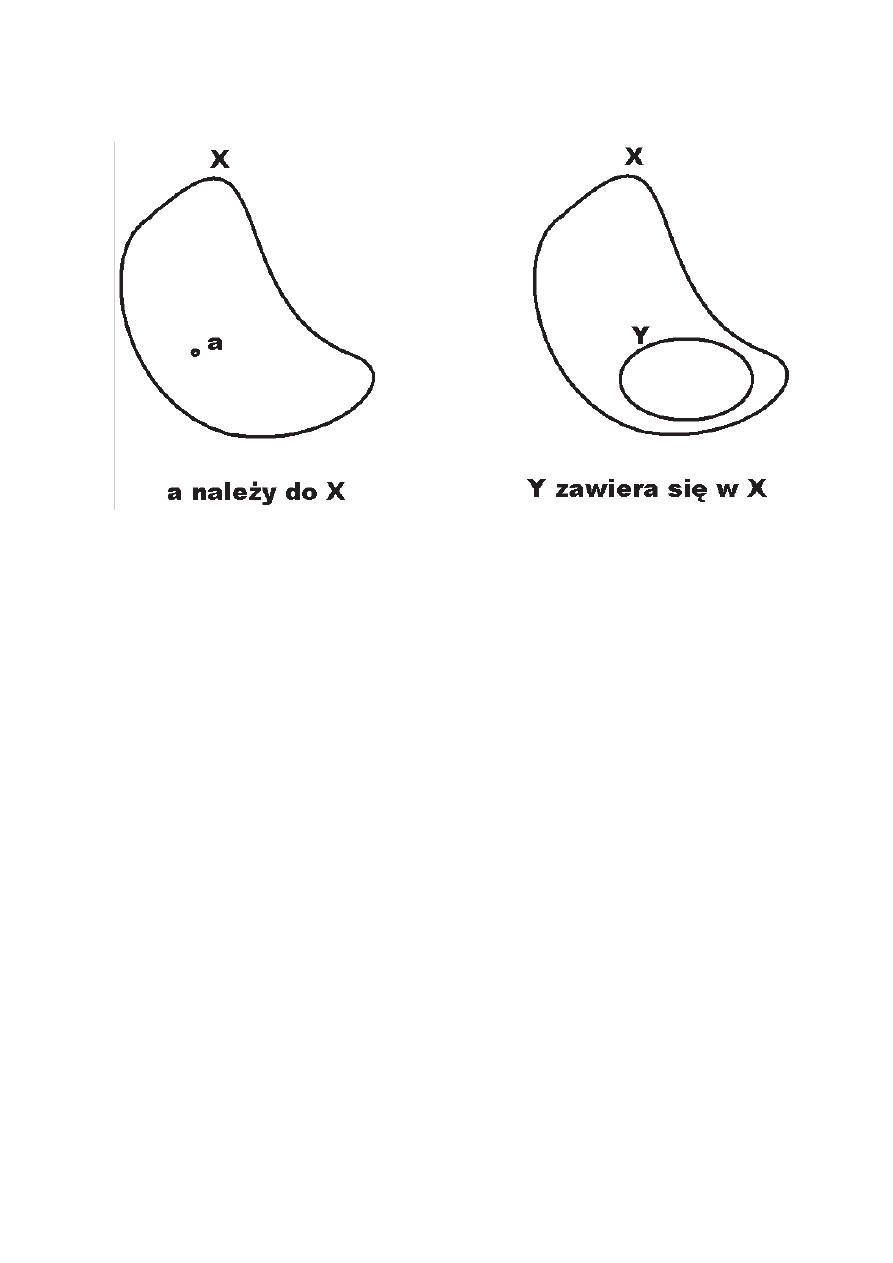
należy vs zawiera

19

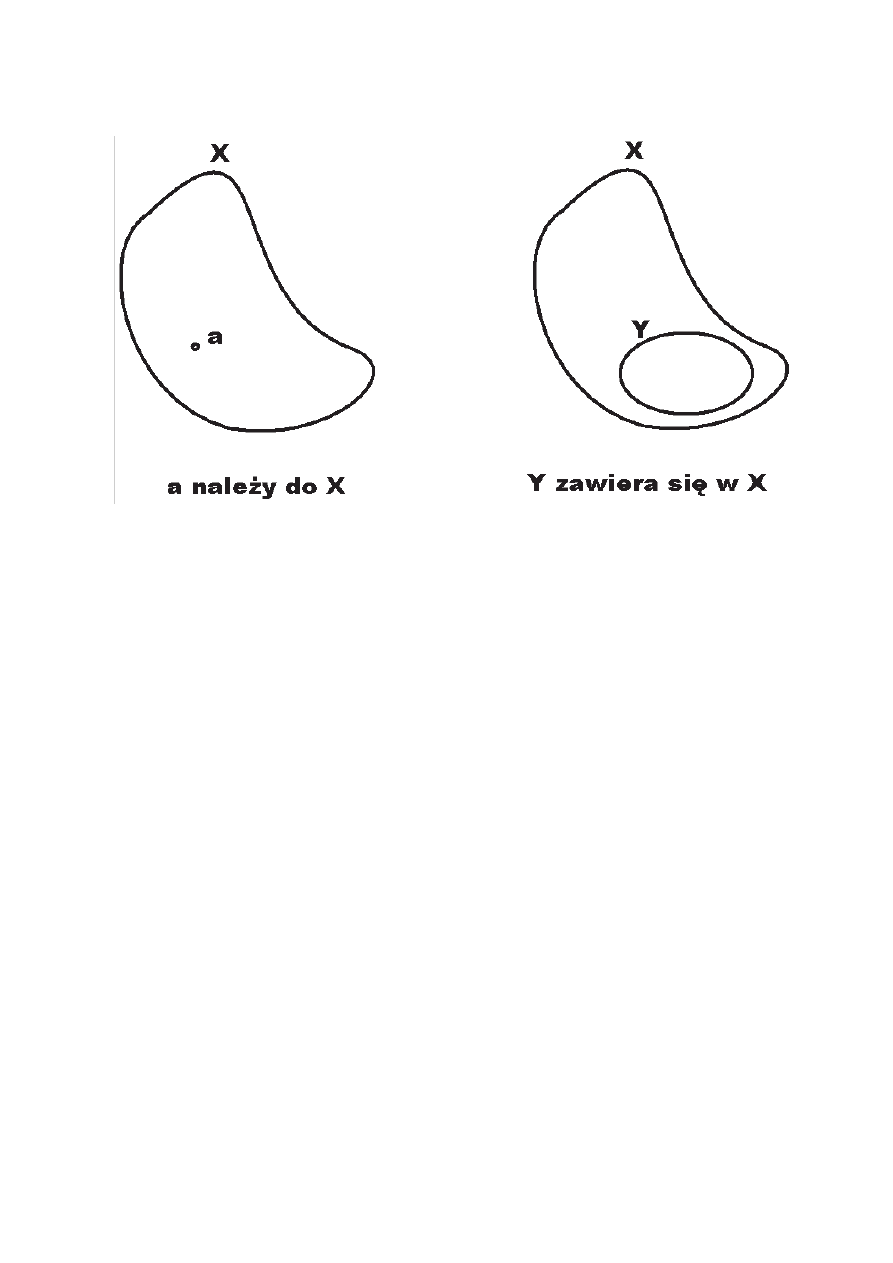
należy vs zawiera

a ∈ X

Y ⊆ X

20

x nie należy do B zapisujemy:

21

x nie należy do B zapisujemy:

x 6∈ B

22

x nie należy do B zapisujemy:

x 6∈ B

C nie zawiera się w D zapisujemy:

23

x nie należy do B zapisujemy:

x 6∈ B

C nie zawiera się w D zapisujemy:

C 6⊆ D

24

Jeśli do zbioru A należą elementy a, b, c, d i żadne inne,
to piszemy:

A = {a, b, c, d}

25

Jeśli do zbioru A należą elementy a, b, c, d i żadne inne,
to piszemy:

A = {a, b, c, d}

Analogicznie, jeśli jedynymi elementami A są elementy
x

1

, x

2

, . . . , x

k

to piszemy:

A = {x

1

, x

2

, . . . , x

k

}

26

Jeśli do zbioru A należą elementy a, b, c, d i żadne inne,
to piszemy:

A = {a, b, c, d}

Analogicznie, jeśli jedynymi elementami A są elementy
x

1

, x

2

, . . . , x

k

to piszemy:

A = {x

1

, x

2

, . . . , x

k

}

Jeśli zbiór A posiada tylko jeden element a to piszemy:

A = {a}

27

Jeśli do zbioru A należą elementy a, b, c, d i żadne inne,
to piszemy:

A = {a, b, c, d}

Analogicznie, jeśli jedynymi elementami A są elementy
x

1

, x

2

, . . . , x

k

to piszemy:

A = {x

1

, x

2

, . . . , x

k

}

Jeśli zbiór A posiada tylko jeden element a to piszemy:

A = {a}

Jeśli A nie posiada w ogóle żadnych elementów to pi-
szemy:

A = ∅

28

Zasada ekstensjonalności

29

Zasada ekstensjonalności

Kiedy dwa zbiory są równe (identyczne)?

30

Zasada ekstensjonalności

Kiedy dwa zbiory są równe (identyczne)?

Wtedy gdy mają takie same elementy.

31

Zasada ekstensjonalności

Kiedy dwa zbiory są równe (identyczne)?

Wtedy gdy mają takie same elementy.

Symbolicznie:

A = B ↔

32

Zasada ekstensjonalności

Kiedy dwa zbiory są równe (identyczne)?

Wtedy gdy mają takie same elementy.

Symbolicznie:

A = B ↔ (dla dowolnego x : x ∈ A ↔ x ∈ B)

33

Przykład. Czy poniższe zbiory są równe?

i.

{1, 2, 3}, {3, 2, 1}

34

Przykład. Czy poniższe zbiory są równe?

i.

{1, 2, 3}, {3, 2, 1}

ii.

{1, 1, 7, 7}, {7, 7, 7, 1, 7, 7, 7}

35

Przykład. Czy poniższe zbiory są równe?

i.

{1, 2, 3}, {3, 2, 1}

ii.

{1, 1, 7, 7}, {7, 7, 7, 1, 7, 7, 7}

iii.

{4}, {4, 4}

36

Przykład. Czy poniższe zbiory są równe?

i.

{1, 2, 3}, {3, 2, 1}

ii.

{1, 1, 7, 7}, {7, 7, 7, 1, 7, 7, 7}

iii.

{4}, {4, 4}

iv.

{1, 6}, {6, 1, 1, 1, 1, . . .}

37

Przykład. Czy poniższe zbiory są równe?

i.

{1, 2, 3}, {3, 2, 1}

ii.

{1, 1, 7, 7}, {7, 7, 7, 1, 7, 7, 7}

iii.

{4}, {4, 4}

iv.

{1, 6}, {6, 1, 1, 1, 1, . . .}

v.

zbiór córek, zbiór kobiet

38

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

39

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

40

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

41

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

42

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

v.

{∅, {∅}, {{∅}}}

43

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

v.

{∅, {∅}, {{∅}}}

vi.

{{{{{{∅, ∅}}}}}}

44

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

v.

{∅, {∅}, {{∅}}}

vi.

{{{{{{∅, ∅}}}}}}

vii.

{{1, 2, 3, 4, 5}}

45

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

v.

{∅, {∅}, {{∅}}}

vi.

{{{{{{∅, ∅}}}}}}

vii.

{{1, 2, 3, 4, 5}}

viii.

{∅, 1, {27, 7, 3 · 9}, 6, {6}}

46

Ćwiczenie. Ile elementów mają poniższe zbiory:

i.

{1, 3, 9, 7, 3}

ii.

{4, 9, 9 − 5}

iii.

{1, ∅}

iv.

{ϑ, {ϑ}}

v.

{∅, {∅}, {{∅}}}

vi.

{{{{{{∅, ∅}}}}}}

vii.

{{1, 2, 3, 4, 5}}

viii.

{∅, 1, {27, 7, 3 · 9}, 6, {6}}

ix.

{{a, b}, b, a, {{b, a, b}}}

47

Rysowanie zbioru pustego...

48

Rysowanie zbioru pustego...

Zbiór pusty ∅ to „puste putełko”:

49

Rysowanie zbioru pustego...

Zbiór pusty ∅ to „puste putełko”:

50

Rysowanie zbioru pustego...

Zbiór {∅} to puste putełko w pudełku:

51

Rysowanie zbioru pustego...

Zbiór {∅} to puste putełko w pudełku:

52

Rysowanie zbioru pustego...

Zbiór {∅, {∅}} to puste putełko i pudełko w którym jest
puste pudełko, w pudełku:

53

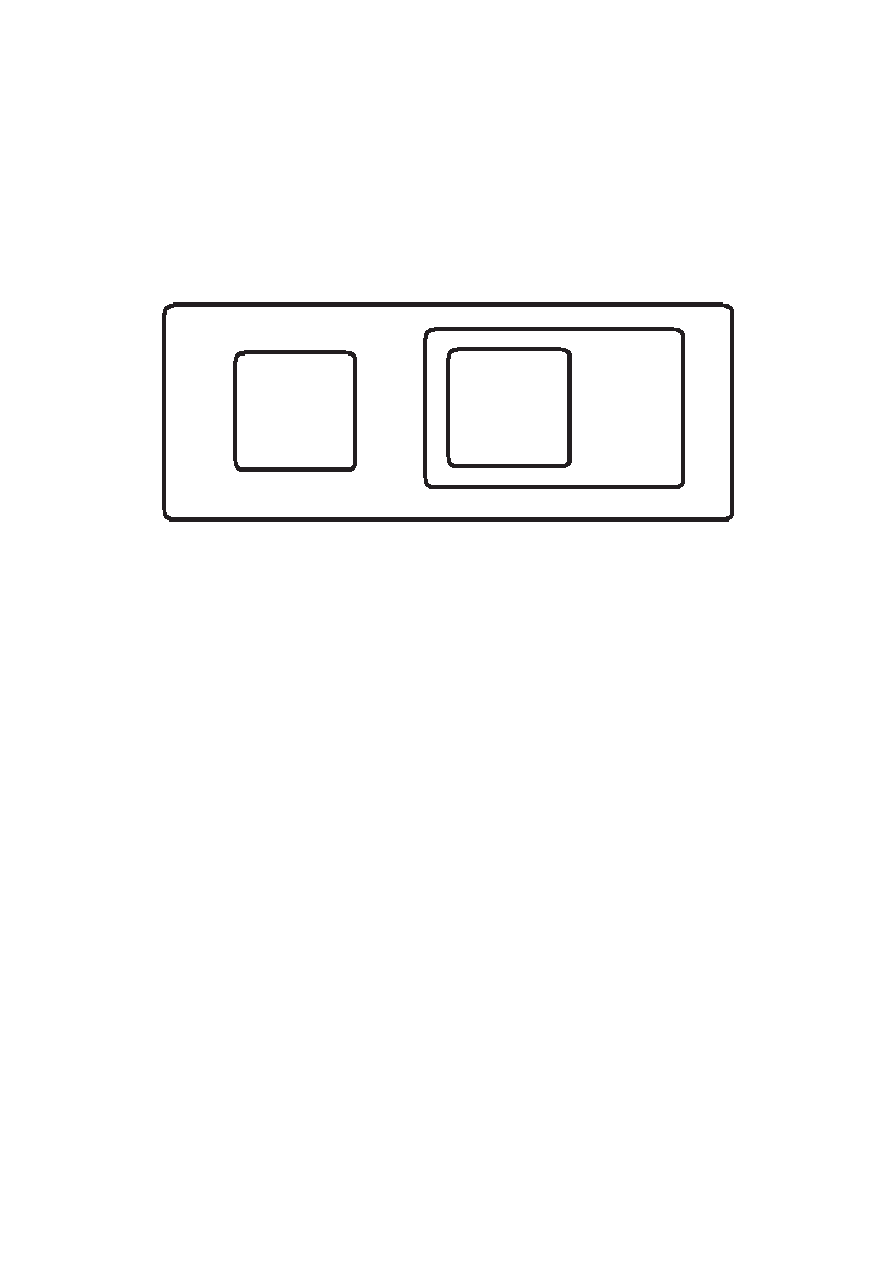
Rysowanie zbioru pustego...

Zbiór {∅, {∅}} to puste putełko i pudełko w którym jest
puste pudełko, w pudełku:

54

i tak dalej...

55

Relacje

56

Zbiór dwuelementowy {x, y} nazywamy parą nieupo-
rządkowaną, ponieważ:

{x, y} = {y, x}.

57

Parę uporządkowaną elementów x i y oznaczamy:

(x, y)

58

Parę uporządkowaną elementów x i y oznaczamy:

(x, y)

Jeśli x 6= y to:

59

Parę uporządkowaną elementów x i y oznaczamy:

(x, y)

Jeśli x 6= y to:

(x, y) 6= (y, x).

60

Parę uporządkowaną elementów x i y oznaczamy:

(x, y)

Jeśli x 6= y to:

(x, y) 6= (y, x).

Kiedy para (x, y) jest równa parze (z, t)?

61

Parę uporządkowaną elementów x i y oznaczamy:

(x, y)

Jeśli x 6= y to:

(x, y) 6= (y, x).

Kiedy para (x, y) jest równa parze (z, t)?

(x, y) = (z, t) ↔ [x = z oraz y = t]

62

Niech A, B będą zbiorami. Zbiór wszystkich par (x, y)
takich, że x ∈ A oraz y ∈ B nazywamy iloczynem
Kartezjańskim zbiorów A i B i oznaczamy:

A × B.

63

Przykład.

{a, b} × {1, 2} =

64

Przykład.

{a, b} × {1, 2} = {

65

Przykład.

{a, b} × {1, 2} = {(a, 1),

66

Przykład.

{a, b} × {1, 2} = {(a, 1), (a, 2),

67

Przykład.

{a, b} × {1, 2} = {(a, 1), (a, 2), (b, 1),

68

Przykład.

{a, b} × {1, 2} = {(a, 1), (a, 2), (b, 1), (b, 2)}

69

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =

70

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =
{(1, 1), (1, 2), (1, 3), (1, 4),

71

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =
{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4),

72

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =
{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4),
(3, 1), (3, 2), (3, 3), (3, 4),

73

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =
{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4),
(3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}

74

Przykład.

{1, 2, 3, 4} × {1, 2, 3, 4} =
{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4),
(3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}

Zatem iloczyn kartezjański ma 4 · 4 = 16 elementów.

75

Ile elementów ma iloczyn kartezjański:

{1, 2, . . . , 20} × {1, 2, . . . , 500}?

76

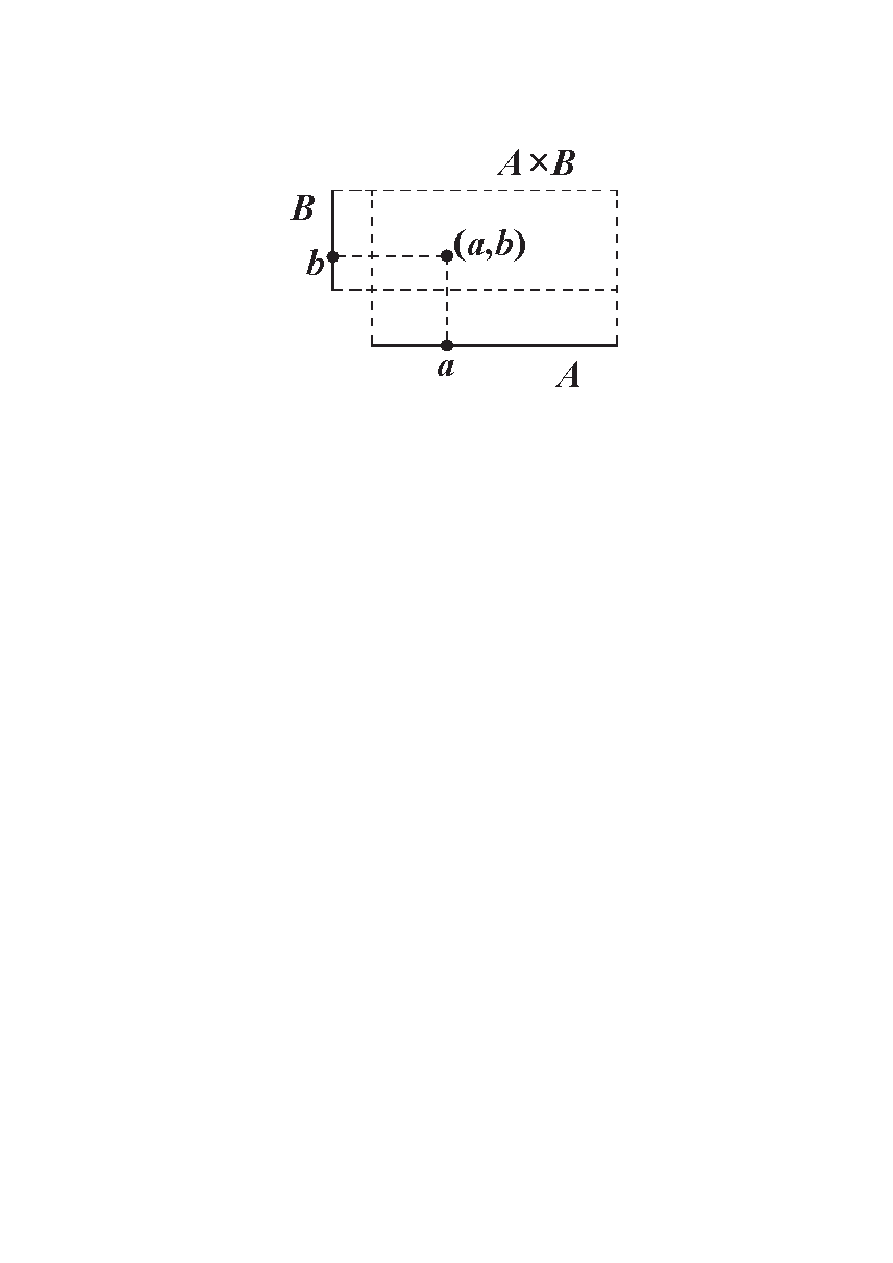
Iloczyn kartrezjański zbirów A i B:

77

Definicja. Niech X, Y będą dowolnymi zbiorami. Re-
lacją pomiędzy elementami zbioru X a elementami zbio-
ru Y nazywamy dowolny podzbiór R ⊆ X × Y .

78

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

79

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

80

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?

81

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

82

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

R

1

= ∅

(relacja „pusta”)

83

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

R

1

= ∅

(relacja „pusta”)

R

2

= {(1, 1)}

84

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

R

1

= ∅

(relacja „pusta”)

R

2

= {(1, 1)}

R

3

= {(1, 2)}

85

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

R

1

= ∅

(relacja „pusta”)

R

2

= {(1, 1)}

R

3

= {(1, 2)}

...

86

Przykład. Rozważmy iloczyn kartezjański {1, 2}×{1, 2}
czyli czteroelementowy (!) zbiór:

{(1, 1), (1, 2), (2, 1), (2, 2)}.

Ile jest różnych relacji w tym zbiorze?
Tyle ile podzbiorów czyli 2

4

= 16, np.:

R

1

= ∅

(relacja „pusta”)

R

2

= {(1, 1)}

R

3

= {(1, 2)}

...
R

16

= {(1, 1), (1, 2), (2, 1), (2, 2)} (relacja „pełna”)

87

Przykład. Ile jest relacji w iloczynie kartezjańskim
{1, 2, . . . , 10} × {1, 2, . . . , 10}?

88

Przykład. Ile jest relacji w iloczynie kartezjańskim
{1, 2, . . . , 10} × {1, 2, . . . , 10}?

2

10·10

=

89

Przykład. Ile jest relacji w iloczynie kartezjańskim
{1, 2, . . . , 10} × {1, 2, . . . , 10}?

2

10·10

= 2

100

=

90

Przykład. Ile jest relacji w iloczynie kartezjańskim
{1, 2, . . . , 10} × {1, 2, . . . , 10}?

2

10·10

= 2

100

=

= 1 267 650 600 228 229 401 496 703 205 376

91

Oznaczenia.

92

Oznaczenia.

Zamiast pisać (x, y) ∈ R, piszemy:

xRy

93

Oznaczenia.

Zamiast pisać (x, y) ∈ R, piszemy:

xRy

Zamiast pisać (x, y) 6∈ R, piszemy:

¬xRy

94

Graf relacji. Przykład.

95

Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

96

Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

97

Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

98

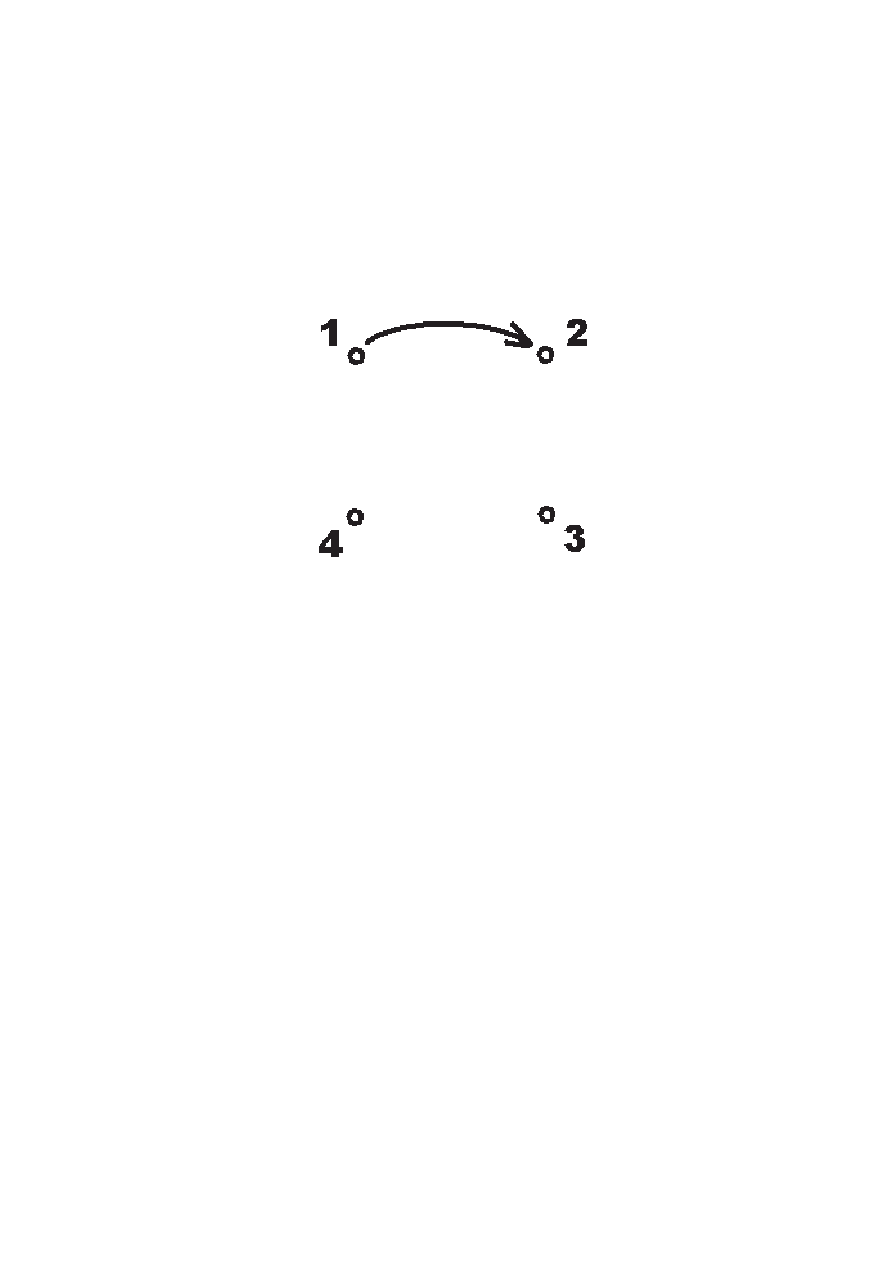
Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

99

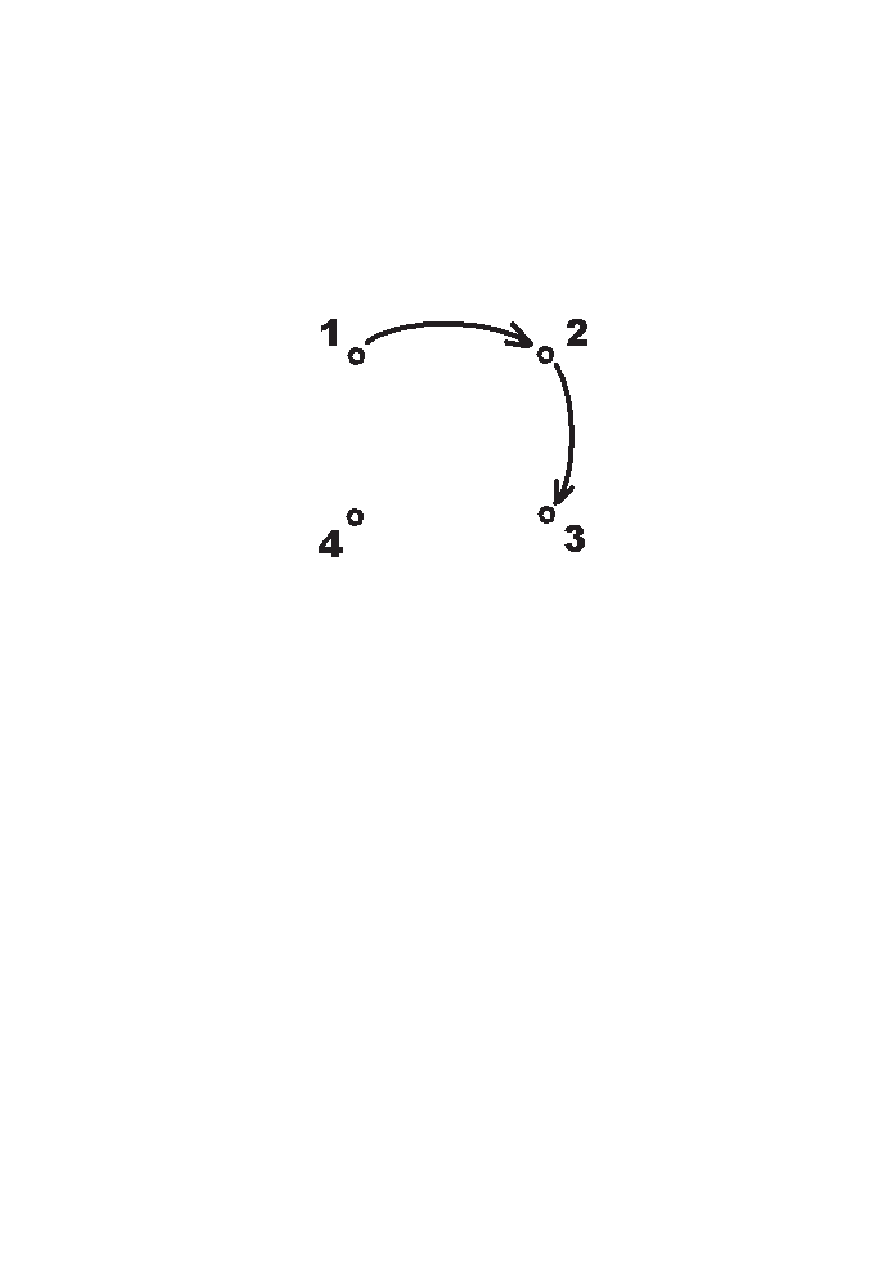
Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

100

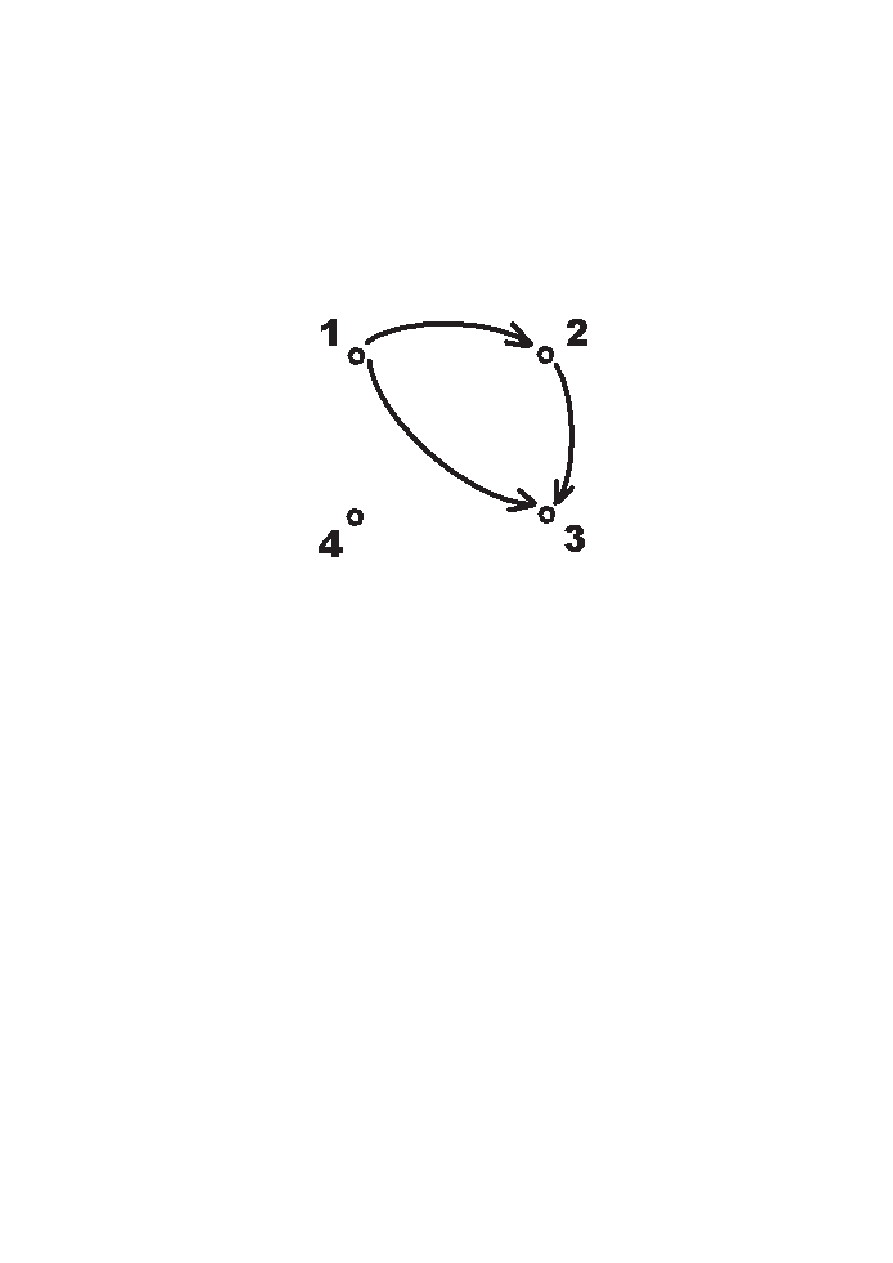
Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

101

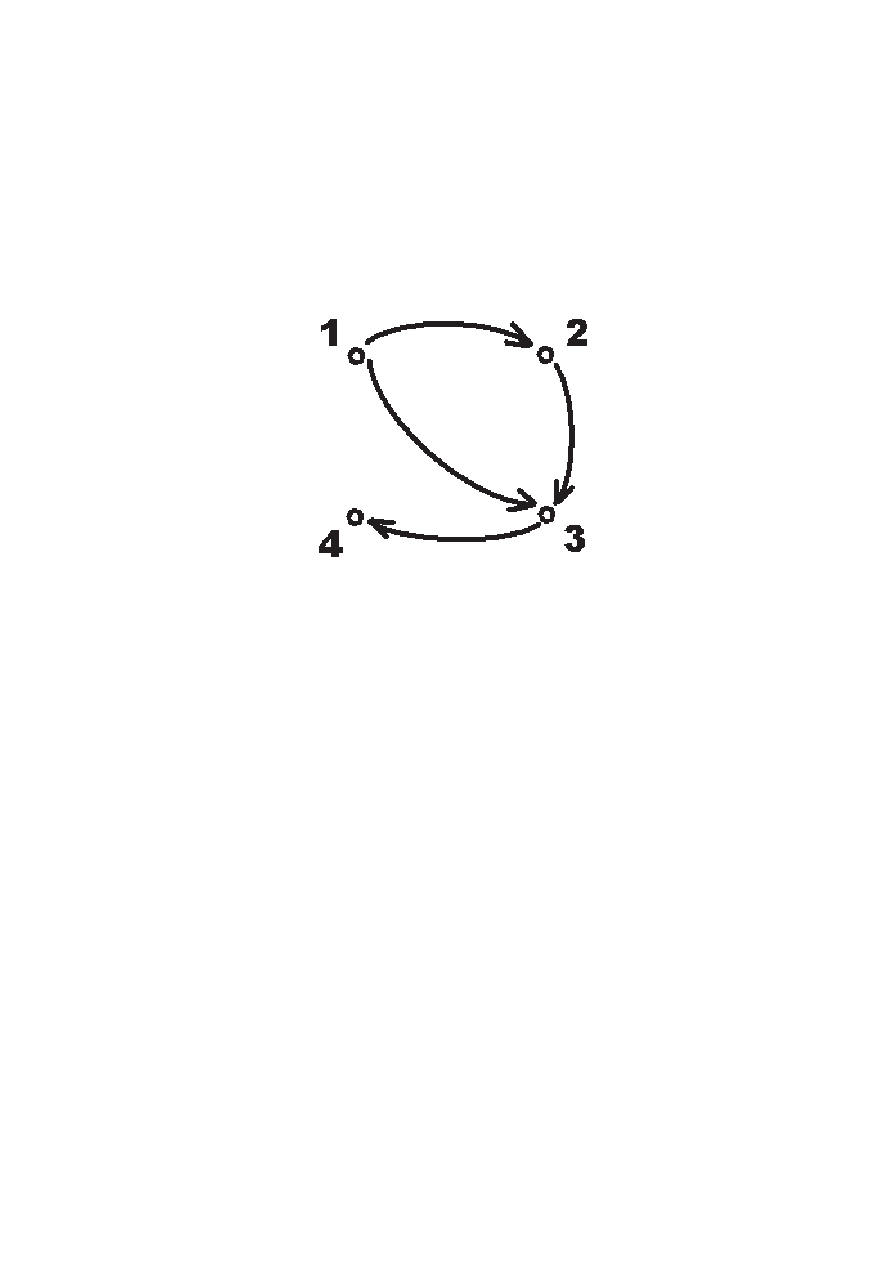
Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

102

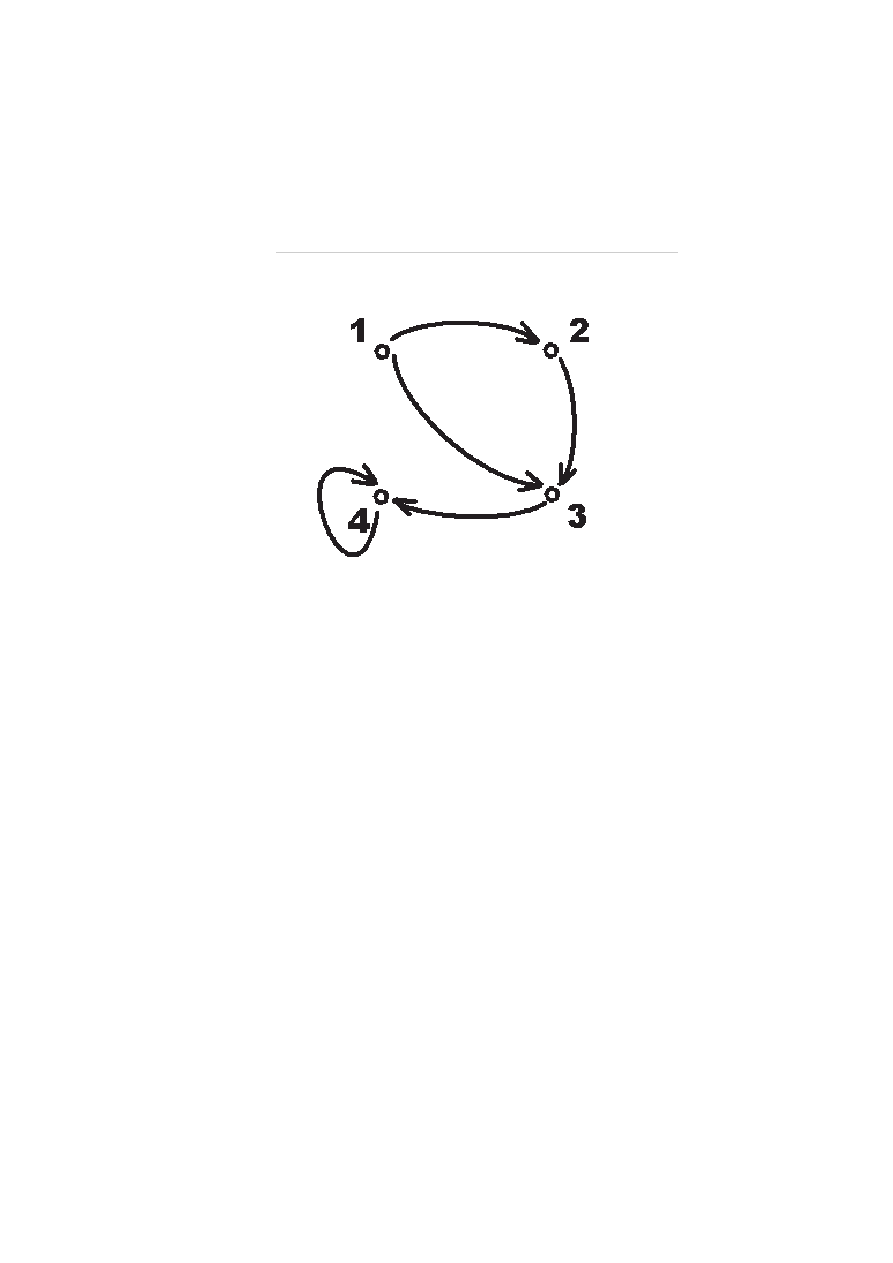
Graf relacji. Przykład. Rozważmy iloczyn kartezjań-
ski {1, 2, 3, 4} × {1, 2, 3, 4} i relację R w tym zbiorze:

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

Sporządzamy graf relacji R w następujący sposób:

103

Własności relacji. Relację R ⊆ X × X nazywamy:

104

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

105

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

106

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

•

symetryczną, gdy ∀x, y (xRy → yRx)

107

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

•

symetryczną, gdy ∀x, y (xRy → yRx)

•

antysymetryczną, gdy ∀x, y (xRy → ¬yRx)

108

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

•

symetryczną, gdy ∀x, y (xRy → yRx)

•

antysymetryczną, gdy ∀x, y (xRy → ¬yRx)

•

słabo-antysymetryczną, gdy ∀x, y

(xRy ∧ yRx) → x = y

109

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

•

symetryczną, gdy ∀x, y (xRy → yRx)

•

antysymetryczną, gdy ∀x, y (xRy → ¬yRx)

•

słabo-antysymetryczną, gdy ∀x, y

(xRy ∧ yRx) → x = y

•

przechodnią, gdy ∀x, y, z

(xRy ∧ yRz) → xRz

110

Własności relacji. Relację R ⊆ X × X nazywamy:

•

zwrotną, gdy ∀x xRx

•

przeciwzwrotną, gdy ∀x ¬xRx

•

symetryczną, gdy ∀x, y (xRy → yRx)

•

antysymetryczną, gdy ∀x, y (xRy → ¬yRx)

•

słabo-antysymetryczną, gdy ∀x, y

(xRy ∧ yRx) → x = y

•

przechodnią, gdy ∀x, y, z

(xRy ∧ yRz) → xRz

•

spójną, gdy ∀x, y (xRy ∨ yRx ∨ x = y)

111

Ćwiczenie 1. Zbadać własności relacji

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

w zbiorze {1, 2, 3, 4}.

112

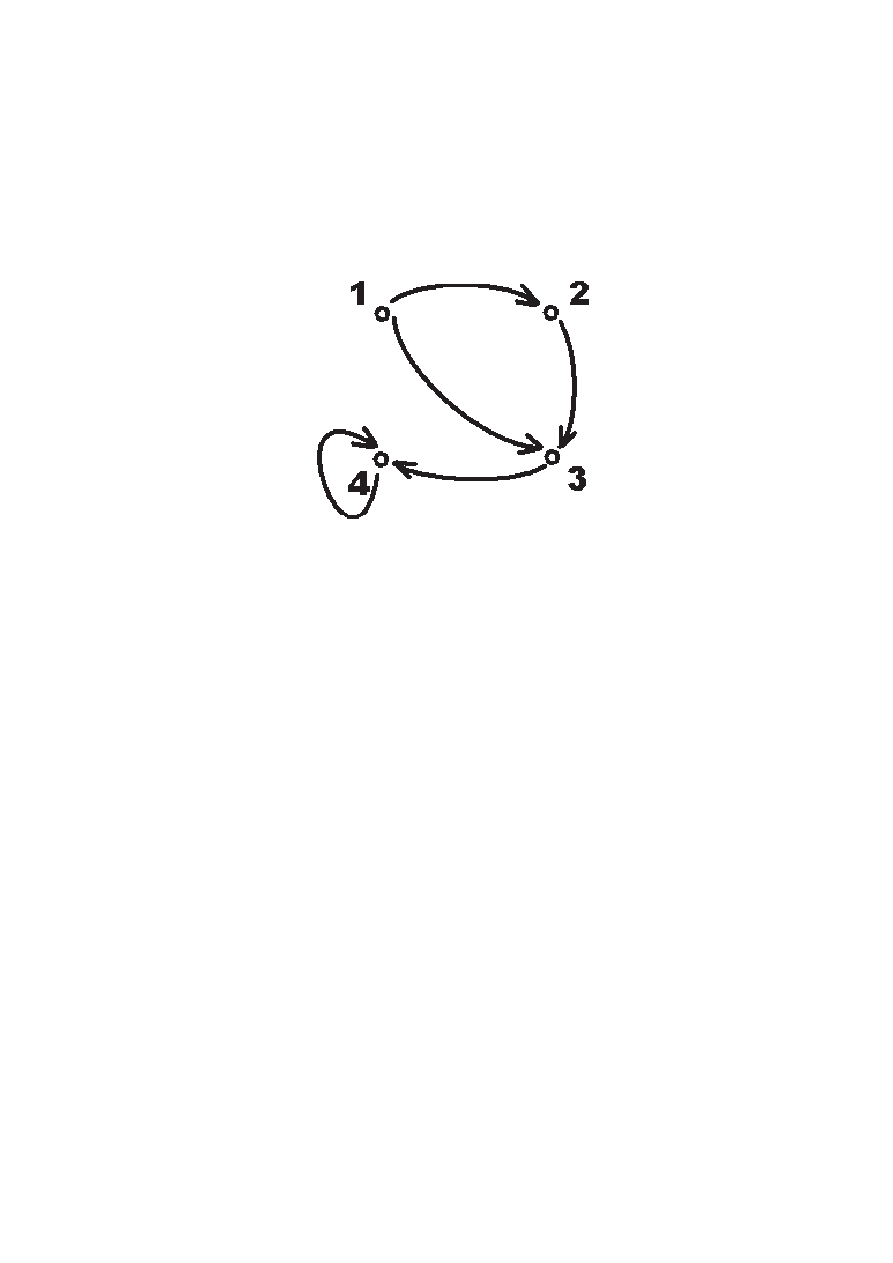
Ćwiczenie 1. Zbadać własności relacji

R = {(1, 2), (2, 3), (1, 3), (3, 4), (4, 4)}

w zbiorze {1, 2, 3, 4}.

113

Ćwiczenie 2. Zbadać własności relacji

R = {(1, 2), (3, 4), (2, 1), (4, 3)}

w zbiorze {1, 2, 3, 4}.

114

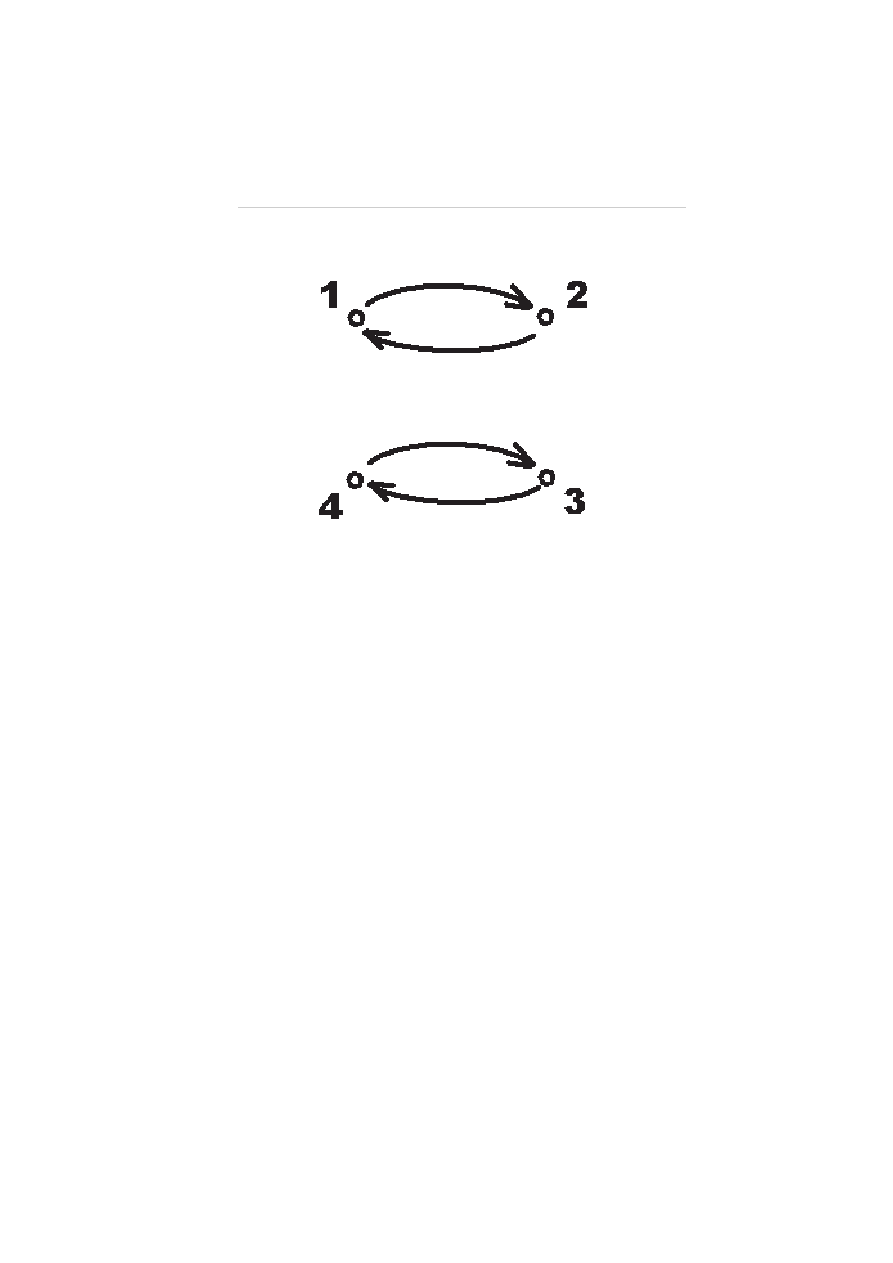
Ćwiczenie 2. Zbadać własności relacji

R = {(1, 2), (3, 4), (2, 1), (4, 3)}

w zbiorze {1, 2, 3, 4}.

115

Ćwiczenie 3. Zbadać własności relacji

R = {(1, 2), (2, 3), (3, 4), (1, 3), (1, 4), (2, 4)}

w zbiorze {1, 2, 3, 4}.

116

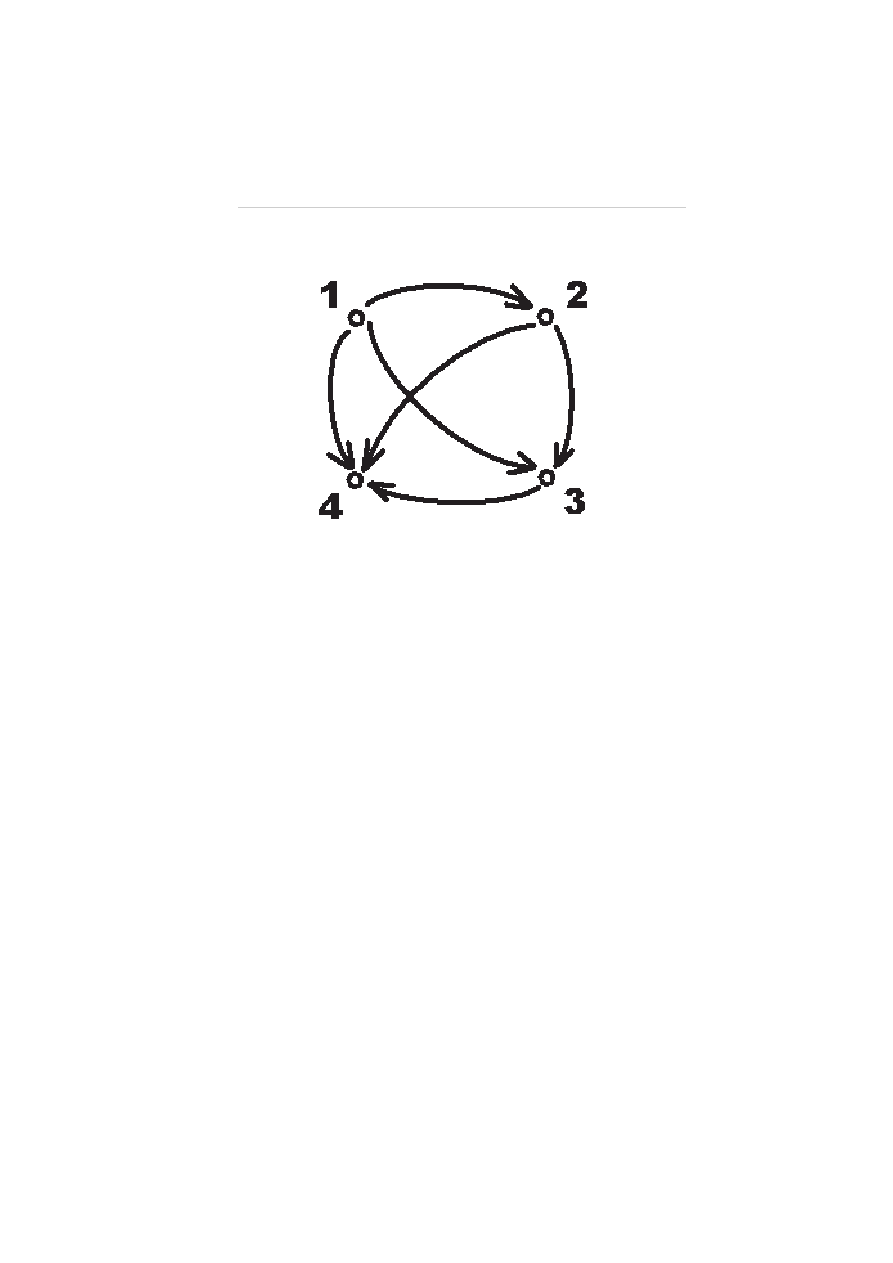
Ćwiczenie 3. Zbadać własności relacji

R = {(1, 2), (2, 3), (3, 4), (1, 3), (1, 4), (2, 4)}

w zbiorze {1, 2, 3, 4}.

117

Ćwiczenie 4. Zbadać własności relacji

R = {(1, 2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1)}

w zbiorze {1, 2, 3, 4}.

118

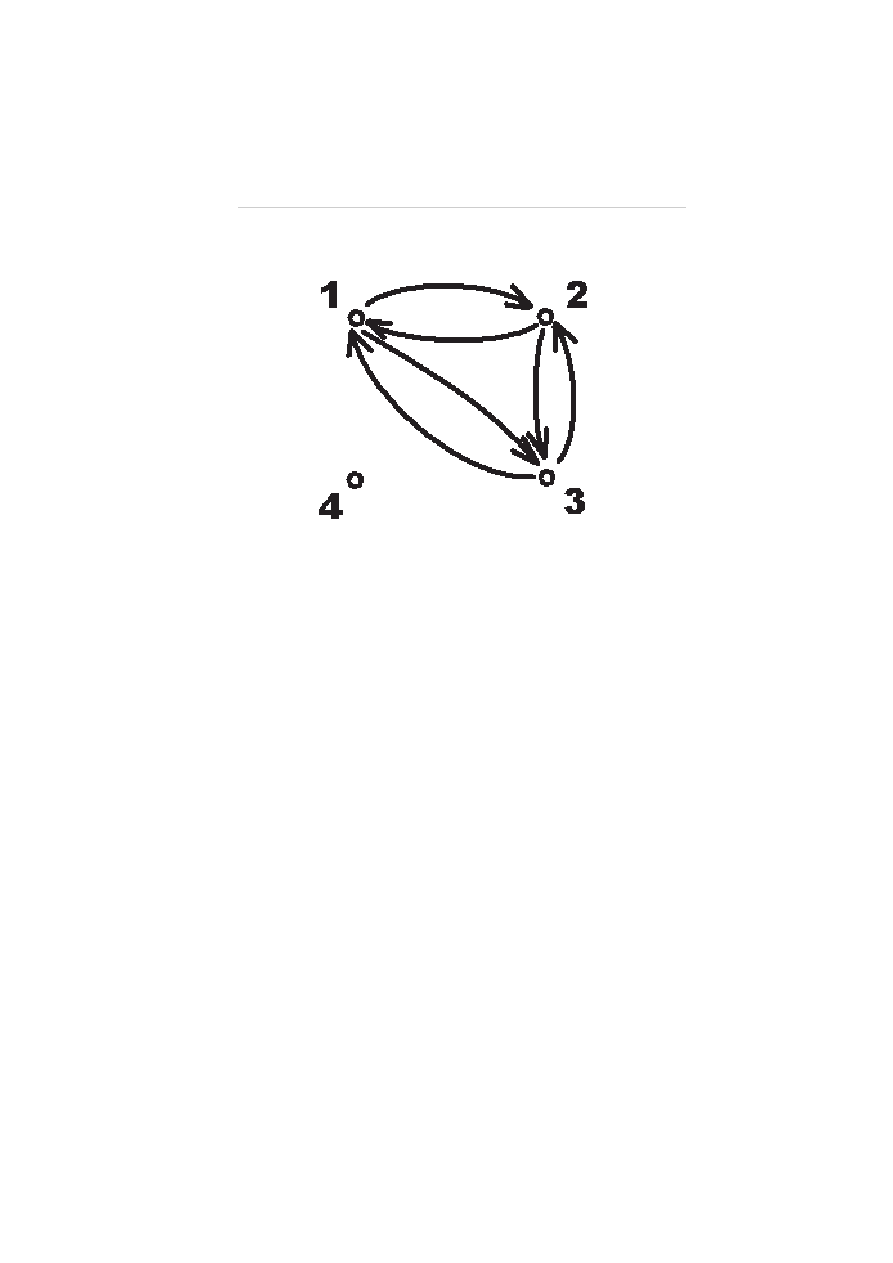
Ćwiczenie 4. Zbadać własności relacji

R = {(1, 2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1)}

w zbiorze {1, 2, 3, 4}.

119

Ćwiczenie 5. Zbadać własności relacji w zbiorze
{1, 2, 3, 4, 5, 6}.

i.

R = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 6)}

ii.

R = {(1, 2), (3, 4), (6, 5)}

iii.

R = {(1, 2), (3, 2), (5, 4), (1, 6), (3, 4), (5, 6)}

iv.

R = {(6, 6), (3, 2), (1, 2), (5, 2), (4, 5), (4, 2)}

v.

R = {(1, 2), (2, 2), (3, 3), (6, 6), (4, 3), (3, 4), (1, 1),
(2, 1), (5, 2), (5, 1), (1, 5), (5, 5), (4, 4), (5, 2)}

120

Relacje rozważane poniżej, są określone w zbiorze ludzi.
Np. relacja „bycia matką” zachodzi między x a y wtedy
i tylko wtedy, gdy x jest matką y.

121

Relacje rozważane poniżej, są określone w zbiorze ludzi.
Np. relacja „bycia matką” zachodzi między x a y wtedy
i tylko wtedy, gdy x jest matką y. Czyli

xRy ↔ x jest matką y.

122

Relacje rozważane poniżej, są określone w zbiorze ludzi.
Np. relacja „bycia matką” zachodzi między x a y wtedy
i tylko wtedy, gdy x jest matką y. Czyli

xRy ↔ x jest matką y.

Jakie własności posiada relacja:

i.

bycia matką

ii.

bycia bratem

iii.

bycia znajomym

iv.

bycia krewnym

v.

zwierzchnictwa (w pracy)

vi.

bycia kochanym

123

vii.

bycia starszym

viii.

bycia o rok starszym

ix.

bycia tego samego wieku

x.

bycia przeciwnej płci

xi.

bycia nie-siostrą

xii.

bycia starszym lub młodszym

xiii.

wyznawania tej samej religii

xiv.

bycia dziadkiem

xv.

bycia najmłodszą siostrą

xvi.

posiadania wspólnego rodzica

124