Zależne uszkodzenia elementów
2
1
gdy jeden z elementów uszkodzi się to intensywność uszkodzeń elementu
pozostającego w stanie zdatności wzrasta do
1
1) ani jeden element nie uszkodzi się do chwili
t
:
t
e
P
2
1
2) element (1) uszkodzi się w pewnej chwili
t
,
element (2) nie uszkodzi się do chwili
t
:
d
t
R
R
f
P
t
)
,
(
)
(
)
(
0
2
e
f
)
(
e
R
)
(
)
(
1
)
,
(
t
e
t
R
d
e
e
d
e
e
e
P
t
t
t
t
)
2
(
0
)
(
0
2
1
1
1
1
2
2
)
2
(
1
0
1
)
2
(
1
1
1
1
t
t
t
t
e
e
e
e
3)
element (2) uszkodzi się w pewnej chwili
t
,
element (1) nie uszkodzi się do chwili
t
:
2
3
P
P
2
1
3
2
1
2
)
(
P
P
P
P
P
t
R
u
1
2
2
)
(
)
2
(
1
2
1
1
t
t
t
u
e
e
e
t
R
t
t
t
e
e
e
1
2
2
2
2
1
2
1
2
t
t
e
e
1
2
2
2
1
2
1
1
dt
e
2
2
e
2
dt
)
t
(
R
)
T
(
E
0
t
1
0
t
2
1
1
0
u
u
1
1
1
2
2
1
1
1
1
1
2
)
2
(
4
1
2
2
2
1
2
1
1
1
1
2
1
2
2
1
)
(
)
(
2
1
t
P
t
P
1
)
(
)
(
2
1
t
t
P
t
t
P
jeżeli:
.
)
(
const
t
.
)
(
const
t
)
(
1
1
T
E
)
(
1
2
T
E
t
t
P
t
t
P
t
t
P
)
(
1
)
(
)
(
2
1
1
)
(
)
(
)
(
)
(
2
1
1
1
t
P
t
P
t
t
P
t
t
P
)
(
)
(
)
(
'
2
1
1
t
P
t
P
t
P
1
)
0
(
1
P
1
2
t
t
t+
t
0
t
1
2
(t)
(t)

)
(
)
(
)
(
1
t
k
e
t
P
g
t
0
t
1
1
P
t
g
k
P
1
e
z
z
nz
z
g
T
T
T
T
T
T
E
T
E
T
E
T
E
T
E
T
E
k
)
(
)
(
)
(
)
(
1
)
(
1
)
(
1
1
2
1
2
1
2
e
T
- całkowity czas eksploatacji
u
T
- całkowity czas użytkowania,
u
T
i
i
o
T
- całkowity czas obsługiwania,
o
T
i
i
i
liczba przejść obiektu do danego stanu
W dwustanowym modelu procesu eksploatacji:
u
z
T
T
,
o
nz
T
T
g
k
nz
z
z
e
z
T
T
T
T
T
o
u
u
T
T
T
W trójstanowym modelu procesu eksploatacji
ou
T
- całkowity czas oczekiwania na użytkowanie,
i
i
ou
T
oo
T
- całkowity czas oczekiwania na obsługiwanie,
i
i
oo
T
'
Przypadek 1
o
ou
u
e
T
T
T
T
ou
u
z
T
T
T
o
nz
T
T
Przypadek 2
oo
o
u
e
T
T
T
T
u
z
T
T
oo
o
nz
T
T
T
e
z
g
T
T
k
o
ou
u
ou
u
g
T
T
T
T
T
k
0
t
1
0
P
1
(t)
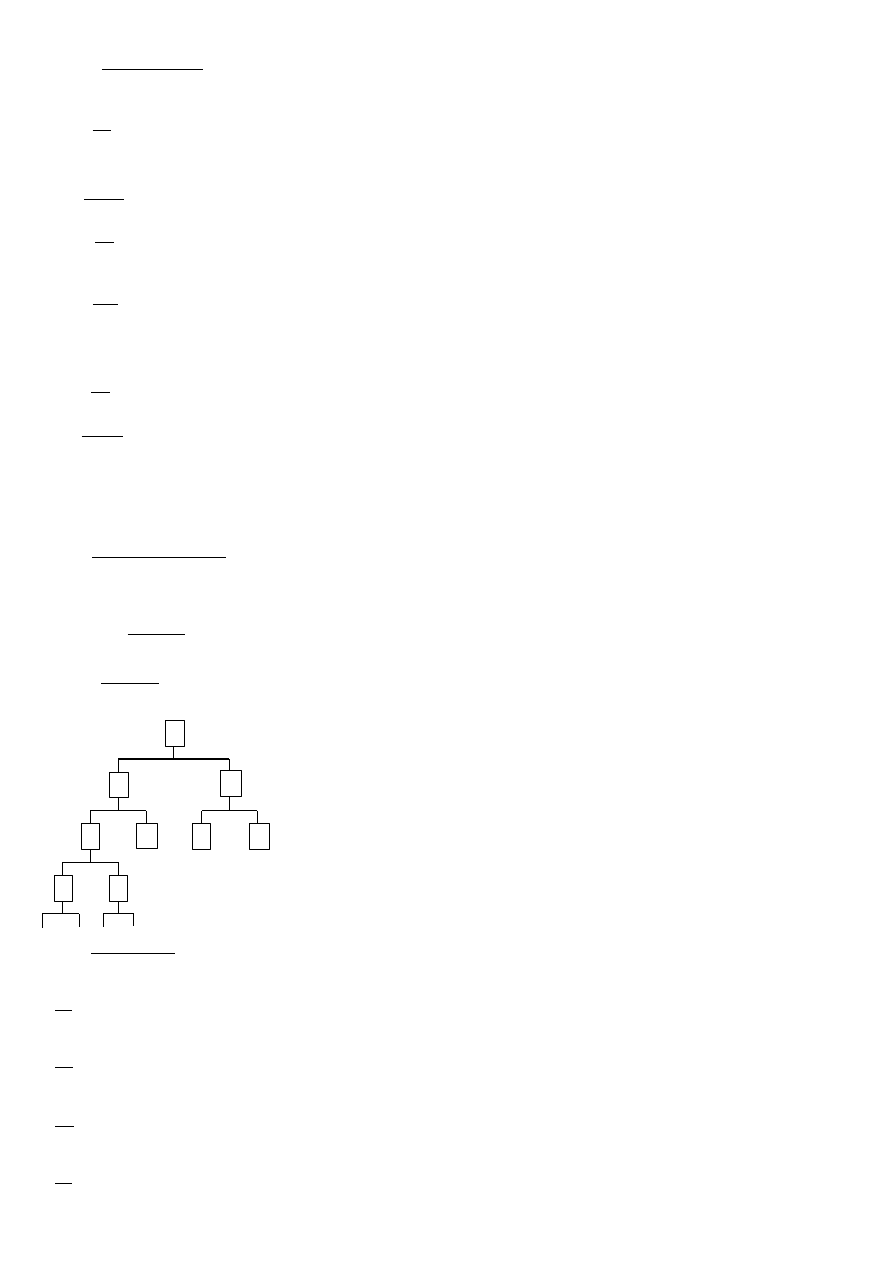
oo
o
u
u
g
T
T
T
T
k
z
u
w
T
T
k
w
k
- wskaźnik wykorzystania obiektu zdatnego
1
ou
u
u
W
T
T
T
k
1
u
u
w
T
T
k
nz
o
e
T
T
k
e
k
- wskaźnik efektywności obsługiwania
obiektu niezdatnego
1
o
o
e
T
T
k
1
oo
o
o
e
T
T
T
k
W czterostanowym modelu procesu eksploatacji:
oo
o
ou
u
e
T
T
T
T
T
oo
o
ou
u
ou
u
g
T
T
T
T
T
T
k
jeżeli:
ou
u
u
w
T
T
T
k
oo
o
o
e
T
T
T
k
o
w
u
e
u
e
g
T
k
T
k
T
k
k
e
e
T
L
-
intensywność eksploatacji
u
z
T
L
-
intensywność użytkowania
e
u
V
T
L
-
prędkość eksploatacyjna
t
j
V
T
L
-
prędkość techniczna
T
j
T
p
T
u
T
ou
T
e
T
o
T
oo
T
z
T
nz
)
(t
N
u
- liczba urządzeń użytkowanych w chwili
t
)
(t
N
o
- liczba urządzeń obsługiwanych w chwili
t
)
(
)
(
t
N
t
N
z
e
)
(t
N
nz
)
(
)
(
t
N
t
N
u
z
)
(
)
(
t
N
t
N
o
nz
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
t
N
t
N
t
N
t
N
t
N
t
N
t
N
t
N
t
k
o
u
u
e
u
nz
z
z
g
)
(t
k
g
- chwilowy wskaźnik gotowości technicznej
W przypadku jednorodnej grupy urządzeń eksploatowanych
w ustalonych warunkach, można potraktować historię
eksploatacji grupy w krótkim przedziale jako
ekwiwalentną historii eksploatacji pojedynczego
urządzenia tej grupy, ale w dłuższym przedziale.
)
(
)
(
)
(
)
(
)
(
)
(
t
N
t
N
t
N
t
T
t
T
t
T
o
u
u
o
u
u
Funkcja wiodąca (skumulowana intensywność uszkodzeń)
dx
x
t
t
0
)
(
)
(
Można ją interpretować jako miarę wyczerpywania się
„zapasu niezawodności obiektu”.
Ponieważ
t
dx
x
e
t
R
0
)
(
)
(
to
)
(
)
(
t
e
t
R
)
(
1
)
(
t
e
t
F
)
(
)
(
t
e
dt
d
t
f
)
(
)
(
t
dt
d
t
)
(
1
ln
)
(
ln
)
(
t
F
t
R
t
t
x
t
t
du
u
f
dx
x
f
dx
x
R
x
f
dx
x
t
0
0
0
)
(
)
(
)
(
)
(
)
(
)
(
dla rozkładu wykładniczego:
t
t
)
(
dla rozkładu jednostajnego w przedziale od 0 do b:
t
b
b
b
t
b
b
t
t
ln
ln
1
ln
)
(
N (t)
N
e
(t)
N
u
(t)
N
o
(t)
t
Oczekiwany pozostały czas zdatności
)
/
(
)
(
t
T
t
T
E
t
r
jest to warunkowa wartość oczekiwana pozostałego czasu zdatności
t
T
pod warunkiem, że w chwili
t
obiekt jest zdatny.
Warunkowa dystrybuanta pozostałego czasu zdatności wynosi:
)
(
)
(
)
(
)
(
)
(
)
/
(
)
,
(
t
R
t
F
x
t
F
t
T
P
x
t
T
t
P
t
T
x
t
T
P
x
t
F
)
(
)
(
)
,
(
)
,
(
t
R
x
t
f
x
t
F
x
x
t
f
0
0
)
(
)
(
1
)
,
(
)
/
(
)
(
dx
x
t
f
x
t
R
dx
x
t
f
x
t
T
t
T
E
t
r
podstawiamy:
z
x
t
stąd:
t
z
x
;
dz
dx
t
dz
z
f
t
z
t
R
t
r
)
(
)
(
)
(
1
)
(
dz
du
t
z
u
)
(
)
(
z
R
v
dz
z
f
dv
t
t
t
dz
z
R
t
R
dz
z
R
z
R
t
z
t
R
t
r
)
(
)
(
1
)
(
)
(
)
(
)
(
1
)
(
t
dx
x
R
t
R
t
r
)
(
)
(
1
)
(
)
(
)
(
)
0
(
1
)
0
(
0
T
E
dx
x
R
R
r
Możemy za pomocą oczekiwanego pozostałego czasu zdatności
)
(t
r
wyrazić poznane uprzednio charakterystyki funkcyjne niezawodności:
dt
t
dr
t
r
t
)
(
1
)
(
1
)
(
)
(
)
0
(
ln
)
(
)
(
0
t
r
r
x
r
dx
t
t
t
x
r
dx
t
r
r
t
R
0
)
(
exp
)
(
)
0
(
)
(
t
x
r
dx
t
r
r
t
F
0
)
(
exp
)
(
)
0
(
1
)
(
t
x
r
dx
dt
t
dr
t
r
r
t
f
0
2
)
(
exp
)
(
1
)
(
)
0
(
)
(
Dla odpowiednio dużych wartości argumentu
t
wartość funkcji
)
(t
r
ulega niewielkim zmianom i dąży do:
)
(
1
lim
)
(
)
(
lim
)
(
)
(
lim
)
(
lim
t
t
f
t
R
t
R
dx
x
R
t
r
t
t
t
t
t
Dla rozkładu wykładniczego:
0
t
t+x
t
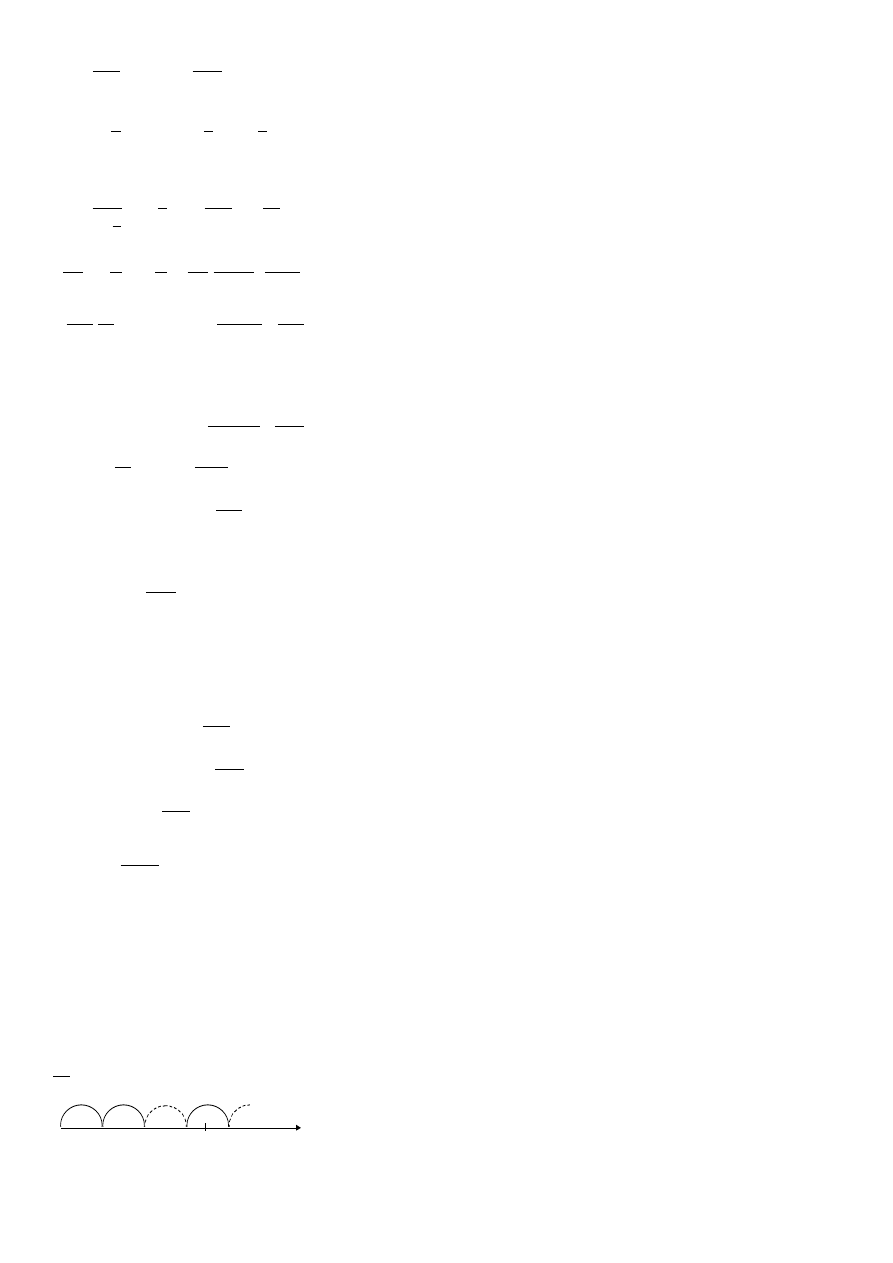
dx
e
e
dx
x
R
t
R
t
r
t
x
t
t
1
)
(
)
(
1
)
(
1
1
1
t
t
t
x
t
e
e
e
e
Dla rozkładu jednostajnego w przedziale od 0 do b:
b
t
b
t
b
x
x
t
b
b
dx
b
x
b
t
t
r
2
)
1
(
1
1
)
(
2
)
2
2
2
2
(
)
2
(
)
2
(
2
2
2
2
2
b
t
bt
b
b
b
t
b
b
b
t
t
b
b
b
t
b
b
2
)
(
2
)
(
)
2
(
2
1
2
2
2
t
b
t
b
t
b
t
bt
b
b
t
b
b
Podobnie możemy wyznaczyć oczekiwany czas zdatności
obiektu jeżeli wiadomo, że uszkodził się do chwili
t
:
)
/
(
t
T
T
E
)
(
)
(
)
(
)
(
)
/
(
)
,
(
t
F
x
F
t
T
P
x
T
P
t
T
x
T
P
x
t
F
)
(
)
(
)
,
(
)
,
(
t
F
x
f
x
t
F
x
x
t
f
t
t
dx
x
f
x
t
F
dx
x
t
f
x
t
T
T
E
0
0
)
(
)
(
1
)
,
(
)
/
(
t
t
t
t
dx
x
R
t
tR
dx
x
R
x
R
x
dx
x
f
x
0
0
0
0
)
(
)
(
)
(
)
(
)
(
t
t
tR
dx
x
R
t
F
t
T
T
E
0
)
(
)
(
)
(
1
)
/
(
)
(
)
(
)
(
)
/
(
)
0
(
t
R
t
r
t
t
F
t
T
T
E
r
t
t
t
R
t
r
dx
x
R
t
R
t
r
t
R
t
t
tR
dx
x
R
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
inaczej:
t
dx
x
R
t
R
dx
x
R
t
r
r
)
(
)
(
1
)
(
)
(
)
0
(
0
t
t
t
dx
x
R
t
R
dx
x
R
dx
x
R
)
(
)
(
1
)
(
)
(
0
t
t
dx
x
R
t
R
dx
x
R
0
)
(
)
(
1
1
)
(
t
t
t
t
r
t
F
dx
x
R
dx
x
R
t
R
t
R
dx
x
R
0
0
)
(
)
(
)
(
)
(
)
(
1
)
(
)
(
t
t
t
R
t
r
dx
x
R
t
r
t
F
t
r
dx
x
R
r
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
0
(
Niezawodność obiektów naprawialnych (odnawialnych)
Rozpatrzmy dwa przypadki:
1)
czas naprawy (odnowy) jest bardzo mały w
stosunku do czasu życia elementu.
Mówimy wówczas, że odnowa jest natychmiastowa
(czas jej trwania
0
)
2)
czas naprawy (odnowy) posiada pewną skończoną
wartość i nie jest pomijalny.
ad. 1.
Chwile uszkodzeń (odnowień) obiektu są następujące:
1
1
T
t
2
1
2
T
T
t
T
1
T
2
T
n+ 1
t
1
t
2
t
n
t
n+ 1
0
t
t

3
2
1
3
T
T
T
t
n
n
T
T
T
t
........
2
1
1
2
1
1
.........
n
n
n
T
T
T
T
t
Chwile uszkodzeń (odnowień) przedstawiają
strumień losowy,
który nazywamy strumieniem odnowy.
Zakładamy, że:
1) proces taki powtarza się nieograniczenie,
2)
.....
,
,
2
1
T
T
są zmiennymi losowymi niezależnymi o
takim samym rozkładzie prawdopodobieństwa
określonym dystrybuantą
)
(
)
(
t
T
P
t
F
n
)
(T
E
)
(
2
T
D
dla wszystkich
n
T
są jednakowe i wynoszą:
dt
t
F
T
E
0
)
(
1
)
(
2
0
2
)
(
)
(
1
2
)
(
T
E
dt
t
F
t
T
D
Niech
)
(t
N
będzie zmienną losową określającą liczbę
uszkodzeń (odnowień) powstałych do chwili
t
.
Zdarzenie
n
t
N
)
(
jest równoważne zdarzeniu
t
t
n
)
(
)
......
(
)
(
)
(
2
1
t
F
t
T
T
T
P
t
t
P
n
t
N
P
n
n
n
Dystrybuantę
)
(t
F
n
można wyznaczyć dla dowolnego
n
:
n=2
t
dF
t
T
P
T
t
T
P
t
T
T
P
t
F
0
1
2
1
2
1
2
)
(
)
(
)
(
)
(
)
(
t
dF
t
F
0
1
)
(
)
(
n=3
)
(
)
(
)
(
3
2
1
3
2
1
3
T
t
T
T
P
t
T
T
T
P
t
F
t
t
dF
t
F
dF
t
T
T
P
0
2
0
2
1
)
(
)
(
)
(
)
(
uogólniając
t
n
n
dF
t
F
t
F
0
1
)
(
)
(
)
(
)
(
)
(
1
t
F
t
F
Wyznaczamy
n
t
N
P
)
(
P
1
)
(
)
(
)
(
n
t
N
n
t
N
P
n
t
N
zdarzenie
n
t
N
)
(
jest równoważne
t
t
n
zdarzenie
1
)
(
n
t
N
jest równoważne
t
t
n
1
)
(
)
(
)
(
)
(
1
1
t
t
t
t
P
t
t
P
t
t
P
n
t
N
P
n
n
n
n
)
(
)
(
)
(
1
t
F
t
F
n
t
N
P
n
n
Nie wystarczy wiedzieć jakie jest prawdopodobieństwo wystąpienia
n
uszkodzeń (odnowień).
Równie ważną informacją jest oczekiwana liczba tych zdarzeń
)
(t
N
E
.
Wielkość ta jest funkcją czasu określoną dla
0
t
oznaczaną
)
(t
H
i nazywaną funkcją odnowy (naprawy).
1
1
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
t
F
t
F
n
n
t
N
P
n
t
N
E
t
H
)
(
)
1
(
)
(
)
(
)
(
2
1
1
1
1
t
F
n
t
F
n
t
F
n
t
F
n
n
n
n
n
n
n
n
n
1
2
2
2
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
n
n
n
n
t
F
t
F
t
F
n
t
F
n
t
F

)
(
)
(
1
t
F
t
H
n
n
W praktyce często posługujemy się pochodna funkcji
odnowy i nazywamy ja gęstością odnowy.
1
1
1
)
(
)
(
)
(
)
(
)
(
n
n
n
n
n
n
t
f
dt
t
dF
t
F
dt
d
dt
t
dH
t
h
Funkcję odnowy można wyznaczyć inaczej:
1
1
1
1
)
(
)
(
)
(
)
(
n
n
n
n
t
F
t
F
t
F
t
H
ale
)
(
)
(
1
t
F
t
F
i
)
(
)
(
)
(
0
1
dF
t
F
t
F
t
n
n
1
0
1 0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
n
n
t
n
t
n
dF
t
F
t
F
dF
t
F
t
F
t
H
)
(
)
(
1
)
(
)
(
)
(
0
0
dF
t
H
dF
t
H
t
F
t
t
)
(t
H
spełnia powyższe równanie całkowe. Równanie to nosi nazwę
równania odnowy (odnowienia).
Funkcję
)
(t
H
wykorzystuje się do wyznaczenia oczekiwanej liczby
uszkodzeń w dowolnym przedziale czasu
2
1
t
,
t
, wynosi ona
)
(
)
(
1
2
t
H
t
H
.
Przy pomocy
)
(t
H
można wyznaczyć wariancję liczby uszkodzeń (odnów)
w przedziale
t
,
0
t
t
H
t
H
dF
t
H
t
N
D
0
2
2
)
(
)
(
)
(
)
(
2
)
(
Badając proces odnowy przy
t
korzysta się z następujących twierdzeń:
Twierdzenie 1 (elementarne twierdzenie odnowy).
Jeżeli czas życia obiektu jest zmienną losową o dystrybuancie
)
(t
F
i skończonej wartości oczekiwanej
)
(T
E
, to
)
(
1
)
(
lim
T
E
t
t
H
t
Oznacza to, że oczekiwana liczba odnowień w jednostce
czasu dąży do odwrotności średniego czasu życia obiektu,
czyli średni odstęp miedzy
uszkodzeniami jest równy średniemu czasowi życia obiektu.
Twierdzenie 2 (Blackwella)
Jeśli czas życia obiektu jest zmienną losowa typu ciągłego
o skończonej wartości oczekiwanej
)
(T
E
to dla
0
zachodzi:
)
(
)
(
)
(
lim
T
E
t
H
t
H
t
Oznacza to, ze po upływie długiego czasu liczba uszkodzeń
w przedziale o długości
zależy tylko od długości
przedziału i średniego czasu życia obiektu.
Twierdzenie 3 (Smitha)
Jeżeli czas życia obiektu jest zmienną losową o skończonej
wartości oczekiwanej
)
(T
E
oraz wariancji
)
(
2
T
D
, to
2
1
)
(
2
)
(
)
(
)
(
lim
2
2
T
E
T
D
T
E
t
t
H
t
stąd wzór przybliżony:
2
1
)
T
(
E
2
)
T
(
D
)
T
(
E
t
)
t
(
H
2
2

Proces odnowy o skończonym czasie odnowy (naprawy)
Zmienne
,
,
2
1
T
T
......
oraz
,
,
2
1
U
U
.....
są zmiennymi losowymi niezależnymi o rozkładach odpowiednio:
)
(
)
(
t
T
P
t
F
n
)
(
)
(
t
U
P
t
G
n
Utwórzmy zmienną losową
1
1
n
n
n
U
T
T
gdzie:
n
n
T
T
T
T
.....
2
1
1
n
n
U
U
U
U
.....
2
1
1
t
n
n
n
dF
t
F
t
F
t
T
P
0
1
1
)
(
)
(
)
(
)
(
)
(
)
(
1
t
F
t
F
t
n
n
n
dG
t
G
t
G
t
U
P
0
1
1
)
(
)
(
)
(
)
(
)
(
)
(
1
t
G
t
G
t
n
n
n
n
dG
t
F
t
t
T
P
0
)
(
)
(
)
(
)
(
1
1 0
)
(
)
(
)
(
)
(
n
n
t
n
n
n
dG
t
F
t
t
H
1
)
(
)
(
n
n
t
t
h
gdzie:
dt
t
d
t
n
n
)
(
)
(
WYMIANA W USTALONYM WIEKU
)
(
)
(
)
(
nw
t
R
w
R
t
P
n
w
w
n
t
nw
)
1
(
gdzie:
)
(t
P
w
- prawdopodobieństwo, że obiekt wymieniany
profilaktycznie w ustalonym czasie (co stały okres w) nie uszkodzi się do chwili t,
)
( w
R
n
- prawdopodobieństwo, że obiekt nie uszkodzi się w kolejnych
przedziałach czasu o długości w,
)
(
nw
t
R
- prawdopodobieństwo, że obiekt nie uszkodzi się
w przedziale
)
,
(
t
nw
;
w
n
t
)
1
(
0
0
)
(
)
(
)
(
)
(
dt
nw
t
R
w
R
dt
t
P
T
E
n
w
w
)
(
w
T
E
- oczekiwany czas do uszkodzenia obiektu;
w
w
w
w
w
n
dt
w
t
R
w
R
dt
w
t
R
w
R
dt
t
R
dt
nw
t
R
w
R
2
3
2
2
0
0
)
2
(
)
(
)
(
)
(
)
(
)
(
)
(
0
)
1
(
)
(
)
(
)
(
)
(
..........
n
w
n
nw
n
nw
n
dt
nw
t
R
w
R
dt
nw
t
R
w
R
T
1
T
2
T
n
U
1
U
2
U
n
0
t
0
nw
w
(n+1)w
2w
t
t
3w

podstawiamy: t - nw = x
dt = dx
dla t = nw→x = 0
t = (n+1)w→x = w
0
0 0
)
1
(
)
(
)
(
)
(
)
(
n
n
w
n
n
w
n
nw
dx
x
R
w
R
dt
nw
t
R
w
R
)
(
)
(
)
(
)
(
0
0
0
0
w
R
dx
x
R
dx
x
R
w
R
w
w
n
n
n
n
w
w
R
dx
x
R
0
)
(
1
1
)
(
gdyż:
x
x
n
n
1
1
0
dla x<1
w
w
dx
x
R
w
R
T
E
0
)
(
)
(
1
1
)
(
)
(
)
(
)
(
)
(
u
T
E
w
F
b
w
R
a
w
C
C(w) – jednostkowy koszt utrzymania obiektu
a – koszt wymiany profilaktycznej
b – koszt naprawy
Zakładamy, że a < b
E(T
u
) – oczekiwany czas użytkowania obiektu (do uszkodzenia
lub wymiany)
)
(
)
/
(
)
(
)
(
w
F
w
T
T
E
w
R
w
T
E
u
w
w
dx
x
f
x
w
F
dx
w
F
x
f
x
w
T
T
E
0
0
)
(
)
(
1
)
(
)
(
)
/
(
w
w
u
dx
x
R
dx
x
f
x
w
R
w
T
E
0
0
)
(
)
(
)
(
)
(
w
w
dx
x
R
b
w
R
b
a
dx
x
R
w
F
b
w
R
a
w
C
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0
)
(
)
(
)
(
)
(
)
(
)
(
'
)
(
)
(
2
0
0
w
w
dx
x
R
w
R
b
w
R
b
a
dx
x
R
w
R
b
a
dw
w
dC
)
(
)
(
)
(
)
(
)
(
'
)
(
0
w
R
b
w
R
b
a
dx
x
R
w
R
b
a
w
w
b
w
R
b
a
dx
x
R
w
R
w
R
a
b
0
)
(
)
(
)
(
)
(
)
(
'
)
(
w
a
b
b
w
R
dx
x
R
w
0
)
(
)
(
)
(
w
a
b
b
w
R
dx
x
R
w
0
)
(
)
(
)
(
a
b
b
w
R
dx
x
R
dx
x
R
w
w
)
(
)
(
)
(
)
(
0
1.
Rozpatrzmy obiekt techniczny składający się z n elementów składowych.
2.
Załóżmy, że elementy są jednakowe w sensie ich niezawodności
3.
Struktura niezawodnościowa obiektu jest szeregowa.
Funkcja niezawodności obiektu do chwili wykonania naprawy
)
(
1
x
R
jest opisana zależnością:
n
e
x
R
x
R
1
gdzie:
)
( x
R
e
- funkcja niezawodności elementu
Jeżeli naprawa wykonana w chwili t polegała na wymianie k spośród n
elementów składowych to funkcja niezawodności obiektu po naprawie
)
(
2
x
R
wynosi:
k
n
e
e
k
e
t
R
x
t
R
x
R
x
R
2
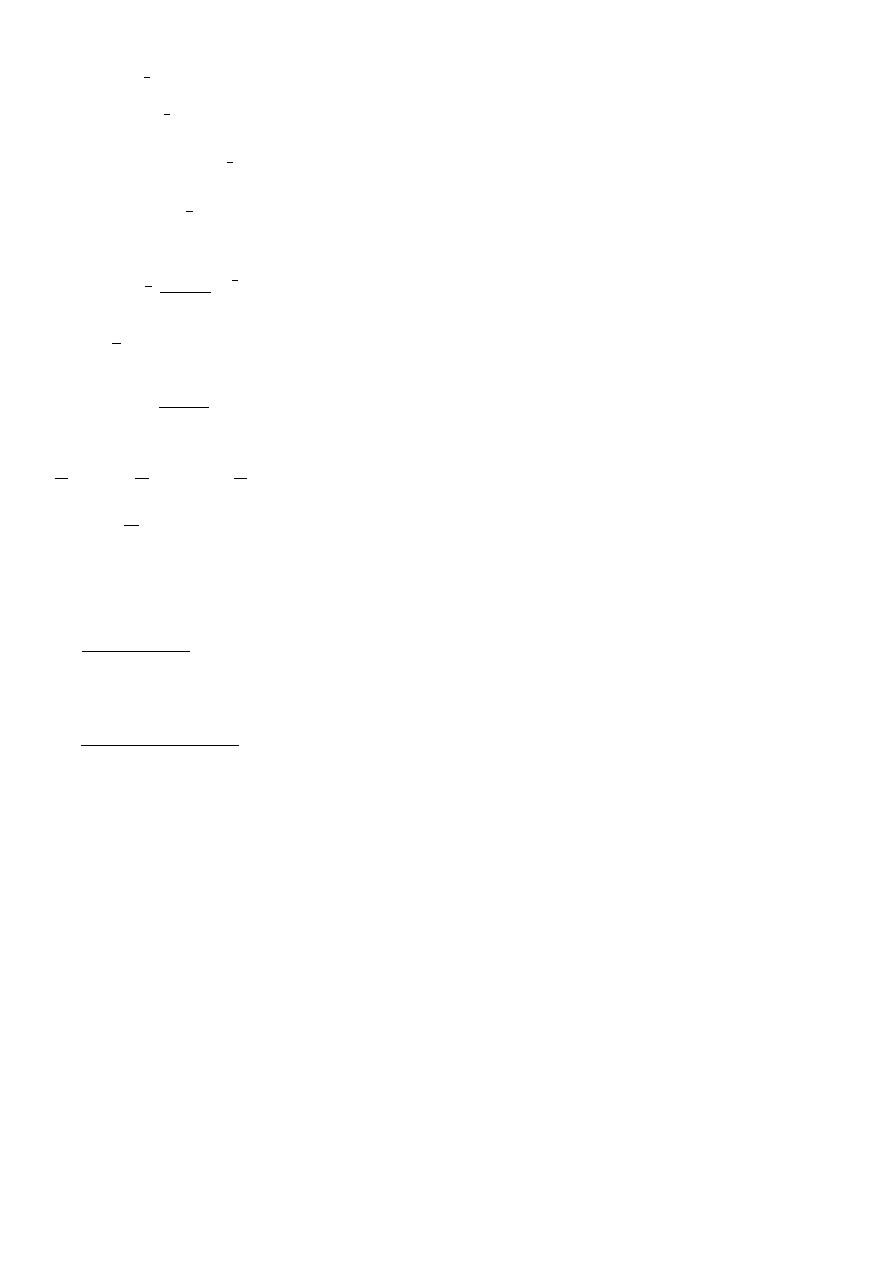
Z wzoru określającego
)
(
1
x
R
wynikają następujące zależności:
n
e
x
R
x
R
1
1
n
k
k
e
x
R
x
R
1
n
k
k
n
e
x
t
R
x
t
R
1
1
n
k
k
n
e
t
R
t
R
1
1
Po podstawieniu do zależności wyrażającej
)
(
2
x
R
otrzymujemy:
n
k
n
k
t
R
x
t
R
x
R
x
R
1
1
1
1
2
Jeżeli stosunek
n
k
potraktujemy jako stopień odnowienia
obiektu (stopień naprawy), to:
1
1
1
1
2
t
R
x
t
R
x
R
x
R
Logarytmując i następnie różniczkując stronami otrzymujemy:
x
t
R
dx
d
α)
(1
x
R
dx
d
α
x
R
dx
d
1
1
2
ln
ln
ln
i podstawiając
x
x
R
dx
d
)
(
ln
otrzymujemy zależność wyrażająca związek między funkcjami
intensywności uszkodzeń
x
2
i
x
1
:
x
t
x
x
1
1
2
)
1
(
czyli
x
x
t
x
x
t
1
1
2
1
Można też współczynnik
przedstawić z wykorzystaniem
funkcji wiodących rozkładów
x
t
x
t
x
t
x
t
1
1
1
2
1
1
)
(
)
(
gdzie:
x
du
u
x
0
)
(
)
(
Wyszukiwarka
Podobne podstrony:
MATERIALY DO WYKLADU CZ IV id Nieznany
MATERIALY DO WYKLADU CZ III id Nieznany
EKON Zast Mat Wyklad 11 12 id Nieznany
PETy, wyklad kolos 1, DRUK id 355133
Chemia wyklady 2007 2008(1) id Nieznany
AP wyklady wersja pelniejsza id Nieznany (2)
LOGIKA WYKLAD ZBIORY RELACJE id Nieznany
OZiRN sciaga zajebista mini id Nieznany
4Chemia (wyklady) 5 01 2008 id Nieznany
MATERIALY DO WYKLADU CZ IV id Nieznany
Kolokwium wyklad do kola id 736 Nieznany
kolokwium probne boleslawiec id Nieznany
Badania operacyjne wyklad 2 id Nieznany
historia gospodarcza wyklady id Nieznany
Anatomia Kolokwium I p4 id 6275 Nieznany
Anatomia Kolokwium I p6 id 6275 Nieznany (2)
MATERIALY DO WYKLADU CZ V id 2 Nieznany
więcej podobnych podstron