Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

1

Wykład 11 -12. Funkcje pierwotne. Całki

Literatura: R.Leitner. ” Zarys matematyki wyższej”, Tom II

M. Dędys. SGH. Materiały dydaktyczne.

Rozważmy funkcję f: X Zakładamy tutaj, że X jest przedziałem
otwartym ograniczonym lub nieograniczonym.

W poprzednich wykładach poszukiwaliśmy pochodnej funkcji f. W
tym wykładzie „odwracamy” problem. Poszukiwać będziemy takiej
funkcji F, której pochodną jest funkcja f. Stąd bierze się określenie: F
jest funkcją pierwotna funkcji f. Następująca definicja precyzuje
pojecie funkcji pierwotnej

I. FUNKCJA PIERWOTNA

Definicja 1. Funkcja pierwotna.
Mówimy, że F jest funkcją pierwotną funkcji f jeśli dla każdego
x

wartość pochodnej funkcji F jest równa wartości f, tzn.

F

, dla każdego x

Wniosek z definicji.
a) Jeżeli F jest funkcją pierwotną dla f, to każda funkcja G postaci
G(x)=F(x)+c, gdzie c jest dowolną stałą, jest także funkcją pierwotną
f. Mamy bowiem G

(x) = (F(x)+c) = F f(x) dla każdego x

Komentarz. Można wykazać, że jeśli F jest funkcją pierwotną
funkcji f, to rodzina funkcji {F+c : c – dowolna stała} obejmuje
wszystkie funkcje pierwotne funkcji f.

Definicja 2. Całka nieoznaczona
Jeżeli F jest funkcją pierwotną funkcji f w przedziale X, to wyrażenie

F(x) + c dla x

nazywamy całką nieoznaczoną funkcji f w przedziale X i zapisujemy
symbolem

( czytamy: całka f od x dx). Mamy więc

F(x) + c dla x ,

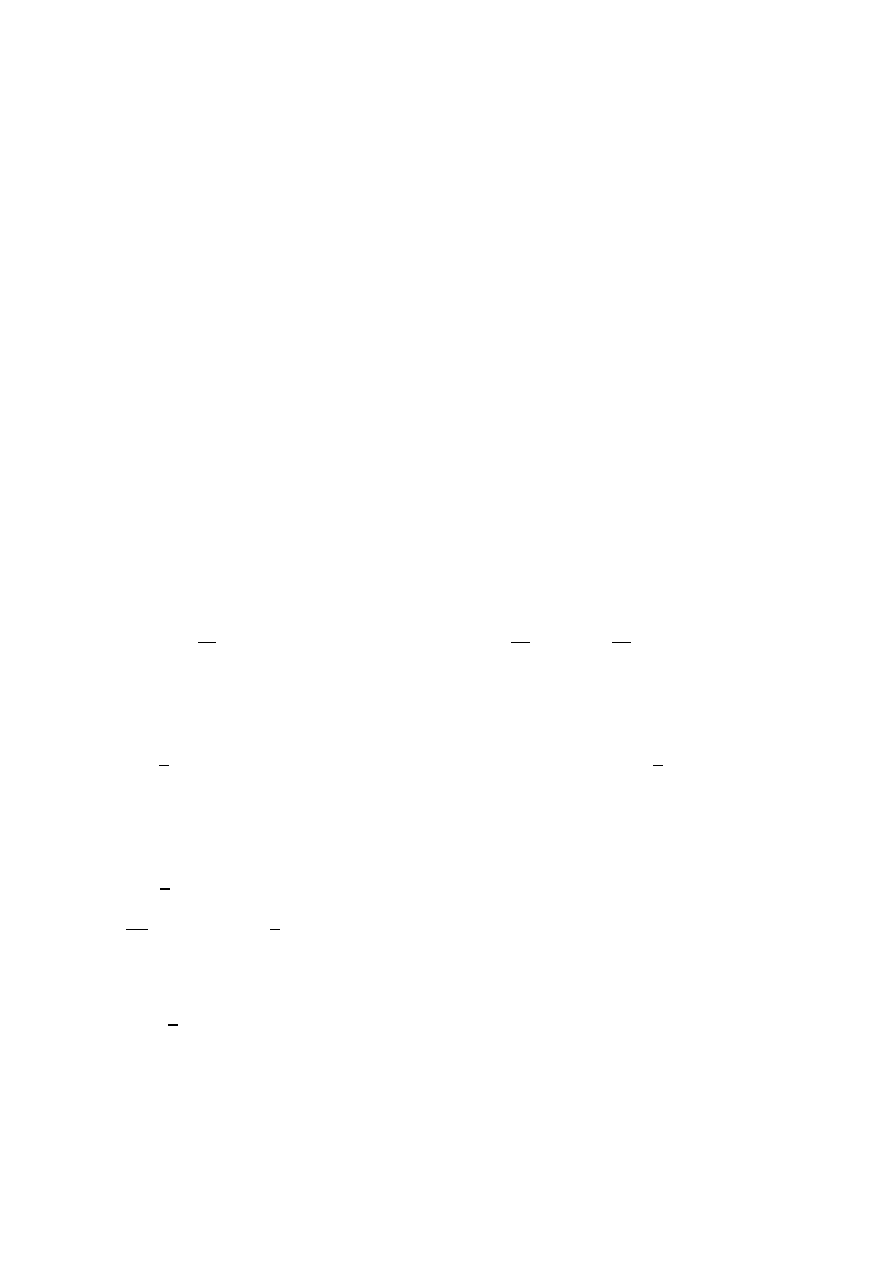
Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

2

Innymi słowy całka nieoznaczona funkcji f, jest dowolną funkcją
pierwotną funkcji podcałkowej f.
Przyjęło się bowiem nazewnictwo: f- funkcja podcałkowa, x-
zmienna całkowania, f(x)dx- wyrażenie podcałkowe, c-stała
całkowania, symbol dx nazywa się różniczką.

Wyznaczenie całki nieoznaczonej funkcji f polega na
odgadnięciu takiej funkcji, której pochodna jest równa funkcji
podcałkowej.


Przykład.1. Wyznaczyć całkę nieoznaczoną funkcji
podcałkowej f(x) gdy

a) f

(x) = x, b) f(x) = 1/x dla x > 0

Ad a)

=

+ c dla x

R, ponieważ (

Ad b)

(i)

= ln x + c dla x > 0, ponieważ (ln x + c) =

.

Zauważmy, że dla x < 0 prawdziwa jest równość

(ii)

= ln( x) + c dla x < 0, ponieważ (ln( x) + c)

=

=

,

zatem obie równości (i) oraz (ii) zapiszemy jednym wzorem:

ln(|x|) +c dla x przy czym c oznacza tu dowolną

stałą w przypadku x >0 oraz dowolną stała w przypadku x< 0.

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

3

I 2. Podstawowe wzory całkowania
( Poniższe wzory są prawdziwe w przedziałach, w których funkcja
podcałkowa jest ciągła. Sprawdzenie poprawności wzorów
zostawiamy jako ćwiczenie).

Zestaw podstawowych funkcji pierwotnych

1.

= c; = x+c

2.

p

3.

ln(|x|) +c dla x 0

4.

5.

6.

= cos x + c

7.

= sin x + c

8.

= ln |cos x| + c

9.

= ln |sin x| + c

10.

11.

Uwaga. Symbol całki nieoznaczonej składa się ze znaku całki:

i ze znaku różniczki: dx. Znak różniczki informuje: która ze
zmiennych jest zmienną całkowania. Czasami bez różniczki jest
trudno to rozpoznać

Przykład 2.

, ponieważ

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

4

, ponieważ

=

=

=

(

W rachunku wykorzystano tożsamość

).

Przykłady:

3.

=

)dx=

dx =

(por. wzór 11)

4.

= x

3

+c bo (x

3

+c)

=3 x

2

Twierdzenie 1.
Jeżeli funkcje f i g mają funkcje pierwotne w przedziale X , to suma

f+g oraz iloczyn a

f, a , a też mają funkcje pierwotne w

tym przedziale przy czym

(i)

dla x oraz

Uwaga. Każda całka nieoznaczona jest sumą funkcji
pierwotnej + stała. W równości (i) mamy zatem 3 stałe i 3
funkcje pierwotne. Przyjął się zapis:
+c
gdzie c jest zależna od wszystkich 3 stałych i 3 funkcji
pierwotnych. Ta uwaga dotyczy wszystkich równości między
funkcjami pierwotnymi.

Twierdzenie 2. Jeżeli

funkcja f jest ciągła

w przedziale X, to

f

posiada funkcję pierwotną

w tym przedziale.

(Dowód pomijamy).

Uwaga. Jeżeli we wzorze na całkę nieoznaczoną nie podaje
się przedziału , to należy rozumieć, że wzór ten jest

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

5

prawdziwy w każdym przedziale otwartym, w którym funkcja
podcałkowa jest ciągła.

Przykład (całkowanie sumy)
5.

=

=

dx = x+ln|x|+c

Przykład (wyłączanie mnożnika)

6.

= a +b = a

+ bx + c



W niektórych przypadkach ułatwieniem w obliczaniu
całki są przytoczone niżej twierdzenia o całkowaniu
przez części i o całkowaniu przez podstawienie.

Twierdzenie3. (O całkowaniu przez części)
Jeżeli funkcje u i v mają ciągłe pochodne w przedziale X, to

= u(x)v(x) – (*)

w skrócie

= uv –

Uzasadnienie wzoru. Wynik uzyskuje się ze wzoru na
pochodną iloczynu : (uv) =

Komentarz. Jeśli chcemy skorzystać ze wzoru (*) przy
całkowaniu funkcji f(x) to musimy przedstawić f w postaci
uv

. Funkcje u i v należy tak dobrać abyśmy byli w stanie

obliczyć całki v =

oraz .

7. Zestaw przykładów.(Całkowanie przez części)

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

6

a)

=

x sinx

∫sinxdx = xsinx+cosx+c

b)

= xln x

= xln x –x + c

c)

=

=

(**)

Potraktujmy

jako niewiadomą. Z (**) wynika, że

2

=

,

stąd

=

.

Tym razem podamy, w poniższym twierdzeniu, wzór ułatwiający
liczenie całki, który jest związany z różniczkowaniem funkcji
złożonej. Przypominamy (przy odpowiednich założeniach) pochodna
funkcji złożonej dana jest wzorem : [F(g(x))] = F

Twierdzenie 3. (O całkowaniu przez podstawienie)
Jeżeli funkcja g ma w przedziale X pochodną g (x), zaś

funkcja f ma w przedziale g(X) (g(X) obraz X przy

przekształceniu g) funkcję pierwotną F, to

= F(g(x)) + c (**)

w przedziale X

Uwaga. Ze względu na to, że F jest funkcją pierwotną funkcji
f, to z definicji

, a zatem wzór (**) przybiera

wykorzystywaną w obliczeniach postać:

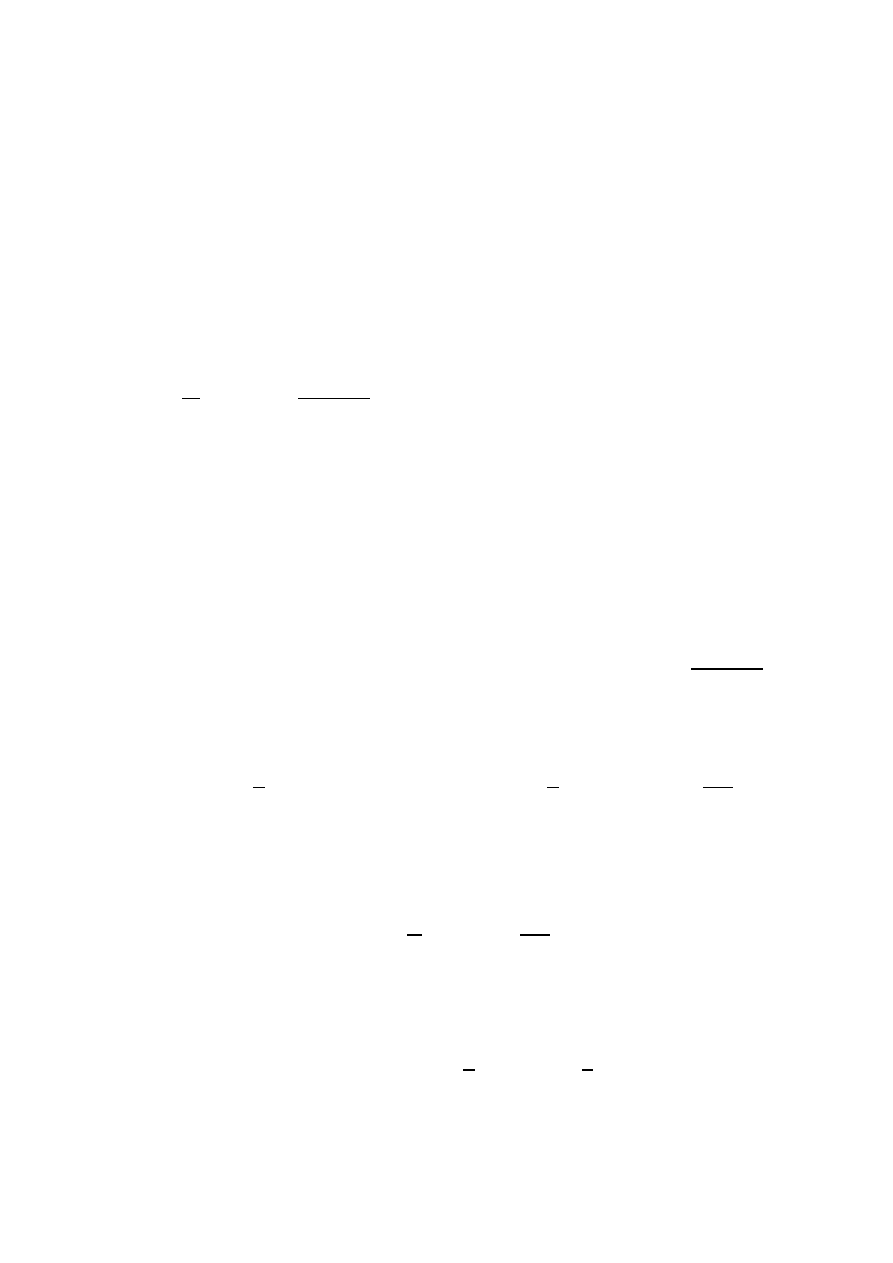
Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

7

gdzie t = g(x) (***)

tzn. obliczmy całkę i podstawiamy t = g(x).
Przykład 8. Przyjmijmy : f( t) =

, g(x) =

zatem

= 2x.

Wykorzystując wzór (***) mamy

=

=

=

=

=

+ c

W praktycznych zagadnieniach zadanie postawione jest
inaczej. W funkcjach podcałkowych należy odszukać (jeśli
to możliwe) funkcje typu f, g i

i zastosować wzór (***).

Przyjęło się więc powyższą całkę, z dodatkowymi
komentarzami w nawiasach „{}”, wyznaczać następująco:

=

=

Przykłady c.d.

9.

=

=

=

+c

W skrócie technicznym rozwiązanie to przebiega w
następujący sposób:

=

=

=

+c

Następne rozwiązania podajemy już w skrócie technicznym.

10.

=

=

=

+ c

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

8

11.

=

+c

12.

=

=

=

Uwaga. Jeżeli w funkcji podcałkowej licznik jest pochodną
mianownika, to funkcją pierwotną jest logarytm modułu
mianownika.

13.

=

=

=ln|sin x| + c

Przykłady do samodzielnych ćwiczeń.
I .Całkowanie przez podstawienie

14.

15.

16.

17.

II. Całkowanie przez części

18.

19.

=

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

9

20.

dx =

dx =

=

+ c

II. Całka oznaczona



Przypominamy , że ciągłość funkcji w przedziale
domkniętym [a,b]oznacza ciągłość w każdym
punkcie przedziału (a,b) i istnienie granic
jednostronnych równych wartościom funkcji w
odpowiednich krańcach .

II1. Pojecie całki oznaczonej
Definicja.

Rozważmy funkcję f, która jest ciągła w

przedziale [a,b]. Całką oznaczoną funkcji f w przedziale [a,b]
nazywamy liczbę

= F(b)

F(a)

gdzie F jest funkcją pierwotną funkcji f w [a,b]

Komentarz (Nazewnictwo)
Przedział [a,b] nazywa się przedziałem całkowania
Początek przedziału, punkt a, nazywa się dolną granicą
całkowania.
Koniec przedziału, punkt b, nazywa się górną granicą
całkowania.
W obliczeniach przyjęło się następujące oznaczenie:

F(a) F(b)

21. Zestaw przykładów

a)

=[

=

=

b)

= [

=0

( 1)=1

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

10

W b) wykorzystaliśmy funkcje pierwotną z Przykładu 20.

II2. Własności całki oznaczonej
Twierdzenie 4. Jeśli funkcje f i g są ciągłe w [a,b], to

a)

dla a

b)

c)

dla dowolnego

c

Własności a) i b) są takie jak dla całki nieoznaczonej.
Zwróćmy uwagę na własność c), która wskazuje na to, że
można liczyć całkę na podprzedziałach” rozbijających”
przedział całkowania.
22. Przykład

=

+2

=

+4+12

II. Interpretacja geometryczna całki oznaczonej

Rozważmy funkcję f(x)=2 dla x

(0,1).

Rys.1.Pole zaznaczonego prostokąta wynosi 2

Zauważmy, że wartość całki w granicach od 0 do 1 przy
funkcji podcałkowej f(x)=2, x jest polem zakreślonego
prostokąta.

0 1

x

2

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

11

Mamy bowiem:

=

=[2x

=2



Pole prostokąta umiemy liczyć bez odwoływania się do
całki. Okazuje się jednak, że za pomocą całki oznaczonej
potrafimy określić pole znacznie bardziej złożonych
figur.

Można udowodnić, że jeżeli f(x) jest nieujemną funkcją
ciągłą określoną w przedziale [a,b], to pole figury K gdzie

K=

(x,y): a 0

wyraża się całką oznaczoną:

y

K
x
a b

Rys.2 Pole K=

23. Zestaw przykładów
a) Oblicz pole figury: K= {(x,y): -1

x 0

}

-1 2

Rys.3. Malo dokładny szkic K. Pole K=

f(x)

Zastosowania matematyki w ekonomii 2014. Wykład 11-12. R.Rempała

12

=[

=

=

=3

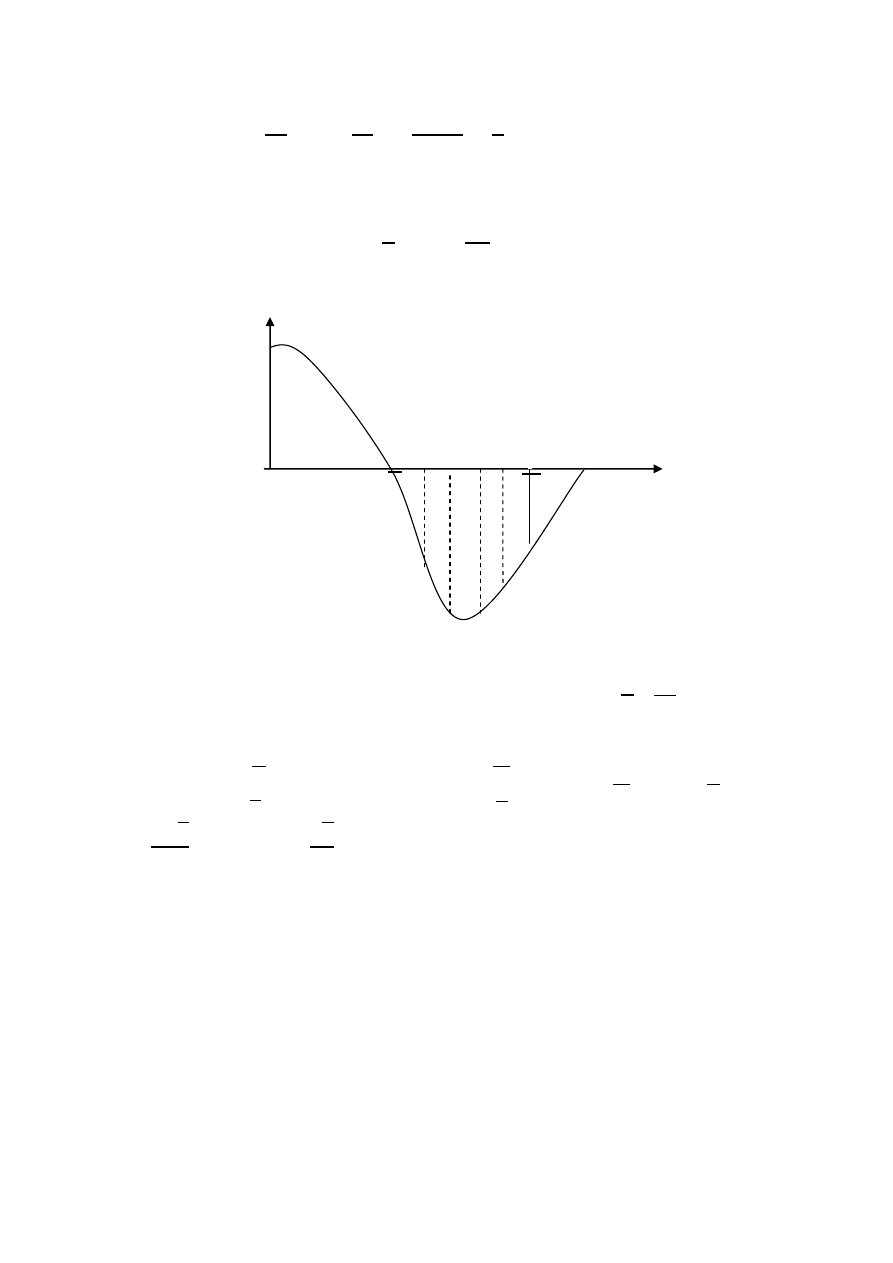
b) Obliczyć pole figury ograniczonej wykresem f(x)=cos x,
osią 0x, oraz prostymi x=

i x=

0

K

Rys.4. Mało dokładny szkic K.

Funkcja f(x)=cos x jest ujemna w przedziale [

,

, zatem

Pole K=

=

[sinx

=

=

[

= 1 +

.