Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

1

Wykłady 1-2a. Macierze i wektory

I. Macierz. Działania na macierzach

Definicja. Macierz o wymiarach m , gdzie m oraz n są ustalonymi
liczbami rzeczywistymi, to prostokątna tablica liczb złożona z m
wierszy i n kolumn.

1. Przykłady macierzy

,

,

Macierz zerowa dowolnych wymiarów zawsze jest oznaczana przez
zero, np.

Z kontekstu będzie wynikało czy chodzi o liczbę zero, czy też macierz
zerową.

W wykładzie liczbę rzeczywistą będziemy nazywali także skalarem.

(i) Ogólny zapis macierzy o wymiarach , m wierszy i n kolumn

Inny zapis macierzy A:
A =

,

i=1,2,…,m; j=1,2,…,n

Liczby

; i=1,2,…,m; j=1,2,…,n nazywają się elementami (wyrazami)

macierzy A.

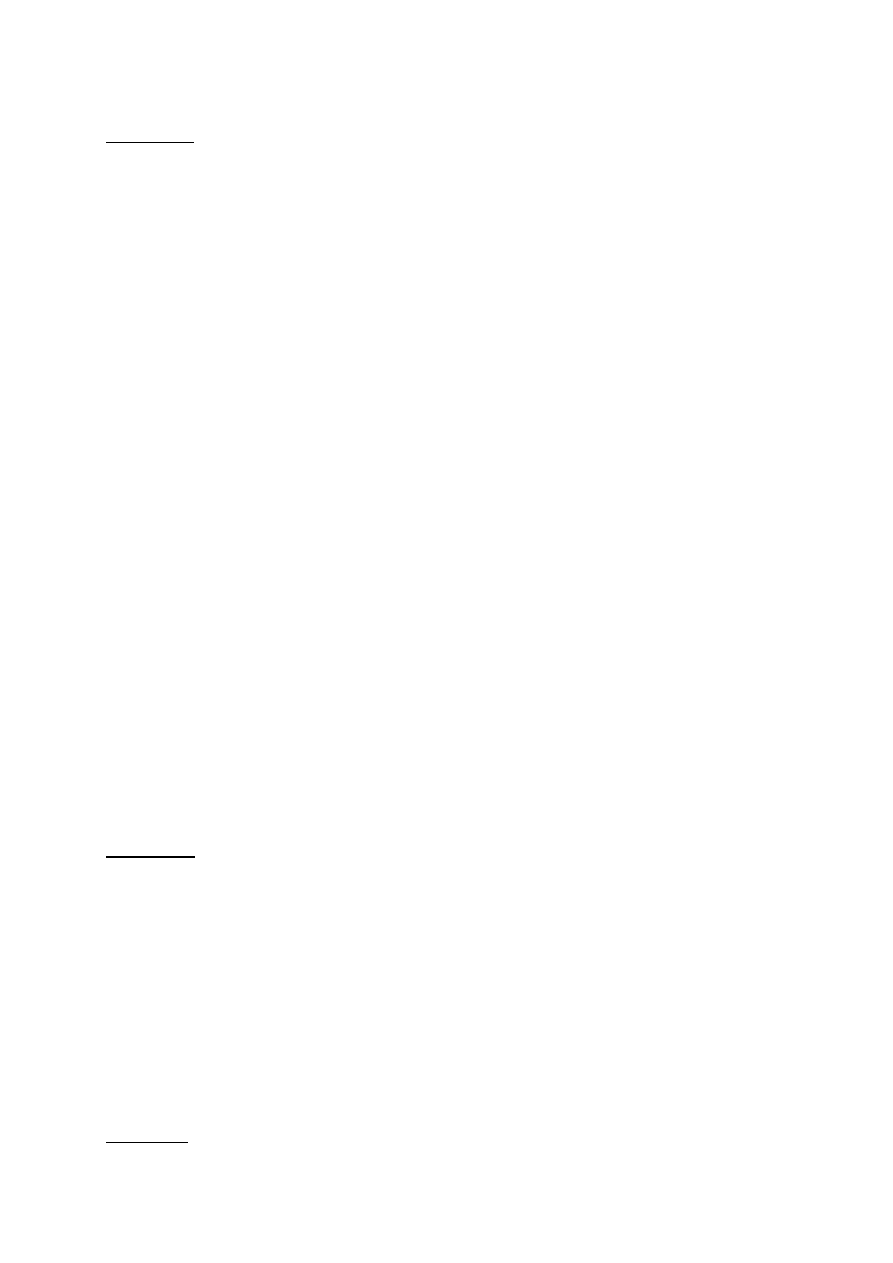
Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

2

Przykład.

, a

23

=5, a

12

= 2,5.

2. Operacje na macierzach

Zbiór wszystkich macierzy o wymiarach oznaczamy przez
M(m,n).

Zauważmy, że

M(2,3)

(i) Dodawanie . Dodawad możemy tylko takie macierze, które mają
ten sam wymiar (obie należą do tego samego zbioru M(m,n)).

Niech A M(m,n), B M(m,n).

Definicja. Sumą A+B nazywamy taką macierz S M(m,n), że

Zauważmy, że dodawanie macierzy podlega prawu przemienności i
łączności. (Wynika to z faktu że dodawanie odpowiadających sobie
elementów macierzy jest dodawaniem liczb). Mamy więc

A+B=B+A

(A+B)+C = A+(B+C)

Przykład:

=

(ii) Mnożenie macierzy przez skalar
Niech A M(m,n), (R-zbiór liczb rzeczywistych)

Definicja. Iloczynem A przez liczbę (zapis nazywamy macierz
C M(m,n) o elementach

, i = 1,2, ; j =1,2, .

Przykład: 2

=

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

3

Zauważmy, że z definicji wynikają już następujące własności

(iii) Iloczyn macierzy.
Iloczyn macierzy A i B ma sens jeśli A ma tyle samo kolumn co B
wierszy. Zatem niech A M(m,r), B M(r,n).

Definicja. Iloczynem AB macierzy A przez macierz B nazywamy taką
macierz C=

M(m,n), że

dla i=1,2,…,m, j=1,2,…,n;

w innym zapisie:

Przykład A B=

=



Zauważmy, że 15,5=

0,5=
6 = 3
11 = 3



Aby otrzymad wyraz macierzy iloczynu o wskaźniku ij należy
elementy i-tego wiersza macierzy A pomnożyd przez
odpowiednie elementy j-tej kolumny macierz B i dodad
otrzymane iloczyny.



Iloczyn dziedziczy po macierzy A liczbę wierszy, po macierzy B
liczbę kolumn.



Mnożenie przez macierz zerową zawsze daje macierz zerową.

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

4

Mnożenie macierzy ma następujące własności:
(AB)C =A(BC)
(A+B)C =AC+BC

A(B+C) =AB+AC

Uwaga . Mnożenie macierzy nie musi być przemienne, to znaczy, że
na ogół nie zachodzi równośd: AB=BA.

(Iv) Transpozycja
Niech A M(m,n), Macierzą transponowaną macierzy A jest
nazywamy macierz A

T

M(n,m), o elementach

, j=1,2,…,n,

i=1,2,…,m
Mówiąc krótko: j-ta kolumna macierzy A staje się i-tym wierszem
macierzy A

T

Przykład : weźmy

, zatem A

T

=

Własności transpozycji

(A

T

)

T

= A

(A+B)

T

= A

T

+B

T

(

T

=

T

(AB)

T

= B

T

A

T

(V) Macierz jednostkowa
Niech A M(n,n). Mówimy, że kwadratowa macierz A jest
macierzą jednostkową jeśli elementy na przekątnej

natomiast pozostałe elementy

dla i .

Przykłady

,

W dalszych rozważaniach macierz

jednostkową będziemy oznaczali przez „I”

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

5

Zauważmy, że

=

=

(VI) Iloczyn macierz przez macierz jednostkową „I”

Dla dowolnej macierzy B, mamy B I=B, I B=B, o ile odpowiednie
mnożenia są wykonalne.


(VII). Bardzo ważne pojecie, tzw. macierzy odwrotnej, wprowadzimy
w późniejszych wykładach.

II Wektory

1.Definicja i uwagi wstępne
Definicja. Macierz należąca do M(n,1)

x=

nazywa się n wymiarowym wektorem kolumnowym.

Macierz należąca do M(1,n) nazywa się n wymiarowym wektorem
wierszowy

x

T

=

W obecnych rozważaniach ograniczamy się do wektorów
kolumnowych nazywając je (prosto) wektorami.

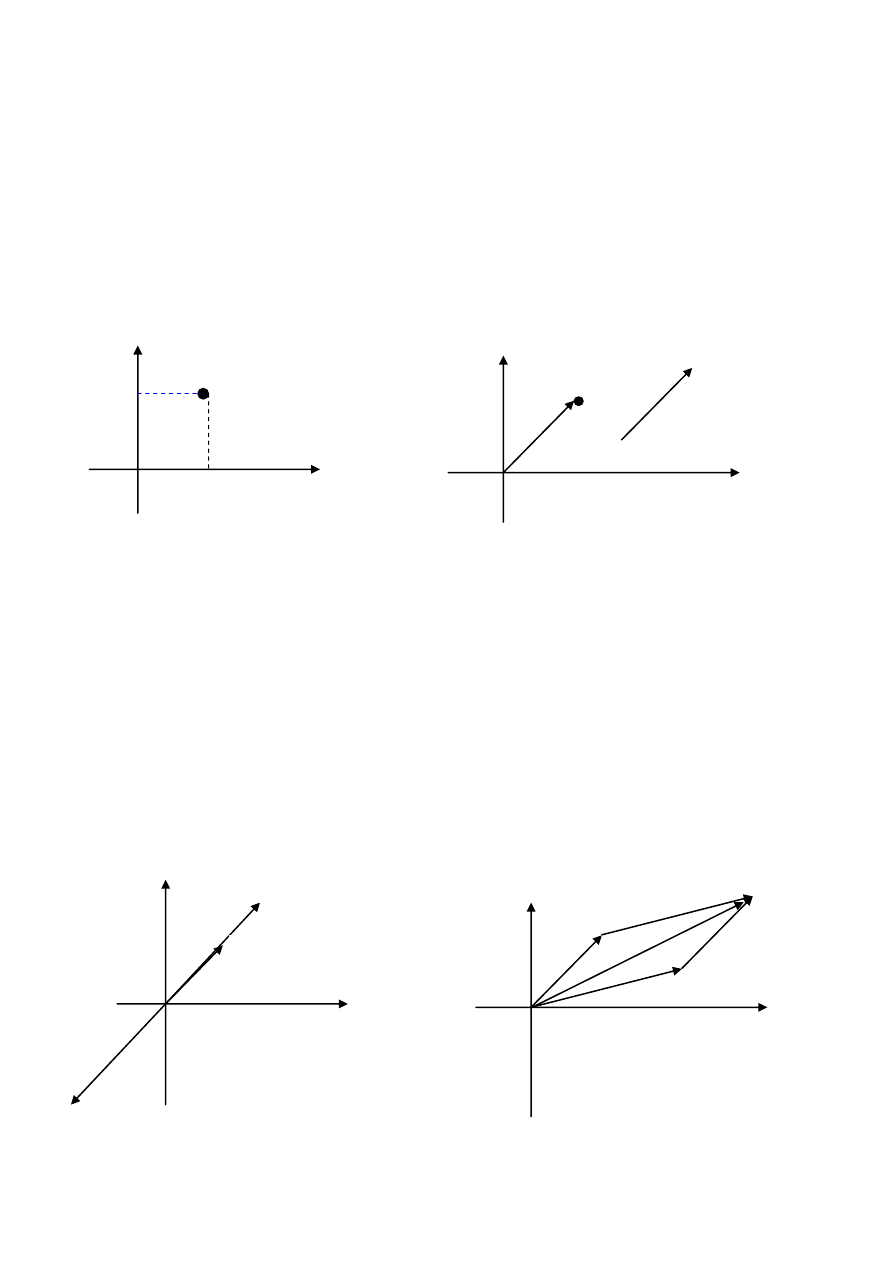
Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

6

Zauważmy, że wektor możemy utożsamiad z ciągiem n liczb. Dlatego
też zbiór wszystkich wektorów n- wymiarowych będziemy oznaczad
przez R

n

.



Na wektory można popatrzed w dwojaki sposób: a) jako
specyfikacja położenia punktu w przestrzeni R

n

, b) jako

specyfikacja przesuwania punktu z R

n

do innego punktu z R

n

.

2.Wektory w R

2

Rys. 1 Interpretacja wektora w R

2

.

R

2

X

R

2

x

2

x

2

X

X


0=(0,0) x

1

x

1

a) specyfikacja położenia, b) specyfikacja przesuwania(tzw.
wektor swobodny zaznaczony strzałką.
Współrzędne wektora wyznaczają
jednoznacznie długośd strzałki, kierunek i zwrot)

2.1 Działania na wektorach w

(Przypominamy działania na

jednokolumnowych macierzach).

Niech x

, y

,

(i) Iloczyn wektora przez liczbę

(ii) Suma wektorów x+y

Rys. 2 Interpretacja geometryczna wyników działao

y

x x+y y

0 0 b)

Wynikiem dodawania

-

a) Mnożenie wektora x przez i (-

). x+y jest wektor będący

przekątną równoległoboku

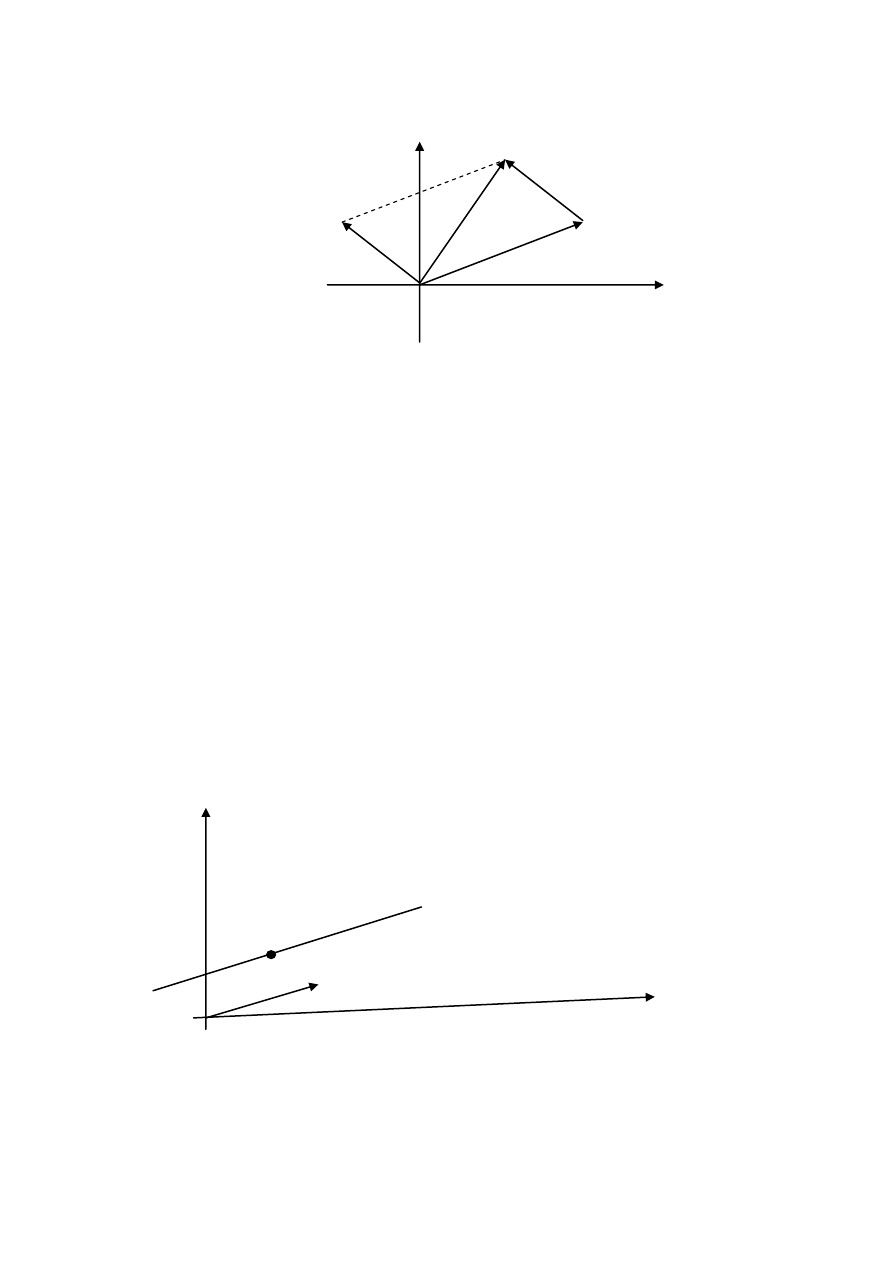
Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

7

x

x-y

y
x-y

0

Rys. 3 Wynik odejmowania x-y, to taki wektor, że y+(x-y)=x


2.2 Równanie parametryczne prostej na płaszczyźnie

Jeśli a=

potraktujemy jako punkt na płaszczyźnie, natomiast

v

jako wektor, to dla wyrażenie a + tv =

można potraktować jako punkt otrzymany przez przesuniecie punktu
a o wektor tv.


Rys.4. Dla różnych t

otrzymamy różne punkty leżące na prostej

przechodzącej przez punkt a i równoległej do wektora v. Por.Rys.2a


x

2

a

v
0 x

1

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

8

2.3. Przedstawienie parametryczne prostej przechodzącej
przez dwa punkty

Niech a=

i b=

będą dwoma różnymi punktami w

. Prosta

przechodząca przez te punkty ma kierunek wyznaczony przez wektor
b-a, por. Rys.3. Zatem jej przedstawienie parametryczne to

a+t (b-a) =

t .

2.4 Przedstawienie parametryczne odcinka

Jeżeli zakres parametru t ograniczymy do przedziału [0,1] , to
odpowiadająca temu część prostej jest odcinkiem [a,b]. Zatem

[a,b]={(1-t)a + t b: t

Przejście od parametrycznego zapisu prostej do zapisu w formie
równania ( i odwrotnie) pozostawiamy jako ćwiczenie.


3. Wektory w

.

Niech z =

, v

, .



Podobnie jak w

, można myśleć o wektorach w

jako o

specyfikacji położenia lub specyfikacji przesunięcia.



Operacje mnożenia przez skalar i dodawania wektorów są
naturalnym uogólnieniem operacji na wektorach z

Mamy:

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

9

(i) iloczyn wektora z R

n

przez liczbę jest następującym wektorem w

R

n

:

(ii) Suma wektorów z

jest następującym wektorem w

z+v

3.1. Przedstawienie parametryczne prostej i odcinka w R

n

Łatwo widać, że przedstawione własności wektorów w R

2

przenoszą

się także na przestrzenie wyższych wymiarów.



Przedstawienie parametryczne prostej o kierunku wektora

v

przechodzącej przez punkt a

, to zbiór punktów

postaci: a+tv=

, t .



Przedstawienie parametryczne prostej przechodzącej przez dwa

różne punkty a

i b

, to zbiór punktów postaci:

a+t (b-a) =

t .



Przedstawienie parametryczne odcinka [a,b], to zbiór punktów

postaci (1-t) a+t b, t

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

10

3.4 Norma wektora

Długośd strzałki reprezentującej n-wymiarowy wektor x nazywa się
jego normą albo modułem tego wektora i oznacza się ||x||. Z
twierdzenia Pitagorasa wynika, że

||x||=

W szczególności jeśli a

i b=

, to odległość miedzy a i b,

rozumianymi jako opisy położenia, ( por. Rys.3) jest równa

||b-a||=

Komentarz. Norma wektora jest liczbą wyrażającą, jak już
wspomniano, długośd strzałki przedstawiającej wektor. Pojawia się
pytanie czy można za pomocą liczb opisad kierunek strzałki?
Okazuje się , ze pomocne w tym jest pojecie iloczynu skalarnego.

3.5 Iloczyn skalarny
Jeżeli x i y są n-wymiarowymi wektorami kolumnowymi to iloczynem
skalarnym x y jest liczbą określoną następująco
x y

Wykorzystując definicję mnożenia macierzy możemy powyższy
iloczyn zapisad jako iloczyn macierzy złożonej z wiersza przez
macierz kolumnę:

x y =x

T

y= [

]



Własności iloczynu skalarnego
a) x x=||x||

2

b) x y=y x
c) x ( = (x y)+ (x ); są liczbami (skalarami).

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

11

Wykorzystując własności a)-c) mamy

(*) ||x-y||

2

= (x-y)

( x-y) = (x-y) x - (x-y) y = x (x-y) - y (x-y)

= x

x- x y - y x + y y = ||x||

2

-2

x y +||y||

2



Inny sposób obliczania długości (normy) wektora x-y, to tzw.
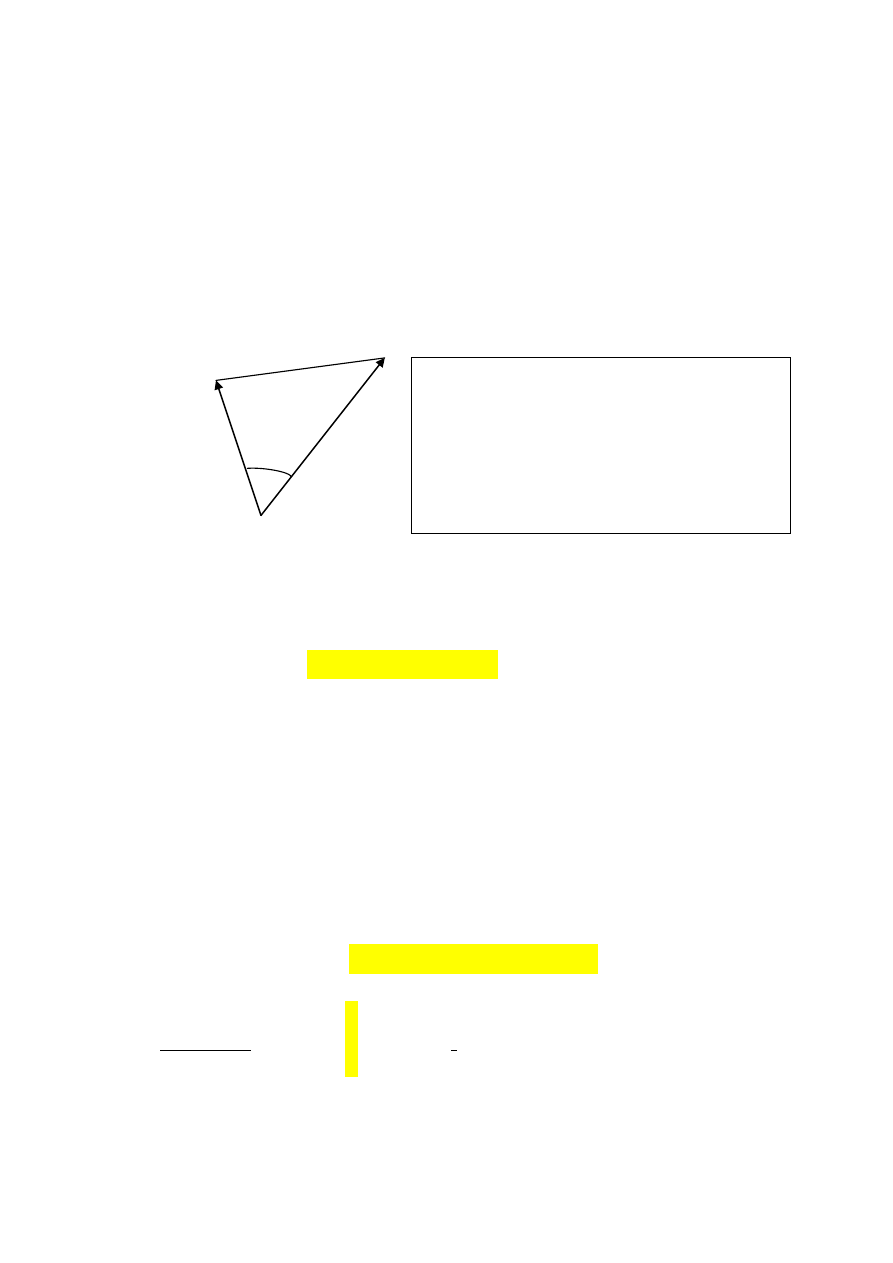
reguła kosinusów. Przypomina ją poniższy rysunek.

Rys.5. Obliczenie ||x-y|| za pomocą reguły cosinusów:
||x-y|| y
x

||x|| ||y||



Porównując wzór na wielkość ||x-y||

2

wynikający z reguły

kosinusów (*) mamy

(**) x y =||x|| ||y||cos(

Otrzymaliśmy w ten sposób wartośd iloczynu skalarnego wyrażoną za
pomocą normy wektorów i cosinusa kąta miedzy nimi.



Z (**) wynika, że w szczególnym przypadku, gdy wektory x i y są
prostopadłe (innymi słowy ortogonalne), to ich iloczyn skalarny
jest równy zero. Mamy bowiem

x

y =||x|| ||y||cos( =0.

Przykład. a) Niech x =

y=

. Wektory x y są

prostopadłe ponieważ x y= 0 13+1 -1 =0..

||x-y||

2

= ||x||

2

+||y||

2

-2 ||x||

||y||cos( ,

przy

mamy cos(

Z reguły cosinusów wynika więc
twierdzenie Pitagorasa

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

12

4. Proste i płaszczyzny

Niech p =

, x=

,



Zauważyć, że p jest ortogonalny do każdego wektora typu x

(dla dowolnych

). Widzimy, że w

3

, zbiór

wektorów typu x tworzy płaszczyznę przechodzącą przez punkt
„0” i prostopadłą do wektora p. Możemy ją opisać
równaniem: p ( x - 0)=0.



Łatwo się przekonać, że jeżeli p

3

jest niezerowym

wektorem, a x

0

dowolnym ustalonym wektorem w

3

, to zbiór

takich wektorów x

3

, że

p

(x- x

0

) = 0

tworzy płaszczyznę przechodzącą przez x

0

i prostopadłą do p.



Ostatnią równość można przekształcić do popularnej postaci
równania opisującego płaszczyznę w

3

. Zauważmy, że

0= p

(x- x

0

)= p

x - p x

0

.

Następnie kładąc k= p

x

0

i przechodząc do współrzędnych

wektorów p x mamy następującą, znaną powszechnie, postać
równania płaszczyzny w

3

:



W przypadku ogólnego wymiaru n, równanie
w postaci

p

(x - x

0

) = 0; p, x

0

- ustalone wektory w

n

,

lub w postaci

k= p x

0

opisuje tzw. hiperpłaszczyznę.



W przypadku n=2 mamy do czynienia z równaniem prostej:

Innymi słowy, przy ustalonych stałych

oraz k

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

13

zbiór punktów (

) spełniających powyższe równanie

tworzy prostą prostopadłą do wektora [

w przestrzeni

2

.

(tzn. dowolny wektor leżący na prostej jest prostopadły do [

).

Zadania.
1.Dane są macierze

,

,

Wykonać każde z następujących działań lub uzasadnić, że nie jest
możliwe.

a) AB-A, b) 2B-A

T

A, c)BA

T

+3A, d) A

T

A-C

T

C.

2. Wykorzystując przedstawienie parametryczne prostej sprawdzić
czy punkty

a=

, b=

, c =

leżą na jednej prostej.

3. Sprawdzić czy wektory są ortogonalne.

a=

, b=

są ortogonalne

4. Dla dowolnych wektorów kolumnowych

x=

, y =

, z =

oblicz a) ||x||, b) ||x-y||, c) x

x, d) x y, e) x z. f) x (2y+3z),

g) jaka jest odległość x od 0, jaka jest odległość x od y

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

14

Sylabus

1. Macierze i wektory
a) Działania na macierzach
b) Wektory. Interpretacja
c) Iloczyn skalarny wektorów
d) Proste , płaszczyzny i hiperpłaszczyzny.
e) Elementy teorii konsumenta. Zbiory budżetowe.


2. Macierze i wyznaczniki
a) Liniowa niezależność, baza przestrzeni
b) Rząd macierzy. Macierz odwrotna
c) Operacje elementarne
d) Wyznaczniki.


3. Układy równań liniowych
a) Rozwiązywanie równań za pomocą operacji elementarnych
b) Twierdzenie Kroneckera-Capelli
c) Wzory Cramera
d) Liniowy model równowagi rynkowej


4.Ciągi liczbowe
a) Własności ciągów liczbowych
b) Zbieżność ciągów
c) Granice pewnych ciągów
d) Szeregi liczbowe jako szczególny rodzaj ciągów
e) Wartość aktualna strumienia dochodów z inwestycji


5. Granice i ciągłość funkcji
a) Pojęcie granicy funkcji
b) Funkcje ciągłe. Przykłady
c) Własności funkcji ciągłych

6. Różniczkowanie funkcji jednej zmiennej
a) Definicja i interpretacja pochodnej

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

15

b) Technika różniczkowania
c) Reguła de l’Hospitala


7. Przebieg zmienności funkcji jednej zmiennej
a) Punkty stacjonarne, monotoniczność
b) Ekstrema lokalne i globalne
c) Druga pochodna, definicja i zastosowanie
d) Funkcje wypukłe

8.Całka
a) Funkcja pierwotna –definicja, przykłady
b) Całki funkcji elementarnych
c) Całkowanie przez podstawienie i przez części
d) Całka oznaczona
e) Interpretacje całki

9. Przykłady zastosowań całek i pochodnych
a) Optymalna partia uzupełniania zapasów. Wzór Wilsona
b) Uproszczony model optymalizacji zysku firmy

10. Funkcje wielu zmiennych.
a) Przykłady funkcji
b) Pojęcia wstępne: otoczenie punktu, zbiory otwarte i domknięte,
zbieżność ciągów w R

n

.

c) Ciągłość funkcji w R

n

.

d) Neoklasyczna funkcja produkcji

11. Pochodne cząstkowe, różniczkowalność
a) Pochodne cząstkowe, interpretacja
b) Gradient, elastyczność cząstkowa funkcji
c) Funkcje różniczkowalne
d) Pochodna kierunkowa



12. Pochodne cząstkowe drugiego rzędu, hesjan.
a) Twierdzenia Schwarza o pochodnych mieszanych.

Zastosowania matematyki w ekonomii. 2014. Macierze i wektory

16

b) Ekstrema lokalne i globalne. Warunki konieczne i dostateczne.
c) Pochodne cząstkowe wyższego rzędu.

13. Elementy teorii konsumenta.

14. Elementy teorii producenta.

15. Elementy teorii równowagi. Model Arrowa-Hurwicza

Literatura
1. Alpha C. Chiang, Podstawy ekonomii matematycznej. PWE,
Warszawa 1994.

2.Adam Ostoja-Ostaszewski, Matematyka w ekonomii. Modele i
metody.Cz.1. Algebra elementarna. PWN, Warszawa 2006.

3. Adam Ostoja-Ostaszewski, Matematyka w ekonomii. Modele i
metody.Cz.2. Elementy rachunku różniczkowego. PWN, Warszawa
2006.

4. Bernard Sozański, Izabela Dziedzic, Algebra analiza w
zagadnieniach ekonomicznych.Wydawnictwo Bila, Rzeszów 2007.

4. Ryszard Antoniewicz, Andrzej Misztal, Matematyka dla studentów
Ekonomii. Wykłady z ćwiczeniami.

PWN, Warszawa 2005.

5.Michał Krych, Analiza matematyczna dla
ekonomistów.Wydawnictwa UW, Warszawa 2010.