R. Rempała. Materiały dydaktyczne
1
Wykład 1b-2. Teoria konsumenta (kontynuacja)
Teoria konsumenta c.d.
Założenie: konsument zachowuje się racjonalnie. Wybiera najlepszy
koszyk na jaki go stać.
Wiemy już co znaczy „na jaki go stać”
Pytanie :
co znaczy „najlepszy”?
Konsument dokonując wyborów wyraża swoje preferencje.
Czy można je opisać? Jakie mają własności?
Relacje dwuargumentowe w zbiorze.
X
= ustalony zbiór.
r = relacja dwuargumentowa w
X
r opisuje
łączenie w uporządkowane pary elementów
X
;
Oznaczenie x
r
y - czytaj element x jest w relacji r z elementem y (x
jest w parze z elementem y).
Dokładniej:
r
jest podzbiorem
produktu kartezjańskiego:
}
,
:
)
,
{(
X
y
X
x
y
x
X
X
)
Typy relacji:
1.
relacja jest zwrotna
def
dla każdego
X
x
, x
r
x,
2.
relacja jest symetryczna
def
dla każdych dwu elementów
X
y
x
,
, jeśli x
r
y, to y
r
x,
R. Rempała. Materiały dydaktyczne
2
3.
relacja jest przechodnia
def
dla
każdych trzech elementów
X
z
y
x
,
,
, jeśli x
r
y i y
r
z to x
r
z,
4.
relacja jest zupełna (całkowita)
def
dla każdych elementów
X
y
x
,
, jeśli x
y to x
r
y lub y
r
x,
5. relacja jest
relacją równoważnością
def
jeśli jest zwrotna ,
symetryczna i przechodnia.
Przykład 1.
X-
zbiór mieszkańców Warszawy.
x
r
y
def
x jest wyższy niż y.
(Wysokość podajemy z dokładnością do centymetra)
.
Relacja ta
1) nie jest zwrotna,
2) nie jest symetryczna,
3) jest przechodnia,
4)
nie jest zupełna (dwie różnie osoby mogą mieć identyczny wzrost),
5)
nie jest równoważnością
Przykład 2
X=R
+
, x
r
y
def
x
y
.
Relacja
ta
1) jest zwrotna ( x
x),
2) nie jest symetryczna (7
2 ale 2
7)
3) jest przechodnia (( x
y i y
z)
x
z)
4) jest zupełna (dla dowolnej pary liczb (x,y) mamy x
y
lub y
x .
5) nie jest relacją równoważności.
R. Rempała. Materiały dydaktyczne
3
Przykład 3
X= {0,1,2,3,......}, x
r
y
def
x i y mają tę samą resztę przy
dzieleniu przez 2.
Relacja ta jest
równoważnością.
Przykład 4
X = ucz
niowie wybranej szkoły podstawowej
x
r
y
def
x jest w tej samej klasie co y.
(1) x
r
x (x jest w tej samej klasie co x)- prawda,
(2) jeśli x
r
y to y
r
x (jeśli x jest w tej samej klasie co y to y
jest w tej samej klasie co x)- prawda,
(3) jeśli x
r
y i y
r
z to x
r
z (jeśli x jest w tej klasie co y, y jest
w tej samej klasie co z to x jest w tej klasie co z)- prawda.
Wniosek. Relacja jest
równoważnością.
Klasy równoważności : klasa 1, klasa 2,.klasa 3, klasa 4, klasa
5, klasa 6.
Własność relacji równoważności - zasada abstrakcji.
Dowolna relacja równoważności w zbiorze niepustym wyznacza
podział tego zbioru na rozłączne, niepuste podzbiory.
Podzbiorami tymi są klasy równoważności tej relacji.
R. Rempała. Materiały dydaktyczne
4
Teoria konsumenta c.d.
X=Z-
zbiór konsumpcyjny. Zakładamy, że przy danych
koszykach x i y konsument potrafi określić relacje między
nimi według swojego stopnia pożądania (upodobania).
x
r
y
def
koszyk x jest lepszy lub tak samo dobry jak y
innymi słowy - x nie jest gorszy niż y,
-
x jest słabo preferowany względem y
Definicja. Relację r, oznaczaną dalej przez ” nazywamy
relacją
słabej preferencji (lub preferencji) jeśli spełnia następujące
aksjomaty:
Aksjomaty
: Relacja słabej preferencji („ ”) jest
1. zwrotna (tzn. x
x) dla każdego x
2. przechodnia (tzn.
dla każdych trzech elementów
Z
z
,
y
,
x
, jeśli x y i y z to x z)
3.
zupełna. ( jeśli
Z
y
,
x
to x y lub y x).
Relacja słabej preferencji (
) wyznacza relację
silnej (ścisłej) preferencji () i relację
indyferencji (~).
Inna nazwa relacji indyferencji -
relacja obojętności.
Definicja . Koszyk x j
est indyferentny (obojętny) względem
y (co zapisujemy
x ~ y) jeśli x y i y x.
R. Rempała. Materiały dydaktyczne
5
Definicja .
Koszyk x jest ściśle preferowany wobec y
(zapis: x
y) jeśli x y i nie jest prawdą, że x ~ y.
Można wykazać, że prawdziwe jest następujące twierdzenie
Twierdzenie
.
R
elacja ścisłej preferencji „” jest
przechodnia, relacja indyferencji
„~” jest relacją
równoważności (tzn. zwrotna, symetryczna i przechodnia)
Niech
)
x
,...,
x
,
x
(
x
m
2
1
-
będzie ustalonym koszykiem.
Klasa równoważności relacji obojętności, w której znajduje
się koszyk x dana jest zbiorem
x
y
:
{
~
}
y
.
Wniosek z zasady abstrakcji. Relacja indyferencji
wyznacza podział zbioru konsumpcji na rozłączne,
niepuste podzbiory. Podzbiorami tymi są klasy
równoważności tej relacji.
Definicja.
Zbiorem obojętności relacji słabej preferencji
„
nazywamy klasę równoważności relacji obojętności
(indyferencji).
R. Rempała. Materiały dydaktyczne
6
Definicja.
Dla koszyków dwu-towarowych zbiór obojętności
nazywa się krzywą obojętności.
Wnioski z zasady abstrakcji
dla koszyków
2- towarowych.
a)
Krzywe obojętności wyznaczają podział zbioru konsumpcyjnego
na rozłączne, niepuste podzbiory.
b)
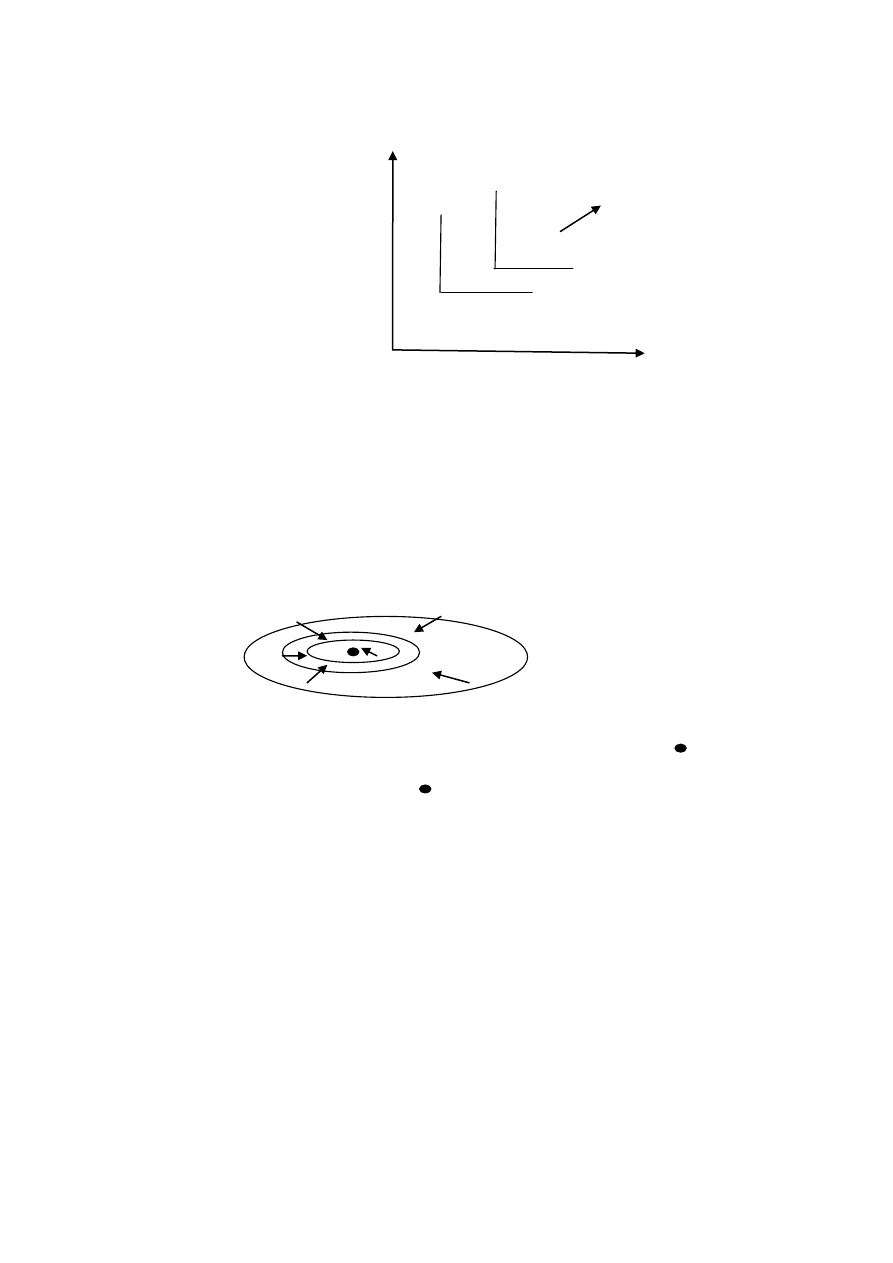
Dwie krzywe obojętności są albo rozłączne albo identyczne.
Rys.a. T
ak nie może być
b)
Punkty na różnych krzywych są względem siebie w relacji
silnej preferencji.
lub
Rys. b
Wniosek.
Krzy
we obojętności prezentują różne poziomy preferencji.
Krzywe obojętności i „relacje między krzywymi” (por
rysunek b) jednoznacznie opisuj
ą relację słabej preferencji
R. Rempała. Materiały dydaktyczne
7
Dla dowolnych trzech koszyków x,y,z mamy
x
y lub
x
y lub x
~y,
Jak wykreślić krzywą obojętności?
1
( x
1
+
1
, x
2
+
2
)
(x
1
,x
2
)
Rys.
Ustalamy koszyk (x
1
,x
2
).
Zwiekszamy drugą współrzędną o
2
. Następnie tak
dobieramy
1
, aby ( x
1
+
1
, x
2
+
2
)
(x
1
,x
2
).
Przykłady preferencji w
Z
=
2
R
Rozważmy następujacą relację:
x
y
def
x
1
+ x
2
y
1
+ y
2
(
Ważne, aby było dużo jednostek w koszyku!)
a)
Czy jest to relacje słabej preferencji? (innymi słowy: czy
spełnia aksjomaty relacji preferencji?)
Pozytywna odpowiedź wynika z własności liczb rzeczywistych.
Mamy bowiem
x
1
+ x
2
x
1
+ x
2
,
zatem x
x
jeśli x
1
+ x
2
y
1
+y
2
i y
1
+y
2
z
1
+z
2
to x
1
+ x
2
z
1
+z
2
zatem
jeśli x y i y z to x z
Z własności liczb wynika, że x
1
+ x
2
y
1
+y
2
lub
y
1
+y
2
x
1
+ x
2
. Zatem x
y lub y x.
2
R. Rempała. Materiały dydaktyczne
8
Relacja jest relacją słabej preferencji. Wyznaczmy krzywe
obojętności.
Przypominamy:
x ~ y jeśli x y i y x
Zatem x ~ y
jeśli x
1
+ x
2
y
1
+y
2
i y
1
+y
2
x
1
+ x
2
Oznacza to, że: x ~ y jeśli x
1
+ x
2
= y
1
+y
2
Wniosek.
W rozważanym przykładzie krzywe obojętności, to
zbiór takich koszyków, w których suma jednostek obu dóbr jest
stała. Zatem rodzinę krzywych obojętności można zapisać:
}
s
x
x
:
)
x
x
(
x
{
K
2
1
2
1
s
, s > 0, (Por. Rys*.)
Opiszmy teraz
relację ścisłej preferencji
Przypominamy :k
oszyk x jest ściśle preferowany wobec y jeśli
x
y i nie jest prawdą, że x ~ y.
Wykorzystując definicję relacji mamy:
x
y jeśli x
1
+ x
2
y
1
+ y
2
i nie jest prawdą, że x
1
+ x
2
=
y
1
+ y
2
. Zatem x
y jeśli x
1
+ x
2
>
y
1
+ y
2
.
Oznacza to, że koszyki należą do różnych krzywych
obojętności. (Koszyk x znajduje się na krzywej bardziej odległej
od środka układu współrzędnych niż koszyk y).
Rys
*.
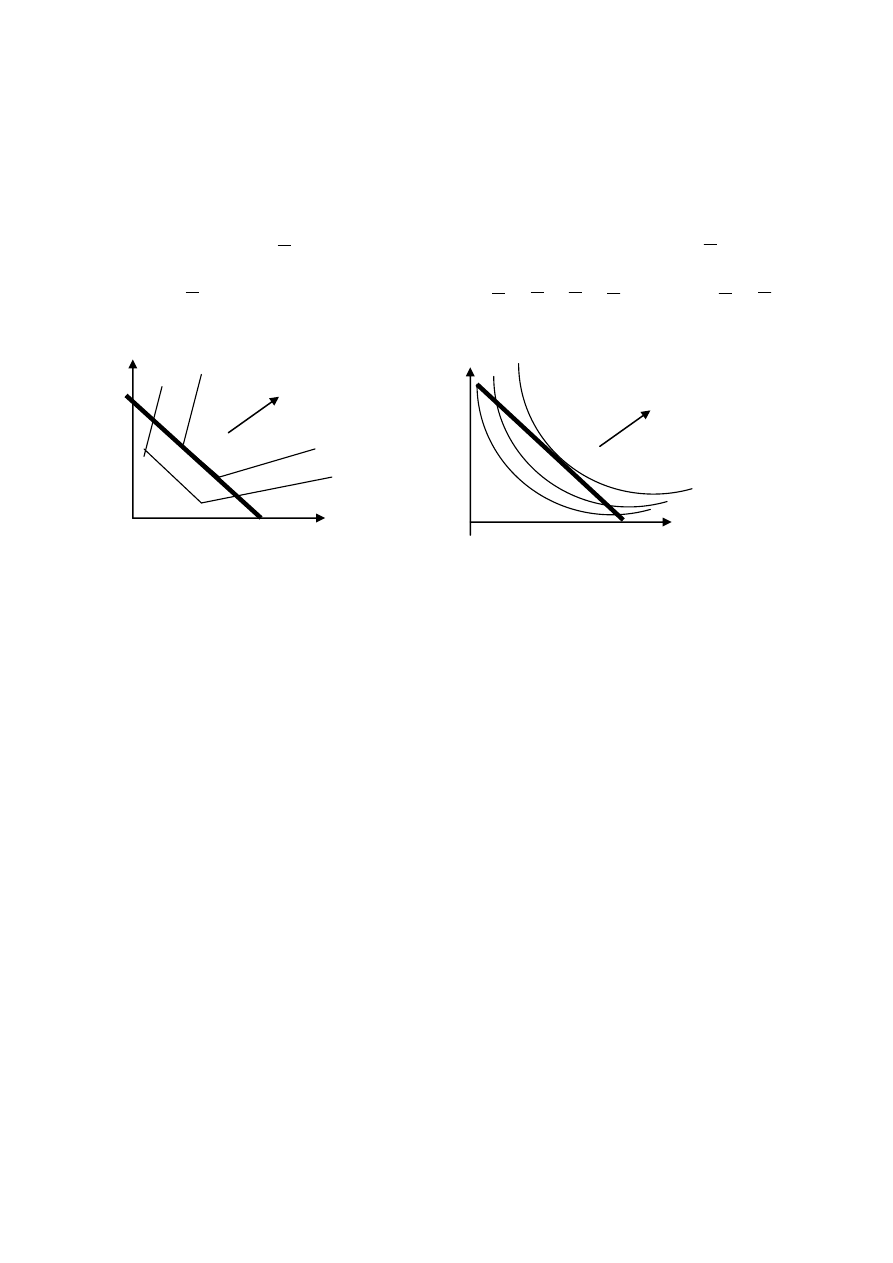
Zauważmy, że dobra 1 i 2 są substytutami doskonałymi.
krzywe obojętności
R. Rempała. Materiały dydaktyczne
9
Przykłady preferencji
(Varian str.55-62).
Rys.
Dobra doskonale komplementarne
x
y
def
min (x
1
, x
2
)
min(y
1
,y
2
).
Na rysunku zaznaczono
krzywe
obojętności {x : min (x
1
,x
2
)=c, c
oraz kierunek
wzrostu preferencji.
B
łogostan
Rys. Krzywe
obojętności otaczają „błogostan” ( ).
Krzywe
obojętności bliższe „ ” są bardziej preferowane.
Dodatkowe założenia o relacji słabej preferencji „
a)
Monotoniczność – „więcej znaczy lepiej”
Relacja „
” nazywa się monotoniczna
def
jeśli dla każdej takiej pary
koszyków
x,y
Z
, że
x
y
oraz
x
1
1
y
,
x
2
2
y
,...,
x
m
m
y
mamy
x
y.
……
….
R. Rempała. Materiały dydaktyczne
10
koszyki
lepsze
x
2
gorsze
x
1
Rys. Przy relacji monotonicznej k
oszyki obojętne względem (x
1
,x
2
)
mogą znaleźć się w obszarach zaznaczonych znakiem „ ”
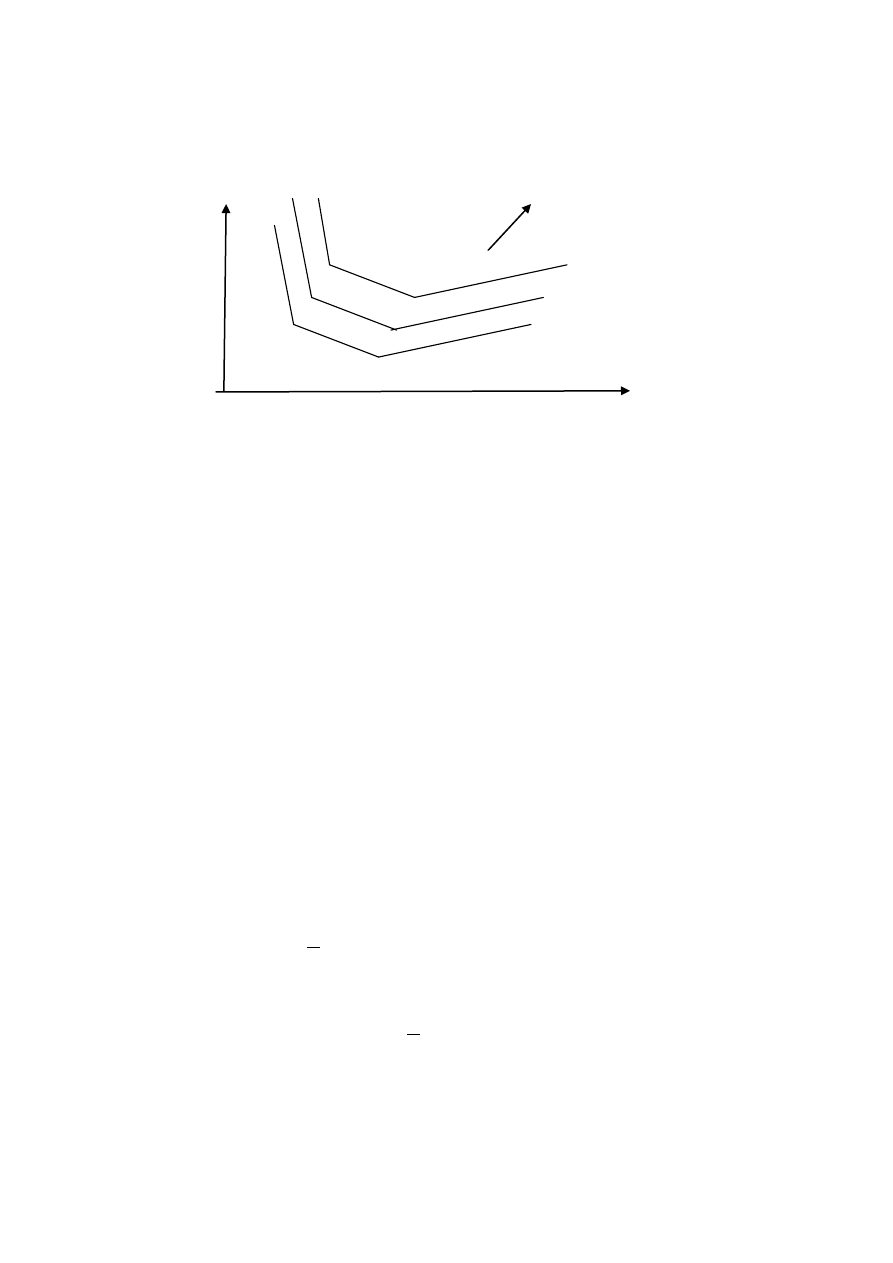
Wniosek
Krzywe obojętności relacji monotonicznej mają ujemne
nachylenie do osi x
1
Rys.Taka krzywa
nie może być krzywą obojętności relacji monotonicznej
b)
Wypukłość słabej preferencji „ ”
Definicja.
Relacja preferencji nazywa się wypukła jeśli dla
każdej pary (x,y)
Z i każdej liczby
]
1
,
0
[
spełniony jest
warunek:
jeśli x
y to
y
1
x
)
(
y
x
Rys. y
Przykład
x =(x
1
,x
2
)=(1,5), y = (y
1
,y
2
)=(2,2). Zdaniem konsumenta
x
y i wiadomo, że relacja jest wypukła.
R. Rempała. Materiały dydaktyczne
11
Czy prawda jest, że (1.3 ,4.1)
(2,2)?
Odpo
wiedź. Tak, bo przy
= 0.7 z własności wypukłości
wynika, że 0.7x + 0.3y
y, a więc 0.7x + 0.3y = (0.7, 3.5) +
(0.6, 0.6) = (1.3, 4.1)
(2,2).
Wniosek z definicji
. Przy wypukłych relacjach:
x ~ y
y
1
x
)
(
y
x ~ y
y
1
x
)
(
x Rys.
Średnie ważone – punkty z odcinka łączącego indyferentne
koszyki -
nie są gorsze niż krańce.
c). Silna
(ścisła) wypukłość
Relacja preferencji „
„ jest silnie (ściśle) wypukła jeśli dla
każdej pary x,y
Z i każdej liczby
)
1
,
0
(
spełniony jest
warunek: (x
y
x
y)
y
)
1
(
x
y
Wniosek.
Przy ściśle wypukłych relacjach
(x ~ y
x
y )
y
)
1
(
x
y
x
(x ~ y
x
y )
y
)
1
(
x
x
y
Rys.
R. Rempała. Materiały dydaktyczne
12
Twierdzenie.
Relacja preferencji jest wypukła na Z
gdy dla
każdego koszyka
a
Z zbiór F(a) =
x
Z
x
:
{
}
a
jest
wypukły
Dowód. Weźmy x F(a). Z zupełności relacji preferencji
wynika, że x y lub y x. Zatem dla wypukłej kombinacji mamy:
jeśli x y to
y
1
x
)
(
y
a
,
jeśli y x to
x
)
1
(
y
x
a
. W obu przypadkach
oznacza to, że odcinek łączący koszyki x i y znajduje się w
zbiorze F(a).
Zakładamy teraz, że dla każdego koszyka
a
Z zbiór
F(a) =
x
Z
x
:
{
}
a
jest wypukły.
Weźmy pod uwagę x y oraz F(y). Z definicji zbioru F(y)
wiadomo, że x oraz y F(y). Rozważmy wektor
z(
=
y
1
x
)
(
, gdzie
Z założenia wypukłości
zbioru F(y)
wynika, że z F(y). Tak więc,
(*) z(
=
y
1
x
)
(
y
co oznacza wypukłość relacji, ponieważ (*) jest prawdziwa dla
każdego λ ϵ [0,1].
a
Rys.
Przykład F(a) .
R. Rempała. Materiały dydaktyczne
13
Przy ściśle wypukłych relacjach krzywe obojętności nie mogą
mieć “ płaskich” fragmentów
relacja jest wypukła ale
Rys. nie jest ściśle wypukła
Definicja. Relcje mon
otoniczne i wypukłe nazywają się
preferencjami dobrze zachowującymi się.
Powrót do problemu wyboru najlepszego koszyka
Z
ałożenie: zbiór konsumpcyjny Z=
m
R
Przypominamy.
Zbiór budżetowy
(Zb)={x
d
x
p
x
p
x
p
R
m
m
2
2
1
1
m
...
:
}
p
1
,p
2
,...,p
m
- ceny,
m
= d -
zasób
.
Koszyki optymalne
Definicja. Koszyk
x
nazywamy optymalnym koszykiem w
zbiorze Zb
jeśli nie jest gorszy od każdego innego koszyka z
tego zbioru, co zapisujemy:
x
x dla każdego x
Zb.
R. Rempała. Materiały dydaktyczne
14
Wniosek z definicji.
Koszyk optymalny nie musi być jedyny.
Koszyki optymalne są indyferentne.
Dowód. Niech
x
będzie optymalny. Gdyby istniał inny
,
Zb
y
taki że
y
x dla każdego x
Zb, to
x
y
i
y
x
a zatem
x
~
y
Zb Zb
Rys. Przykłady koszyków optymalnych.