Ekonomia matematyczna. Wykład 13            R. Rempała. Materiały dydaktyczne 
 

1 

 

Liniowy model duopolu Cournota 

(

Por. T. Tokarski Ekonomia Matematyczna . Modele Makroekonomjczne. PWE,Warszawa 

2011, 256-269). 
 



 

Na rynku  mamy 2 producentów.  Obaj produkują taki 
sam produkt.  
 



 

Funkcje kosztów produkcji są liniowe: 
C

i

(y

i

) =c

i 

y

i 

+ f

i

;  c

i 

> 0, f

i 

 > 0 ;     i=1,2. 

             y

i  

- wielkość produkcji i-tego producenta. 

 



 

Zakładamy, że popyt na dobro (zgłaszany przez 
konsumentów) jest liniową funkcją ceny p i zapisuje się 
y

d

(p) = 

      . 

 



 

Produkcja dostosowuje się do popytu: 

y

1+

y

2

                               

 zatem cena równowagi staje się funkcją zależną od  
poziomu y

1+

y

2

 i przyjmuje  następującą  postać:   

 

                           p(y

1

,y

2

) = p(y

1+

y

2

) = 

 

 

  

   

 

 

  

 

 

 

Niech  a

  

 

 

 , b

  

 

 

 , zatem 

                           p(y

1

,y

2

) = a 

– b (y

1+

y

2

)                       

Założenie1 c

1

< a,  c

2

 < a

 (koszty krańcowe niższe od ceny startu)

 

Założenie2 Producenci są duopolistami.  Mogą sprzedać  
 całą swoją produkcję dostosowaną do popytu. 
 
                       Funkcje zysków  
 
 

1

(y

1,

y

2

) = y

1 

p(y

1

,y

2

)

 – C

1

(y

1

)   

zysk producenta nr 1; 

 
 

2

(y

1,

y

2

) = y

2 

p(y

1

,y

2

)

 – C

2

(y

2

) 

zysk producenta nr 2. 

Ekonomia matematyczna. Wykład 13            R. Rempała. Materiały dydaktyczne 
 

2 

 

           
Wykorzystując wzory na p

i

 oraz C

i 

otrzymujemy 

 
 

1

(y

1,

y

2

) = y

1 

[a 

– b (y

1+

y

2

)]

  c

1 

y

1 

– f

1

, 

 
 

2

(y

1,

y

2

) = y

2 

[a 

– b (y

1+

y

2

)]

  c

2 

y

2 

– f

2

. 

 

 Producenci, aby zmaksymalizować  swoje zyski, zachowują 
się jak gracze i stosują następujące strategie: 



  producent nr 1  przy produkcji producenta 2 na poziomie 

y

2 

wybiera taką wielkość y

1

(y

2

), która maksymalizuje  

1.

 



  producent nr 2  przy produkcji producenta 1 na poziomie 

y

1 

wybiera taką wielkość y

2

(y

1

), która maksymalizuje  

2.

 

 
Pokażemy, że taka strategia prowadzi do punktu równowagi 
Cournota  tzn do 

takiej para (



1

y

,)



2

y

, że  

(a) 



1

(



1

y

,



2

y

) = 

)

y

,

y

(

max

2

1

1

0

1

y







 

(b) 



2

(



1

y

,



2

y

) = 

)

y

,

y

(

max

2

1

2

0

2

y







 

 

Wyznaczanie optymalnej odpowiedzi  producenta (gracza)  

przy  ustalonym poziomie  produkcji konkurenta 

 



 

Funkcje zysków są funkcjami liniowymi. Możemy 
stosować  tradycyjne metody  rachunku różniczkowego. 
 

    1).Ustalamy y

2

. Warunki konieczne i dostateczne 

optymalnego wybory 

 

 

 są nastepujące: 

a) 

 



 

  

 

 

 

 

     

       

    

    

 

     

 

    

b) 

  

 



 

  

 

 

 

 

 

     

      < 0 

Ekonomia matematyczna. Wykład 13            R. Rempała. Materiały dydaktyczne 
 

3 

 

2) Ustalamy y

1

. Warunki konieczne i dostateczne optymalnego 

wybory  

 dpowiedzi 2 producenta  

 

   są następujące: 

a) 

 



 

  

 

 

 

 

     

       

    

    

 

     

 

    

b) 

  

 



  

 

 

 

 

 

     

      < 0 

  
Ze względu na założenie b >0, warunki 1b) i 2b są spełnione. 
Z rozwiązań równań 1a) i 2a) otrzymujemy następujące 
optymalne odpowiedzi producentów nazywane  liniami   
reakcji   
 
LR

1

: 

 

 

 

 = 

   

 

 

  

 

 

 

 

    linia reakcji producenta 1 

LR

2

: 

 

 

 

 = 

   

 

 

  

 

 

 

 

    linia reakcji producenta 2 

Dla uproszczenia  w dalszych rozważaniach opuszczamy * 

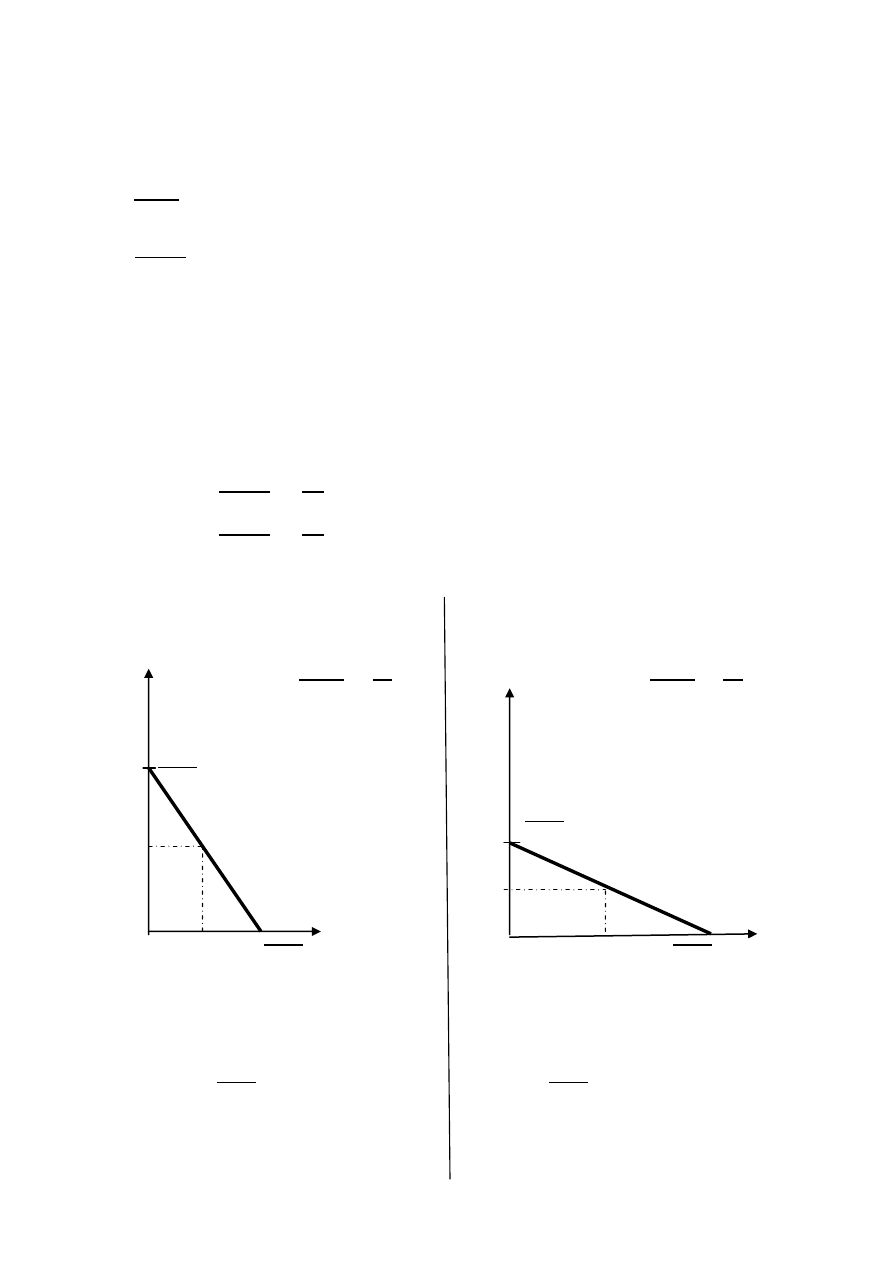
Rys1

.  

Linia reakcji producenta nr.1     Rys2. Linia reakcji producenta nr.2

 

 

   

                

 

  

y

2

        

LR

1

: 

 

 

 = 

   

 

 

  

 

 

 

 

                

y

2

      LR

2

: 

 

 

 = 

   

 

 

  

 

 

 

 

   

 

     

  

     

 

 

B

1  

     

 

   

 

 

 

 

 

                                                              

   

 

 

  

                            

                                                       

A

2 

 
 

                                                   

 

 

 

 

 

                

A

1 

  

                                                                                                                          

B

2

   

                  

 

 

 

 

           

 

   

 

 

  

   y

1

                                                 

 

 

 

 

           

   

 

 

 

     y

1 

 
Zauważmy, że odpowiedzią na  

 

 

 jest 

 

 

 

                  Zauważmy, że odpowiedzią na 

 

 

 

 jest 

 

 

 

 

 
W szczególności odpowiedzią producenta 1

                

W szczególności odpowiedzią producenta 2 

na wybór producenta 2: y

2

=0 jest                             na wybór producenta 1: y

1

=0 jest       

                   y

1

=

   

 

 

  

                                                   

y

2

=

   

 

 

  

 

 

 Punkty A

1

,B

1

 – wyznaczają

 

przecięcia LR

1              

Punkty A

2

,B

2

 – wyznaczają

 

przecięcia LR

2   

 z   osiami współrzędnych.                                     z   osiami współrzędnych.     

 

 

 

 

 

Ekonomia matematyczna. Wykład 13            R. Rempała. Materiały dydaktyczne 
 

4 

 

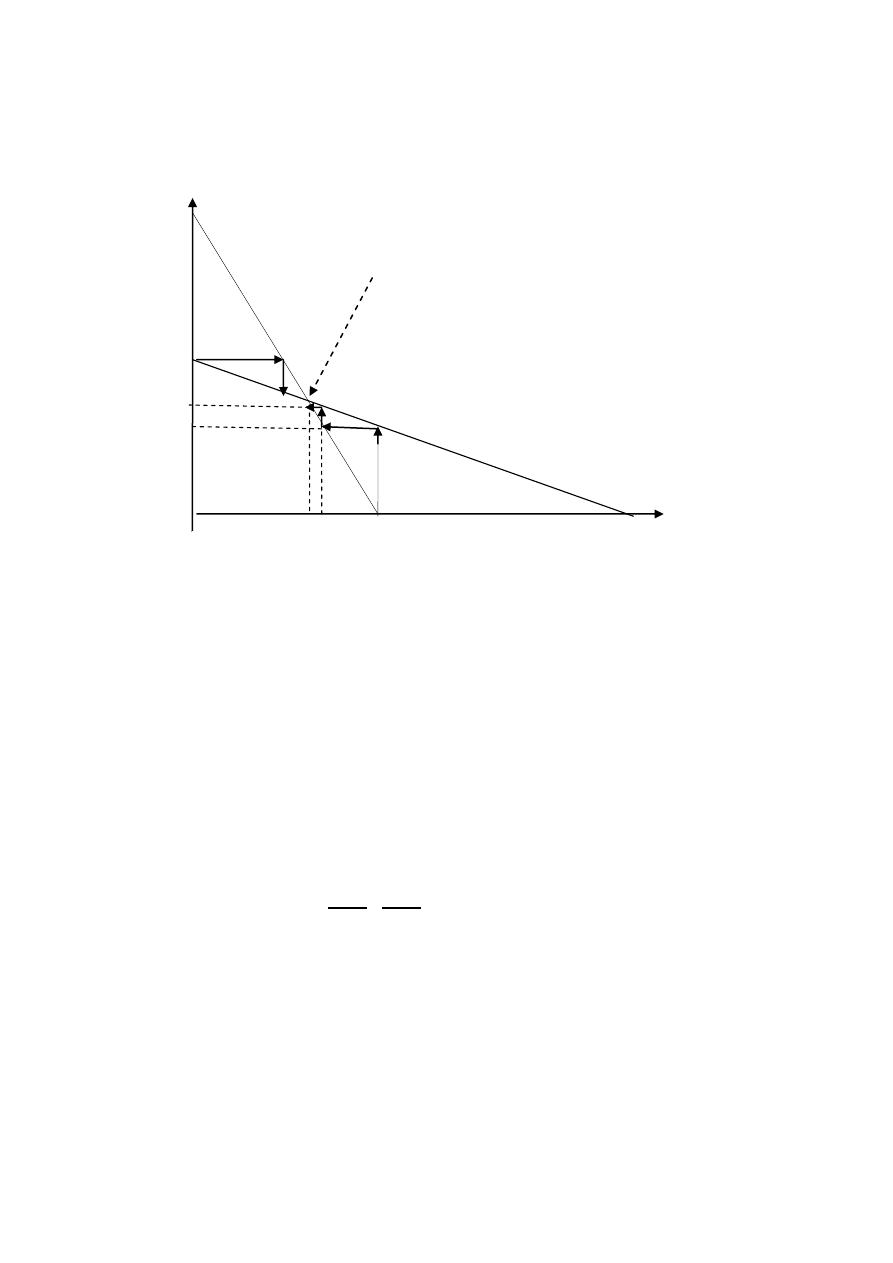
Rys.3 Linie reakcji LR

1 

 i LR

2 

 oraz dochodzenie do równowagi 

Cournota. 
          y

2

       

         

 

                              punkt równowagi Cournota 
 
 
 
                                     

 

                          

D

1

 

                                           

 

                       

 

 

                          

                          A

1

                                             

B

2

  y

1 

 

 

 

Prosta B

1

A

1

,

 

 to LR

1 

–linia reakcji pierwszego producenta. 

Prosta A

2 

B

2

,

 

 to LR

2 

–linia reakcji pierwszego producenta. 

 
Niech LR

1

(y) (LR

2 

(y))oznacza odpowiedź  pierwszego 

(drugiego) producenta  na y oznaczający poziom produkcji   
konkurenta. 
 



 

Jeżeli spełnione jest założenie 

                B

1 

> A

2

 tzn. 

   

 

 

 

> 

   

 

 

  

 (por. Rys.3), 

 

  

 

to następujący  ciąg   optymalnych odpowiedzi startujący z  
zerowego poziomu produkcji pierwszego producenta:   
 

 

 

 

   ,  

 

 

  LR

2

( 

 

 

      

 

 

    

1

( 

 

 

 ,  

 

 

  LR

2

( 

 

 

 ,   

 

 

 =   

1

( 

 

 

    

 
  zbiega do punktu równowagi Cournota.  

        B

1

                   

 
 
 
 
 
 
        A

2

  

 
          

 

 

        

          

 

 

    

         
 
 
          0

 

               

       

 

 

 

 

 

 

       

 

 

 

 

                                                                          

 
D

2 

Ekonomia matematyczna. Wykład 13            R. Rempała. Materiały dydaktyczne 
 

5 

 



 

Taki sam wynik zbieżności otrzymamy dla ciągu 
startujacego  z zerowego poziomu produkcji drugiego 
producenta (na rysunku punkt z punktu A

2

) 

 
       
  Zauważmy, że punkt równowagi jest punktem przecięcia 
prostych reakcji LR

1

 i LR

2

, zatem jest rozwiązaniem układu 

równao liniowych: 
                                   

 

 = 

   

 

 

  

 

 

 

 

    

                                

 

 

= 

   

 

 

  

 

 

 

 

 

 
Rozwiązaniem układu jest para ( 

 

 

   

 

 

) gdzie 

                              

 

 

 

 

    

 

  

 

  

   

                               

 

 

 

 

   

 

   

 

  

 

Dokładne wyznaczenie  rozwiązanie zostawiamy  jako 
dwiczenie.